dr Józef Szymczak
Politechnika Opolska

LICZBY ZESPOLONE

– notatki z wykładu

1.

Ciało liczb zespolonych.

Niech

R

R

Z

×

=

. W zbiorze

Z

traktowanym jako zbiór par liczb rzeczywistych określamy dodawanie i

mnożenie w następujący sposób:

)

,

(

)

,

(

)

,

(

2

1

2

1

2

2

1

1

b

b

a

a

b

a

b

a

+

+

=

+

,

)

,

(

)

,

(

)

,

(

1

2

2

1

2

1

2

1

2

2

1

1

b

a

b

a

b

b

a

a

b

a

b

a

⋅

+

⋅

⋅

−

⋅

=

⋅

.

Algebra

)

,

,

(

⋅

+

Z

jest ciałem, które nazywamy ciałem liczb zespolonych. Każdą parę

Z

b

a

∈

)

,

(

nazywamy liczbą

zespoloną i oznaczamy

)

,

(

b

a

z

=

.

Przykładowo, jeżeli

)

1

,

0

(

),

2

,

3

(

),

4

,

2

(

),

2

,

3

(

4

3

2

1

=

=

=

−

=

z

z

z

z

, to mamy

)

2

,

5

(

)

4

2

,

2

3

(

)

4

,

2

(

)

2

,

3

(

2

1

=

+

−

+

=

+

−

=

+

z

z

,

)

8

,

14

(

)

4

2

1

,

8

6

(

)

2

)

2

(

4

3

,

4

)

2

(

2

3

(

)

4

,

2

(

)

2

,

3

(

2

1

=

−

+

=

⋅

−

+

⋅

⋅

−

−

⋅

=

⋅

−

=

⋅

z

z

,

)

0

,

13

(

)

6

6

,

4

9

(

)

3

)

2

(

2

3

,

2

)

2

(

3

3

(

)

2

,

3

(

)

2

,

3

(

3

1

=

−

+

=

⋅

−

+

⋅

⋅

−

−

⋅

=

⋅

−

=

⋅

z

z

,

)

0

,

1

(

)

0

0

,

1

0

(

)

0

1

1

0

,

1

1

0

0

(

)

1

,

0

(

)

1

,

0

(

4

4

−

=

+

−

=

⋅

+

⋅

⋅

−

⋅

=

⋅

=

⋅

z

z

.

Pierwszy element pary

)

,

(

b

a

, czyli liczbę

a

, nazywamy częścią rzeczywistą liczby zespolonej z, natomiast drugi

element pary

)

,

(

b

a

nazywamy częścią urojoną liczby zespolonej z. Oznaczamy:

.

Im

,

Re

b

z

a

z

=

=

(Skrót Re pochodzi od łacińskiego słowa realis, skrót Im pochodzi od łacińskiego słowa imaginarius).

Liczby zespolone postaci

)

0

,

(

a

będziemy dalej oznaczać krótko przez

a

, natomiast liczbę zespoloną

)

1

,

0

(

nazywamy jednostką urojoną i będziemy oznaczać ją symbolem

i

. Zauważmy, że

1

2

−

=

=

⋅

i

i

i

.

Ze względu na te oznaczenia każdą liczbę zespoloną

)

,

(

b

a

z

=

zapisaną w postaci pary, będziemy mogli zapisać

w postaci algebraicznej:

bi

a

z

+

=

(ponieważ

)

,

(

)

,

0

(

)

0

,

(

)

0

0

1

,

1

0

0

(

)

0

,

(

)

1

,

0

(

)

0

,

(

)

0

,

(

b

a

b

a

b

b

a

b

a

bi

a

z

=

+

=

⋅

+

⋅

⋅

−

⋅

+

=

⋅

+

=

+

=

).

Postać

algebraiczna jest najczęściej używana przy zapisywaniu liczb zespolonych. Łatwo jest przy jej pomocy zapisywać

działania algebraiczne na liczbach zespolonych, pamiętając przy tym, że

1

2

−

=

i

.

Przykładowo jeżeli

i

z

i

z

4

2

,

6

2

1

+

−

=

−

=

, wtedy

i

i

i

z

z

3

4

4

)

2

(

6

2

1

+

=

+

−

+

−

=

+

,

i

i

i

i

i

i

i

i

i

i

z

z

26

8

4

2

24

12

4

)

(

)

2

(

)

(

4

6

)

2

(

6

)

4

2

(

)

6

(

2

2

1

+

−

=

−

+

+

−

=

⋅

−

+

−

⋅

−

+

⋅

+

−

⋅

=

+

−

⋅

−

=

⋅

,

i

i

i

i

i

z

16

12

16

16

4

16

4

)

2

(

2

4

)

4

2

(

2

2

2

2

−

−

=

−

−

=

+

⋅

−

⋅

+

=

+

−

=

.

Jaka liczba zespolona jest elementem neutralnym dodawania, a jaka liczba zespolona jest elementem

neutralnym mnożenia liczb zespolonych? Sprawdzić, że dodawanie i mnożenie liczb zespolonych to działania
przemienne i łączne oraz że zachodzi rozdzielność mnożenia względem dodawania.

2.

Interpretacja geometryczna liczb zespolonych.

Liczby zespolone

bi

a

z

+

=

interpretujemy geometrycznie jako punkty

)

,

(

b

a

P

płaszczyzny z określonym

prostokątnym układem współrzędnych. Taką płaszczyznę nazywamy płaszczyzną zespoloną lub płaszczyzną
Gaussa.

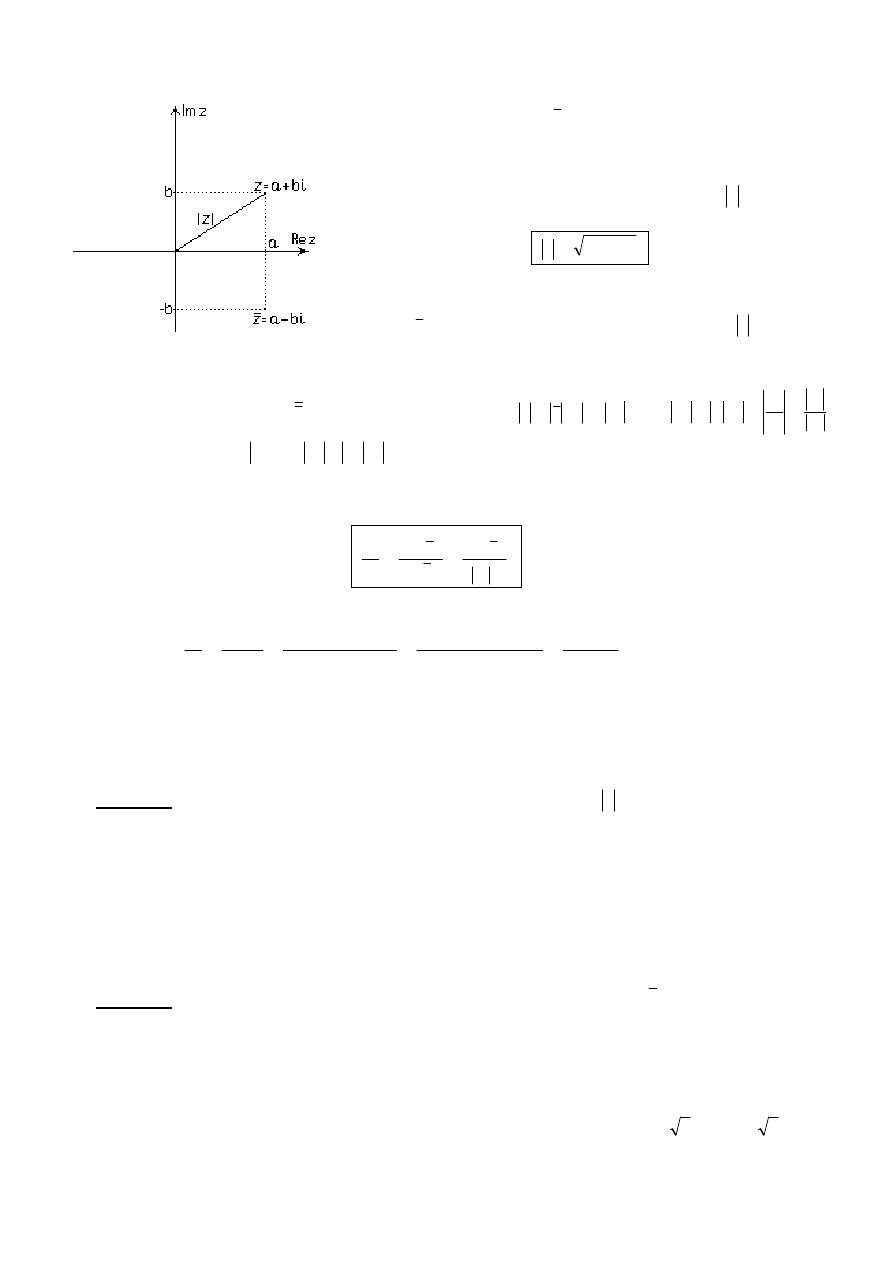
Liczbą sprzężoną do liczby zespolonej

bi

a

z

+

=

nazywamy liczbę

bi

a

z

−

=

.

Ma ona taką samą część rzeczywistą jak liczba

z

, natomiast przeciwną

część urojoną.

Moduł liczby zespolonej

z

oznaczamy symbolem

z

i określamy

go wzorem:

2

2

b

a

z

+

=

(geometrycznie jest to odległość punktu

)

,

(

b

a

od punktu

)

0

,

0

(

).

Zauważmy, że

2

2

2

2

2

2

)

(

)

(

z

b

a

i

b

a

bi

a

bi

a

z

z

=

+

=

−

=

−

⋅

+

=

⋅

,

czyli iloczyn liczby zespolonej przez jej sprzężenie jest równy sumie
kwadratów części rzeczywistej i urojonej.

Mamy oczywiście równość

z

z

=

. Zachodzą też równości:

z

z

z

−

=

=

,

2

1

2

1

z

z

z

z

⋅

=

⋅

,

2

1

2

1

z

z

z

z

=

oraz oczywista nierówność

2

1

2

1

z

z

z

z

+

≤

+

.

Wykorzystując sprzężenie liczb zespolonych, możemy w prosty sposób wykonać dzielenie dwóch liczb

zespolonych:

2

2

2

1

2

2

2

1

2

1

z

z

z

z

z

z

z

z

z

⋅

=

⋅

=

⋅

Przykładowo, jeżeli

i

z

i

z

3

1

,

2

3

2

1

+

−

=

−

=

, wtedy

i

i

i

i

i

i

i

i

i

i

i

z

z

7

,

0

9

,

0

10

7

9

9

1

6

2

9

3

)

3

1

)(

3

1

(

)

3

1

)(

2

3

(

3

1

2

3

2

2

1

−

=

−

−

=

+

+

+

−

−

=

−

−

+

−

−

−

−

=

+

−

−

=

.

Równość dwóch liczb zespolonych określamy warunkiem:

)

Im(

)

Im(

)

Re(

)

Re(

2

1

2

1

2

1

z

z

z

z

z

z

=

∧

=

⇔

=

,

czyli że liczby zespolone są równe jeżeli mają takie same części rzeczywiste i takie same części urojone. Zwróćmy
uwagę, że nie da się wprowadzić relacji nierówności między liczbami zespolonymi innymi niż czysto rzeczywiste.

Przykład 1. Rozwiązać następujące równanie w zbiorze liczb zespolonych:

i

z

z

2

6

2

+

=

−

.

Zakładając, że

yi

x

z

+

=

, możemy napisać dane równanie w formie:

i

yi

x

y

x

2

6

2

2

+

=

−

−

+

.

Porównując części rzeczywiste i części urojone obu stron tego równanie otrzymamy układ dwóch równań:







=

−

=

−

+

2

6

2

2

y

x

y

x

. Z drugiego równania mamy, że

2

−

=

y

, czyli że

4

2

=

y

i po podstawieniu do pierwszego

równania przekształci się ono do postaci

0

2

2

=

−

−

x

x

, skąd otrzymujemy, że

2

,

1

2

1

=

−

=

x

x

. Przy znanej już

wartości

y

otrzymujemy zatem, że równanie spełniają dwie liczby zespolone:

i

z

i

z

2

2

,

2

1

2

1

−

=

−

−

=

.

Przykład 2. Rozwiązać następujące równanie w zbiorze liczb zespolonych:

0

2

2

=

+

z

z

.

Zakładając, że

yi

x

z

+

=

, możemy napisać dane równanie w formie:

0

2

2

2

2

2

=

−

+

−

+

yi

x

y

xyi

x

.

Porównując części rzeczywiste i części urojone obu stron tego równanie otrzymamy układ dwóch równań:







=

−

=

+

−

0

2

2

0

2

2

2

y

xy

x

y

x

. Z drugiego równania mamy, że

0

)

1

(

2

=

−

x

y

, które jest spełnione gdy

1

=

x

lub gdy

0

=

y

.

Jeżeli

1

=

x

, to z pierwszego równania po podstawieniu wynika, że

3

2

=

y

, czyli

3

−

=

y

lub

3

=

y

. Jeżeli

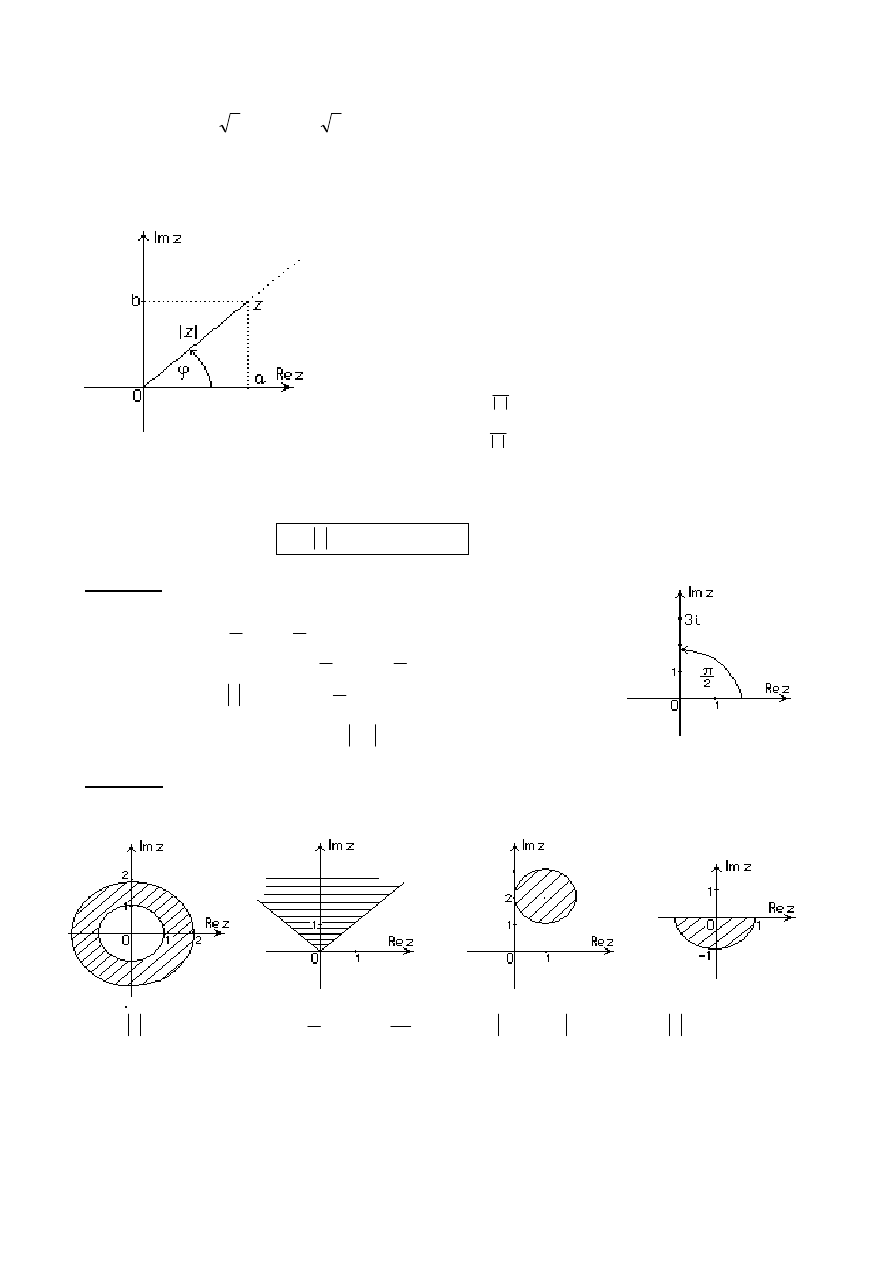
0

=

y

, to z pierwszego równania po podstawieniu wynika, że

0

2

2

=

+

x

x

, czyli

0

=

x

lub

2

−

=

x

. Zatem mamy

cztery liczby zespolone spełniające wyjściowe równanie:

2

,

0

,

3

1

,

3

1

4

3

2

1

−

=

=

+

=

−

=

z

z

i

z

i

z

.

3.

Postać trygonometryczna liczb zespolonych.

Argumentem niezerowej liczby zespolonej

z

nazywamy jakikolwiek

kąt

ϕ

między osią rzeczywistą a półprostą Oz.

Argumentem głównym liczby zespolonej

z

(oznaczenie

z

arg

)

nazywamy ten z kątów

ϕ

, który spełnia nierówność:

π

ϕ

2

0

<

≤

(czasem wygodnie jest przyjmować

π

ϕ

π

≤

<

−

).

Każdy argument

ϕ

liczby zespolonej

0

≠

z

ma postać

π

ϕ

k

z

2

arg

+

=

, gdzie

C

k

∈

.

Argument

ϕ

liczby zespolonej

bi

a

z

+

=

spełnia układ równań:









=

=

.

sin

,

cos

z

b

z

a

ϕ

ϕ

Ze względu na powyższy układ równań, każdą niezerową liczbę zespoloną

bi

a

z

+

=

możemy przedstawić w

postaci trygonometrycznej:

)

sin

(cos

ϕ

ϕ

i

z

z

+

⋅

=

Przykład 3.

a) Jeżeli liczba zespolona ma postać trygonometryczną

)

sin

(cos

3

2

2

π

π

i

z

+

=

,

to jest to liczba

i

z

3

=

(ponieważ

1

,

0

2

2

sin

cos

=

=

π

π

).

Dla tej liczby mamy, że

3

=

z

,

2

arg

π

=

z

.

b)

)

sin

(cos

4

4

π

π

i

+

=

−

, ponieważ

4

4

=

−

,

0

sin

,

1

cos

=

−

=

π

π

.

Przykład 4. Poniżej przedstawione są graficzne interpretacje warunków, jakie spełniają określone zbiory liczb

zespolonych (zbiory punktów na płaszczyźnie zespolonej):

a)

2

1

≤

≤

z

b)

4

4

3

arg

π

π

≤

≤

z

c)

1

2

1

≤

−

−

i

z

d)

1

≤

z

oraz

π

π

2

arg

≤

≤

z

Wyznaczyć w podobny sposób inne graficzne interpretacje różnych warunków, które spełniają zbiory liczb

zespolonych.

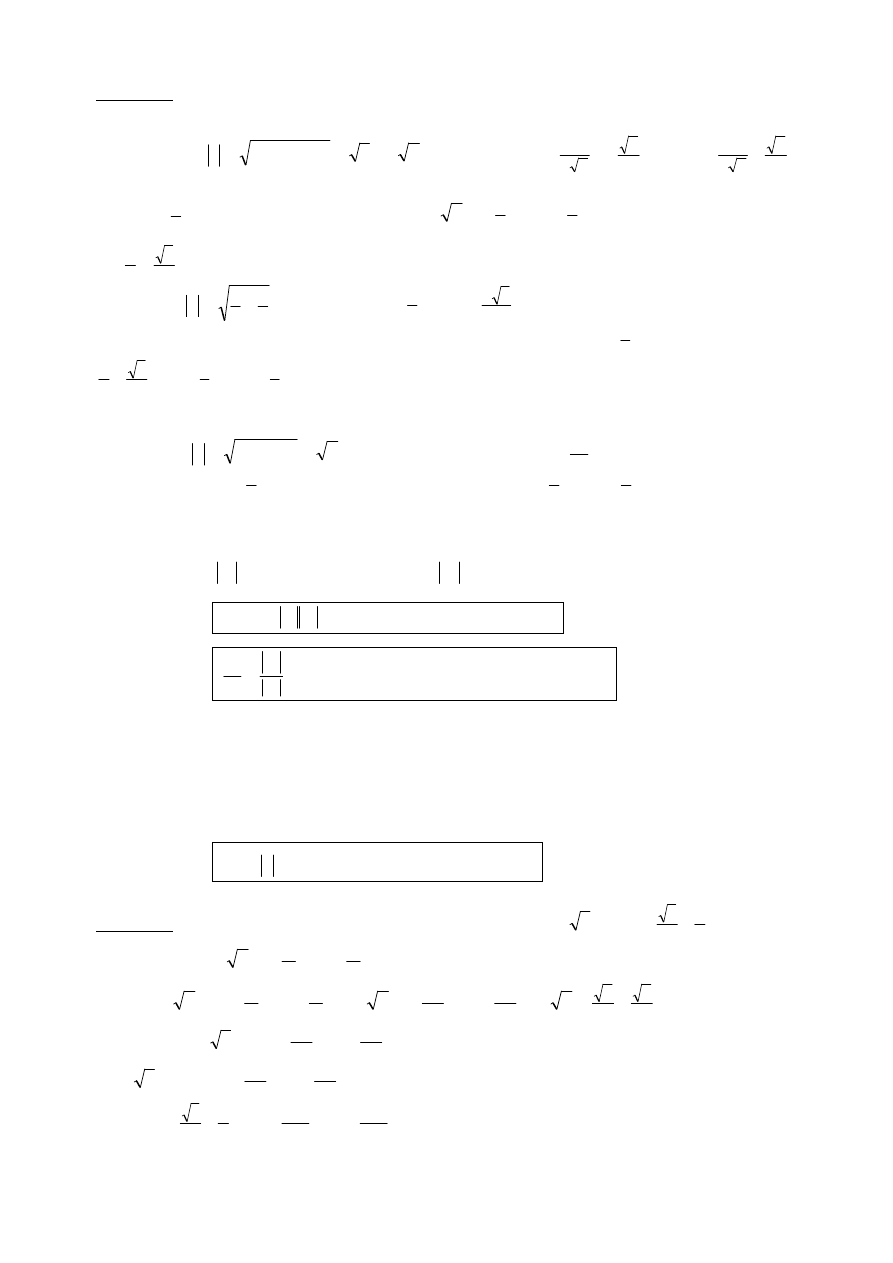
Przykład 5. Przedstawić w postaci trygonometrycznej podaną liczbę zespoloną.

a)

i

z

2

2

+

−

=

.

Mamy tutaj:

2

2

8

2

)

2

(

2

2

=

=

+

−

=

z

. Zatem

2

2

2

2

2

cos

−

=

−

=

ϕ

,

2

2

2

2

2

sin

=

=

ϕ

. Na

podstawie przebiegu funkcji

x

sin i

x

cos wynika, że kąt

ϕ

jest kątem z drugiej ćwiartki kąta pełnego i

wynosi on

π

4

3

. Możemy więc zapisać

)

sin

(cos

2

2

2

2

4

3

4

3

π

π

i

i

+

=

+

−

.

b)

i

z

2

3

2

1

−

=

.

Mamy tutaj:

1

4

3

4

1

=

=

+

z

. Zatem

2

1

cos

=

ϕ

,

2

3

sin

−

=

ϕ

. Z przebiegu funkcji

x

sin i

x

cos wynika, że

kąt

ϕ

jest kątem z czwartej ćwiartki kąta pełnego i wynosi on

π

3

5

. Możemy więc zapisać

π

π

3

5

3

5

2

3

sin

cos

2

1

i

i

+

=

−

.

c)

i

z

2

−

=

.

Mamy tutaj:

2

4

0

)

2

(

2

=

=

=

+

−

z

. Zatem

0

cos

=

ϕ

,

1

2

2

sin

−

=

−

=

ϕ

. Z przebiegu funkcji

x

sin i

x

cos wynika, że

π

ϕ

2

3

=

, czyli możemy napisać, że

)

sin

(cos

2

2

2

3

2

3

π

π

i

i

+

=

−

.

Mając liczby zespolone zapisane w postaci trygonometrycznej, możemy w łatwy sposób wykonywać na nich

operacje mnożenia i dzielenia.

Jeżeli zatem

)

sin

(cos

1

1

1

1

ϕ

ϕ

i

z

z

+

=

oraz

)

sin

(cos

2

2

2

2

ϕ

ϕ

i

z

z

+

=

, to wtedy

))

sin(

)

(cos(

2

1

2

1

2

1

2

1

ϕ

ϕ

ϕ

ϕ

+

+

+

=

⋅

i

z

z

z

z

))

sin(

)

(cos(

2

1

2

1

2

1

2

1

ϕ

ϕ

ϕ

ϕ

−

+

−

=

i

z

z

z

z

, gdzie

0

2

≠

z

Przy mnożeniu liczb zespolonych w postaci trygonometrycznej ich moduły mnożymy, a argumenty dodajemy.

Natomiast przy dzieleniu liczb zespolonych w postaci trygonometrycznej ich moduły dzielimy, a argumenty
odejmujemy.

Wzór dotyczący mnożenia liczb zespolonych jest słuszny również dla dowolnej liczby czynników. Z tego

względu w łatwy sposób otrzymujemy wzór na potęgowanie liczb zespolonych w postaci trygonometrycznej,
zwany wzorem Moivre’a:

)

sin

(cos

ϕ

ϕ

n

i

n

z

z

n

n

+

⋅

=

, gdzie

N

n

∈

Przykład 6. Wykonać następujące potęgowania: a)

5

)

1

(

i

+

, b)

6

)

3

1

(

i

−

, c)

11

)

2

1

2

3

(

i

−

.

Ad a) Ponieważ

)

sin

(cos

2

1

4

4

π

π

i

i

+

=

+

, więc

i

i

i

i

i

4

4

)

(

2

4

)

sin

(cos

2

4

)

sin

(cos

)

2

(

)

1

(

2

2

2

2

4

5

4

5

4

4

5

5

5

−

−

=

−

=

+

=

+

=

+

−

π

π

π

π

.

Ad b) Ponieważ

)

sin

2(cos

3

1

3

5

3

5

π

π

i

i

+

=

−

, więc

64

)

0

sin

0

(cos

64

)

sin10

(cos10

4

6

)

sin

(cos

2

)

3

1

(

6

6

6

3

5

3

5

=

+

=

+

=

+

=

−

i

i

i

i

π

π

π

π

.

Ad c) Ponieważ

6

11

6

11

2

1

sin

cos

2

3

π

π

i

i

+

=

−

, więc

=

+

+

+

=

+

=

+

=

−

)

20

sin(

)

20

cos(

sin

cos

)

sin

(cos

)

6

6

6

121

6

121

6

11

6

11

2

1

11

11

2

3

(

π

π

π

π

π

π

π

π

i

i

i

i

i

i

2

1

6

6

2

3

sin

cos

+

=

+

=

π

π

.