Paulina Szewczyk 221218 pon 15:15

27.04.2015

Ćwiczenie 84

Wyznaczanie długości fali świetlnej za pomocą siatki dyfrakcyjnej

I.

Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie stałej siatki dyfrakcyjnej, wyznaczenie
chromatycznej zdolności rozdzielczej oraz dyspersji kątowej siatki
dyfrakcyjnej.

II.

Wstęp teoretyczny

Siatka dyfrakcyjna jest to przyrząd do przeprowadzania analizy widmowej
światła. Tworzy ją układ równych, równoległych i jednakowo
rozmieszczonych szczelin. Stała siatki dyfrakcyjnej to parametr
charakteryzujący siatkę dyfrakcyjną. Wyraża on rozstaw szczelin siatki
(odległość między środkami kolejnych szczelin). Aby wyznaczyć stałą siatki
dyfrakcyjnej, należy wiązkę światła z monochromatora o znanej długości fali
λ skierować na siatkę dyfrakcyjną. Na ekranie po lewej i prawej stronie
plamki centralnej obserwuje się plamki ±1 i ±2 rzędu dyfrakcji. Mierząc ich
odległości S

m

od środka plamki centralnej należy wyznaczyć odpowiedni kąt

ugięcia θ

m

dla pierwszego i drugiego rzędu dyfrakcji. Korzystamy przy tym

ze wzoru:

sin θ

n

=

x

n

√x

x

2

+ L

2

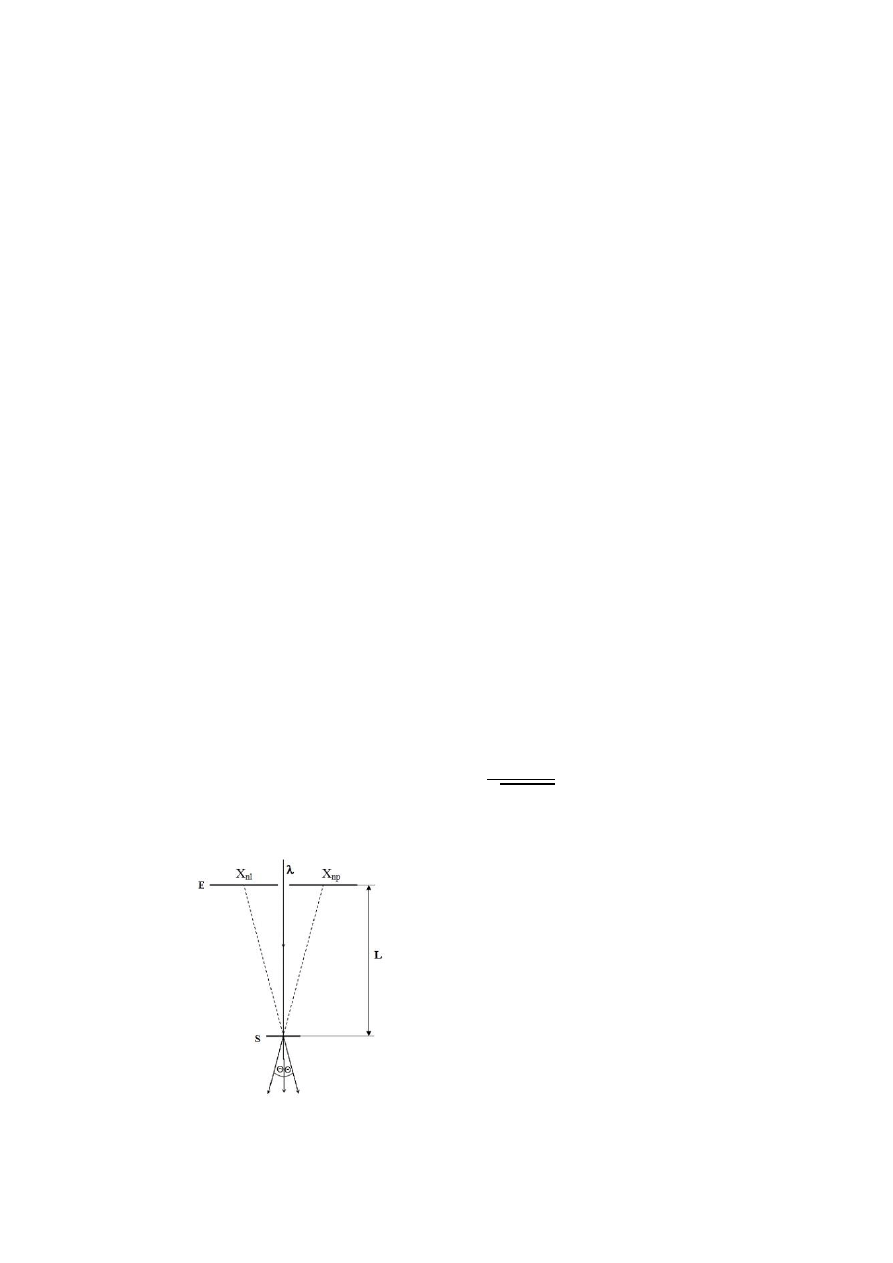
E

– ekran z podziałką milimetrową

S

– siatka dyfrakcyjna

λ – promień światła o długości fali λ
L

– odległość siatki dyfrakcyjnej od ekranu

x

nl

,

x

np

– odległość pozornych obrazów n-tego

rzędu od oświetlonej szczeliny

Rys. 1. Schemat rysunku pomiarowego

III.

Wyniki pomiarów i obliczenia

1.

Wyniki pomiarów

Lp.

x

nl

[m]

x

np

[m]

λ

L

[m]

1.

0,07

0,07

441

0,3

±0,00001

2.

0,08

0,08

500

3.

0,085

0,085

550

4.

0,095

0,095

600

5.

0,105

0,105

650

6.

0,115

0,115

700

x̅

0,092

0,092

573,5

-

S

x̅

0,0068

0,0068

39,17

-

x -

średnia arytmetyczna















n

i

i

n

x

n

n

x

x

x

x

1

2

1

1

...

S

x̅

- odchylenie standardowe wartości średniej

S

x̅



 









































n

i

i

n

x

x

n

n

x

x

x

x

x

x

n

n

1

2

2

2

2

2

1

)

1

(

1

...

)

1

(

1

2. Obliczenia



Wyznaczenie stałej siatki dyfrakcyjnej

Średnia wartość x

n

odległości pozornego obrazu od oświetlonej szczeliny

x

n

=

x

nl

+ x

np

2

x

n

= 91,7 mm

Sinus kąta ugięcia dla n-tego rzędu obrazu dyfrakcyjnego

sin θ

n

=

x

n

√x

n

2

+ L

2

sin θ

n

≈ 0,3

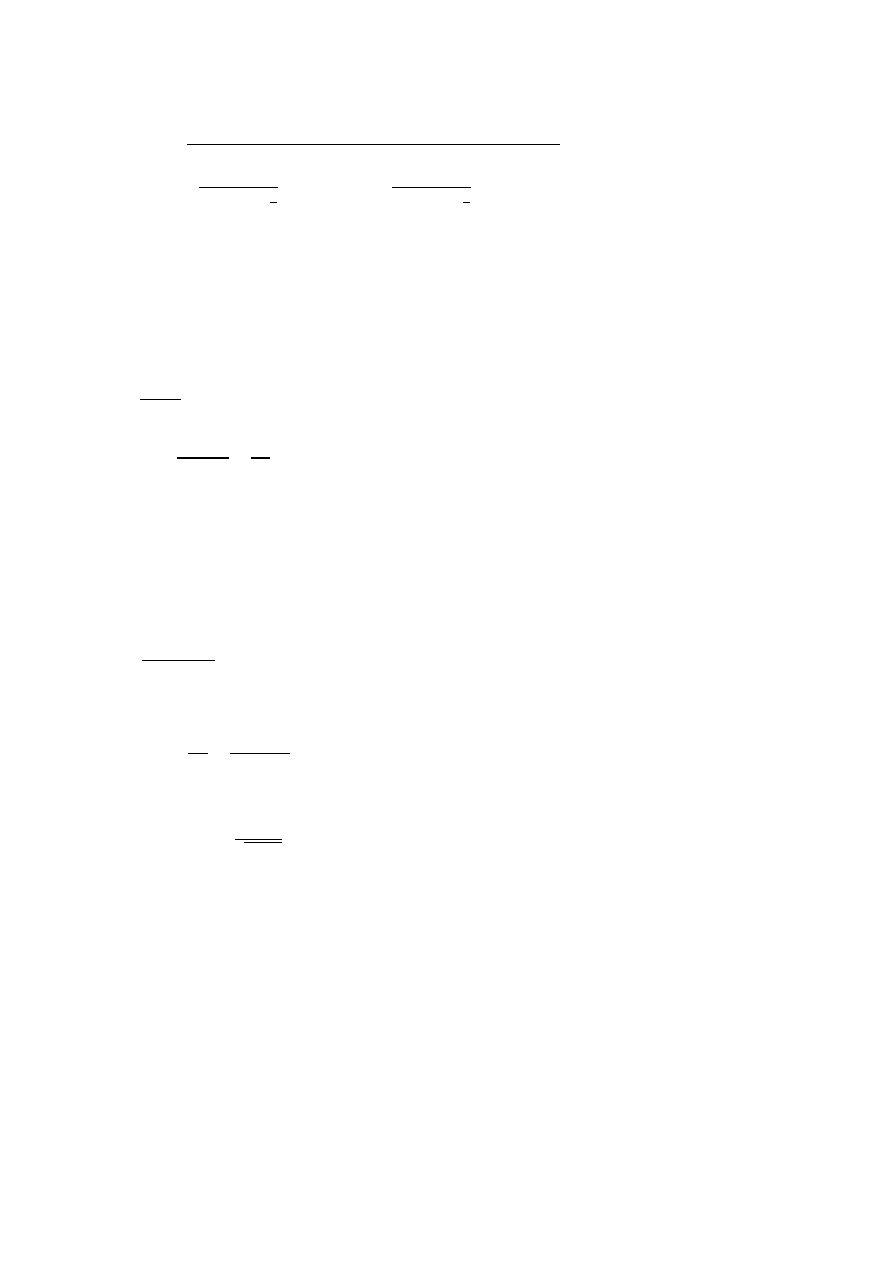
Niepewność sin kąta ugięcia

∆sinθ = √(

L ∗ x

n

(L

2

+ x

n

2

)

3
2

)

2

∗ (∆L)

2

+ (

L

2

(L

2

+ x

n

2

)

3
2

)

2

∗ (∆x

n

)

2

∆sinθ ≈ 0,00039

Stała siatki dyfrakcyjnej dla n–tego rzędu obrazu dyfrakcyjnego

d =

n ∗ λ

sinθ

n

d = ±d {

∆sinθ

n

sinθ

n

+

∆λ

λ

}

d ≈ 248,9

d = (3823,3 ± 263,8)nm



Dyspersja kątowa siatki dyfrakcyjnej

D =

n

d ∗ cos θ

n

D = (0,0055 ± 0,000037)rad/m

∆D = ±D {

∆d

d

+

∆ cos θ

n

cos θ

n

}

∆D ≈ 0,000037

gdzie

cos θ

n

=

L

√L

2

+x

n

2

∆ cos θ

n

≈0,00091

cos θ

n

≈0,97

IV.

Wnioski

Błędy zależały przede wszystkim od dokładności odczytu odległości plamek
interferencyjnych od plamki centralnej.