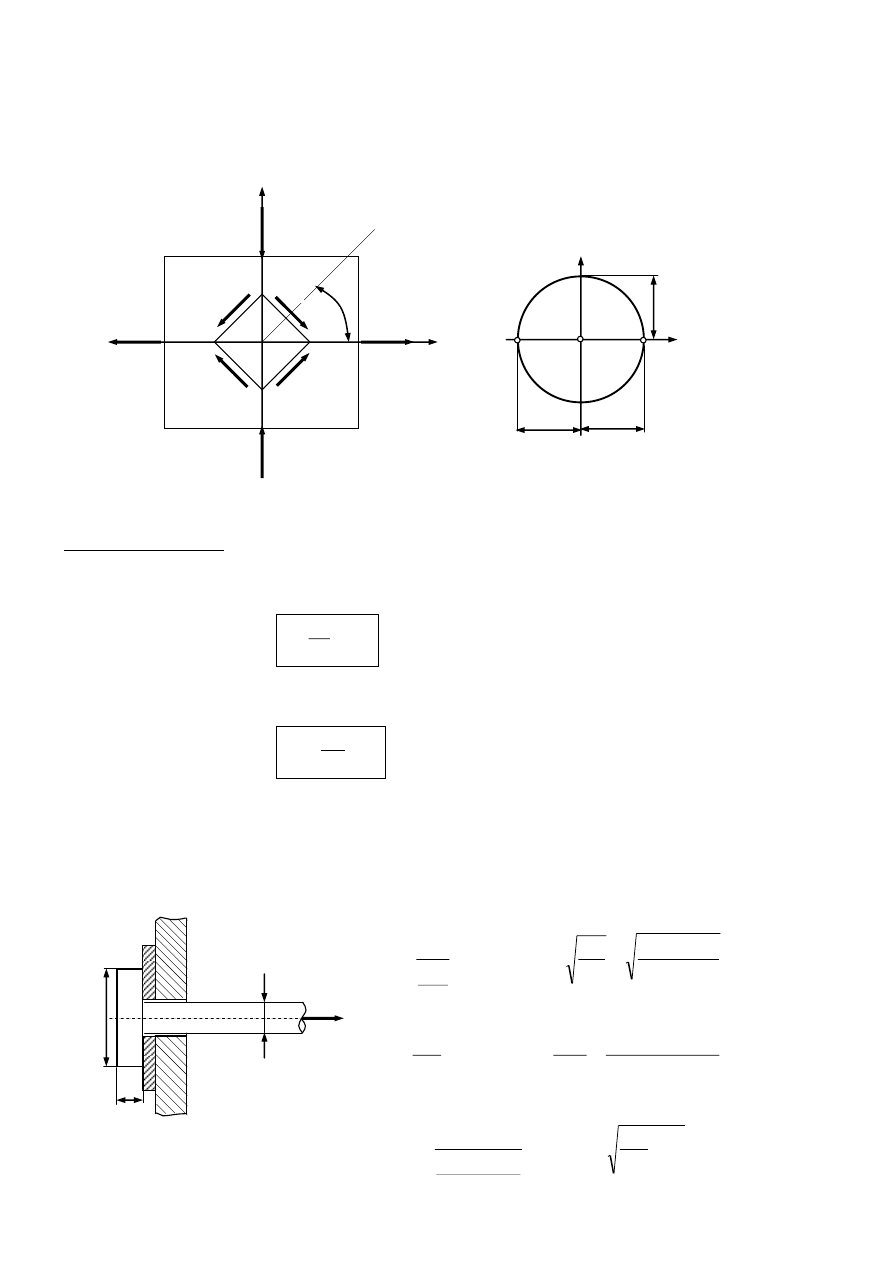
ŚCINANIE

Czyste ścinanie – stan naprężenia wywołujący wyłącznie odkształcenia postaciowe. Praktyczna

realizacja takiego stanu jest niemożliwa bez udziału dodatkowego obciążenia
zewnętrznego np. sile tnącej przy zginaniu towarzyszy moment gnący.

Rozpatrzmy

płaski stan naprężenia:



1

=





2

= -



W przekroju obróconym o kąt 45



mamy stan czystego ścinania





= 0,





=



.

Ścinanie techniczne – można wyodrębnić grupę elementów w których naprężenia styczne

odgrywają zasadniczą rolę: nity, sworznie, kołki, kliny, wpusty, spoiny.

W tych przypadkach przyjmujemy założenie o równomiernym rozkładzie naprężeń stycznych w
przekroju poprzecznym

dop

t

A

T









A

t

– całkowity przekrój przenoszący siłę tnącą

Ścinaniu towarzyszy zwykle docisk powierzchniowy pomiędzy współpracującymi elementami.
Czynimy tu również założenie, że docisk rozkłada się równomiernie.

d

d

d

k

A

P







gdzie: A

d

– powierzchnia docisku

-

rzeczywista, dla elementów płaskich;

-

umowna (średnicowa), dla elementów okrągłych.

Przykład Wyznaczyć najmniejszą dopuszczalną średnicę d, średnicę głowy D, oraz wysokość

głowy h, pręta obciążonego jak na rysunku. Siła P=37 kN,
Dla materiału pręta: k

r

=120 MPa, k

t

=70 MPa, k

d

=180 MPa.

1.

Z warunku na zerwanie pręta

]

[

02

,

0

10

120

10

37

4

4

4

6

3

2

m

k

P

d

k

d

P

r

r





























2.

Z warunku na ścięcie

]

[

85

,

0

10

70

02

,

0

10

37

6

3

cm

dk

P

h

k

dh

P

t

t





























3. Z warunku na docisk powierzchniowy

]

[

6

,

2

.....

4

4

)

(

2

2

2

cm

d

k

P

D

k

d

D

P

d

d

d























2

1

2



1



1



2









45



n





S



2

=-





1

=





max

=



P

d

D

h

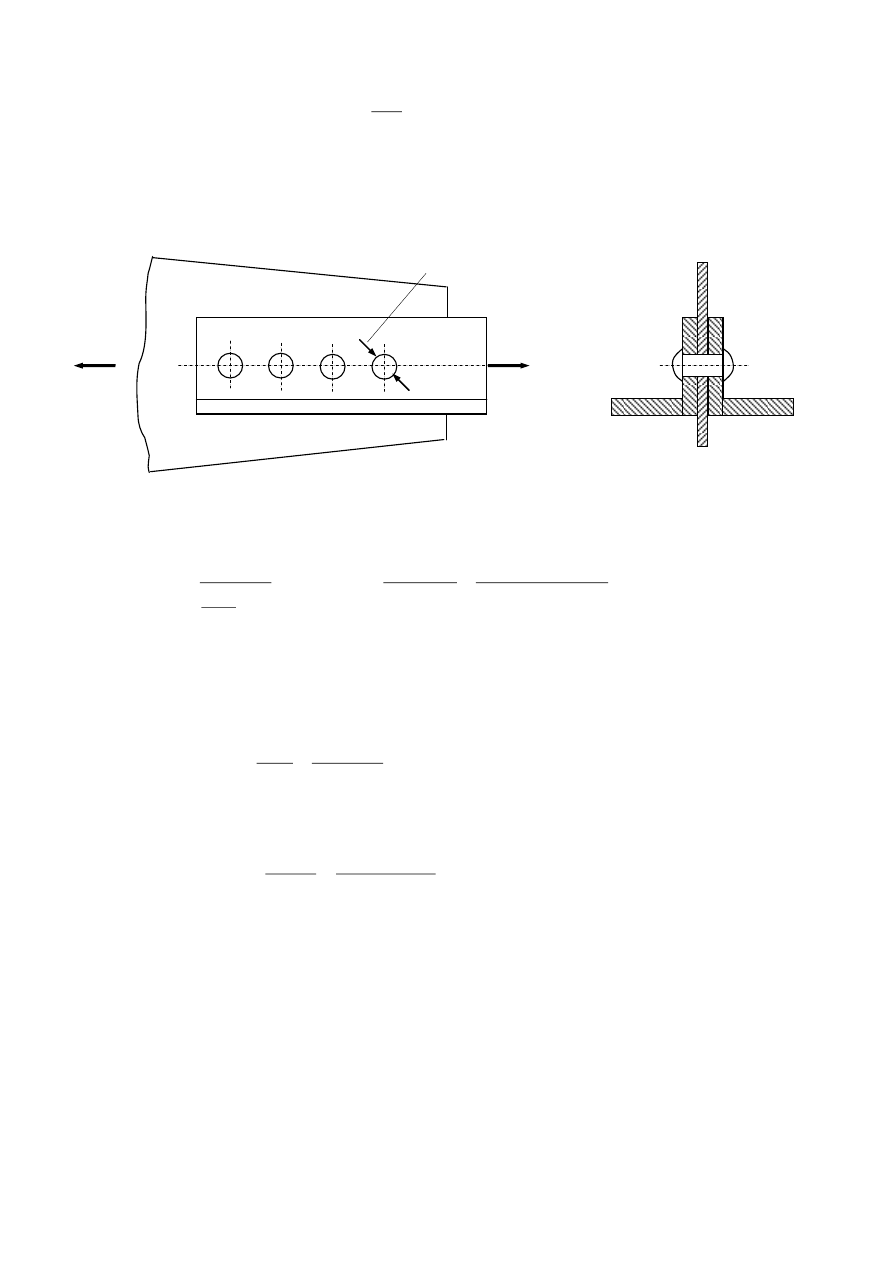
Przykład

Obliczanie nitów

m

n

d

A

n

t





4

2



n

– liczba nitów,

m

– liczba przekrojów ścinanych w nicie,

d

n

= średnica nita

Do blachy o grubości g=12,5 mm przynitowano dwa kątowniki równoramienne 80x80x8.

Siła rozciągająca połączenie T=200 kN. Wyznaczyć liczbę n nitów potrzebnych do przeniesienia
siły tnącej, gdy k

t

=80 MPa, k

d

=200 MPa, oraz k

r

=100 MPa.

Średnicę nita przyjmuje się zwykle równą 1,5



2,5 grubości łączonych części,

tu przyjmujemy d

n

= 20 mm, m = 2.

z

98

,

3

10

80

2

02

,

0

10

200

4

4

4

6

2

3

2

2



































t

n

t

n

k

m

d

P

n

k

m

n

d

T

przyjmujemy

n = 4 nity

Sprawdzenie naprężeń:

1)

w przekrojach osłabionych otworami: z tablic A

L

= 12,3 cm

2

; A

netto

=2(12,3-

2·0,8)=21,4 cm

2

MPa

k

MPa

A

T

r

netto

100

5

,

93

10

4

,

21

10

200

4

3



















2)

naprężenia docisku powierzchniowego:

MPa

k

MPa

d

g

T

d

d

200

200

10

)

2

25

,

1

(

2

10

200

4

4

3























T

T

d

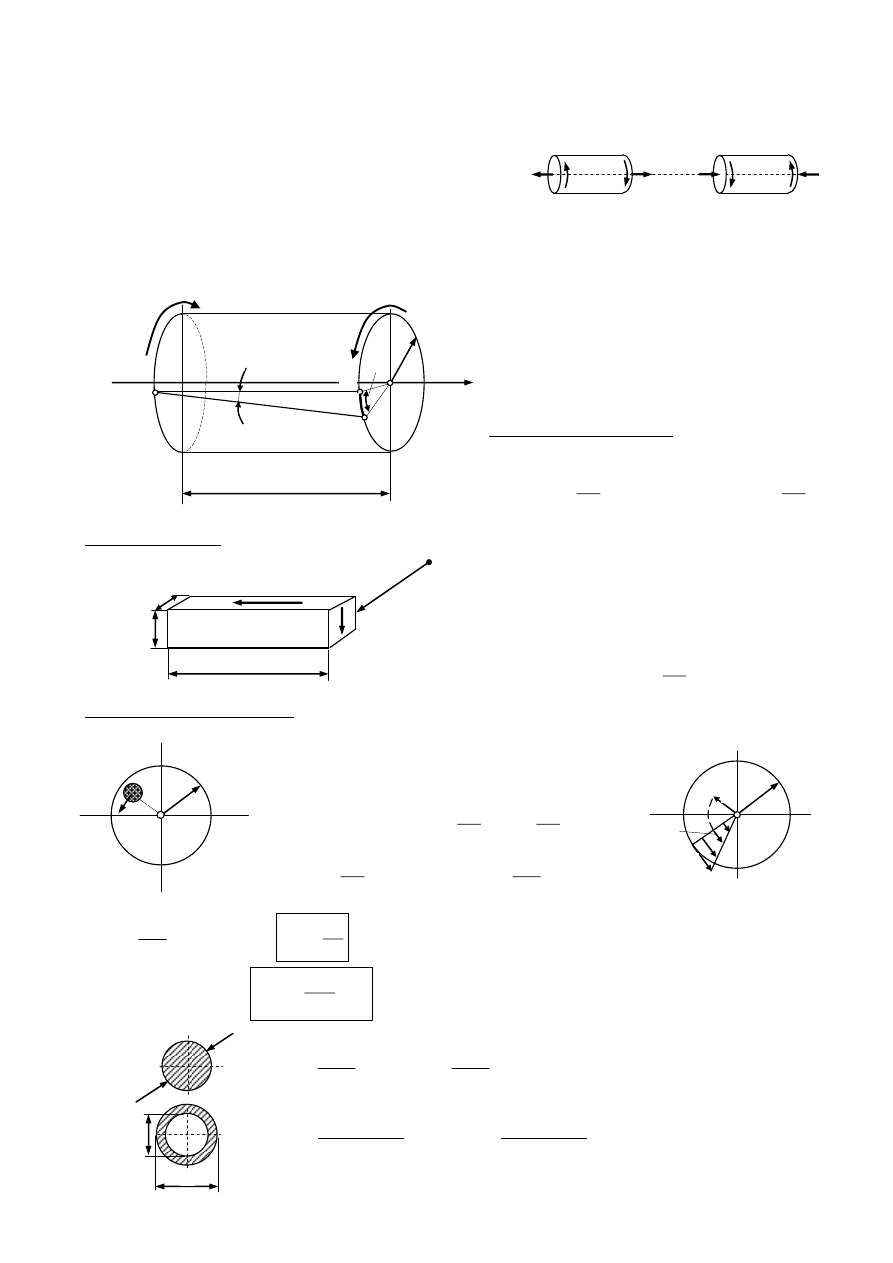
SKRĘCANIE PRĘTÓW PROSTYCH

I.

Pręty o przekroju kołowym.

znak momentu

Skręcanie – gdy na pręt działają dwie pary sił

w dwóch różnych płaszczyznach

prostopadłych do osi pręta.

Taką parę sił nazywamy momentem skręcającym M

s

.

Przeanalizujmy charakter odkształceń powstających w skręcanym pręcie kołowym.

Wnioski i założenia:

1.

Hipoteza płaskich przekrojów
-

przekroje tylko się obracają.

2.

Brak wydłużeń i przewężeń
wskazuje na występowanie tylko
naprężeń stycznych



.

Warunki geometryczne

Długość łuku AA’=ds=rd



oraz ds=



dx

stąd

dx

d

r







a dla



<r

dx

d











Warunki fizyczne -

wytnijmy z pręta element ds., d



, dx

– jego stan odkształcenia odpowiada

czystemu ścinaniu.

Zatem prawo Hooke’a:





= G





Wykorzystując war. geometryczny

dx

d

G











Warunek równowagi pręta











A

s

x

dM

M

M

0

dA

dT

dM

























A

A

A

s

dA

dx

d

G

dA

dx

d

G

dA

M

2

2























0

0

J

M

J

dx

d

G

M

s

s







s

s

k

r

J

M





0

max



r

J

W

0

0



W

0

– wskaźnik wytrzymałości na skręcanie

s

S

k

W

M





0

max



- warunek wytrzymałościowy na skręcanie

dla

16

32

3

0

4

0

d

W

d

J









D

d

D

W

d

D

J

16

)

(

32

)

(

4

4

0

4

4

0













(+)

M

s

M

s

(-)

M

s

M

s

M

s

M

s

B

A

’

A

r

x

dx

d



0



ds

dx



ds

d











r

0

dA







r

0









max

d

D

d

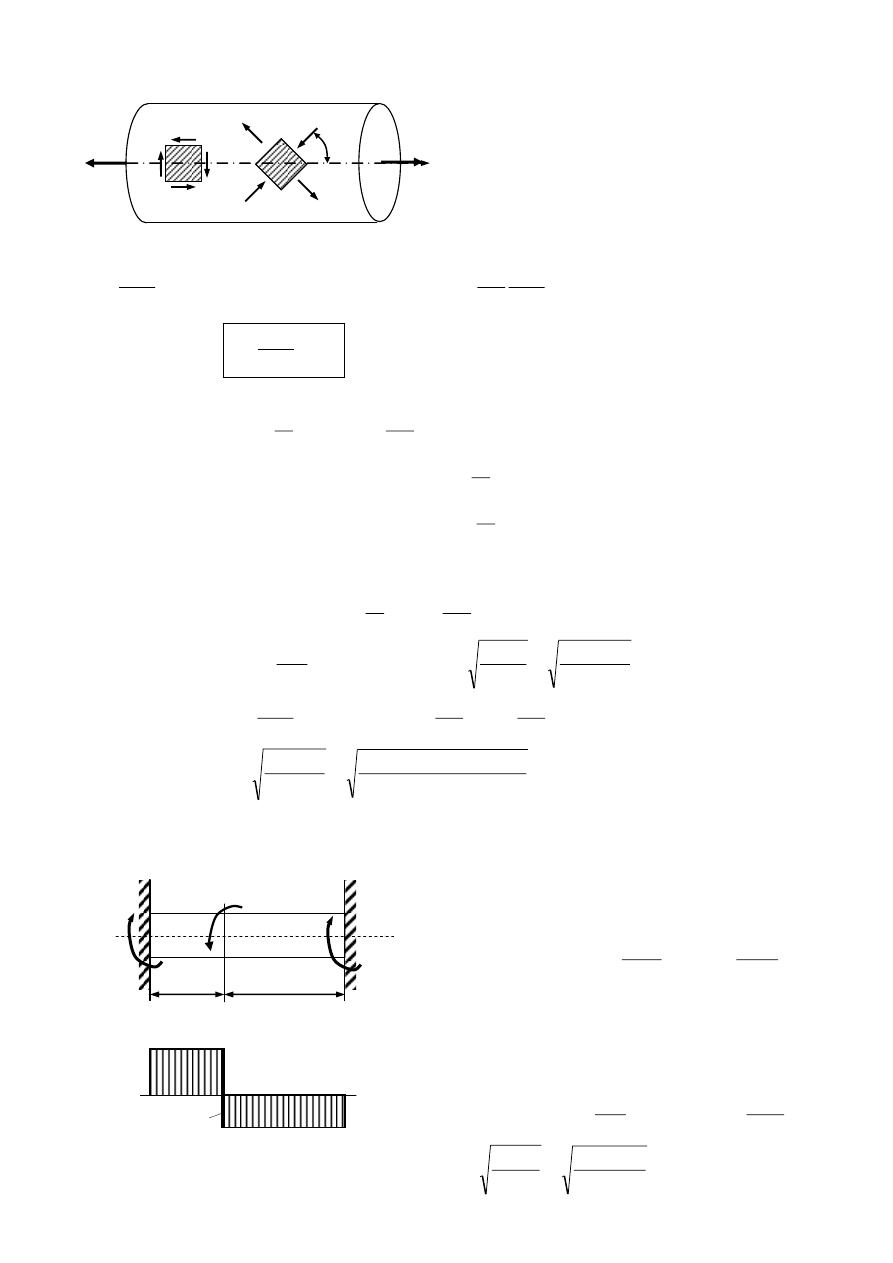
Rozpatrzmy stan naprężenia na powierzchni elementu skręcanego.

Jest to ścinanie niejednorodne.

Kierunki główne leżą pod kątem 45



do osi



= I



1

I = I



2

I

Przemieszczenie w pręcie skręcanym – jest to kąt skręcenia

]

[

0

rad

GJ

l

M

S





w mierze stopniowej

0

180

GJ

l

M

S









GJ

0

– sztywność skręcania

dop

S

GJ

l

M









0

- warunek

sztywnościowy, zwykle



dop

= 0,25



/m

Często dana jest moc i obroty a moment skręcający trzeba wyliczyć ze wzorów,

ogólnie:

30

;

n

N

M

S













-

prędkość kątowa

gdy

N w [kW]

]

[

9550

Nm

n

N

M

S



N w [kM]

]

[

2

,

716

kGm

n

N

M

S



Przykład Wał stalowy przenosi moc 5 kW, wykonując n=950 obr/min. Obliczyć średnicę

wału jeżeli k

s

=30 MPa,



dop

= 0,25



/m, G=8,1 10

4

MPa.

]

[

3

,

50

950

5

9550

9550

Nm

n

N

M

S







z war wytrzym.

s

S

k

W

M





0

max





]

[

0205

,

0

10

30

3

,

50

16

16

3

6

3

m

k

M

d

s

S















z war. sztywn.

]

[

00435

,

0

180

25

,

0

180

]

[

0

rad

rad

GJ

l

M

dop

S

























d

]

[

0348

,

0

10

10

1

,

8

00435

,

0

3

,

50

32

32

4

6

4

4

m

G

M

dop

S



















Przykład Obliczyć minimalną średnicę wału. k

s

=50 MPa, M=100 Nm, l

1

=20 cm, l

2

=30 cm.

Warunek równowagi:

-M

1

+M-M

2

=0 -

układ 1 krotnie hiperstatyczny

należy ułożyć dodatkowe równanie rozpatrując
odkształcenia

0

2

2

2

0

1

1

1

2

1

GJ

l

M

GJ

l

M















zatem

M

1

l

1

=M

2

l

2

M

2

=M

1

l

1

/l

2

M=M

1

+M

2

M=M

1

+M

1

⅔=5/3M

1

M

1

=3/5M=60 Nm

M

2

=M-M

1

=40 Nm

war. wytrz.

s

S

k

W

M





0

max



16

3

0

d

W





]

[

0182

,

0

10

50

60

16

16

3

6

3

m

k

M

d

s

S















M

s

M

s











2



2



1



1

45



l

1

l

2

M

M

1

M

2

M

1

=60

M

2

=40

M=100
0

M

max

= M

1

=60 Nm