Prof. Piotr Chrzan
RYNKI FINANSOWE
1
2. Teoria portfela wielu spółek
Oczekiwana stopa zwrotu z portfela n akcji
n
n
n
1
k
2
2
1
1
k
k
p
r
w
r
w
r
w
r
w
r
+
+
+
=
=
∑
=
L
(13)
gdzie:
r
p
– oczekiwana stopa zwrotu portfela,
w
k
– udział k-tej spółki w portfeli (0
≤ w
k
≤ 1)
r
k
-oczekiwana stopa zwrotu akcji k-tej spółki
n – liczba akcji w portfelu
Wariancja stopa zwrotu portfela n akcji
∑
∑ ∑
=
−
=
+
=
ρ
+
=
n
1
k
1
n
1
k
n
1
k
j
kj
j
k
j
k
2
k
2
k
2
p
s
s
w
w
2
s
w
s
(14)
∑
∑ ∑
=
−
=
+
=
+
=
n
1
k
1
n
1
k
n
1
k
j
kj
j
k
2
k
2
k
2
p
cov
w
w
2
s
w
s
(15)
gdzie:
– wariancja stopy zwrotu portfela,
2
p
s
– wariancja akcji k-tej spółki,
2
k
s
Prof. Piotr Chrzan
RYNKI FINANSOWE
2
– odchylenia standardowe k-tej spółki,
k
s
– udział k-tej spółki w portfelu (0
≤ w
k
w
i
≤ 1)
cov
kj
– kowariancja stóp zwrotu akcji k-tej spółki i j-tej
spółki
ρ
kj
– współczynniki korelacji stóp zwrotu akcji k-tej
spółki i j-tej spółki
Zapis macierzowy wariancji stopy zwrotu z portfela
Cw
w
s
2
p
′
=
(16)
gdzie: w
′ =[w
1
,w
2
, . . . w
n
]–wektor udziałów akcji spółek w
portfelu (wektor transponowany – wierszowy)
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
2
n
3
n
2
n
1
n
n
2
23
2
2
21
n
1
13
12
2
1
s
cov
cov
cov
cov
cov
s
cov
cov
cov
cov
s
C
L
L
L
L
L
L
L
L
C – macierz wariancji i kowariancji stóp zwrotu akcji spółek
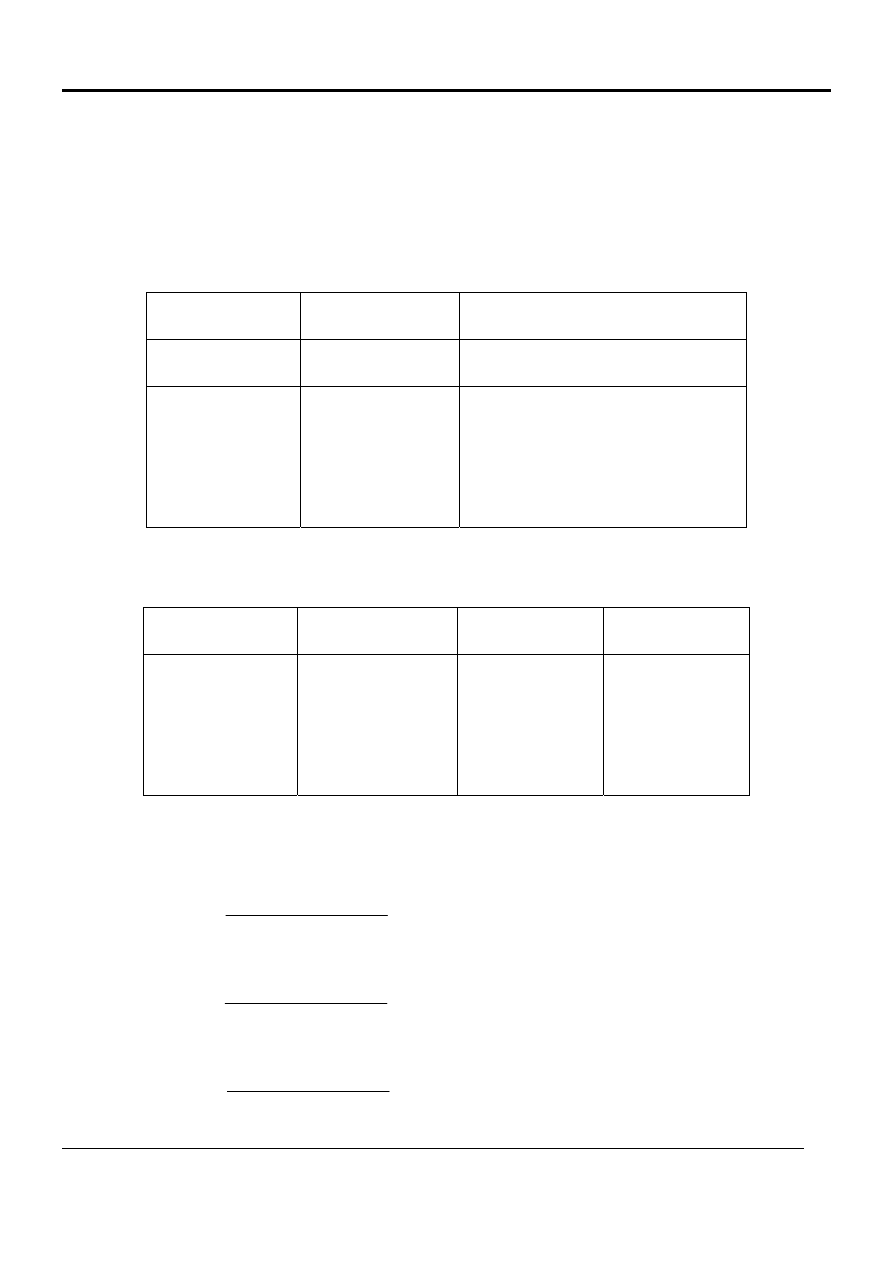
Prof. Piotr Chrzan
RYNKI FINANSOWE
3
Przykład 5
Rozpatrzmy portfel trzech akcji dla danych od stycznia 2000
do marca 2002 – tygodniowe stopy zwrotu GPW w Warszawie
Spółka Stopa
zwrotu Odchylenie
standardowe
k r
k
s
k
Compland
Świecie
Pekao
0,0091
0,0077
0,0064
0,0956
0,0643
0,0447
Macierz wariancji i kowariancji
cov
kj
Compland-1
Świecie-2 Pekao-3
Compland-1
Świecie-2
Pekao-3
0,009129
0,000996
0,001258
0,000996
0,004129
0,000479
0,001258
0,000479
0,001990
Współczynniki korelacji
162
,
0
0643
,
0
0956
,
0
000996
,
0
12
=
⋅
=
ρ
294
,
0
0447
,
0
0643
,
0
001258
,
0
13
=
⋅
=
ρ
166
,
0
0447
,
0
0643
,
0
000479
,
0
23
=
⋅
=
ρ
Prof. Piotr Chrzan
RYNKI FINANSOWE
4
Zapis wektorowa oczekiwanej stopy zwrotu z portfela
r
p
= w
′r
gdzie: w
′ – wektor udziałów akcji
r– wektor stóp zwrotu akcji
r
′
=[r
1,
r
2
. . . r
n
]
Przyjmujemy wektor udziałów
w
′ = [0,2; 0,3; 0,5]
r
′=[0,0091; 0,0077; 0,0064]
[
]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0064
,
0
0077
,
0
0091
,
0
5
,
0
3
,
0
2
,
0
r
p
00733
,
0
0064
,
0
5
,
0
0077
,
0
3
,
0
0091
,
0
2
,
0
r
p
=
⋅
+
⋅
+
⋅
=
Wariancja portfela
[
]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
5
,
0
3
,
0
2
,
0
001990
,
0
000479
,
0
001258
,
0
000479
,
0
004129
,
0
000996
,
0
001258
,
0
000996
,
0
009129
,
0
5
,
0
3
,
0
2
,
0
s
2
p
[
]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
5
,
0
3
,
0
2
,
0
0013903
,
0
0016774
,
0
0027536
,
0
s
2
p
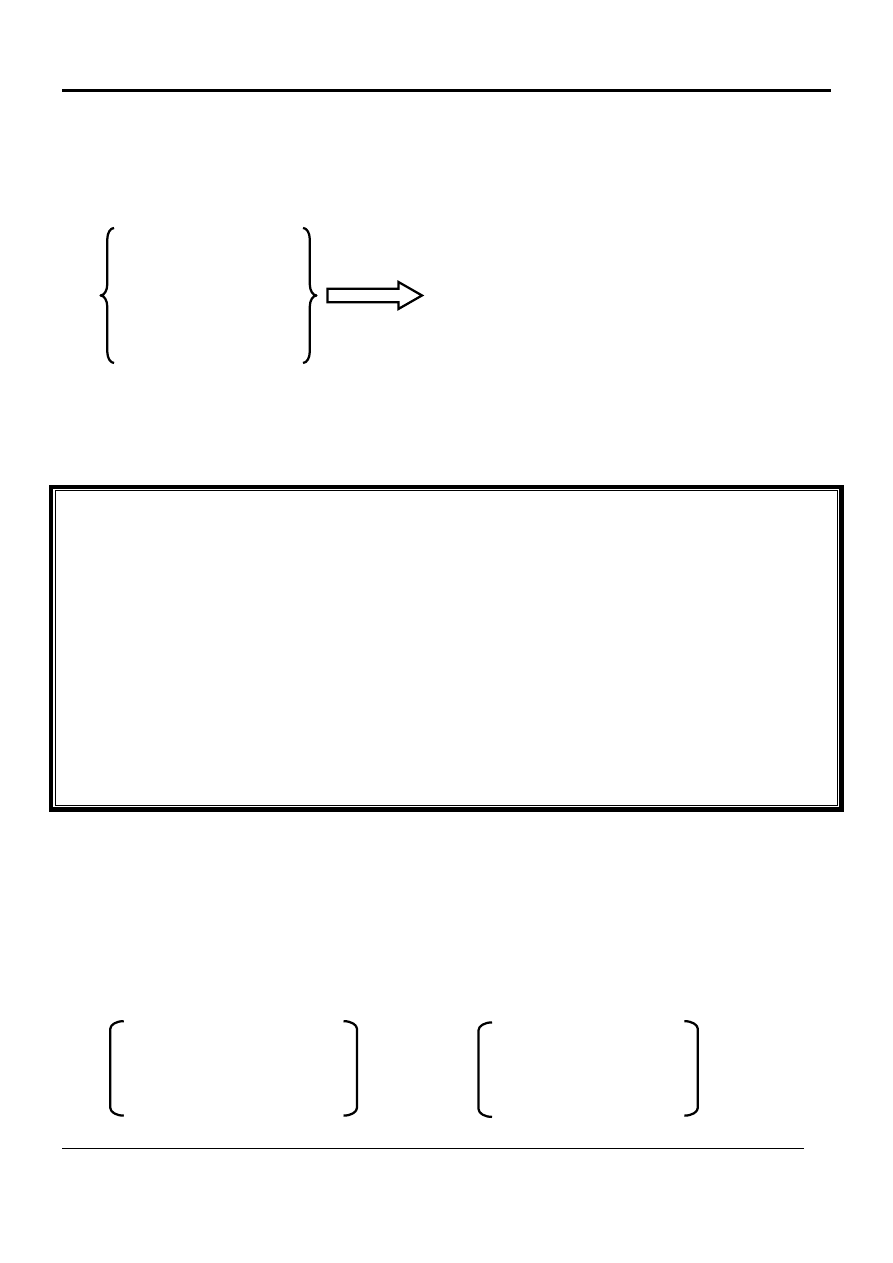
Prof. Piotr Chrzan
RYNKI FINANSOWE
5
001744909
,
0
s
2
p
=
s
p
= 0,0418
Portfel
20% Compland
30% Świecie
50% Pekao
Portfel efektywny
Portfel efektywny (efficient portfolio)
Pojedyncza inwestycja lub portfel aktywów jest uznawany za
efektywny, jeżeli żadna inna inwestycja lub portfel aktywów
nie przyniesie wyższego oczekiwanego zwrotu przy tym sa-
mym (lub niższym) ryzyku albo niższego ryzyka przy tym sa-
mym (lub wyższym) oczekiwanym zwrocie.
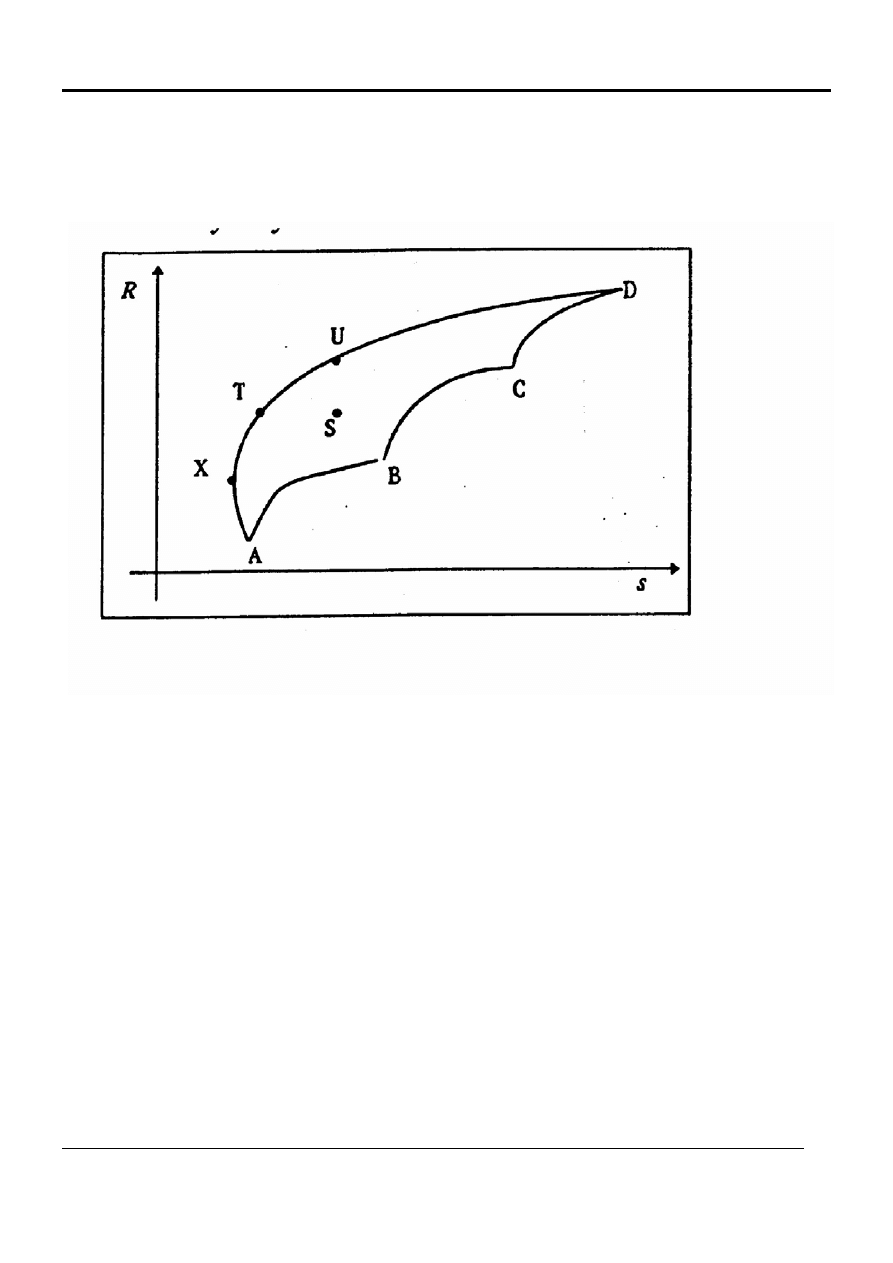
Zbiór możliwości (opportunity set)
Zbiór możliwości tworzą wszystkie możliwe portfele spółek
dostępne dla inwestora.
Zbiór
efektywny
efficient
set
Granica
efektywna efficient
frontier
r
p
= 0,00733 (0,733%)
s
p
= 0,0418 (4,18%)
Prof. Piotr Chrzan
RYNKI FINANSOWE
6
Zbiór efektywny tworzą wszystkie możliwe portfele efektywne
Rys. 5. Zbiór efektywny
3. Teoria użyteczności w analizie portfelowej
Prof. Piotr Chrzan
RYNKI FINANSOWE
7
Zadanie 1
max r
p
= w
′r
min = w
′Cw
2
k
s
Przy ograniczeniach
w
1
+ w
2
+ . . .+ w
n
= 1
w
1
≥0, w
2
≥0, . . . w
n
≥0
Teoria użyteczności
Użyteczność można interpretować jako satysfakcję, zadowo-
lenie czy też komfort psychiczny inwestora
U(r
p
, ) = – A + r
2
p
s
2
p
s
p
→ max
Zasada maksymalizacji wartości oczekiwanej użyteczności
A > 0 – wskaźnik skłonności do podejmowania ryzyka
Za każdą jednostkę ryzyka mierzonego wariancją stopy zwrotu
inwestor oczekuje wzrostu dochodu o A jednostek.
)
r
(
s
v
r
r
2
1
A
M
2
f
M
⋅
−
⋅
=
(17)
gdzie:
Prof. Piotr Chrzan
RYNKI FINANSOWE
8
r
M
– spodziewana stopa zwrotu rynku (najczęściej jest to repre-
zentatywny indeks giełdowy np. WIG)
r
f
–stopa zwrotu inwestycji wolnej od ryzyka (np. stopa zwrotu
bonów skarbowych obligacji skarbu państwa)
v – udział środków ulokowanych przez inwestora w portfelu
rynkowym
Przykład 6
WIG –– indeks rynkowy
r
M
= 10%, s(r
M
) = 15%,
v = 100%
r
f
= 5%
11
,
1
15
,
0
1
05
,
0
10
,
0
2
1
A
2
≈
⋅
−
⋅
=
Za wzrost wariancji stopy zwrotu o 1% inwestor oczekuje
wzrostu stopy zwrotu o 1,11%.
W zastosowaniach praktycznych najczęściej przyjmuje się war-
tość A = 3 co oznacza, że: za wzrost wariancji stopy zwrotu o
1% oczekuje się wzrostu stopy zwrotu o 3%.
Krzywe obojętności (indifference curves)
Krzywe jednakowej użyteczności (iso– utility curves)
Założenie: A = 3; U(r,s)= –3s
2
+ r
Prof. Piotr Chrzan
RYNKI FINANSOWE
9
U(r,s)=1 – krzywa o użyteczności 1
U(r,s)=2 – krzywa o użyteczności 2
–3s
2
+ r=1
⇒r= 3s
2
+ 1
przesunięte parabole
–3s
2
+ r=2
⇒r= 3s
2
+ 2
r= 3%
⇒ 3 = 3s
2
+ 2
⇒ s
2
= 1/3
⇒ s ≈ 0,577%
B = (r=3%, s = 0,577%)
R = 5%
⇒ 5 = 3s
2
+ 2
⇒ s
2
= 3/3 =1
⇒ s =1%
A = (r=5%, s = 1%)
U(A) = U(B) = 2
Decyzje A i B mają takie same znaczenie dla inwestora (krzy-
we obojętności)
Rys. 6 Krzywe jednakowej użyteczności
U=2 U=1
•
4
3
2
5
•
R(%)
Stopa
zwrotu
B
1
A
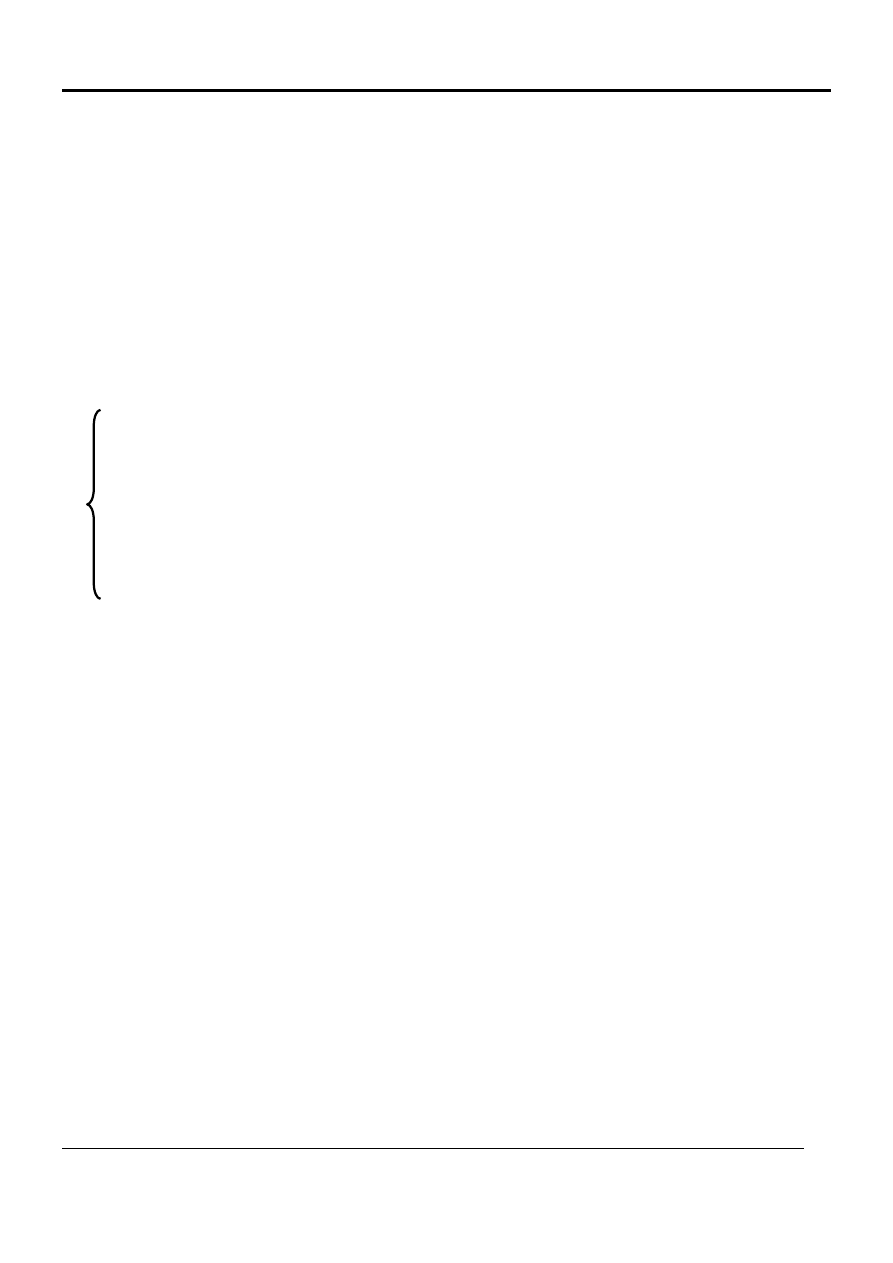
Prof. Piotr Chrzan
RYNKI FINANSOWE
10
Model Markowitza
U(r
p
,s
p
)= – A + r
2
p
s
p
→ max
1
w
n
1
k
k
=
∑
=
w
k
≥ 0
Rys. 7 Rozwiązanie graficzne modeli Markowitza
Z – Decyzja optymalna Markowitza
Przykład 7.
Prof. Piotr Chrzan
RYNKI FINANSOWE
11
Wyznaczmy optymalny portfel Markowitza dla A= 3 oraz da-
nych z przykładu 5
Model Markowitza dla trzech spółek
0
w
,
0
w
,
0
w
1
w
w
w
max
w
0064
,
0
w
0077
,
0
w
0091
,
0
)
w
001990
,
0
w
w
00479
.
0
2
w
004129
.
0
w
w
001258
.
0
2
w
w
000996
.
0
2
w
00912
,
0
(
3
)
s
,
r
(
U
3
2
1
3
2
1
3
2
1
2
3
3
2
2
2
3
1
2
1
2
1
p
p
≥
≥
≥
=
+
+
→
+
+
+
+
⋅
+
+
⋅
+
⋅
+
−
=
Excel – Solver
Optymalne rozwiązanie Markowitza
U(r
p
,s
p
) = 0,0025
w
1
= 0,028; w
2
= 0,338; w
3
= 0,634
2,8%
akcji
Compland
Portfel Markowitza 33,8% akcji Świecie
63,4%
akcji
Pekao
Prof. Piotr Chrzan
RYNKI FINANSOWE
12
Wady Modelu Markowitza
n=100 spółek w portfelu, liczba kowariancji do policzenia
L
C
= (99 + 98 + 97 + . . . +1) =4950
Liczba wariancji do policzenia
100
L
2
s
=
Liczba stóp zwrotu do policzenia L
r
=100
Możliwe źródło błędów, jakie pojawia się przy tych oblicze-
niach, nazywane jest ryzykiem estymacji.