
Eugeniusz Rosołowski, e-mail:
eugeniusz.rosolowski@pwr.wroc.pl
3.
ANALIZA SYSTEMÓW ZA POMOCĄ METOD
OPERATOROWYCH
3.1. Przekształcenie Fouriera
W klasycznym podejściu, przekształcenie Fouriera
1
wywodzi się z szeregów Fouriera,
które odnoszą się do przebiegów okresowych. Okresowa funkcja f(t) (w ogólnym
przypadku funkcja zespolona) ciągłej niezależnej zmiennej t (zazwyczaj jest to czas,
chociaż można rozważać także inną wielkość) z okresem T może być przedstawiona w
postaci następującego szeregu, zwanego szeregiem Fouriera:
∑
+∞
−∞
=
=
k
t
jk
k
e
a
t
f
0
)
(
ω
dla
2
/
2
/
T
t
T
≤
≤
−
(3.1)
gdzie:
ω
0
= 2π/T, natomiast zespolone współczynniki a
k
są określone następującym
związkiem:
∫
+
−
−
=
2
/
2
/
0
)
(
1
T
T
t
jk
k
t
e
t
f
T
a
d
ω
(3.2)
Równość (3.1) jest zachowana, jeśli funkcja f(t) spełnia warunki Dirichleta
2
[Director]:
• funkcja f(t) jest jednowartościowa w rozpatrywanym przedziale
2
/
2
/
T
t
T
≤
≤
−
;
• f(t) może mieć tylko skończoną liczbę maksimów i minimów w dowolnym skoń-
czonym przedziale czasu;
• f(t) może mieć tylko skończoną liczbę nieciągłości w przedziale
2
/
2
/
T
t
T
≤
≤
−
;
• spełniona jest nierówność:
∞
<
∫
+
−
2
/
2
/
)
(
T
T
t
t
f
d
.
Warunki te spełnia większość praktycznych sygnałów. W punktach nieciągłości
funkcji f(t) jej wartość należy przyjąć jako średnią z lewej i prawej granicy obliczanej
zgodnie z (3.1) w punkcie nieciągłości.
1
Jean Baptiste Joseph Fourier (1768-1830), matematyk francuski. Prace z zakresu teorii
funkcji, rachunku całkowego, równań różniczkowych i fizyki matematycznej.
2
Johann Peter Gustav Lejeune Dirichlet (1805-1859), niemiecki matematyk francuskiego
pochodzenia. Był wykładowcą uniwersytetów we Wrocławiu, Berlinie i Getyndze.

2
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
Współczynniki a
k
można interpretować jako zespoloną amplitudę sygnału f(t) dla
częstotliwości k
ω
0
(k-tej harmonicznej przy pulsacji podstawowej
ω
0
):
}
Im{
}
Re{
k
k
k
a
a
a
j
+
=
(3.3)
Łatwo więc określić amplitudę i fazę poszczególnych współczynników rozkładu (3.1),
które w ten sposób tworzą amplitudowe i fazowe widmo okresowego sygnału f(t).
W przypadku, gdy f(t) jest rzeczywistym sygnałem okresowym, reprezentacja (3.1)
redukuje się do postaci:
∑
∑
+∞
=
+∞
=
+
=
1
0
0
0
)
sin(
)
cos(
)
(
k
k
k
k
t
k
c
t
k
b
t
f
ω
ω
(3.4)
przy czym:
∫
−
=
2
/
2
/
0
)
(
1
T
T
t
t
f
T
b
d ,
∫
−
=
2
/
2
/
0
)
cos(
)
(
1
T
T
k
t
t
k
t
f
T
b
d
ω
, dla k > 1,
∫
−
=
2
/
2
/
0
)
sin(
)
(
1
T
T
k
t
t
k
t
f
T
c
d
ω
.
Można zauważyć, że widmo sygnału okresowego (a więc zbiór współczynników
a
k
) jest dyskretne względem pulsacji. Okres dyskretyzacji jest równy pulsacji podsta-
wowej
ω
0
. Całkowe przekształcenie Fouriera, które odnosi się również do przebiegów
nieokresowych, można uzyskać przez wydłużenie okresu sygnału w zależnościach
(3.1) i (3.2) w granicy do nieskończoności, co także oznacza, że szerokość przedziału
pulsacji podstawowej
ω
0
zmierza do zera: T→
∞,
ω
0
→0. Sumowanie w (3.1) zostaje
wówczas zastąpione operacją całkowania. Prowadzi to do następującej pary prze-
kształceń całkowych [Osiowski]:
∫
+∞
∞
−
−
=
t
e
t
f
F
t
d
j
j
ω
ω
)
(
)
(
(3.5)
∫
+∞
∞
−
=
ω
ω
π
ω
d
j
j t
e
F
t
f
)
(
2
1
)
(
(3.6)
znanych jako proste (3.5) i odwrotne (3.6) przekształcenie Fouriera. Są one często za-
pisywane w następującej skróconej formie:
{ }
{
}
)
(
)
(
)
(
)
(
1
ω
ω
j
j
F
t
f
t
f
F
-
F
F
=
=
Transformata F(j
ω
) jest funkcją względem pulsacji
ω
i stała ‘j’ jest niekiedy opusz-
czana, jednak w tym zapisie podkreślona jest zespolona postać transformaty Fouriera,
a ponadto, zachowany zostaje jej związek z omawianą dalej transformatą Laplace’a.
Wystarczającym warunkiem istnienia transformaty Fouriera F(j
ω
) dla danej funk-
cji f(t) jest spełnienie przez tę funkcję ostatniego z podanych warunków Dirichleta dla

3.1. Przekształcenie Fouriera
3
T→
∞ [Director]. Ten warunek już nie jest tak łatwo spełnić i dlatego istnieje pewna
klasa funkcji, dla których transformata Fouriera nie istnieje.
Przekształcenie Fouriera odgrywa bardzo ważną rolę w zakresie przetwarzania sy-
gnałów ciągłych i dyskretnych, projektowania filtrów, a także jako wydajne narzędzie
do rozwiązywania równań różniczkowych i analizy systemów.
W praktycznych zastosowaniach najczęściej korzysta się z różnych właściwości
przekształcenia oraz znanych par przekształceń F(j
ω
)
↔f(t) typowych funkcji, które
zostały określone na podstawie zależności (3.5) i (3.6).
Przykład 3.1.
Określić transformatę Fouriera impulsu Diraca.
Zgodnie z (3.5) możemy napisać:
{ }
1
)
(
)
(
0
=
=
=
−
+∞
∞
−
−
∫
ω
ω
δ
δ
j
j
d
e
t
e
t
t
t
F
co wprost wynika z (2.14).
Przykład 3.2.
Określić transformatę Fouriera pochodnej funkcji.
Posługując się definicją transformaty odwrotnej można napisać:
{
}
)
(
)
(
2
1
)
(
2
1
)
(
1
ω
ω
ω
ω
ω
π
ω
ω
π
ω
ω
j
j
d
j
j
d
j
d
d
d
d
j
j
F
e
F
e
F
t
t
f
t
t
t
−
+∞
∞
−
+∞
∞
−
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
∫
∫
F
.
Stąd:
)
(
)
(
ω
ω
j
j
d
d
F
t
f
t
=
⎭
⎬
⎫
⎩
⎨
⎧
F
.
A więc, różniczkowanie funkcji prowadzi do pomnożenia jej transformaty przez czynnik j
ω.
Otrzymany wynik jest poprawny dla zerowych warunków początkowych.
W przypadku analizy systemów sterowania, funkcja względem czasu jest ograni-
czona do przedziału
∞
<
≤ t
0
, przyjmując zerową wartość poza nim. Wobec tego w
(3.5) granicę całkowania można także ograniczyć do tego przedziału:
∫
+∞
−
=
=
0
)
(
)
(
)
(
t
e
t
f
F
F
t
d
j
j
j
I
ω
ω
ω
(3.7)
gdzie indeks I wskazuje na przekształcenie jednostronne.
Mówimy wówczas o jednostronnym przekształceniu Fouriera, które ma zastoso-
wanie w analizie systemów dynamicznych. Wspomniane ograniczenia nie obejmują
dziedziny częstotliwości (pulsacji), więc przekształcenie odwrotne (3.6) pozostaje bez
zmian, przy czym f(t) = 0 dla
0
<
t
.
Ograniczenie przedziału całkowania w (3.7) jest równoważne pomnożeniu funkcji
czasu przez skok jednostkowy 1(t). Można to zapisać następująco:
4
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
{ }
{
}
)
(
1
)
(
)
(
t
t
f
t
f
F
F
=
I
(3.8)
Podstawowe właściwości przekształcenia Fouriera są zebrane w Tabeli 3.1.
Tabela 3.1. Podstawowe właściwości przekształcenia Fouriera
liniowość:
{
}
{ }
{ }
)
(
)
(
)
(
)
(
t
q
t
p
t
q
t
p
F
F
F
β
α
β
α
+
=
+
oraz:
{
}
{ }
{ }
)
(
)
(
)
(
)
(
1
1
1
t
q
t
p
t
q
t
p
-
-
-
F
F
F
β
α
β
α
+
=
+
przesunięcie w dziedzinie czasu:
{
}
ωτ
ω
τ
j
e
F
t
f
−
=
−
)
j
(
)
(
F
przesunięcie w dziedzinie częstotliwości (o modulacji):
{
}
(
)
)
j(
)
(
0
0
ω
ω
ω
−
= F
e
t
f
t
j
F
skalowanie:
{
}
⎟
⎠
⎞
⎜
⎝
⎛
=
a
j
1
)
(
ω
F
a
at
f
F
różniczkowanie po czasie (zerowe warunki początkowe):
{ }
( )
ω
ω
j
j
)
(
'
F
t
f
=
F
( )
ω
ω
j
)
j
(
d
)
(
d
F
t
t
f
k
k
k
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
F
różniczkowanie po częstotliwości (zerowe warunki początkowe):
{
}
( )
ω
ω
d
j
d
j
)
(
F
t
f
t
=
⋅
F
{
}
( )
n
n
n
n
F
t
f
t
ω
ω
d
j
d
j
)
(
=
⋅
F
splot:
{
}
( ) ( )
ω
ω
τ
τ
τ
j
j
d
)
(
)
(
)
(
)
(
G
F
t
g
f
t
g
t
f
⋅
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
−
=
⊗
∫
∞
∞
−
F
F
mnożenie
{
}
( ) ( )
ω
ω
ξ
ξ
ω
ξ
j
j
d
)
j(
(
)
j
(
)
(
)
(
G
F
G
F
t
g
t
f
⊗
=
−
=
⋅
∫
∞
∞
−
F
transmitancja:
( )
{ } ( )
( )
ω
ω
ω
j
j
)
(
j
U
Y
t
g
G
=
= F
symetria przekształcenia:
jeżeli:
{ }
)
(
)
(
t
f
F
F
=
ω
j
, to wówczas:
{
}
)
(
2
)
(
1
ω
π
−
=
f
t
F
-
F
W Tabeli 3.2 podane są transformaty Fouriera podstawowych funkcji względem
czasu.
3.1. Przekształcenie Fouriera
5
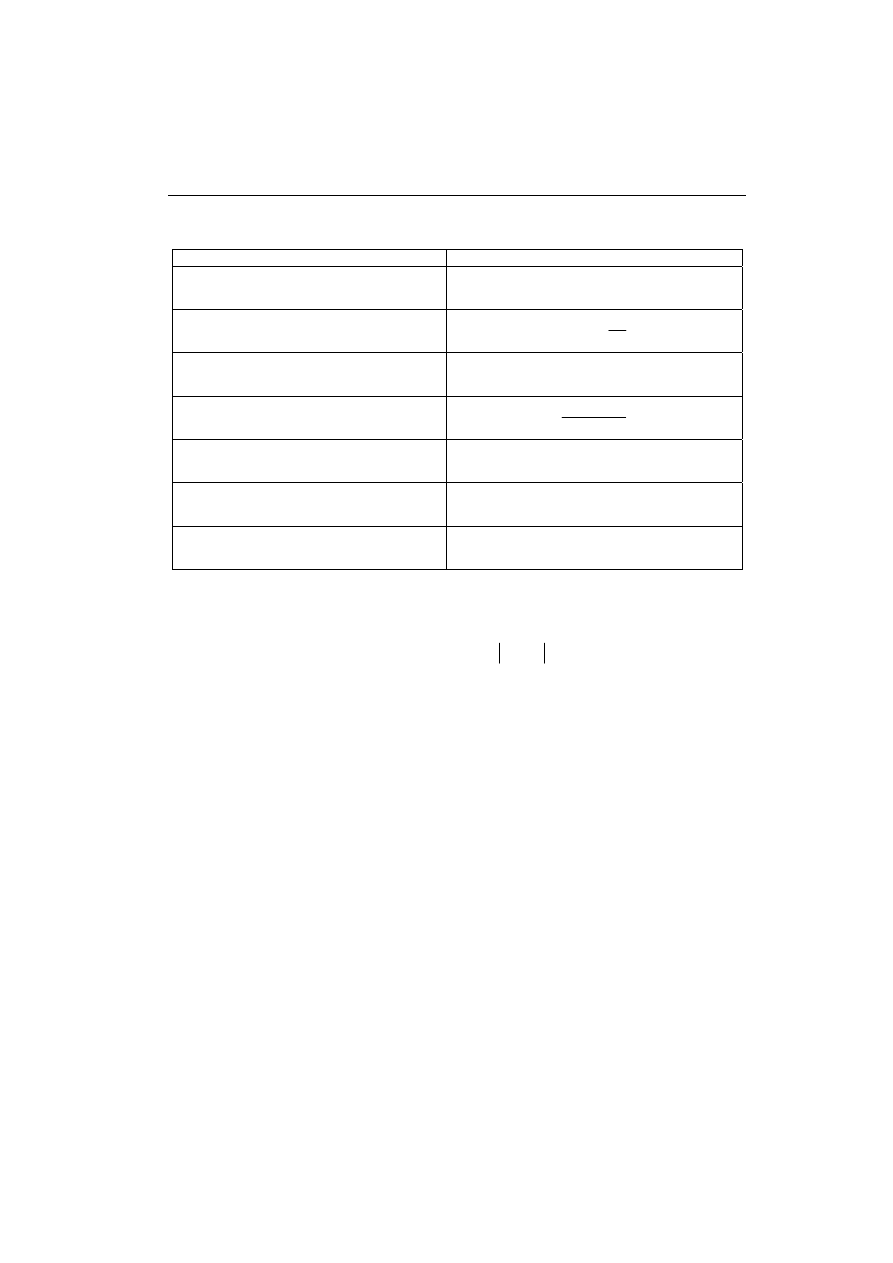
Tabela 3.2. Transformaty Fouriera wybranych funkcji
f(t)
F(j
ω
)
)
(t
δ
1
1(t)
ω
ω
πδ
j
1
)
(
+
1
)
(
2
ω
πδ
t
a
e
t
)
j
(
)
(
1
β
+
−
,
α ≥ 0
ω
β
j
j
1
+
+
a
t
e
β
j
)
(
2
β
ω
πδ
−
t
α
sin
(
)
)
(
)
(
j
α
ω
δ
α
ω
δ
π
+
−
−
−
t
α
cos
(
)
)
(
)
(
α
ω
δ
α
ω
δ
π
+
+
−
Transformata Fouriera funkcji względem czasu (sygnału): F(j
ω
)
↔f(t) jest obrazem
widma tej funkcji. W ogólnym przypadku jest to funkcja zespolona:
)
(
j
e
)
j
(
)
(
j
)
(
)
j
(
ω
ϕ
ω
ω
ω
ω
F
B
A
F
=
+
=
(3.9)
gdzie |F(j
ω
)| przedstawia amplitudę widma (charakterystykę amplitudową), natomiast
ϕ
(
ω
) jest funkcją reprezentującą fazę tego widma (charakterystyką fazową).
Posługując się w (3.5) zależnością:
t
t
t
ω
ω
ω
sin
j
cos
e
j
−
=
−
można określić rzeczywistą i urojoną część transformaty F(j
ω
) rzeczywistej funkcji
f(t) (3.5):
(
)
(
)
∫
∫
∞
+
∞
−
+∞
∞
−
−
=
=
=
=
t
t
t
f
F
B
t
t
t
f
F
A
d
sin
)
(
)
j
(
Im
)
(
d
cos
)
(
)
j
(
Re
)
(
ω
ω
ω
ω
ω
ω
(3.10)
Widać stąd, że część rzeczywista transformaty F(j
ω
) jest funkcją parzystą: A(–
ω
) =
A(
ω
), natomiast jej część urojona – funkcją nieparzystą: B(–
ω
) = –B(
ω
). Podobnie jest
z reprezentacją wykładniczą funkcji F(j
ω
): widmo amplitudowe |F(j
ω
)| jest funkcją
parzystą, a charakterystyka fazowa
ϕ
(
ω
) – funkcją nieparzystą.

6
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
Ważna właściwość przekształcenia Fouriera dotyczy transformaty splotu dwóch
funkcji. Jeżeli (2.31):
)
(
)
(
)
(
)
(
)
(
t
g
t
u
t
g
u
t
y
⊗
=
−
=
∫
+∞
∞
−
τ
τ
τ
d
,
to transformatę tej operacji można określić następująco:
∫
∫
∫
∫
∞
∞
−
∞
∞
−
−
∞
∞
−
∞
∞
−
−
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
=
=
τ
τ
τ
τ
τ
τ
ω
ω
ω
d
d
)
(
e
)
(
d
d
)
(
)
(
e
)]
(
[
)
(
j
j
t
t
g
u
t
t
g
u
t
y
j
Y
t
t
F
A ponieważ:
ωτ
ω
ω
τ
j
j
e
)
j
(
d
)
(
e
−
∞
∞
−
−
=
−
∫
G
t
t
g
t
, co wynika z transformaty funkcji przesuniętej w
czasie, to:
)
j
(
)
j
(
e
)
(
)
j
(
)
j
(
j
ω
ω
τ
τ
ω
ω
ωτ
U
G
d
u
G
Y
=
=
∫
∞
∞
−
−
(3.11)
co jest bardzo ważnym praktycznym wynikiem transformaty splotu dwóch funkcji.
Przykład 3.3.
Przedstawić graficznie amplitudę i fazę widma funkcji
T
t
e
t
t
u
/
)
(
1
)
(
−
=
T = 0,02s.
Posługując się Tabelą 3.2 można wyznaczyć transformatę podanej funkcji:
{
}
ω
ω
j
j
+
=
=
−
T
e
t
U
T
t
/
1
1
)
(
1
)
(
/
F
.
Amplituda i faza transformaty są zatem następujące:
2
2
/
1
1
)
(
ω
ω
+
=
T
U j
,
)
(
)
(
T
ω
ω
ϕ
arctg
−
=
.
Przebiegi funkcji związanych z tym przykładem dla podanej wartości T = 0,02s są pokazane na
rys. 3.1.
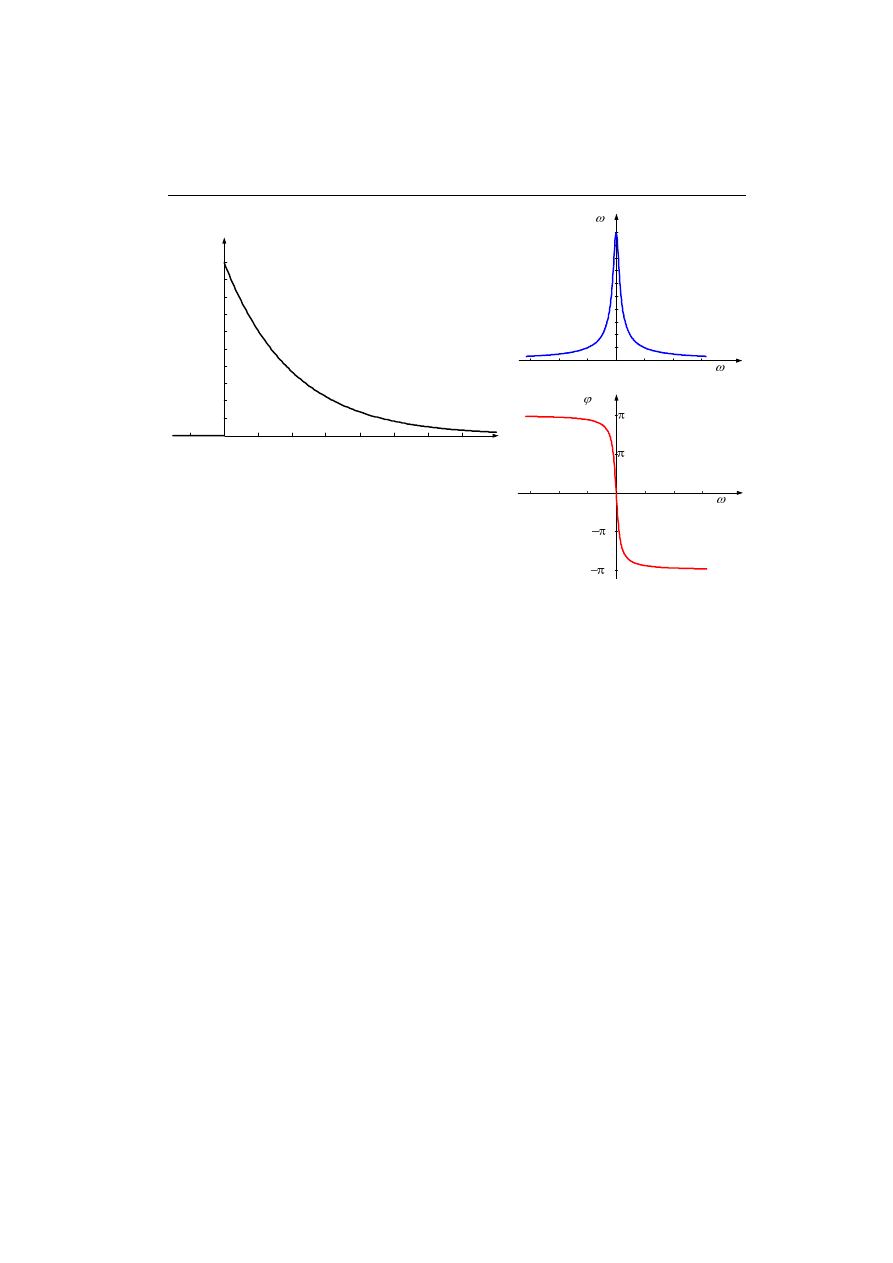
3.1. Przekształcenie Fouriera
7
0
0,01 0,02 0,03
0,04 0,05 0,06 0,07 t, s
0,2
0,4
0,6
0,8
1
-0,01
1(t)e
-t/T
/2
-1500 -1000 -500 0
500 1000 1500 , 1/s
/4
/4
/2
, rad
-1500 -1000 -500
0
500 1000 1500
0,004
0,008
0,012
0,016
0,02
, 1/s
|U(j )|
u(t)
a)
b)
c)
Rys. 3.1. Sygnał a) oraz jego charakterystyka widmowa amplitudy b) i fazy c)
Przyjrzyjmy się rezultatom otrzymanym w powyższym przykładzie. Analizowana
funkcja przedstawia wykładniczo zanikający sygnał, który ma zerową wartość dla 0> t
(rys. 3.1a). Jej charakterystyka częstotliwościowa ma przebieg jak na rys. 3.1b. Dla
pulsacji
ω
= 0 wartość amplitudy jest równa składowej stałej, czyli wartości średniej
analizowanego sygnału. Łatwo sprawdzić na podstawie (3.5), że
∫
+∞
∞
−
=
t
t
f
F
d
)
(
)
0
(
(3.12)
Jeśli analizowana funkcja jest funkcją wagi g(t) jakiegoś układu, to jej transformata
Fouriera jest nazywana transmitancją widmową (widmową funkcją przejścia) układu:
{ }
∫
+∞
∞
−
−
=
=
t
e
t
g
t
g
G
t
d
j
j
ω
ω
)
(
)
(
)
(
F
(3.13)
Znaczenie transmitancji widmowej wynika bezpośrednio z transformaty Fouriera
splotu dwóch funkcji (Tabela 3.1):
{
} ( ) ( ) ( )
ω
ω
ω
j
j
j
)
(
)
(
Y
G
U
t
g
t
u
=
⋅
=
⊗
F
(3.14)
skąd:
8
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
( )
( )
( )
ω
ω
ω
j
j
j
U
Y
G
=
(3.15)
Ilustracja operacji (3.14) jest pokazana na rys. 3.2. Najważniejszą praktyczną kon-
sekwencją przejścia z opisu systemu w dziedzinie czasu do podobnego opisu za po-
mocą przekształcenia Fouriera jest zastąpienie operacji splotu funkcji wymuszenia i
wagi przez mnożenie ich transformat. Ponadto, na podstawie (3.15), transmitancję
układu można wyznaczyć na podstawie transformat sygnałów: wyjściowego i wej-
ściowego. Odpowiedź czasowa może być określona przez odwrotne przekształcenie
Fouriera tego właśnie iloczynu transformat:
( ) ( )
{
}
( )
{
}
ω
ω
ω
j
j
j
Y
G
U
t
y
-
-
1
1
)
(
F
F
=
⋅
=
(3.16)
∫
−
=
t
t
g
u
t
y
0
d
)
(
)
(
)
(
τ
τ
τ
Rys. 3.2. Opis układu w dziedzinie czasu i częstotliwości
Transmitancję systemu można także bezpośrednio określić na podstawie równania
różniczkowego opisującego jego dynamikę. Rozpatrzmy ogólne równanie różniczko-
we systemu o postaci jak w (2.19):
)
(
)
(
)
(
...
)
(
)
(
)
(
)
(
)
(
...
)
(
)
(
0
'
1
''
2
)
1
(
1
)
(
0
'
1
''
2
)
1
(
1
)
(
t
u
b
t
u
b
t
u
b
t
u
b
t
u
b
t
y
a
t
y
a
t
y
a
t
y
a
t
y
m
m
m
m
n
n
n
+
+
+
+
+
=
+
+
+
+
+
−
−
−
−
(3.17)
przy czym, n
≥ m.
Równanie to można obustronnie poddać przekształceniu Fouriera. Posługując się
właściwością transformaty pochodnej funkcji przy zerowych warunkach początko-
wych (Tabela 3.1), otrzymamy:
)
(
)
(
)
(
...
)
(
)
(
)
(
)
(
)
(
)
(
)
(
...
)
(
)
(
)
(
)
(
0
1
1
1
0
1
1
1
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
j
U
b
j
U
j
b
j
U
j
b
j
U
j
b
j
Y
a
j
Y
j
a
j
Y
j
a
j
Y
j
m
m
m
m
n
n
n
+
+
+
+
=
+
+
+
+
−
−
−
−
(3.18)
Po uporządkowaniu powyższego równania otrzymamy następującą relację:

3.1. Przekształcenie Fouriera
9
)
(
)
(
...
)
(
)
(
)
(
...
)
(
)
(
)
(
)
(
0
1
1
1
0
1
1
1
ω
ω
ω
ω
ω
ω
ω
ω
ω
j
G
a
j
a
j
a
j
b
j
b
j
b
j
b
j
U
j
Y
n
n
n
m
m
m
m
=
+
+
+
+
+
+
+
+
=
−
−
−
−
(3.19)
Widać zatem, że transmitancja układu, którego dynamika jest opisana równaniem
różniczkowym jest funkcją wymierną
3
. Na podstawie warunków zapisu dynamiki sys-
temu (3.17) widać, że rząd wielomianu w mianowniku transmitancji (3.19) nie może
być mniejszy od rzędu wielomianu w liczniku tej funkcji. Jest to związane z zakładaną
przyczynowością rozpatrywanych systemów.
Przykład 3.4.
Określić transmitancję widmową układu opisanego następującym równa-
niem różniczkowym:
)
(
)
(
)
(
)
(
)
(
0
'
1
0
'
1
''
2
t
u
b
t
u
b
t
y
a
t
y
a
t
y
a
+
=
+
+
.
Obliczając transformatę Fouriera obu stron równania różniczkowego otrzymamy (3.18):
(
)
(
)
0
1
0
1
2
2
)
(j
)
j
(
)
(j
)
(j
)
j
(
b
b
U
a
a
a
Y
+
=
+
+
ω
ω
ω
ω
ω
.
Skąd:
)
j
(
)
j
(
)
j
(
)
(j
)
(j
)
(j
)
j
(
0
1
2
2
0
1
ω
ω
ω
ω
ω
ω
ω
U
G
U
a
a
a
b
b
Y
=
+
+
+
=
.
A zatem, poszukiwana transmitancja jest następująca:
∫
+∞
∞
−
−
=
+
+
−
+
=
dt
t
g
a
a
a
b
b
G
t
ω
ω
ω
ω
ω
j
1
0
2
2
1
0
e
)
(
j
j
)
j
(
.
Przykład 3.5.
Posługując się transformatą Fouriera określić odpowiedź układu opisane-
go równaniem różniczkowym:
t
y
t
y
t
y
=
+
+
d
d
d
d
2
2
2
.
Niestety, jak łatwo sprawdzić, funkcja leżąca po prawej stronie powyższego równania (wymu-
szenie) nie spełnia warunku istnienia transformaty Fouriera, gdyż nie jest bezwzględnie całko-
walna, gdyż wynik całki:
∞
+∞
∞
−
=
∫
0
2
t
dt
t
z pewnością nie jest ograniczony.
Zatem, podane równanie różniczkowe nie może być przetwarzane za pomocą przekształcenia
Fouriera.
Wniosek płynący z przykładu 3.5 wskazuje na duże ograniczenie zastosowania
przekształcenia Fouriera do analizy systemów.
3
Funkcja wymierna jest ilorazem dwóch wielomianów.
3.2. Przekształcenie Laplace’a
3.2.1. Wprowadzenie
Nawiązując do przykładu 3.5 można zauważyć, że funkcja będąca wymuszeniem w
rozpatrywanym równaniu różniczkowym:
t
t
u
=
)
(
,
spełni warunek przekształcenia Fouriera, jeśli pomnożyć ją przez funkcję wykładniczą
e
–
σ
t
, o szczególnych wartościach liczby rzeczywistej
σ
. Załóżmy, że chcemy określić
jednostronną transformatę Fouriera dla tak ograniczonej funkcji:
{
}
∫
∞
+
−
−
=
0
)
j
(
I
d
e
)
(
t
t
e
t
u
t
t
ω
σ
σ
F
.
Podstawiając:
ω
σ
j
+
=
s
otrzymamy:
2
0
2
0
1
e
1
e
1
d
e
)
(
)
j
(
s
s
t
s
t
t
s
U
U
st
st
st
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
=
=
+
∞
−
−
∞
−
∫
ω
σ
dla Re(s) =
σ
> 0. (3.20)
Powyższy związek określa transformatę Laplace’a
4
funkcji u(t) = t. Formalnie
transformata Laplace’a jest definiowana za pomocą pary następujących przekształceń:
{ }
∫
+∞
−
=
=
0
d
)
(
)
(
)
(
t
e
t
f
t
f
s
F
st
L
(3.21)
{ }
∫
∞
+
∞
−
=
=
j
j
j
1
d
e
)
(
2
j
1
)
(
)
(
σ
σ
π
s
s
F
s
F
t
f
st
-
L
(3.22)
gdzie
ω
σ
j
+
=
s
.
Podobnie jak w przypadku całki Fouriera, związek (3.21) jest nazywany prostym
przekształceniem Laplace’a (jednostronnym), a (3.22) – przekształceniem odwrotnym.
Bardziej ogólne przekształcenie dwustronne Laplace’a różni się granicą całkowa-
nia:
{ }
∫
+∞
∞
−
−
=
=
t
e
t
f
t
f
s
F
st
d
)
(
)
(
)
(
II
II
L
(3.23)
4
Pierre Simon de Laplace (1749-1827), matematyk i fizyk francuski, jeden z twórców teo-
rii prawdopodobieństwa.
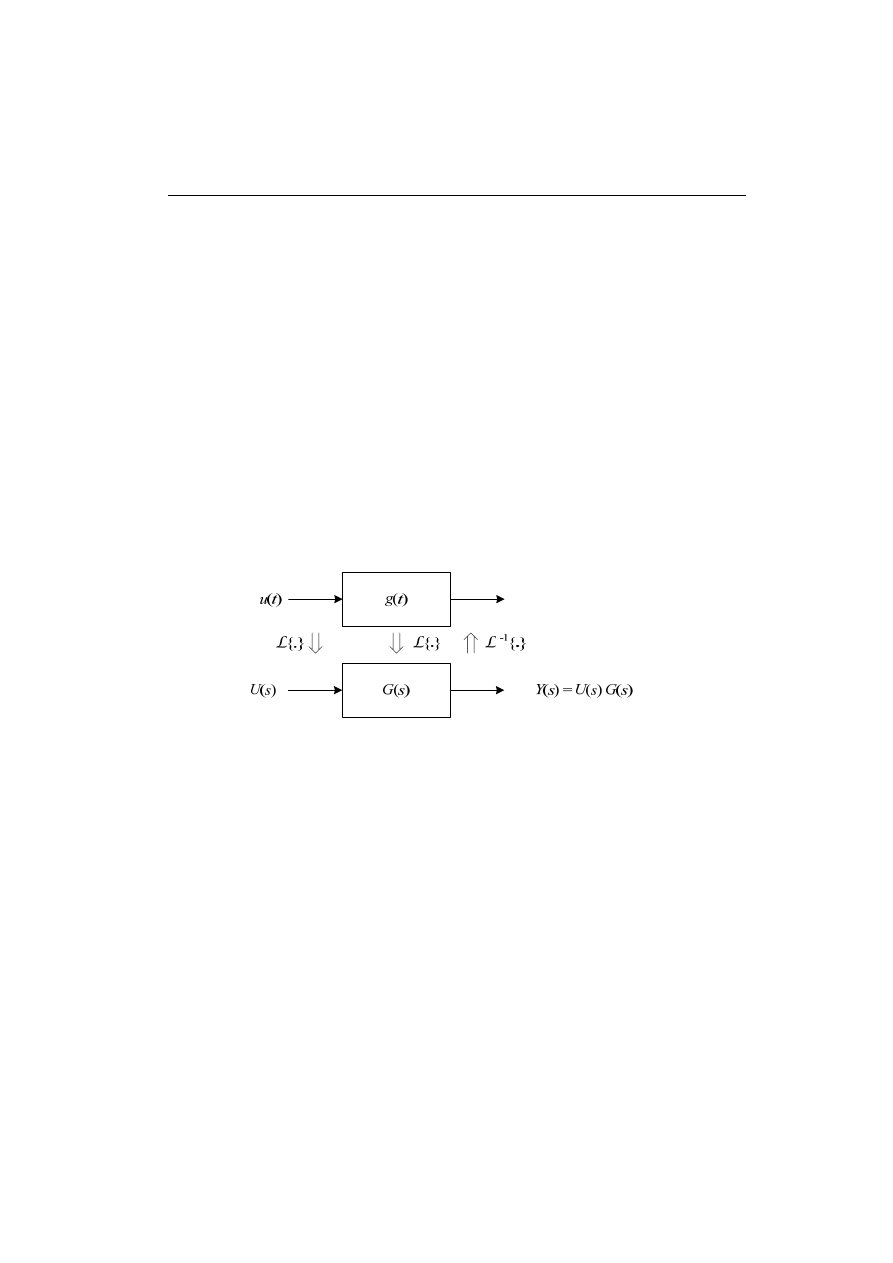
3.2. Przekształcenie Laplace’a
11
W przypadku analizy systemów, kiedy f(t) = 0 dla t < 0, powszechnie stosuje się prze-
kształcenie jednostronne.
Jak było pokazane powyżej, odpowiednia wartość części rzeczywistej zmiennej ze-
spolonej s =
σ
+ j
ω
zapewnia istnienie ograniczonej wartości całki (3.21) dla bardzo
szerokiej klasy funkcji. Dzięki temu, przekształcenie Laplace’a może być stosowane
praktycznie do analizy niemal wszystkich liniowych przyczynowych systemów dyna-
micznych. Warunek istnienia przekształcenia Laplace’a jest związany z bezwzględną
zbieżnością całki:
∫
∞
∞
−
−
t
t
f
t
)d
(
e
0
σ
.
Wartość
σ
=
σ
0
, która wyznacza zbieżność powyższej całki jest wartością współrzęd-
nej rzeczywistej w granicach całkowania w przekształceniu odwrotnym (3.22). Jeśli
σ
0
= 0, to przekształcenie Laplace’a nie różni się od przekształcenia Fouriera.
Zasady posługiwania się przekształceniem Laplace’a do analizy systemów dyna-
micznych są analogiczne do tych związanych z przekształceniem Fouriera. Wobec te-
go, schemat przetwarzania z rys. 3.2 można przenieść do postaci, jak na rys. 3.3.
∫
−
=
t
t
g
u
t
y
0
d
)
(
)
(
)
(
τ
τ
τ
Rys. 3.3. Struktura przetwarzania związana z posługiwaniem się przekształceniem Laplace’a
Widać, że zachodzą tu następujące relacje:
{ }
)
(
)
(
t
u
s
U
L
=
,
{ }
)
(
)
(
t
g
s
G
L
=
,
{ }
)
(
)
(
t
y
s
Y
L
=
.
Ponadto, transformata Laplace’a splotu jest określona następująco:
)
(
)
(
)
(
)
)
(
)
(
)
(
)
(
0
0
)
(
0
0
s
Y
s
G
s
U
t-
t
g
u
t
t
g
u
t
t
s
s
st
t
=
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
∫
∫
∫ ∫
∞
−
−
−
∞
−
τ
τ
τ
τ
τ
τ
τ
τ
τ
d(
e
d
e
d
e
d
L
L
(3.24)
co staje się oczywiste, gdy w drugiej całce dokonamy podstawienia: t – τ = x.
Na podstawie (3.24) widać, że transmitancja układu jest określona podobnie, jak w
przypadku transformaty Fouriera:

12
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
{ }
)
(
)
(
)
(
)
(
t
g
s
U
s
Y
s
G
L
=
=
(3.25)
Charakterystykę widmową transformowanej funkcji można uzyskać przez podsta-
wienie
σ
= 0 do jej transformaty Laplace’a. Na przykład:
{ }
)
(
)
(
)
(
)
(
0
ω
ω
σ
σ
j
j
G
G
t
g
s
G
=
+
→
=
=
L
(3.26)
przy czym, G(j
ω
) nie musi być transformatą Fouriera funkcji g(t) (może ona nie speł-
niać warunku istnienia transformaty Fouriera).
Transformaty Laplace’a funkcji można określić bezpośrednio na podstawie prze-
kształcenia (3.21), posługując się także właściwościami przekształcenia (Tabela 3.3).
Poniżej podane są niektóre przykłady.
{ } {}
s
t
t
st
1
1
)
(
1
0
∫
∞
−
=
=
=
d
e
L
L
– co wynika stąd, że dla t
≥ 0,
∫
∫
∞
−
∞
−
⋅
=
0
0
1
)
(
1
t
t
t
st
st
d
e
d
e
.
{ }
a
s
t
t
t
a
s
st
at
at
+
=
=
=
∫
∫
∞
+
−
∞
−
−
−
1
d
e
d
e
e
e
0
)
(
0
L
.
{
}
(
)
2
2
0
2
2
0
cos
sin
e
1
d
e
sin
sin
s
t
t
s
s
t
t
t
st
st
+
=
+
+
−
=
=
∞
−
∞
−
∫
ω
ω
ω
ω
ω
ω
ω
ω
L
.
Do obliczenia transformaty funkcji cos
ω
t można się posłużyć zależnością:
2
e
e
-j
j
t
t
t
ω
ω
ω
+
=
cos
, zatem:
{
}
{ }
{ }
2
2
)
(
2
1
)
(
2
1
2
1
2
1
cos
s
s
t
s
t
s
t
t
t
+
=
+
+
−
=
+
=
ω
ω
ω
ω
ω
ω
j
j
e
e
j
-
j
L
L
L
.
{
}
2
2
)
(
sin
a
s
t
at
+
+
=
−
ω
ω
ω
e
L
– na podstawie twierdzenia o przesunięciu zespolonym.
{ }
{ }
2
)
(
1
1
a
s
a
s
s
s
t
at
at
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
−
=
−
−
d
d
e
d
d
e
L
L
.
{
}
{
}
(
)
2
2
2
2
2
2
2
cos
cos
ω
ω
ω
ω
ω
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
−
=
s
s
s
s
s
t
s
t
t
d
d
d
d L
L
.
{ }
1
1
lim
)
(
1
)
(
1
lim
)
(
0
0
=
−
=
⎭
⎬
⎫
⎩
⎨
⎧
−
−
=
−
→
→
sa
e
a
a
t
t
t
sa
a
a
L
L
δ
– stosowana jest tu definicja funkcji
impulsowej jako impulsu o szerokości a i amplitudzie 1/a, przy czym a
→ 0 (patrz
rys. 2.5). Impuls ten jest formowany z różnicy dwóch skoków jednostkowych, z któ-
rych drugi jest opóźniony o czas a. Transformaty Laplace’a niektórych funkcji są
przedstawione w Tabeli 3.4.
3.2. Przekształcenie Laplace’a
13
Tabela 3.3. Podstawowe twierdzenia i właściwości przekształcenia Laplace’a
liniowość:
{
}
{ }
{ }
)
(
)
(
)
(
)
(
t
q
t
p
t
q
t
p
L
L
L
β
α
β
α
+
=
+
oraz:
{
}
{ }
{ }
)
(
)
(
)
(
)
(
1
1
1
t
q
t
p
t
q
t
p
-
-
-
L
L
L
β
α
β
α
+
=
+
przesunięcie w dziedzinie czasu:
{
}
τ
τ
s
e
s
F
t
f
−
=
−
)
(
)
(
L
przesunięcie w dziedzinie zespolonej:
{
}
(
)
a
s
F
e
t
f
at
−
=
)
(
L
skalowanie:
{
}
⎟
⎠
⎞
⎜
⎝
⎛
=
a
s
F
a
at
f
1
)
(
L
różniczkowanie po czasie:
{ }
( )
)
0
(
)
(
'
f
s
sF
t
f
−
=
L
( )
1
1
'
2
1
)
0
(
...
)
0
(
)
0
(
)
(
−
−
−
−
−
−
−
−
=
⎭
⎬
⎫
⎩
⎨
⎧
k
k
k
k
k
k
k
t
f
f
s
f
s
s
F
s
t
t
f
d
d
d
d
L
różniczkowanie w dziedzinie zespolonej:
{
}
( )
s
s
F
t
f
t
d
d
−
=
⋅
)
(
L
{
}
( )
n
n
n
n
s
s
F
-
t
f
t
d
d
)
1
(
)
(
=
⋅
L
całkowanie w czasie:
( )
s
s
F
f
t
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
∫
0
)
(
τ
τ
d
L
całkowanie w dziedzinie zespolonej:
( )
∫
∞
=
⎭
⎬
⎫
⎩
⎨
⎧
0
)
(
s
s
F
t
t
f
d
L
splot:
{
}
( ) ( )
s
G
s
F
t
g
f
t
g
t
f
t
⋅
=
⎪⎭
⎪
⎬
⎫
⎪⎩
⎪
⎨
⎧
−
=
⊗
∫
0
)
(
)
(
)
(
)
(
τ
τ
τ
d
L
L
mnożenie
{
}
( ) ( )
s
G
s
F
s
G
F
t
g
t
f
⊗
=
−
=
⋅
∫
∞
+
∞
−
j
j
d
j
ξ
ξ
ξ
ξ
ξ
π
)
(
)
(
2
1
)
(
)
(
L
transmitancja:
( ) { } ( )
( )
s
U
s
Y
t
g
s
G
=
=
)
(
L
wartości graniczne:
)
(
lim
)
(
lim
0
s
sF
t
f
s
t
∞
→
→
=
)
(
lim
)
(
lim
0
s
sF
t
f
s
t
→
∞
→
=

14
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
Tabela 3.4. Transformaty Laplace’a wybranych funkcji
f(t)
F(s) Uwagi
)
(t
δ
1
−∞
>
σ
1(t)
s
1
0
>
σ
at
−
e
a
s
+
1
a
−
>
σ
at
t
−
e
2
)
(
1
a
s
+
a
−
>
σ
at
−
− e
1
)
(
a
s
s
a
+
a
−
>
σ
t
ω
sin
2
2
s
+
ω
ω
0
>
σ
t
ω
cos
2
2
s
s
+
ω
0
>
σ
t
t
ω
sin
(
)
2
2
2
2
s
s
+
ω
ω
0
>
σ
t
t
ω
cos
(
)
2
2
2
2
2
s
s
+
−
ω
ω
0
>
σ
k
t
1
1
)!
1
(
+
−
k
s
k
0
>
σ
t
at
ω
sin
e
−
2
2
)
(
ω
ω
+
+ a
s
a
−
>
σ
t
at
ω
cos
e
−
2
2
)
(
ω
+
+
+
a
s
a
s
a
−
>
σ
3.2.2. Transmitancja
układu
Zgodnie z (3.25) transmitancję operatorową G(s) układu można wyznaczyć na pod-
stawie znanych transformat wymuszenia U(s) i odpowiedzi Y(s) lub jako transformatę
funkcji wagi g(t). Można także posłużyć się rozwiązaniem równania różniczkowego w
dziedzinie s
5
, przy czym zakłada się, że w transmitancji (funkcji przejścia) przyjmuje
się zerowe warunki początkowe – inaczej niż w przypadku rozwiązywania równań
różniczkowych.
5
W literaturze można spotkać różne określenia: dziedzina (przestrzeń) Laplace’a, dziedzina
zespolona, dziedzina s.
3.2. Przekształcenie Laplace’a
15
Przykład 3.6.
Określić transmitancję układu analizowanego w przykładzie 2.2 i zbadać
jego charakterystyki częstotliwościowe.
Rozpatrywany układ jest opisany następującym równaniem różniczkowym:
t
t
y
t
y
t
y
+
=
+
+
3
2
2
d
d
2
d
d
.
Wymuszeniem jest więc funkcja:
t
t
t
u
+
=
3
)
(
.
Poddając obie strony równania różniczkowego transformacji Laplace’a, otrzymamy:
)
(
1
2
)
(
)
(
2
)
(
2
4
2
s
U
s
s
s
Y
s
sY
s
Y
s
=
+
=
+
+
W kolejnych krokach obliczamy transformatę sygnału wyjściowego:
4
2
2
2
)
1
2
)(
(
s
s
s
s
s
Y
+
=
+
+
,
)
1
2
(
2
)
(
2
4
2
+
+
+
=
s
s
s
s
s
Y
.
A zatem:
1
2
1
2
)
1
2
(
2
)
(
)
(
)
(
2
2
4
2
4
2
+
+
=
+
⋅
+
+
+
=
=
s
s
s
s
s
s
s
s
s
U
s
Y
s
G
.
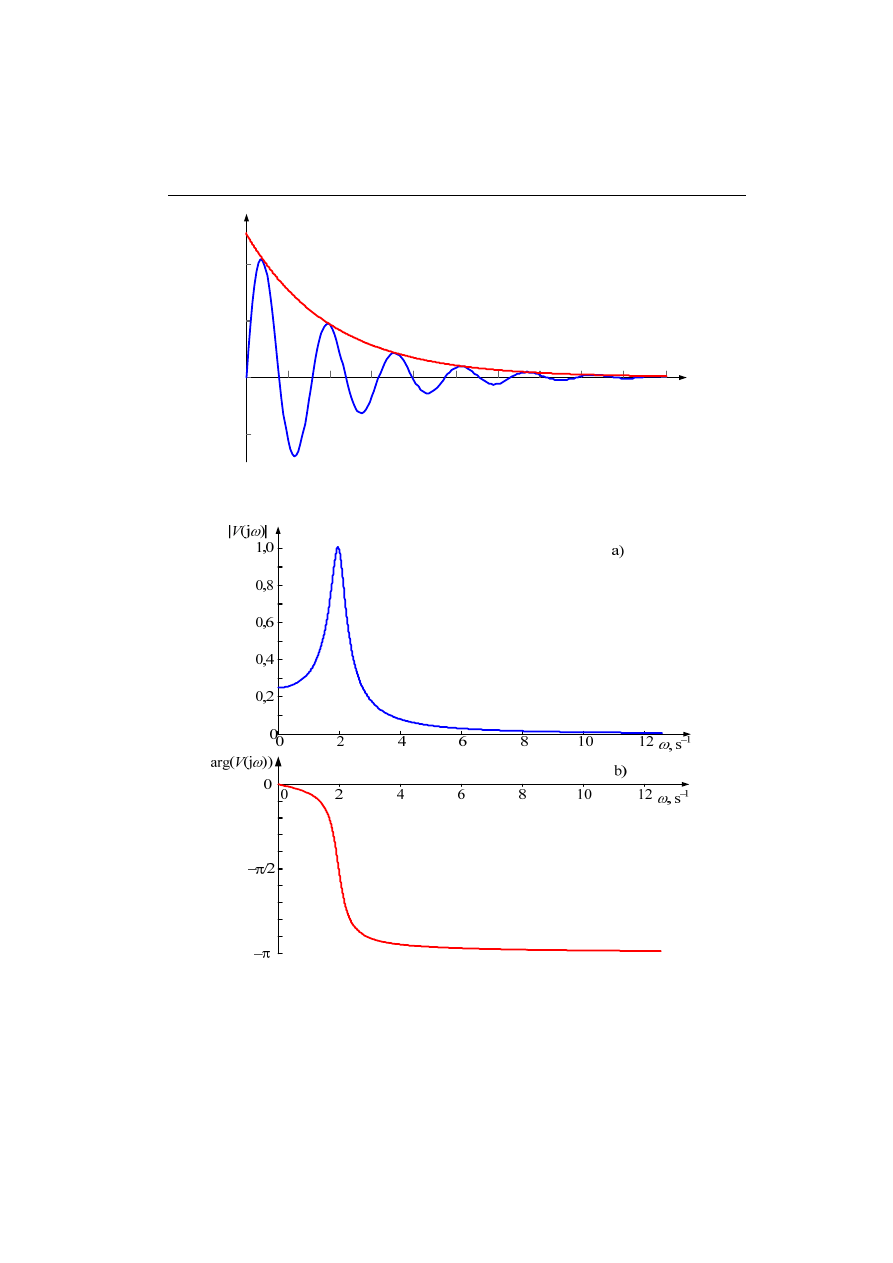
Przechodząc do analizy charakterystyki częstotliwościowej, określamy transmitancję widmową
układu:
)
(
j
2
2
2
2
j
2
e
)
j
(
1
2
j
1
1
2
j
1
1
1
2
1
)
j
(
ω
ϕ
ω
ω
ω
ω
ω
ω
ω
ω
ω
G
s
s
G
s
=
+
−
+
−
=
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
=
,
gdzie:
2
1
1
)
j
(
ω
ω
+
=
G
,
(
)
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
=
2
1
2
arctg
)
j
(
arg
)
(
ω
ω
ω
ω
ϕ
G
.
Wykresy obu charakterystyk widmowych transmitancji: amplitudy i fazy, są pokazane na rys.
3.4. Można zauważyć, że maksymalna wartość amplitudy |G(j
ω)| = 1 odpowiada zerowej pul-
sacji, natomiast ekstrema charakterystyki fazowej występują dla
ω = ±1, co łatwo sprawdzić
analizując funkcję
ϕ(ω). Dla tych wartości pulsacji, odpowiednio: ϕ(ω) = ±π/4.
W ogólnym przypadku, gdy znane jest równanie różniczkowe opisujące dynamikę
układu, jego transmitancja ma postać funkcji wymiernej:
)
(
...
...
)
(
)
(
0
1
1
1
0
1
1
1
s
G
a
s
a
s
a
s
b
s
b
s
b
s
b
s
U
s
Y
n
n
n
m
m
m
m
=
+
+
+
+
+
+
+
+
=
−
−
−
−
, m
≤ n, (3.27)
co ma miejsce wówczas, gdy dynamika układu jest opisana równaniem różniczkowym
(3.19).
Zauważmy, że ze względu na jednoznaczność prostego i odwrotnego przekształce-
nia Laplace’a, transmitancja G(s) zawiera pełną informację o właściwościach układu.

16
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
- /10
-8
-6
-4
-2
0
2
4
6
8
, 1/s
0
0,2
0,4
0,6
0,8
|G(j )|
-8
-6
-4
-2
0
2
4
6
8
, 1/s
0
- /5
/5
/10
a)
b)
m
Rys. 3.4. Przebieg amplitudy a) i fazy b) widmowej transmitancji badanego układu
Przykład 3.7.
Funkcja wagi określona w przykładzie 2.4 ma następującą postać:
)
(
1
)
(
/
t
e
t
g
T
t
−
=
. Wyznaczyć jego transmitancję.
Transmitancję wyznaczamy według zależności:
{ }
{ }
1
/
1
1
)
(
)
(
/
+
=
+
=
=
=
−
sT
T
T
s
e
t
g
s
G
T
t
L
L
.
Mnożenie przez funkcję skoku jednostkowego w wyrażeniu na funkcję wagi nie zmienia trans-
formaty jednostronnej.
Transmitancję badanego układu można także określić na podstawie równania różniczkowego.
Równanie jednorodne jest następujące (przykład 2.4):
0
1
=
+ y
T
t
y
d
d
.

3.2. Przekształcenie Laplace’a
17
Załóżmy, że w charakterze wymuszenia występuje funkcja:
t
t
t
u
ω
cos
)
(
1
)
(
=
. Zatem pełne
równanie ma postać:
t
y
T
t
y
ω
cos
1
d
d
=
+
(przy stosowaniu przekształcenia jednostronnego funkcję 1(t) można pomi-
nąć.
Obustronne przekształcenie powyższego równania daje:
2
2
)
(
1
)
(
s
s
s
Y
T
s
sY
+
=
+
ω
, przy czym:
2
2
)
(
s
s
s
U
+
=
ω
.
Transformata odpowiedzi jest zatem następująca:
(
)
(
)
1
)
(
2
2
+
+
=
sT
s
sT
s
Y
ω
(przy zerowych warunkach początkowych).
Ostatecznie, transmitancję obliczamy według następującej zależności:
(
)
(
)
(
)
1
1
)
(
)
(
)
(
2
2
2
2
+
=
+
⋅
+
+
=
=
sT
T
s
s
sT
s
sT
s
U
s
Y
s
G
ω
ω
.
3.2.3. Transformata
odwrotna
Transformata odwrotna w interesującym nas przypadku analizy systemów jest funkcją
czasu, która formalnie może być określona na podstawie danej transformaty Laplace’a
zgodnie z (3.22). Należy zwrócić uwagę na to, że całka definiująca przekształcenie
odwrotne odnosi się do funkcji zespolonych i sprawne posługiwanie się tym narzę-
dziem wymaga znajomości zaawansowanych metod dotyczących tych funkcji. W
większości praktycznych przypadków wystarczy posługiwać się podstawowymi wła-
ściwościami przekształcenia i tablicami transformat typowych funkcji.
a)
Rozkład transformaty na ułamki
Załóżmy, że transformata funkcji f(t) ma postać jak (3.27), gdzie wielomian mianow-
nika M(s) został przedstawiony w formie iloczynowej:
)
)...(
)(
(
)
(
)
(
)
(
)
(
2
1
n
s
s
s
s
s
s
s
L
s
M
s
L
s
F
−
−
−
=
=
, (3.28)
przy czym:
0
1
1
1
...
)
(
b
s
b
s
b
s
b
s
L
m
m
m
m
+
+
+
+
=
−
−
, m
≤ n.
Prawa strona (3.28) może być rozłożona na sumę prostych transformat w formie
ułamków o postaci:
t
s
k
k
k
k
e
A
s
s
A
↔
−
,
których transformaty odwrotne są znane. Szczegóły obliczeń zależą od krotności po-
szczególnych pierwiastków wielomianu mianownika (3.28).
1. Wszystkie pierwiastki są jednokrotne (różne). Wówczas:

18
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
n
n
s
s
A
s
s
A
s
s
A
s
M
s
L
−
+
+
−
+
−
=
...
)
(
)
(
2
2
1
1
(3.29)
Współczynniki A
1
, A
2
, …, A
n
można określić z warunku równowagi wielomianu
liczników obu stron (3.29). Jest to ekwiwalentne następującej zależności:
(
)
k
k
s
s
s
s
k
k
s
M
s
L
s
M
s
L
s
s
A
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
)
(
)
(
)
(
)
(
'
(3.30)
Przykład 3.8.
Określić funkcję czasu, której transformata Laplace’a jest następująca:
s
s
s
s
s
F
3
4
2
)
(
2
3
+
+
+
=
Obliczając pierwiastki mianownika transformaty F(s) otrzymamy:
(
)
( )(
)
3
1
3
4
3
4
)
(
2
2
3
+
+
=
+
+
=
+
+
=
s
s
s
s
s
s
s
s
s
s
M
, czyli: s
1
= 0, s
2
= –1, s
3
= –3.
Do obliczenia współczynników rozkładu stosujemy regułę (3.30):
( )(
)
( )(
)
3
2
3
1
2
3
1
2
0
0
1
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
=
=
=
s
s
s
s
s
s
s
s
s
s
A
( )(
)
(
)
2
1
3
2
3
1
2
)
1
(
1
1
2
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
−
=
−
=
s
s
s
s
s
s
s
s
s
s
A
( )(
)
( )
6
1
1
2
3
1
2
)
3
(
3
3
3
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
−
=
−
=
s
s
s
s
s
s
s
s
s
s
A
Wzorując się na (3.29), obliczamy:
3
1
6
1
1
1
2
1
1
3
2
)
(
+
⋅
−
+
⋅
−
⋅
=
s
s
s
s
F
.
Dla tych prostych składników transformaty otrzymujemy:
t
t
s
s
s
t
f
3
1
e
6
1
e
2
1
3
2
3
1
6
1
1
1
2
1
1
3
2
)
(
−
−
−
−
−
=
⎭
⎬
⎫
⎩
⎨
⎧
+
⋅
−
+
⋅
−
⋅
= L
Jeśli pierwiastki mianownika M(s) transmitancji są zespolone, to zawsze występują
pary pierwiastków wzajemnie sprzężonych: s
k
= a + jb oraz s
k
+1
= a – jb. Zasada po-
stępowania przy obliczaniu odpowiednich współczynników rozkładu jest podobna do
tej przedstawionej powyżej, z tym, że w ogólnym przypadku otrzymujemy zespolone
współczynniki.
Przykład 3.9.
Określić funkcję czasu, której transformata Laplace’a jest następująca:
(
)
)
3
(
5
2
1
)
(
2
+
+
+
+
=
s
s
s
s
s
F
Transformatę tę można przedstawić w następującej formie:
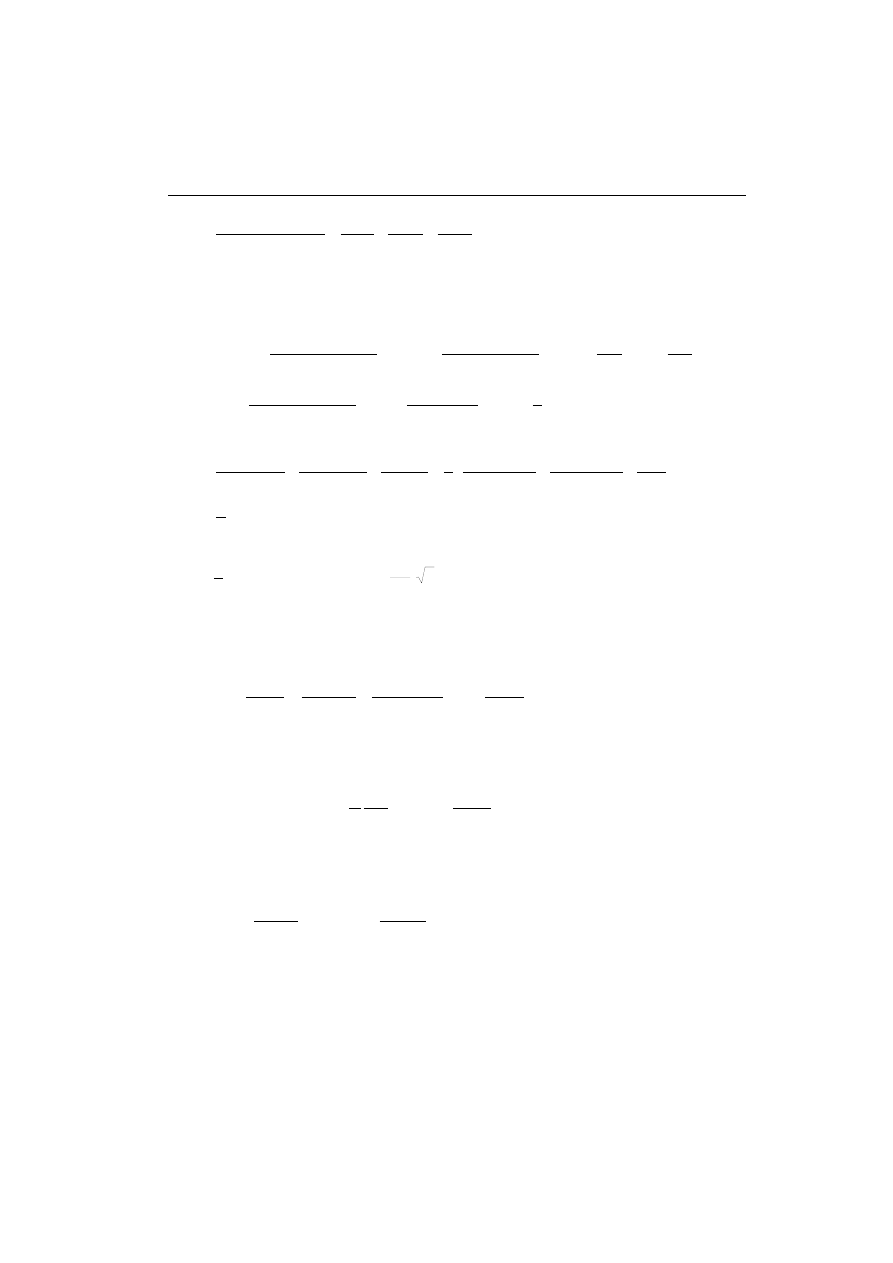
3.2. Przekształcenie Laplace’a
19
(
)
)
3
(
5
2
1
)
(
2
+
+
+
+
=
s
s
s
s
s
F
=
3
3
2
2
1
1
s
s
A
s
s
A
s
s
A
−
+
−
+
−
Obliczając pierwiastki mianownika transformaty F(s) otrzymamy:
s
1
= –1 + j2, s
2
= –1 – j2, s
3
= –3.
Współczynniki obliczamy według (3.30), przy czym A
1
, A
2
są liczbami zespolonymi sprzężo-
nymi, więc wystarczy obliczyć jedną z nich. Zatem:
(
)
(
)
(
)
(
)(
)
8
1
3
2
1
1
3
5
2
1
2
1
2
1
2
1
2
1
j
j
j
j
j
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
−
+
=
+
−
=
+
−
=
s
s
s
s
s
s
s
s
s
s
A
,
8
1
2
j
−
=
A
,
(
)
(
)
(
)
4
1
5
2
1
3
5
2
1
)
3
(
3
2
3
2
3
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
+
=
−
=
−
=
s
s
s
s
s
s
s
s
s
s
A
.
Po podstawieniu otrzymamy:
(
) (
)
(
) (
)
{
} {
} { }
(
)
t
t
t
t
t
s
s
s
s
s
s
s
s
F
3
2
2
2
sin
2
cos
4
1
3
1
4
)
1
(
2
4
)
1
(
1
4
1
)
3
(
4
1
2
1
8
1
2
1
8
1
)
(
−
−
−
−
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
+
+
+
+
+
+
=
+
−
−
+
−
+
+
+
+
=
e
e
e
j
j
j
j
L
L
L
Ostatecznie, funkcja względem czasu jest następująca:
(
)
(
)
(
)
t
t
t
t
t
t
t
t
f
2
3
4
/
2
sin
2
4
)
2
sin
2
(cos
4
1
)
(
−
−
−
−
−
+
=
−
+
=
e
π
e
e
e
.
2. Niektóre pierwiastki są wielokrotne.
Jeśli pierwiastek s
k
w (3.29) jest l-krotny, to związane z nim składniki (ułamki)
rozkładu są następujące:
(
) (
)
{
}
ułamki
pozostałe
+
−
+
+
−
+
−
=
−
−
k
k
l
k
l
k
l
k
kl
s
s
A
s
s
A
s
s
A
s
M
s
L
1
)
1
(
)
1
(
...
)
(
)
(
(3.31)
Ogólna formuła na obliczanie współczynników rozkładu w przypadku wielokrot-
nych pierwiastków mianownika transformaty jest następująca [Tripathi]:
(
)
k
s
s
l
k
r
r
r
l
k
s
M
s
L
s
s
s
r
A
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
−
=
)
(
)
(
!
1
)
(
d
d
, r = 0, 1, ... l–1 (3.32)
Ułamkom związanym z wielokrotnym pierwiastkiem wielomianu M(s) mianowni-
ka transformaty (3.31) odpowiadają następujące składniki funkcji czasu:
{
}
składniki
pozostałe
e
e
e
+
+
+
−
+
−
=
−
−
−
t
s
k
t
s
l
l
k
t
s
l
kl
k
k
k
A
l
t
A
l
t
A
t
f
1
2
)
1
(
1
...
)!
2
(
)!
1
(
)
(
(3.33)
co wynika z twierdzenia o różniczkowaniu w dziedzinie zespolonej.

20
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
Przykład 3.10.
Określić funkcję czasu, której transformata Laplace’a jest następująca:
(
)
)
3
(
2
1
)
(
3
+
+
+
=
s
s
s
s
F
.
Pierwiastki mianownika transformaty: s
1
= –2, l-krotny, l = 3 oraz s
2
= –3. Poszukujemy
współczynników następującego rozkładu:
(
)
)
3
(
2
1
)
(
3
+
+
+
=
s
s
s
s
F
=
(
) (
)
3
2
2
2
2
11
2
12
3
13
+
+
+
+
+
+
+
s
A
s
A
s
A
s
A
Posługując się (3.32) określamy współczynniki związane z pierwiastkiem wielokrotnym:
(
) ( )
2
3
3
2
2
13
)
3
(
2
1
2
2
1
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
s
s
s
s
s
s
A
d
d
=
2
)
3
(
2
)
3
(
1
2
1
2
3
2
2
2
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
−
=
−
=
s
s
s
s
s
s
d
d
,
(
) ( )
2
3
3
12
)
3
(
2
1
2
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
s
s
s
s
s
s
A
d
d
=
2
)
3
(
2
)
3
(
1
2
2
2
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
−
=
−
=
s
s
s
s
s
s
d
d
,
(
) ( )
2
3
3
11
)
3
(
2
1
2
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
s
s
s
s
s
A
=
1
)
3
(
1
2
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
−
=
s
s
s
,
(
)( )
3
3
2
)
3
(
2
1
3
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
s
s
s
s
s
A
=
2
)
2
(
1
3
3
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
−
=
s
s
s
.
Zatem, otrzymujemy:
(
) (
)
3
2
2
1
2
2
2
2
)
(
2
3
+
+
+
−
+
+
+
+
−
=
s
s
s
s
s
F
,
co daje następującą funkcję czasu:
(
)
(
)
t
t
t
t
t
t
s
s
s
s
t
f
3
2
2
2
2
1
1
2
1
3
1
e
2
e
e
2
e
3
2
2
1
2
2
2
2
)
(
−
−
−
−
−
−
−
−
+
−
−
−
=
⎭
⎬
⎫
⎩
⎨
⎧
+
+
⎭
⎬
⎫
⎩
⎨
⎧
+
−
+
⎭
⎬
⎫
⎩
⎨
⎧
+
+
⎭
⎬
⎫
⎩
⎨
⎧
+
−
=
L
L
L
L
.
W przypadku dwóch pierwszych składników ma zastosowanie następujące twierdzenie:
{
}
( )
n
n
n
n
s
s
F
-
t
f
t
d
d
)
1
(
)
(
=
⋅
L
, gdzie
2
1
)
(
+
=
s
s
F
.
Przedstawione metody mają zastosowanie do transformat, które są przedstawione
w postaci funkcji wymiernych. Pozwalają one określić transformaty odwrotne szero-
kiej klasy funkcji. W ten sposób można rozwiązywać równania różniczkowe lub obli-
czać odpowiedzi układów zgodnie ze schematem z rys. 3.3. Ilustrują to kolejne przy-
kłady.
Przykład 3.11.
Określić odpowiedź układu mechanicznego opisanego równaniem róż-
niczkowym (2.4):
0
)
(
d
)
(
d
d
)
(
d
2
2
=
+
+
t
Kv
t
t
v
D
t
t
v
M

3.2. Przekształcenie Laplace’a
21
przy warunkach początkowych: v(0) = 0, v
’
(0) = 1. Przyjąć następujące
parametry układu: K = 4, D = 0,5, M = 1 (patrz przykład 2.8).
Zauważmy, że powyższe równanie różniczkowe układu z rys. 2.1b powstało z różniczkowania
równania ruchu tego układu:
∫
+
+
=
t
t
v
K
t
t
v
M
t
Dv
t
f
d
d
d
)
(
)
(
)
(
)
(
.
Początkowa wartość pierwszej pochodnej prędkości ma wówczas fizyczną wartość przyśpie-
szenia: v
’
(0) = f(0)/M, gdzie M jest masą, natomiast f(0) jest siłą początkową.
Po podstawieniu podanych parametrów, otrzymamy:
0
)
(
4
)
(
5
,
0
)
(
2
=
+
+
t
v
t
t
v
t
t
v
d
d
d
d
2
, v(0) = 0, v
’
(0) = 1.
Stosując jednostronne przekształcenie Laplace’a uzyskujemy:
(
)
0
)
(
4
)
0
(
)
(
5
,
0
)
0
(
)
0
(
)
(
'
2
=
+
−
+
−
−
s
V
v
s
sY
v
sv
s
V
s
,
co po uporządkowaniu prowadzi do wyrażenia:
(
)
)
5
,
0
)(
0
(
)
0
(
4
5
,
0
)
(
'
2
+
+
=
+
+
s
v
v
s
s
s
V
.
Zauważmy, że warunki początkowe pełnią tu podobną funkcję, jak wymuszenia. W tym przy-
padku transformatą wymuszenia jest wartość v
’
(0) = 1. Po podstawieniu ich wartości, mamy
następującą transformatę odpowiedzi:
)
(
)
(
4
5
,
0
1
)
(
2
s
U
s
G
s
s
s
V
=
+
+
=
,
1
)
(
=
s
U
.
W celu określenia odpowiedzi czasowej należy odpowiednio przekształcić transformatę V(s).
Widać, że można ją ‘dopasować’ do transmitancji wykładniczo tłumionej sinusoidy:
t
at
ω
sin
e
−
↔
2
0
2
0
)
(
ω
ω
+
+ a
s
, skąd widać kierunek przekształceń:
2
2
2
2
2
25
,
0
4
)
25
,
0
(
25
,
0
4
4
5
,
0
1
)
(
⎟
⎠
⎞
⎜
⎝
⎛
−
+
+
−
⋅
=
+
+
=
s
A
s
s
s
V
, przy czym:
1
25
,
0
4
2
=
−
⋅
A
.
Otrzymujemy stąd:
t
A
t
v
at
ω
sin
e
)
(
−
=
,
gdzie:
5039
,
0
63
4
≈
=
A
, a = 0,25,
984
,
1
1
0
≈
=
A
ω
s
–1
.
Można zauważyć, że przebieg odpowiedzi istotnie się zmieni, jeśli także wartość początkowa
prędkości v(0) będzie różna od zera.
Uzyskane przebiegi są prezentowane na rys. 3.5. Funkcja Ae
–at
tworzy obwiednię odpowiedzi
układu. Zauważmy, że ponieważ
1
)
(
=
s
U
, to transmitancja układu:
)
(
)
(
s
V
s
G
=
Charaktery-
styki częstotliwościowe układu można zatem określić badając transmitancję widmową:
ω
ω
ω
ω
ω
ω
ω
5
,
0
4
1
4
5
,
0
)
(
1
4
5
,
0
1
)
(
)
(
2
2
2
j
j
j
j
j
j
+
−
=
+
+
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
=
=
=
s
s
s
V
G
.
Charakterystyki częstotliwościowe są pokazane na rys. 3.6.
22
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
0
2
4
6
8
10
12
14
16
18
t, s
–0,2
0
0,2
0,4
Ae
–at
v(t)
Rys. 3.5. Przebieg odpowiedzi v(t) oraz jej obwiedni
Rys. 3.6. Charakterystyka amplitudowa (a) i fazowa (b) analizowanego układu
3.2. Przekształcenie Laplace’a
23
Można zauważyć, że charakterystyka amplitudowa ma silnie zaznaczone maksimum, które wy-
stępuje dla pulsacji rezonansowej
ω
r
, zbliżonej do pulsacji drgań
ω
0
występujących w odpo-
wiedzi układu. Pulsację rezonansową można obliczyć analizując moduł transmitancji:
(
)
2
2
2
)
5
,
0
(
4
1
)
(
ω
ω
ω
+
−
=
j
G
.
Rozwiązując równanie:
0
)
(
=
ω
ω
j
d
d
G
, otrzymujemy pulsację rezonansową:
ω = ω
r
≈ 1,968,
która tylko nieznacznie różni się od pulsacji
ω
0
oscylacji z rys. 3.5. Problem ten jest dyskuto-
wany w przykładzie 4..
b)
Metoda residuów
Przed omówieniem tej metody przypomnimy podstawowe terminy odnoszące się do
funkcji zmiennej zespolonej. Pochodna funkcji zespolonej w punkcie z
0
jest definio-
wana następująco:
0
0
0
'
)
(
)
(
lim
)
(
)
(
0
0
z
z
z
f
z
f
z
f
z
z
f
z
z
z
z
−
−
=
=
→
=
d
d
(3.34)
Jeśli granica ta istnieje, to mówimy, że funkcja f(z) jest różniczkowalna w sensie ze-
spolonym w punkcie z
0
.
Funkcja zespolona jest holomorficzna w obszarze liczb zespolonych, jeśli jest róż-
niczkowalna w sensie zespolonym w każdym punkcie z
0
obszaru wraz z jego pewnym
otoczeniem
6
. Każda funkcja holomorficzna jest funkcją analityczną w obszarze liczb
zespolonych, co oznacza, że spełnia warunki Cauchy’ego
7
-Riemanna
8
[Leja]:
,
)
,
(
)
,
(
,
)
,
(
)
,
(
x
y
x
v
y
y
x
u
y
y
x
v
x
y
x
u
∂
∂
=
∂
∂
−
∂
∂
=
∂
∂
(3.35)
przy czym:
)
,
(
)
,
(
)
(
)
(
y
x
v
y
x
u
y
x
f
z
f
j
j
+
=
+
=
.
Zależności (3.35) definiują warunek konieczny różniczkowalności funkcji f(z) (ist-
nienia jej pochodnej). Punkty w obszarze liczb zespolonych, w których funkcja f(z)
przestaje być holomorficzna nazywa się punktami osobliwymi funkcji.
6
Funkcja może mieć pochodną, w punkcie z
0
i nie być holomorficzną w tym punkcie, jeśli
nie ma pochodnej w żadnym otoczeniu punktu z
0
.
7
Augustin Louis Cauchy (1789 – 1857), matematyk francuski charakteryzujący się wielką
precyzją i ścisłością formułowania i dowodzenia twierdzeń. Prace z zakresu analizy matema-
tycxznej.
8
Georg Friedrich Bernhard Riemann (1826 – 1866), matematyk niemiecki, twórca wielo-
wymiarowej geometrii, która jest podstawą ogólnej teorii względności.

24
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
Funkcja meromorficzna jest określona jako iloraz funkcji holomorficznych f
1
(z),
f
2
(z) w całym obszarze liczb zespolonych:
)
(
)
(
)
(
2
1
z
f
z
f
z
f
=
, (3.36)
przy czym, f
2
(z) nie może być stale równa zero. Zbiór biegunów funkcji f(z) jest zbio-
rem zer funkcji f
2
(z). Funkcja meromorficzna w skończonym obszarze nie ma innych
osobliwości oprócz biegunów (wszystkie osobliwości są biegunami). Przykładami
funkcji meromorficznych są funkcje wymierne, czy ilorazy funkcji trygonometrycz-
nych, jak sinz/cosz lub cosz/sinz.
Całkowa formuła Cauchy’ego podaje sposób obliczania całki funkcji holomorficz-
nej w dowolnym punkcie z
0
objętym przez dowolną krzywą C (całka krzywoliniowa)
wewnątrz której i na jej granicach funkcja jest holomorficzna []:
∫
−
=
C
z
z
z
z
f
z
f
d
πj
0
0
)
(
2
1
)
(
(3.37)
Residuum (pozostałość) funkcji zespolonej f(z) w punkcie z
0
jest liczbą, której war-
tość określa wynik całkowania tej funkcji wzdłuż krzywej C w kierunku dodatnim
(odwrotnym do wskazówek zegara), otaczającej obszar, w którym znajduje się punkt
z
0
i żaden inny punkt osobliwy:
∫
=
C
z
z
z
f
z
f
d
πj
res
)
(
2
1
)
(
0
(3.38)
Z twierdzeń analizy zespolonej wynika, że całka ta nie zależy od rodzaju wybranej
drogi całkowania (wybranej krzywej C). Ponadto, jeśli krzywa zamknięta C obejmuje
jeden raz (w wyniku jednego okrążenia) n punktów osobliwych: z
1
, z
2
, ..., z
n
funkcji
f(z), to:
∑
∫
=
=
n
i
z
C
z
f
z
z
f
i
1
)
(
)
(
2
1
res
d
πj
(3.39)
Jeżeli z
0
jest pojedynczym biegunem funkcji f(z), to residuum w tym punkcie moż-
na obliczyć następująco:
)
(
)
(
lim
)
(
0
0
0
z
f
z
z
z
f
z
z
z
−
=
→
res
(3.40)
Gdy punkt z
0
jest l-krotnym biegunem funkcji f(z), to residuum w tym punkcie
określa następująca formuła:
)
(
)
(
lim
)!
1
(
1
)
(
0
1
)
1
(
0
0
z
f
z
z
z
l
z
f
l
l
l
z
z
z
−
−
=
−
−
→
d
d
res
(3.41)
3.2. Przekształcenie Laplace’a
25
Przeniesienie tych właściwości zespolonych funkcji w obszarze zmiennych zespo-
lonych na obliczanie odwrotnej transformaty Laplace’a (3.22) wymaga odpowiednie-
go zdefiniowania krzywej obejmującej wszystkie punkty osobliwe całkowanej funkcji,
tak aby można było zastosować zależność (3.39). Zauważmy, że w tym przypadku
funkcja podcałkowa jest utworzona przez iloczyn: F
1
(s) = F(s)e
st
, a zatem należy obli-
czyć całkę:
∫
∫
∞
+
∞
−
∞
+
∞
−
=
=
j
j
j
j
d
j
d
e
j
0
0
0
0
)
(
2
1
)
(
2
1
)
(
1
σ
σ
σ
σ
π
π
s
s
F
s
s
F
t
f
st
, gdzie:
ω
σ
j
+
=
s
. (3.42)
Wielkość
σ
0
określa granicę zbieżności całki w przekształceniu prostym, rozdziela-
jąc płaszczyznę liczb zespolonych równolegle do osi urojonej (rys. 3.7)
j
0
0
R =
|s|
R = |s|
C
1
C
2
A
B
Rys. 3.7. Kontury całkowania dla odwrotnego przekształcenia Laplace’a
Obliczanie całki liniowej w granicach nieskończonych wzdłuż osi wyznaczonej
przez parametr
σ
0
można zastąpić przez obliczanie całki krzywoliniowej wzdłuż okrę-
gu o promieniu R
→ ∞.
Kolejny pomysł zmierzający do zastosowania w tej procedurze właściwości funkcji
zespolonych polega na rozdzieleniu tego obszaru na dwie części wzdłuż prostej
σ
=
σ
0
. W ten sposób powstają dwa obszary zakreślone, odpowiednio, przez zamknięte
krzywe C
1
oraz C
2
(rys. 3.7). Całka krzywoliniowa obliczana wzdłuż pełnego okręgu
jest równa sumie całek obliczanych oddzielnie dla konturów C
1
oraz C
2
. (całki obli-
czane dla wspólnej części związanej z odcinkiem AB znoszą się ze względu na prze-

26
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
ciwne kierunki całkowania). Zauważamy dalej, że dla t > 0 funkcja podcałkowa F
1
(s)
= F(s)e
st
w (3.42) nie może mieć żadnych punktów osobliwych w obszarze zakreślo-
nym przez krzywą C
2
. Podobnie, dla czasu t < 0 funkcja ta nie ma punktów osobli-
wych w obszarze C
1
. Uwzględniając twierdzenie o residuach można pokazać, że [Le-
ja, Osowski]:
(
)
(
)
⎪
⎪
⎩
⎪⎪
⎨
⎧
<
−
>
=
=
∑
∑
∫
=
=
∞
+
∞
−
2
1
0
0
1
1
,
0
)
(
,
0
)
(
)
(
2
1
)
(
n
i
st
s
n
i
st
s
st
t
s
F
t
s
F
s
s
F
t
f
i
i
dla
e
res
dla
e
res
d
e
j
j
j
σ
σ
π
(3.43)
przy czym, n
1
, n
2
oznaczają liczby punktów osobliwych w obszarach, odpowiednio: C
1
dla t > 0 oraz C
2
dla t < 0.
Jeśli rozważane jest przekształcenie jednostronne Laplace’a, to odwrotne prze-
kształcenie Laplace’a można określić następująco (t > 0):
{ }
(
)
∑
∫
=
−
∞
+
∞
−
=
=
=
n
i
st
s
st
s
F
s
F
L
s
s
F
t
f
i
1
1
)
(
)
(
)
(
2
1
)
(
0
0
e
res
d
e
j
j
j
σ
σ
π
(3.44)
gdzie n jest liczbą punktów osobliwych w obszarze zbieżności całki przekształcenia
prostego.
Dla różnych szczegółowych postaci funkcji F(s) korzysta się z odpowiednich skró-
towych formuł. W szczególności:
• Dla transformaty o postaci:
)
(
)
(
)
(
s
M
s
L
s
F
=
, przy czym M(s) ma pojedyncze zera:
∑
∑
=
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
⎭
⎬
⎫
⎩
⎨
⎧
=
n
i
t
s
i
i
n
i
st
s
i
i
s
M
s
L
s
M
s
L
s
M
s
L
L
t
f
1
'
1
1
)
(
)
(
)
(
)
(
)
(
)
(
)
(
e
e
res
(3.45)
• Jeśli s
i
jest biegunem l-krotnym, to związane z nim residuum jest obliczane nastę-
pująco:
st
l
i
l
l
s
s
st
s
s-s
s
M
s
L
s
l
s
M
s
L
i
i
e
)
(
d
d
(
e
res
)
(
)
(
lim
)!
1
1
)
(
)
(
1
1
−
−
→
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
, (3.46)
• Jeśli funkcję
F(s)
można przedstawić w postaci:
)
(
)
(
)
(
s
sM
s
L
s
F
=
,
przy
czym
M(0)
≠
0, to:
∑
=
−
+
=
⎭
⎬
⎫
⎩
⎨
⎧
=
n
i
t
s
i
i
i
i
s
M
s
s
L
M
L
s
sM
s
L
L
t
f
1
'
1
)
(
)
(
)
0
(
)
0
(
)
(
)
(
)
(
e (3.47)

3.2. Przekształcenie Laplace’a
27
Jeśli F(s) jest funkcją meromorficzną, to n w (3.45) oraz (3.47) może przyjmować
wartość nieskończoną: n =
∞.
Przykład 3.12.
Określić transformatę odwrotną h(t) gdy transformata Laplace’a tej funk-
cji jest następująca:
( )
1
1
)
(
2
+
=
s
s
s
H
.
Przedstawimy trzy sposoby obliczenia funkcji h(t).
1. Funkcję H(s) można przedstawić w postaci:
( )
1
1
1
)
(
2
+
=
s
s
s
H
=
)
(
1
s
G
s
,
( )
1
1
)
(
2
+
=
s
s
G
.
Na podstawie tablicy transformat (Tabela 3.4) widać, że:
{ }
( )
t
s
s
G
t
g
sin
1
1
)
(
)
(
2
1
1
=
⎭
⎬
⎫
⎩
⎨
⎧
+
=
=
−
−
L
L
(
ω = 1).
Wobec tego:
{
}
t
t
g
s
G
s
s
H
t
h
t
t
t
cos
1
cos
sin
)
(
)
(
1
)
(
)
(
0
0
0
1
1
−
=
−
=
=
=
⎭
⎬
⎫
⎩
⎨
⎧
=
=
∫
∫
−
−
τ
τ
τ
τ
d
d
L
L
.
2. Stosując rozkład na ułamki proste otrzymamy:
1
1
)
(
2
+
−
=
s
s
s
s
H
.
Zatem:
t
s
s
s
t
g
cos
1
1
1
)
(
2
1
1
−
=
⎭
⎬
⎫
⎩
⎨
⎧
+
−
⎭
⎬
⎫
⎩
⎨
⎧
=
−
−
L
L
.
3. Aby posłużyć się zależnością (3.47) zauważmy, że:
( )
⎭
⎬
⎫
⎩
⎨
⎧
=
⎭
⎬
⎫
⎩
⎨
⎧
+
=
−
−
)
(
)
(
1
1
)
(
1
2
1
s
sM
s
L
L
s
s
L
t
h
, gdzie:
1
)
(
=
s
L
,
1
)
(
2
+
= s
s
M
.
Bieguny funkcji H(s) są zerami funkcji M(s):
0
1
2
=
+
s
, a więc:
j
±
=
2
,
1
s
.
Zatem, na podstawie (3.47):
( )
=
+
+
=
⎭
⎬
⎫
⎩
⎨
⎧
=
∑
=
=
−
2
1
0
2
1
)
2
(
1
1
1
)
(
)
(
)
(
i
t
s
i
i
s
i
s
s
s
s
sM
s
L
L
t
h
e
t
e
e
e
e
t
t
t
t
cos
1
2
1
2
1
1
2
2
−
=
+
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
−
−
j
j
j
j
j
j
.
Przykład 3.13.
Określić odwrotną transformatę Laplace’a funkcji:
2
3
4
2
2
2
2
2
2
)
(
s
s
s
s
s
s
H
+
+
+
+
=
.
Bieguny funkcji są zerami jej mianownika:
(
)
0
2
2
2
2
)
(
2
2
2
3
4
=
+
+
=
+
+
=
s
s
s
s
s
s
s
M
, skąd znaj-
dujemy pierwiastki: s
1
= 0 (podwójny) oraz: s
2
= 1 + j, s
3
= 1 – j.
Residuum funkcji H(s)e
st
dla podwójnego bieguna obliczamy zgodnie z (3.46):
t
s
s
s
s
s
s
H
s
st
st
s
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
=
=
0
2
2
0
2
2
2
2
2
)
)
(
(
e
d
d
e
res
,
natomiast dla kolejnych dwóch biegunów pojedynczych zgodnie z (3.45):
t
s
st
t
s
st
s
s
s
s
s
s
s
M
s
L
s
M
s
L
)
1
(
1
2
3
2
2
'
2
2
4
6
4
2
2
2
)
(
)
(
)
(
)
(
2
2
j
j
e
j
e
e
e
res
+
−
+
−
=
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
,

28
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
t
s
st
t
s
st
s
s
s
s
s
s
s
M
s
L
s
M
s
L
)
1
(
1
2
3
2
3
'
3
2
4
6
4
2
2
2
)
(
)
(
)
(
)
(
3
3
j
j
e
j
e
e
e
res
−
−
−
−
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
+
+
+
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
.
Sumując te residua otrzymamy:
{
}
(
)
t
t
s
H
s
H
L
t
h
t
i
st
s
i
sin
)
(
)
(
)
(
3
1
1
−
=
−
+
=
=
=
∑
e
e
res
.
Można zauważyć, że metoda residuów w odniesieniu do funkcji wymiernych (ilo-
razu funkcji holomorficznych) jest równoważna metodzie rozkładu na ułamki proste.
Obejmuje ona jednak znacznie szerszą klasę funkcji.
3.2.4. Transformata Laplace’a w równaniach zmiennych stanu
Prezentowane w p. 2.5 wprowadzenie do metody przestrzeni stanów w zastosowaniu
do opisu systemów dynamicznych odnosiło się do czasowej analizy odpowiednich
równań stanu. Główny problem obliczeniowy, który tam występuje polega na oblicze-
niu macierzy przenoszenia
Φ(t) (2.60). Zobaczmy, co można uzyskać stosując w od-
niesieniu do równań stanu przekształcenie Laplace’a.
Poddając różniczkowe równanie stanu (2.44):
Bu
Ax
x
+
=
&
przekształceniu Laplace’a, otrzymamy:
)
(
)
(
)
0
(
)
(
s
s
s
s
Bu
Ax
x
x
+
=
−
,
co po kolejnych przekształceniach przyjmuje następującą postać:
(
)
(
)
)
(
)
0
(
)
(
1
1
s
s
s
s
Bu
A
I
x
A
I
x
−
−
−
+
−
=
(3.48)
Podstawiając:
(
)
1
)
(
−
−
=
A
I
Φ
s
s
, otrzymamy:
)
(
)
(
)
0
(
)
(
)
(
s
s
s
s
Bu
Φ
x
Φ
x
+
=
(3.49)
Obliczając odwrotne przekształcenie Laplace’a z (3.49) otrzymamy:
{
}
{
}
∫
−
+
=
+
=
−
−
t
d
t
t
s
s
s
t
0
1
1
)
(
)
(
)
0
(
)
(
)
(
)
(
)
0
(
)
(
)
(
τ
τ
τ
Bu
Φ
x
Φ
Bu
Φ
x
Φ
x
L
L
, (3.50)
co jest identyczne z (2.60) dla t
0
= 0.
Wynika stąd następująca równość:
{
}
(
)
{
}
1
1
1
)
(
)
(
−
−
−
−
=
=
A
I
Φ
Φ
s
s
t
L
L
, (3.51)
a także, na podstawie (2.54):
(
)
{
}
1
1
)
(
−
−
−
=
=
A
I
Φ
A
s
t
t
L
e
, (3.52)
co jest kolejnym sposobem obliczania funkcji e
At
.

3.2. Przekształcenie Laplace’a
29
Analizując prawą stronę (3.50) widać, że macierz przenoszenia
Φ(t) odgrywa w
stanowej reprezentacji systemu zbliżoną rolę, jak funkcja wagi w systemie z jednym
wejściem i jednym wyjściem: jej splot z wektorem wejść u(t), po uwzględnieniu wa-
runków początkowych, daje wynik w postaci wektora stanu x(t). Podobne relacje za-
chodzą także w przestrzeni transformaty Laplace’a (3.49), gdzie
Φ(s) jest swego ro-
dzaju wielowymiarową transmitancją pomiędzy wektorem wejść i wektorem stanu.
Po uwzględnieniu w (3.50) równania wyjść (2.45):
)
(
)
(
)
(
t
t
t
Du
Cx
y
+
=
,
otrzymamy:
)
(
)
(
)
(
)
0
(
)
(
)
(
0
t
d
t
t
t
t
Du
Bu
CΦ
x
CΦ
y
+
−
+
=
∫
τ
τ
τ
, (3.53)
lub w postaci transformaty s:
(
)
(
)
(
)
)
(
)
0
(
)
(
1
1
s
s
s
s
u
D
B
A
I
C
x
A
I
C
y
+
−
+
−
=
−
−
. (3.54)
Przykład 3.14.
Jednorodne równanie stanu badanego układu ma postać:
)
(
)
(
t
t
Ax
x
=
&
,
gdzie
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
2
1
1
0
A
. Określić funkcję przenoszenia tego układu.
Zgodnie z (3.51) należy najpierw obliczyć macierz:
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
−
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
−
=
−
−
2
2
2
2
2
1
1
)
1
(
)
1
(
1
)
1
(
1
)
1
(
2
1
1
2
1
2
1
2
1
1
)
(
s
s
s
s
s
s
s
s
s
s
s
s
s
s
A
I
Φ
Łatwo określić transformatę odwrotną macierzy
Φ(s):
{
}
⎥
⎦
⎤
⎢
⎣
⎡
−
−
+
=
=
=
−
−
−
−
−
t
t
t
t
t
t
t
t
t
s
t
e
e
e
e
e
)
1
(
)
1
(
)
(
)
(
1
A
Φ
Φ
L
.
Przykład 3.15.
Posługując się przekształceniem Laplace’a obliczyć macierz przenoszenia
układu z przykładu 2.8.
Macierz stanu w przykładzie 2.8 jest następująca:
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
5
,
0
1
4
0
A
.
Postępując jak w poprzednim przykładzie otrzymamy:
(
)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
+
+
+
−
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
−
+
+
+
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
−
−
−
2
0
2
2
0
2
2
0
2
2
0
2
2
1
1
)
25
,
0
(
)
25
,
0
(
1
)
25
,
0
(
4
)
25
,
0
(
5
,
0
1
4
5
,
0
4
5
,
0
1
5
,
0
1
4
ω
ω
ω
ω
s
s
s
s
s
s
s
s
s
s
s
s
s
A
I
,

30
3. ANALIZA SYSTEMÓW ZA POMOCĄ METOD OPERATOROWYCH
gdzie
2
2
0
25
,
0
4
−
=
ω
=63/16=1,9843
2
.
Transformaty odwrotne poszczególnych elementów otrzymanej macierz prowadzą do następu-
jącej macierzy przenoszenia badanego układu:
(
)
{
}
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
+
=
=
−
=
−
−
−
t
t
t
t
t
t
s
t
t
t
0
0
0
0
0
0
0
0
0
0
25
,
0
1
1
sin
25
,
0
cos
sin
1
sin
4
sin
25
,
0
cos
)
(
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
e
e
A
A
I
Φ
L
.
Widać, że wynik ten jest zgodny z rezultatem uzyskanym w przykładzie 2.8.
Zadania
3.1. Posługując się przekształceniem Fouriera określić charakterystyki częstotliwościowe
transmitancji widmowej układu opisanego równaniem różniczkowym z przykładu 3.5:
t
y
t
y
t
y
=
+
+
d
d
d
d
2
2
2
.
3.2. Określić transmitancję układu, który jest opisany podanym równaniem różniczkowym.
Obliczyć funkcję wagi tego układu.
a)
t
t
t
d
x
t
x
t
t
x
−
=
+
+
∫
e
)
(
1
)
(
4
)
(
5
d
)
(
d
0
τ
τ
,
b)
)
(
)
(
4
)
(
3
)
(
2
)
(
'
''
'''
t
u
t
y
t
y
t
y
t
y
=
+
+
+
,
c)
)
(
)
(
2
)
(
2
)
(
5
)
(
'
'
''
t
u
t
u
t
y
t
y
t
y
+
=
+
+
.
3.3. Dla układu o podanej transmitancji określić funkcję wagi.
a)
)
2
(
1
)
(
+
+
=
s
s
s
s
G
,
b)
2
5
1
2
)
(
2
+
+
+
=
s
s
s
s
G
,
c)
5
2
1
)
(
2
+
+
=
s
s
s
G
.
3.4. Określić odpowiedź na skok jednostkowy układów z zadania 3.3.
3.5. Określić równania różniczkowe opisujące układy z zadania 3.3.
3.6. Określić transformaty Laplace’a podanych sygnałów. Narysować przebiegi tych sygna-
łów w czasie.
a)
)
(
1
)
(
a
t
t
y
−
=
,
0
>
a
,
b)
)
(
1
)
(
1
)
(
b
t
a
t
t
y
−
−
−
=
,
0
>
> a
b
,
c)
)
(
1
)
(
)
(
a
t
a
t
m
t
y
−
−
=
,
d)
)
(
1
)
(
)
(
2
a
t
a
t
t
y
−
−
=
.
3.7. Określić przebiegi sygnałów, o podanych transformatach Laplace’a.

3.2. Przekształcenie Laplace’a
31
a)
s
s
Y
π
e
)
(
−
=
,
b)
2
2
1
)
(
ω
+
=
s
s
Y
,
c)
6
5
3
)
(
2
+
+
−
=
s
s
s
s
Y
, d)
)
1
(
1
3
2
)
(
2
2
3
+
+
+
+
=
s
s
s
s
s
s
Y
,
e)
2
)
(
1
)
(
a
s
s
Y
−
=
,
f)
2
2
)
(
1
)
(
ω
+
−
=
a
s
s
Y
.
3.8. Wyznaczyć transformaty Laplace’a podanych funkcji.
a)
)
cos
1
(
2
)
(
at
t
t
y
−
=
,
b)
kt
t
t
y
sin
1
)
(
=
,
c)
t
t
t
y
2
3
e
5
e
6
)
(
−
−
−
=
,
d)
(
)
at
bt
t
e
e
1
−
.
Wyszukiwarka
Podobne podstrony:
06 pomiar mocy za pomoca oscylo Nieznany (2)
Kodowanie pilota za pomoca VAG Nieznany
06 pomiar mocy za pomoca oscylo Nieznany (2)
Microsoft Excel 2007 PL Analiza danych za pomoca tabel przestawnych Akademia Excela e27aae
Microsoft Excel 2007 PL Analiza danych za pomoca tabel przestawnych Akademia Excela 2
Analiza wykresu za pomocą formacji cenowych
Microsoft Excel 2007 PL Analiza danych za pomoca tabel przestawnych Akademia Excela
Analiza wykresu za pomocą formacji cenowych
Microsoft Excel 2007 PL Analiza danych za pomoca tabel przestawnych Akademia Excela e27aae 2
analiza skladu gazu za pomoca c Nieznany
Rozwiązywanie problemów z uruchamianiem systemu Windows za pomocą konsoli odzyskiwania, windows XP i
Metody organizacji i zarządzania, BCG, Analiza i projektowanie portfela produkcji za pomocą macierzy
Motywowanie za pomoca plac id 3 Nieznany
Analiza systemu dystrybucji pal Nieznany
Prowadzenie ksiąg rachunkowych za pomocą systemu komputerowego
Analiza długich list za pomocą funkcji?zy?nych
Naprawa systemu plików NTFS za pomocą mini Windows XP startującego z dysku CD, Sbs
więcej podobnych podstron