W

W

Y

Y

M

M

I

I

A

A

N

N

A

A

(

(

T

T

R

R

A

A

N

N

S

S

P

P

O

O

R

R

T

T

)

)

C

C

I

I

E

E

P

P

Ł

Ł

A

A

Trzy podstawowe mechanizmy transportu ciepła

(wymiany ciepła):

1.

P

P

P

R

R

R

Z

Z

Z

E

E

E

W

W

W

O

O

O

D

D

D

Z

Z

Z

E

E

E

N

N

N

I

I

I

E

E

E

- przekazywanie energii od jednej cząstki do

drugiej, za pośrednictwem ruchu drgającego tych cząstek. Proces ten
trwa dopóty, dopóki temperatura ciała nie zostanie wyrównana w
całej rozpatrywanej objętości. Dotyczy to bezpośredniego kontaktu
ciała z ciałem, części ciała z ciałem.

2.

P

P

P

R

R

R

O

O

O

M

M

M

I

I

I

E

E

E

N

N

N

I

I

I

O

O

O

W

W

W

A

A

A

N

N

N

I

I

I

E

E

E

- przekazywanie ciepła w postaci energii

promieniowania, którego natura jest taka sama jak energii świetlnej.
Energia cieplna przekształca się w energię promieniowania, przebywa

określoną przestrzeń z prędkością światła, aby w innym miejscu
przekształcić się całkowicie lub częściowo w energię cieplną.

3.

K

K

K

O

O

O

N

N

N

W

W

W

E

E

E

K

K

K

C

C

C

J

J

J

A

A

A

(

(

(

W

W

W

N

N

N

I

I

I

K

K

K

A

A

A

N

N

N

I

I

I

E

E

E

)

)

)

- wiąże się z ruchem konwekcyjnym

gazów lub cieczy, wywołanym bądź różnicą gęstości (różnicą
temperatur), bądź przez wymuszenie czynnikami zewnętrznymi.

PRZEWODZENIE

PRZEWODZENIE

Stan cieplny ciała określa temperatura. Miejsca geometryczne o

jednakowej temperaturze tworzą powierzchnie izotermiczne, linie o
jednakowej temperaturze tworzą izotermy.
Temperatura ciała zmienia się najszybciej w kierunku
prostopadłym do izoterm.

Przewodzenie dotyczy głównie ciał stałych, gdyż to ciała stałe
najlepiej przewodzą ciepło.

PODSTAWOWE

DEFINICJE

PODSTAWOWE DEFINICJE

NATĘŻENIE PRZEPŁYWU CIEPŁA

(GĘSTOŚĆ STRUMIENIA CIEPLNEGO) Q

*

ilość ciepła jaka przepływa przez dane ciało w jednostce czasu

[W]

s]

J

[

*

=

=

dt

dQ

Q

gdzie:
Q-ciepło,
t-czas,

STRUMIEŃ CIEPLNY q (OBCIĄŻENIE CIEPLNE)

natężenie przepływu ciepła odniesione do jednostki powierzchni (straty

ciepła przypadające na jednostkę powierzchni)

]

m

W

[

2

*

A

Q

q

=

gdzie:
A-powierzchnia,

Natężenie przepływu ciepła

[W]

*

A

q

Q

⋅

=

Przewodzenie ciepła jest USTALONE gdy

dQ/dt=const lub

Q

*1

= Q

*2

= Q

*3

Przewodzenie ciepła jest NIEUSTALONE gdy

dQ/dt≠const lub

Q

*1

≠ Q

*2

≠ Q

*3

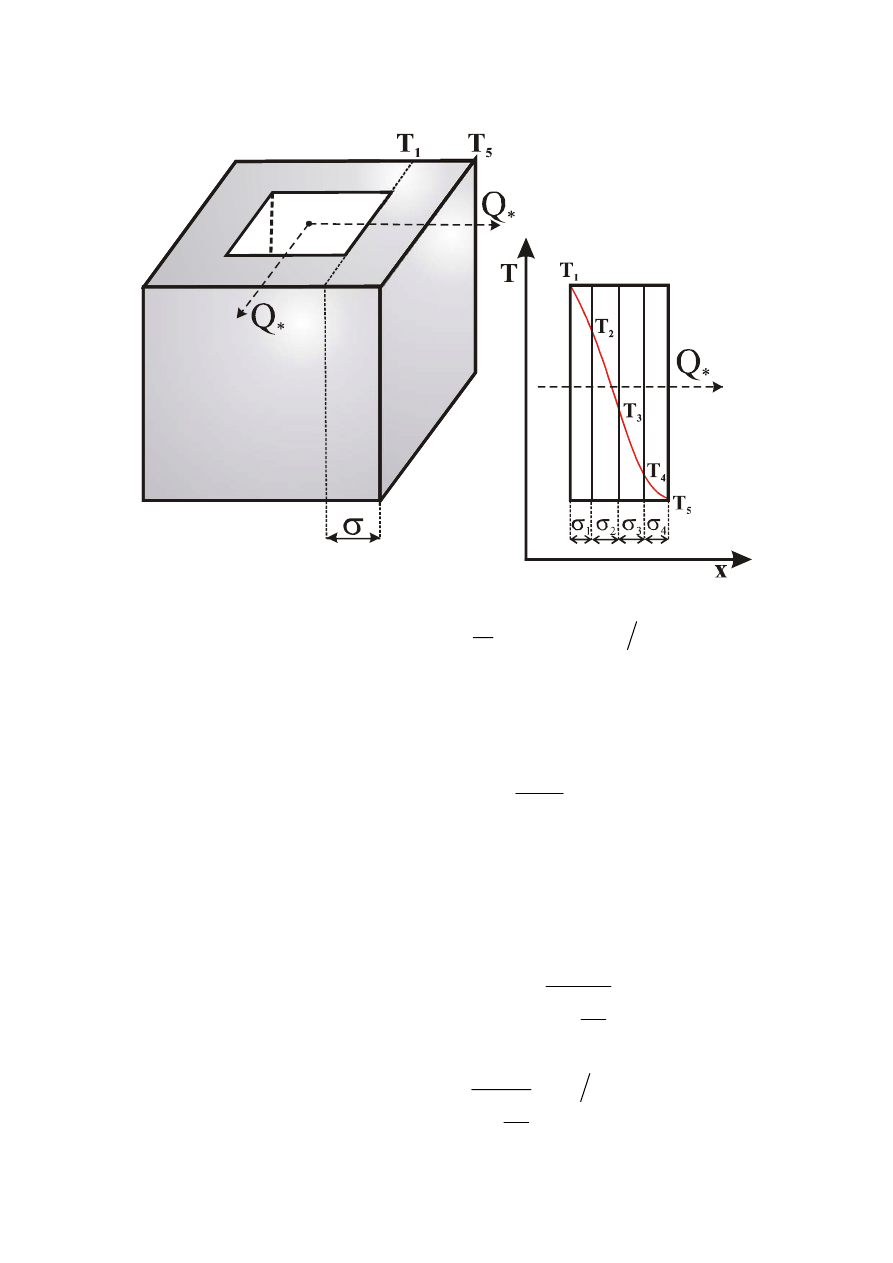
Ś

Ś

C

C

I

I

A

A

N

N

K

K

A

A

P

P

Ł

Ł

A

A

S

S

K

K

A

A

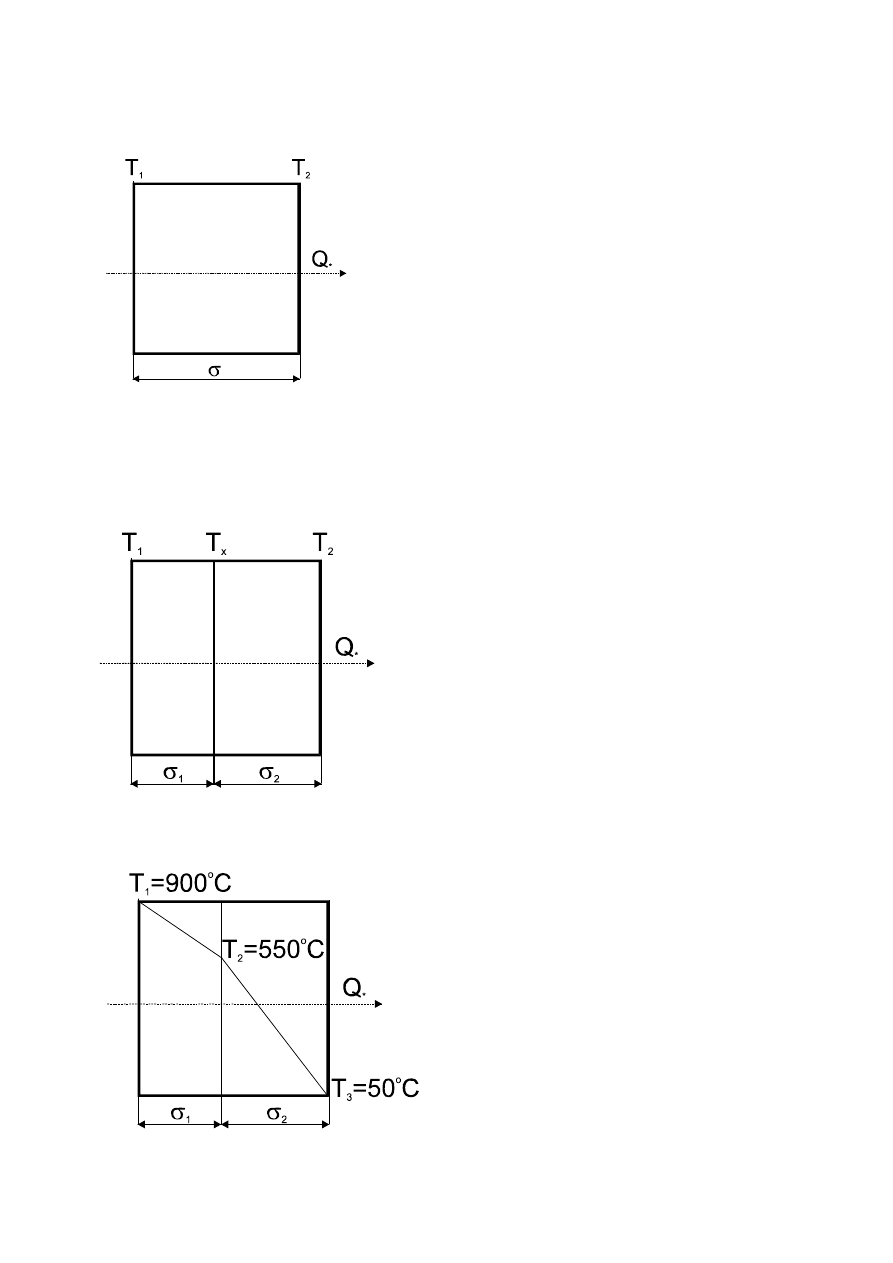
Ścianka płaska jednowarstwowa:

strumień cieplny

]

m

W

[

)

(

2

2

1

T

T

q

−

⋅

=

σ

λ

temperatura T

1

>temperatury T

2

gdzie:
σ-grubość warstwy (ścianki),

natężenie przepływu ciepła

[W]

)

(

*

2

1

T

T

A

Q

−

⋅

⋅

=

σ

λ

Całkowita ilość przewodzonego ciepła przez ciało:

[J]

t

A

q

Q

⋅

⋅

=

Ścianka płaska wielowarstwowa:

natężenie przepływu ciepła

[W]

*

∑

=

Δ

⋅

=

n

i

i

i

T

A

Q

1

λ

σ

strumień cieplny

]

m

W

[

2

∑

=

Δ

=

n

i

i

i

T

q

1

λ

σ

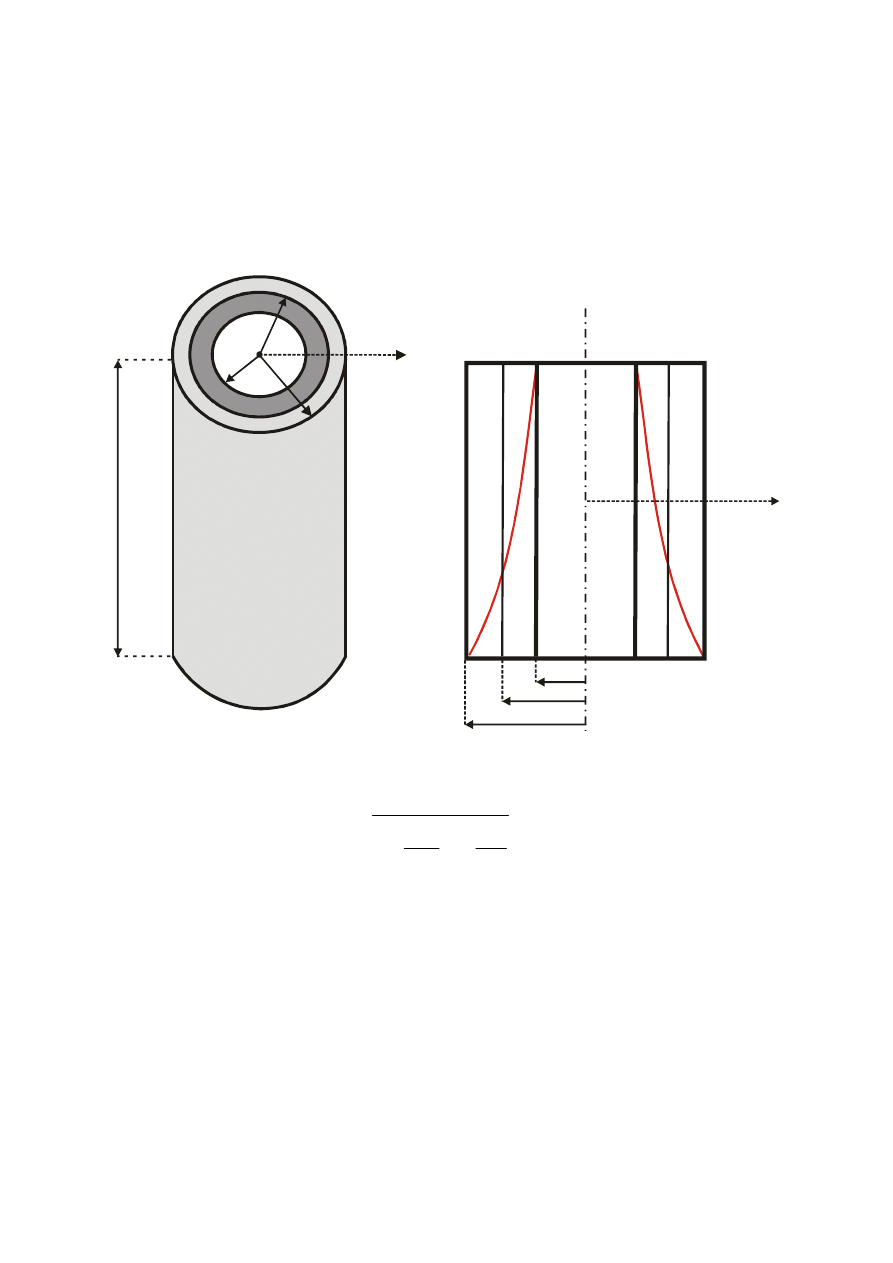
Ś

Ś

C

Przewodzenie ciepła przez ściankę cylindryczną:

1

2

*

1

1

(

)

[W]

1

ln

2

n

i

i

i

i

L T T

Q

r

r

π

λ

+

=

⋅ ⋅

−

=

⋅

∑

C

I

I

A

A

N

N

K

K

A

A

C

C

Y

Y

L

L

I

I

N

N

D

D

R

R

Y

Y

C

C

Z

Z

N

N

A

A

Q

*

Q

*

T

1

T

1

T

2

T

3

T

3

L

r

3

r

2

r

1

r

1

r

2

r

3

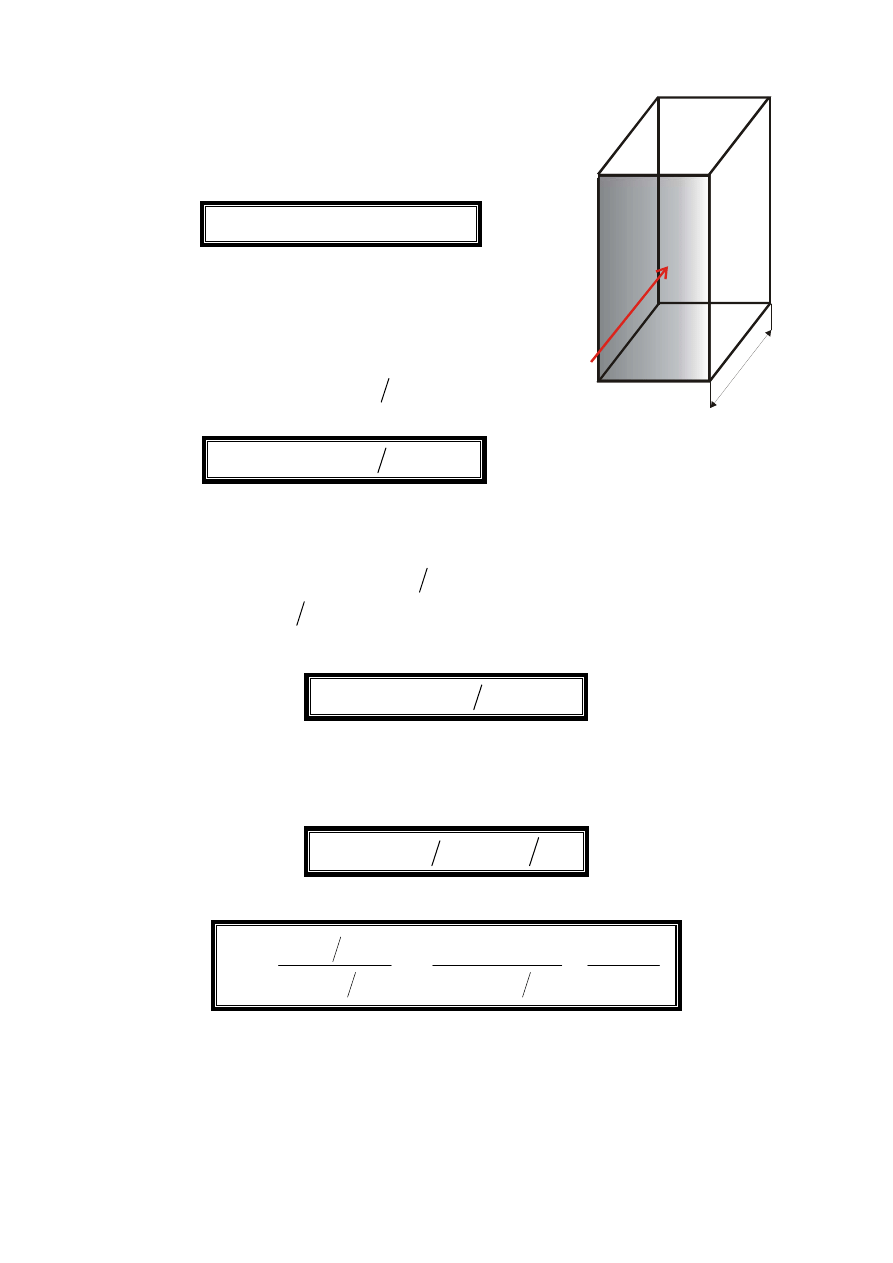
PRZEWODZENIE

opiera się na prawie

FOURIERA

mówiącym o ilości ciepła

przewodzonego przez powierzchnię A prostopadłą

do kierunku ruchu ciepła:

T

1

Q

T

2

x( )

σ

)

(

τ

λ

d

gradT

A

dQ

⋅

⋅

⋅

−

=

gdzie:
T-temperatura,
λ-współczynnik przewodzenia ciepła,
τ-czas,

podstawiając za:

dx

dT

gradT

=

otrzymujemy:

)

(

)

(

τ

λ

d

dx

dT

A

dQ

⋅

⋅

⋅

−

=

gdzie:
x (

σ)-grubość warstwy,

dalej:

*

Q

d

dQ

=

τ

zakładamy

const

d

dQ

=

τ

– ustalone przewodzenie ciepła

otrzymujemy:

[W]

)

(

*

dx

dT

A

Q

⋅

⋅

−

=

λ

rozważając dalej:

A

q

Q

⋅

=

*

stąd:

]

m

W

[

)

(

2

dx

dT

q

⋅

−

=

λ

Z powyższych równań wynika, że:

⎥

⎦

⎤

⎢

⎣

⎡

⋅

=

⋅

⋅

−

=

deg

m

W

)

m

deg

(m

W

)

(

2

dx

dT

A

d

dQ

τ

λ

zatem

współczynnik przewodzenia ciepła (λ)

jest to ilość

ciepła przewodzona przez ciało o powierzchni 1m

2

, grubości

ścianki 1m, gdy różnica temperatur pomiędzy przeciwległymi
ściankami wynosi 1deg, w ciągu 1s.

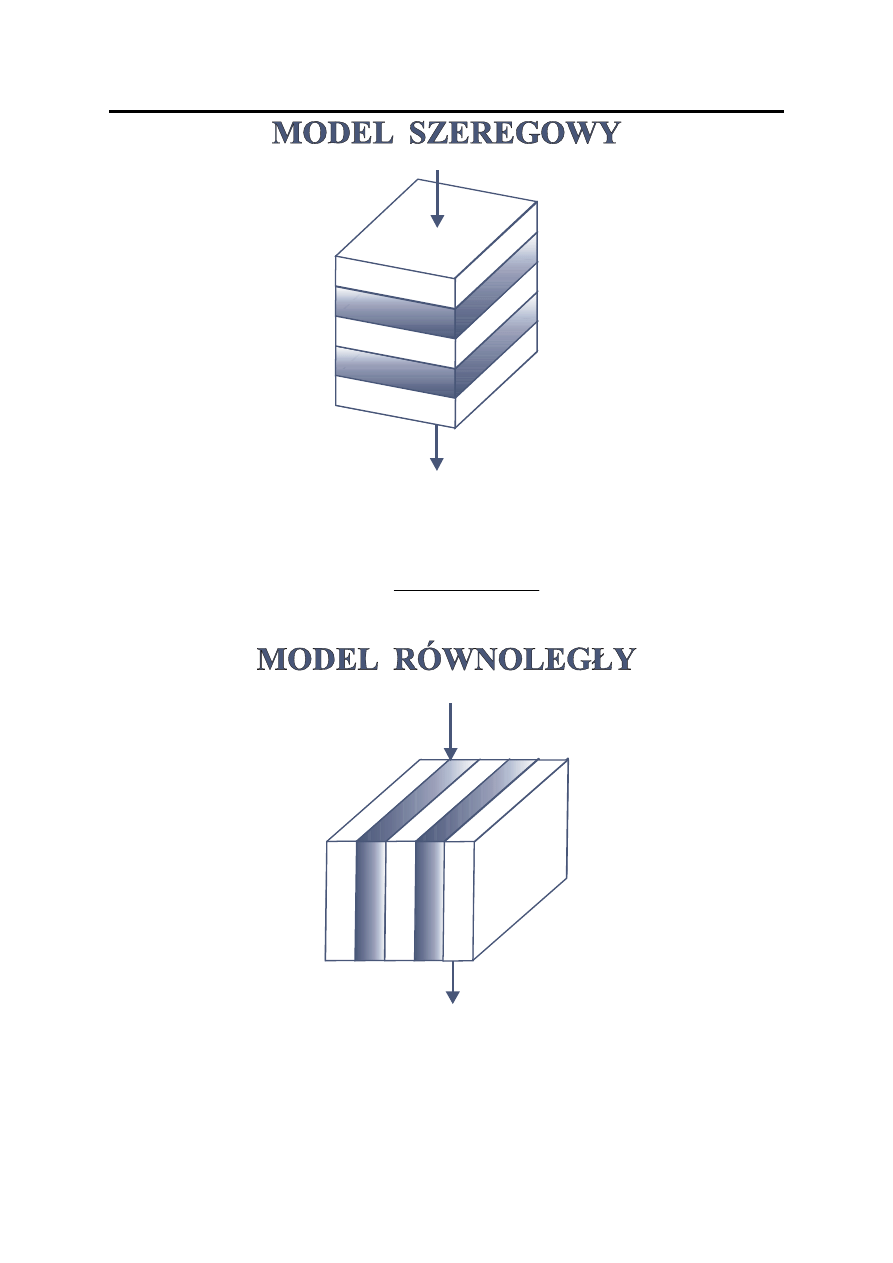
WSPÓŁCZYNNIK PRZEWODZENIA CIEPŁA KOMPOZYTÓW

Przewodzenie w kierunku prostopadłym do warstw

(model szeregowy):

1

2

2

1

2

1

V

V

⋅

⋅

⋅

+

=

λ

λ

λ

λ

λ

Przewodzenie w kierunku równoległym do warstw

(model równoległy):

2

2

1

1

V

V

⋅

+

⋅

=

λ

λ

λ

gdzie:
V

1

, V

2

– udziały objętościowe składników kompozytu,

ZADANIA

ZADANIE 1

Dane:

σ=0,2 m T

1

=300

°C

λ=0,252 [W/m·deg] T

2

=275

°C

A=3,5 m

2

Obliczyć natężenie przepływu ciepła,
strumień cieplny oraz wyznaczyć izotermę,

dla której temperatura ścianki będzie równa
280

°C.

Ponadto:

1) tak dobrać współczynnik przewodzenia

ciepła żeby

ΔT=45°C;

2) obliczyć całkowite ciepło przewodzone
przez tą ściankę w ciągu 1s ?

ZADANIE 2

Dane:

σ

1

=0,5 m

σ

2

=0,2 m

λ

1

= 2 [W/m·deg]

λ

2

= 0,07 [W/m·deg]

T

1

= 2500

°C T

2

= 200

°C

Obliczyć natężenie przepływu ciepła

wiedząc, że A=2m

2

. Obliczyć strumień

cieplny tej ścianki, opór termiczny oraz
wyznaczyć temperaturę T

x

. Następnie

dobrać grubość warstwy drugiej tak, żeby
T

2

wynosiła 80

°C oraz wyznaczyć izotermę

gdzie temperatura ścianki wynosi 2000

°C?

ZADANIE 3

Określić minimalną grubość ściany
paleniska, jeśli wiadomo, że ściana
składa się z dwóch warstw:

wewnętrznej z cegły szamotowej i
zewnętrznej z cegły czerwonej, straty
cieplne 1m

2

ściany wynoszą 1,2 kW.

Współczynniki przewodzenia ciepła
obu materiałów są następujące: cegła
szamotowa

λ

1

=1,3 W/m·deg, cegła

czerwona

λ

2

=0,5 W/m·deg.

Temperaturowy przekrój przez ścianę
przedstawiono na rysunku.

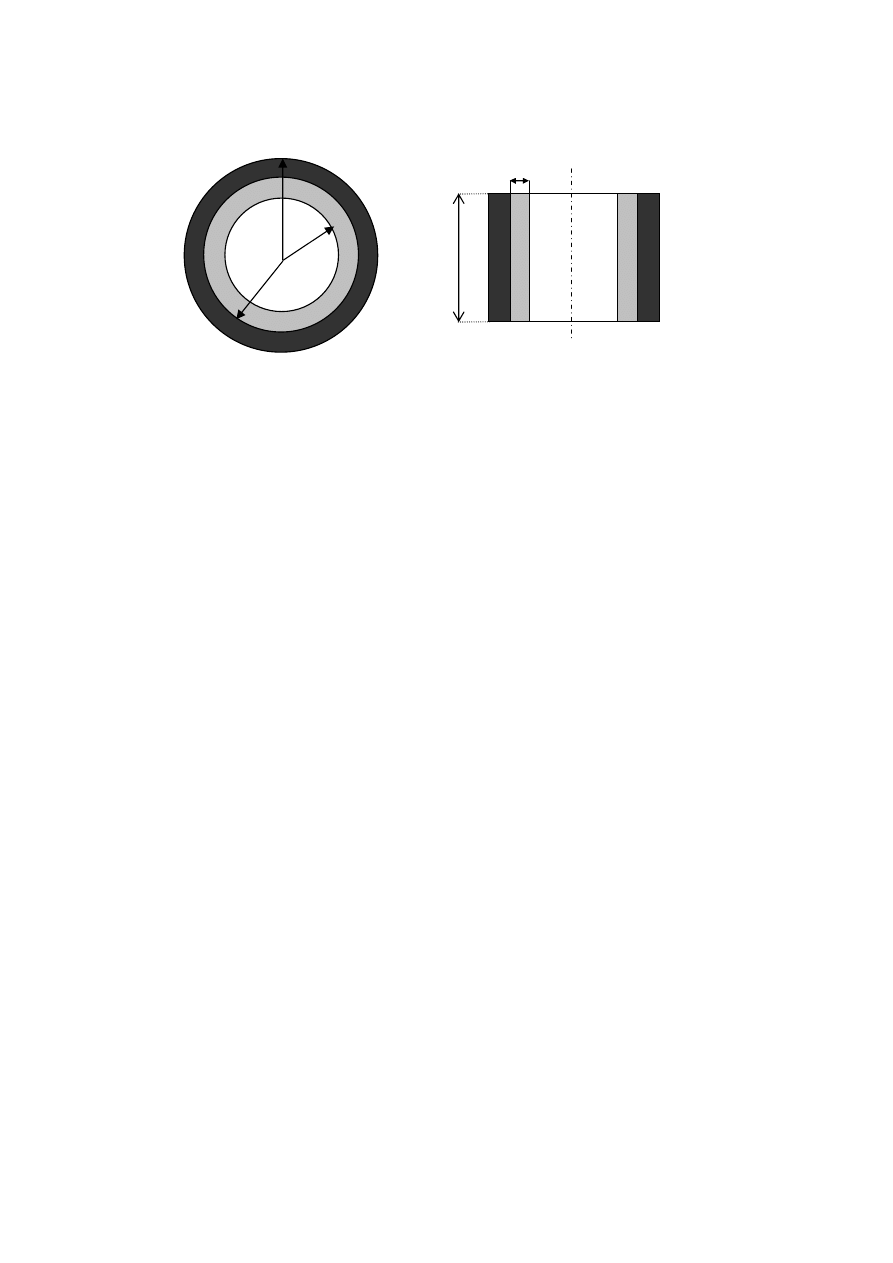
ZADANIE 4

Dany jest rurociąg, którego podstawowe parametry są następujące:

r

1

= 0,1 m r

3

= 0,5 m

σ

1

=0,05 m

λ

1

= 3,8 [W/m·deg]

λ

2

= 0,05 [W/m·deg]

L= 2 m

Temperatura wewnętrznej ścianki wynosi 500

°C, zaś zewnętrznej 50°C.

Wyznaczyć natężenie przepływu ciepła na drodze przewodzenia
i temperaturę na połączeniu warstw. Następnie dobrać grubość warstwy
iyolacji tak, żeby temperatura powierzchni zewnętrznej rury wynosiła

20ºC.

ZADANIE 5
Z dużym przybliżeniem cegła dziurawka jest przykładem kompozytu
warstwowego złożonego z warstw cegły (ciała stałego) i warstw porów.
Wyznaczyć współczynniki przewodzenia ciepła w kierunku równoległym
i prostopadłym do warstw, wiedząc, że:

V

ciała stałego

=78%

λ

ciała stałego

=0,2 W/m·deg

V

porów

=22%

λ

porów

=0,001 W/m·deg

ZADANIE 6

Obliczyć natężenie przepływu ciepła na drodze przewodzenia przez
ściankę szamotową o powierzchni 10m

2

i grubości 200mm, jeżeli

temperatury wewnętrznej i zewnętrznej powierzchni ściany wynoszą
odpowiednio 800

°C i 40°C. Współczynnik przewodzenia ciepła szamotu

wynosi 0,7 W/m·deg.

ZADANIE 7
Jaka jest temperatura wewnętrznej powierzchni ściany o grubości
210mm , wykonanej z kształtek bazaltowych, jeżeli straty cieplne ściany
od powierzchni zewnętrznej do otoczenia wynoszą 840 W/m

2

, a

temperatura zewnętrznej powierzchni ściany równa jest 40

°C.

Współczynnik przewodzenia ciepła bazaltu wynosi 2,8 W/m·deg.

T

z

L

T

w

r

3

r

1

r

2

σ

1

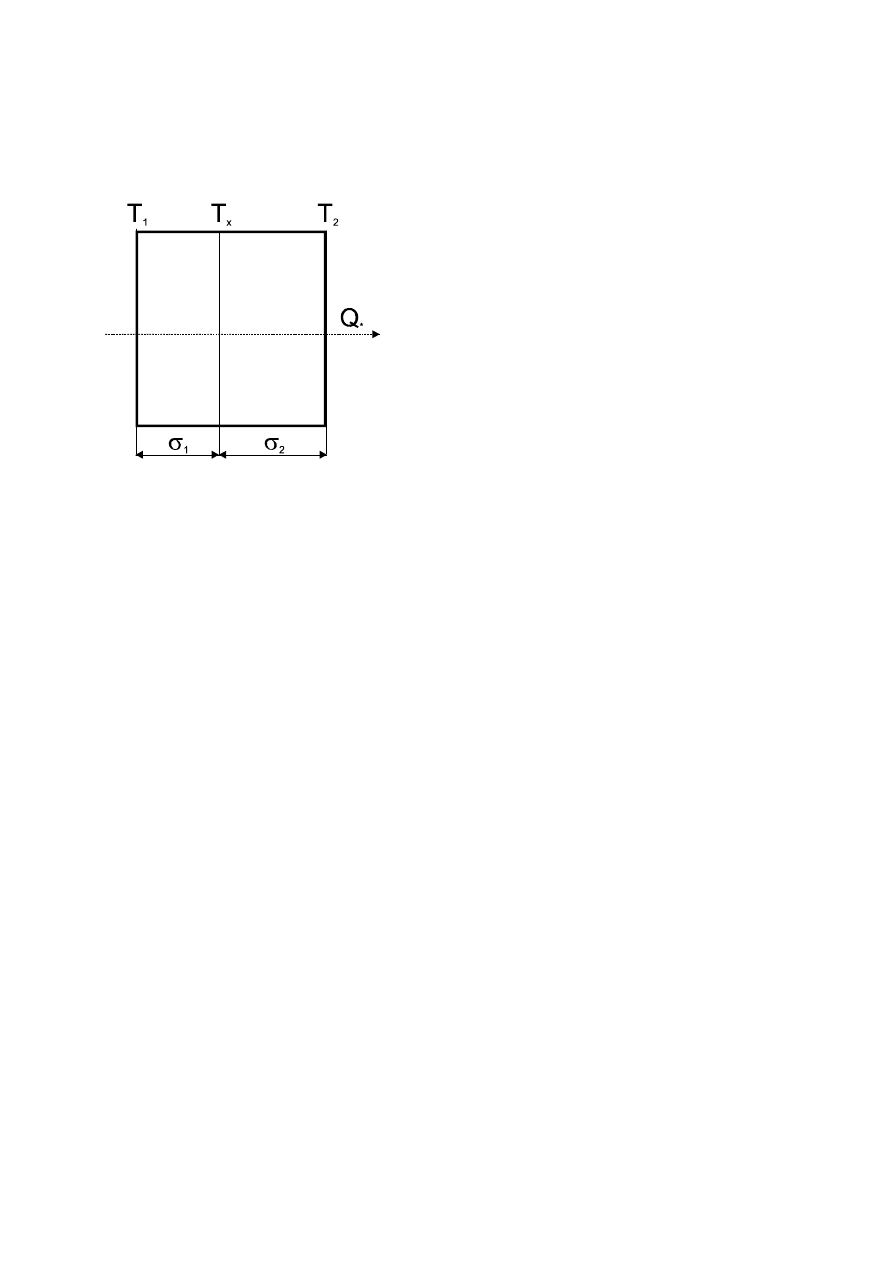
ZADANIE 8

Dane:
T

1

=1000

°C

T

2

=70

°C

σ

1

=0,5 m

σ

2

=0,6 m

λ

1

=1 [W/m·deg]

λ

2

=0,45 [W/m·deg]

Przewodzenie ciepła ustalone Q

*1

=Q

*2

.

Obliczyć strumień cieplny i natężenie przepływu ciepła tej ścianki,

wyznaczyć temperaturę T

x

? Powierzchnia tej ścianki wynosi 1 m

2

.

ZADANIE 9
Rura stalowa o średnicy 102/112 mm jest zaizolowana warstwą waty

azbestowej o grubości

σ=70mm. Różnica temperatur pomiędzy

powierzchnią wewnętrzną a zewnętrzną wynosi 200

°C. Obliczyć

natężenie przepływu ciepła, jeżeli długość rury wynosi 15m.

Współczynniki przewodzenia ciepła wynoszą: 50 W/m·deg dla stali, zaś
dla waty azbestowej

λ=0,05 W/m·deg.

ZADANIE 10
Ściana pieca składa się z trzech warstw. Wewnętrzną warstwę stanowi
cegła ognioodporna o grubości

σ

1

=0,1 m i współczynniku przewodzenia

ciepła

λ

1

=0,95 W/m·deg. Środkową warstwą jest cegła zwykła o

σ

2

=0,2m i

λ

2

=0,65 W/m·deg, zewnętrzną natomiast izolacja o σ

3

=0,06m

i

λ

3

=0,1 W/m·deg. Pomiary temperatury wykazały, że temperatura

wewnętrzna ściany wynosi 750

°C, a ściany zewnętrznej 80°C. Obliczyć

straty cieplne pieca z 1m

2

powierzchni ściany oraz zakres temperatur, w

jakim znajduje się warstwa cegły zwykłej.

ZADANIE 11
Dana jest ścianka wielowarstwowa (A=1x2 m). Przewodzenie ciepła
ustalone.
Wiedząc, że: T

1

=800

°C σ

1

=0,2 m

λ

1

=25 W/m·deg

T

2

=799,4

°C σ

2

=0,1 m

λ

2

=1,0 W/m·deg

T

3

=791,9

°C σ

3

=0,2 m

λ

3

=0,02 W/m·deg

T

4

=40

°C

Obliczyć:
Natężenie przepływu ciepła Q

*

; strumień cieplny q i znaleźć izotermę

100

°C.

ZADANIE 12

Dany jest kompozyt warstwowy. Współczynnik przewodzenia ciepła

λ

II

dla tego kompozytu wynosi 0,872 W/m·deg. Udział objętościowy jednej z
faz wynosi 18% zaś jej

λ=4,3 W/m·deg. Wyznaczyć współczynnik

przewodzenia ciepła dla drugiej z faz i zakwalifikować tą fazę do
odpowiedniego rodzaju materiału? Wyznaczyć także

λ dla przewodzenia

ciepła w kierunku prostopadłym do warstw?

ZADANIE 13
Dana jest cylindryczna ścianka o długości 0,7 m. Obliczyć natężenie
przepływu ciepła dla tej ścianki przyjmując jej grubość = 0,12 m. Dobrać
tak materiał (wyznaczyć współczynnik przewodzenia ciepła), żeby

ΔT=20°C? Przewodzenie ciepła ustalone.
Dane do zadania:

λ=0,04 W/m·deg

ΔT=50°C r

1

=0,12 m