Wyb

oczenie pręta

Katedra Wytrzymałości Materiałów i Metod

Komputerowych Mechaniki

POLITECHNIKA ŚLĄSKA W GLIWICACH

R

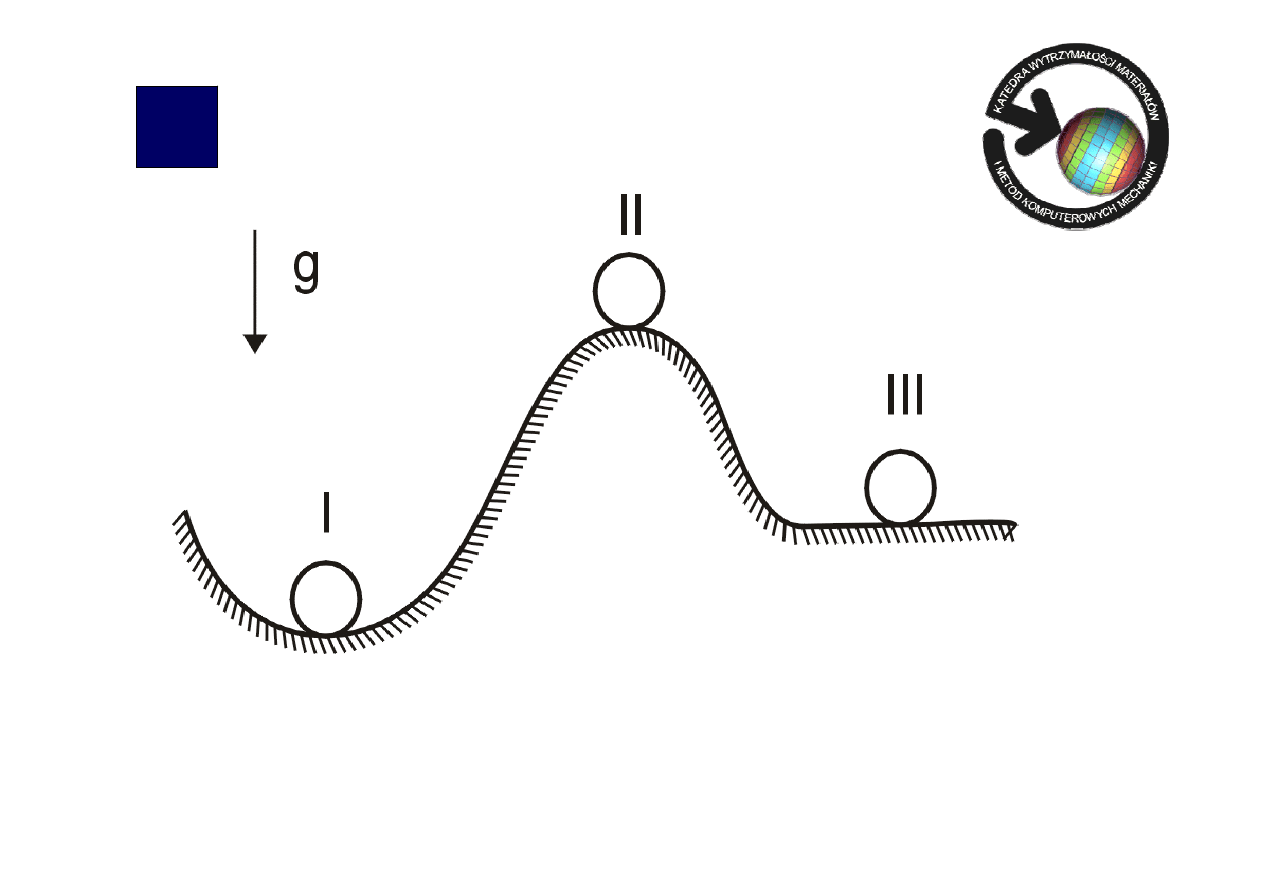
ównowaga ciał - przykład

Stan równowagi statecznej

(trwałej)

minimum energii potencjalnej

Równowaga niestateczna

max energii potencjalnej

Równowaga obojętna

R

ównowaga ciał

•Równowaga stateczna (trwała)

- taka forma

równowagi w której ciało wychylone z położenia
pierwotnego z powrotem do niego powraca.

•Równowaga niestateczna

– ciało wychylone z

położenia pierwotnego nie wraca do niego, ale
przechodzi do innego.

•Równowaga obojętna

– ciało wychylone z

położenia pierwotnego pozostaje w nowym
położeniu.

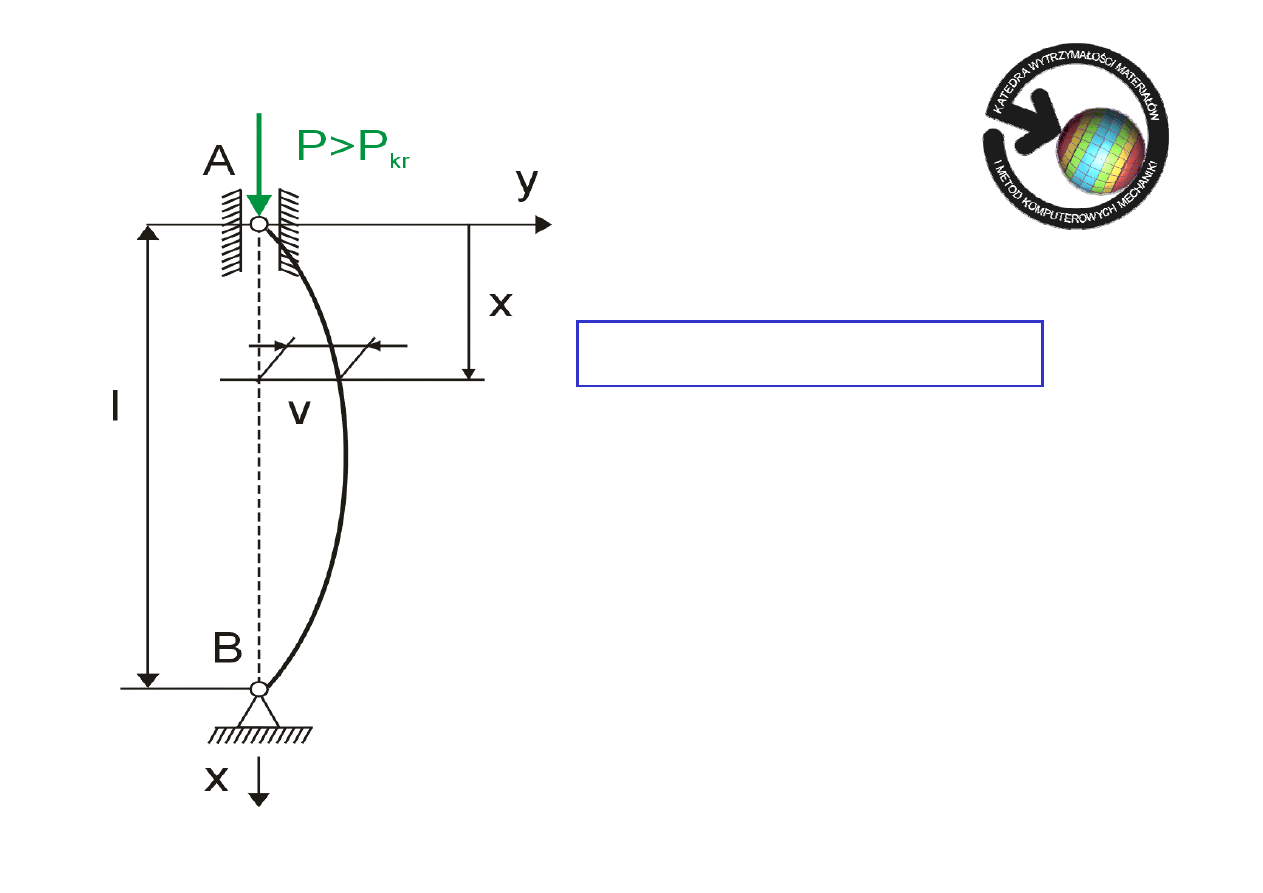
W

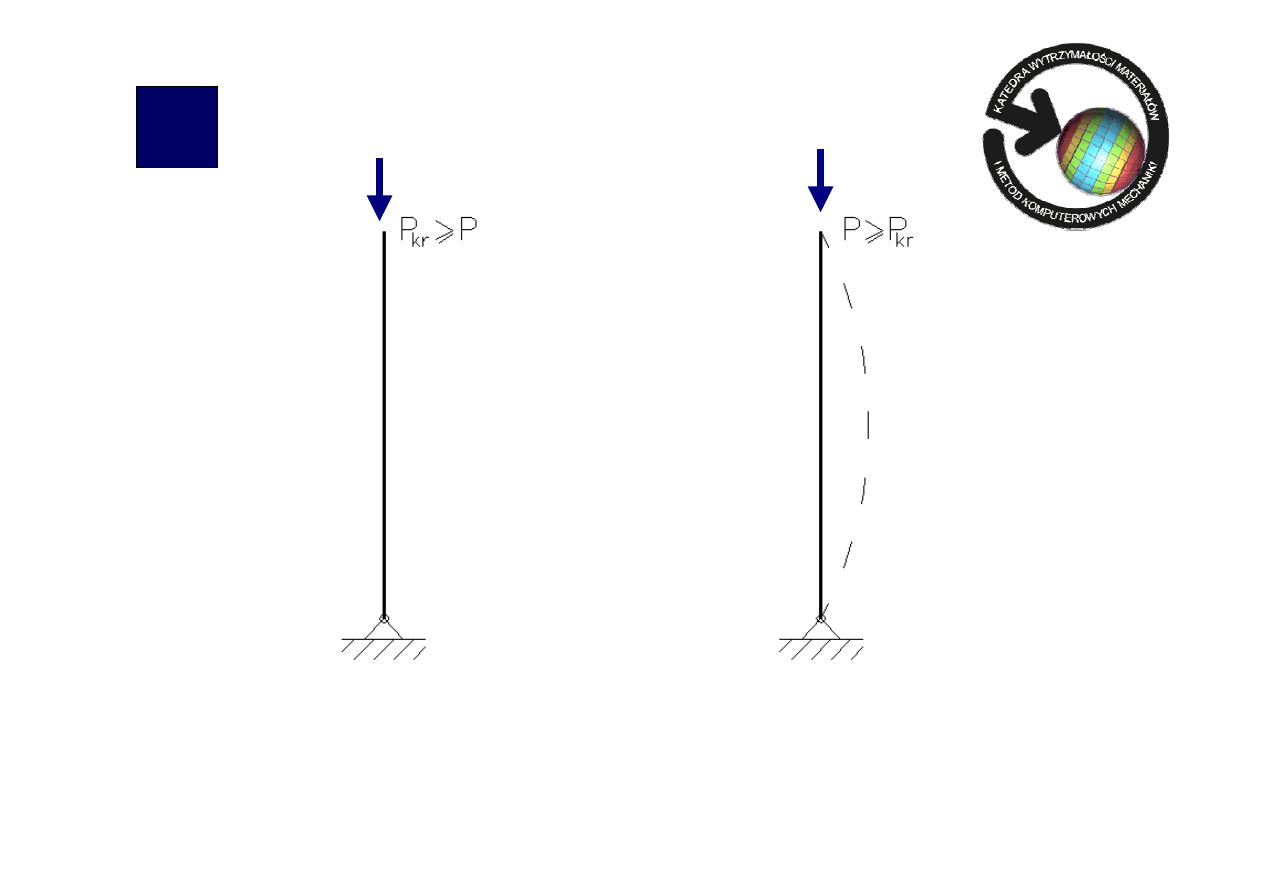
yboczenie pręta

Wygięcie pręta spowodowane przekroczeniem
przez siłę ściskającą wartości krytycznej P

kr

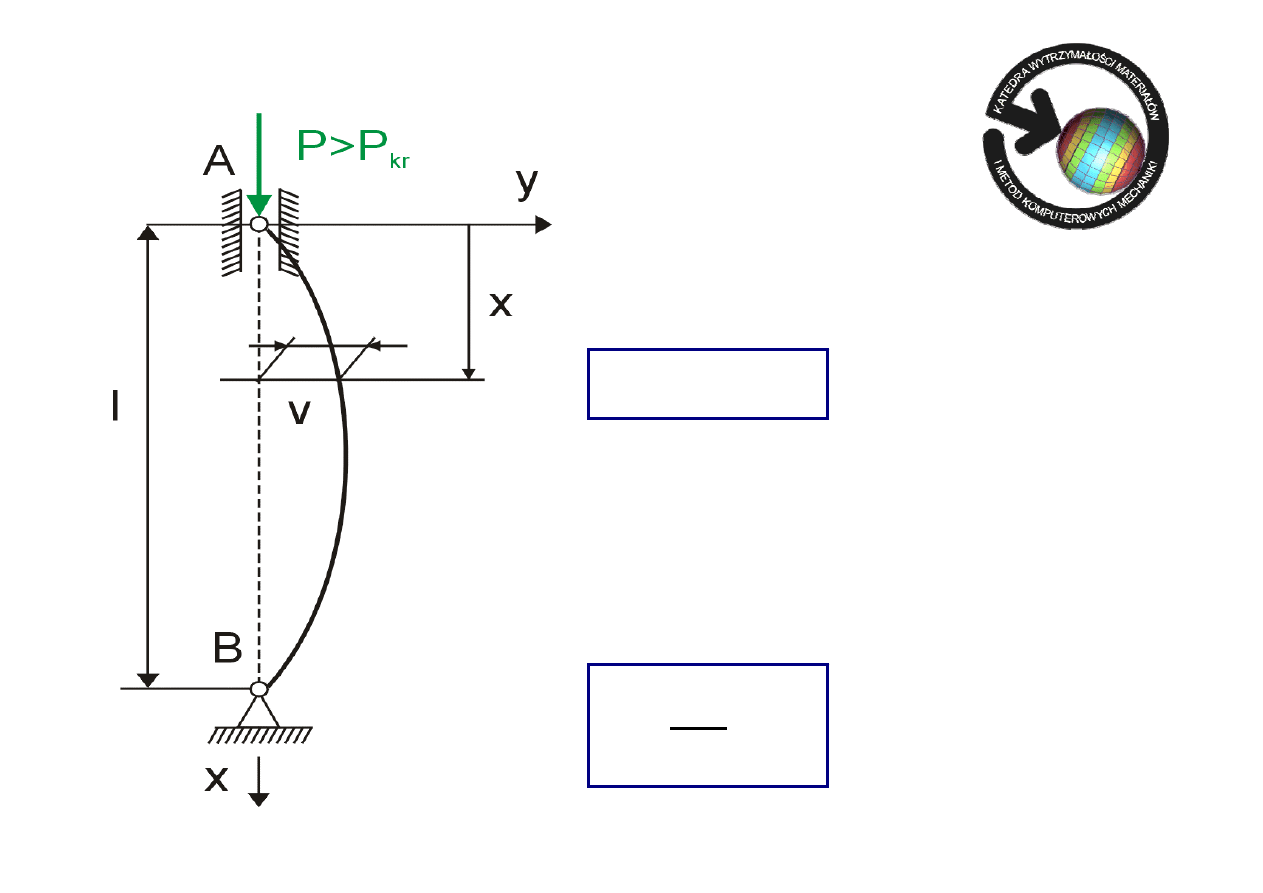
Formuła Eulera

na siłę krytyczną

przy wyboczeniu sprężystym pręta:

E – moduł Younga
I – moduł przekroju poprzecznego pręta

"

( )

g

v EI

M x

= −

( )

g

kr

M x

P v

=

⋅

"

kr

EIv

P v

= −

Po uporządkowaniu:

"

0

kr

P

v

v

EI

+

=

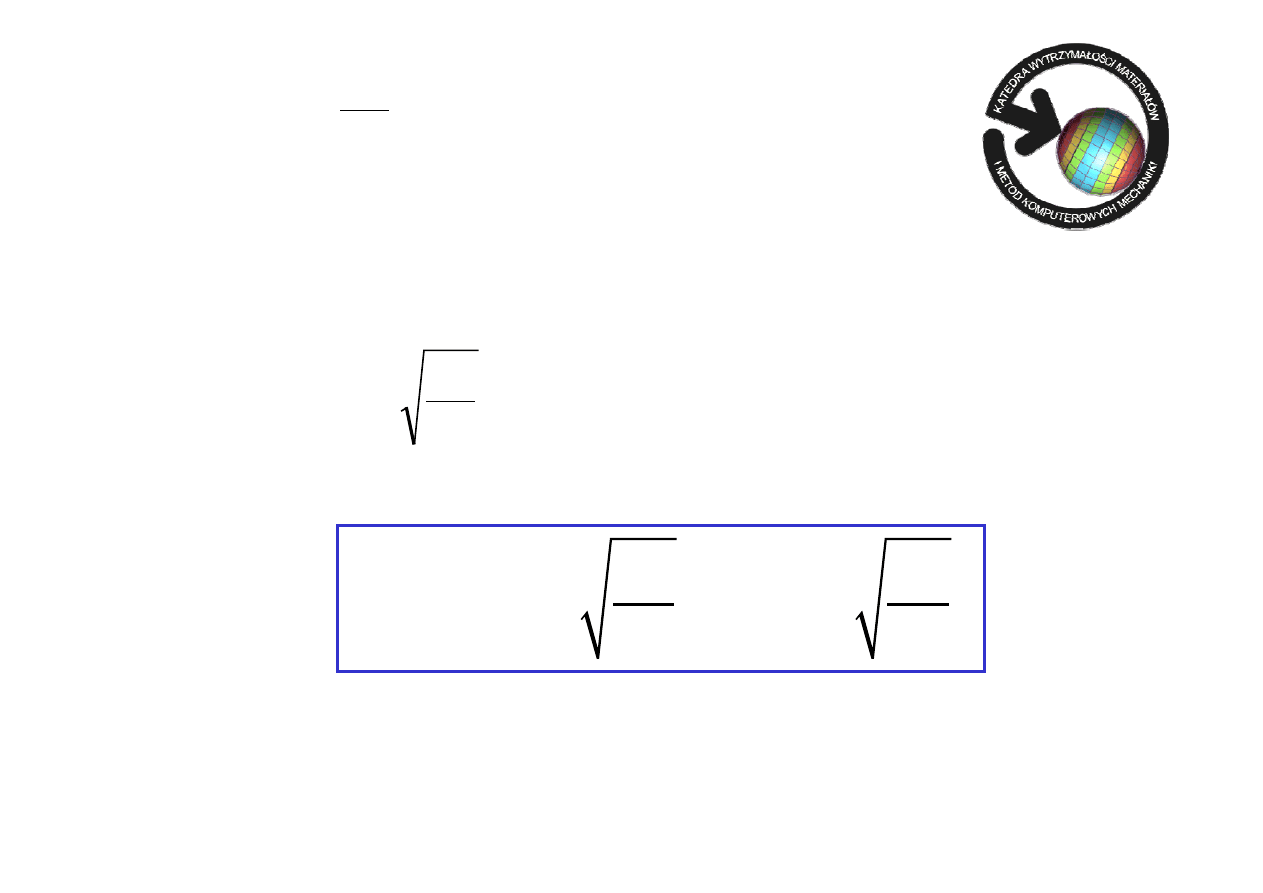
Podstawiając

2

k

EI

P

kr

=

( )

sin

cos

v x

A

kx B

kx

=

+

otrzymujemy:

2

"

0;

v

k v

+

=

Całka ogólna ma postać:

( )

sin

cos

kr

kr

P

P

v x

A

x B

x

EI

EI

=

+

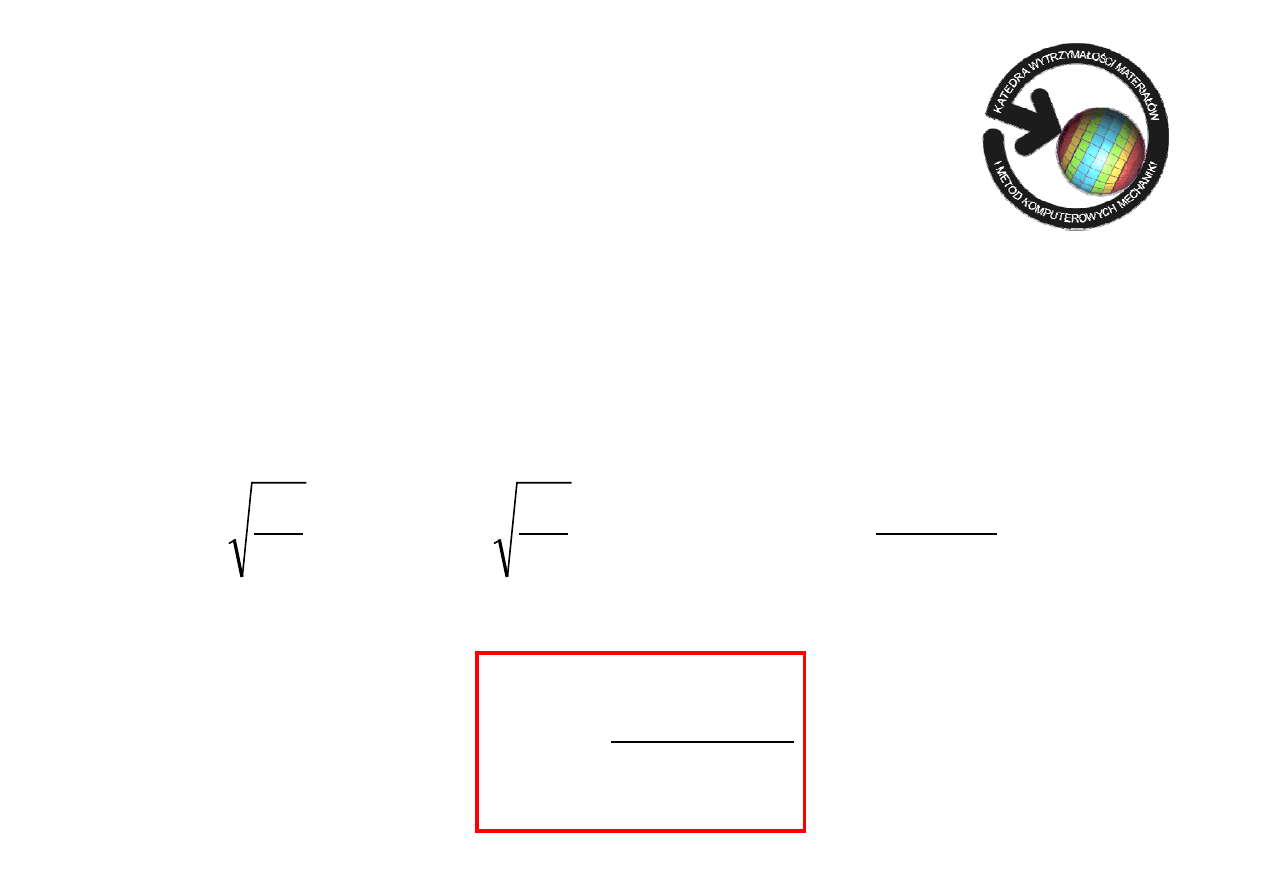
Podstawiając:

EI

P

k

kr

=

otrzymujemy:

Warunki brzegowe:

0,

0,

0

Dla x

v

B

=

= ⇒

=

( )

sin

cos

v x

A

kx B

kx

=

+

,

0,

sin

0

Dla x l v

A

kl

=

= ⇒

=

Warunek

⇒

lub gdy:

czyli:

,...

3

,

2

,

1

,

=

=

n

n

kl

π

podstawiając:

0

sin

=

kl

A

jest spełniony gdy A=0,

0

sin

=

kl

EI

P

k

kr

=

π

n

l

EI

P

kr

=

⇒

2

2

2

l

EI

n

P

kr

π

=

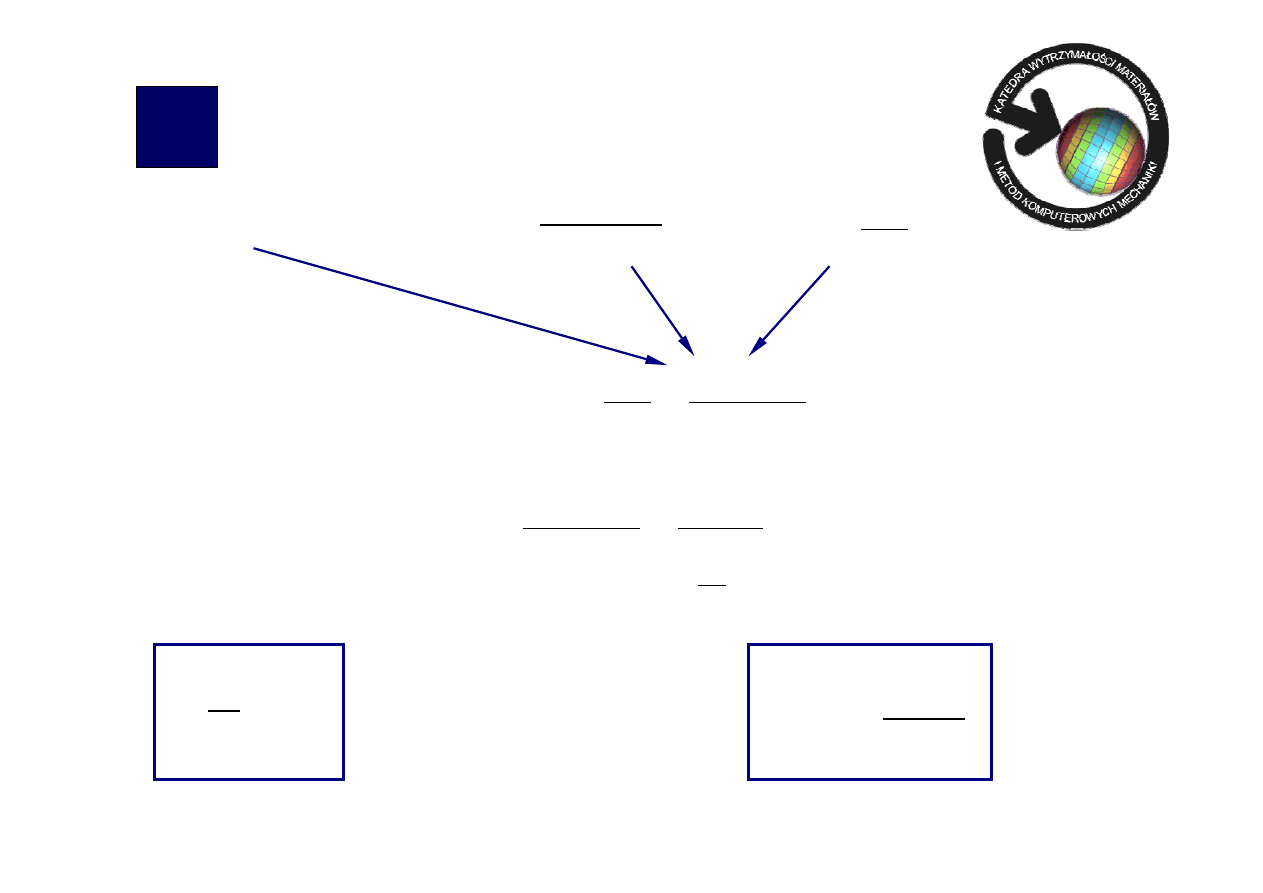
Wzór na Eulerowską siłą krytyczną:

2

2

2

r

kr

l

EI

n

P

π

=

2

2

2

r

kr

l

EI

n

P

π

=

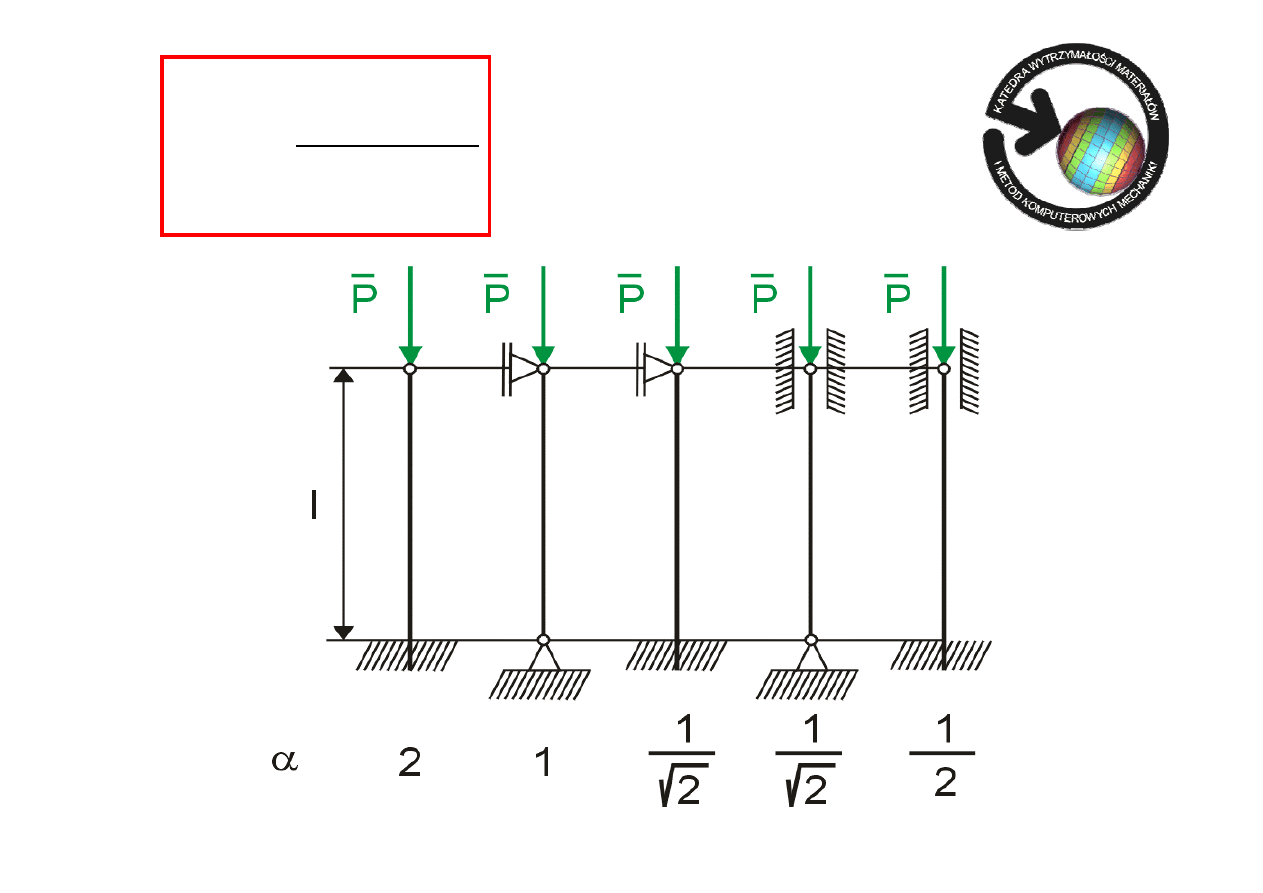
Gdzie:

l

l

r

⋅

=

α

N

aprężenia

Naprężenie krytyczne :

A

l

EAi

A

P

r

kr

kr

2

2

2

π

σ

=

=

2

Ai

I

=

2

2

2

r

kr

l

EI

n

P

π

=

A

P

kr

kr

=

σ

2

2

2

2

2

⎟

⎠

⎞

⎜

⎝

⎛

=

=

i

l

E

A

l

EAi

r

r

kr

π

π

σ

Przekształcając:

smukłość pręta

λ

=

i

l

r

eulerowskie naprężenie krytyczne

2

2

λ

π

σ

E

kr

=

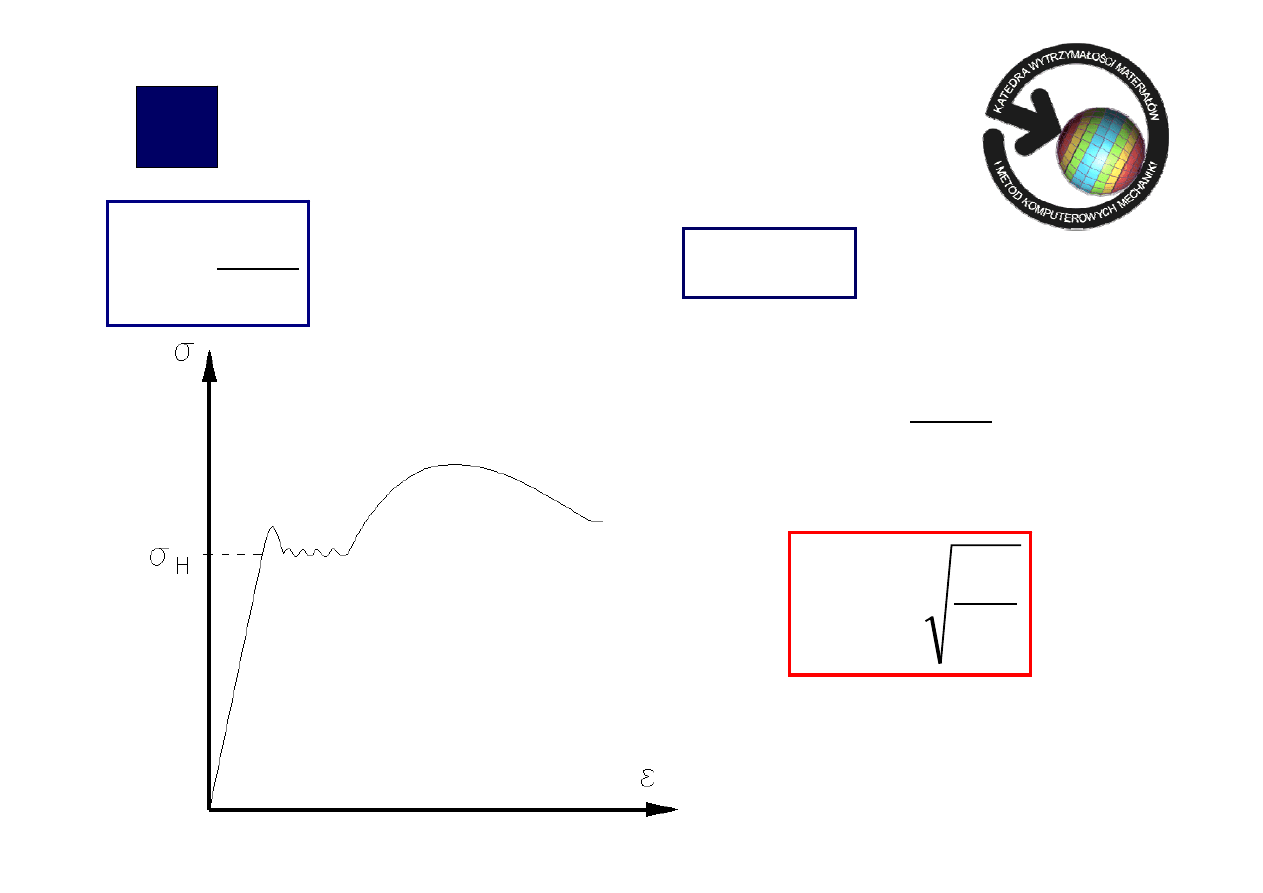
N

aprężenia

2

2

λ

π

σ

E

kr

=

jest prawdziwe tylko gdy

H

kr

σ

σ

≤

(granica
proporcjonalności)

2

2

gr

H

E

λ

π

σ

=

⇓

H

gr

E

σ

π

λ

=

smukłość graniczna

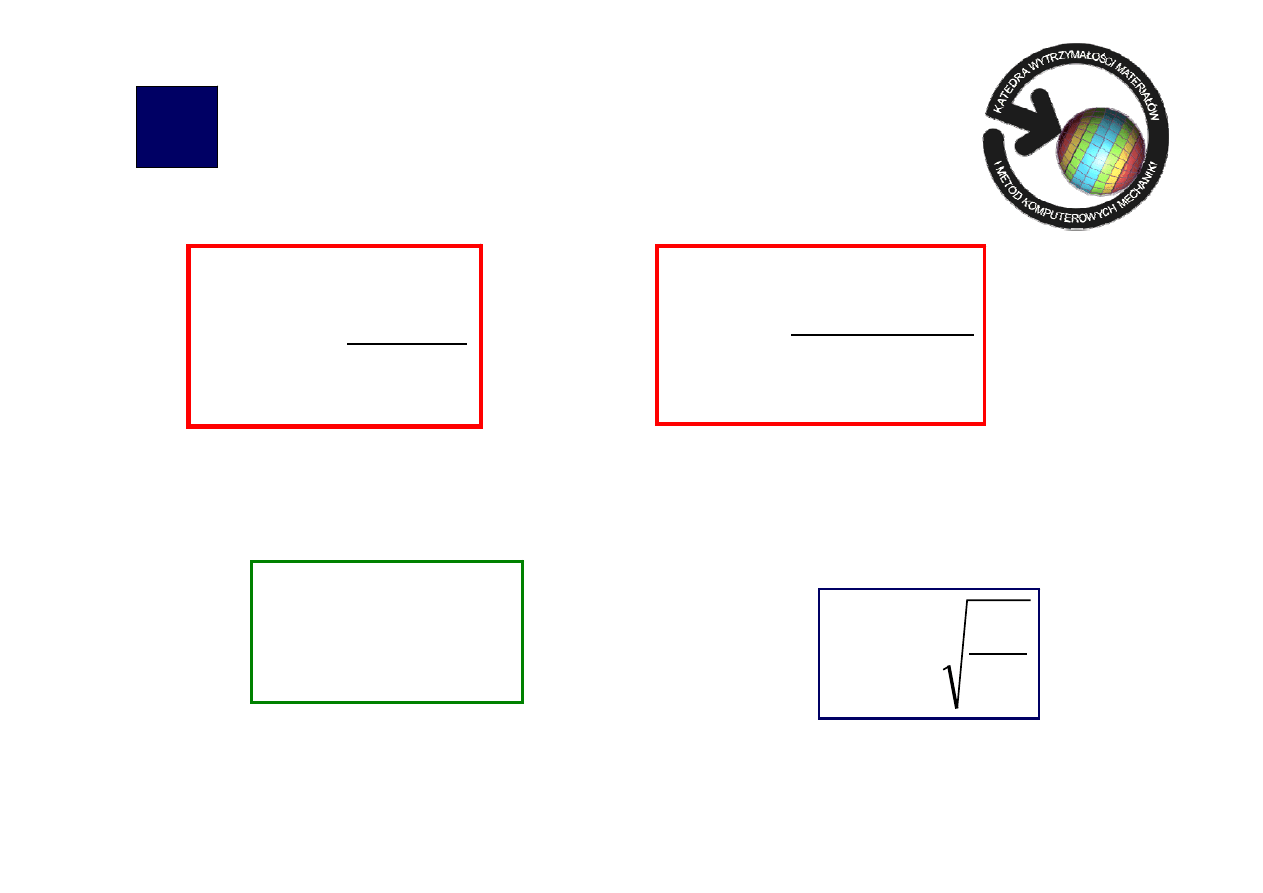
P

odsumowanie

2

2

λ

π

σ

E

kr

=

2

2

2

r

kr

l

EI

n

P

π

=

Siła krytyczna

Naprężenie krytyczne

TYLKO WTEDY GDY:

gr

λ

λ

>

H

gr

E

σ

π

λ

=

smukłość graniczna

gdzie

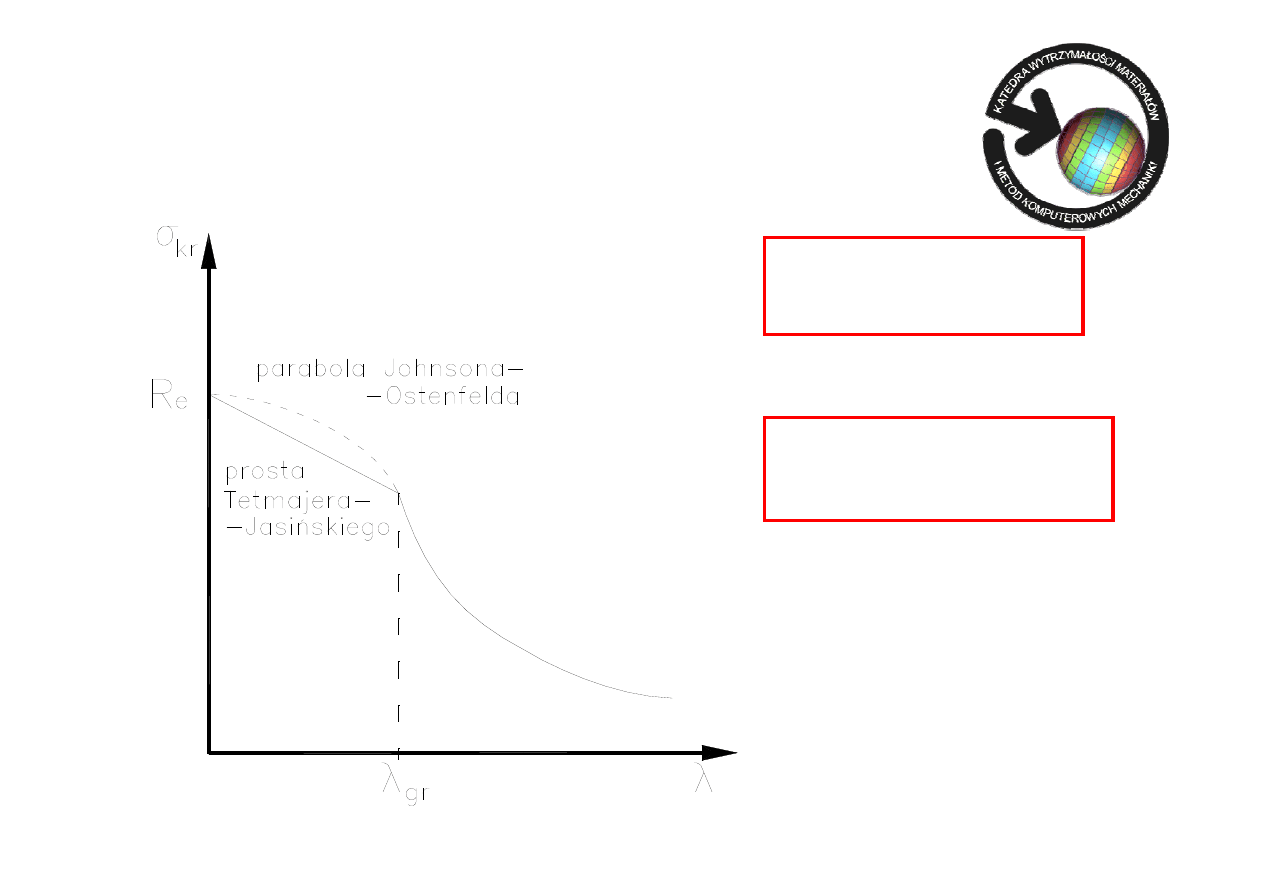
Gdy

i

e

kr

R

<

σ

Stosujemy zależności eksperymentalne:

λ

σ

b

a

kr

−

=

2

λ

σ

B

A

kr

−

=

Wzór Tetmajera-Jasińskiego

Wzór Johnsona-Ostenfelda

Gdzie:

A, B, a, b – stałe materiałowe

ustalone doświadczalnie

gr

λ

λ

<

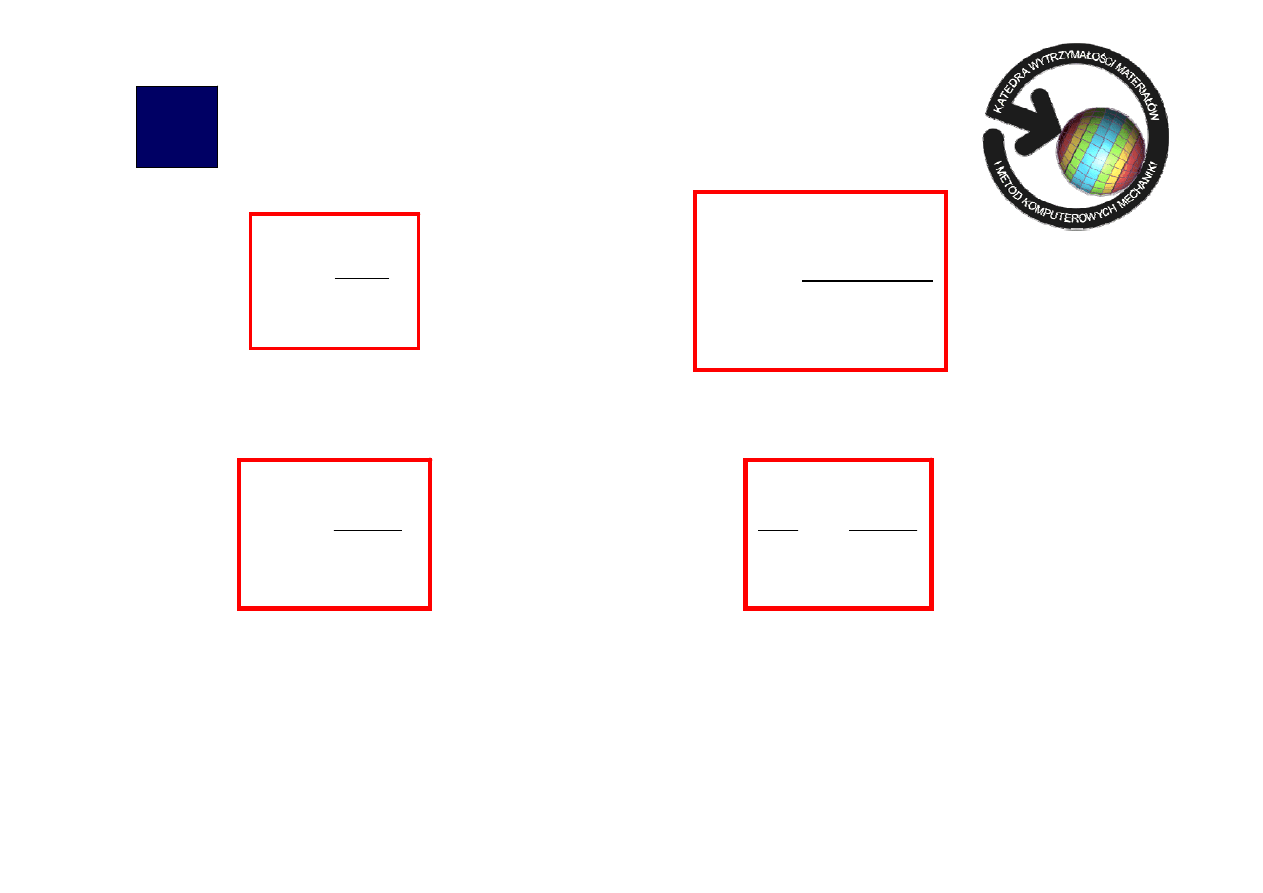
K

ryteria wyboczenia

,

w

kr

n

σ

σ

≤

2

2

r

w

l

n

EI

P

π

≤

,

w

kr

n

P

P

≤

w

kr

n

A

P

σ

≤

n

w

– współczynnik bezpieczeństwa ze względu na wyboczenie

czyli

czyli

U

proszczone kryterium wyboczenia

,

c

k

β

σ

≤

c

k

A

P

β

≤

k

c

– dopuszczalne naprężenie materiału na ściskanie

czyli

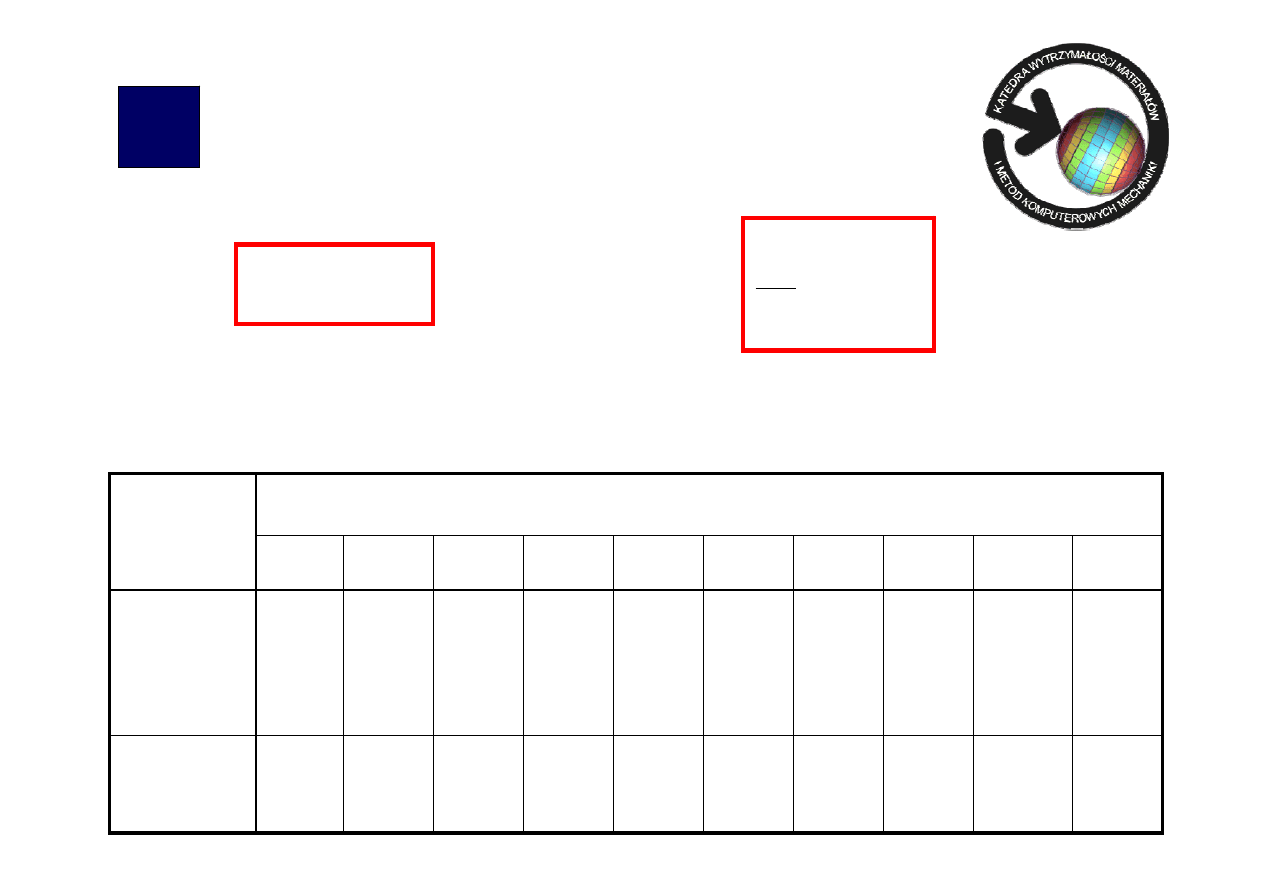
β – współczynnik zależny od smukłości pręta i rodzaju materiału

0,110

0,140

0,180

0,230

0,300

0,410

0,600

0,770

0,880

0,950

18G2
18G2A

0,160

0,200

0,250

0,320

0,420

0,550

0,680

0,800

0,890

0,950

St05
St35
St35x

200

180

160

140

120

100

80

60

40

20

λ

Materiał