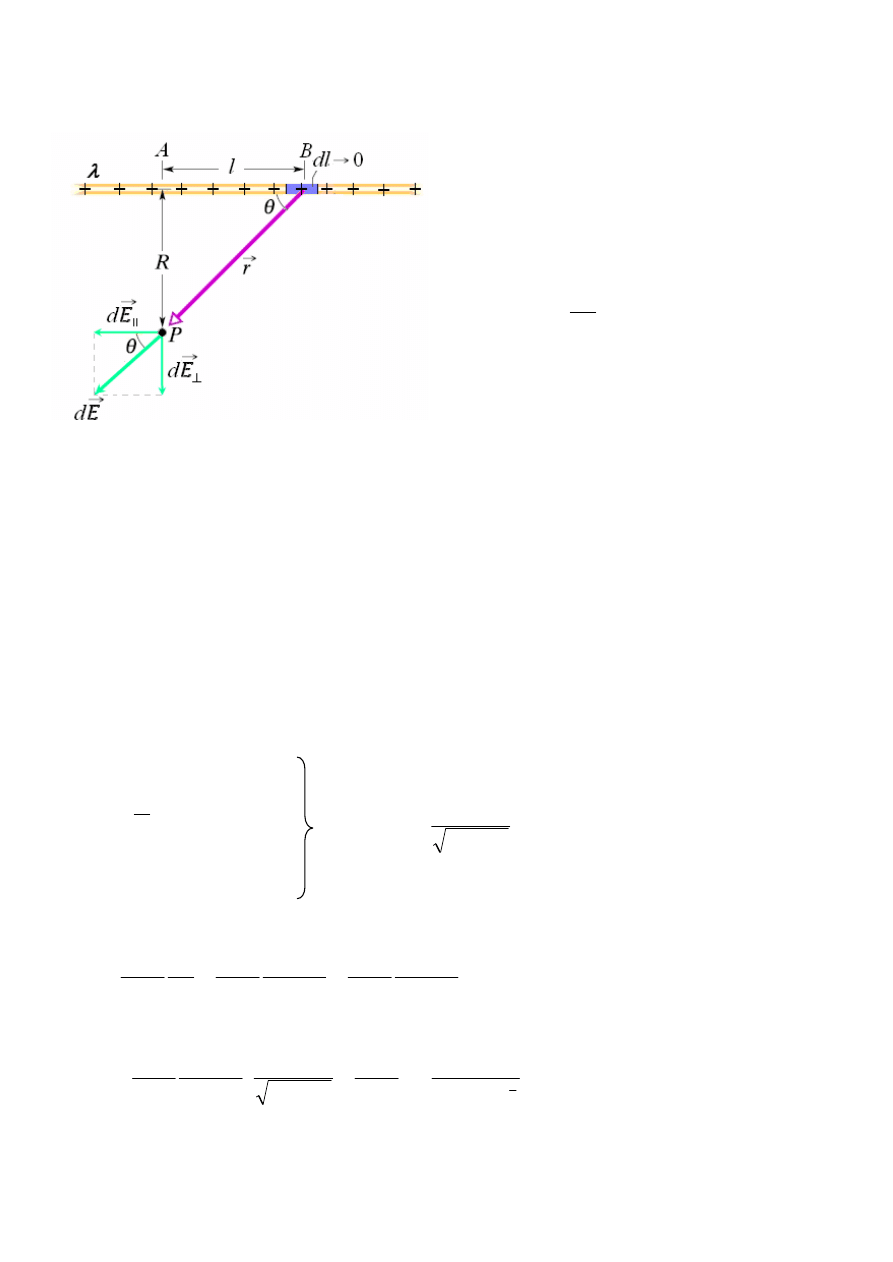
Natężenie pola elektrostatycznego wytworzonego przez cienki nieskończenie
długi jednorodnie naładowany pręt – na podstawie prawa Coulomba

suma składowych równoległych do osi pręta (dE

||

) w punkcie P wynosi 0 – dla każdego

(nieskończenie małego) odcinka dl można znaleźć inny odcinek dl’ (po przeciwnej stronie
punktu A, który wytwarza w punkcie P pole elektryczne o wartości dE’ równej co do wartości
lecz przeciwnie skierowanej

∫

=

=

0

||

||

dE

E

składowe prostopadłe do osi pręta (dE

⊥

) sumują się:

∫

⊥

⊥

=

dE

E

gdzie

θ

sin

dE

dE

=

⊥

z

∆

ABP:

r

R

=

θ

sin

z twierdzenia Pitagorasa:

2

2

2

R

l

r

+

=

przyczynek od odcinka dl do natężenia pola elektrycznego w punkcie P:

2

2

0

2

2

0

2

0

4

1

4

1

4

1

R

l

l

d

R

l

q

d

r

q

d

dE

+

=

+

=

=

λ

πε

πε

πε

składowa prostopadła do osi pręta:

l

d

R

l

R

R

l

R

R

l

l

d

dE

2

3

)

(

1

4

1

4

1

2

2

0

2

2

2

2

0

+

=

+

⋅

+

=

⊥

λ

πε

λ

πε

gęstość liniowa ładunku

l

d

q

d

≡

λ

→

2

2

sin

R

l

R

+

=

θ

suma składowych prostopadłych – dwukrotna wartość całki w granicach od punktu A do



...

l

d

R

l

R

l

d

R

l

R

E

E

∫

∫

∞

∞

⊥

=

+

=

+

=

=

0

2

2

0

0

2

2

0

2

3

2

3

)

(

1

2

1

)

(

1

4

1

2

λ

πε

λ

πε

całka funkcji niewymiernej

korzystamy ze wzoru:

2

1

2

3

)

(

)

(

2

2

2

2

2

a

x

a

x

a

x

dx

+

=

+

∫

(np. Halliday, Resnick, Walker „Podstawy fizyki” t.3, dodatek E, s. A13)

stąd

2

2

2

2

0

2

2

2

0

2

2

1

0

0

1

1

1

1

)

(

1

2

2

3

R

R

R

R

l

l

R

l

d

R

l

R

=

















+

−

+

=













+

=

+

∞

∞

∞

∫

= 1

= 0

po podstawieniu otrzymujemy

R

R

R

...

λ

πε

λ

πε

0

2

0

2

1

1

2

1

=

=

R

E

λ

πε

0

2

1

=

gdzie R – odległość punktu obserwacji od osi pręta