Budownictwo WIŚ

Projekt nr 2. Stan naprężenia w punkcie. Prawo Hooke’a.

a) przypadek 3D (trójwymiarowy stan naprężenia)
b) przypadek 2D (płaski stan naprężenia)

Celem ćwiczenia jest opanowanie podstawowych pojęć i algorytmów, oraz ich wizualizacja.
Szczegółowy zakres podaje się poniżej.

a.

Dla zadanej macierzy (tensora) naprężeń w 3D

σ

T i pewnej płaszczyzny

π

o kierunku

wersora normalnej zewnętrznej n należy:

1.

Narysować kostkę naprężeń (zgodnie z zasadami rzutu aksonometrycznego, przyjmując
jednolitą skalę dla wszystkich składowych naprężeń)

2.

Narysować (w aksonometrii) ślad przecięcia się kostki i płaszczyzny

π

. Wyznaczyć

(podać współrzędne i długości) i narysować (w skali naprężeń) wektor naprężenia p dla

pł.

π

oraz jego składowe styczną

τ

i normalną

n

σ .

3.

Znaleźć naprężenia główne (rozwiązanie równania 3-go stopnia metodą Cardano) i
dokonać sprawdzenia wyznaczając niezmienniki przez naprężenia główne

4.

Wyznaczyć analitycznie i narysować (w aksonometrii) kierunki działania naprężeń
głównych. Sprawdzić warunek ich ortogonalności. Narysować kostkę naprężeń
obróconą do kierunków głównych (używać tej samej skali co w p. 1 i 2)

5.

Wykonać konstrukcję kół Mohra dla wyznaczonych naprężeń głównych (p 1.18
wykładu)

6.

Dokonać sprawdzenia rozkładu wektora naprężenia

n

σ

τ

p

+

=

(z p. 2) metodą

konstrukcyjną (p. 1.18 wykładu) na podstawie kół Mohra

7.

Dokonać rozkładu tensora naprężeń na aksjator i dewiator. Wyznaczyć niezmienniki
J

2

, J

3

dewiatora.

8.

Wyznaczyć niezmienniki (p,q,

θ)

(ciśnienie, intensywność, kąt Lode’go) i narysować je

w przestrzeni naprężeń głównych.

9.

Wyznaczyć tensor odkształceń, zakładając że naprężenia dane są w MPa oraz
przyjmując wartości modułów E i

ν

jak dla stali.

10. Wyznaczyć odkształcenie liniowe wzdłuż kierunku n

b.

Mając daną macierz naprężeń

σ

T dla płaskiego stanu naprężeń należy:

1.

Wyznaczyć naprężenia i kierunki główne analitycznie

2.

Narysować kostkę naprężeń (w skali) w początkowym układzie współrzędnych i w
kierunkach głównych

3.

Wyznaczyć naprężenia główne graficznie (koło Mohra 2D)

4.

Wyznaczyć tensor odkształceń, zakładając że naprężenia dane są w kPa oraz przyjmując
wartości modułów E i

ν

jak dla betonu B30.

Uwagi:

1. Dane wg nr PESEL
2. Wykonując stosowne rysunki należy używać linijki z podziałką mm i cyrkla.
3. Ich skale należy dobrać tak by a) mieściły się na formacie A4 b) były czytelne bez

użycia lupy

4. Obliczenia wykonywać z dokładnością 3±5 cyfr znaczących (nie mylić z ilością

miejsc po przecinku.

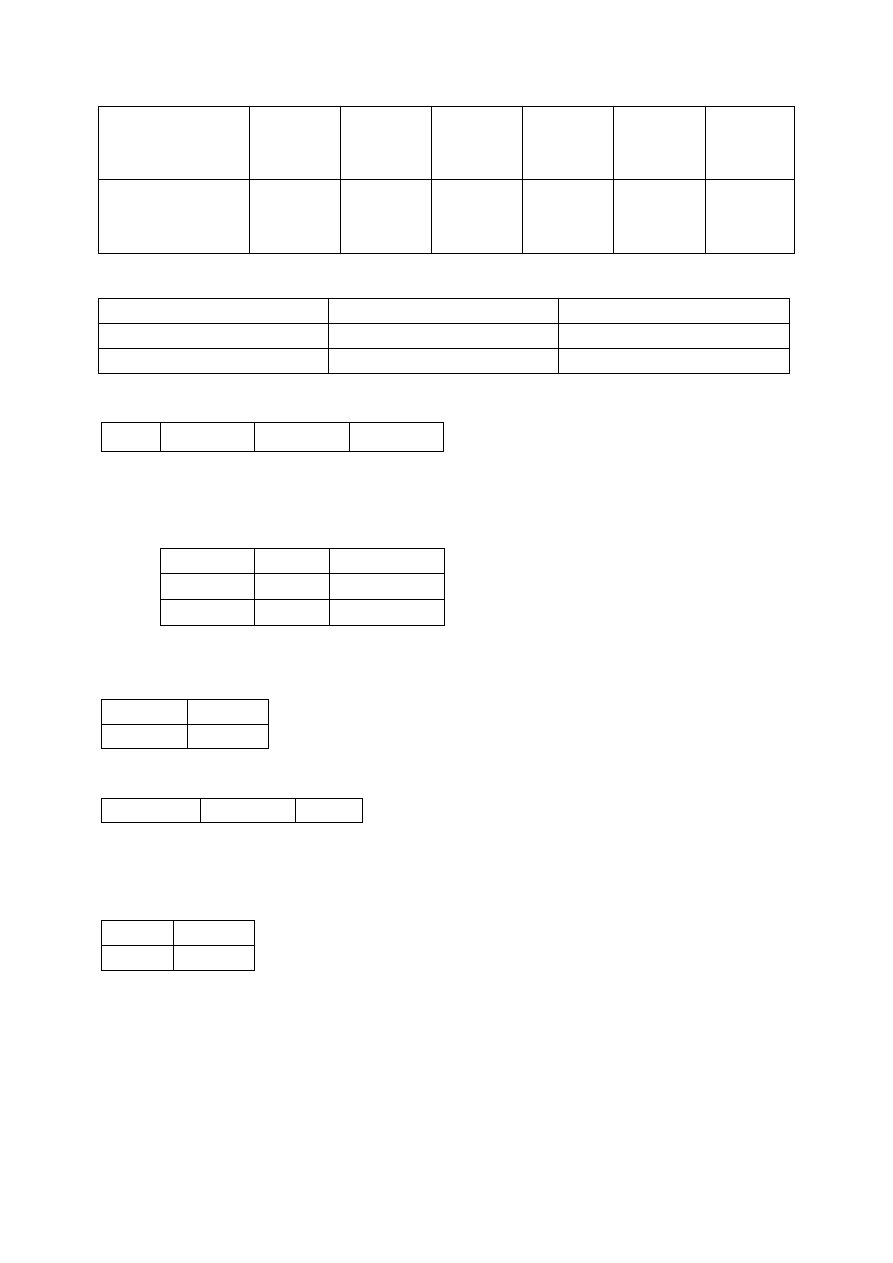
PESEL
Kolejne cyfry
pogrupowane

87

06

07

02

97

3

OZNACZENIE
Liczb do
tematu

L1

L2

L3

L4

L5

L6

a) T

σ

3D =

L1/3 – L2

L2 – L3

L3

sym.

L4

L4 – L5

sym.

sym.

Cz. całk. (L5/L6)*

wektor normalny do płaszczyzny (przed unormowaniem):
m

L2

L3

L4

przykład:

T

σ

3D= m=(6,7,2)

23

-1

7

-1

2

-95

7

-95

32

b) T

σ

2D=

L2-L3

L4-L5

sym.

L3

wektor normalny do płaszczyzny (przed unormowaniem):
m

L2

L6

przykład:

T

σ

2D=

m=(6,3)

-1

-95

-95

7