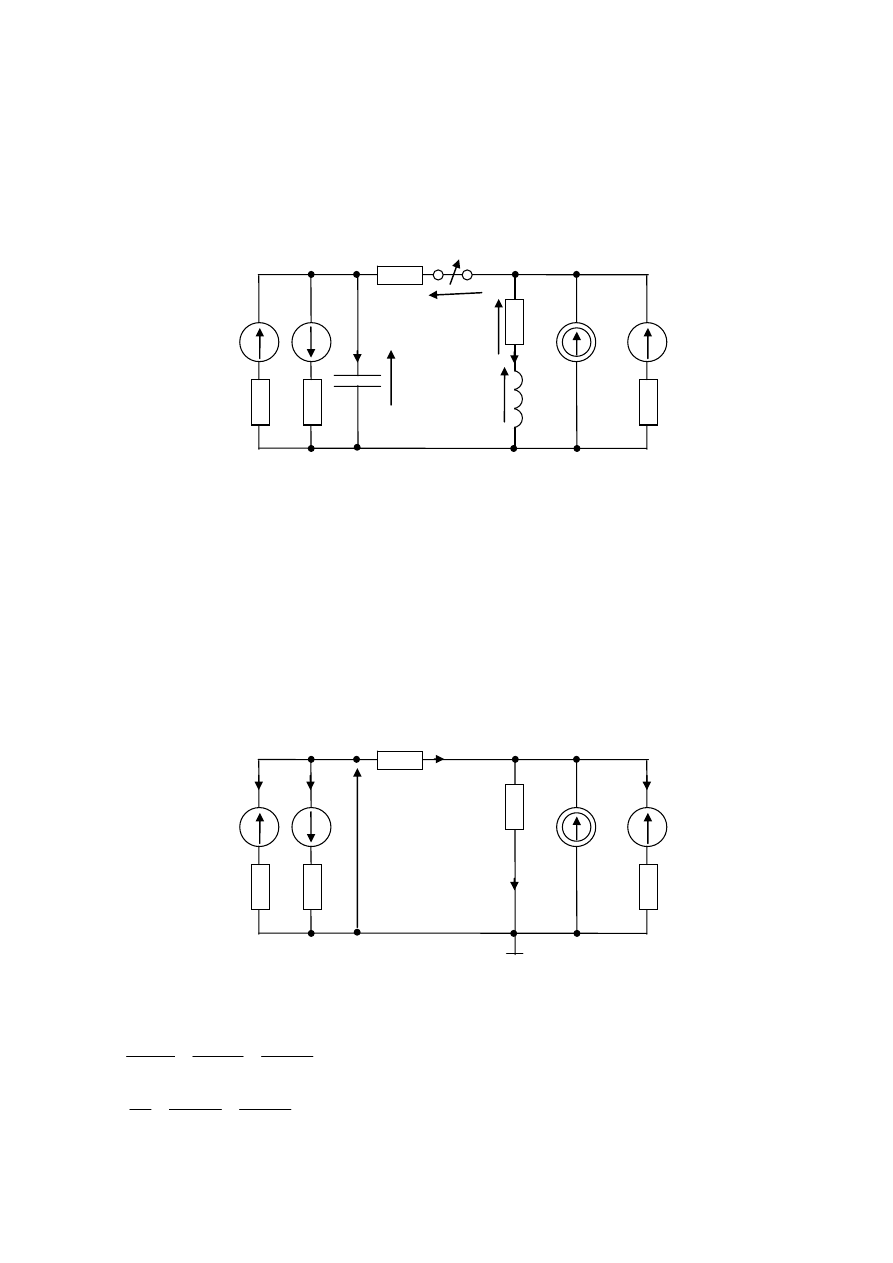
A. Oblicz napięcie na wyłączniku

( )

t

u

w

A

j

1

5

=

w stanie nieustalonym. Przed komutacją układ był w

stanie ustalonym. Narysuj przebiegi napięcia i prądu w cewce i kondensatorze. Dane:

,

,

,

,

V

e

6

1

=

V

e

4

2

=

V

e

6

4

=

Ω

=

=

2

2

1

R

R

,

Ω

=

=

=

1

6

4

3

R

R

R

,

,

.

H

L

1

.

0

6

=

F

C

1

.

0

7

=

e

1

i

C

i

L

R

6

L

6

R

3

C

7

u

w

R

1

t=0

u

C

u

L

u

R6

j

5

e

2

R

2

e

4

R

4

Rozwiązanie:
Po otwarciu wyłącznika układ można podzielić na dwie części (dwa układy I rzędu).
Poszukiwane napięcie, po wyznaczeniu napięcia i prądu cewki oraz napięcia na
kondensatorze, można obliczyć z napięciowego prawa Kirchhoffa

L

L

C

w

u

R

i

u

u

−

−

=

6

1. Wyznaczamy warunki początkowe – wyłącznik zamknięty
Ponieważ wszystkie źródła są źródłami napięcia i prądu stałego cewkę idealna zastępujemy
zworą, a kondensator idealny traktujemy jako przerwę. Otrzymujemy więc schemat, w
którym dowolną metodą wyznaczamy zaznaczone wielkości

( )

−

0

C

u

oraz

( )

−

0

L

i

.

e

1

i

L

(0)

R

6

R

3

R

1

u

C

(0)

j

5

e

2

R

2

1

2

i

1

i

2

i

4

i

3

e

4

R

4

Najłatwiej wyznaczyć te wielkości korzystając z metody napięć węzłowych:

0

:

2

0

:

1

5

3

4

3

2

1

=

−

−

+

=

+

+

j

i

i

i

i

i

i

L

0

:

2

0

:

1

5

3

2

1

4

4

2

6

2

3

2

1

2

2

1

1

1

1

=

−

−

−

−

+

=

−

+

+

+

−

j

R

V

V

R

e

V

R

V

R

V

V

R

e

V

R

e

V

1

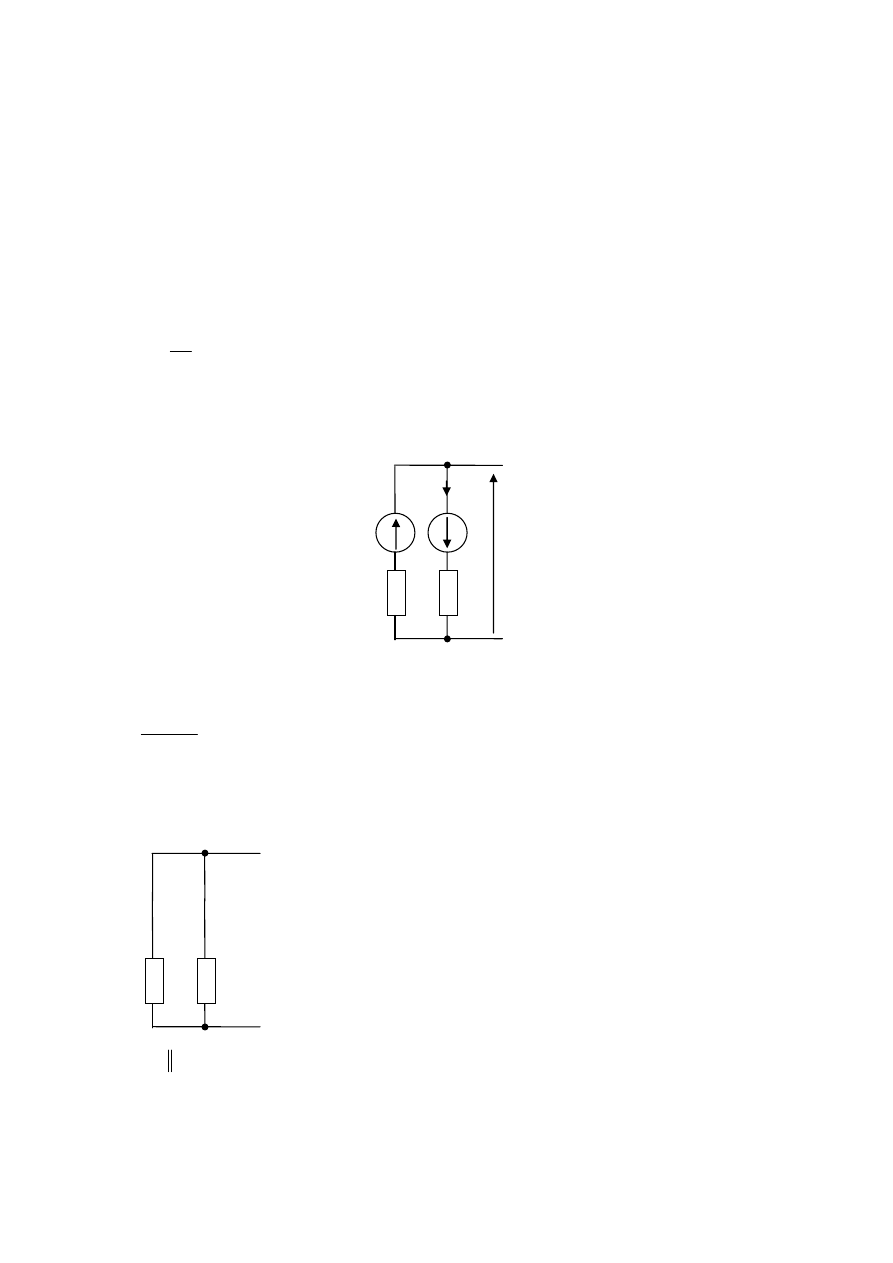
Podstawiając dane liczbowe otrzymujemy układ dwóch równań liniowych:

7

3

1

2

2

1

2

1

=

+

−

=

−

V

V

V

V

którego rozwiązaniem są napięcia węzłowe:

V

V

V

V

3

2

2

1

=

=

Na tej podstawie wyznaczamy warunki początkowe:

( )

( )

A

R

V

i

V

V

u

L

C

3

0

2

0

6

2

1

=

=

=

=

−

−

2. Obecnie rozpatrzymy prawą część układu: RC
Wyznaczamy dwójnik Thevenina widziany z zacisków kondensatora

e

1

R

1

u

AB

e

2

R

2

1

i

2

A

B

Napięcie

wyznaczyć można wieloma metodami. Zauważmy, że w układzie płynie jeden

prąd

AB

u

2

i

A

R

R

e

e

i

5

.

2

2

1

2

1

2

=

+

+

=

z NPK :

V

e

R

i

u

AB

1

2

2

2

=

−

=

Następnie obliczamy rezystancję zastępczą

R

1

R

2

A

B

Ω

=

=

1

2

1

R

R

R

Z

Z zatem dwójnik Thevenina ma postać:

2

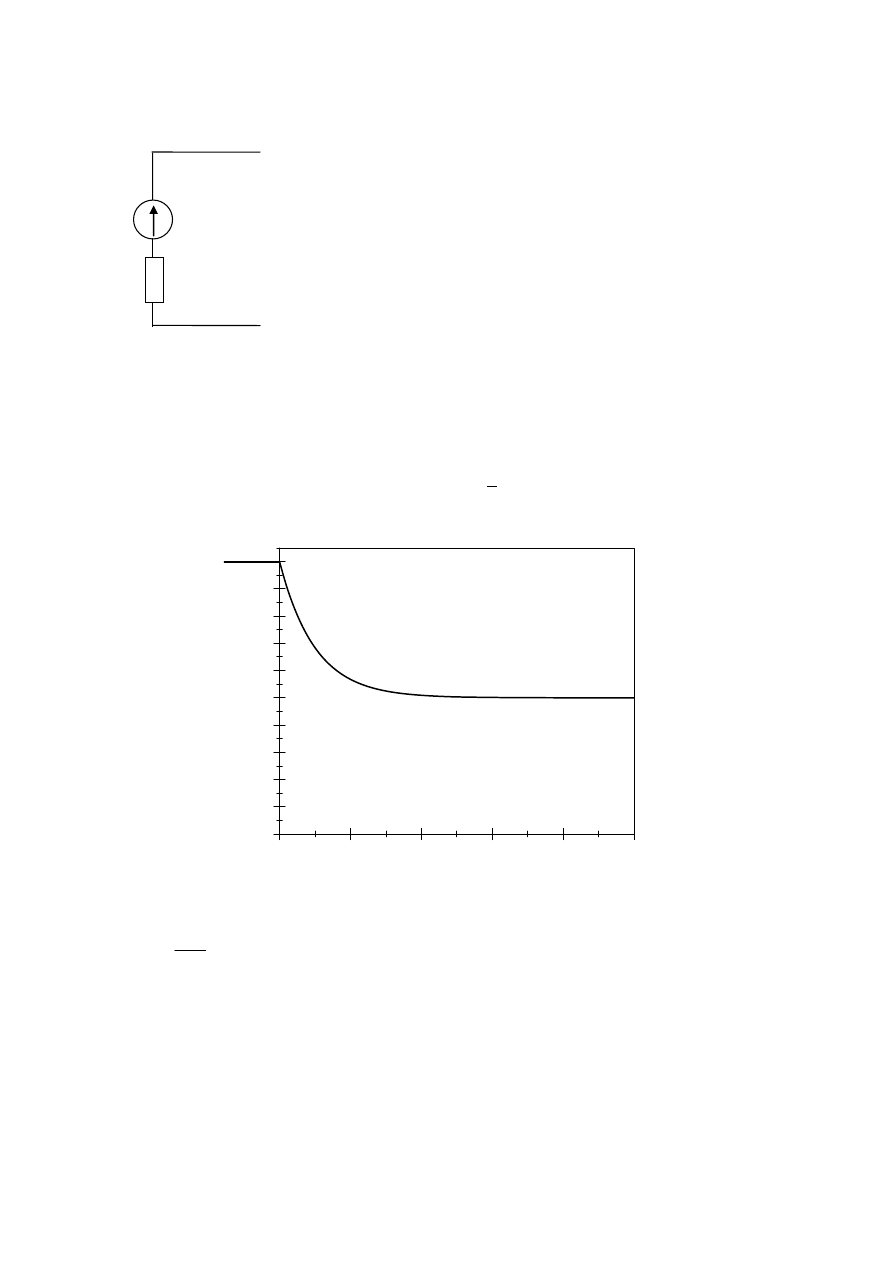
e

z

=1V

R

Z

=1

Ω

A

B

Stąd obliczamy:
składową wymuszoną:

V

e

u

Z

Cw

1

=

=

stałą czasową:

s

C

R

Z

1

.

0

7

=

=

τ

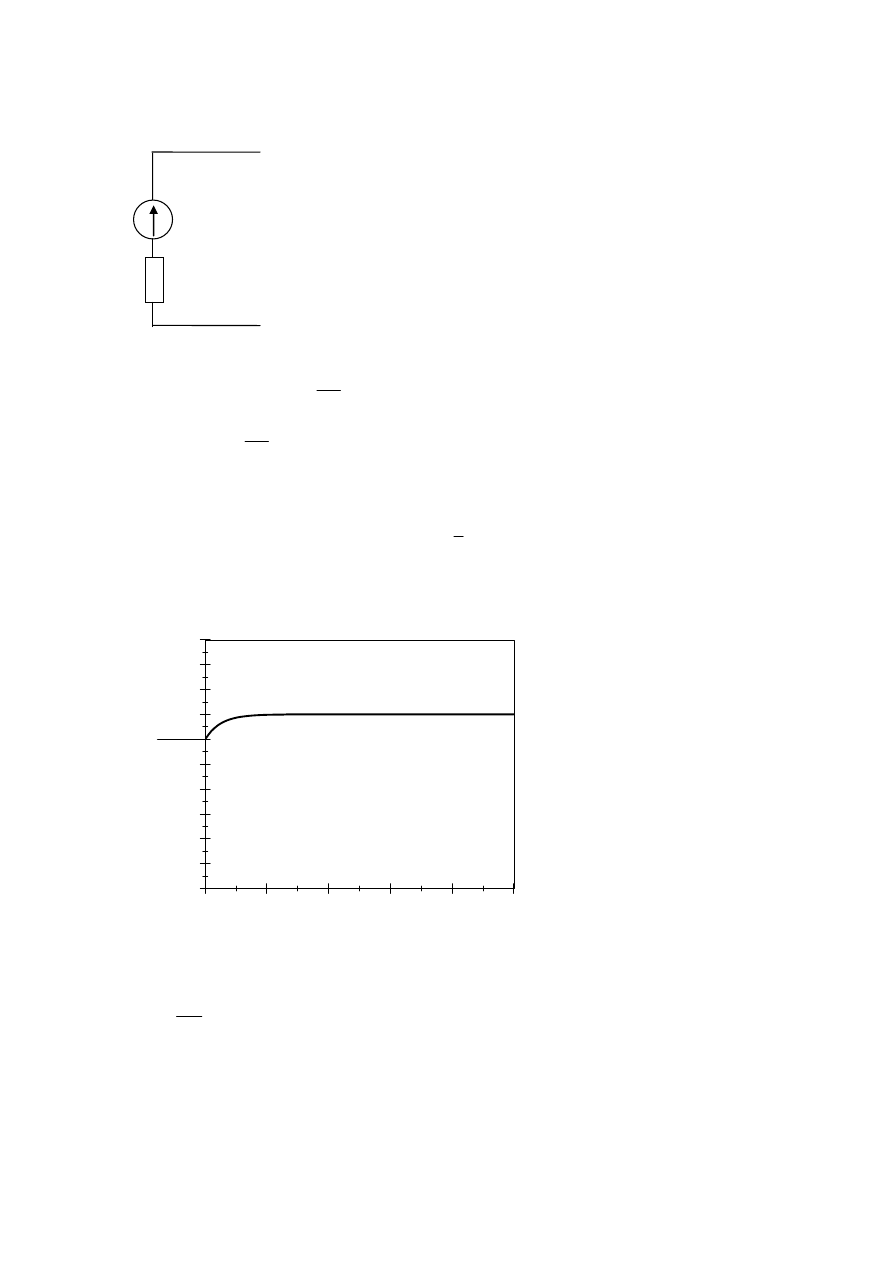
W efekcie napięcie na kondensatorze wyraża się wzorem:

( )

( )

( )

( )

(

)

t

-

Cw

C

Cw

C

u

u

t

u

t

u

10

t

-

e

1

e

0

0

+

=

⋅

−

+

=

τ

0,0

0,2

0,4

0,6

0,8

1,0

0,0

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

1,8

2,0

uc

t[s]

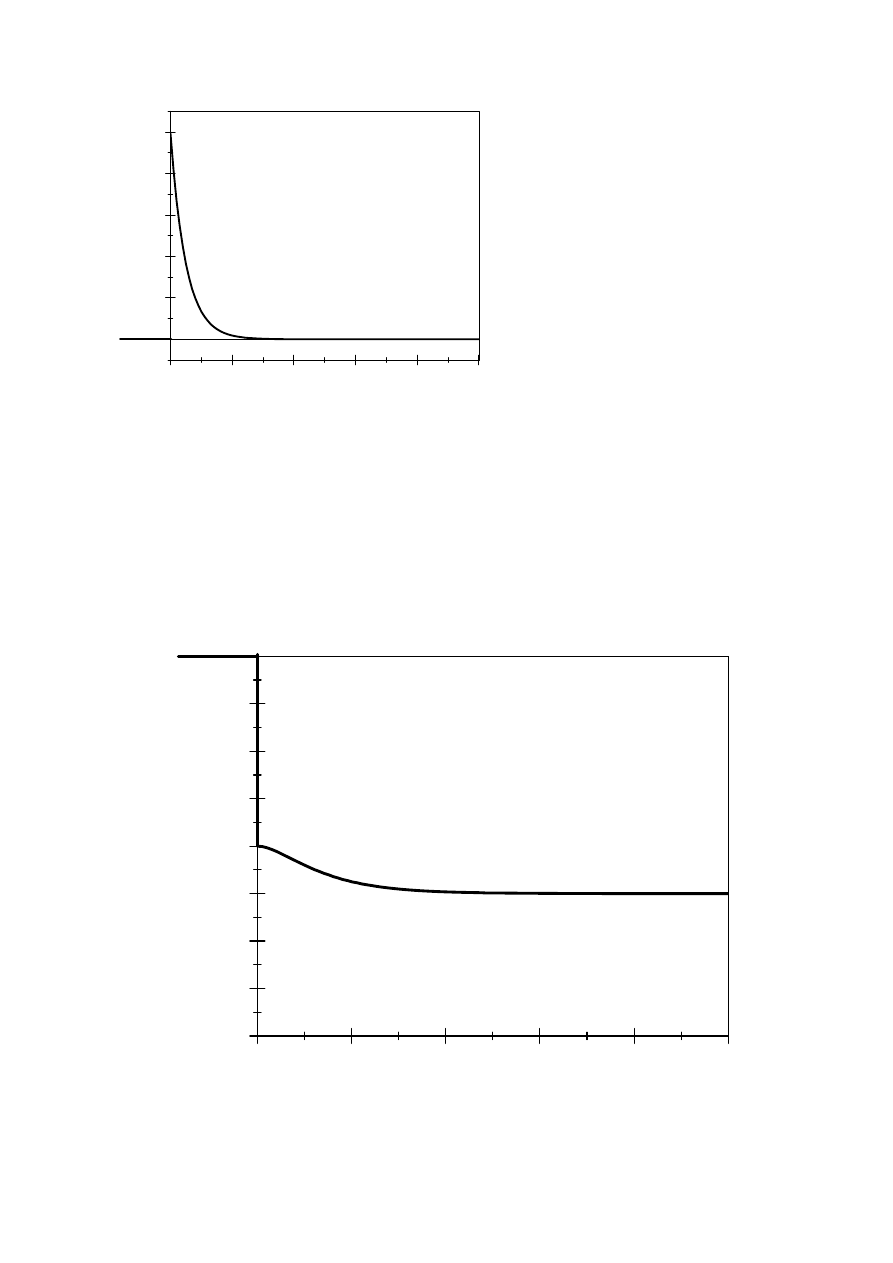
Prąd kondensatora wyznaczamy z zależności:

( )

t

C

C

dt

du

C

t

i

10

e

−

−

=

=

3

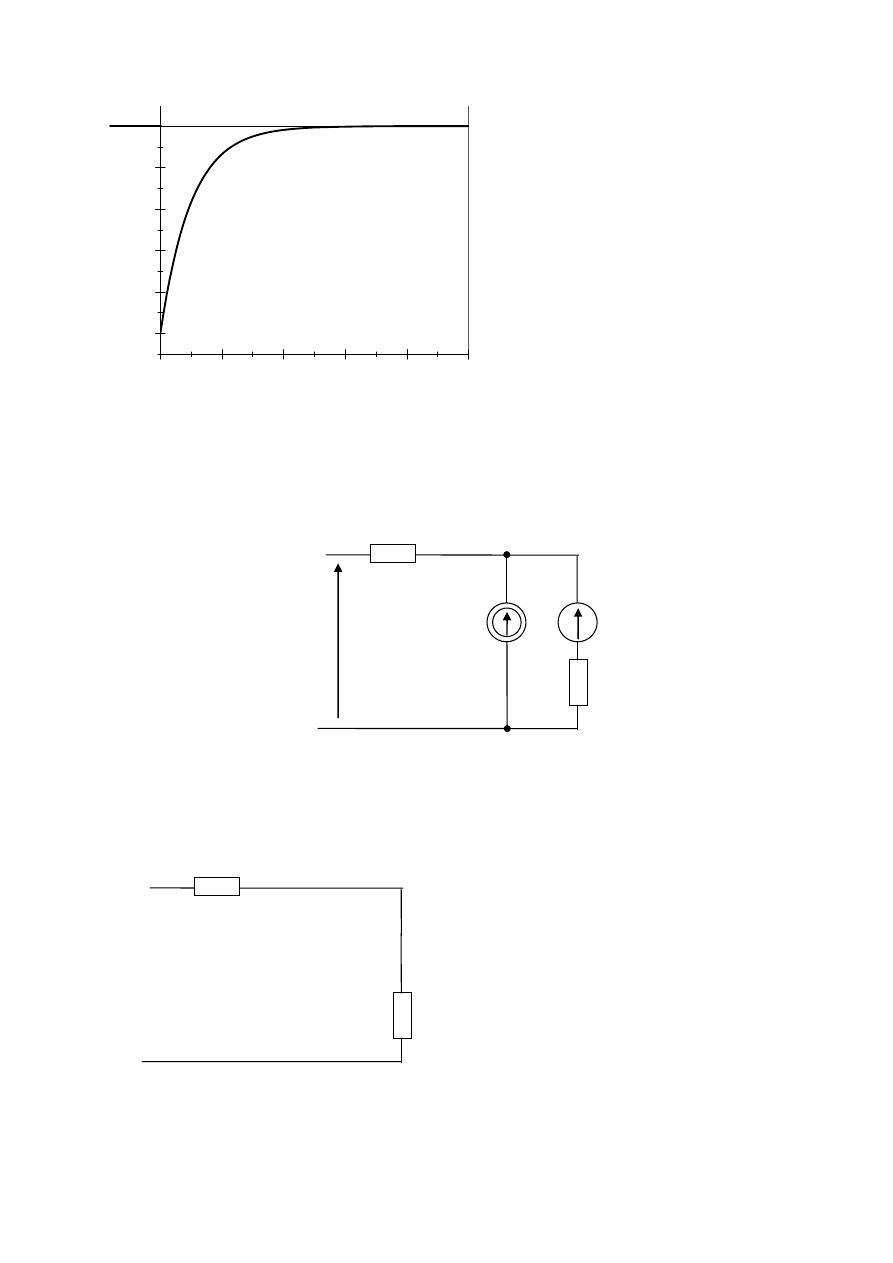
0,0

0,2

0,4

0,6

0,8

1,0

-1,0

-0,8

-0,6

-0,4

-0,2

0,0

ic

t[s]

Obecnie analogicznie rozpatrujemy układ RL (prawą część układu wyjściowego)


Wyznaczamy dwójnik Thevenina widziany z zacisków cewki

R

6

j

5

A

B

u

AB

e

4

R

4

Napięcie

wyznaczyć można wieloma metodami. Zauważmy, że w układzie płynie jeden

prąd

AB

u

A

1

=

j

5

z NPK :

V

e

R

i

u

AB

7

4

4

5

=

+

=

Następnie obliczamy rezystancję zastępczą

R

6

A

B

R

4

Ω

=

+

=

2

6

4

R

R

R

Z

Z zatem dwójnik Thevenina ma postać:

4

e

z

=7V

R

Z

=2

Ω

A

B

Stąd obliczamy:

składową wymuszoną:

A

R

e

i

Z

Z

Lw

5

.

3

=

=

stałą czasową:

s

R

L

Z

05

.

0

=

=

τ

W efekcie prąd kondensatora wyraża się wzorem:

( )

( )

( )

( )

(

)

t

-

Lw

L

Lw

L

i

i

t

i

t

i

20

t

-

e

5

.

0

5

.

3

e

0

0

−

=

⋅

−

+

=

τ

0,0

0,2

0,4

0,6

0,8

1,0

0,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

5,0

uL

t[s]

Napięcie na cewce wyznaczamy z zależności:

( )

t

L

L

dt

di

L

t

u

20

e

−

=

=

5

0,0

0,2

0,4

0,6

0,8

1,0

0,0

0,2

0,4

0,6

0,8

1,0

ic

t[s]

W efekcie

t

t

L

L

C

w

u

R

i

u

u

-20

-10

6

e

5

.

0

e

5

.

2

−

+

−

=

−

−

=

(tego rysować nie trzeba na sprawdzianie)

0,0

0,2

0,4

0,6

0,8

1,0

-4,0

-3,5

-3,0

-2,5

-2,0

-1,5

-1,0

-0,5

0,0

iL

t[s]

6

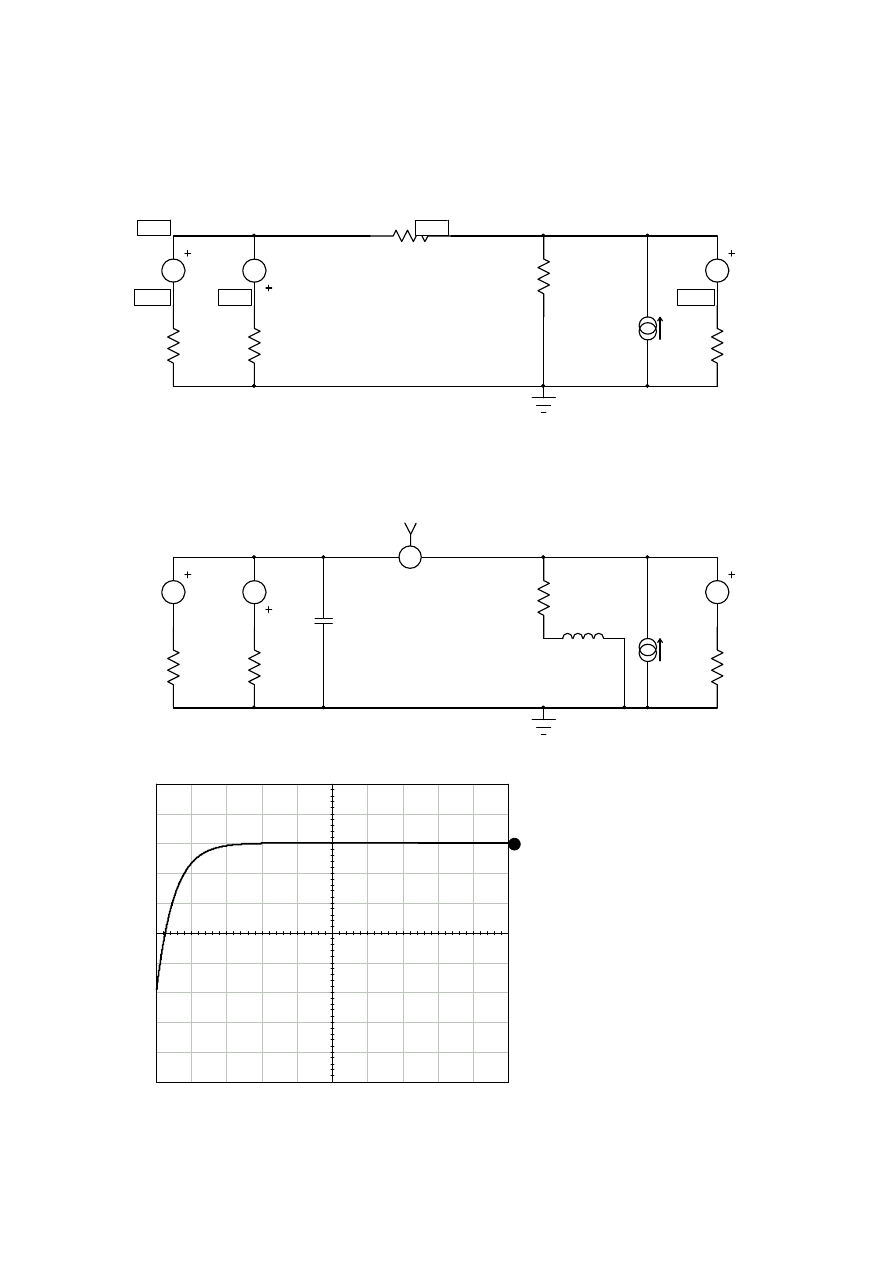
Wyniki ze SPICEa
1. warunki poczatkowe

4

1

V1
6

R1
2

2

V2
4

R2
2

5

R3
1

3

R4
1

R6
1

I1
1

V4
6

2.00

-4.00

6.00

3.00

-3.00

stan nieustalony

4

1

V1
6

R1
2

2

V2
4

R2
2

3

R4
1

5

6

R6
1

I1
1

V4
6

Δ

Uw
volts

C1
0.1
IC = 2
0.1

L1
0.1H
IC = 3

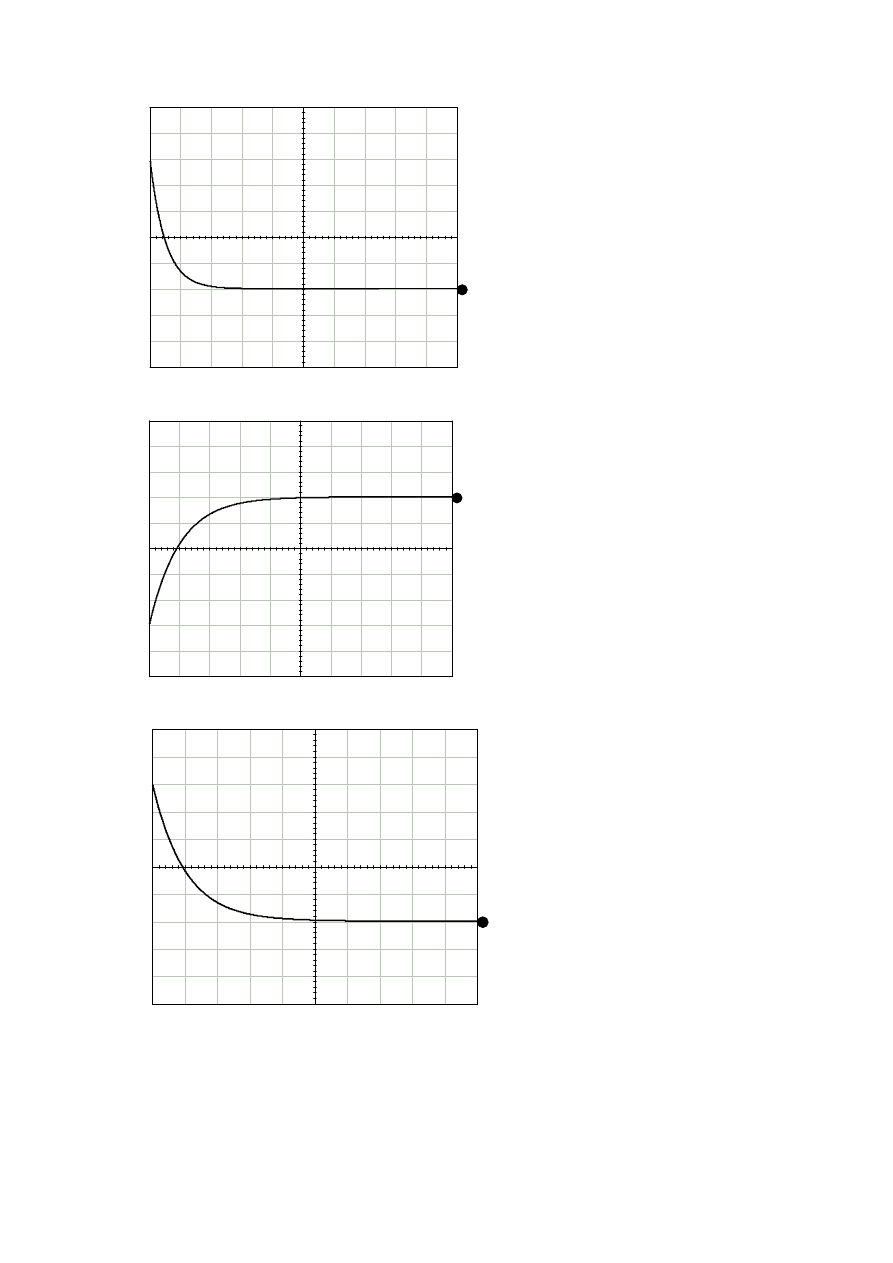
prąd cewki

1

100.0M

300M

500M

700M

900M

WFM.1 @l1[i] vs. time in Secs

3.60

3.40

3.20

3.00

2.80

@

l1[

i]

i

n A

m

ps

napięcie na cewce

7

1

100.0M

300M

500M

700M

900M

WFM.1 UL vs. time

1.20

800M

400M

0

-400M

UL

in

V

o

lt

s

prąd kondensatora

1

100.0M

300M

500M

700M

900M

WFM.1 ICvs. time in Secs

400M

0

-400M

-800M

-1.20

IC

i

n

Am

p

s

napięcie na kondensatorze

1

100.0M

300M

500M

700M

900M

WFM.1 V(4) vs. time in

2.20

1.80

1.40

1.00

600M

V(

4

) i

n

Vo

lt

s

8

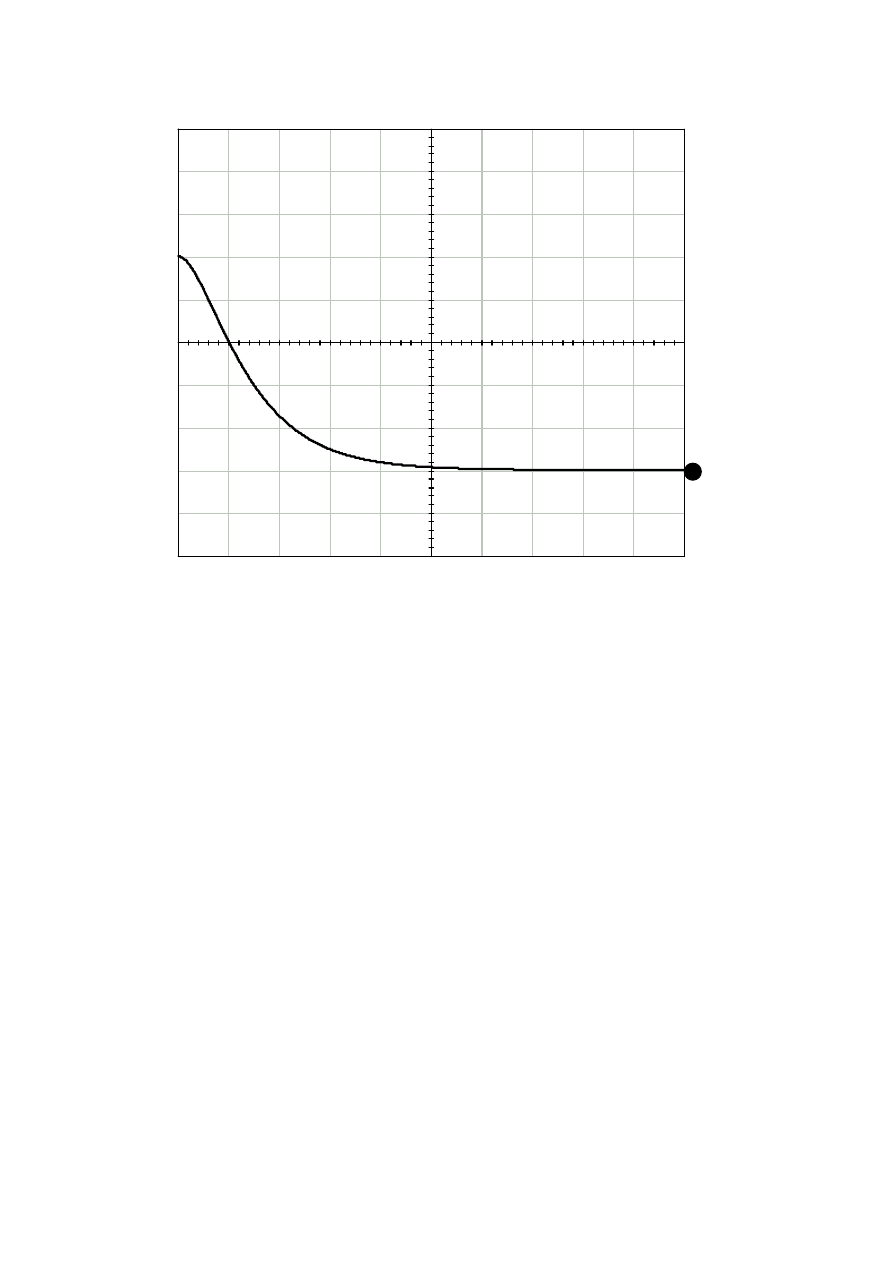
napięcie na wyłączniku

1

100.0M

300M

500M

700M

900M

WFM.1 UW vs. TIME in Secs

-1.80

-2.00

-2.20

-2.40

-2.60

UW

in

V

o

lt

s

Wyniki te w pełni potwierdzają obliczenia ręczne.

9