
17
.
dxdy
y
P
x
Q
dxdz
x
R
z
P
dydz
z
Q
y
R
Rdz
Qdy
Pdx
K
S
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
=
+
+
∫
∫∫
.
dS
V
rot
dK
V
Rdz
Qdy
Pdx
K
S
K
∫
∫∫
∫
=
⋅
=
+
+
………………………………………………….
Całka krzywoliniowa skierowana inaczej cyrkulacja pola wektorowego
po zamkniętej dodatnio skierowanej krzywej regularnej K równa jest
strumieniowi rotacji wektora pola przez powierzchnię S,
której brzegiem jest dodatnio skierowana krzywa K
…………………………………………………………………………………
Wniosek z tw. Stokesa
Jeżeli
0
=
V
rot
r
w obszarze
3
R
V
⊂
, to całka krzywoliniowa w tym obszarze
nie zależy od drogi – zależy jedynie od początku i końca krzywej –
a ponadto:
)
A
(
F
)
B
(
F
Rdz
Qdy
Pdx
B
A
−
=
+
+
∫
16
Def.
Dywergencję pola wektorowego
]
R
,
Q
,
P
[
V
=
r
określamy wzorem:
z
R
y
Q
x
P
V
div
∂
∂
+
∂
∂
+
∂
∂
=
r
……………………………………………………………………………..
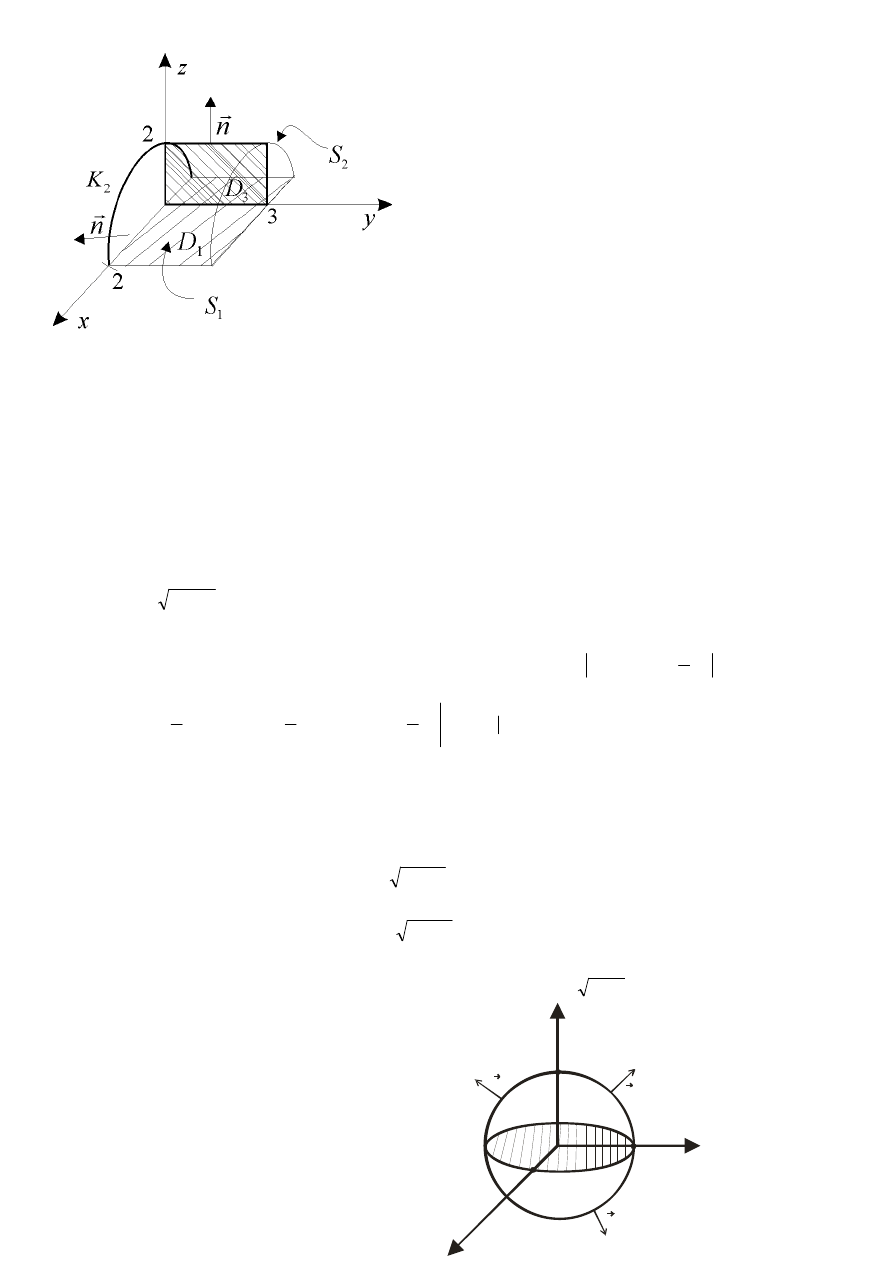
Twierdzenie (Gaussa – Ostrogradskiego)
Jeśli S – powierzchnia regularna zamknięta ograniczająca obszar przestrzenny V normalny
względem trzech płaszczyzn układu współrzędnych
oraz pole wektorowe
[
]
)
V
(
C
R
,
Q
,
P
F
1
∈
=
→
,
to
dxdydz
S
V
V
div
)
(
dS
n
V
S
Rdxdy
Qdxdz
Pdydz
∫∫
∫∫∫
+
=
⋅
∫∫
+
=
+
+
.
…………………………………………………….
Całka powierzchniowa zorientowana jako strumień wektora pola przez zorientowaną
powierzchnię zamkniętą S równa jest całce potrójnej z dywergencji wektora pola
V
r
po obszarze V, ograniczonym tą powierzchnią.
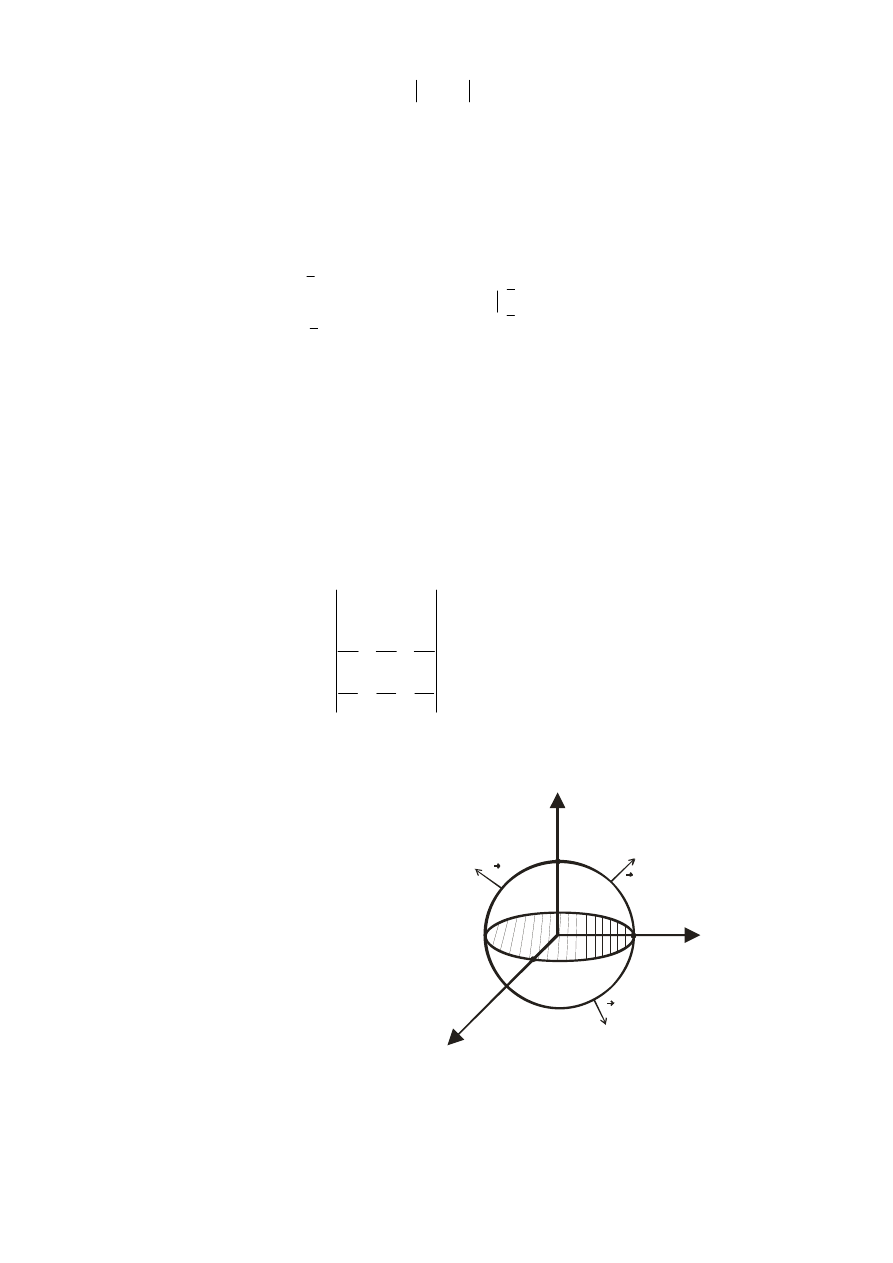
Twierdzenie (Stokesa)
Jeżeli
[
]
)
(
,
,
1
S
C
R
Q
P
F
∈
=
→
, gdzie S jest dwustronną powierzchnią gładką
ograniczoną krzywą regularną przestrzenną zamkniętą K,
oraz orientacja powierzchni S jest zgodna z orientacją krzywej
K
,
to
x
y
z
n
n
n
D
S
1
S
2
R
R
R

15
czyli, że:
0
=
∂
∂
−
∂
∂
x
R
z
P
,
0
=
∂
∂
−
∂
∂
y
P
x
Q
…………………………………………………………………………..
ad b)
∫
+
+
+
+
+
+
+
+
=
)
,
,
(
)
0
,
0
,
1
(
2
2
2
2
2
2
2
2
2
)
,
,
(
z
y
x
dz
z
y
x
z
dy
z
y
x
y
dx
z
y
x
x
z
y
x
u
Zał: x>0, y>0, z>0
[ ]
x
t
dz
z
dy
y
dt
dx
t
x
,
1
,
0
,
0
0
,
0
,
∈
=
=
=
=
=
=
[
]
y
t
dz
z
dt
dy
t
y
dx
x
x
,
0
,
0
,
0
,
0
,
∈
=
=
=
=
=
=
[
]
z
t
dt
dz
t
z
dy
y
y
dx
x
x
,
0
,
,
0
,
0
,
∈
=
=
=
=
=
=
…………………………………………………………………..
Wobec tego:
[ ]
[ ]
=
=
=
=
+
+
+
+
+
+
=
∫
∫
∫
x
u
x
t
udu
tdt
u
t
C
dt
t
y
x
t
dt
t
x
t
dt
t
t
z
y
x
u
z
y
x
,
1
:
,
1
:
)
,
,
(
2
0
2
2
2
0
2
2
1
2
C
y
x
z
y
x
x
y
x
x
C
z
y
x
t
x
u
z
y
x
+
+
−
+
+
+
−
+
+
−
=
+
+
+
+
+
+
=
2
2
2
2
2
2
2
2
0
2
2
2
0
2
2
1
1
Czyli:
C
z
y
x
z
y
x
u
+
+
+
=
2
2
2
)
,
,
(
………………………………………………………………….
Znajdź funkcję F (potencjał) pola wektorowego -jak w r.r.
…………………………………………………………….
ad c)
6
5
)
1
,
2
,
1
(
)
2
,
1
,
0
(
)
2
,
1
,
0
(
)
1
,
2
,
1
(
−
=
−
−
=
+
+
∫
−
u
u
Rdz
Qdy
Pdx
…………………………………………………………………………………
L
1
:
L
3
:
L
2
:
x
y
z
L
1
(1,0,0)
L
2
(x,0,0)
L
3
(x,y,z)
(x,y,0)
14
Zatem:
,
oraz
dF(x,y,z) =
= P dx + Q dy + R dz
………………………………………………………………………………….
Def. Rotację pola wektorowego
[
]
)
z
,
y
,
x
(
R
),
z
,
y
,
x
(
Q
),
z
,
y
,
x
(
P
określamy wzorem:
rot
∇x
[
]
)
z
,
y
,
x
(
R
),
z
,
y
,
x
(
Q
),
z
,
y
,
x
(
P
=
=
=
∂
∂
−
∂
∂
∂
∂
−
∂
∂
∂
∂
−
∂
∂
y
P
x
Q
,
x
R
z
P
,
z
Q
y
R
………………………………………………………………………………..
Tw.
Pole wektorowe
V
r
jest potencjalne wtedy i tylko wtedy, gdy
0
V
rot
=
r
.
……………………………………………………………………………..
Przykład.
Dane jest pole wektorowe:
]
z
,
y
,
x
[
z
y
x
1
W
2
2
2
+
+
=
a)
sprawdź, czy
W
jest potencjalne,
b)
oblicz potencjał,
c)
oblicz
∫
−
+
+
)
2
,
1
,
0
(
)
1
,
2
,
1
(
Rdz
Qdy
Pdx
ad a)
(
)
3
2
2
2
z
y
x
yz
y
R
+
+
−
=
∂
∂
(
)
3
2
2
2
z
y
x
yz
z
Q
+
+
−
=
∂
∂
Analogicznie sprawdzamy dla pozostałych współrzędnych,
0
=
∂
∂
−
∂
∂
z
Q
y
R
13
Def.
Powiemy, że pole skalarne jest gładkie, jeżeli pochodne cząstkowe pierwszego rzędu
funkcji opisującej pole skalarne są ciągłe.
……………………………………………………………………………………..
Def.
Polem wektorowym lub funkcją wektorową nazywamy funkcję,
która każdemu punktowi pewnego obszaru
3
przyporządkowuje
określony wektor.
……………………………………………………………………………….
Pole wektorowe
3
3
R
R
:
W
→
czyliw
3
R :
)]
z
,
y
,
x
(
R
),
z
,
y
,
x
(
Q
),
z
,
y
,
x
(
P
[
)
z
,
y
,
x
(
W
=
.
……………………………………………………………………………
Def.
Powiemy, że pole wektorowe
W
jest gładkie, jeżeli pochodne cząstkowe
pierwszego rzędu funkcji opisującej pole wektorowe są ciągłe.
…………………………………………………………………………………
Def.
Operator Hamiltona (nabla) określamy wzorem:
∇ =
.
………………………………………………………………………………
Def.
Jeżeli funkcja skalarna F ma pochodne cząstkowe pierwszego rzędu,
to gradientem funkcji skalarnej F nazywamy wektor:
= grad F.
……………………………………………………………………
Gradient F = [0,0,0] wtedy i tylko wtedy, gdy pole skalarne jest stałe.
…………………………………………………………………………………
Def.
Pole wektorowe
W
=
[
]
)
z
,
y
,
x
(
R
),
z
,
y
,
x
(
Q
),
z
,
y
,
x
(
P
- nazywamy
potencjalnym
w obszarze
3
wtedy i tylko wtedy,
gdy istnieje taka funkcja F: V
, że grad F =
=
W
= [P,Q,R],
przy czym funkcję F = F(x,y,z) nazywamy potencjałem pola wektorowego
W
.
12
Twierdzenie (Stokesa).
Jeżeli
[
]
)
(
,
,
1
S
C
R
Q
P
F
∈
=
→
, gdzie S jest dwustronną powierzchnią gładką
ograniczoną krzywą regularną przestrzenną zamkniętą K,
oraz orientacja powierzchni S jest zgodna z orientacją krzywej K ,
to
.
dxdy
y
P
x
Q
dxdz
x
R
z
P
dydz
z
Q
y
R
Rdz
Qdy
Pdx
K
S
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
+
∂
∂
−
∂
∂
=
+
+
∫
∫∫
Zatem
.
dxdy
)
z
,
y
,
x
(
R
dxdz
)
z
,
y
,
x
(
Q
dydz
)
z
,
y
,
x
(
P
Rdz
Qdy
Pdx
1
1
K
S
1
+
+
=
+
+
∫
∫∫
∫
K
--- całka po łuku zamkniętym.
Uwaga
Jeśli powierzchnia S jest płaskim obszarem w płaszczyźnie OXY, to
0
=
z
,
i z twierdzenia Stokesa otrzymujemy twierdzenie Greena.
………………………………………………………………………….
Twierdzenie (Gaussa – Ostrogradskiego)
Jeśli S – powierzchnia zamknięta ograniczająca obszar przestrzenny V
oraz
pole wektorowe
[
]
)
(
,
,
1
V
C
R
Q
P
F
∈
=
→
,
to
(
)
dxdydz
R
Q
P
Rdxdy
Qdxdz
Pdydz
S
V
z
y
x
∫∫
∫∫∫
+
+
+
=
+
+
.
……………………………………..……………………………………………..
TEORIA POLA
Def.
Polem skalarnym lub funkcją skalarną F nazywamy funkcję, która każdemu
punktowi pewnego obszaru
3
,
R
3
R
:
F
→
, przyporządkowuje określoną liczbę.
…………………………………………………………………………………….

11
Sfera S ma następującą parametryzację:
=
=
=
θ
ϕ
θ
ϕ
θ
sin
sin
cos
cos
cos
R
z
R
y
R
x
, gdzie
[
]
π
ϕ
π
π
θ
2
,
0
,
2
,
2
∈
−
∈
i wtedy wektor normalny jest postaci
n
r
=
]
cos
sin
,
sin
cos
,
cos
[cos
R
z
y
x
z
y
x
k
j
i
2
2
2
θ
θ
ϕ
θ
ϕ
θ
∂θ
∂
∂θ
∂
∂θ
∂
∂ϕ
∂
∂ϕ
∂
∂ϕ
∂
=
]
cos
sin
,
sin
cos
,
cos
[cos
R
n
2
2
2
θ
θ
ϕ
θ
ϕ
θ
=
r
dla
,
)
,
(
Ω
∈
ϕ
θ
gdzie
[
]
.
2
,
0
2
,
2
π
π
π
×
−
=
Ω
Stąd
[
]
(
)
[
]
(
)
[
]
[
]
(
)
(
)
(
)
3
2
0
2
2
2
2
3
3
3
2
3
3
2
2
3
2
3
3
2
2
2
4
sin
2
cos
cos
cos
sin
cos
cos
sin
sin
cos
cos
cos
cos
sin
,
sin
cos
,
cos
cos
sin
,
sin
cos
,
cos
cos
)
,
(
)
,
(
),
,
(
),
,
(
)
,
(
)
,
(
)
,
(
),
,
(
),
,
(
R
R
d
R
d
d
d
R
d
d
R
d
d
R
d
d
R
R
R
R
d
d
n
z
y
x
d
d
n
n
z
y
x
I
e
π
θ
π
θ
θ
ϕ
ϕ
θ
θ
ϕ
θ
θ
θ
θ
ϕ
θ
θ
θ
ϕ
θ
ϕ
θ
ϕ
θ
θ
θ
ϕ
θ
ϕ
θ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
π
π
π
π
π
=
⋅
=
=
=
=
+
=
+
+
=
=
=
=
=
=
⋅
=
∫∫
∫
∫
∫∫
∫∫
∫∫
∫∫
∫∫
Ω
−
+
−
Ω
Ω
Ω
Ω
Ω
o
r
o
r
r
o
Dowód
[
]
(
) (
) (
)
[
]
(
) (
) (
)
[
]
=
×
=
=
=
=
=
+
+
∫∫
∫∫
∫∫
∫∫
Ω
Ω
+
dudv
v
u
r
v
u
r
v
u
z
v
u
y
v
u
x
R
v
u
z
v
u
y
v
u
x
Q
v
u
z
v
u
y
v
u
x
P
dudv
v
u
n
v
u
z
v
u
y
v
u
x
R
v
u
z
v
u
y
v
u
x
Q
v
u
z
v
u
y
v
u
x
P
dS
n
R
Q
P
Rdxdy
Qdxdz
Pdydz
v
u
S
S
e
)
,
(
)
,
(
)
,
(
),
,
(
),
,
(
,
)
,
(
),
,
(
),
,
(
,
)
,
(
),
,
(
),
,
(
)
,
(
)
,
(
),
,
(
),
,
(
,
)
,
(
),
,
(
),
,
(
,
)
,
(
),
,
(
),
,
(
,
,
r
r
o
r
o
r
o
dudv
v
z
v
y
v
x
u
z
u
y
u
x
R
Q
P
∫∫
Ω
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
10
,
∫∫
+
+
=
S
zdxdy
ydzdx
dydz
x
I
Stąd
[
]
(
)
[
]
(
)
[
]
[
]
(
)
(
)
(
)
3
2
0
2
2
2
2
3
3
3
2
3
3
2
2
3
2
3
3
2
2
2
4
sin
2
cos
cos
cos
sin
cos
cos
sin
sin
cos
cos
cos
cos
sin
,
sin
cos
,
cos
cos
sin
,
sin
cos
,
cos
cos
)
,
(
)
,
(
),
,
(
),
,
(
)
,
(
)
,
(
)
,
(
),
,
(
),
,
(
R
R
d
R
d
d
d
R
d
d
R
d
d
R
d
d
R
R
R
R
d
d
n
z
y
x
d
d
n
n
z
y
x
I
e
π
θ
π
θ
θ
ϕ
ϕ
θ
θ
ϕ
θ
θ
θ
θ
ϕ
θ
θ
θ
ϕ
θ
ϕ
θ
ϕ
θ
θ
θ
ϕ
θ
ϕ
θ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
ϕ
θ
π
π
π
π
π
=
⋅
=
=
=
=
+
=
+
+
=
=
=
=
=
=
⋅
=
∫∫
∫
∫
∫∫
∫∫
∫∫
∫∫
∫∫
Ω
−
+
−
Ω
Ω
Ω
Ω
Ω
o
r
o
r
r
o
Twierdzenie
Jeśli płat powierzchniowy S zadany jest równaniami parametrycznymi
=
=
=
)
,
(
)
,
(
)
,
(
:
v
u
z
z
v
u
y
y
v
u
x
x
S
, gdzie
Ω
∈
)
,
( v
u
,
oraz
[
]
)
(
,
,
S
C
R
Q
P
F
∈
=
r
,
to
dudv
v
z
v
y
v
x
u
z
u
y
u
x
R
Q
P
Rdxdy
Qdxdz
Pdydz
S
∫∫
∫∫
+
Ω
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
+
+
.
= = = = = = = = = = = = = = = = = = = = = = = = = = =
Przykład
Obliczyć całkę
gdzie S jest zewnętrzną stroną powierzchni sfery
.
2
2
2
2
R
z
y
x
=
+
+
Skorzystamy z definicji całki powierzchniowej zorientowanej,
a następnie z twierdzenia o zamianie całki powierzchniowej niezorientowanej
na całkę podwójną.
[
]
dS
n
z
y
x
I
e
S
r
o
∫∫
=
,
,
x
y
z
n
n
n
D
S
1
S
2
R
R
R
9
Obliczyć całkę
gdzie S jest zewnętrzną stroną powierzchni sfery
.
2
2
2
2
R
z
y
x
=
+
+
I sposób.
Oczywiście
∫∫
∫∫
∫∫
=
=
S
S
S
zdxdy
ydzdx
dydz
x
.
Wystarczy więc obliczyć tylko jedną z tych całek, np.
.
∫∫
S
zdxdy
Sferę S rozbijamy na dwie półsfery:
górną (względem płaszczyzny OXY)
1
S
i dolną
2
S
; a następnie korzystamy z twierdzenia.
(
)
(
)
.
4
3
1
2
6
6
6
3
3
3
3
0
2
0
0
2
3
2
2
2
2
2
2
2
2
2
2
2
2
2
1
2
R
r
R
rdr
r
R
d
dxdy
y
x
R
dxdy
y
x
R
dxdy
y
x
R
zdxdy
zdxdy
zdxdy
I
R
R
D
D
D
S
S
S
π
π
ϕ
π
=
−
−
⋅
=
⋅
−
=
=
−
−
=
−
−
−
−
−
−
=
=
+
=
=
∫ ∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
+
−
II sposób.
Tym razem skorzystamy z definicji całki powierzchniowej zorientowanej, a następnie z twierdzenia o
zamianie całki powierzchniowej niezorientowanej na całkę podwójną.
[
]
dS
n
z
,
y
,
x
I
e
S
r
o
∫∫
=
Sfera S ma następującą parametryzację:
=
=
=
θ
ϕ
θ
ϕ
θ
sin
sin
cos
cos
cos
R
z
R
y
R
x
, gdzie
[
]
π
ϕ
π
π
θ
2
,
0
,
2
,
2
∈
−
∈
i wtedy wektor normalny jest postaci
n
r
=
i
j
k
x
u
y
u
z
u
x
v
y
v
z
v
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
≠ 0
]
cos
sin
,
sin
cos
,
cos
[cos
2
2
2
θ
θ
ϕ
θ
ϕ
θ
R
n
=
r
dla
,
)
,
(
Ω
∈
ϕ
θ
gdzie
[
]
.
2
,
0
2
,
2
π
π
π
×
−
=
Ω
8
,
∫∫
+
+
=
S
zdxdy
ydzdx
dydz
x
I
Rozłóżmy całkę I na sumę trzech całek I
I
I
I
=
+
+
1
2
3
, gdzie
(
)
I
x
yz dxdy
S
1
2
2
=
+
∫∫
,
I
xyzdxdz
S
2
=
∫∫
,
I
x zdydz
S
3
2
=
∫∫
i dla każdej z całek I
k
skorzystajmy z Twierdzenia k , gdzie k
= 1 2 3
, , .
1
o
Ponieważ powierzchnia S jest płatem powierzchniowym zadanym równaniem
(
)
S z
x
x y
D
:
,
,
=
−
∈
4
2
1
, gdzie
[
] [ ]
D
1
2 2
0 3
= −
×
,
,
zatem
(
)
(
)
(
)
(
)
(
)
I
x
y
x
dxdy
dx
x
y
x
dy
x y
x
y
dx
D
1
2
2
2
2
2
2
0
3
2
0
3
2
2
0
3
2
2
4
4
4
1
2
1
= +
+
−
=
+
−
=
+
−
⋅
=
∫∫
∫ ∫
∫
−
−
=
+
−
=
−
+
=−
+
= − +
=
−
−
−
−
∫
∫
3
18
9
2
3
2
18
1
2
18
8
72
64
2
2
2
2
2
2
2
3
2
2
2
2
x
x
dx
x
dx
x
x
2
o
I
2
0
= - bo rzut powierzchni S jest krzywą K
2
(a nie obszarem).
3
o
Rzutujemy S na płaszczyznę OYZ . Rzut
( )
[ ]
[ ]
{
}
D
y z
y
z
3
0 3
0 2
=
∈
∈
, :
, ,
,
powstaje zatem
z rzutowania zarówno części S
1
powierzchni S dla której x
> 0 oraz z części S
2
dla której x
< 0 .
Rozłóżmy zatem S na sumę S
S
S
=
∪
1
2
, gdzie
( )
S
x=
z
y z
D
1
2
3
4
:
,
dla
−
∈
oraz
( )
S
x=
z
y z
D
2
2
3
4
:
,
dla
−
−
∈
.
Stąd
(
)
(
)
I
x zdydz
x zdydz
z
zdydz
z
zdydz
S
S
D
D
3
2
2
2
2
1
2
3
3
4
4
0
=
+
=
−
−
−
−
=
+
−
∫∫
∫∫
∫∫
∫∫
Z 1
o
, 2
o
, 3
o
otrzymujemy I
= 64 .
Przykład
x
y
z
n
n
n
D
S
1
S
2
R
R
R
7
Twierdzenie 3
Niech S
− płat powierzchniowy zorientowany,
( )
( )
S x
h y z
y z
D
:
, ,
,
gdzie
=
∈
3
,
r
F
C S
∈ ( ) .
Wtedy 1
o
całka powierzchniowa po górnej stronie płata S :
(
)
( )
(
)
P x y z dydz
P h y z y z dydz
S
D
, ,
, , ,
∫∫
∫∫
=
3
,
2
o
całka powierzchniowa po dolnej stronie płata S :
(
)
( )
(
)
P x y z dydz
P h y z y z dydz
S
D
, ,
, , ,
∫∫
∫∫
= −
3
.
= = = = = = = = = = = = = = = = = = = = = = = = = = = =
Najczęściej i najwygodniej stosować następujące :
Twierdzenie.
Niech
S
−
płat powierzchniowy zorientowany,
(
)
(
)
D
y
,
x
gdzie
,
y
,
x
f
z
:
S
∈
=
( S
)
R
,
S
(
C
]
R
,
Q
,
P
[
F
3
∈
=
r
to
∫∫
=
+
+
S
dxdy
)
z
,
y
,
x
(
R
dxdz
)
z
,
y
,
x
(
Q
dydz
)
z
,
y
,
x
(
P
=
∫∫
+
∂
∂
−
∂
∂
⋅
−
D
dxdy
)]
y
,
x
(
f
,
y
,
x
(
R
y
)
y
,
x
(
f
)
y
,
x
(
f
,
y
,
x
(
Q
x
)
y
,
x
(
f
)
y
,
x
(
f
,
y
,
x
(
P
[
.
gdzie
Przykład
1.
Obliczyć całkę
dxdy
z
dxdz
y
dydz
x
I
S
∫∫
+
+
=
gdzie S: …
Przykład
2.
Obliczyć całkę
(
)
I
x zdydz
xyzdxdz
x
yz dxdy
S
=
+
+
+
∫∫
2
2
2
po zewnętrznej stronie powierzchni
(
)
{
}
S
x y z
y
z
x
z
=
≤
≤
≥
+
=
, , :
,
,
0
3
0
4
2
2
.
6
Dowód
Ponieważ płat S zadany jest w postaci jawnej
(
)
z
f x y
=
,
, więc wektor normalny jest postaci
[
]
r
n
f
f
x
y
= −
−
'
'
,
,1 lub
[
]
r
n
f
f
x
y
=
−
'
'
,
, 1 .
1
o
Niech S
S
=
+
Wtedy
[
]
r
n
f
f
x
y
= −
−
'
'
,
,1 oraz
( )
( )
( )
( )
( )
( )
r
n
f
f
f
f
f
f
f
f
e
x
x
y
y
x
y
x
y
=
−
+
+
−
+
+
+
+
'
'
'
'
'
'
'
'
,
,
.
2
2
2
2
2
2
1
1
1
1
Zatem
(
)
(
)
(
)
(
)
( )
( )
( )
( )
(
)
(
)
R x y z dxdy
R x y z
dS
R x y f x y
f
f
f
f
dxdy
R x y f x y dxdy
S
def
S
tw
x
y
x
y
D
D
, ,
, ,
cos
, ,
,
, ,
,
.
'
'
'
'
+
∫∫
∫∫
∫∫
∫∫
=
=
=
+
+
+
+
=
γ
1
1
1
2
2
2
2
1
1
2
o
Dowodzimy analogicznie.
Twierdzenie 2
Niech S
− płat powierzchniowy zorientowany,
(
)
(
)
S
y
g x z
x z
D
:
, ,
,
gdzie
=
∈
2
,
r
F
C S
∈ ( ) .
Wtedy 1
o
całka powierzchniowa po górnej stronie płata S :
(
)
(
)
(
)
Q x y z dxdz
Q x g x z z dxdz
S
D
, ,
,
, ,
∫∫
∫∫
=
2
,
2
o
całka powierzchniowa po dolnej stronie płata S :
(
)
(
)
(
)
Q x y z dxdz
Q x g x z z dxdz
S
D
, ,
,
,
,
∫∫
∫∫
= −
2
.
……………………………………………………………………………..

5
Definicja
Całkę powierzchniową niezorientowaną funkcji
r
o
r
F n
e
, czyli
(
)
r
o
r
F n dS
P
Q
R
dS
e
S
S
∫∫
∫∫
=
+
+
cos
cos
cos
α
β
γ
nazywamy całką powierzchniową zorientowaną funkcji wektorowej
r
F na płacie zorientowanym
S i
oznaczamy symbolem
Pdydz
Qdxdz
Rdxdy
S
+
+
∫∫
.
Uwaga
Jeśli zmienimy orientację płata S na przeciwną, to
czyli
Pdydz
Qdxdz
Rdxdy
Pdydz
Qdxdz
Rdxdy
S
S
+
+
= −
+
+
−
∫∫
∫∫
.
……………………………………………………………………
Niech S
− powierzchnia regularna dwustronna,
2
1
S
S
S
∪
=
,
gdzie S
i
− płat gładki dla i
n
= 1,..., .
Wtedy
∑ ∫∫
+
+
∫∫
+
+
=
2
1
i
Si
S
i
Rdxdy
Qdxdz
Pdydz
:=
Rdxdy
Qdxdz
Pdydz
.
Uwaga
Pdydz
Qdxdz
Rdxdy
Pdydz
Qdxdz
Rdxdy
S
S
S
S
+
+
=
+
+
∫∫
∫∫
∫∫
∫∫
bo
[
]
Pdydz
Qdxdz
Rdxdy
P
Q
R
dS
S
S
+
+
=
+
+
=
∫∫
∫∫
cos
cos
cos
α
β
γ
=
+
+
=
∫∫
∫∫
∫∫
P
dS
Q
dS
R
dS
S
S
S
cos
cos
cos
α
β
γ
=
+
+
∫∫
∫∫
∫∫
Pdydz
Qdxdz
Rdxdy
S
S
S
……………………….…………………………………
Twierdzenie 1
Niech S
− płat powierzchniowy zorientowany,
(
)
(
)
S z
f x y
x y
D
:
,
,
,
gdzie
=
∈
1
,
r
F
C S
∈ ( ) .
Wtedy 1
o
całka powierzchniowa po górnej stronie płata S :
(
)
(
)
(
)
R x y z dxdy
R x y f x y dxdy
S
D
, ,
, ,
,
∫∫
∫∫
=
1
,
2
o
całka powierzchniowa po dolnej stronie płata S :
(
)
(
)
(
)
R x y z dxdy
R x y f x y dxdy
S
D
, ,
, ,
,
∫∫
∫∫
= −
1
.
r
o
r
r
o
r
F n dS
F n dS
e
S
e
S
−
∫∫
∫∫
= −
4
Uwaga
Istnieją powierzchnie jednostronne (np. wstęga Möbiusa)
Zatem nie każdą powierzchnię regularną można zorientować.
…………………………………………………………………………
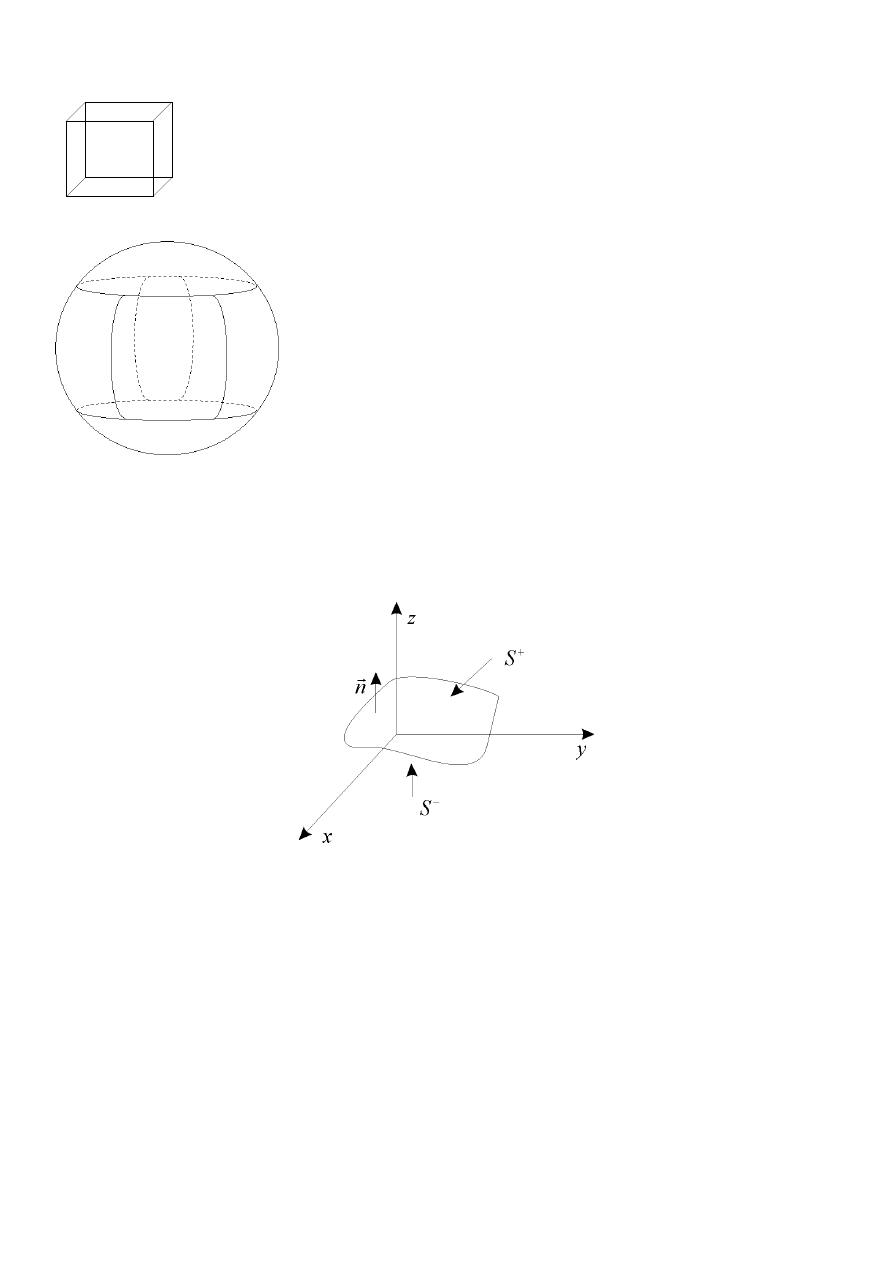
Niech
r
n
e
- wersor normalny do płata S. Ponieważ
r
n
e
= 1, więc wersor normalny zadany jest wzorem
[
]
r
n
e
= cos , cos ,cos
α
β
γ
,
gdzie
α β γ
, , są kątami między wektorem
r
n
e
a dodatnimi półosiami
OX
OY
OZ
+
+
+
,
,
.
Niech
r
F - pole wektorowe określone na płacie S,
[
]
r
F
P Q R
S
=
→
, ,
:
R
3
,
oraz niech
r
F
C S
∈ ( ) .
W każdym punkcie płata S tworzymy iloczyn skalarny
r
o
r
F n
P
Q
R
e
=
+
+
cos
cos
cos
α
β
γ
.
Ponieważ
r
o
r
F n
C S
e
∈
⇒ ∃
( )
całka powierzchniowa niezorientowana
r
o
r
F n dS
e
S
∫
.
………………………………………………………………………………..
3
Przykład
- powierzchnia regularna
- półsfera nie jest powierzchnią regularną, bo dla jej brzegu
(największego okręgu) nie istnieją pochodne cząstkowe, natomiast
sfera jest powierzchnią regularną bo można ją podzielić na 6 płatów
gładkich.
Całka powierzchniowa zorientowana
(całka powierzchniowa funkcji wektorowej)
Niech S – gładki płat powierzchniowy.
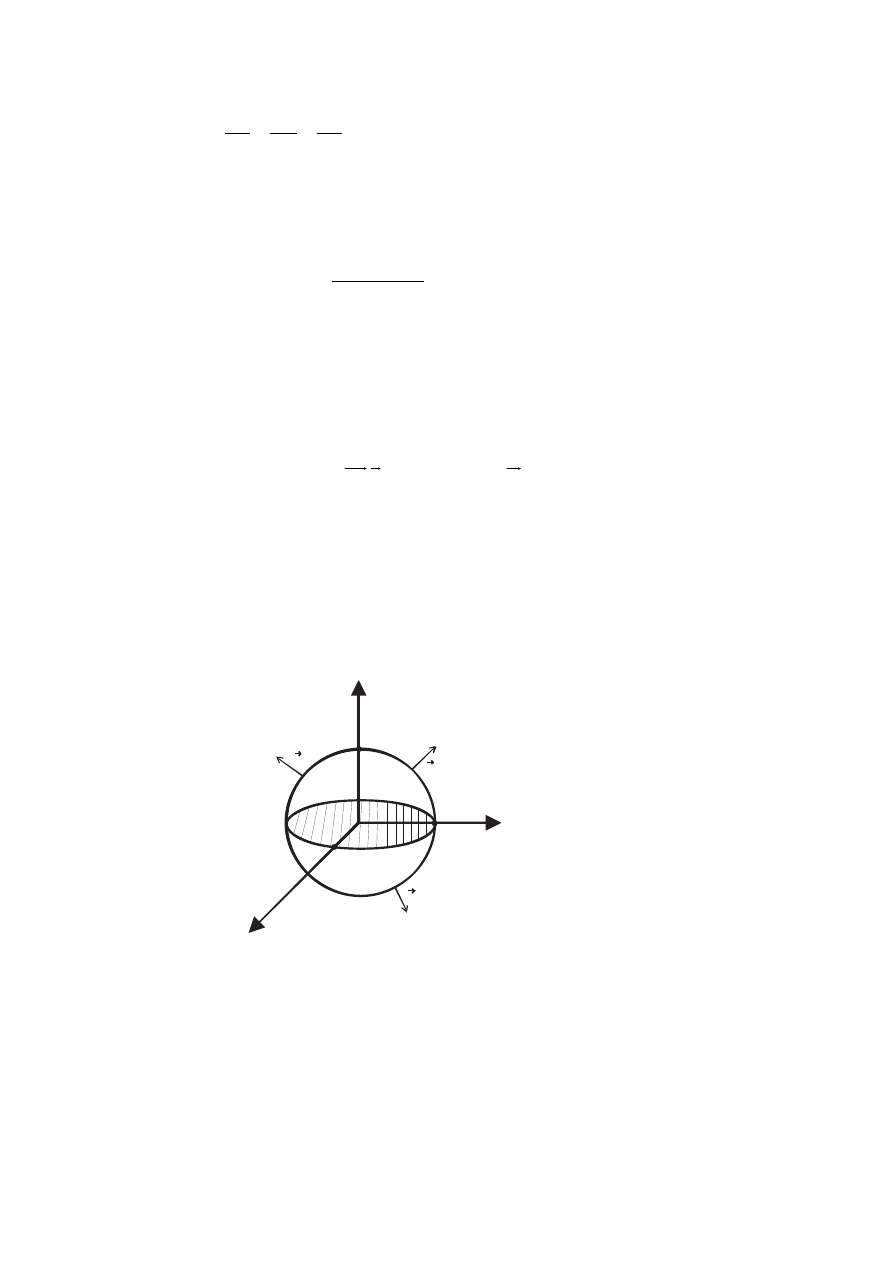
Płat orientujemy czyli rozróżniamy jego strony: dodatnią S
S
+
−
i ujemną
. W każdym punkcie płata
zorientowanego prowadzimy wektor normalny
r
n o zwrocie od strony ujemnej do dodatniej.
……………………………………………………………………….
Orientacja płata S wyznacza jednoznacznie orientację krzywej K
S
⊂
.
……………………………………………………………………….
Krzywa K jest zorientowana dodatnio, gdy obiegając krzywą K zgodnie ze wzrostem parametru
wektor normalny mamy po stronie lewej.
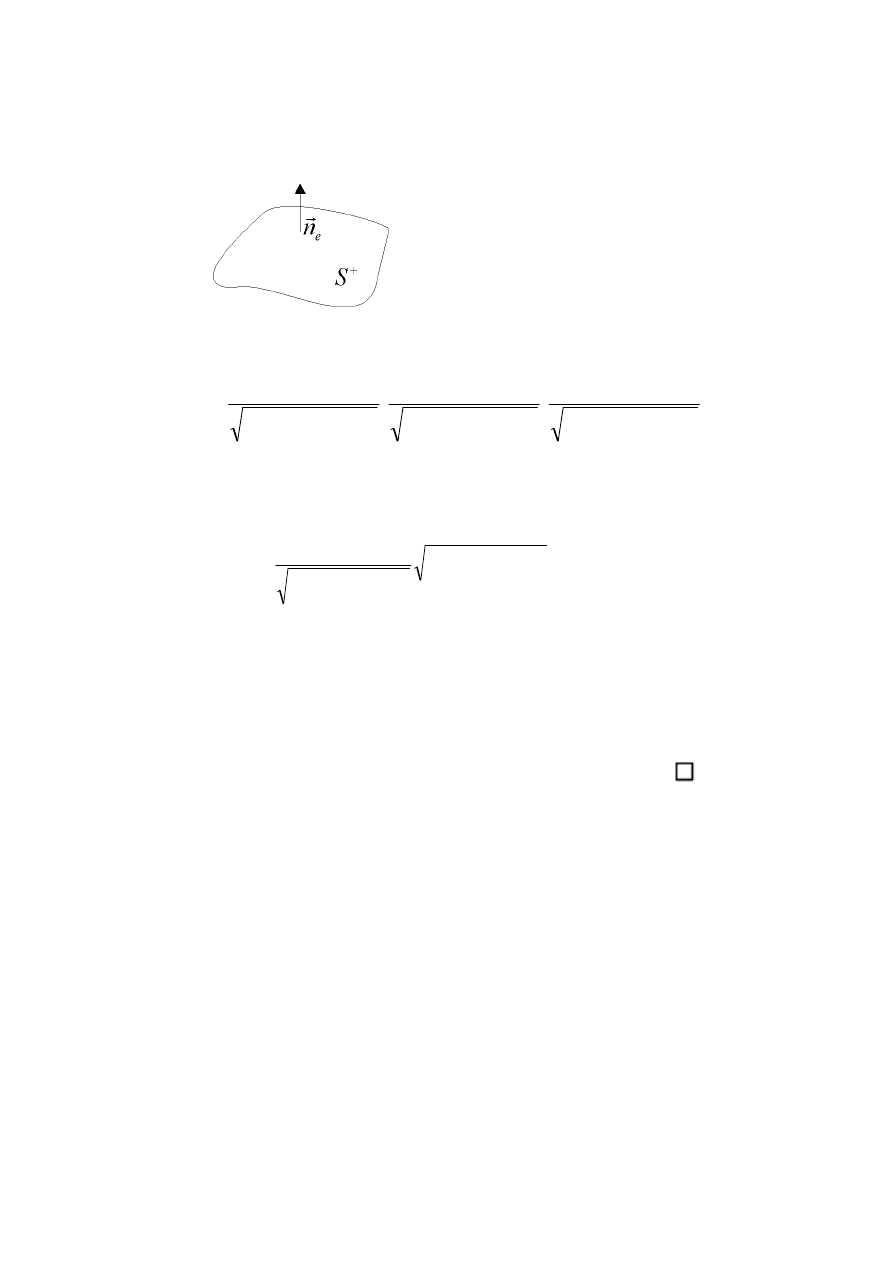
…………………………………………………………………………
Jeśli S jest powierzchnią zamkniętą, to przyjmujemy, że jej zewnętrzna strona jest stroną dodatnią; a
wewnętrzna – ujemną.
…………………………………………………………………………
2
r
r
r
n
r
r
x
u
y
u
z
u
x
v
y
v
z
v
i
j
k
x
u
y
u
z
u
x
v
y
v
z
v
u
v
=
×
=
×
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
,
,
,
,
przy założeniu, że wyznacznik
i
j
k
x
u
y
u
z
u
x
v
y
v
z
v
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
≠ 0 .
………………………………………………………………………………
Jeśli dany jest wektor normalny
[
]
r
n
A B C
=
, ,
do powierzchni S, to płaszczyzna
π
styczna do
powierzchni S w punkcie
(
)
M x
y z
0
0
0
,
,
jest postaci
(
)
(
)
(
)
π
: A x
x
B y
y
C z
z
−
+
−
+
−
=
0
0
0
0 .
…………………………………………………………
Zatem w przypadku *
(
)
(
)
(
)
(
)
(
)
(
)
π
∂
∂
∂
∂
∂
∂
:
F
x
M x
x
F
y
M y
y
F
z
M z
z
−
+
−
+
−
=
0
0
0
0 .
…………………………………………………………………………………..
Natomiast w przypadku **
(
)
(
)
(
)
(
)
π
∂
∂
∂
∂
:
−
−
−
−
+ −
=
F
x
M x
x
F
y
M y
y
z
z
0
0
0
0 ,
stąd
( )
(
)
( )
(
)
π
∂
∂
∂
∂
: z
z
F
x
M
x
x
F
y
M
y
y
−
=
−
+
−
0
0
0
.
……………………………………………………………………………….
Definicja
Powierzchnia gładka jest to powierzchnia, która w każdym swoim punkcie ma płaszczyznę styczną,
która zmienia się w sposób ciągły przy zmianie punktu styczności.
…………………………………………………………………………………
Definicja
Płatem nazywamy figurę określoną równaniem
(
)
(
)
z
f x y
x y
D
=
∈
,
,
,
gdzie
,
D - domknięty obszar jednospójny,
(
)
( )
f
C
D
f
C D
∈
∈
1
int
,
.
…………………………………………………………………………………..
Definicja
Płat nazywamy gładkim, gdy
( )
f
C D
∈
1
.
………………………………………………………………………….
Definicja
Powierzchnia regularna jest to powierzchnia, którą można podzielić na skończenie wiele płatów
gładkich.

1
CAŁKA POWIERZCHNIOWA ZORIENTOWANA
Powierzchnie
Powierzchnia jest to zbiór punktów S(x,y,z) spełniających pewne równanie,
które jest klasy C
1
i ma jedną z trzech postaci:
* postać uwikłana:
(
)
F x y z
, ,
= 0
** postać jawna:
(
)
(
)
z
f x y
x y
D D
D
OXY
=
∈
⊂
,
,
,
, gdzie
- obszar,
*** postać parametryczna:
(
)
(
)
(
)
(
)
x
x u v
y
y u v
z
z u v
u v
=
=
=
∈
,
,
,
,
,
, gdzie
Ω Ω
- obszar w R
2
………………………………………………………………………..
Definicja
Wektorem normalnym do powierzchni S w punkcie M
S
∈ nazywamy niezerowy wektor prostopadły
do wszystkich krzywych leżących na S i przechodzących przez M .
Jeśli S zadana jest w postaci:
* uwikłanej, to
(
)
(
)
(
)
(
)
r
n
F M
F
x
M
F
y
M
F
z
M
=
=
grad
∂
∂
∂
∂
∂
∂
,
,
,
gdzie M jest punktem, w którym gradient nie zeruje się, gradF(M) ≠ 0 .
………………………………………
** jawnej, to przekształcając równanie
(
)
z
f x y
=
,
otrzymujemy postać uwikłaną
(
)
z
f x y
−
=
,
0
gdzie
(
)
(
)
F x y z
z
f x y
, ,
,
= −
i korzystając ze wzoru na wektor normalny w przypadku * dostajemy
(
)
(
)
(
)
r
n
F x y z
f
x
M
f
y
M
=
= −
−
grad
, ,
,
,
∂
∂
∂
∂
1
………………………………………………..
*** parametrycznej, to w punkcie jednokrotnym powierzchni S, tzn. punkcie odpowiadającym tylko
jednej parze
(
)
u v
,
wektor normalny zadany jest wzorem
Wyszukiwarka
Podobne podstrony:
3.Całka powierzchniowa zorientowana, MATEMATYKA, CAŁKI, CAŁKI KRZYWOLINIOWE I POWIERZCHNIOWE, 02Całk
Matematyka Sem 2 Wykład Całki Powierzchniowe
Calka powierzchniowa zorientowana
całki powierzchniowe
02Całki powierzchniowe, 1.Powierzchnie, CAŁKI POWIERZCHNIOWE
Objetosci, calki powierzchniowe
4. całka powierzchniowa zorientowana
Zadania.Calki powierzchniowe, Oceanotechnika. PG, Semestr 2
Całki powierzchniowe
calka powierzchniowa zorientowana
Całki powierzchniowe, zadania
Matematyka Sem 2 Wykład Całki Powierzchniowe
Calka powierzchniowa zorientowana
calki pow zorientowane
więcej podobnych podstron