Podstawowe wzory

∫

dx=xC       

∫

x

a

=

x

a1

a1



C , a≠−1

∫

dx

x

=

ln∣x∣C , x ≠0

∫

e

x

dx=e

x



C

∫

a

x

dx=

a

x

ln a



C

∫

cos x dx=sin xC

∫

sin x dx =−cos xC

∫

tg x=−ln∣cos x∣C

∫

ctg x=ln∣sin x∣C

∫

dx

cos

2

x

=

tg xC , cos x ≠0

∫

dx

sin

2

x

=−

ctg xC ,sin x≠0

∫

dx



1− x

2

=

arcsin xC ,−1 x1

∫

dx

x

2



1

=

arctg xC

∫

dx

x

2



a

2

=

1
a

arctg

x

a



C

∫

dx



a

2

−

x

2

=

arcsin

x

∣

a∣



C ,∣x∣∣a∣

∫

[

f  xg  x]dx=

∫

f  x dx

∫

g  x dx

∫

[

f  x− g  x ] dx=

∫

f  x  dx−

∫

g  x  dx

∫

kf  x dx=k

∫

f  x dx

Całkowanie przez części

∫

f  x g '  x dx= f  x g  x −

∫

f '  x g  x  dx

∫

xcosx dx=

∣

f  x =x

f '  x=1

g  x=sin x g '  x =cos x

∣

=

xsin x−

∫

1sinx dx=x sin xcos xC

Całkowanie przez podstawienie

∫

f  x dx=

∫

f t'  t dt gdzie x=t 

∫



2x−1

3

dx=

∣

2 x−1=t

2d x=dt

d x=

1
2

dt

∣

=

1
2

∫

t

3

du=

1
8

t

4



C=

1
8



2 x−1

4



C  

Kilka dodatkowych wzorów wartych zapamiętania

∫

f '  x

f  x 

dx=ln∣ f  x∣C

     

∫

f '  x e

f  x

dx =e

f x



C  

∫

f '  x

1[ f  x]

2

dx=arctan f  x C

∫

f '  x



f  x 

dx=2



f  x C      

∫

f '  x cos f  x dx=sin f  xC

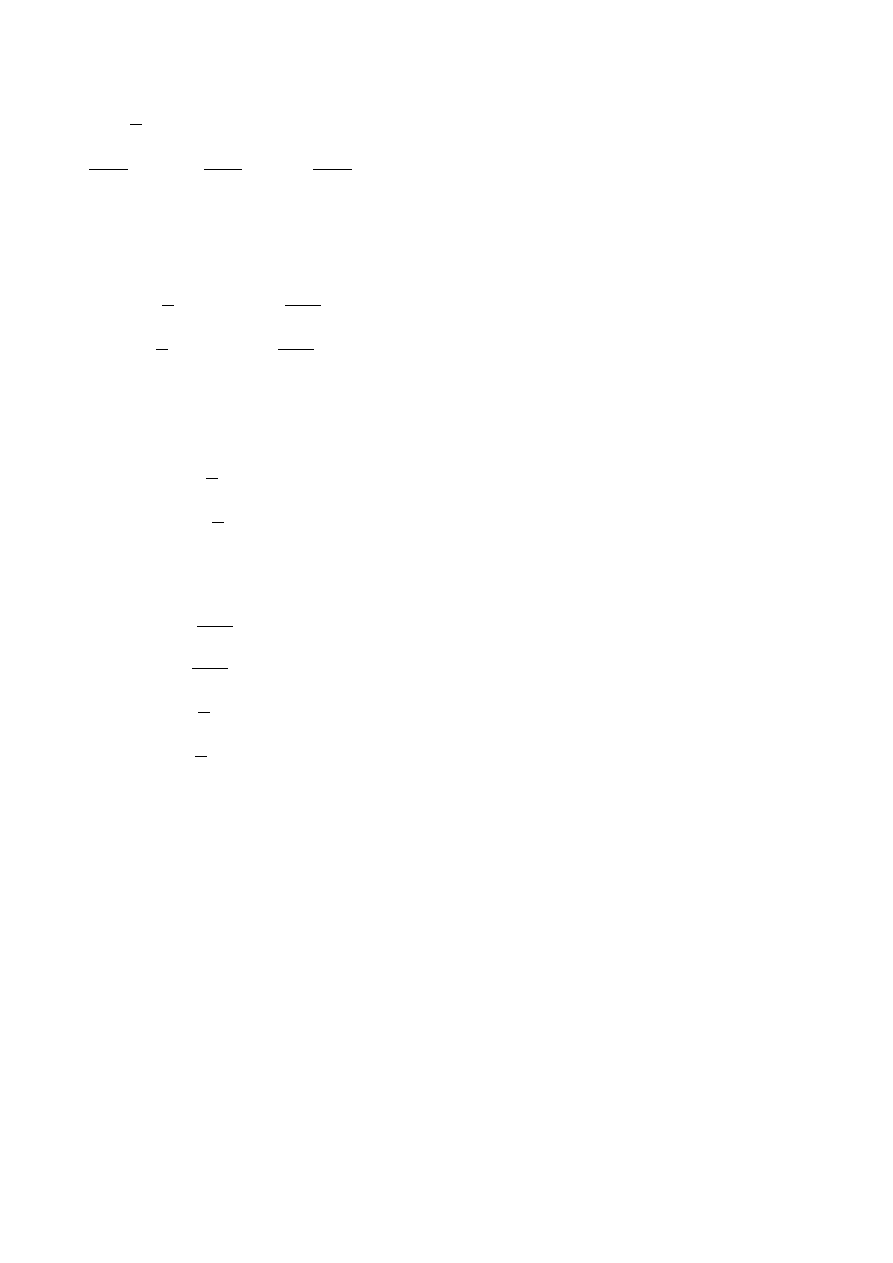
Całki trygonometryczne
Podstawienie uniwersalne.

tan

x

2

=

t ⇒ x=2 arctan t

dx =

2 dt

1t

2

sin x=

2t

1t

2

cos x=

1−t

2

1t

2

Wzory redukcyjne:

n=±1,±2, ...

∫

sin

n

x dx=−

1
n

sin

n−1

x cos x

n−1

n

∫

sin

n−2

x dx

∫

cos

n

x dx=

1
n

cos

n−1

x sin x

n−1

n

∫

cos

n− 2

x dx

Przydatne wzory trygonometryczne:

sin

2

xcos

2

x=1

cos 2x=cos

2

x−sin

2

x=2cos

2

x−1=1−2 sin

2

x

cos

2

x=

1

2



cos2x1

sin

2

x=−

1
2



cos 2x−1

sin 2x=2 sin x cos x

Warto pamiętać, że:

∫

sin x cos

n

xdx=−

1

n1

cos

n1

xC

∫

cos x sin

n

xdx=

1

n1

sin

n1

xC

∫

sin nx dx=−

1
n

cosnxC

∫

cos nx dx=

1
n

sin nxC