6. Naprężenia w podłożu gruntowym – zadania przykładowe
Zadanie 6.1
Dla warunków gruntowo-wodnych wykopu fundamentowego w ściankach szczelnych jak
w zadaniu 3.3, wyznaczyć wartości i rozkłady naprężeń geostatycznych całkowitych i efektywnych
w podłożu gruntowym tuż przy ściankach szczelnych, po obu stronach ścianek – zewnętrznej
i wewnętrznej. Wykorzystać wyniki obliczeń z zadania 3.3.
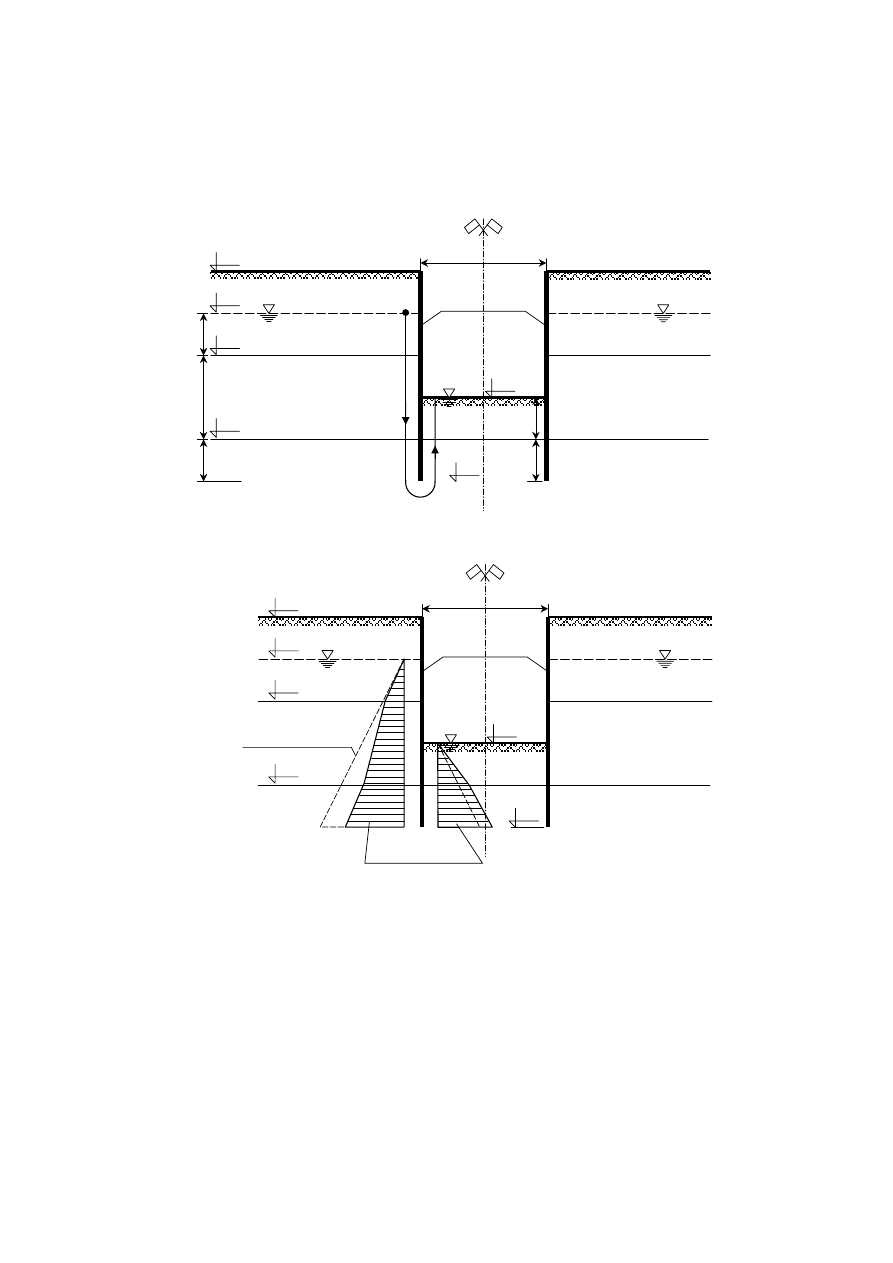
Z obliczeń w zadaniu 3.3 otrzymano rozkłady ciśnień u wody w podłożu gruntowym przedstawione
na rysunku poniżej.
Wartości naprężeń geostatycznych w poszczególnych poziomach:
a) strona lewa :
0
.
37
5
.
18
0
.
2
=
⋅
=
′
=
zA
zA
γ
γ
σ
σ
kPa
0
.
76
5
.
19
0
.
2
0
.
37
=
⋅
+
=
zB
γ
σ
kPa,
5
.
17
=
B
u
kPa,
5
.
58
5
.
17
0
.
76
=
−
=
′
zB
γ
σ
kPa
0
.
156
0
.
20
0
.
4
0
.
76
=
⋅
+
=
zC
γ
σ
kPa,
8
.
37
=
C
u
kPa,
2
.
118
8
.
37
0
.
156
=
−
=
′
zB
γ
σ
kPa
0
.
197
5
.
20
0
.
2
0
.
156
=
⋅
+
=
L
zD
γ
σ
kPa,
9
.
53
=
D
u
kPa,
1
.
143
9
.
53
0
.
197
=
−
=
′
L
zD
γ
σ
kPa
b) strona prawa :
0
.
0
=
′
=
zF
zF
γ
γ
σ
σ
kPa
0
.
40
0
.
20
0
.
2
=
⋅
=
zE
γ
σ
kPa,
0
.
30
=
E
u
kPa,
0
.
10
0
.
30
0
.
40
=
−
=
′
zB
γ
σ
kPa
0
.
81
5
.
20
0
.
2
0
.
40
=
⋅
+
=
P
zD
γ
σ
kPa,
9
.
53
=
D
u
kPa,
1
.
27
9
.
53
0
.
81
=
−
=
′
P
zD
γ
σ
kPa
± 0.0
- 2.0
- 4.0
- 8.0
- 10.0
- 6.0
zwg
zwg
zwg
Ps,
γ = 18.5 kN/m
3
γ’ = 9.5 kN/m
3
k
1
= 8
⋅10
-4
m/s
Pd,
γ’ = 10 kN/m
3
k
2
= 2
⋅10
-4
m/s
Ps,
γ’ = 10.5 kN/m
3
k
3
= 5
⋅10
-4
m/s
Ps, k
3
Pd, k
2
h
1
=2 m
h
2
=4 m
h
3
=2 m
h
4
=2 m
h
4
=2 m
i
1
i
2
i
3
i
4
i
5
B = 6 m
ścianki szczelne
A
B
C
D
E
F
± 0.0
- 2.0
- 4.0
- 8.0
- 10.0
- 6.0
zwg zwg
zwg
Ps
Pd
Ps
Ps
Pd,
B = 6 m
ścianki szczelne
A
B
C
D
E
F
53.9
(80)
37.8
17.5
30.0
53.9
(40)
rozkłady ciśnień wody
u [kPa]
rozkład hydrostatyczny
Wartości naprężeń efektywnych można obliczyć również, wykorzystując ciśnienie spływowe:
(
)
∑
±
⋅
=
′
i
i
i
zi
j
h
)
(,
γ
σ
γ
, (znak (+) dajemy gdy woda płynie w dół, znak (-) – gdy do góry)
Wartości ciśnień spływowych (według obliczeń w zad. 3.3):
23
.
1
10
123
.
0
1
1
=
⋅
=
⋅
=
w
i
j
γ
kN/m
3
,
93
.
4
10
493
.
0
2
2
=
⋅
=
⋅
=
w
i
j
γ
kN/m
3
,
97
.
1
10
197
.
0
3
4
3
=
⋅
=
⋅
=
=
w
i
j
j
γ
kN/m
3
,
93
.
4
2
5
=
= j
j
kN/m
3
Wartości naprężeń efektywnych:
0
.
37
5
.
18
0
.
2
=
⋅
=
′
zA
γ
σ
kPa
5
.
58
)
23
.
1
5
.
9
(
0
.
2
0
.
37
=
+
⋅
+
=
′
zB
γ
σ
kPa
2
.
118
)
93
.
4
0
.
10
(
0
.
4
5
.
58
=
+
⋅
+
=
′
zC
γ
σ
kPa
1
.
143
)
97
.
1
5
.
10
(
0
.
2
2
.
118
=
+
⋅
+
=
′
L
zD
γ
σ
kPa
1
.
10
)
93
.
4
0
.
10
(
0
.
2
=
−
⋅
=
′
zE
γ
σ
kPa
2
.
27
)
97
.
1
5
.
10
(
0
.
2
1
.
10
=
−
⋅
+
=
′
P
zD
γ
σ
kPa
(Niewielkie różnice w stosunku do wartości z pkt. b) wynikają jedynie z zaokrągleń).
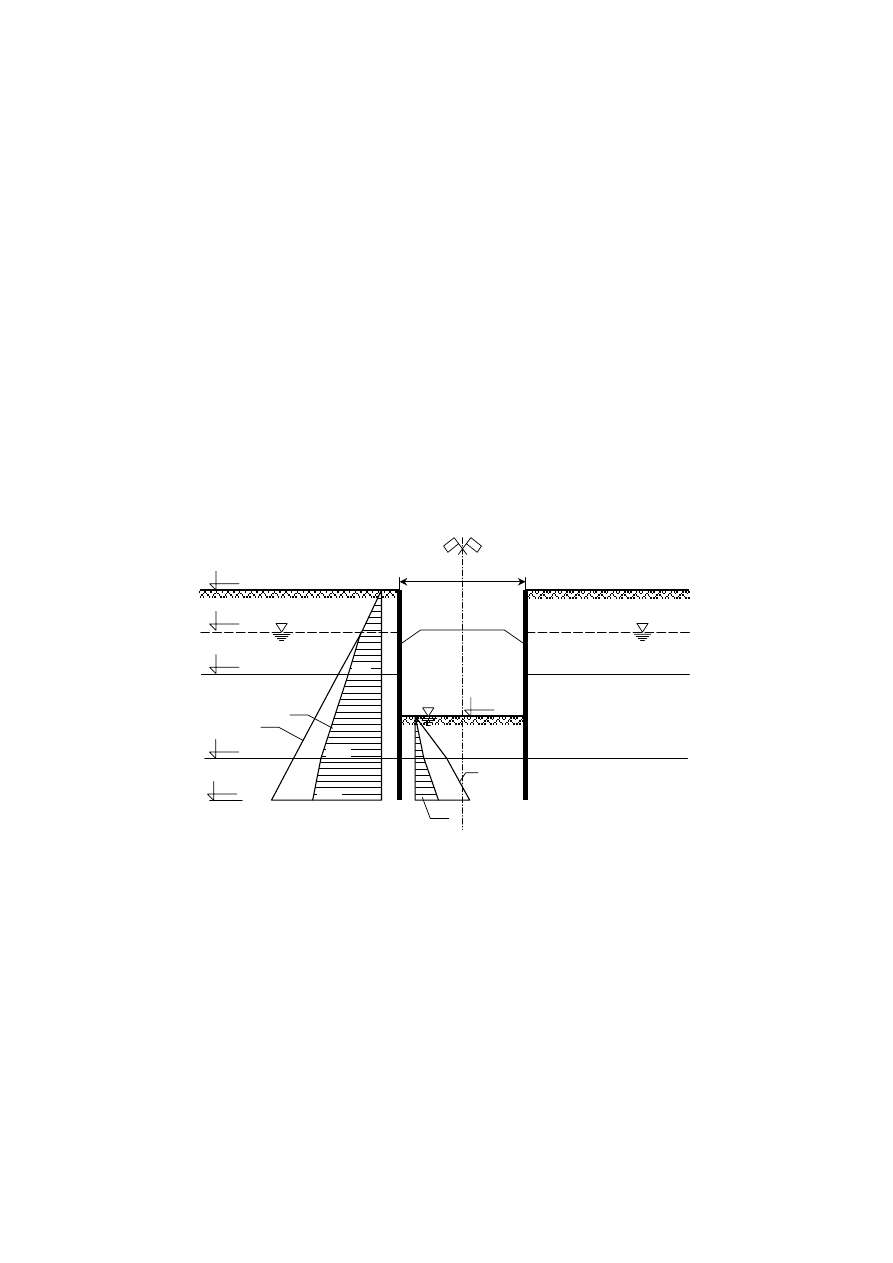
Wyniki obliczeń przedstawiono graficznie na rysunku poniżej.
± 0.0
- 2.0
- 4.0
- 6.0
zwg
zwg
zwg
Ps
Pd
Ps
Ps
Pd,
B = 6 m
ścianki szczelne
A
B
C
D
E
F
76.0
40.0
81.0
σ’
γz
37.0
156.0
197.0
58.5
118.2
143.1
u
- 8.0
- 10.0
10
27.1
u
σ’
γz
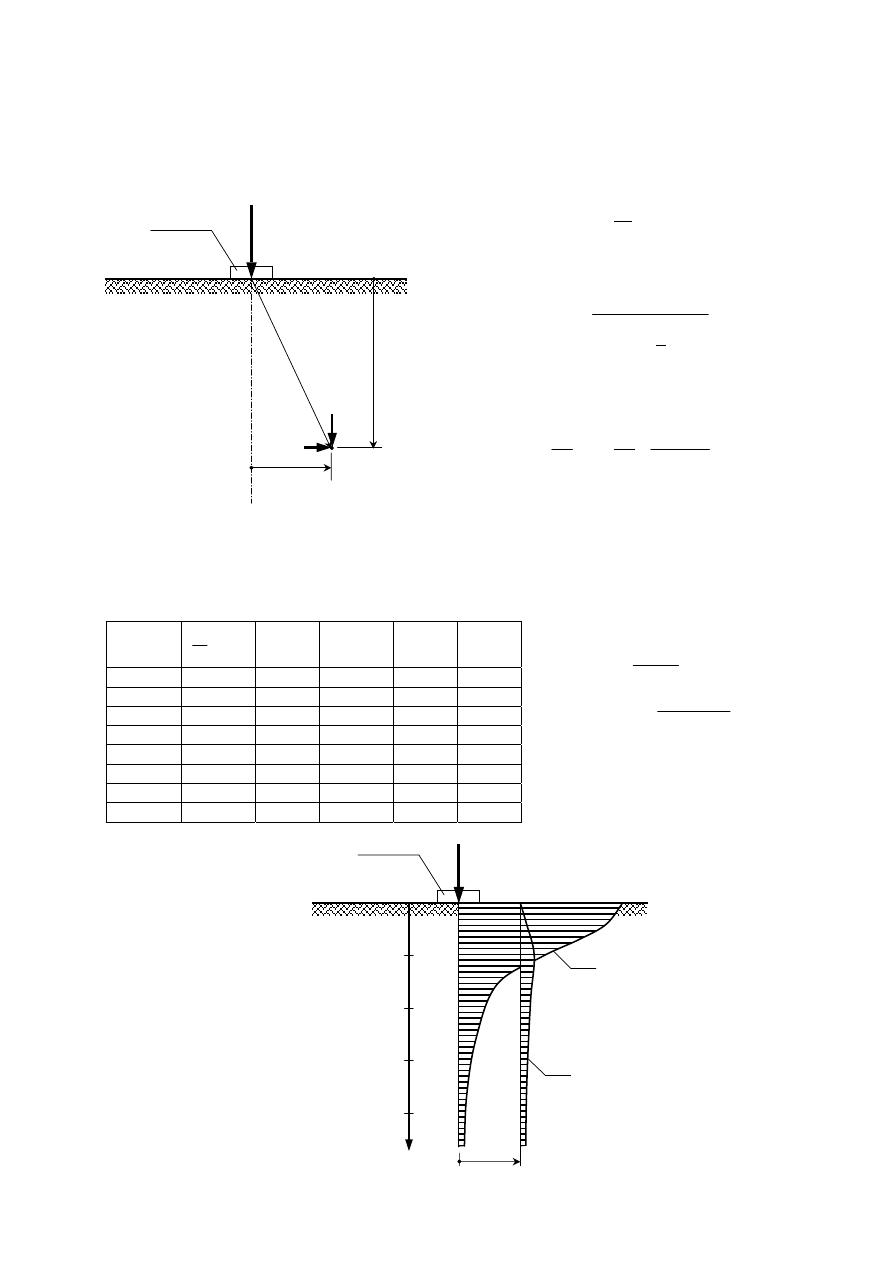
Zadanie 6.2.
Obliczyć wartości i narysować wykres rozkładu naprężeń pionowych
σ
Qz
w ośrodku gruntowym od
obciążenia skupionego Q = 200 kN ze stopy fundamentowej o wymiarach 0.8
× 0.8 m. Wyznaczyć
rozkład w osi działania siły Q i w odległości 1.0 m od tej osi.
W rozwiązaniu zadania wykorzystany zostanie wzór
Boussinesqa o następującej postaci:
η
σ
⋅
=
2
z
Q
Qz
[kPa]
(1)
w którym
η
jest współczynnikiem zaniku napręże-nia,
obliczanym według wzoru:
2
/
5
2
1
2
3
+
⋅
=
z
r
π
η
Można także policzyć naprężenie poziome radialne
σ
Qr
ze wzoru:
+
−
−
=
)
(
)
2
1
(
1
3
2
5
2
z
R
R
R
z
r
Q
Qr
ν
π
σ
[kPa]
w którym
ν
jest współczynnikiem Poissona dla gruntu.
W rozwiązaniu Boussinesqua zakłada się, że siła Q działa w punkcie, więc wartość naprężenia
σ
Qz
tuż pod
siłą równa jest nieskończoność. W rzeczywistości siła Q działa za pośrednictwem jakiegoś fundamentu
o określonej powierzchni F=B
×L, a więc tuż pod tym fundamentem naprężenia wyniosą
σ
qz
(z=0) = Q/F.
Wartości naprężeń
σ
Qz
według wzoru (1) można liczyć dopiero od pewnej głębokości, na której
σ
Qz
< Q/F.
Tabela obliczeń
Głębokość
z [m]
2
z
Q
[kPa]
η
1
(r = 0)
η
1
(r = 1.0 m)
σ
Qz1
[kPa]
σ
Qz2
[kPa]
0 - - 0
312.5
0
0.5 800.0 0.48 0.009 ~200.0 7.2
1.0 200.0 0.48 0.084 96.0 16.9
1.5 89.0 0.48 0.19 42.7 16.3
2.0 50.0 0.48 0.27 24.0 13.7
2.5 32.0 0.48 0.33 15.4 10.5
3.0 22.0 0.48 0.37 10.7 8.1
4.0 12.5 0.48 0.41 6.0 5.1
R
z
r
σ
Qz
σ
Qr
Q=200 kN
stopa
0.8
×0.8 m
Q
stopa
0.8
×0.8 m
1.0
2.0
3.0
4.0
z [m]
σ
Qz1
σ
Qz2
r = 1.0 m
5
.
312
8
.
0
8
.
0
200
)
0
(
=
⋅
=
=
r
Qz
σ
kPa
200
2
0
96
5
312
5
0
≈
+
=
=
.
.
)
m
.
r
(
Qz
σ
kPa
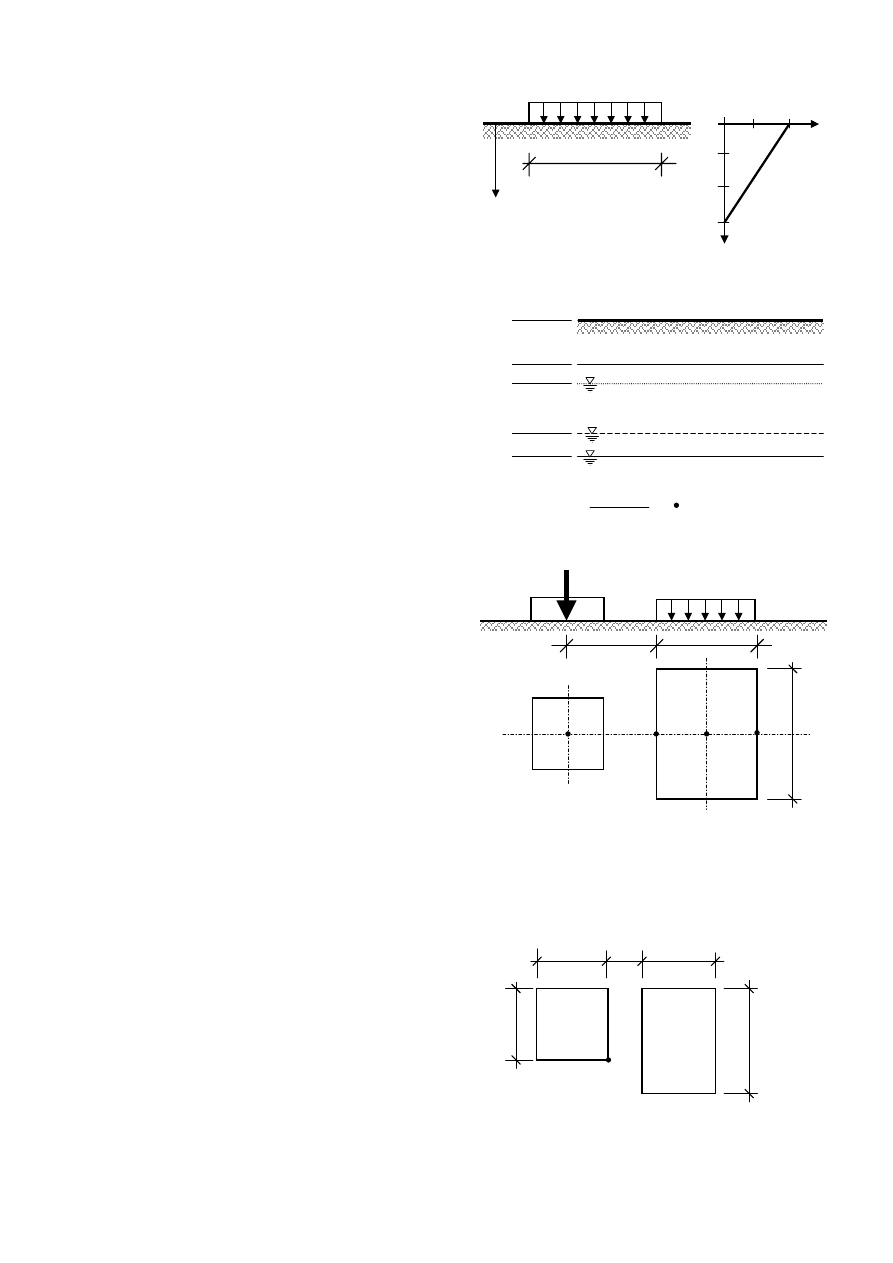
Zadania do rozwiązania
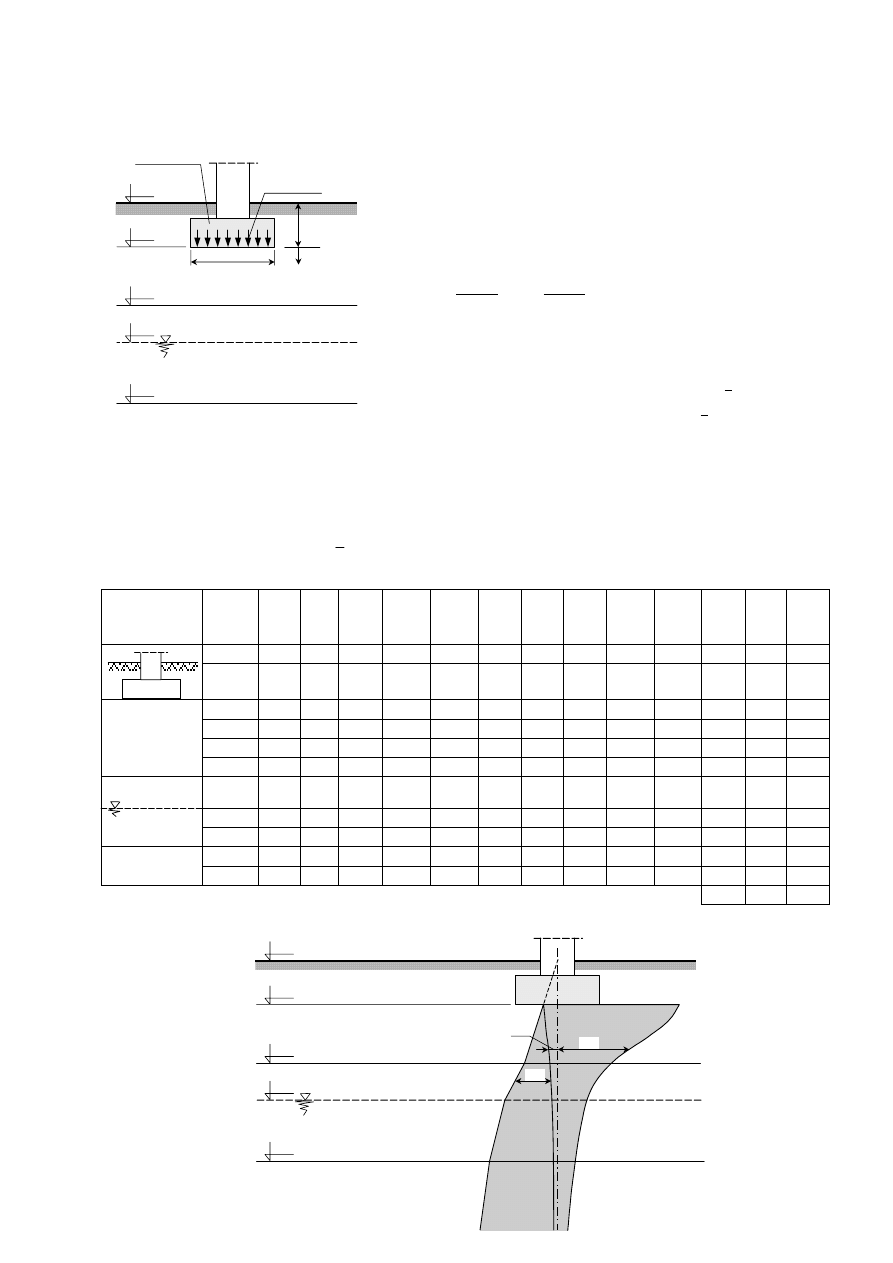
Zad. 6.3.
Na jakiej głębokości „z” naprężenia
dodatkowe od nacisków q=100 kPa przekazy-
wanych przez fundament o szerokości B=2,0 m
zrównają się z naprężeniami geostatycznymi
w podłożu gruntowym. Rozkład
η przyjąć
liniowy do głębokości z =3B.
Odp.: z = 2.73 m
Zad. 6.4.
W podłożu gruntowym obniżono
zwierciadło wody gruntowej o 5,0 m, w wyniku
czego wystąpiła kapilarność bierna h
kb
= 2,0 m.
Policzyć wartość efektywnych naprężeń
geostatycznych w gruncie w punkcie A przed
i po obniżeniu zwierciadła wody gruntowej.
Odp.: przed obniżeniem –
σ’
z
γ
A
= 166 kPa
po obniżeniu –
σ’
z
γ
A
=207 kPa
Zad. 6.5.
Pod punktami A, B i C, na
głębokościach z = 1.0m, 3.0m i 5.0m wyzna-
czyć wartości pionowych naprężeń dodat-
kowych od oddziaływania fundamentów I i II.
Naprężenia od fundamentu I policzyć jak od siły
skupionej Q według wzoru Bussinesqu’a.
Naprężenia od fundamentu II policzyć jak pod
wiotkim obszarem prostokątnym obciążonym
obciążeniem q (wykorzystać nomogramy na
η).
Odp.:
punkt A
punkt B
punkt C
z
σ
zI
σ
zII
σ
zI
σ
zII
σ
zI
σ
zII
1.0 21.3 92.0
2.0 180.0
∼0.0 92.0
3.0 52.5 60.0
15.5 84.0
4.8 60.0
5.0 32.9 32.0
17.6 40.0
8.4 32.0
Zad. 6.6.
W punkcie A, na głębokościach
z = 2.0m i 4.0m wyznaczyć wartości naprężeń
pionowych od oddziaływania fundamentów I i
II. Obliczenia wykonać metodą punktu
narożnego (wykorzystać nomogram na
η
n
).
Odp.: z = 2.0m
σ
zA
=
σ
zI
+
σ
zII
= 34.0 + 12.0 = 46.0 kPa
z = 4.0m
σ
zA
=
σ
zI
+
σ
zII
= 16.0 + 9.2 = 25.2 kPa
q = 100 kPa
B = 2,0 m
z
P
d
,
γ = 20 kN/m
3
z/B
0
1
2
3
1
0.5
η
± 0.0
- 3.0
- 4.0
- 7.0
- 9.0
A
P
g
,
γ = 20 kN/m
3
P
d
,
γ = 18 kN/m
3
γ‘ = 11 kN/m
3
,
γ
sr
= 21 kN/m
3
zwg (pierw.)
zwg (kap.)
zwg (obniż.)
- 12.0
q = 200 kPa
B = 3,0 m
Q = 2500 kN
II
I
2,0 m
L = 4.5 m
I
II
A B
q=200kPa
Q = 2500 kN
C
3.0 m
I
II
A
q=200kPa
q=100kPa
2.0 m
2.0 m
1.0 m
2.0 m
7. Osiadania podłoża gruntowego – zadania przykładowe
Zadanie 7.1
Wyznaczyć rozkład naprężeń w gruncie pod fundamentem przedstawionym na rysunku poniżej oraz
obliczyć wartość średnich osiadań podłoża gruntowego pod tym fundamentem.
Rozkład naprężeń w gruncie pod fundamentem wyznaczony zostanie
z wykorzystaniem współczynnika
η
s
do wyznaczanie składowej pionowej
σ
z
naprężenia średniego pod całym wiotkim obszarem prostokątnym,
obciążonym równomiernie.
1) Obliczenie osiadań metodą odkształceń jednoosiowych
Wartość osiadania podłoża gruntowego obliczona zostanie ze wzoru:
∑
∑
⋅
⋅
+
⋅
=
+
=
i
i
szi
i
i
dzi
M
h
M
h
"
s
's
s
σ
λ
σ
0
[mm]
w którym:
s’ , s” - osiadania pierwotne i wtórne
M
0i
, M
i
– edometryczny moduł ściśliwości pierwotnej i wtórnej
h
i
– miąższość warstwy obliczeniowej (h
i
≤ B/2)
σ
dzi
– naprężenia dodatkowe na głębokości z
i
(
q
si
dzi
⋅
=
η
σ
)
σ
szi
– naprężenia wtórne na głębokości z
i
(
q
si
szi
⋅
=
η
σ
)
głębokość z
i
przyjmuje się w połowie miąższości h
i
.
λ – współczynnik uwzględniający stopień odprężenia gruntu w dnie
wykopu (
λ = 0 ÷ 1.0)
Sumowanie osiadań przeprowadza się do głębokości z
i
, na której spełnia się
warunek:
σ
dzi
< 0.3
⋅σ
γzi
.
Obliczenia pomocnicze:
q
D
=
γ
D
⋅D = 17.0⋅1.5 = 25.5 kPa, q = q - γ
D
⋅D = 300 – 25.5 = 274.5 kPa, L/B = 4.0/2.0 = 2.0, λ = 1.0
Tabela obliczeń naprężeń i osiadań
Profil
geotech.
Rzędna
spodu
warstwy
h
i
[m]
z
i
[m]
σ
γzi
[kPa]
0.3
σ
γzi
[kPa]
z
i
/B
η
si
σ
dzi
[kPa]
σ
szi
[kPa]
M
0i
[MPa]
M
i
[MPa]
i
's
[mm]
i
"
s
[mm]
i
s
[mm]
+1.5
0.0
0.0
0.0
0.0
22.5
6.8
0
1.0
274.5
25.5
60.0
75.0
0.0
0.0
0.0
-0.5 0.5
0.25
26.75
8.0 0.125
0.85
233.0
22.0 60.0 75.0 1.94 0.15 2.09
-1.0 0.5
0.75
35.25
10.5
0.375
0.72
198.0
18.0 60.0 75.0 1.65 0.12 1.77
-1.5 0.5
1.25
43.75
13.1
0.625
0.52
143.0
13.0 60.0 75.0 1.19 0.09 1.28
P
d
γ = 17 kN/m
3
-2.0 0.5
1.75
52.25
15.7
0.875
0.42
115.0
11.0 60.0 75.0 0.96 0.07 1.03
-3.0 1.0
2.50
66.00
19.8 1.25
0.30
82.0 8.0 35.0 47.0 2.34 0.17 2.51
-4.0 1.0
3.50
80.50
24.2 1.75
0.22
60.0 6.0 35.0 47.0 1.71 0.13 1.84
P
g,
γ =19 kN/m
3
γ’=10 kN/m
3
-5.0 1.0
4.50
90.50
27.2 2.25
0.15
41.0 4.0 35.0 47.0 1.17 0.09 1.26
-6.0 1.0
5.50
100.3
30.1 2.75
0.11
30.0 3.0 25.0 33.0 1.21 0.09 1.30
G
γ’ = 9.5 kN/m
3
-7.0 1.0
6.50
109.8
32.9 3.25
0.08 22.0 2.0 25.0 33.0 -
-
-
12.18
0.90 13.08
Rezultat: osiadania podłoża gruntowego wyniosą około s = 13.0 mm
zwg
Piasek drobny (P
d
)
γ = 17.0 kN/m
3
M
0
= 60 MPa, M = 75 MPa
stopa
B= 2m, L = 4m
0.00
+ 1.50
- 2.00
Piasek gliniasty (P
g
)
γ = 19.0 kN/m
3
γ’ = 10 kN/m
3
M
0
= 35 MPa, M = 47 MPa
Glina (G)
γ = 18.5 kN/m
3
γ’ = 9.5 kN/m
3
M
0
= 25 MPa, M = 33 MPa
- 3.00
- 5.00
D = 1.5 m
q = 300 kPa
B
zwg
z
Piasek drobny (P
d
)
γ = 17.0 kN/m
3
M
0
= 60 MPa, M = 75 MPa
0.00
+ 1.50
- 2.00
Piasek gliniasty (P
g
)
γ = 19.0 kN/m
3
γ’ = 10 kN/m
3
M
0
= 35 MPa, M = 47 MPa
Glina (G)
γ = 18.5 kN/m
3
γ’ = 9.5 kN/m
3
M
0
= 25 MPa, M = 33 MPa
- 3.00
- 5.00
zwg
σ
sz
σ
dz
σ
γz
2) Obliczenie osiadań metodą odkształceń trójosiowych
Wartość osiadania podłoża gruntowego obliczona zostanie ze wzoru:
∑
∑
−
⋅
∆
⋅
⋅
⋅
+
−
⋅
∆
⋅
⋅
=
+
=
i
i
i
D
i
i
i
E
)
(
B
q
E
)
(
B
q
"
s
's
s
2
0
2
1
1
ν
ω
λ
ν
ω
[mm]
w którym:
∆ω
i
=
ω
2i
–
ω
1i
(
ω
1i
– współczynnik wpływu dla stropu warstwy „i” na głębokości z
1i
,
ω
2i
– współczynnik wpływu dla
spągu warstwy „i” na głębokości z
2i
, współczynniki
ω
1
i
ω
2
zależą od z
1
/B i z
2
/B oraz L/B)
ν
i
– współczynnik Poissona dla gruntu w warstwie „i”,
E
0i
, E
i
- odpowiednio pierwotny i wtórny moduł odkształcenia ogólnego gruntu
B – szerokość fundamentu
a) osiadanie warstwy 1 – P
d
Przyjęto
ν
1
= 0.27
→
80
.
0
)
27
.
0
1
(
)
27
.
0
2
1
(
)
27
.
0
1
(
1
=
−
⋅
−
⋅
+
=
δ
→
48
60
80
.
0
01
=
⋅
=
E
MPa,
60
75
80
.
0
1
=
⋅
=
E
MPa
z
11
= 0
→ ω
11
= 0, z
21
= 2.0 m , z
21
/B = 2.0/2.0 = 1, L/B = 4.0/2.0 = 2
→
ω
21
= 0.47,
→
∆ω
1
= 0.47 – 0.0 = 0.47
=
+
=
−
⋅
⋅
⋅
⋅
+
−
⋅
⋅
⋅
=
37
0
98
4
60
27
0
1
47
0
0
2
5
25
0
1
48
27
0
1
47
0
0
2
5
274
2
2
1
.
.
)
.
(
.
.
.
.
)
.
(
.
.
.
s
5.35 mm
b) osiadanie warstwy 2 – P
g
Przyjęto
ν
2
= 0.30
→
74
.
0
)
30
.
0
1
(
)
30
.
0
2
1
(
)
30
.
0
1
(
2
=
−
⋅
−
⋅
+
=
δ
→
26
35
74
.
0
02
=
⋅
=
E
MPa,
35
47
74
.
0
2
=
⋅
=
E
MPa
z
21
= 2.0
→ ω
21
= 0.47, z
22
= 5.0 m , z
22
/B = 5.0/2.0 = 2.5, L/B = 2
→
ω
22
= 0.86,
→
∆ω
2
= 0.86 – 0.47 = 0.39
=
+
=
−
⋅
⋅
⋅
⋅
+
−
⋅
⋅
⋅
=
52
.
0
49
.
7
35
)
30
.
0
1
(
39
.
0
0
.
2
5
.
25
0
.
1
26
)
30
.
0
1
(
39
.
0
0
.
2
5
.
274
2
2
2
s
8.01 mm
c) osiadanie warstwy 3 – G
Przyjęto
ν
3
= 0.32
→
70
.
0
)
32
.
0
1
(
)
32
.
0
2
1
(
)
32
.
0
1
(
3
=
−
⋅
−
⋅
+
=
δ
→
5
.
17
25
70
.
0
03
=
⋅
=
E
MPa,
23
33
70
.
0
3
=
⋅
=
E
MPa
z
31
= 5.0
→ ω
31
= 0.86, z
32
=
∞ , z
32
/B =
∞, L/B = 2 →
ω
32
= 1.22,
→
∆ω
3
= 1.22 – 0.86 = 0.36
=
+
=
−
⋅
⋅
⋅
⋅
+
−
⋅
⋅
⋅
=
72
.
0
14
.
10
23
)
32
.
0
1
(
36
.
0
0
.
2
5
.
25
0
.
1
5
.
17
)
32
.
0
1
(
36
.
0
0
.
2
5
.
274
2
2
3
s
10.86 mm
d) osiadanie całkowite
s = s
1
+ s
2
+ s
3
= 5.35 + 8.01 + 10.86 = 24.22 mm
Wniosek: Obliczenia metodą odkształceń trójosiowych dają większe wartości osiadań.
Zadania do rozwiązania
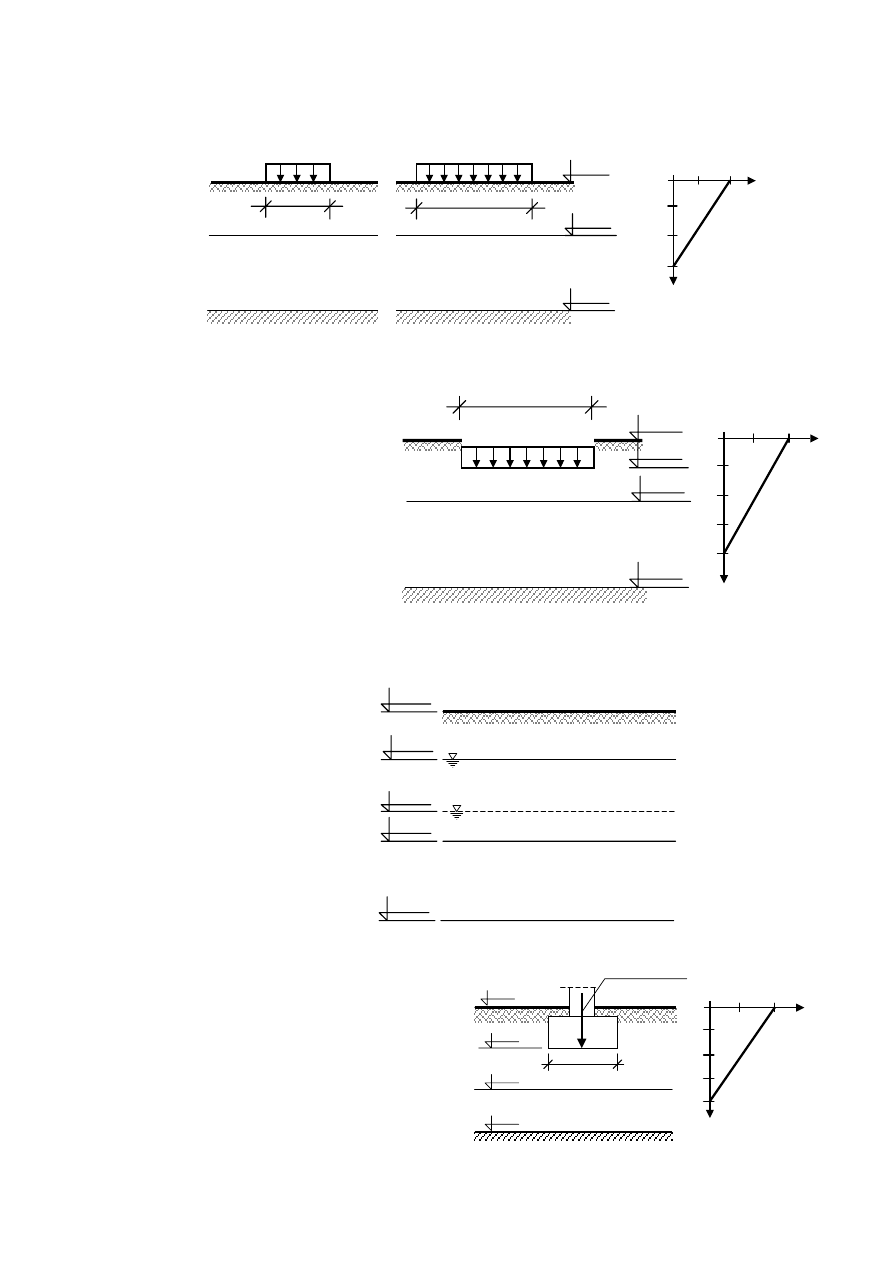
Zad. 7.2.
Który fundament osiądzie więcej? Spróbować powiedzieć najpierw bez obliczeń.
Policzyć wartości osiadań fundamentów. Rozkład
η przyjąć liniowy do głębokości z = 3B.
Odp.: więcej osiądzie fundament B, s
A
= 38.07 mm, s
B
= 57.8 mm.
Zad. 7.3.
Policzyć osiadanie warstwy
G
π
od nacisków dodatkowych q
przekazywanych przez fundament.
Rozkład
η przyjąć liniowy do
głębokości 4B.
Odp.: s
G
π
= 27.96 mm
Zad. 7.4.
Policzyć osiadanie warstwy namułu w wyniku obniżenia zwierciadła wody gruntowej
o 4.0 m. Przyjąć, że obniżenie wody wykonano na znacznym obszarze, stąd
η = 1 w całej
miąższości namułu.
Odp.: s
Nm
= 120 mm
Zad. 7.5.
Jaką szerokość powinna mieć
ława fundamentowa, aby osiadania podłoża
gruntowego nie przekroczyły 20 mm?
Obliczenia wykonać metodą odkształceń
jednoosiowych, przyjmując liniowy rozkład
współczynnika
η, jak pokazano na
wykresie.
Odp.: B
≥ 3.0 m.
- 2.0
q = 250 kPa
B = 3,0 m
± 0.0
- 6.0
M
0
= 25 MPa
z/B
0
1
2
3
1
0.5
η
- 1.0
G
π
,
Pd,
γ = 17 kN/m
3
4
podłoże nieściśliwe
B
- 2.0
q = 200
B = 3,0 m
A
q = 200
B = 1,5 m
± 0.0
- 6.0
M
0
= 10 MPa
M
0
= 20 MPa
M
0
= 10 MPa
M
0
= 20 MPa
z/B
0
1
2
3
1
0.5
η
podłoże nieściśliwe
podłoże nieściśliwe
± 0.0
- 2.0
- 6.0
- 7.0
P
d
,
γ = 18 kN/m
3
γ‘ = 11 kN/m
3
γ
sr
= 21 kN/m
3
zwg (pierw.)
zwg (obniż.)
- 10.0
Nm, M
0
= 1,0 MPa
η
z/B
0
1
2
4
1
0.5
± 0.00
- 3.5
M
0
= 25 MPa
- 1.0
3
B= ?
M
0
= 15 MPa
- 7.0
podłoże nieściśliwe
N = 250 kN/m?