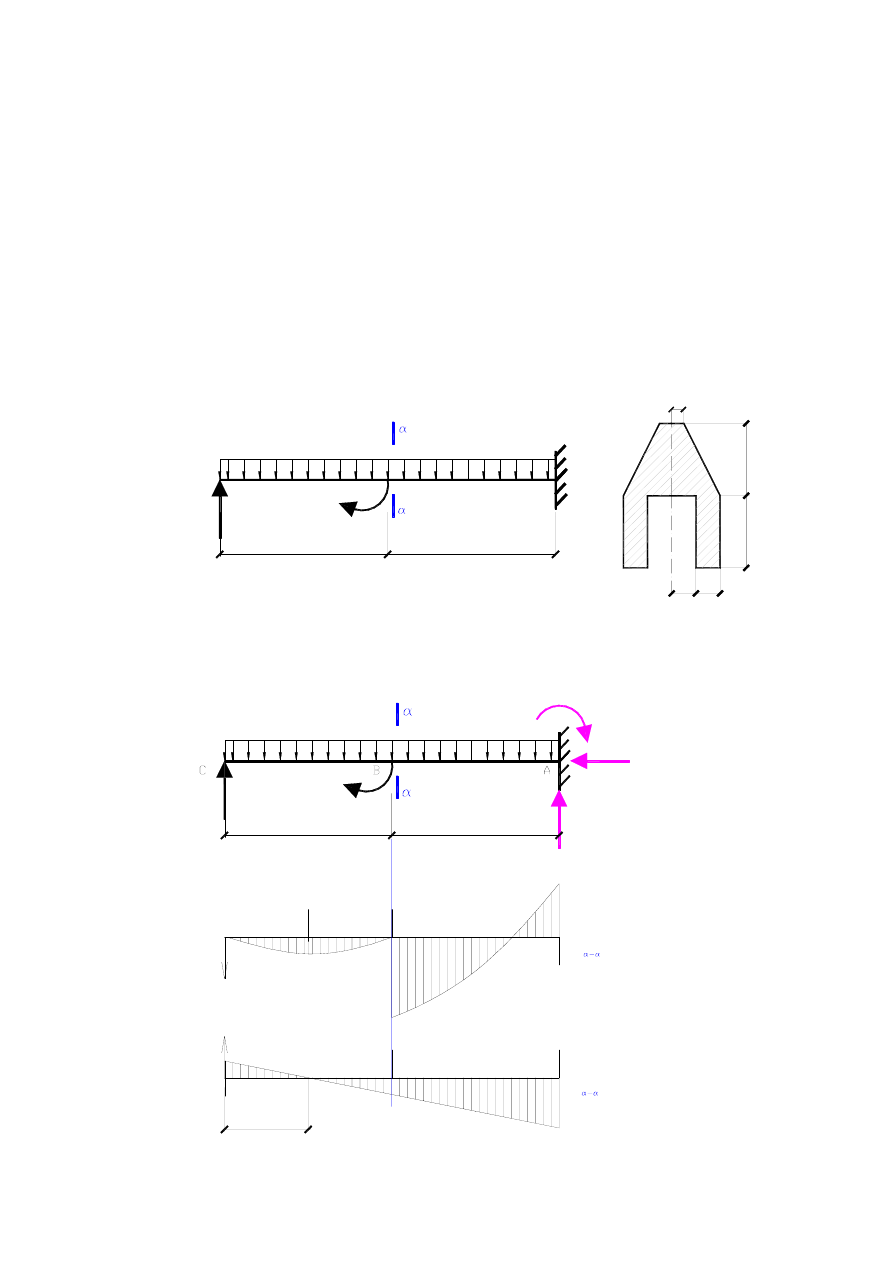
Zadanie 2. Zginanie proste belek.

Dla

belki

zginanej

obciążonej jak na

Rys.1

wyznaczyć:

1. Wykres momentów zginających M(x) oraz sił poprzecznych Q(x).

2. Położenie osi obojętnej.

3. Wartość maksymalnego naprężenia normalnego

σ

x

.

4. Wartość maksymalnego naprężenia stycznego

τ

xz

.

5. Wartości naprężeń głównych

σ

1

,

σ

2

i ich kierunki główne w oznaczonym punkcie K

belki przekroju poprzecznego

α – α

.

10 KN

12.0KNm

1.0 m

20 KN/m

C

B

1.0 m

A

2.0 2.0

1.0

6.

0

6.

0

cm

Rys1.

1. Wykres momentów zginających M(x) oraz sił poprzecznych Q(x) –

Rys2.

-8.0

+2.5

10 KN

20 KN/m

M(x)

[KNm]

Q(x)

[KN]

-30.0

+10.0

H

A

= 0.0KN

M

A

= 8.0KN

V

A

= 30.0KN

1.0 m

1.0 m

12.0KNm

0.

0

M

= +12.0KNm

Q

= -10.0KN

+12.0

0.5 m

-10.0

Rys.2

M

max

= +12.0KNm

Q

max

= -30.0KN

_____________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

1/6

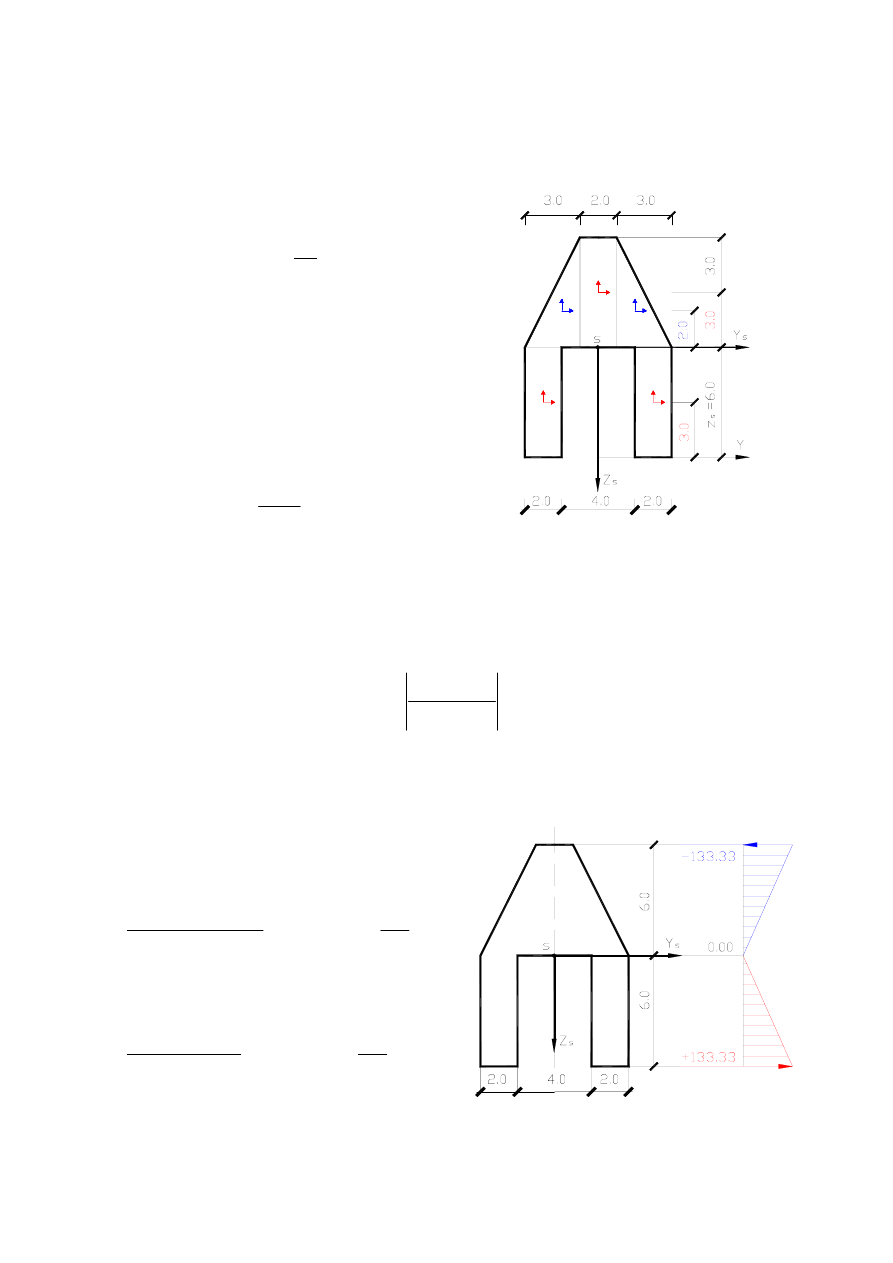
2. Wyznaczenie położenia osi obojętnej

.

Oś obojętna przechodzi przez środek ciężkości przekroju i jest prostopadła do płaszczyzny obciążenia
- wymiary przekroju podane są w centymetrach

Rys3

.

Środek ciężkości przekroju wyznaczamy z zależności:

A

S

z

y

s

=

gdzie:

S

y

- moment statyczny przekroju poprzecznego belki

względem przyjętej osi y.

A – pole powierzchni przekroju poprzecznego belki.

S

y

= 2*2*6*(-3) + 2*6*(-9) + 2*(3*6/2)*(-8) =

−324cm

2

A = 3*2*6 + 2*(3*6/2) = 54cm

2

cm

6

54

324

z

s

−

=

−

=

Rys.3

3. Wyznaczenie wartości maksymalnego naprężenia normalnego

σ

x

.

Największe naprężenie normalne rozciągające i ściskające (

Rys.4

) co do bezwzględnej wartości

występują odpowiednio w dolnych i górnych skrajnych włóknach belki

i wynoszą:

s

y

max

max

max

J

z

M

=

σ

(1)

Maksymalny moment zginający wynosi

M

max

=12KNm

(patrz

Rys.2

)

Obliczenia na podstawie wzoru

(1)

Włókna górne belki są ściskane:

2

3

8

2

g

m

KN

10

*

33

.

133

10

*

540

)

10

*

0

.

6

(

*

12

−

=

−

+

=

σ

−

−

Włókna dolne belki są rozciągane:

2

3

8

2

d

m

KN

10

*

33

.

133

10

*

540

10

*

0

.

6

*

12

+

=

+

=

σ

−

−

Wykres

σ

x

[MPa]

Rys.4

Wykres naprężeń

normalnych

_____________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

2/6

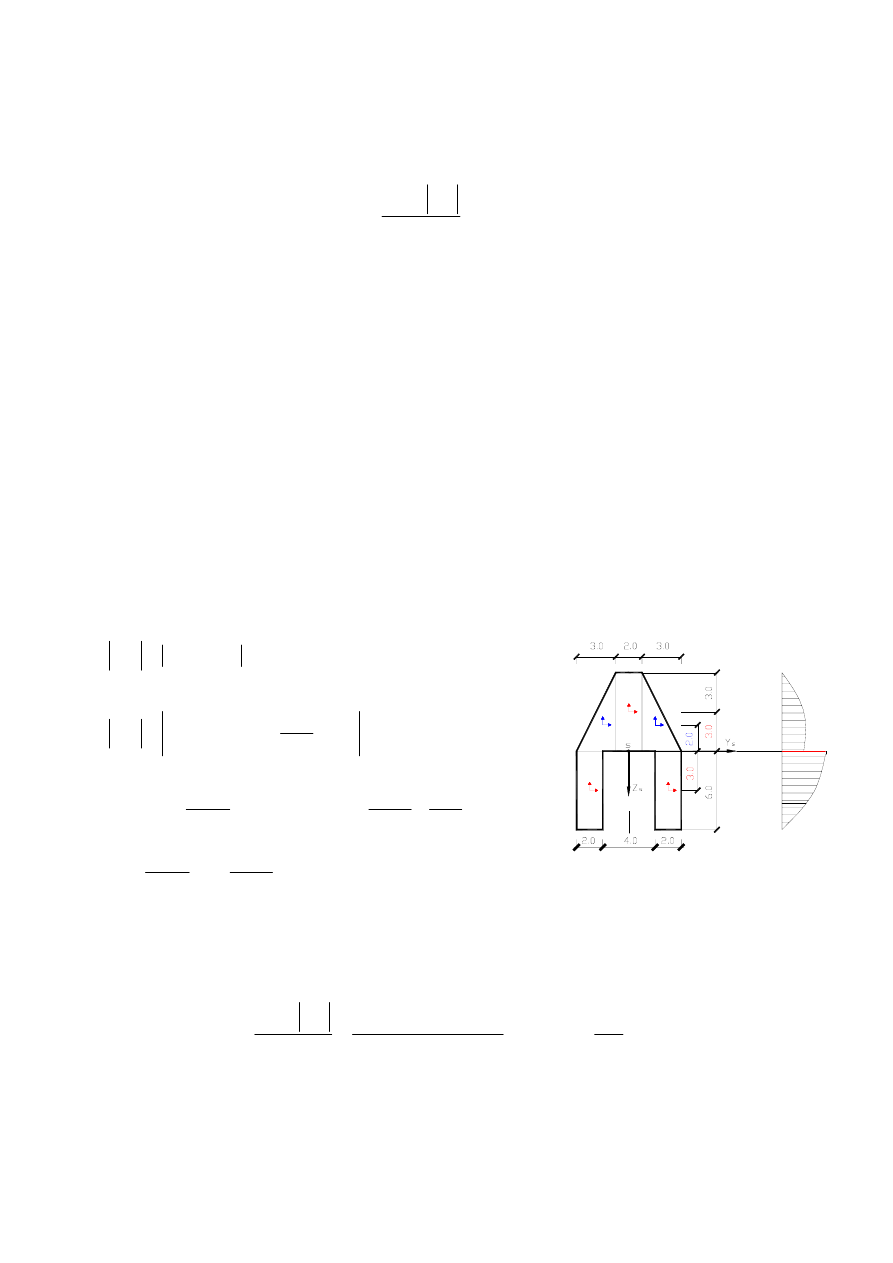
4. Wyznaczenie wartości maksymalnego naprężenia

stycznego

τ

xz

.

Maksymalne naprężenie styczne

τ

xz

wyznaczamy ze wzoru

(2)

:

b

J

S

Q

s

s

y

y

max

xz

=

τ

(2)

gdzie:

Q

max

– maksymalna siła poprzeczna w belce zginanej.

s

y

S

– moment statyczny względem osi obojętnej części przekroju poprzecznego zawartej między

poziomem punktu, dla którego obliczamy naprężenia, a włóknami dolnymi lub górnymi
przekroju.

s

y

J

– główny centralny moment bezwładności przekroju poprzecznego belki względem osi y

s

.

b – szerokość przekroju poprzecznego belki w poziomie punktu dla którego obliczamy naprężenia.

Maksymalna siła poprzeczna wynosi

Q

max

=

−30 KN

(patrz

Rys.2

)

Obliczenia na podstawie wzoru

(2)

3

y

cm

72

3

*

6

*

2

*

2

S

s

=

=

lub

3

y

cm

72

)

2

(

*

2

6

*

3

*

2

)

3

(

*

6

*

2

S

s

=

−

+

−

=

4

3

3

2

3

2

3

y

cm

540

12

6

*

3

*

2

3

6

*

2

*

3

2

*

2

6

*

3

36

6

*

3

*

2

3

*

6

*

2

12

6

*

2

*

3

J

s

=

+

=

=















+

+















+

=

cm

4

2

2

b

=

+

=

wykres

τ

xz

[MPa]

Rys.5 Wykres

naprężeń stycznych

-10.0

MPa

10

m

KN

10

*

10

10

*

4

*

10

*

540

10

*

72

*

30

b

J

S

Q

2

3

2

8

6

y

y

max

xz

s

s

=

−

=

−

=

=

τ

−

−

−

_____________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

3/6

5. Wyznaczenie wartości naprężeń głównych

σ

1

,

σ

2

i ich kierunków głównych

w oznaczonym punkcie K belki przekroju poprzecznego

α – α

.

Moment zginający i siła poprzeczna w przekroju poprzecznym belki

α – α

wynoszą odpowiednio:

M

α

-

α

= +12 KNm

,

Q

α

-

α

=

−10 KN

(patrz

Rys.2

).

5.1. Naprężenie normalne rozciągające w punkcie K wyznaczamy ze wzoru

(3)

:

s

y

k

k

J

z

M

α

−

α

=

σ

(3)

gdzie:

M

α-α

– moment zginający w przekroju poprzecznym belki

α – α

z

k

– odległość punktu K od osi obojętnej

s

y

J

– główny centralny moment bezwładności przekroju poprzecznego belki

względem osi y

s

.

MPa

889

.

88

m

KN

10

*

889

.

88

10

*

540

10

*

4

*

12

2

3

8

2

k

=

=

=

σ

−

−

5.2. Naprężenie styczne

τ

k

w punkcie K

wyznaczamy ze wzoru

(4)

:

b

J

S

Q

s

s

y

y

k

α

−

α

=

τ

(4)

gdzie:

Q

α-α

– siła poprzeczna w belce zginanej w przekroju poprzecznym belki

α – α

.

s

y

S

– moment statyczny względem osi obojętnej

części przekroju

poprzecznego zawartej

między poziomem punktu K, dla którego obliczamy naprężenia, a włóknami dolnymi.
Na poniższym rysunku (

Rys.6)

część przekroju zakreskowana jest na kolor czerwony

.

s

y

J

– główny centralny moment bezwładności przekroju poprzecznego belki względem osi y

s

b

– szerokość przekroju poprzecznego belki w poziomie punktu K dla którego obliczamy

naprężenia.

3

y

cm

40

5

*

2

*

2

*

2

S

s

=

=

MPa

852

.

1

m

KN

10

*

852

.

1

10

*

4

*

10

*

540

10

*

40

*

10

2

3

2

8

6

k

−

=

−

=

−

=

τ

−

−

−

_____________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

4/6

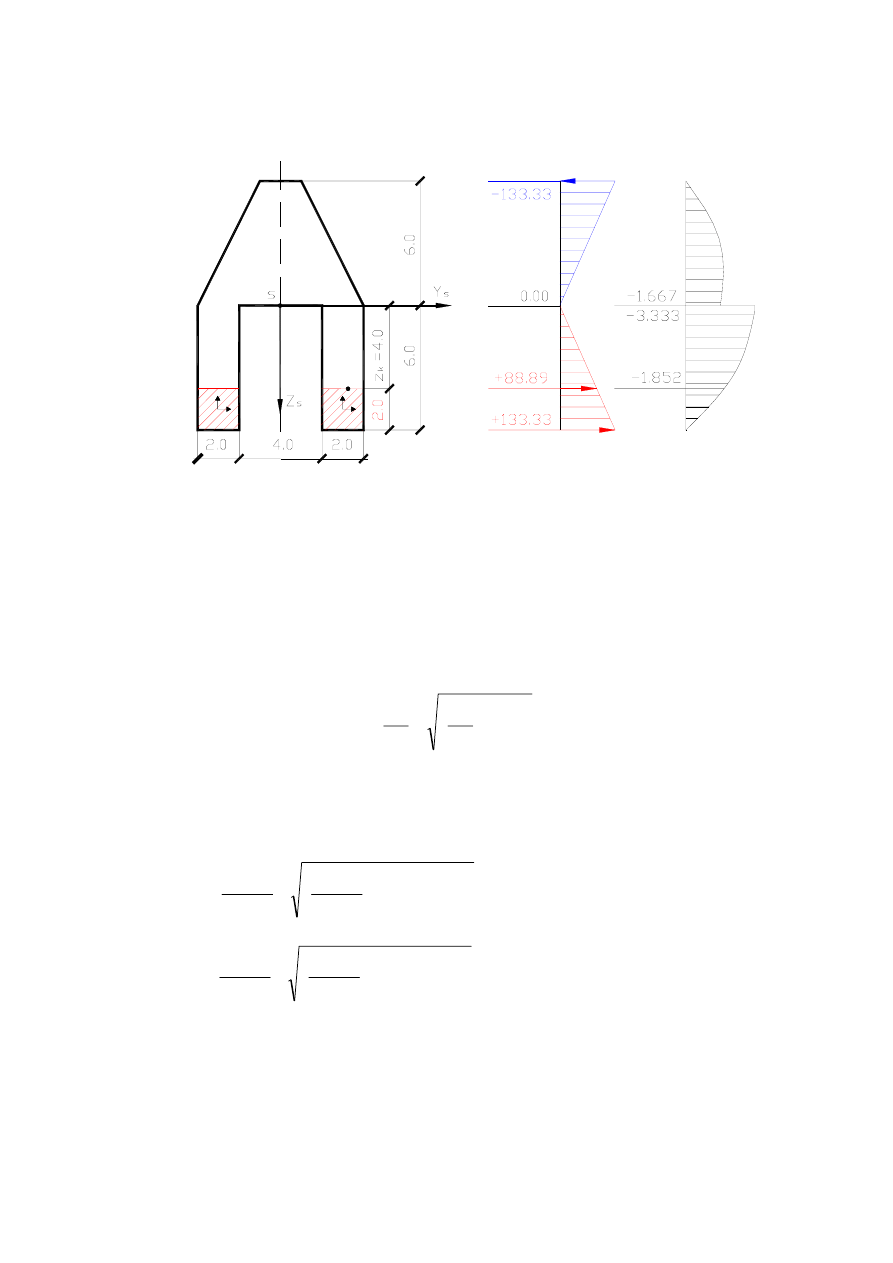
5.3. Wykresy naprężeń normalnych i stycznych w przekroju poprzecznym

α – α

.

wykres

σ

α-α

wykres

τ

α-α

K

Rys. 6 Wykresy naprężeń normalnych i stycznych

w przekroju

α-α

belki.

a). Obliczenie naprężeń głównych

σ

1

,

σ

2

w oznaczonym punkcie K belki

przekroju poprzecznego

α – α

.

Naprężenia główne w punkcie K belki zginanej obliczamy ze wzoru

(5)

2

k

2

k

k

min

max,

2

2

τ

+











 σ

±

σ

=

σ

(5)

Do wzoru

(5)

wstawiamy wartości obliczone na stronie 4

(

)

MPa

928

.

88

852

.

1

2

889

.

88

2

889

.

88

2

2

max

+

=

−

+













+

=

σ

(

)

MPa

039

.

0

852

.

1

2

889

.

88

2

889

.

88

2

2

min

−

=

−

+













−

=

σ

MPa

928

.

88

1

max

+

=

σ

=

σ

MPa

039

.

0

2

min

−

=

σ

=

σ

_____________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

5/6

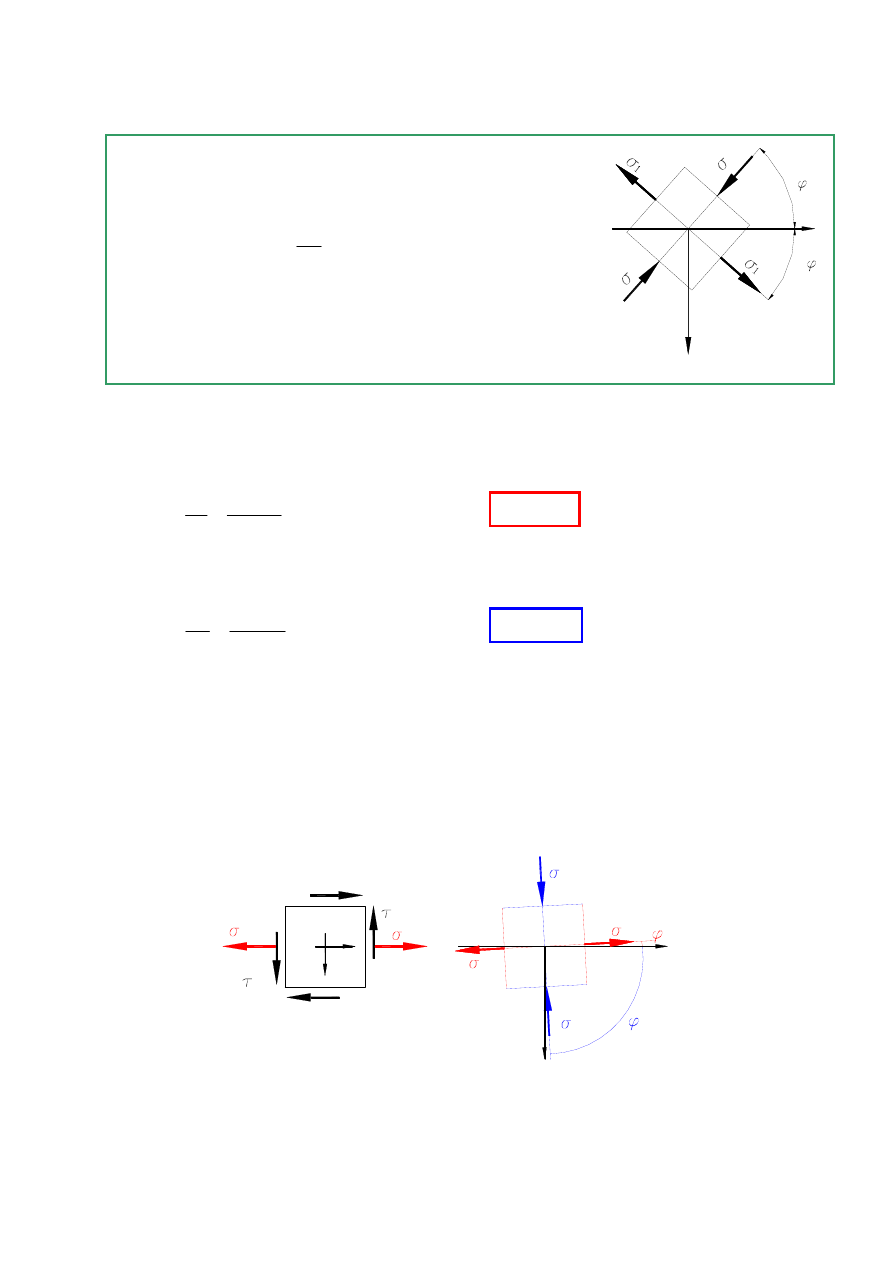
b). Obliczenie kierunków naprężeń głównych

σ

1

,

σ

2

w oznaczonym punkcie K belki przekroju

poprzecznego

α – α

.

Położenie kierunków naprężeń

głównych

σ

1

,

σ

2

i odpowiadających im płaszczyzn głównych przechodzących
przez dany punkt K wyznaczamy ze wzoru

(6)

n

k

n

tg

σ

τ

=

ϕ

n = 1,2

(6)

Np. dla n = 1,

ϕ

jest to kąt zawarty miedzy kierunkiem osi x,

a kierunkiem naprężenia głównego

σ

1

1

.

Dodatni kąt odmierzamy w pierwszej ćwiartce układu osi
współrzędnych xz jak na rysunku poglądowym obok –

Rys7

+

1

2

Z

X

-

2

2

Rys.7

i tak w naszym zadaniu wyznaczamy na podstawie wzoru

(6)

- kierunek naprężenia głównego

σ

1

:

0.0208

28

88.9

1.852

σ

τ

tg

1

k

1

−

=

−

=

=

ϕ

'

12

1

1

o

−

=

ϕ

- kierunek naprężenia głównego

σ

2

:

487

.

47

039

.

0

852

.

1

tg

2

k

2

+

=

−

−

=

σ

τ

=

ϕ

88

=

ϕ

'

48

2

o

Na rysunku (

Rys.8a

) przedstawiony jest płaski stan naprężenia w punkcie K belki przekroju

poprzecznego

α – α

.

Wartości

σ

x

=

σ

k

oraz

τ

xz

=

τ

k

obliczone są na stronie 4

– odpowiednio wzór

(3)

,

(4)

.

Na rysunku (

Rys.8b

) przedstawione są kierunki naprężeń głównych i odpowiadające im

płaszczyzny główne w punkcie K belki przekroju poprzecznego

α – α

.

2

Z

X

Z

X

xz

xz

2

2

1

x

x

1

1

Rys.8a

Rys.8b

_____________________________________________________________________________________

http://riad.usk.pk.edu.pl/~iwroblew/dydaktyka/

6/6