
Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
dr inż. Mirosław Jan Nowakowski
Obliczanie pochylenia zastępczego
Ostatnie zmiany: listopada r., godz. :
Wszelkie prawa zastrzeżone
Spis treści
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. Opory ruchu pociągu
Na pociąg będący w ruchu, oprócz siły pociągowej, działa wiele sił różnego rodzaju
i pochodzenia, których większość skierowana jest zwykle przeciw ruchowi pociągu.
Rzuty tych wszystkich sił, odniesionych do obwodu kół pociągu, na kierunek jego biegu
nazywamy o p o r a m i r u c h u.
Oporom ruchu przypisujemy znak ,,+”, gdy są skierowane przeciw ruchowi pociągu
i znak ,,–”, gdy ich kierunek jest zgodny z ruchem pociągu.
Wszystkie opory składowe jak i całkowite określa się jako siłę wyrażoną w [N] lub
w postaci oporów jednostkowych, odniesionych do kN ciężaru pociągu, wyrażonych
w [N/kN] lub [h].
Siły przeciwdziałające ruchowi składu pociągu po torze wyidealizowanym, doskonale
prostym i poziomym, nazywamy o p o r e m z a s a d n i c z y m. Po jego odniesieniu
do ciężaru pociągu otrzymujemy o p ó r j e d n o s t k o w y.
Wartość oporu zasadniczego pociągu można wyrazić za pomocą ogólnego wzoru
W
zas
= W
k
+ W
L
+ W
γ
+ W
A
()
gdzie:
W
k
łączne opory kontaktowe,
W
L
opory łożysk osiowych,
W
γ
opory dyssypacji energii,
W
A
opór aerodynamiczny,

Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
przy czym:
(W
k
+ W
L
) = const
W
γ
= W
γ
(v)
W
A
= W
A
(v
)
gdzie:
v
prędkość pojazdu szynowego [m/s].
Zgodnie z fizycznymi aspektami poszczególnych składników oporu ruchu pociągu,
można zapisać:
W
zas
= (a + b ⋅ v) ⋅ Q + c ⋅ A ⋅ v
()
lub w postaci bardziej ogólnej:
W
zas
= A ⋅ Q + B ⋅ v + D ⋅ v
,
()
gdzie:
D
= c ⋅ A
Stosowane na świecie wzory służące do obliczania oporu zasadniczego mają charakter
empiryczny i uwzględniają specyfikę oraz doświadczenia poszczególnych zarządów kole-
jowych. W Polsce stosuje się wzory opracowane przez Instytut Kolejnictwa
(w skrócie:
IK) — osobno dla lokomotyw, wagonów oraz zespołów trakcyjnych (zarówno elektrycz-
nych, jak i spalinowych).
Wzór IK dla lokomotyw ma postać
W
zas L
= (, + , ⋅ v) ⋅ Q
L
+ ⋅ n + , ⋅ v
[N]
()
przy czym
Q
L
= g ⋅ m
L
gdzie:
Q
L
nacisk lokomotywy na tor [kN];
m
L
masa lokomotywy [t];
g
przyspieszenie ziemskie (, m/s
);
n
liczba osi lokomotywy;
v
prędkość jazdy lokomotywy [m/s].
Wzór IK na opór zasadniczy dla wagonów ma postać
W
zas W
= (K + , ⋅ v) ⋅ Q
W
+ ⋅ n + f ⋅ (, + z) ⋅ v
[N] ,
()
przy czym
Q
W
= g ⋅ m
W
gdzie:
K
współczynnik rodzaju łożysk, wynoszący , dla łożysk ślizgowych i , dla
łożysk tocznych;
Jest to nowa nazwa Centrum Naukowo-Technicznego Kolejnictwa( CNTK).

Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
Q
W
nacisk wagonów na tor [kN];
m
W
masa wagonów [t];
n
liczba osi w pociągu;
z
liczba wagonów w pociągu;
f
współczynnik zależny od rodzaju wagonów, który dla wagonów towarowych
wynosi ,, a dla wagonów osobowych — ,;
v
prędkość jazdy wagonów [m/s].
Na całkowity opór zasadniczy pociągu składa się opór pojazdu trakcyjnego oraz opór
wagonów. Wyraża się on zatem wzorem
W
= W
zas L
+ W
zas W
[N] ,
natomiast jednostkowy opór ruchu pociągu wyznaczamy z zależności
w
=
W
Q
L
+ Q
W
=
W
g
⋅ (m
L
+ m
W
)
[N/kN].
()
Nieco inaczej należy traktować zespoły trakcyjne, w których wagony silnikowe oraz
wagony doczepne tworzą nierozłączną eksploatacyjnie całość. Według zaleceń IK do
obliczenia ich oporu zasadniczego należy stosować wzór
W
zas Z T
= (, + , ⋅ v) ⋅ Q
Z T
+ ⋅ n + , ⋅ (, + z) ⋅ v
[N] ,
()
przy czym
Q
Z T
= g ⋅ m
Z T
gdzie:
Q
Z T
nacisk na tor zapełnionego zespołu trakcyjnego [kN];
m
Z T
masa zespołu trakcyjnego [t];
z
liczba wagonów w zespole trakcyjnym;
n
liczba osi w zespole trakcyjnym;
v
prędkość jazdy zespołu trakcyjnego [m/s].
Opór jednostkowy zespołu trakcyjnego wyznaczamy odnosząc jego opór zasadniczy
do nacisku na tor, tzn.
w
=
W
zas Z T
Q
Z T
[N/kN].
()
W powyższych wzorach, przy braku dokładnych danych odnośnie mas pojazdów, do
obliczeń należy przyjmować wartości średnie przedstawione w tab.
. Trzeba przy tym
pamiętać, że występujące w niej masy dla wagonów w zespole trakcyjnym podane są
bez pasażerów, których masę trzeba uwzględnić. Do obliczeń przyjmuje się zapełnienie
każdego wagonu osobami o masie kg.
Poza oporem zasadniczym na pociąg będący w ruchu oddziałują opory wynikające
z kształtu geometrycznego linii kolejowej w profilu podłużnym oraz w planie.
Opór na pochyleniu jest składową ciężaru pociągu Q równoległą do niwelety toru
(rys.
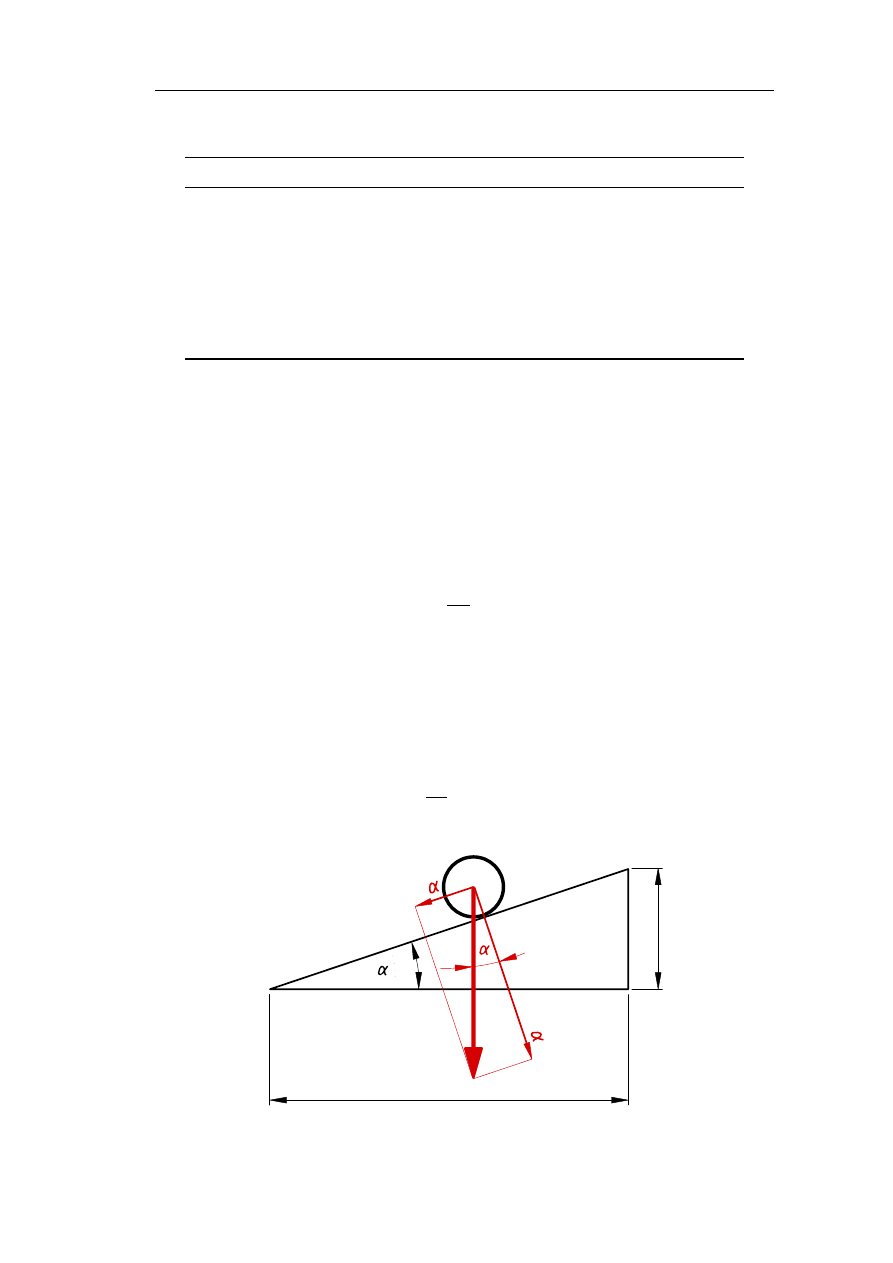
Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
Tab. . Średnie masy pojazdów przyjmowane do obliczeń wg zaleceń IK
Rodzaj pojazdu
Masa [t]
-osiowy wagon pasażerski z obciążeniem
wagon towarowy -osiowy całkowicie załadowany
wagon towarowy -osiowy całkowicie załadowany
lokomotywa -osiowa
lokomotywa -osiowa
lokomotywa -osiowa
wagon silnikowy w zespole trakcyjnym
wagon doczepny w zespole trakcyjnym
Ponieważ ciężar pociągu Q wyrażany jest w [kN], wzór na dodatkowy opór na
wzniesieniu wyrażony w [N] będzie miał postać:
W
i
= ⋅ Q ⋅ sin α [N]
Z kolei p o c h y l e n i e m niwelety toru kolejowego łączącego punkty A i B (rys.
nazywamy stosunek różnicy wysokości ∆h tych punktów do poziomej odległości między
nimi wyrażony w promilach, czyli:
i
= tg α =
∆h
l
⋅ [h].
()
Dla spotykanych w praktyce małych wartości kąta α możemy przyjąć sin α
≈ tg α,
a wtedy
W
i
= Q ⋅ i
[N],
skąd wynika wzór na opór jednostkowy na wzniesieniu w postaci
w
i
=
W
i
Q
= i
[h]
()
Q
Q sin
Q
cos
A
B
Δ
h
l
i
Rys. . Pochylenie toru i opór na pochyleniu

Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
Na wzniesieniach wartość oporu dodaje się do oporów zasadniczych, na spadkach —
odejmuje.
Opory na krzywiznach poziomych oblicza się zwykle według różnych wzorów
empirycznych. Na PKP na liniach normalnotorowych stosowany jest wzór
w
k
=
R
[h]
()
gdzie:
R
promień łuku poziomego [m].
Całkowite opory ruchu są sumą oporów zasadniczych, oporów profilu linii i ewentu-
alnie oporów dodatkowych ośrodka (np. podczas jazdy w tunelu):
W
c
= Q ⋅ w
c
= Q ⋅ (w
± i + w
k
)
()
. Pochylenia linii kolejowej
P o c h y l e n i e m m i a r o d a j n y m i
m
nazywamy największe dopuszczalne pochy-
lenie, na którym — przy danym typie lokomotywy — może odbywać się ruch najcięższego
dla danej linii pociągu z założoną stałą prędkością. Jest ono wyznaczane na długości
równej co najmniej długości najcięższego pociągu towarowego kursującego po danym
odcinku linii kolejowej.
Pochylenia o wielkości w granicach pochylenia miarodajnego — w zależności od tego,
czy są nie większe, czy większe od oporu jednostkowego pociągu — różnie wpływają na
wielkości pracy siły pociągowej.
P o c h y l e n i a n i e s z k o d l i w e to pochylenia mniejsze lub równe oporowi
jednostkowemu, które nie mają wpływu na średnią pracę lokomotywy przy jeździe w dół.
Średnia praca lokomotywy — przy uwzględnieniu jazdy w obu kierunkach — wynosi
wówczas tyle samo, co praca lokomotywy na odcinku poziomym.
P o c h y l e n i a s z k o d l i w e to pochylenia o oporze większym od oporu
jednostkowego. Przy jeździe w dół po pochyleniu szkodliwym przewaga pochylenia
(spadku) nad oporem ruchu powoduje ruch przyspieszony pociągu. Aby nie przekroczyć
dopuszczalnej prędkości, pociąg musi być hamowany. W ten sposób część pracy siły
pociągowej nie może być odzyskana, gdyż zostaje zużyta przez pracę hamulców.
Właściwości pochyleń nieszkodliwych i szkodliwych znajdują zastosowanie przy
trasowaniu kolei w terenach nizinnych, na których właśnie z takimi pochyleniami ma
się do czynienia. Zastosowanie w takim terenie pochyleń nieszkodliwych — zamiast
układania toru w poziomie lub jednym niewielkim pochyleniu — umożliwia zmniejszenie
objętości robót ziemnych przy tym samym koszcie eksploatacji linii.
. Pochylenie zastępcze
.. Wprowadzenie teoretyczne
P o c h y l e n i e z a s t ę p c z e to pochylenie, na którym praca siły pociągowej
lokomotywy jest równa jej pracy rzeczywistej na linii o tej samej długości i zadanych
(projektowanych) zmiennych pochyleniach.

Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
Pochylenie zastępcze jest wykorzystywane do porównania pracy siły pociągowej
w zależności od układu projektowanej linii w profilu i w planie. Ma to znaczenie przy
analizie wariantów projektowanej linii i ostatecznym wyborze realizowanego rozwiązania.
Przyjmijmy dla uproszczenia, że obciążenie linii przewozami jest jednakowe w obu
kierunkach. Średnia praca siły pociągowej przy jeździe w obydwu kierunkach na części
linii o pochyleniach nieszkodliwych (tj. odcinkach poziomych i o pochyleniach i
⩽ w
)
wynosi
Z
+ Z
⋅ L
= P ⋅ w
⋅ L
()
gdzie L
— łączna długość pochyleń nieszkodliwych. Natomiast średnia pracy siły
pociągowej przy jeździe w obu kierunkach na części odcinka o pochyleniach szkodliwych
(pochylenia i
> w
) wynosi:
Z
+ Z
⋅ L
= P ⋅
(w
+ i)
⋅ L
()
gdzie L
— łączna długość pochyleń szkodliwych.
Na łukach poziomych — położonych zarówno na pochyleniach nieszkodliwych, jak
i szkodliwych — konieczna jest dodatkowa praca siły pociągowej. Jej wartość obliczamy
dla każdego łuku, mnożąc opór w łuku obliczony ze wzoru (
) przez długość toru, na
jakiej opór ten występuje. Długość toru położonego na łuku wyznaczamy z zależności:
L
k
=
π
⋅ R ⋅ α
gdzie:
L
k
długość łuku kołowego;
R
promień łuku poziomego;
α
kąt zwrotu trasy.
Wobec tego dodatkowa praca siły pociągowej na łuku o promieniu R i długości L
k
wynosi:
Z
R
= i
R
⋅ L
k
=
R
⋅
π
⋅ R ⋅ α
= , ⋅ α
()
Oznaczając sumę kątów zwrotu wszystkich łuków poziomych położonych na pochyle-
niach nieszkodliwych przez α
, a na pochyleniach szkodliwych — przez α
, otrzymamy:
,
⋅ α
dodatkową jednostkową pracę siły pociągowej na łukach położonych na
pochyleniach nieszkodliwych;
,
⋅ α
dodatkową jednostkową pracę siły pociągowej na łukach położonych na
pochyleniach szkodliwych.
Łączna praca siły pociągowej na całym analizowanym odcinku wynosi
(Z
+ Z
)
⋅ L = Q ⋅ (w
L
+ ,α
) +
P
[(w
+ i)L
+ ,α
]
=
= Q ⋅ (w
L
+ ,α
+
w
L
+
i L
+
,α
) =
= Q ⋅ [w
L
+
w
L
+
h
+ , (α
+
α
)]

Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
Należy ją porównać z pracą siły pociągowej na umownym pochyleniu zastępczym i
z
o wartości
(Z
+ Z
)
⋅ L = Q ⋅
(w
+ i
z
)
⋅ L
Mamy zatem:
Q
⋅
(w
+ i
z
)
⋅ L = Q [w
L
+
w
L
+
h
+ , (α
+
α
)]
w
⋅ L + i
z
⋅ L = w
L
+ w
L
+ h
+ ,(α
+ α
)
w
⋅ L + i
z
⋅ L = w
L
+ w
L
+ w
L
+ h
+ ,(α
+ α
)
i
z
=
L
[w
L
+ h
+ ,(α
+ α
)]
()
Ponieważ we wzorze (
) następuje powiązanie oporów z pochyleniami, należy opory
ruchu podawać w wartościach bezwzględnych. Oznacza to, że:
o
ponieważ jednostką w
jest [N/kN], we wzorze wartość tę należy przemnożyć przez
,;
o
ponieważ wartość , także ma miano [N/kN], należy ją podać jako ,.
Ostatecznie wzór na pochylenie zastępcze będzie miał zatem postać:
i
z
=
L
[, ⋅ w
⋅ L
+ h
+ ,( ⋅ α
+ α
)] ⋅ [h].
()
We wzorze tym wartości L, L
i h
są wyrażone w [m], a kąty α
i α
— w stopniach.
.. Przykład obliczeń
Dane
o
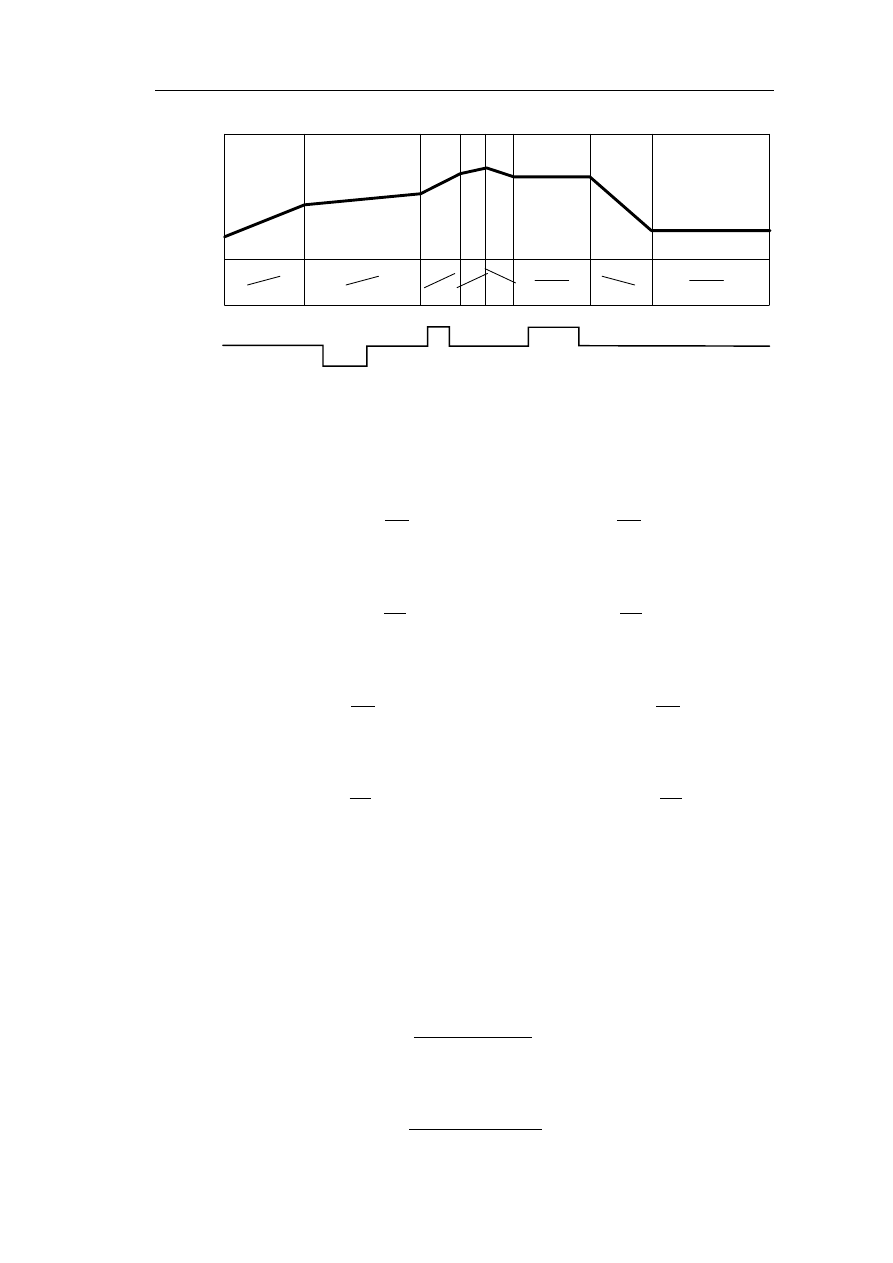
profil podłużny linii kolejowej wg rys.
o
masa wagonów składu osobowego t;
o
liczba wagonów składu osobowego ;
o
liczba osi wszystkich wagonów w składzie osobowym ;
o
konstrukcja łożysk w wagonach składu osobowego — łożyska toczne;
o
masa wagonów składu towarowego t;
o
liczba wagonów składu towarowego ;
o
liczba osi w składzie towarowym ;
o
konstrukcja łożysk w wagonach składu towarowego — łożyska toczne;
o
masa lokomotywy składu osobowego t;
o
liczba osi w lokomotywie składu osobowego ;
o
masa lokomotywy składu towarowego t;
o
liczba osi w lokomotywie składu osobowego ;
o
prędkość pociągów osobowych km/h;
o
prędkość pociągów towarowych km/h;
o
udział w ruchu pociągów osobowych/towarowych % : %.
Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
Numer
odcinka
Pochylenie
i długość
Proste
i łuki
1
2
3
4 5
6
7
8
8
1000
3
1500
10
500
3
300
0
1000
10
800
0
1500
3
300
1 = 15º30'
β
2 = 20º00'
β
3 = 10º10'
β
Rys. . Dany profil fragmentu linii kolejowej
Rozwiązanie
o
Opór zasadniczy lokomotywy pociągu osobowego:
W
z l o
= (, + , ⋅
,
) ⋅ , ⋅ + ⋅ + , ⋅ (
,
)
= N
o
Opór zasadniczy lokomotywy pociągu towarowego:
W
z l t
= (, + , ⋅
,
) ⋅ , ⋅ + ⋅ + , ⋅ (
,
)
= N
o
Opór zasadniczy wagonów pociągu osobowego (-osiowych o łożyskach tocznych):
W
z w o
= (, + , ⋅
,
)⋅,⋅+⋅+,⋅(,+)⋅(
,
)
= N
o
Opór zasadniczy wagonów pociągu towarowego (o łożyskach tocznych):
W
z w t
= (, + , ⋅
,
)⋅,⋅+⋅+,⋅(,+)⋅(
,
)
= N
o
Opór zasadniczy pociągu osobowego:
W
z o
= + = N
o
Opór zasadniczy pociągu towarowego:
W
z t
= + = N
o
Opór jednostkowy pociągu osobowego:
w
os
=
,
⋅ ( + )
= , h
o
Opór jednostkowy pociągu towarowego:
w
tow
=
,
⋅ ( + )
= , h

Po
mo
ce
dy
da
kt
yczne
Katedra Transportu Szynowego, Politechnika Gdaska
o
Opór jednostkowy przy danej strukturze ruchu:
w
= , ⋅ , + , ⋅ , = , h
o
Całkowita długość odcinka:
L
= + + + + + + + = m
o
Długość pochyleń nieszkodliwych (tzn. na odcinkach , , , i ):
L
= + + + + = m
o
Różnica wysokości pokonywana na pochyleniach szkodliwych:
h
= ⋅ , + ⋅ , + ⋅ , = + + = , m
o
Obliczenie kątów na pochyleniach nieszkodliwych (tzn. łuków β
i β
):
α
= ,
○
+ ,
○
= ,
○
o
Obliczenie kątów na pochyleniach szkodliwych (tzn. łuku β
)
α
=
○
o
Obliczenie pochylenia zastępczego:
i
z
=
⋅ [, ⋅ + + , ⋅ ( ⋅ , + )] ⋅ =
= , ⋅ = , h
Document Outline
Wyszukiwarka
Podobne podstrony:
BSP018 pochylenie zastepcze profil
BSP018 pochylenie zastepcze profil
prezentacja slajdy trening zastepowania agresji(1)
Integrowanie wsparcia społecznego dziecka i rodziny zastępczej wyzwaniem
6 ZBIOREK ZASTEPU id 43998 Nieznany (2)
DOM DZIECKA JAKO ŚRODOWISKO WYCHOWAWCZE, PSYCHOLOGIA, adopcja, dom dziecka, rodzina zastępcza, opiek
PRIDE-III (1), Studia, Rodzicielstwo zastępcze i system wsparcia rodziny
Zajęcia kursu kasa (finanse zastępu), Kurs zastępowych
schody i pochylnie, Analiza i ocena zagrożeń
Ustawa o wspieraniu rodziny i systemie pieczy zastepczej
WALCOWE KOŁA ZASTĘPCZE
DOKUMENTACJA W ZASTĘPIE
BSP018 rysunki landscape
System zastępowy, HARCERZE
więcej podobnych podstron