Podstawy Robotyki

Sprawozdanie

Kinematyka odwrotna

Krzysztof Gruba

grupa 23

rok IID

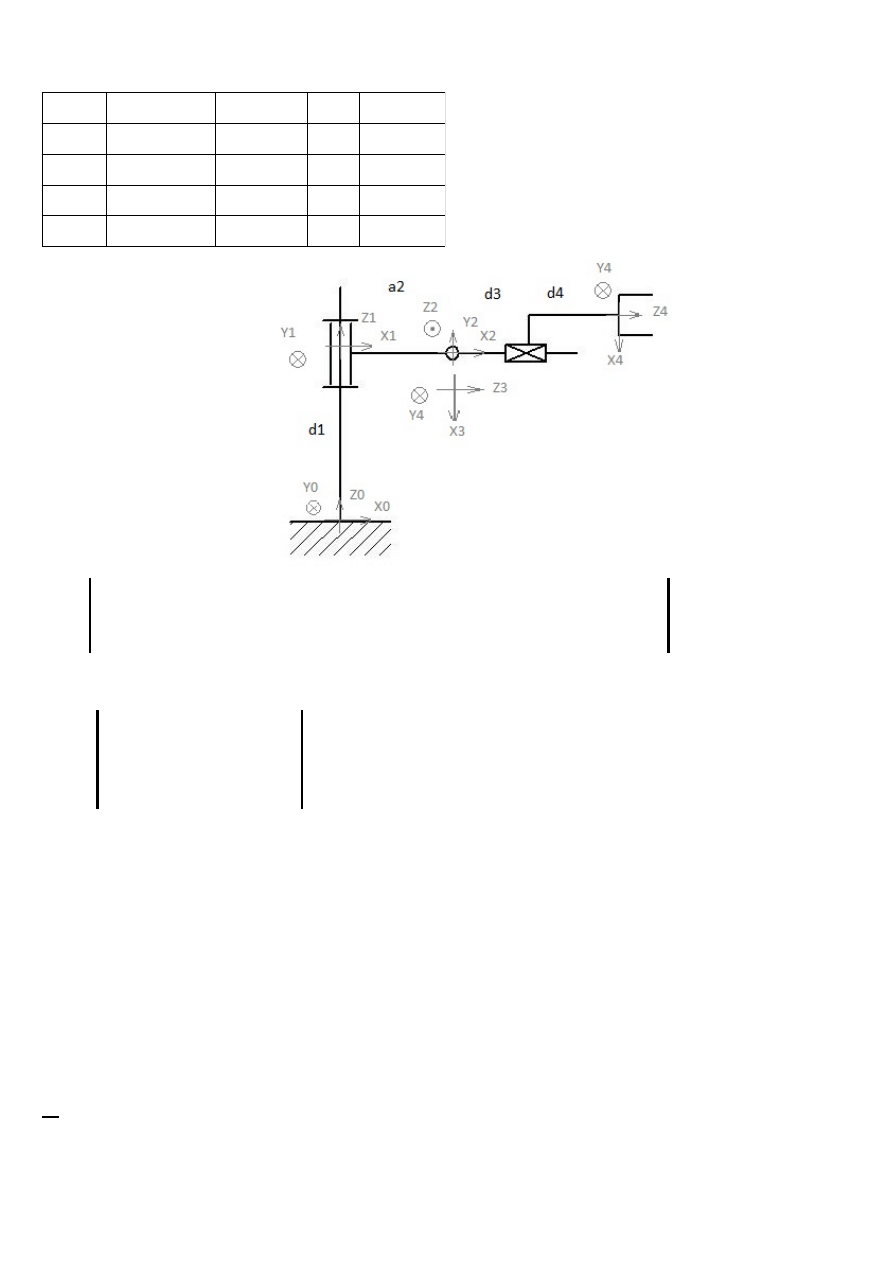
1)

układ

θ

i

d

i

a

i

α

i

1

0

d

1

0

0

2

Θ

2 VAR

0

a

2

90

o

3

Θ

3 VAR

-90

o

0

0

-90

o

4

0

d

3 VAR

+d

4

0

0

d

1

= 400

Θ

2

= 30

o

a

2

= 200

Θ

3

= 60

o

d

3

= 250

d

4

=150

T

7,0

=

Po podstawieniu danych:

T

7,0

=

Współrzędne wynoszą:
x = 346,4
y = 200
z = 746,4

Równania kinematyki odwrotnej mają postać:

-cos(θ

2

)sin(θ

3

-90

0

)(d

3

+150) + 200cos(θ

2

) = 356,4

-sin(θ

2

)sin(θ

3

-90

0

)(d

3

+150) + 200sin(θ

2

) = 200

400 + cos(θ

3

-90

0

)(d

3

+150) = 746,4

Rozwiązując układ równań za pomocą programu Maple otrzymuje się 4 rozwiązania:

1)

d

3

= 249,99 mm

θ

2

= 29,8

0

θ

3

= -29,8

0

0,75 -0,5 0,43 346,4
0,43 0,866 0,25 200

-0,5

0

0,87 746,4

0

0

0

1

cosθ2cos(θ3-90)

-sinθ2

sinθ2cos(θ3-90)

cosθ2

sin(θ3-90)

0

0

0

0

1

-cosθ2sin(θ3-90) -cosθ2sin(θ3-90)(d3+d4) + a2cosθ2

-sinθ2sin(θ3-90)

-sinθ2sin(θ3-90)(d3+d4) + a2sinθ2

cos(θ3-90)

cos(θ3-90)(d3+d4) + d1

2)

d

3

= -549,99 mm

θ

2

= 29,8

0

θ

3

= 240,1

0

3)

d

3

= 542,8 mm

θ

2

= -150,1

0

θ

3

= 147,3

0

4)

d

3

= -842,8 mm

θ

2

= -150,1

0

θ

3

= 210,3

0

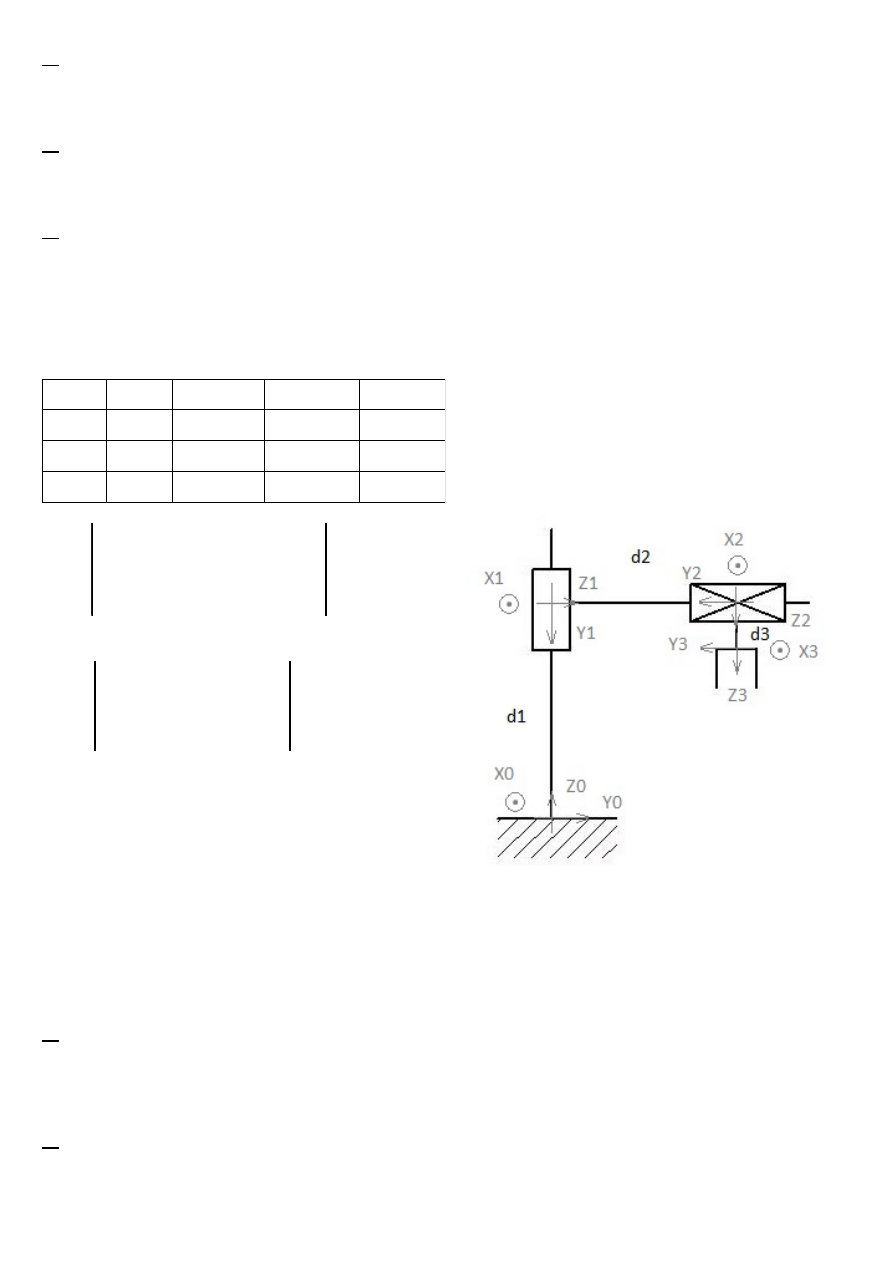
2)

układ

θ

i

d

i

a

i

α

i

1

Θ

1 VAR

d

1 VAR

0

-90

o

2

0

d

2 VAR

0

-90

o

3

0

d

3

0

0

Θ

1

= 30

o

d

1

= 150

d

2

= 200

d

3

= 50

T

6,0

=

Po podstawieniu danych:

T

6,0

=

Współrzędne wynoszą:
x = -100
y = 173,2
z = 100

Równania kinematyki odwrotnej mają postać:

-sin(θ

1

)d

2

= -100

cos(θ

1

)d

2

= 173,2

-50 + d

1

= 100

Rozwiązując układ równań za pomocą programu Maple otrzymuje się 2 rozwiązania:

1)

d

1

= 150 mm

d

2

= 199,99 mm

θ

1

= 29,8

0

2)

d

1

= 150 mm

d

2

= -199,99

θ

1

= -150,1

0

0,87

0,5

0

-100

0,5

-0,87 0 173,2

0

0

-1

100

0

0

0

1

cosθ1

sinθ1

0 -d2sinθ1

sinθ1 -cosθ1 0 d2cosθ1

0

0

-1 -d3+d1

0

0

0

1