kurs: Inżynieria chemiczna (ćwiczenia)
kierunek: Biotechnologia II rok
prowadzący: dr inż. Wojciech Budzianowski
Lista zadań A
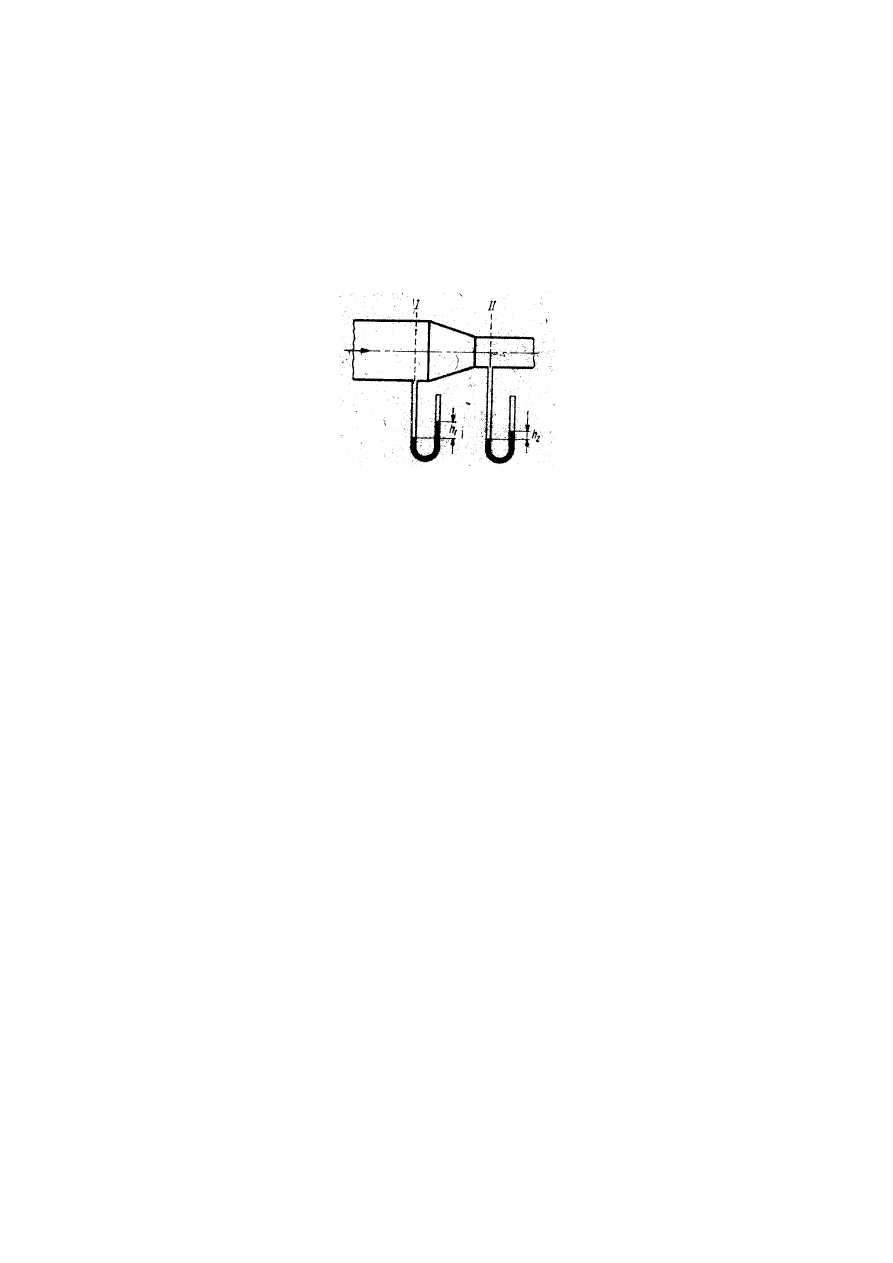
1. Rurociąg o średnicy wewnętrznej 200 mm zwęża się łagodnie do średnicy 100 mm. Przez
rurociąg przepływa 1700 m
3
/h metanu o temperaturze 30 °C. Otwarty do atmosfery manometr
wodny w kształcie litery U na szerszej części rurociągu wskazuje nadciśnienie 40 mm H
2
O. Jakie
będzie wskazanie manometru zainstalowanego na wąskiej części rurociągu?
Rys. Schemat układu pomiarowego
Dane:
V = 1700 m
3
/h, T = 30 °C, d
1
= 200 mm, d
2
= 100 mm, Δh
1
= p
1
-p
atm
= 40 mm H
2
O
w – prędkość przepływu m/s
A – pole przekroju rurociągu, m
2
Rozwiązanie:
Wyznaczamy pola przekroju rurociągu:
A=Pi d
2
/4
A
1
= 3.14*(0.2*0.2)/4 = 0.0314 m
2
A
2
= 3.14*(0.1*0.1)/4 = 0.00785 m
2
Wyznaczamy prędkości średnie w rurociągu:
w = V/A
w
1
= 1700/3600/0.0314 = 15.04 m/s
w
2
= 1700/3600/0.00785 = 60.16 m/s
Wyznaczamy gęstość metanu:
q = pM/RT = 1.013 10
5
* 16 10
-3
/ (8.314*303) = 643.39 g/m3 = 0.643 kg/m
3
Przeliczamy jednostki ciśnienia na jednostki SI:
Δp
1
=qgΔh
1
=1000*9.81*40*10
-3
= 392.4 Pa
Wyznaczamy ciśnienie statycznego absolutne w przekroju 1.
p
1
= p
atm
+ Δp
1
= 101300 + 392.4 = 101692.4 Pa
Wyznaczamy ciśnienie statyczne absolutne:
Mamy ten sam poziom geometryczny, wobec tego qgh jest stałe w obu przekrojach i można je
pominąć, a stąd prawo Bernoulliego upraszcza się do.
p+w
2
q/2=const
p
1
+w
1
2
q/2 = p
2
+w
2
2
q/2
p
2
= p
1
+(w
1
2
-w
2
2
)q/2 = 101692.4+(15.04
2
– 60.16
2
) * 0.64339 / 2 = 100 606 Pa
Wyznaczamy wskazanie manometru w przekroju 2:
Δp
2
= p
2
- p
atm
= 100606 - 101300 = -694 Pa
Δh
2
= Δp
2
/ qg = -694/1000/9.81 = -0.07074 m = -70.74 mm H
2
O
Odpowiedź:
Manometr zainstalowany na wąskiej części rurociągu (w przekroju 2) wskaże podciśnienie
statyczne 70.74 mm H
2
O.
2. Rurociągiem o średnicy d = 0.1m przepływa woda z natężeniem przepływu V = 5 m3/h. Obliczyć
spadek ciśnienia na odcinku rurociągu o długości L = 1 km. Przyjąć gęstość wody 1000 kg/m3,
lepkość wody = 0.8937 10
-3
Pa s.
3. Ze zbiornika znajdującego się w oczyszczalni ścieków spływa woda rurociągiem o średnicy d =
0.1m o długości L = 1 km. Poziom wody w zbiorniku jest stale utrzymywany na poziomie H
zb
=
10m. Z jakim objętościowym natężeniem przepływu popłynie woda w tym rurociągu? Dane: ρ
w
=
1000 kg/m3, η
w
= 0.8937 10
-3
Pa s.
4. Dzwon mokrego zbiornika gazowego do przechowywania azotu ma średnicę 6m i z
uzupełniającym obciążeniem waży 2900 kg (Rys). Pomijając straty ciężaru części dzwonu
zanurzonej w wodzie, proszę obliczyć nadciśnienie gazu w napełnionym zbiorniku.
6m
p
gazu
Rys. Dzwon mokrego zbiornika gazowego
5. Rurowy wymiennik ciepła posiada rurę zewnętrzną o średnicy wewnętrznej 80
∅ mm i 4 rury
wewnętrzne o średnicach wewnętrznych
∅20 mm, w których płynie produkt spożywczy. Woda
jako nośnik ciepła przepływa w przestrzeni międzyrurowej z wydajnością 10 m3/h. Jaki jest
charakter przepływu wody w przestrzeni międzyrurowej aparatu, którego przekrój poprzeczny
przedstawia poniższy szkic? Wyznacz spadek ciśnienia w aparacie o długości 1m. Dane: ρ
w
= 1000
kg/m3, η
w
= 0.8937 10
-3
Pa s.
Rys. Przekrój poprzeczny wymiennika ciepła.
6. Jakie ciśnienie musi wytworzyć pompa pracująca w układzie, jak na poniższym rysunku? Średnia
prędkość czynnika w przewodzie wynosi 1 m/s, średnica rury 40 mm, całkowita długość odcinków
prostych L= 60 m, ζ
1
= ζ
4
= 0.5, ζ
2
= 0.2, ζ
3
= 1.5, L
e
= 13 m, H = 3.3 m. Dane: ρ
w
= 1000 kg/m3, η
w
= 0.8937 10
-3
Pa s.
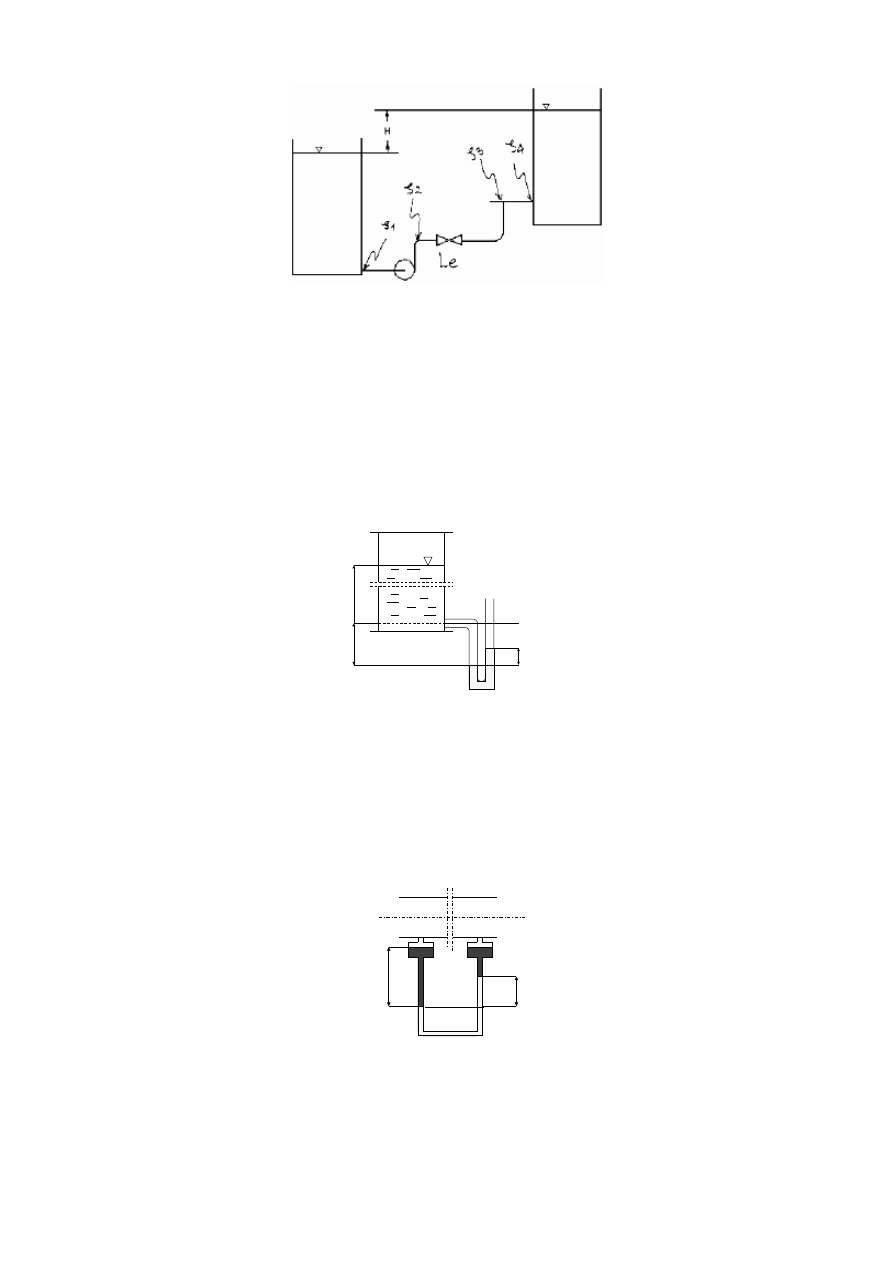
Rys. Układ pracy pompy.
7. Rurociągiem o średnicy Ø 72x3 mm płynie woda. Średnia prędkość przepływu wynosi 1.5 m/s.
Obliczyć masowe natężenie przepływu strumienia cieczy. Czy w podanych warunkach można
zrealizować proces mycia instalacji jeżeli wymagany jest burzliwy charakter przepływu cieczy
myjącej. Dane: ρ
w
= 1000 kg/m3, η
w
= 0.8937 10
-3
Pa s.
8. Wyznaczyć ciśnienie absolutne na poziomie A-A aparatu, gdzie umieszczony jest rtęciowy
manometr (Rys.). Wysokość słupa rtęci wynosi 180 mm Hg. Wysokość warstwy cieczy o gęstości
870 kg/m
3
wynosi h
1
= 2.0 m, a wysokość cieczy w lewym ramieniu manometru od poziomu rtęci
do poziomu A-A wynosi h
2
= 0.4 m. Jakie jest ciśnienie absolutne nad powierzchnią cieczy, jeśli
ciśnienie atmosferyczne wynosi 746 mm Hg?
A
A
h1
h2
h3
p
p0
Rys. Schemat zbiornika z manometrem rtęciowym.
9. Manometr dwucieczowy, w którym zastosowano jako ciecz cięższą czterochlorek węgla (CCl
4
) o
gęstości 1596 kg/m
3
, a jako ciecz lżejszą - wodę o gęstości 998 kg/m
3
, podłączono do dwóch
punktów przewodu o średnicy wewnętrznej 35 mm (rys.3), odległych o 3 metry. Przewodem tym
płynie powietrze o temperaturze 20
o
C i pod ciśnieniem 160 kPa. Zanotowano różnicę poziomów
cieczy cięższej równą 45 mm. Obliczyć jaką różnicę ciśnień wyrażoną w Pa zmierzył manometr
cieczowy.
p1
p2
h1
45
Rys. Manometr dwucieczowy.
10. Obliczyć poziom oleju w zbiorniku (Rys.), jeśli manometr w kształcie litery „S” wskazuje
różnicę poziomów słupa rtęci h
m
= 250 mm Hg a wysokość h
1
= 0.2 m. Gęstość oleju wynosi 860
kg m
-3
.
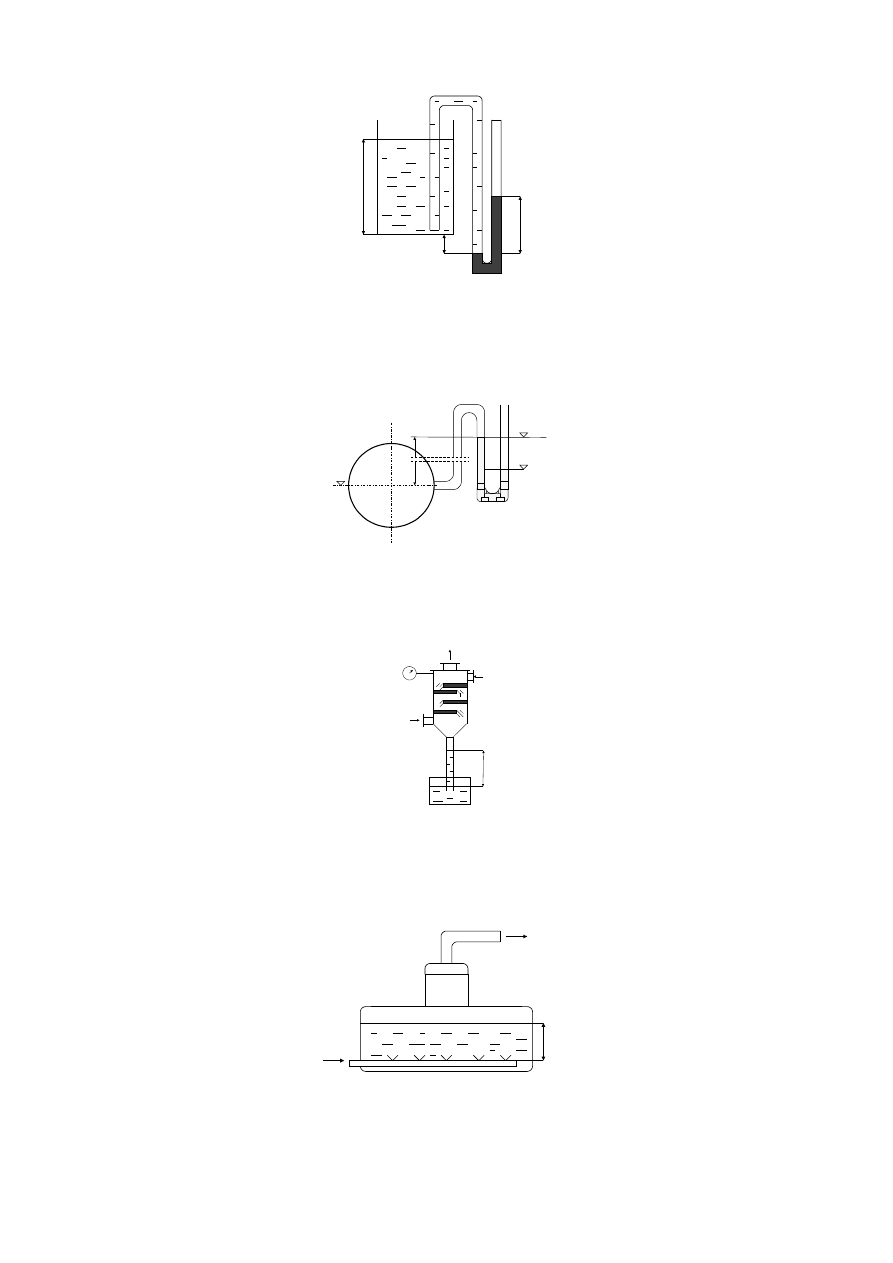
hm
h1
H
po
Rys. Zbiornik oleju z manometrem.
11. Obliczyć ciśnienie absolutne wody w rurociągu, jeśli U-rurkowy manometr rtęciowy
przyłączony do rurociągu (Rys.) pokazuje różnicę poziomów słupa rtęci
∆
h = 500 mm Hg.
Ciśnienie atmosferyczne wynosi p
atm
= 760 mm Hg.
0,0
1,36
0,86
pabs
patm
I
I
Rys. Schemat rurociągu z manometrem.
12. Próżniomierz umiejscowiony na skraplaczu barometrycznym (Rys.) wskazuje podciśnienie
równe 600 mm Hg. Ciśnienie atmosferyczne wynosi 748 mm Hg. Oblicz: a) ciśnienie absolutne w
skraplaczu, b) na jaką wysokość podniesie się woda w rurze barometrycznej.
P
gaz
ciecz
H
Rys. Próżniomierz umiejscowiony na skraplaczu barometrycznym.
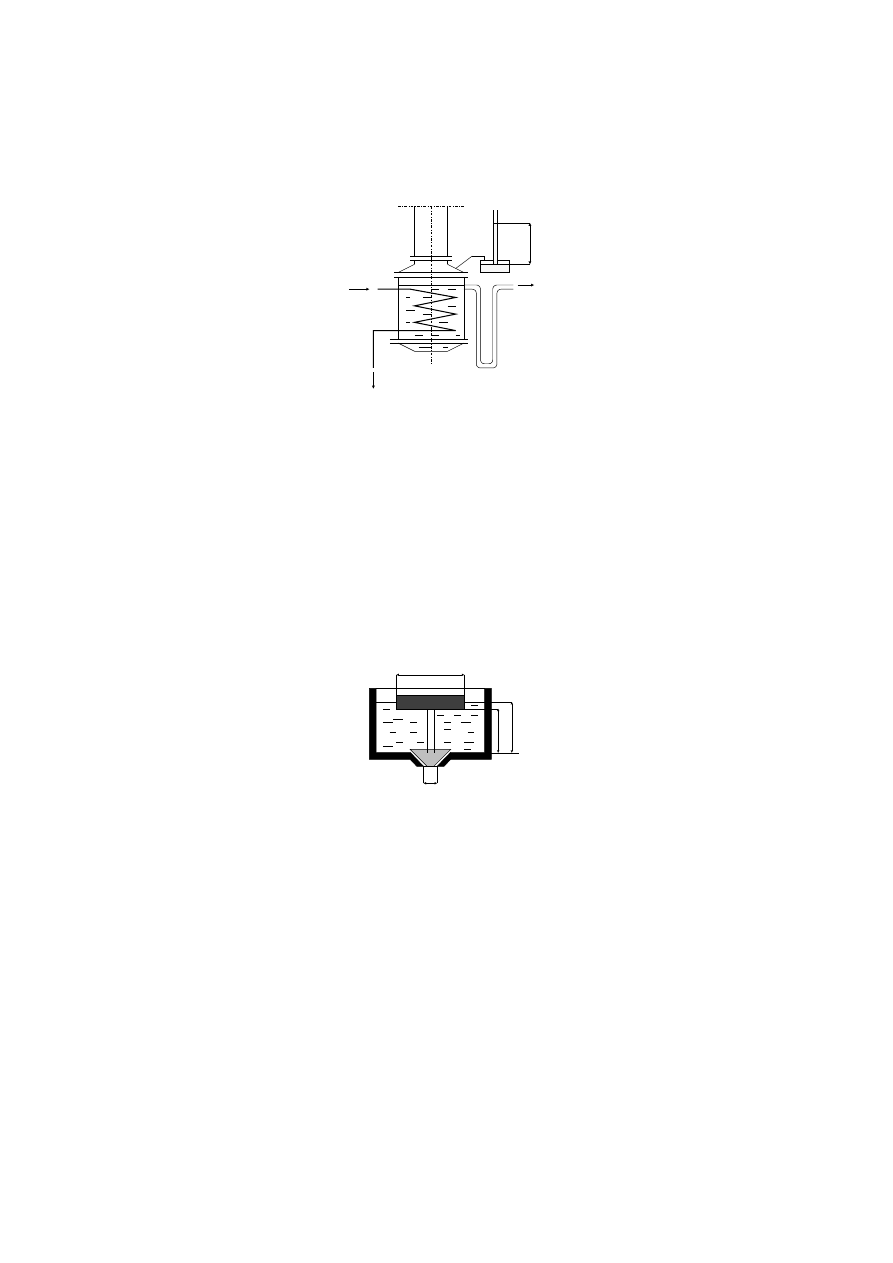
13. Gorącą parę wodną doprowadza się do akumulatora ciepła wypełnionego wodą (Rys.),
perforowaną rurą zanurzoną w wodzie na głębokość 1 metra. Proszę obliczyć minimalne ciśnienie
gorącej pary, jeśli ciśnienie pary wtórnej, opuszczającej zbiornik akumulatora ciepła wynosi 0.2
MPa.
h=1m
para grzejna
para
wtorna
Rys. Schemat wodnego akumulatora ciepła.
14. W kolumnie rektyfikacyjnej o działaniu ciągłym rektyfikuje się układ dwuskładnikowy: alkohol
etylowy-woda. Do kotła kolumny (Rys.) dołączony jest manometr, który wskazuje, że ciśnienie
wewnątrz kotła (p
1
) jest o 1,6 m słupa wody wyższe od ciśnienia atmosferycznego (p
0
= 752 mm
Hg). Przyjmując, że ciecz wyczerpaną w kotle stanowi czysta woda, wyznacz temperaturę wrzenia
tej wody w warunkach zadania. Dla porównania wyznacz temperaturę wrzenia wody pod
ciśnieniami 0.2 i 0.02 MPa.
p1
ciecz
wyczerpana
para
grzejna
kondensat
po
h
Rys. Schemat wyparki kolumny rektyfikacyjnej.
15. Oblicz „ciąg” w kominie (tzn. różnicę ciśnienia pomiędzy wnętrzem komina u jego podstawy i
atmosferą wokół komina u jego podstawy) o wysokości 50 metrów, jeśli średnia temperatura gazów
w kominie wynosi 227
o
C a temperatura otoczenia 27
o
C. Gęstości gazu i powietrza w temperaturze
0
o
C i przy ciśnieniu 760 mm Hg wynoszą odpowiednio:
ρ
g
=1.27 kg/m
3
,
ρ
pow.
=1.29 kg/m
3
.
16. Zbiornik napełniony wodą ma w płaskim poziomym dnie okrągły otwór zamykany za pomocą
zaworu (grzybek o średnicy d). Zawór połączony jest poprzez pręt (Rys.) z pływakiem o średnicy
D. Podniesienie zaworu następuje w momencie, gdy poziom cieczy w zbiorniku osiągnie wysokość
„h”. Przyjmując masę pływaka, pręta i grzybka równą m i długość pręta równą l wyznacz zależność
h = f (m , l, d, D). Oblicz poziom cieczy dla następujących danych: m = 20 kg, D = 0.5 m (średnica
pływaka), d = 0.1 m (średnica grzybka) i l = 1 m.
d
D
l
h
Rys. Schemat zbiornika z otworem w dnie.
17. Pompa pobiera zimną wodę ze studni. Wydajność pompy wynosi V
= 180 m
3
/h. Średnica rury
ssawnej wynosi d
wlot
= 250 mm. Oblicz maksymalną wysokość na jakiej może być oś pompy,
powyżej poziomu wody w studni, jeśli dopuszczalne ciśnienie na wlocie do pompy wynosi p
wlot
=
0.03 MPa. Całkowite straty ciśnienia w rurociągu ssawnym
∆
p
strat
= 8 kPa. Gęstość wody 1000 kg/
m
3
.
kurs: Inżynieria chemiczna (ćwiczenia)
kierunek: Biotechnologia II rok
prowadzący: dr inż. Wojciech Budzianowski
Lista zadań B
1. Oblicz prędkość opadania w wodzie cząstki piasku kwarcowego o kształcie kulistym i średnicy
0.8 mm, jeśli gęstość piasku wynosi 2600 kg/m
3
, a lepkość wody 10
-3
Pa s.
2. Obliczyć średnicę największych kulistych cząstek kredy, które będą unoszone przez strumień
wody płynący do góry z prędkością 1 m/s. Rozważyć dwa przypadki a) temperatura wody wynosi 0
o
C (
η
w
= 1.9 10
-3
Pa s) i 50
o
C (
η
w
= 1.0 10
-3
Pa s). Gęstość kredy wynosi 2700 kg/m
3
.
3. Wyznaczyć prędkość opadania cząstek cementu o średnicy 1 mm w wodzie o temperaturze 20 °C
przyjmując kulisty kształt ziaren. Gęstość cementu ρ
c
= 2900 kg/m
3
. W obliczeniach wykorzystaj
liczbę Archimedesa.
4. Ziarno skrobi o gęstości 1500 kg/m
3
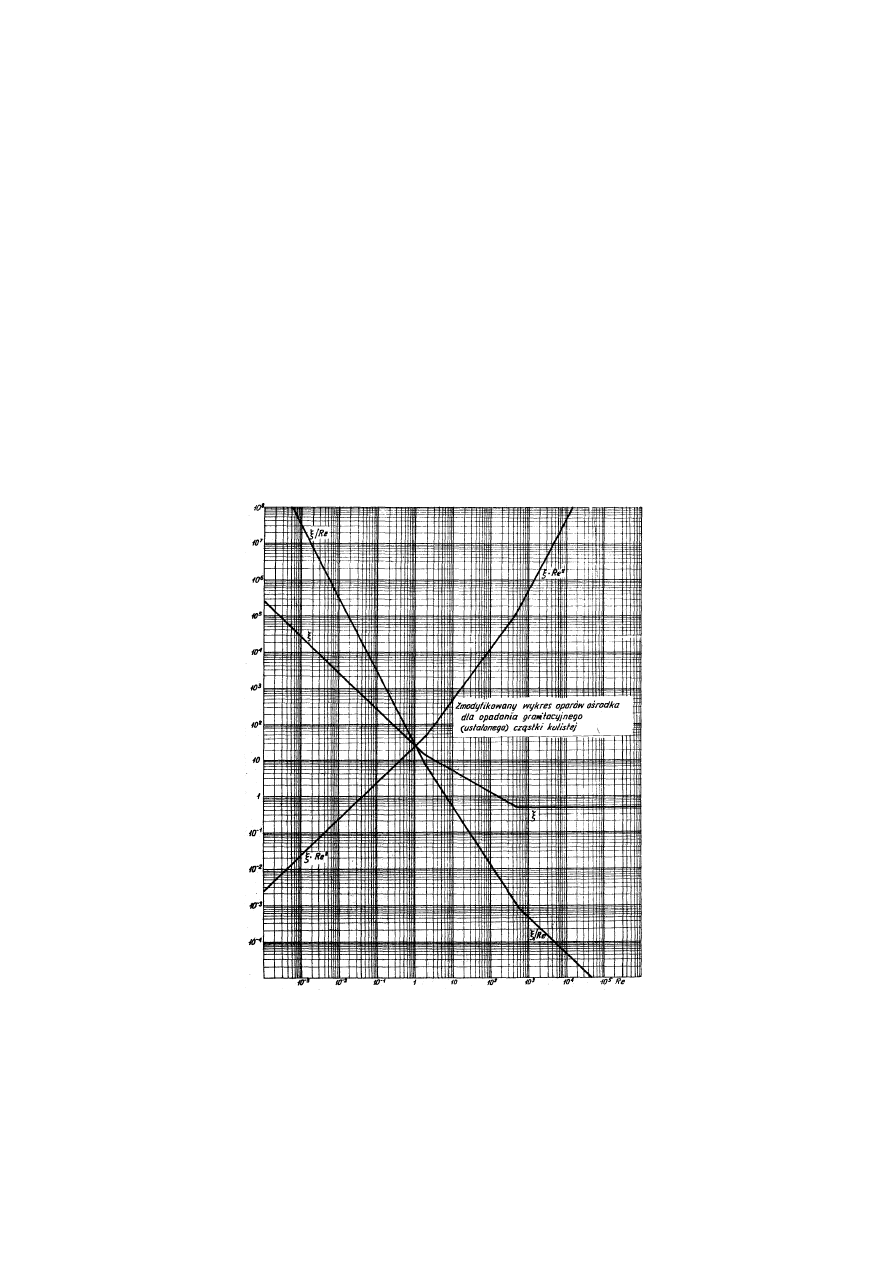
opada w powietrzu z prędkością 0.1 m/s. Jaka jest średnica
ziarna, jeżeli przyjąć kulisty kształt cząstek skrobi. Temperatura powietrza 20 °C, ciśnienie 1 at.
Wykorzystaj poniższy wykres (Rys).
Rys. Wykres oporów ośrodka dla opadania grawitacyjnego (ustalonego) cząstki kulistej.
5. 500 kg/h zapylonego gazu, o temperaturze 100
o
C, wpływa do cyklonu przewodem o średnicy
0.15 m (Rys.). Obliczyć najmniejszą średnicę cząstek usuwanych z powietrza w cyklonie o średnicy
0.5 m, długości l = 1 m i liczbie zwojów n = 1.5. Gęstość cząstek wynosi 1900 kg/m
3
, gęstość
powietrza w warunkach normalnych
ρ
pow
= 1.29 kg/m
3
, lepkość powietrza w 100
o
C
η
pow
= 2.22
⋅
10
-5
Pa
⋅
s.
R
wlot do
cyklonu
ro
Rys. Przekrój cyklonu.
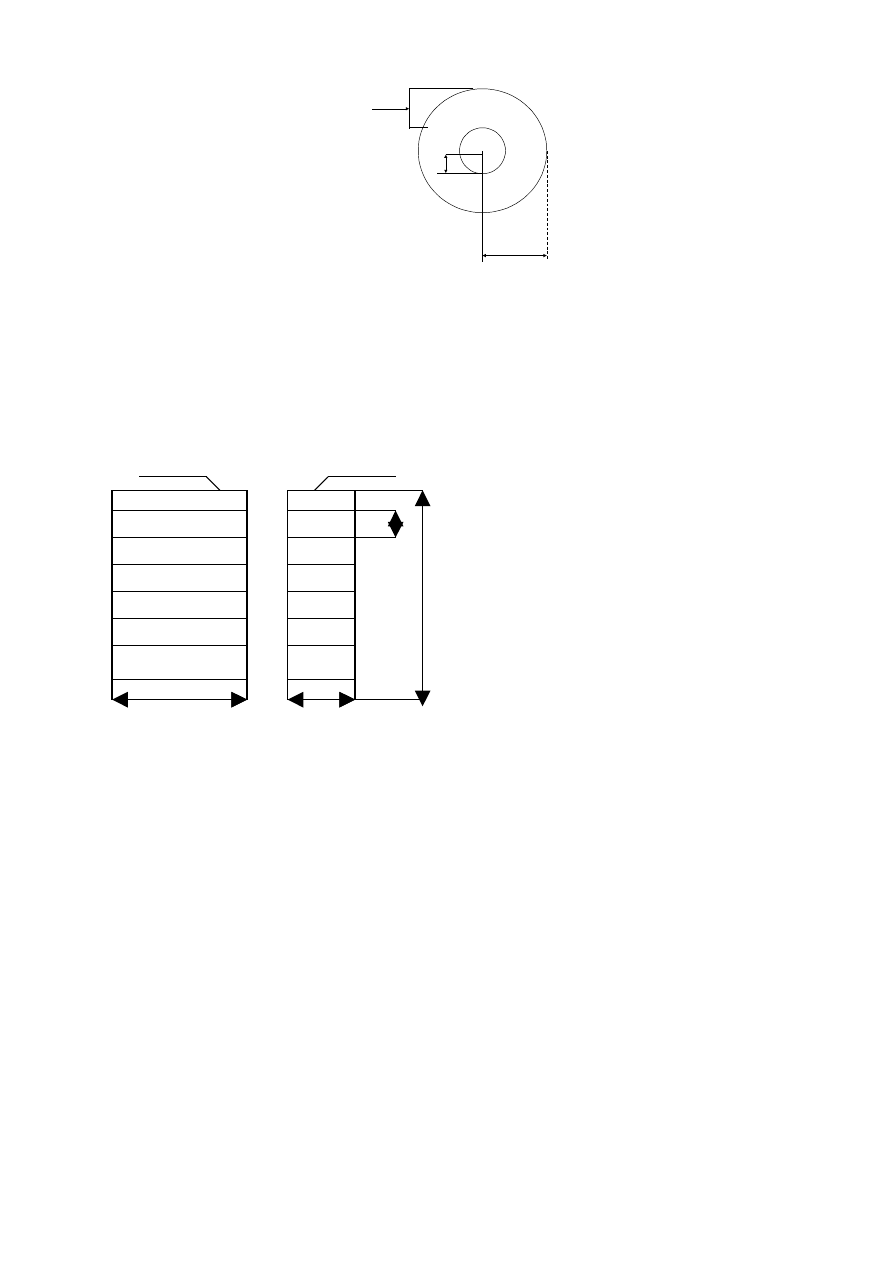
6. Jaką wysokość h powinny mieć półki komory pyłowej (Rys.), aby osiadały w niej cząstki pirytu
o średnicy d
p
= 8
µ
m przy natężeniu przepływu gazu piecowego V
0
= 0.6 m
3
/s ( w przeliczeniu na
warunki normalne)? Długość komory pyłowej wynosi L = 4.1 m. Średnia temperatura gazu w
komorze wynosi 427
o
C. Lepkość gazu w tej temperaturze
η
g
= 0.034
⋅
10
-3
Pa
⋅
s, gęstość pyłu
ρ
p
=
4000 kg/m
3
, gęstość gazu
ρ
g
= 0.5 kg/m
3
.
Przekrój komory z boku Przekrój komory z przodu
Rys. Półki komory pyłowej
7. Oblicz powierzchnię filtru, przy której uzyska się 2 m
3
przesączu w ciągu 30 min.podczas
filtracji pewnej zawiesiny. Filtrację prowadzi się przy różnicy ciśnień Δp = 150 kPa. Stałe filtracji
odniesione do 1 m
2
powierzchni filtracyjnej (F
0
) można wyrazić następującymi zależnościami:
K
0
= 1.5 10
-8
* Δp
0.65
C
0
= 0.13 * Δp
-0.35
8. Podczas wstępnych badań filtracji prowadzonej pod stałym ciśnieniem na filtrze o powierzchni 1
m
2
, uzyskano następujące dane doświadczalne: po czasie τ
1
= 3.2 min zebrano V
1
= 1.5 10
-3
m
3
przesączu, a po czasie τ
2
= 22 min zebrano V
2
= 4.3 10
-3
m
3
przesączu. Obliczyć, po upływie
jakiego czasu będzie można uzyskać 12 litrów filtratu?
L=4,1m m
H=4,2m
2,8
h