1

Transport ciepła i masy

©Ryszard A. Białecki

ustalone przewodzenie

ustalone przewodzenie

ciep

ciep

ł

ł

a, rozwi

a, rozwi

ą

ą

zania analityczne

zania analityczne

Transport ciepła i masy

©Ryszard A. Białecki

Redukcja wymiarowo

Redukcja wymiarowo

ś

ś

ci zagadnienia przewodzenia ciep

ci zagadnienia przewodzenia ciep

ł

ł

a

a

w wielu przypadkach przewodzenie w jednym kierunku dominuje

w wielu przypadkach przewodzenie w jednym kierunku dominuje

nad przep

nad przep

ł

ł

ywem energii w innych kierunkach. Pozwala to

ywem energii w innych kierunkach. Pozwala to

zredukowa

zredukowa

ć

ć

wymiar geometryczny zagadnienia, przez pomini

wymiar geometryczny zagadnienia, przez pomini

ę

ę

cie

cie

sk

sk

ł

ł

adnika strumienia ciep

adnika strumienia ciep

ł

ł

a w nieistotnych kierunkach.

a w nieistotnych kierunkach.

Najcz

Najcz

ęś

ęś

ciej uproszcze

ciej uproszcze

ń

ń

takich mo

takich mo

ż

ż

na dokona

na dokona

ć

ć

w obszarach o

w obszarach o

kszta

kszta

ł

ł

tach wyd

tach wyd

ł

ł

u

u

ż

ż

onych w jednym lub kierunkach. Zadanie

onych w jednym lub kierunkach. Zadanie

tr

tr

ó

ó

jwymiarowe sprowadza si

jwymiarowe sprowadza si

ę

ę

wtedy odpowiednio do dwu lub

wtedy odpowiednio do dwu lub

jednowymiarowego.

jednowymiarowego.

Aby zastosowa

Aby zastosowa

ć

ć

takie uproszczenie, warunki brzegowe wzd

takie uproszczenie, warunki brzegowe wzd

ł

ł

u

u

ż

ż

kierunk

kierunk

ó

ó

w wyd

w wyd

ł

ł

u

u

ż

ż

onych musz

onych musz

ą

ą

by

by

ć

ć

sta

sta

ł

ł

e. Zadania ch

e. Zadania ch

ę

ę

tnie

tnie

upraszcza si

upraszcza si

ę

ę

do 1D, bowiem dla takich przypadk

do 1D, bowiem dla takich przypadk

ó

ó

w znane s

w znane s

ą

ą

proste

proste

rozwi

rozwi

ą

ą

zania analityczne.

zania analityczne.

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

2

Transport ciepła i masy

©Ryszard A. Białecki

(

)

r

q

T

T

∞

= α

−

(

)

l

q

T

T

∞

= α

−

b

T

T

=

u

q

q

=

izolacja

0

q

=

izolacja

0

q

=

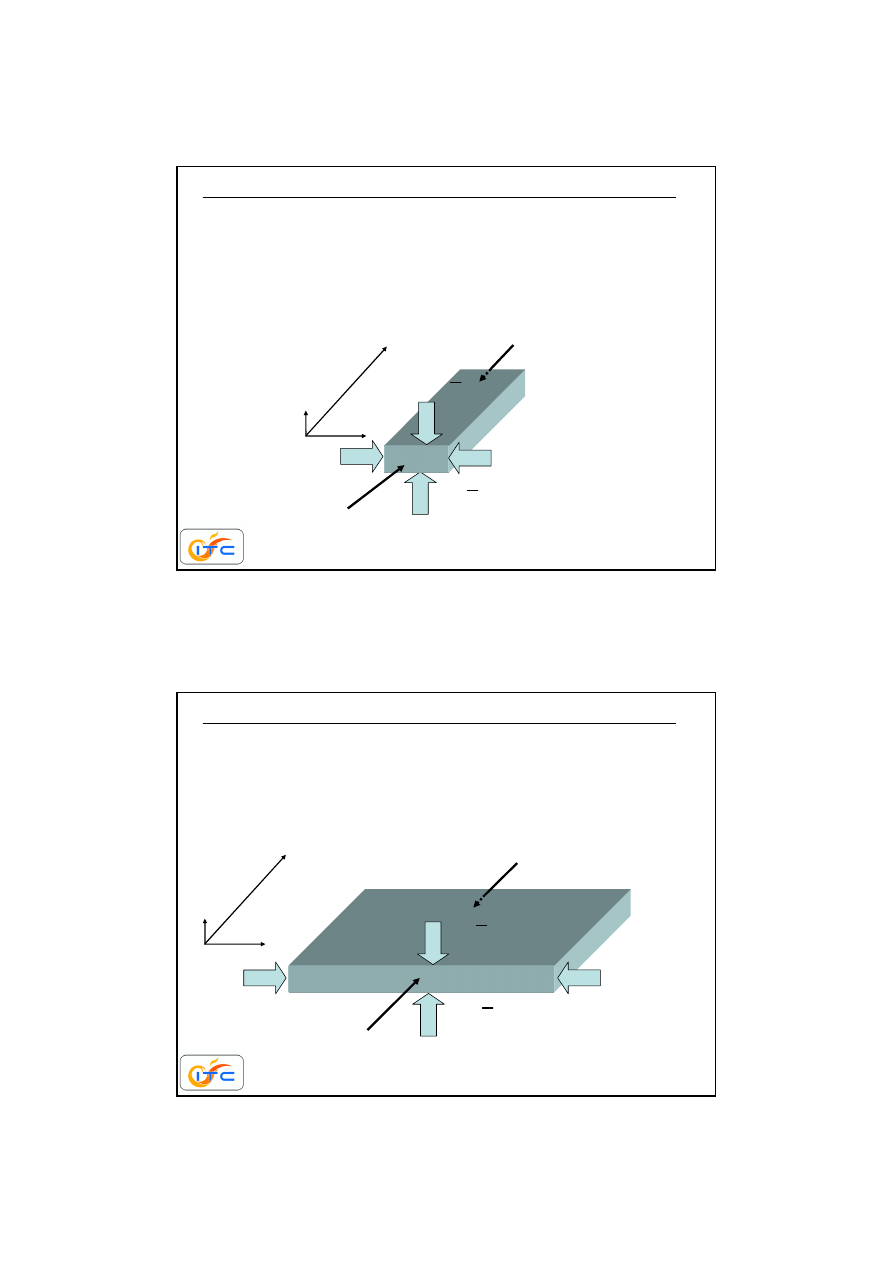
przykład zadania dwuwymiarowego

pole temperatury w ka

ż

dym przekroju

x y

jest

identyczne (nie zale

ż

y od

z

).

z

y

x

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

Transport ciepła i masy

©Ryszard A. Białecki

b

T

T

=

u

q

q

=

izolacja

0

q

=

izolacja

0

q

=

przykład zadania jednowymiarowego

pole temperatury wzdłu

ż

ka

ż

dej linii równoległej do osi

y

jest

identyczne (nie zale

ż

y ani od

z

ani od

x

).

z

y

izolacja

0

q

=

izolacja

0

q

=

x

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

3

Transport ciepła i masy

©Ryszard A. Białecki

(

)

e

e

q

T

T

∞

= α

−

(

)

i

i

q

T

T

∞

= α

−

izolacja

0

q

=

izolacja

z

r

φ

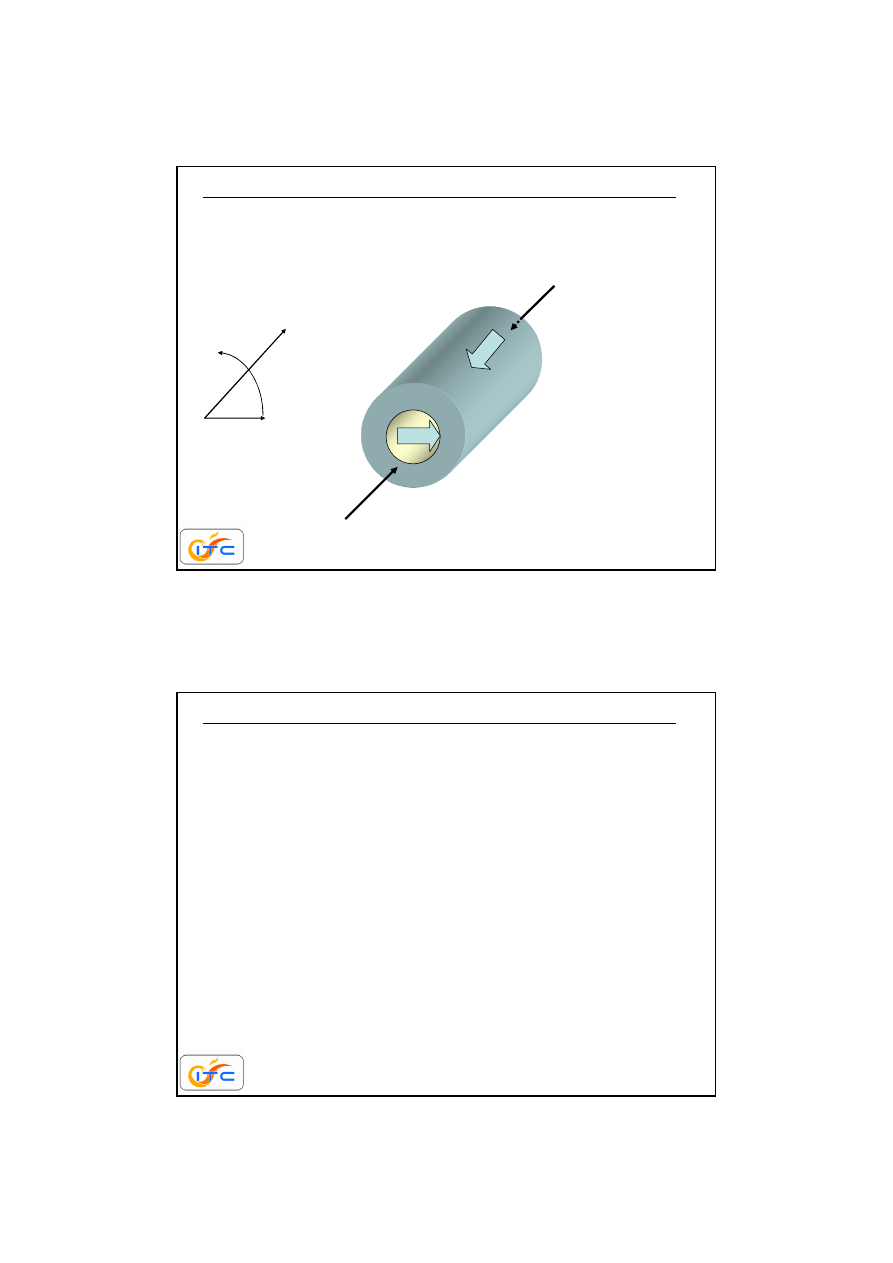
przykład zadania jednowymiarowego

pole temperatury wzdłu

ż

ka

ż

dego promienia

r

jest

identyczne (nie zale

ż

y ani od

z

ani od k

ą

ta

φ

).

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

Transport ciepła i masy

©Ryszard A. Białecki

ś

ci

ś

le rzecz bior

ą

c, redukcja zadania 3D do 2D

wymaga aby na powierzchniach prostopadłych do
wynikowego pola 2D, panowały warunki adiabatyczne.
W praktyce, je

ś

li warunki w tych przekrojach nie ró

ż

ni

ą

si

ę

znacznie, zadanie mo

ż

na i tak traktowa

ć

jak 2 wymiarowe,

bowiem zakłócenia pola 2D koncentruj

ą

si

ę

tylko w okolicach

tych powierzchni.

Podobnie rzecz si

ę

ma przy redukcji zada

ń

2D do 1D.

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

4

Transport ciepła i masy

©Ryszard A. Białecki

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

2

50(

300)

/

q

T

W m

=

−

2

1200 /

q

W m

=

400

T

K

=

2

50(

300)

/

q

T

W m

=

−

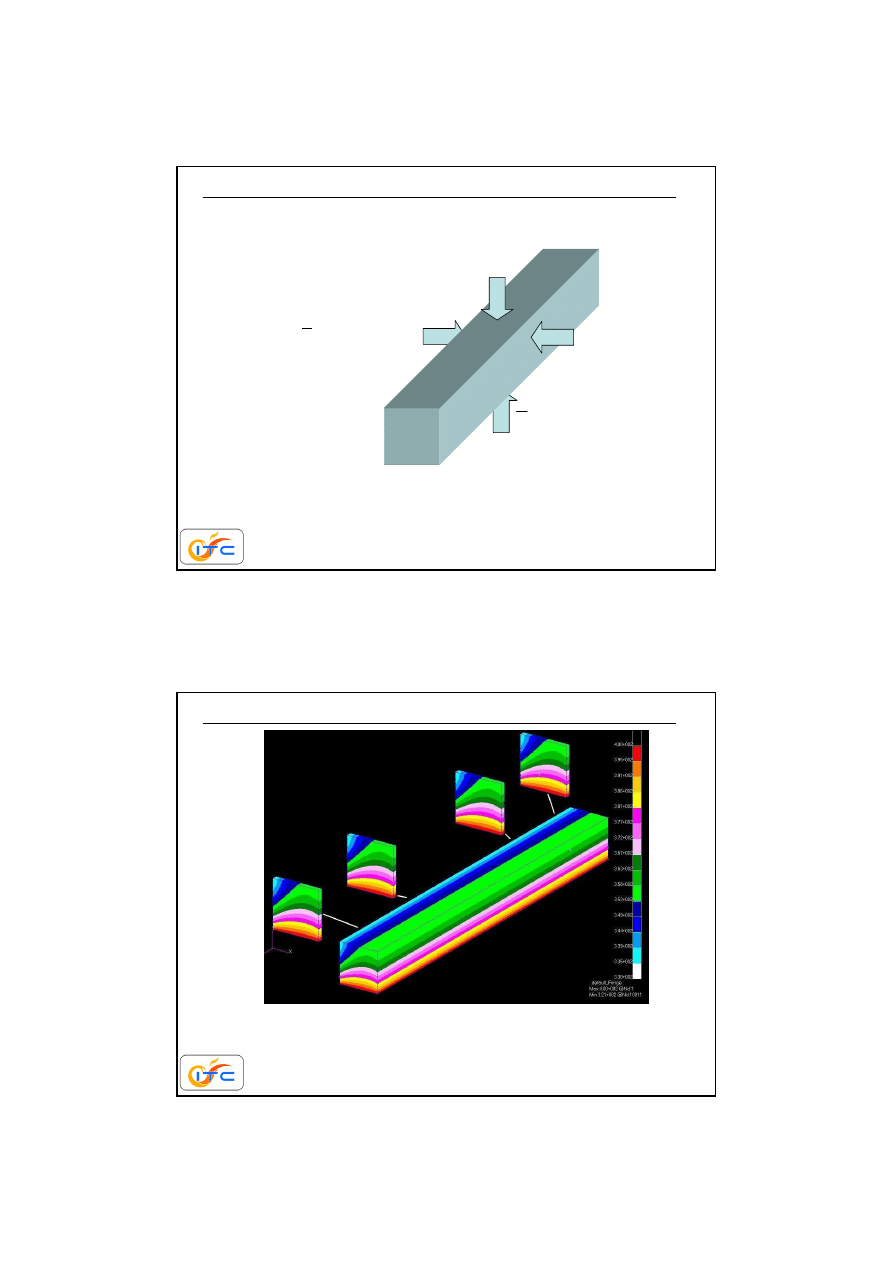
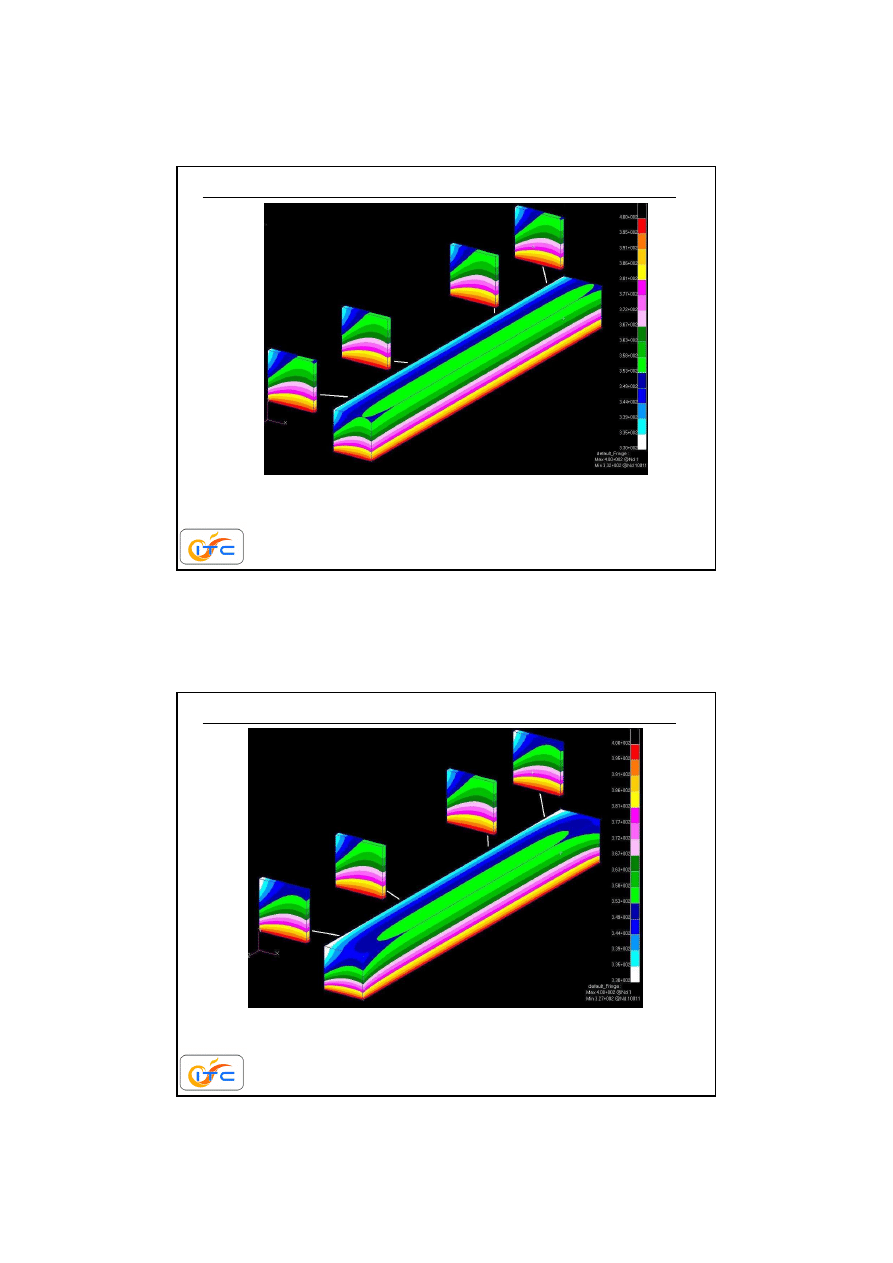
warunki brzegowe na czołowych (kwadratowych)
powierzchniach zmieniaj

ą

si

ę

od izolacji do

intensywnej wymiany konwekcyjnej

przykład redukcji wymiarowo

ś

ci zagadnienia

Transport ciepła i masy

©Ryszard A. Białecki

powierzchnie czołowe zaizolowane. Zadanie 2D

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

5

Transport ciepła i masy

©Ryszard A. Białecki

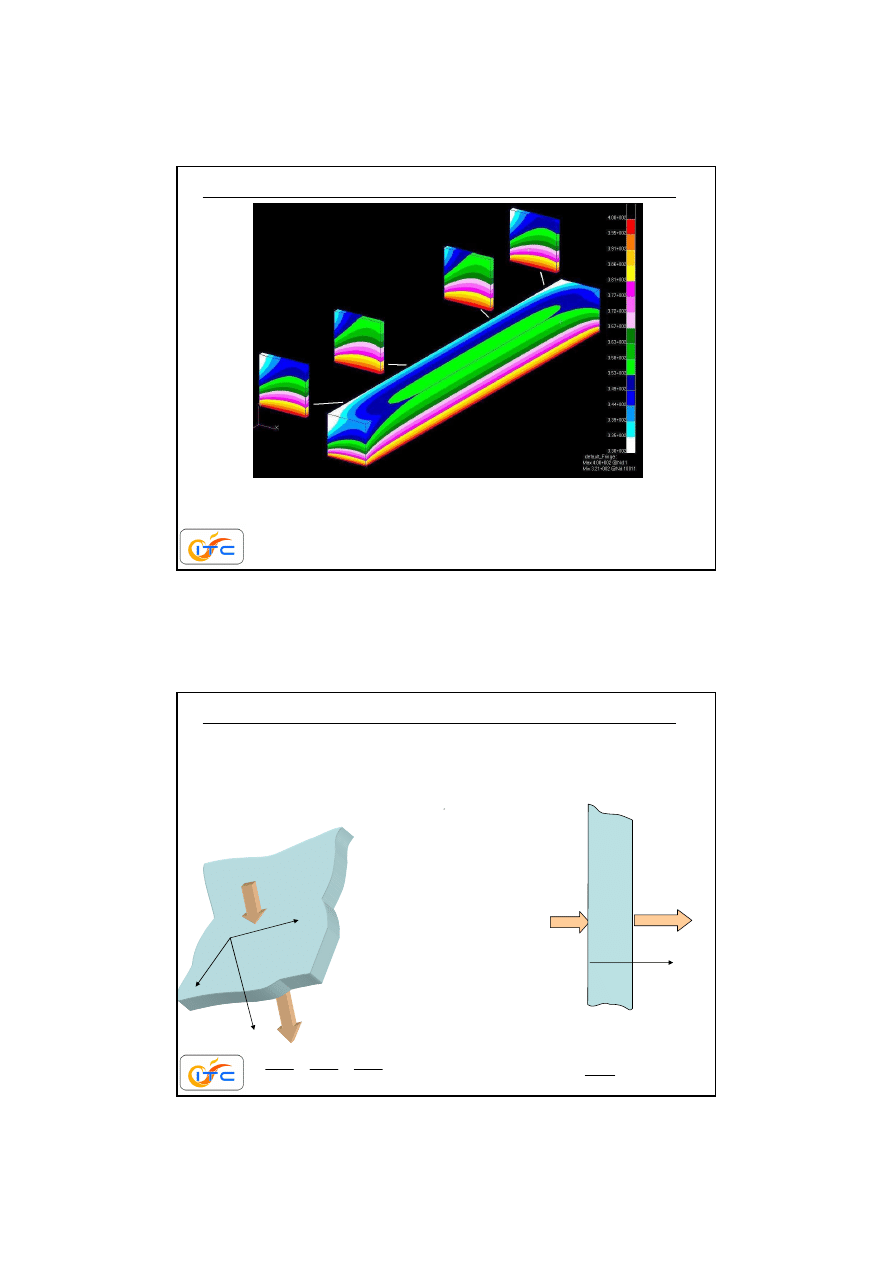
powierzchnie czołowe słabo wymieniaj

ą

ce ciepło przez

konwekcj

ę

αααα

=20 W/m

2

K temperatura płynu 300K.

Wpływ wnikania z tych powierzchni ogranicza si

ę

do

bardzo małego obszaru w ich s

ą

siedztwie

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

Transport ciepła i masy

©Ryszard A. Białecki

powierzchnie czołowe wymieniaj

ą

ce ciepło przez konwekcj

ę

ze

ś

redni

ą

intensywno

ś

ci

ą

αααα

=50 W/m

2

K temperatura płynu 300K.

Wpływ wnikania z tych powierzchni nadal w niewielkim obszarze
w s

ą

siedztwie powierzchni czołowych

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

6

Transport ciepła i masy

©Ryszard A. Białecki

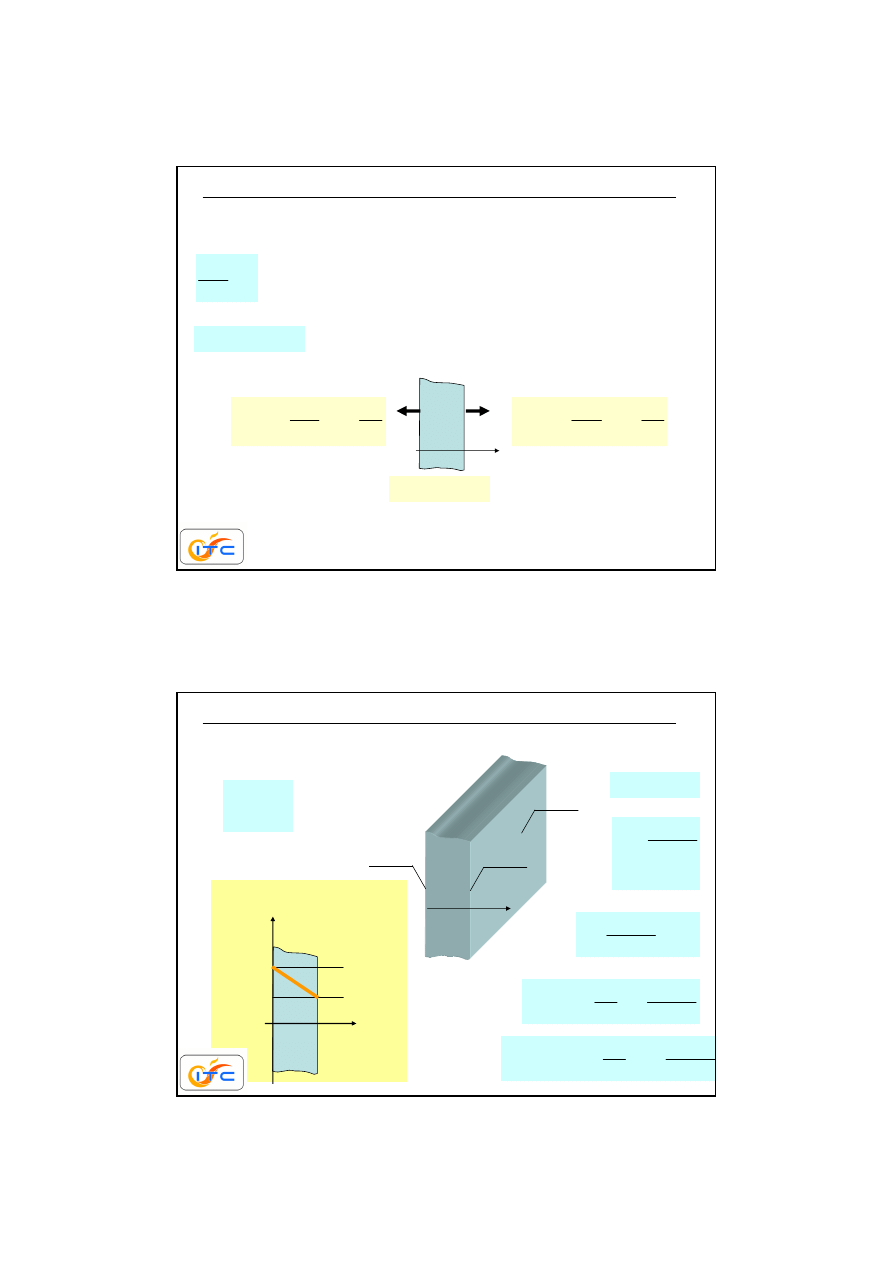
powierzchnie czołowe wymieniaj

ą

ce ciepło przez konwekcj

ę

z du

żą

intensywno

ś

ci

ą

αααα

=100 W/m

2

K,temperatura płynu 300K.

Wpływ wnikania z tych powierzchni jest jeszcze wi

ę

kszy ni

ż

poprzednio. W

ś

rodku obszaru pole jest nadal dwuwymiarowe

redukcja wymiarowo

redukcja wymiarowo

ś

ś

ci

ci

Transport ciepła i masy

©Ryszard A. Białecki

Ustalone zadania jednowymiarowe

Ustalone zadania jednowymiarowe

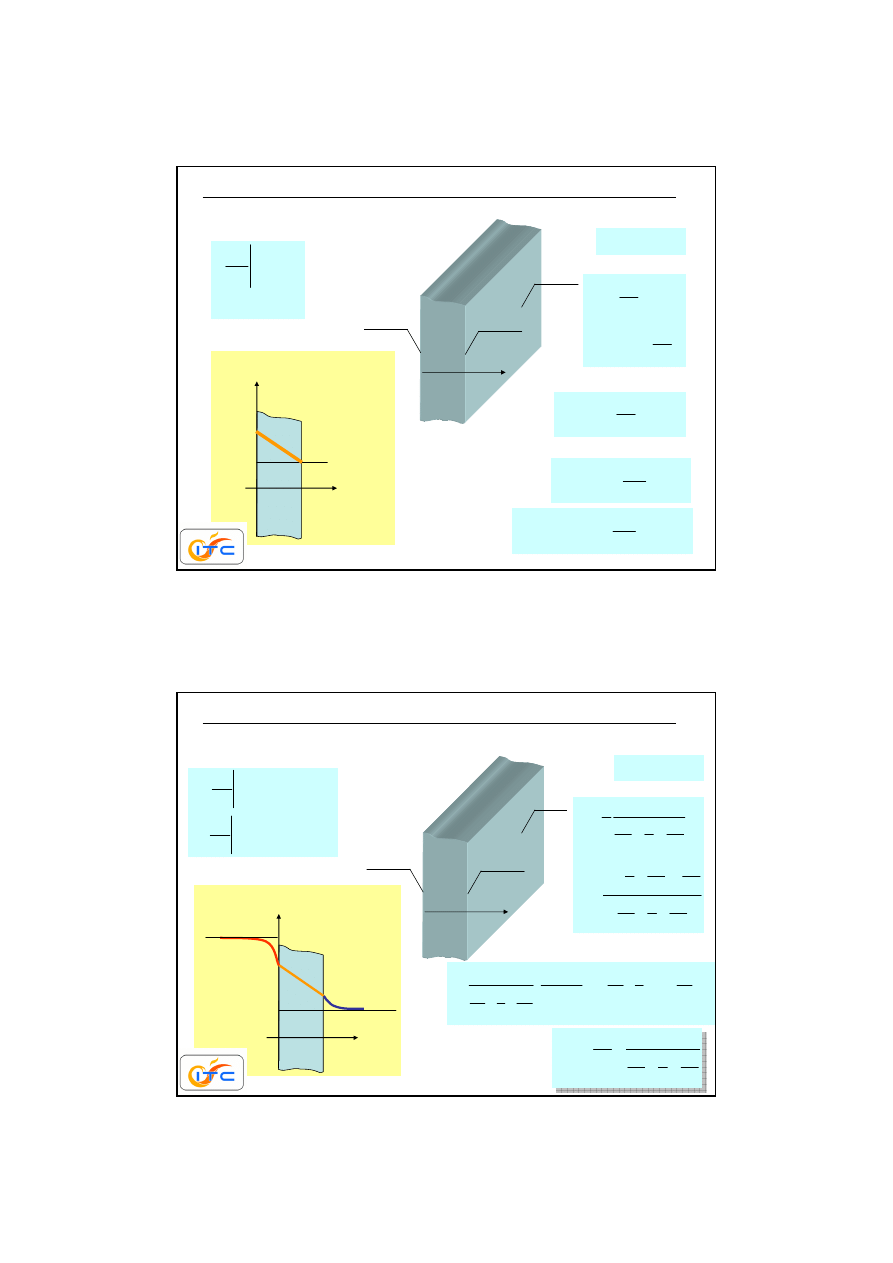
P

P

ł

ł

aska niesko

aska niesko

ń

ń

czona p

czona p

ł

ł

yta

yta

wektor strumienia ciepła
normalny do powierzchni

q=q

x

y

z

q

q

x

obiekt 3D

obiekt 3D

model 1D

model 1D

2

2

2

2

2

2

0

v

T

T

T

q

x

y

z





∂

∂

∂

λ

+

+

+ =





∂

∂

∂





2

2

0

v

d T

q

dx

λ

+ =

q=q

x=0

x=

δ

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

7

Transport ciepła i masy

©Ryszard A. Białecki

2

2

0

d T

dx

=

Sta

Sta

ł

ł

y wsp

y wsp

ó

ó

ł

ł

czynnik przewodzenia ciep

czynnik przewodzenia ciep

ł

ł

a.

a.

P

P

ł

ł

aska niesko

aska niesko

ń

ń

czona p

czona p

ł

ł

yta, pole bez

yta, pole bez

ź

ź

r

r

ó

ó

d

d

ł

ł

owe

owe

pole bez

ź

ródłowe

0

v

q

=

rozwi

ą

zanie (całka ogólna)

1

2

( )

T x

C x C

=

+

stałe

C

1

i

C

2

wyznacza si

ę

z warunków brzegowych

x

R

R

dT

dT

q

d

dx

= −λ

= −λ

n

R

n

L

n

L

L

dT

dT

q

d

dx

= −λ

= +λ

n

strumienie na skrajnych powierzchniach maja przeciwne znaki.
W praktyce u

ż

ywa si

ę

jednego ze strumieni (zwykle dodatniego)

0

0

x

x

q

q

=δ

=

+

=

notka o kierunku strumienia ciepła

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

Transport ciepła i masy

©Ryszard A. Białecki

(0)

( )

L

R

T

T

T

T

=

δ =

znane obie temperatury skrajne

R

L

L

T

T

T

x T

−

=

+

δ

( )

L

R

T

T

dT

q x

dx

−

= −λ

= λ

δ

x

0

δ

L

T

R

T

rozwi

ą

zanie

x

0

δ

T

R

T

L

T

1

2

R

L

L

T

T

C

C

T

−

=

δ

=

1

2

T

C x C

=

+

przebieg temperatury

λ

A

L

R

T

T

dT

Q

qA

A

A

dx

−

=

= − λ

= λ

δ

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

8

Transport ciepła i masy

©Ryszard A. Białecki

0

( )

L

x

R

dT

q

dx

T

T

=

λ

=

δ =

znana temperatura i strumie

ń

ciepła

(

)

L

R

q

T

T

x

=

−

δ −

λ

( )

L

dT

q x

q

dx

= −λ

= −

x

0

δ

L

q

R

T

x

0

δ

T

R

T

1

2

L

L

R

q

C

q

C

T

=

λ

=

−

δ

λ

1

2

T

C x C

=

+

rozwi

ą

zanie

λ

przebieg temperatury

A

L

dT

Q

qA

A

q A

dx

=

= −λ

= −

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

Transport ciepła i masy

©Ryszard A. Białecki

0

(

)

(

)

L

fL

x

R

fR

x

dT

T

T

dx

dT

T

T

dx

=

=δ

+ λ

= α

−

−λ

= α

−

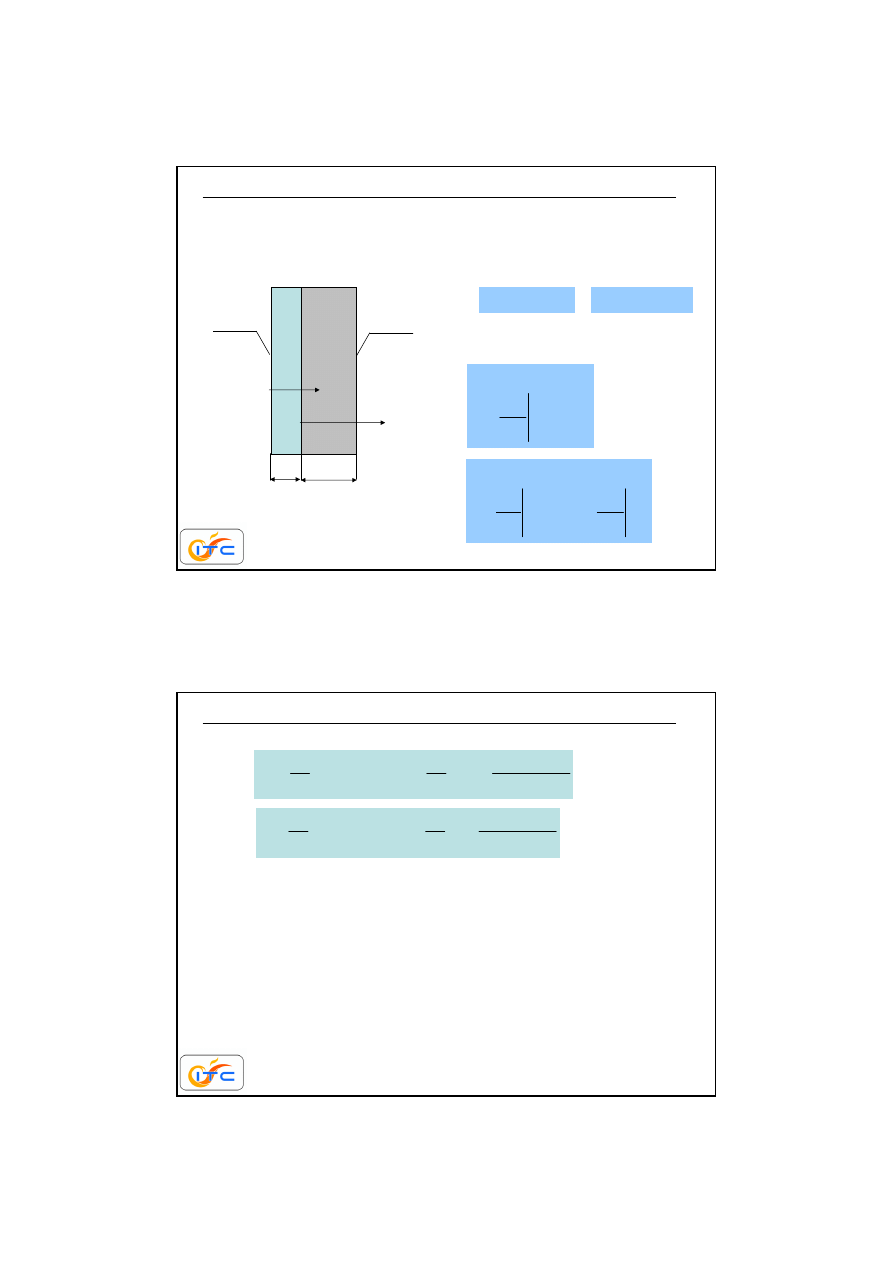
konwekcyjna wymiana ciepła na obu powierzchniach

x

0

δ

,

L

fL

T

α

x

0

δ

,

R

fR

T

α

1

2

1

1

1

1

(

)

1

1

fR

fL

L

R

fR

fL

R

L

L

R

T

T

C

T

T

C

−

=

δ

λ

+ +

α

λ α

δ +

+

λ α

α

=

δ

+ +

α

λ α

1

1

1

1

1

fR

fL

fL

fR

R

L

L

R

T

T

T

x

T

T





−





δ

=

+

+

+









δ

λ

α

λ

α









+ +

α λ α

1

1

fL

fR

L

R

T

T

dT

q

dx

−

= −λ

=

δ

+ +

α

λ α

λ

1

2

T

C x C

=

+

rozwi

ą

zanie

T

fL

T

fR

T

płyn
ciepły

płyn
chłodny

przebieg temperatury

A

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

9

Transport ciepła i masy

©Ryszard A. Białecki

płyta dwuwarstwowa 1

znany strumie

ń

ciepła i temperatura na brzegu. Idealny styk warstw

L

T

R

q

1

x

2

x

1

1 1

2

T

C x

C

=

+

2

3 2

4

T

C x

C

=

+

1

λ

2

λ

1

δ

2

δ

0

0

2

2

1

1

2

2

2

(

0)

L

R

x

T x

T

dT

q

dx

=δ

= =

−λ

=

1

1

2

1

1

1

2

2

1

2

1

2

1

2

0

(

)

(

0)

x

x

T x

T x

dT

dT

dx

dx

=δ

=

= δ =

=

−λ

= −λ

rozwi

ą

zanie w ka

ż

dej z warstw

nieznane stałe wyznacza si

ę

z warunków brzegowych

brzegi
zewn

ę

trzne

styk

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

Transport ciepła i masy

©Ryszard A. Białecki

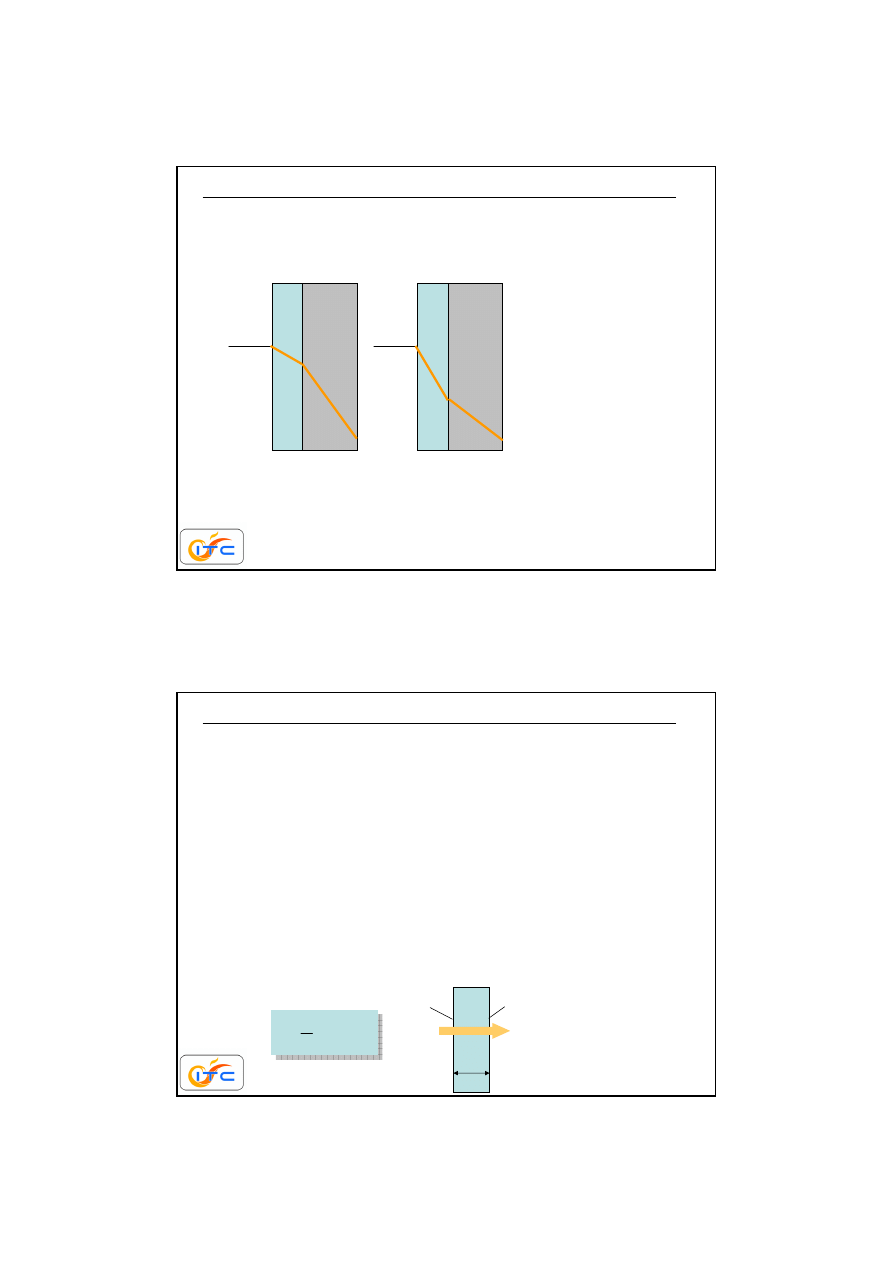
płyta dwuwarstwowa 2

podej

ś

cie uniwersalne, wymaga do

ść ż

mudnych rachunków

1

1

1

2

3

4

1

2

2

;

;

;

R

R

L

R

L

q

q

T

q

C

C

T C

C

λ

− δ

=

=

= −

=

λ

λ

λ

mo

ż

e by

ć

stosowane do zada

ń

o

• dowolnej liczbie warstw,
• dowolnych liniowych warunków brzegowych
• zale

ż

nych od współrz

ę

dnej

ź

ródeł ciepła

lub
•zale

ż

nych od temperatury współczynnikach przewodzenia ciepła

1

1

1

1

2

2

1

2

1

;

R

R

L

R

L

q

q

T

q

T

x

T

T

x

λ

− δ

=

+

= −

+

λ

λ

λ

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

10

Transport ciepła i masy

©Ryszard A. Białecki

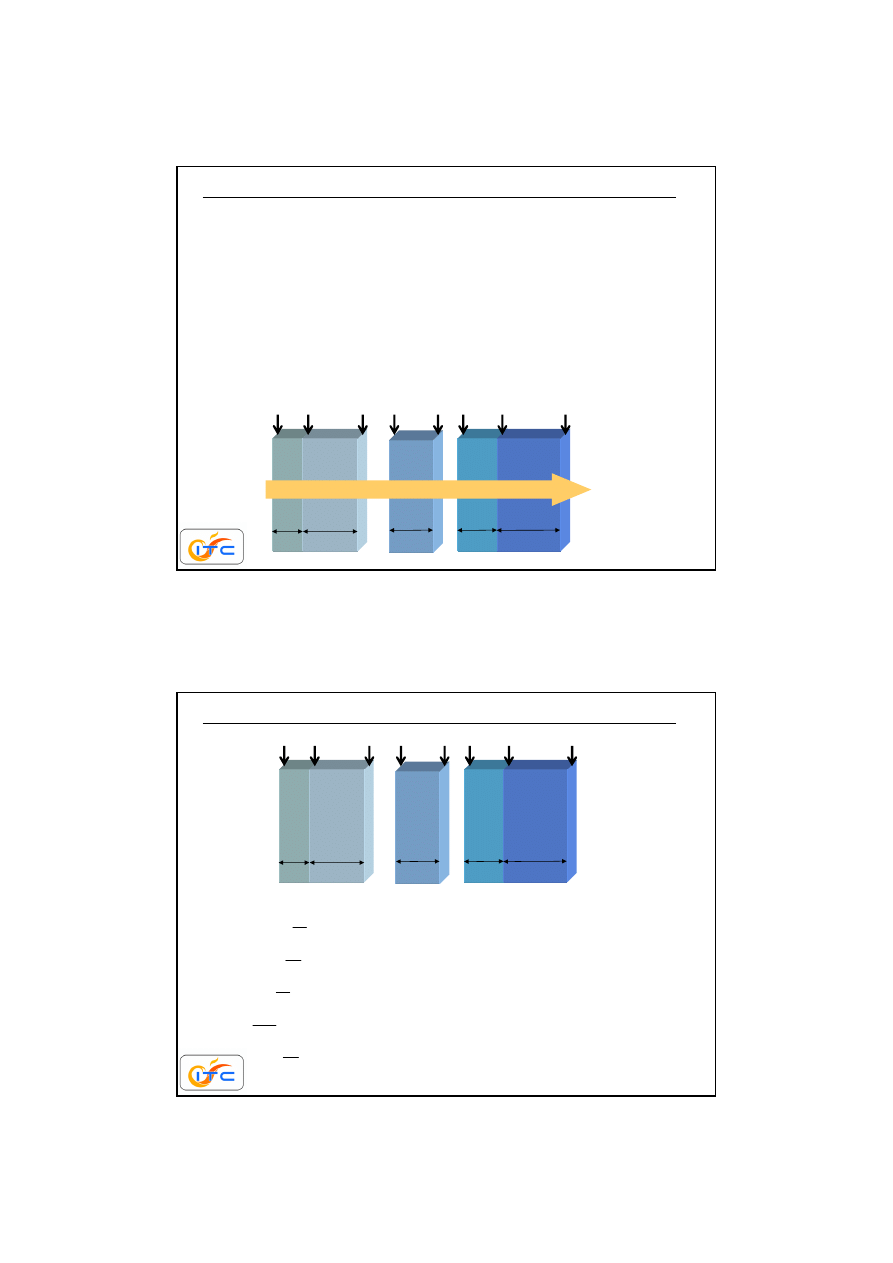
płyta dwuwarstwowa 3

L

T

1

λ

2

λ

L

T

1

λ

2

λ

1

2

λ < λ

1

2

λ > λ

przebieg temperatury

bardziej strome przebiegi w gorszych przewodnikach ciepła

p

p

ł

ł

aska p

aska p

ł

ł

yta

yta

Transport ciepła i masy

©Ryszard A. Białecki

• jednowymiarowych
• ustalonych
• bez

ź

ródłowych

• o stałym współczynniku przewodzenia ciepła
Rachunki mo

ż

na znacznie upro

ś

ci

ć

, je

ś

li zamiast wyznaczania

rozkładu temperatury, okre

ś

la si

ę

wpierw strumie

ń

ciepła.

Wykorzystuje si

ę

stało

ść

strumienia ciepła w czasie

(stan

ustalony i pole bez

ź

ródłowe). Zwi

ą

zek mi

ę

dzy temperaturami

na powierzchni płyty a g

ę

sto

ś

ci

ą

strumienia ciepła

(niezale

ż

nie od zadanych warunków brzegowych)

analogia elektryczna.
Szybka metoda rozwi

ą

zywania zada

ń

(

)

L

R

q

T

T

λ

=

−

δ

L

T

δ

R

T

λ

q

op

op

ó

ó

r cieplny

r cieplny

11

Transport ciepła i masy

©Ryszard A. Białecki

…

…

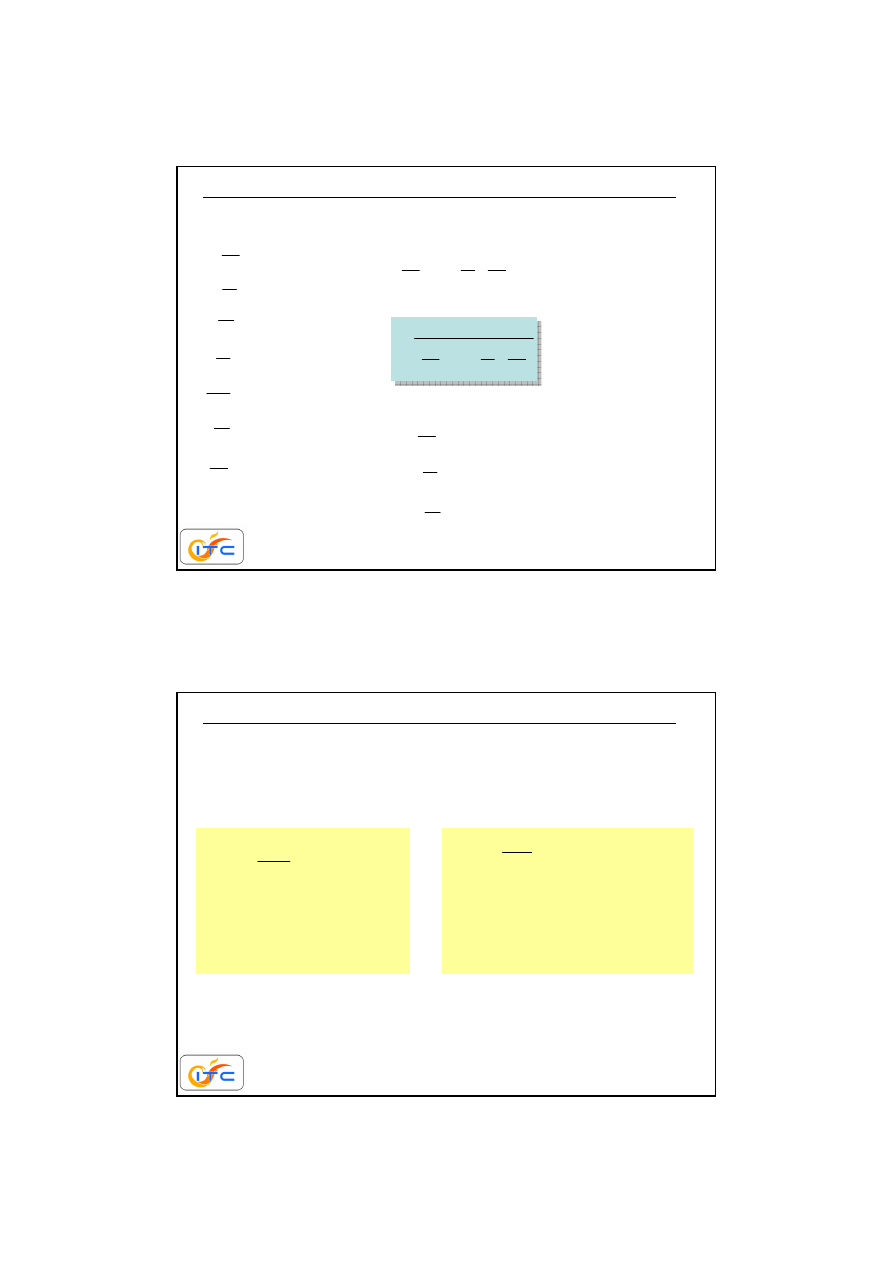
ś

cianka płaska, wielowarstwowa, idealny kontakt cieplny

konwekcyjna wymiana ciepła z obu stron

ś

cianki

przenikanie ciepła

Dane:

L

T

1,2

T

2,3

T

1,

i

i

T

−

, 1

i i

T

+

2,

1

n

n

T

−

−

1,

n

n

T

−

R

T

temperatury granic warstw s

ą

nieznane

1

δ

2

δ

i

δ

1

n

−

δ

n

δ

,

1, 2,...

i

i

n

δ =

grubo

ś

ci warstw

1

λ

2

λ

i

λ

1

n

−

λ

n

λ

,

1, 2,...

i

i

n

λ =

współczynniki przewodzenia ciepła warstw

,

fL

fR

T

T

fL

T

fR

T

temperatury płynów omywaj

ą

cych

ś

ciank

ę

L

α

R

α

,

L

R

α α

współczynniki wnikania ciepła

q

op

op

ó

ó

r cieplny

r cieplny

Transport ciepła i masy

©Ryszard A. Białecki

…

…

1

δ

2

δ

i

δ

1

n

−

δ

n

δ

1

λ

2

λ

i

λ

1

n

−

λ

n

λ

L

α

R

α

L

T

1,2

T

2,3

T

1,

i

i

T

−

, 1

i i

T

+

2,

1

n

n

T

−

−

1,

n

n

T

−

R

T

fL

T

fR

T

(

)

L

fL

L

q

T

T

= α

−

1

1,2

1

(

)

L

q

T

T

λ

=

−

δ

2

1,2

2,3

2

(

)

q

T

T

λ

=

−

δ

1,

, 1

(

)

i

i

i

i i

i

q

T

T

−

+

λ

=

−

δ

…

…

1

2,

1

1,

1

(

)

n

n

n

n

n

n

q

T

T

−

−

−

−

−

λ

=

−

δ

1,

(

)

n

n

n

R

n

q

T

T

−

λ

=

−

δ

(

)

R

R

fR

q

T

T

= α

−

wnikanie do lewej powierzchni

przewodzenie w 1. warstwie

przewodzenie w 2. warstwie

przewodzenie w i-tej warstwie

przewodzenie w n-1-szej warstwie

przewodzenie w n-tej warstwie

wnikanie do prawej powierzchni

op

op

ó

ó

r cieplny

r cieplny

12

Transport ciepła i masy

©Ryszard A. Białecki

1

fL

L

L

q

T

T

=

−

α

1

1,2

1

L

q

T

T

δ = −

λ

2

1,2

2,3

2

q

T

T

δ = −

λ

1,

, 1

i

i

i

i i

i

q

T

T

−

+

δ =

−

λ

1

2,

1

1,

1

n

n

n

n

n

n

q

T

T

−

−

−

−

−

δ

=

−

λ

1,

n

n

n

R

n

q

T

T

−

δ =

−

λ

1

R

fR

R

q

T

T

=

−

α

z ka

ż

dego z równa

ń

wyznacza si

ę

ró

ż

nic

ę

temperatur

dodawanie stronami eliminuje wszystkie (nieznane)
po

ś

rednie temperatury

1

1

1

n

i

fL

fR

i

L

i

R

q

T

T

=





δ

+

+

=

−





α

λ

α





∑

1

1

1

fL

fR

n

i

i

L

i

R

T

T

q

=

−

=





δ

+

+





α

λ

α





∑

ostatecznie g

ę

sto

ść

strumienia ciepła wyznaczy

ć

mo

ż

na ze wzoru

znaj

ą

c g

ę

sto

ść

strumienia ciepła, temperatury na stykach

(je

ś

li s

ą

potrzebne) wyznacza si

ę

kolejno

1

L

fL

L

T

q

T

=

+

α

1

1,2

1

L

T

q

T

δ

=

+

λ

2

2,3

1,2

2

T

q

T

δ

=

+

λ

itd

poniewa

ż

temperatury w warstwach zmieniaj

ą

si

ę

liniowo, wystarcza

to do jednoznacznego wyznaczenia pełnego pola temperatury w przegrodzie

op

op

ó

ó

r cieplny

r cieplny

Transport ciepła i masy

©Ryszard A. Białecki

poj

ę

cie oporu cieplnego

U

i

R

∆

=

analogia mi

ę

dzy ustalonym przepływem pr

ą

du stałego

a ustalonym, jednowymiarowym przewodzeniem ciepła.

i

nat

ęż

enie pr

ą

du

∆∆∆∆

U

ró

ż

nica potencjałów

R

opór elektryczny

Q

T

Q

R

∆

=

Q

g

ę

sto

ść

strumienia ciepła

∆∆∆∆

T

ró

ż

nica temperatur

R

Q

opór cieplny

op

op

ó

ó

r cieplny

r cieplny

13

Transport ciepła i masy

©Ryszard A. Białecki

1

1

1

fL

fR

n

i

i

i

L

L

i

R

R

T

T

Q

A

A

A

=

−

=





δ

+

+





α

λ

α





∑

1

fL

fR

n

L

i

R

i

T

T

Q

R

R

R

α

λ

α

=

−

=





+

+





∑

1

R

A

α

=

α

opór wnikania

R

A

λ

δ

=

λ

opór przewodzenia

tak zdefiniowane opory cieplne mo

ż

na ł

ą

czy

ć

tylko szeregowo

jednak

ż

e dla pól zbli

ż

onych do jednowymiarowych, ł

ą

czenie

równoległe i szeregowe oporów jest dopuszczalne, gdy

ż

prowadzi do niewielkich bł

ę

dów

op

op

ó

ó

r cieplny

r cieplny

Transport ciepła i masy

©Ryszard A. Białecki

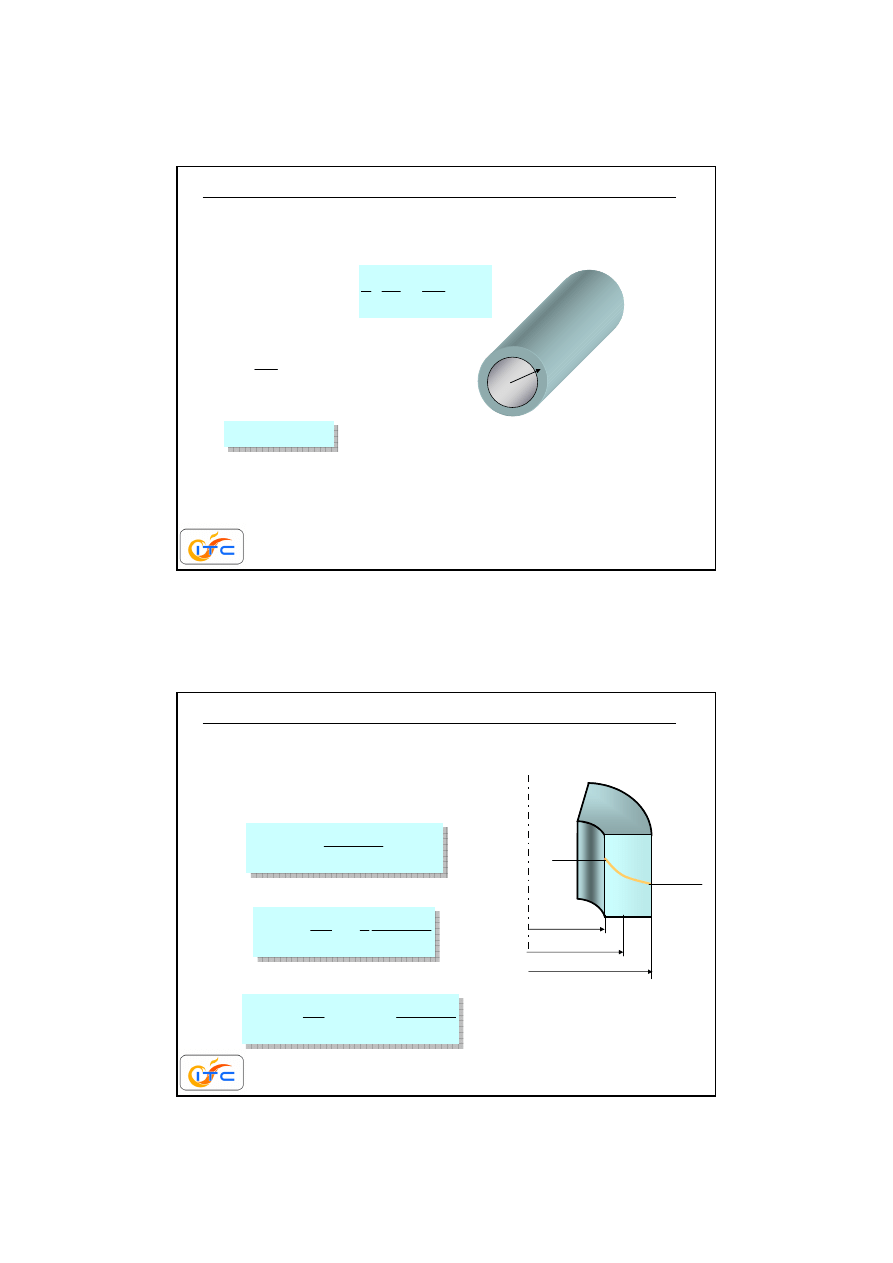
L

α

R

α

fL

T

a

δ

b

δ

R

α

fR

T

1

A

2

A

3

A

1

λ

2

λ

3

λ

4

λ

4

A

4

1

1

1

2

2

2

L

L

a

a

A

R

R

A

R

A

α

λ

λ

=

α

δ

=

λ

δ

=

λ

3

3

3

4

4

4

4

a

b

R

R

R

A

R

A

A

R

λ

λ

α

δ

=

λ

δ

=

λ

=

α

4

1

2

3

1

1

1

1

fL

fR

L

R

T

T

Q

R

R

R

R

R

R

α

λ

α

λ

λ

λ

−

=

+

+

+

+

+

współczynniki przewodzenia ciepła powinny by

ć

do siebie

zbli

ż

one. W przeciwnym wypadku, zało

ż

enie o

jednowymiarowo

ś

ci pola temperatury jest obarczone du

ż

ym

bł

ę

dem

op

op

ó

ó

r cieplny

r cieplny

14

Transport ciepła i masy

©Ryszard A. Białecki

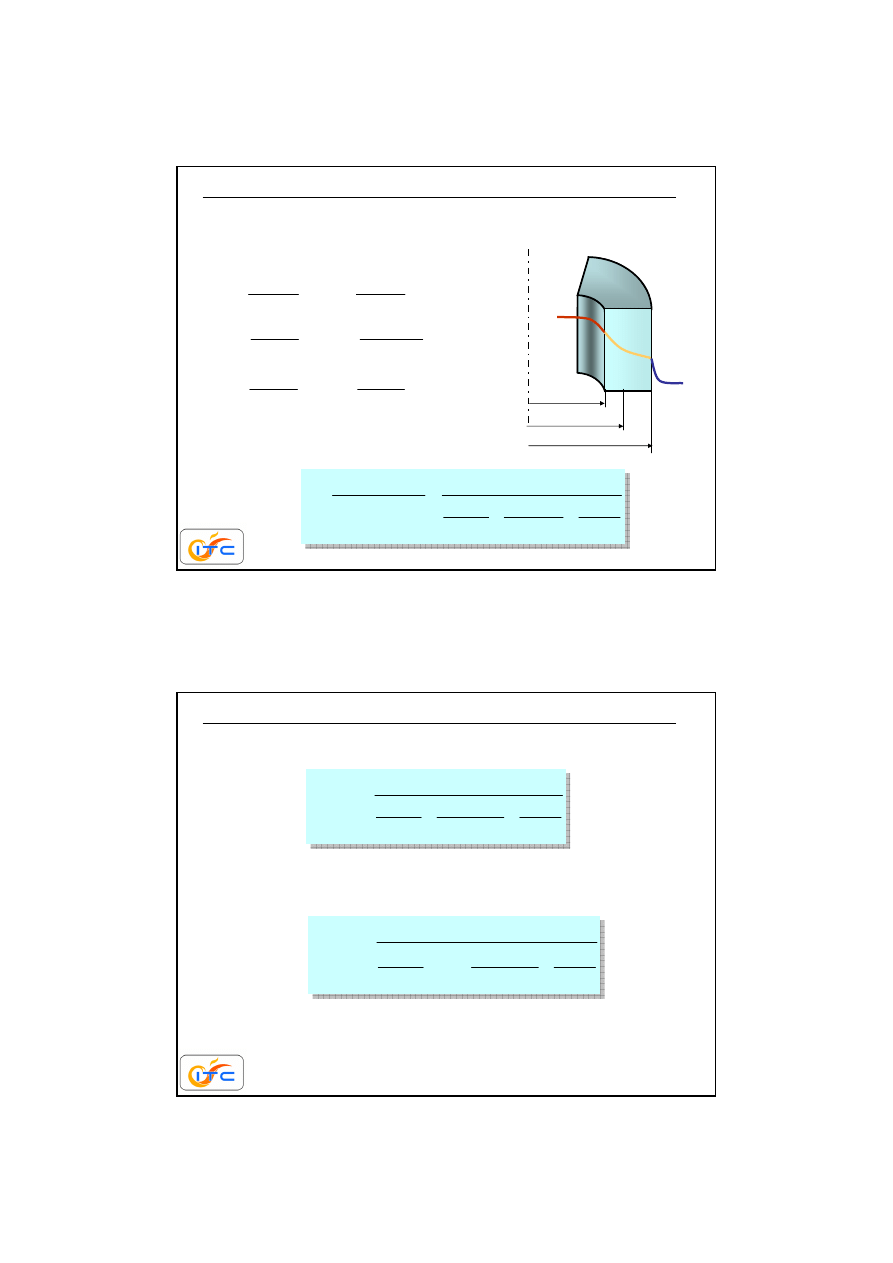
przewodzenie ciepła w układzie cylindrycznym.

Powłoka walcowa, pole bez

ź

ródłowe, jednowymiarowe.

Stały współczynnik przewodzenia ciepła

1

0

d

dT

r

r dr

dr









=

















r

1

dT

r

C

dr

=

jednokrotne całkowanie daje

powtórne całkowanie

1

2

ln

T

C

r

C

=

+

stałe wyznacza si

ę

z warunków brzegowych na wewn

ę

trznej

i zewn

ę

trznej powierzchni powłoki.

cylinder

cylinder

Transport ciepła i masy

©Ryszard A. Białecki

zadane temperatury na obu powierzchniach

( )

( )

w

w

z

z

T r

T

T r

T

=

=

w

T

z

T

w

r

r

z

r

ln( / )

( )

(

)

ln( / )

w

w

z

w

z

w

r r

T r

T

T

T

r r

= +

−

rozwi

ą

zanie

g

ę

sto

ść

strumienia ciepła zale

ż

y od promienia

krzywoliniowy przebieg temperatury!

1

( )

ln( / )

z

w

z

w

T

T

dT

q r

dr

r

r r

−

= λ

= λ

( )

2

2

ln( / )

z

w

l

z

w

T

T

dT

q r

r

dr

r r

−

= λ

π = πλ

strumie

ń

jednostkowy

odniesiony do jednostki

długo

ś

ci walca [W/m]

strumie

ń

jednostkowy jest stały (nie zale

ż

y od promienia)

cylinder

cylinder

15

Transport ciepła i masy

©Ryszard A. Białecki

konwekcyjna wymiana ciepła na obu powierzchniach

2

(

)

l

w

w

fw

w

q

r

T

T

= π α

−

1

;

2

fw

w

w

l

l

w

l

w

w

T

T

q

R

R

r

α

α

−

=

=

π α

rozwi

ą

zanie metod

ą

oporu cieplnego

fw

T

fz

T

w

r

r

z

r

2

(

)

lz

z

z

fz

z

q

r

T

T

= π α

−

ln( /

)

;

2

w

z

z

w

l

l

l

T

T

r

r

q

R

R

λ

λ

−

=

=

πλ

1

;

2

z

fz

z

l

l

z

l

z

z

T

T

q

R

R

r

α

α

−

=

=

π α

eliminuj

ą

c po

ś

rednie temperatury

ln( / )

1

1

2

fw

fz

fw

fz

l

w

z

z

w

l

l

l

w

w

z

z

T

T

T

T

q

r r

R

R

R

d

d

α

λ

α

−

−

=

=

+

+

+

+

π α

πλ

π α

cylinder

cylinder

Transport ciepła i masy

©Ryszard A. Białecki

strumie

ń

ciepła z rury o długo

ś

ci

L

(

)

ln(

/

)

1

1

2

fw

fz

l

z

w

w

w

z

z

T

T L

Q q L

d

d

d

d

−

=

=

+

+

π α

πλ

π α

1

(

)

ln(

/

)

1

1

2

fw

fz

l

i

i

n

z

w

i

i

w

w

z

z

T

T L

Q q L

d

d

d

d

=

−

=

=

+

+

π α

πλ

π α

∑

wielowarstwowa przegroda cylindryczna

,

i

i

w

z

d d

wewn

ę

trzna i zewn

ę

trzna

ś

rednica i-tej warstwy

,

w

z

d d

wewn

ę

trzna i zewn

ę

trzna

ś

rednica przegrody

cylinder

cylinder