Transport ciepła i masy

©Ryszard A.
Białecki

ustalone przewodzenie

ustalone przewodzenie

ciepła, rozwiązania analityczne

ciepła, rozwiązania analityczne

Transport ciepła i masy

©Ryszard A.
Białecki

Redukcja wymiarowości zagadnienia przewodzenia ciepła

Redukcja wymiarowości zagadnienia przewodzenia ciepła

w wielu przypadkach przewodzenie w jednym kierunku

w wielu przypadkach przewodzenie w jednym kierunku

dominuje

dominuje

nad przepływem energii w innych kierunkach. Pozwala to

nad przepływem energii w innych kierunkach. Pozwala to

zredukować wymiar geometryczny zagadnienia, przez

zredukować wymiar geometryczny zagadnienia, przez

pominięcie składnika strumienia ciepła w nieistotnych

pominięcie składnika strumienia ciepła w nieistotnych

kierunkach.

kierunkach.

Najczęściej uproszczeń takich można dokonać w

Najczęściej uproszczeń takich można dokonać w

obszarach o kształtach wydłużonych w jednym lub

obszarach o kształtach wydłużonych w jednym lub

kierunkach. Zadanie trójwymiarowe sprowadza się wtedy

kierunkach. Zadanie trójwymiarowe sprowadza się wtedy

odpowiednio do dwu lub jednowymiarowego.

odpowiednio do dwu lub jednowymiarowego.

Aby zastosować takie uproszczenie, warunki brzegowe

Aby zastosować takie uproszczenie, warunki brzegowe

wzdłuż kierunków wydłużonych muszą być stałe. Zadania

wzdłuż kierunków wydłużonych muszą być stałe. Zadania

chętnie upraszcza się do 1D, bowiem dla takich

chętnie upraszcza się do 1D, bowiem dla takich

przypadków znane są proste rozwiązania analityczne.

przypadków znane są proste rozwiązania analityczne.

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

(

)

r

q

T T

�

=a

-

(

)

l

q

T T

�

=a

-

b

T T

=

u

q q

=

izolacja

0

q=

izolacja

0

q=

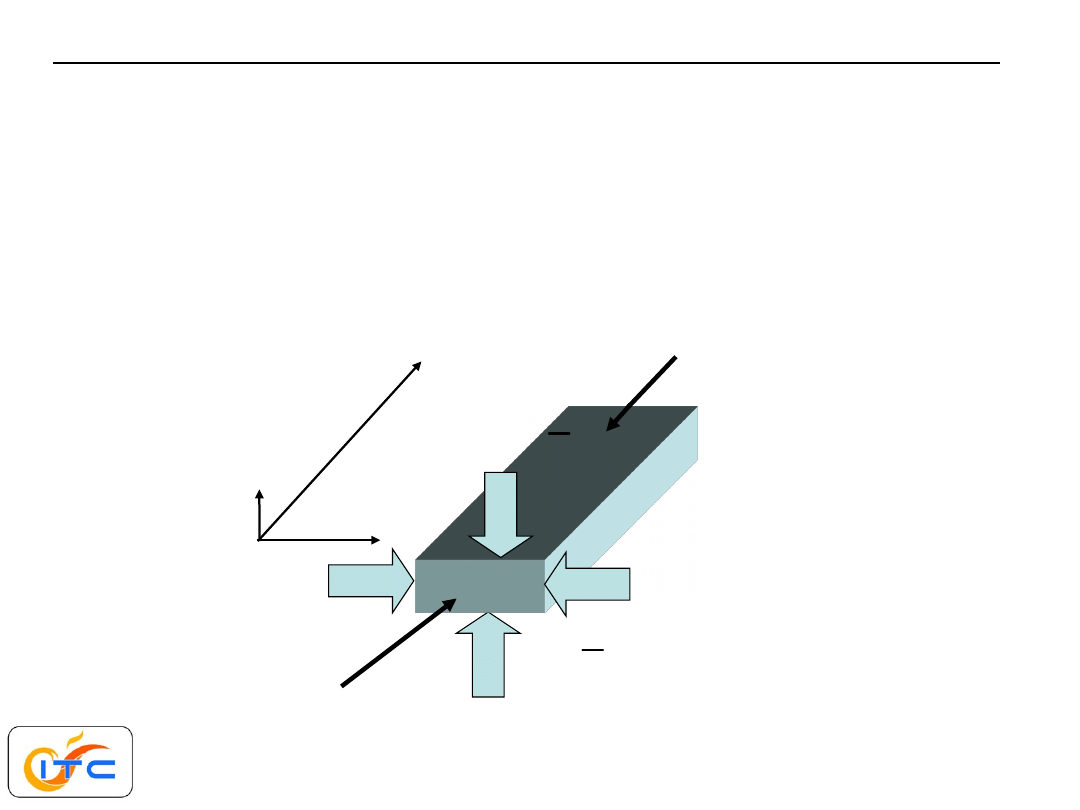
przykład zadania dwuwymiarowego

pole temperatury w każdym przekroju

x y

jest

identyczne (nie zależy od

z

).

z

y

x

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

b

T T

=

u

q q

=

izolacja

0

q=

izolacja

0

q=

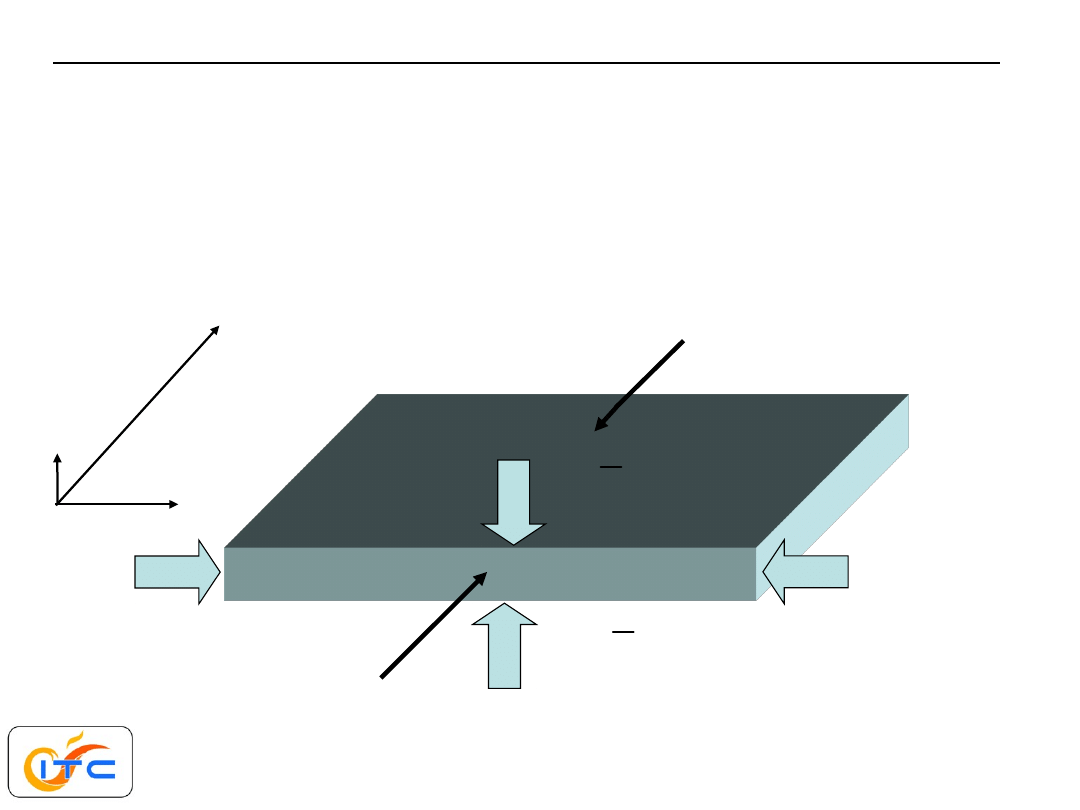
przykład zadania jednowymiarowego

pole temperatury wzdłuż każdej linii równoległej do osi

y

jest

identyczne (nie zależy ani od

z

ani od

x

).

z

y

izolacja

0

q=

izolacja

0

q=

x

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

(

)

e

e

q

T T

�

=a

-

(

)

i

i

q

T T

�

=a

-

izolacja

0

q=

izolacja

z

r

f

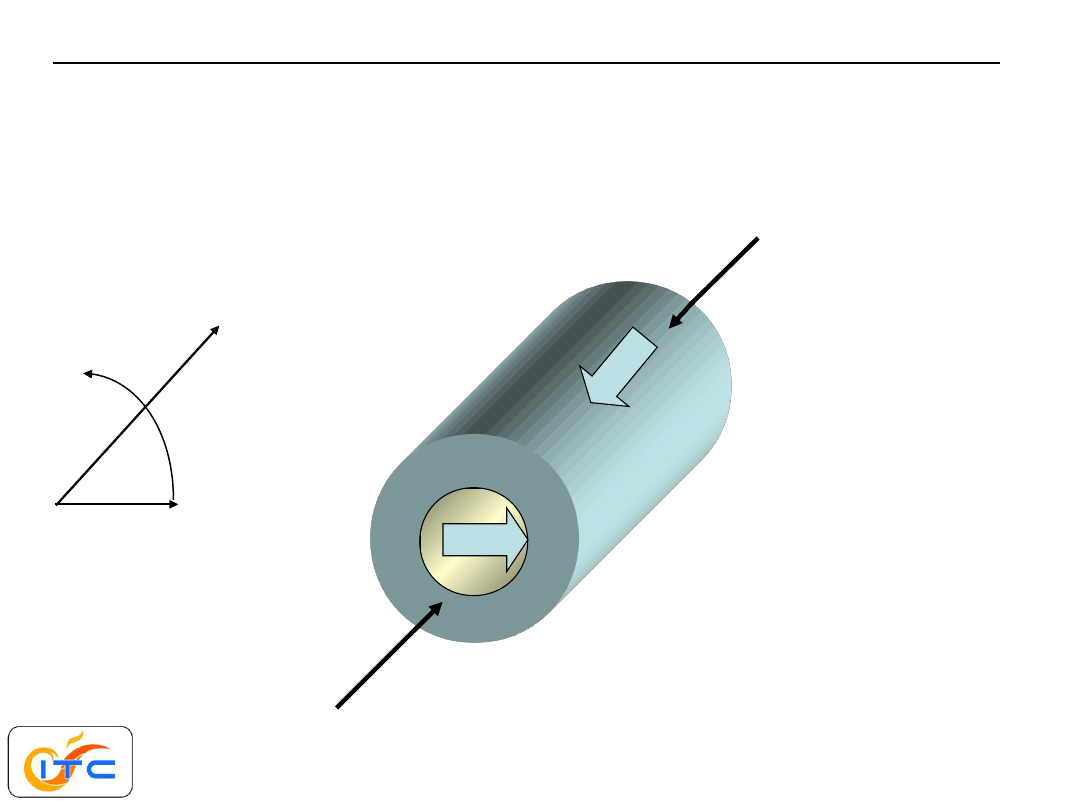
przykład zadania jednowymiarowego

pole temperatury wzdłuż każdego promienia

r

jest

identyczne (nie zależy ani od

z

ani od kąta



).

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

ściśle rzecz biorąc, redukcja zadania 3D do 2D
wymaga aby na powierzchniach prostopadłych do
wynikowego pola 2D, panowały warunki adiabatyczne.
W praktyce, jeśli warunki w tych przekrojach nie różnią się
znacznie, zadanie można i tak traktować jak 2 wymiarowe,
bowiem zakłócenia pola 2D koncentrują się tylko w okolicach
tych powierzchni.

Podobnie rzecz się ma przy redukcji zadań 2D do 1D.

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

redukcja wymiarowości

redukcja wymiarowości

2

50(

300) /

q

T

W m

=

-

2

1200 /

q

W m

=

400

T

K

=

2

50(

300) /

q

T

W m

=

-

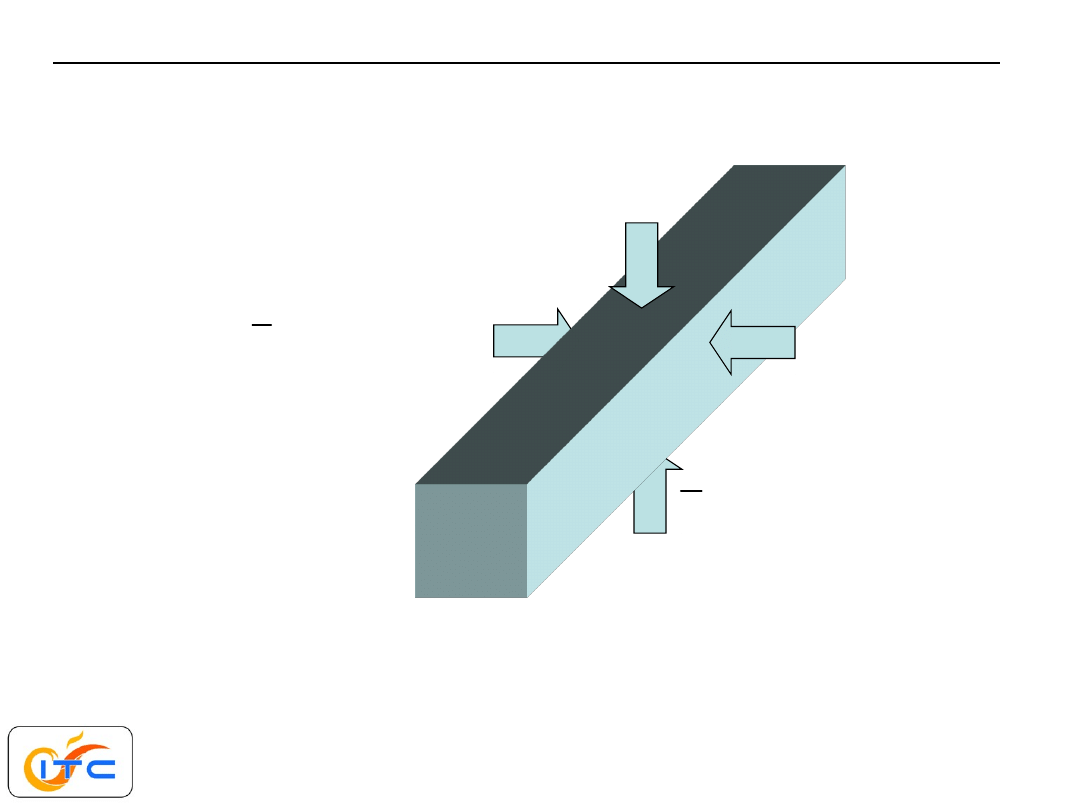
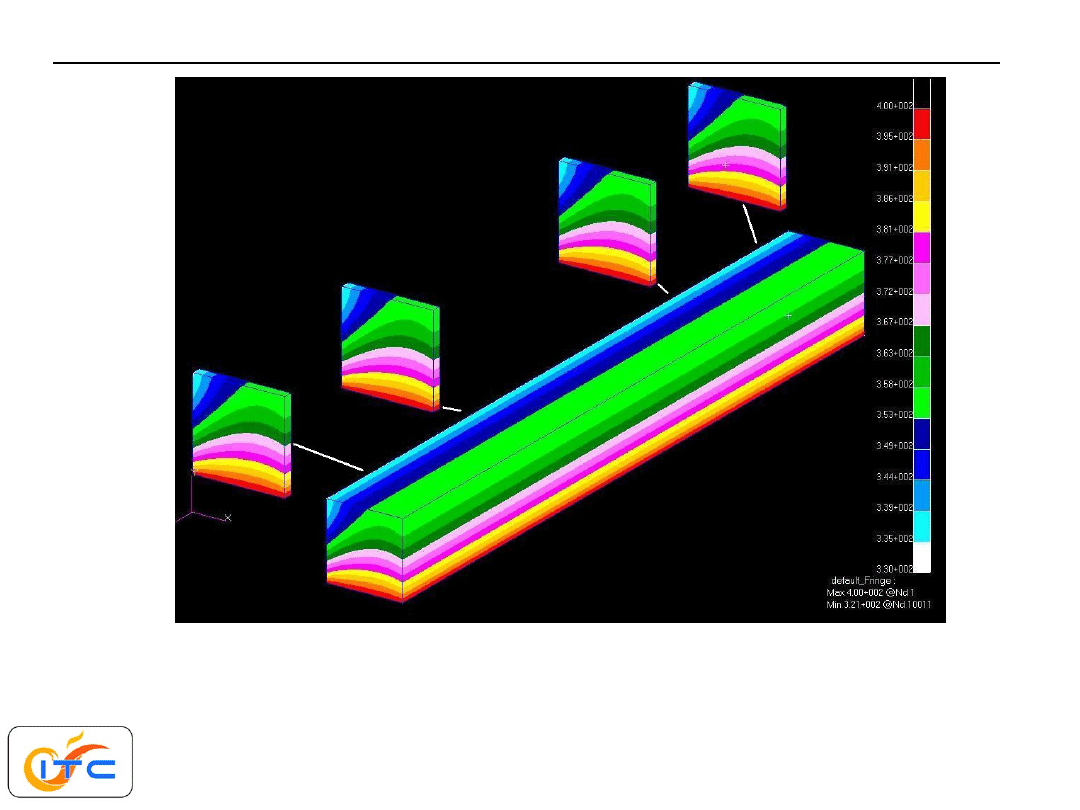
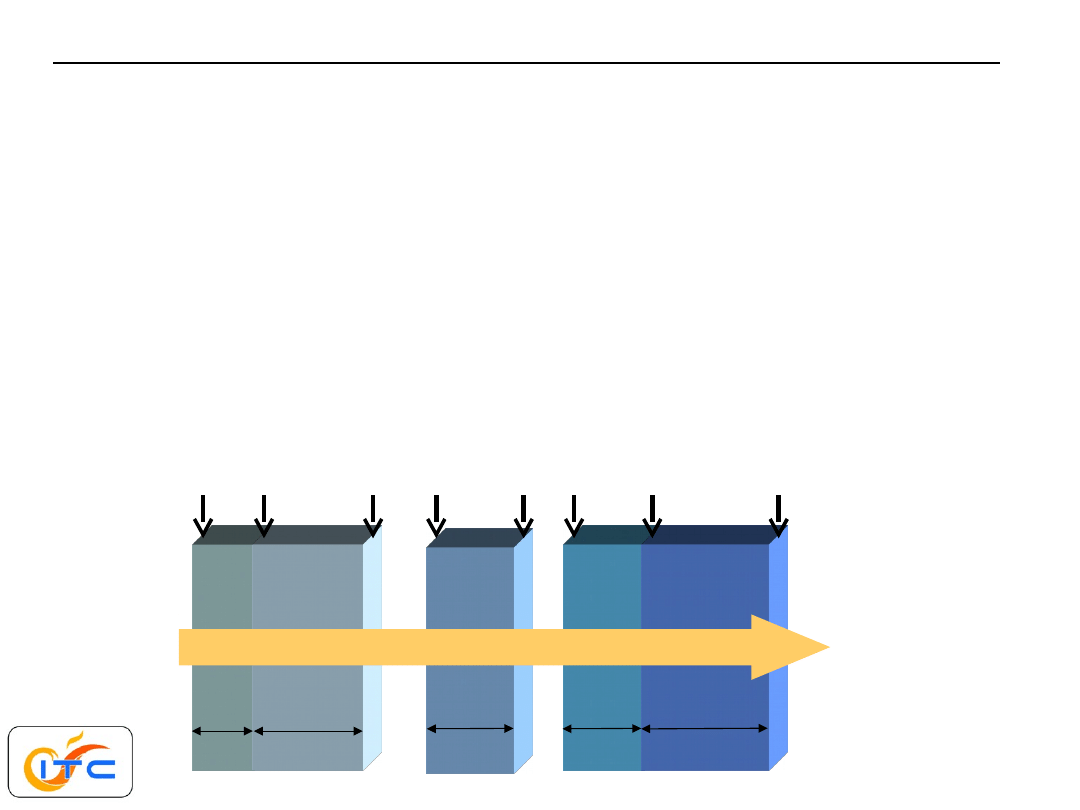
warunki brzegowe na czołowych (kwadratowych)
powierzchniach zmieniają się od izolacji do
intensywnej wymiany konwekcyjnej

przykład redukcji wymiarowości zagadnienia

Transport ciepła i masy

©Ryszard A.
Białecki

powierzchnie czołowe zaizolowane. Zadanie 2D

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

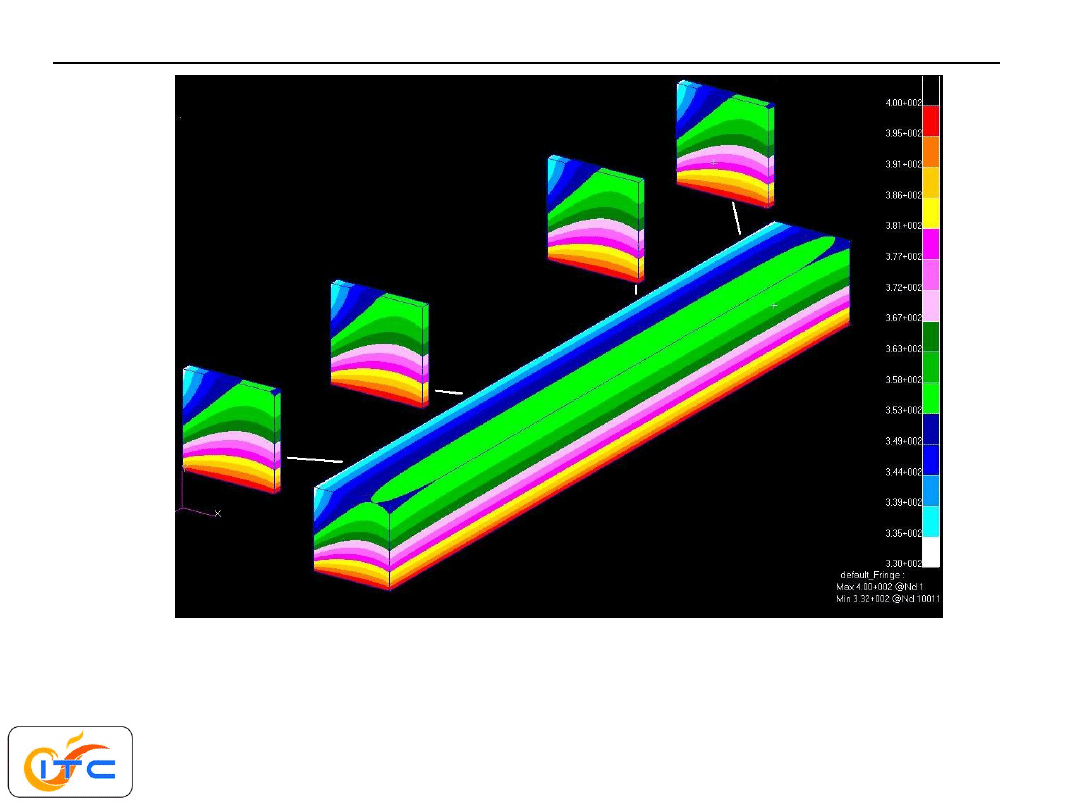
powierzchnie czołowe słabo wymieniające ciepło przez
konwekcję



=20 W/m

2

K temperatura płynu 300K.

Wpływ wnikania z tych powierzchni ogranicza się do
bardzo małego obszaru w ich sąsiedztwie

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

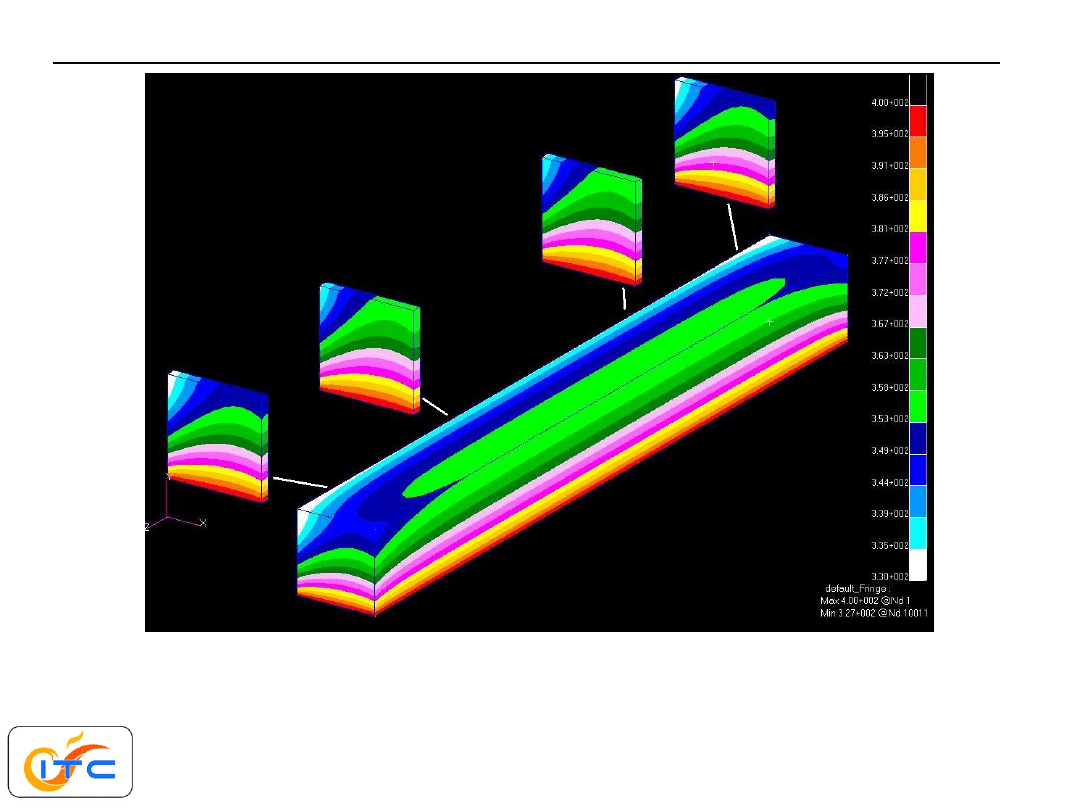
powierzchnie czołowe wymieniające ciepło przez konwekcję
ze średnią intensywnością



=50 W/m

2

K temperatura płynu 300K.

Wpływ wnikania z tych powierzchni nadal w niewielkim obszarze
w sąsiedztwie powierzchni czołowych

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

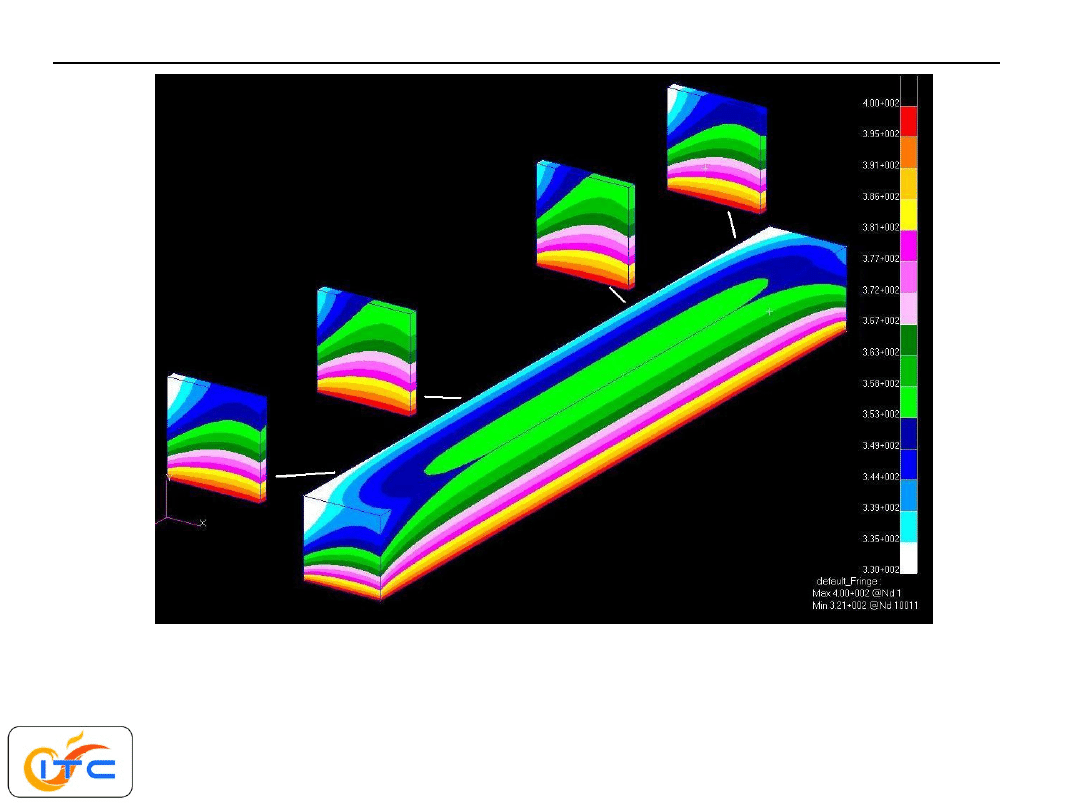
powierzchnie czołowe wymieniające ciepło przez
konwekcję
z dużą intensywnością



=100 W/m

2

K,temperatura

płynu 300K. Wpływ wnikania z tych powierzchni jest
jeszcze większy niż poprzednio. W środku obszaru
pole jest nadal dwuwymiarowe

redukcja wymiarowości

redukcja wymiarowości

Transport ciepła i masy

©Ryszard A.
Białecki

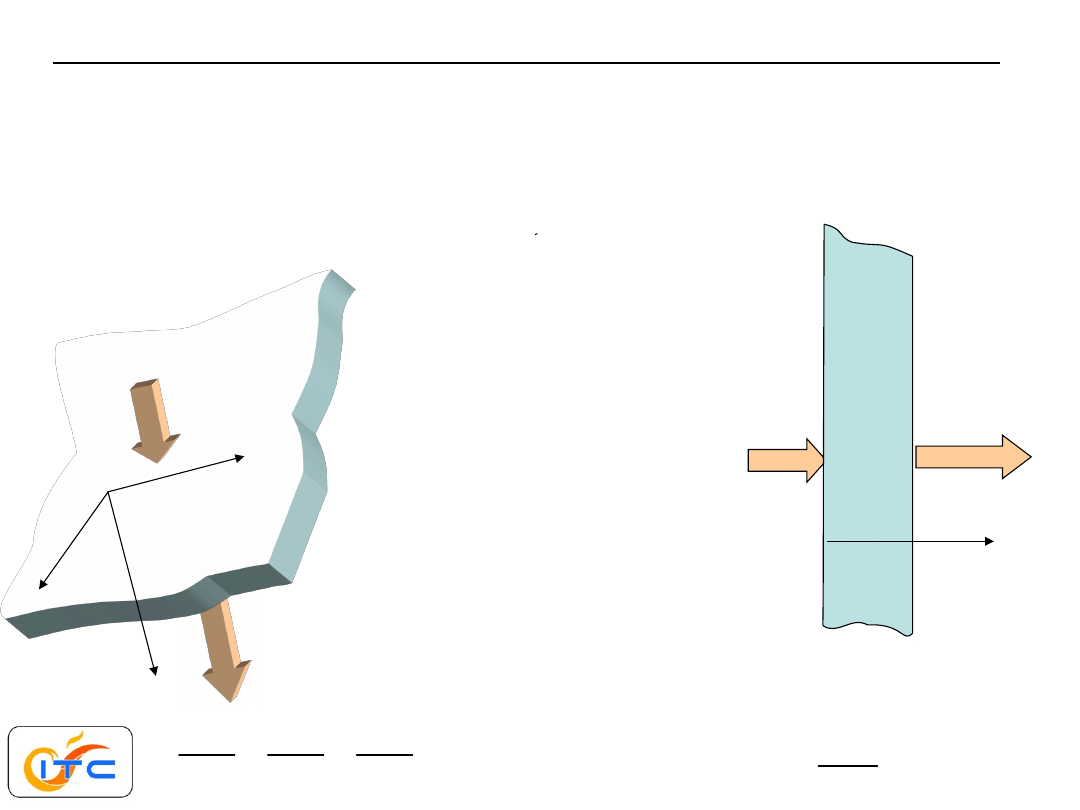
Ustalone zadania jednowymiarowe

Ustalone zadania jednowymiarowe

Płaska nieskończona płyta

Płaska nieskończona płyta

wektor strumienia ciepła
normalny do powierzchni

q=q

x

y

z

q

q

x

obiekt 3D

obiekt 3D

model 1D

model 1D

2

2

2

2

2

2

0

v

T

T

T

q

x

y

z

�

�

�

�

�

l

+

+

+ =

�

�

�

�

�

�

�

2

2

0

v

d T

q

dx

l

+ =

q=q

x=0

x=



płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

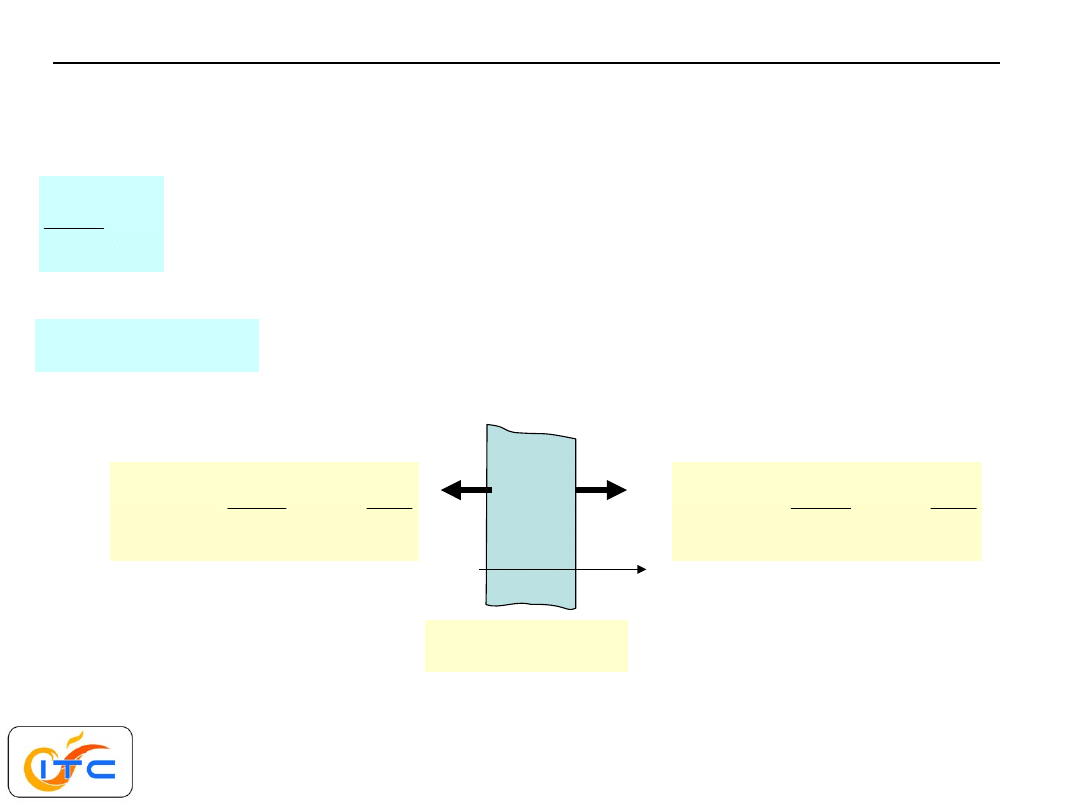
2

2

0

d T

dx

=

Stały współczynnik przewodzenia ciepła.

Stały współczynnik przewodzenia ciepła.

Płaska nieskończona płyta, pole bezźródłowe

Płaska nieskończona płyta, pole bezźródłowe

pole bezźródłowe

0

v

q =

rozwiązanie (całka ogólna)

1

2

( )

T x

C x C

=

+

stałe

C

1

i

C

2

wyznacza się z warunków brzegowych

x

R

R

dT

dT

q

d

dx

=- l

=- l

n

R

n

L

n

L

L

dT

dT

q

d

dx

=- l

=+l

n

strumienie na skrajnych powierzchniach maja przeciwne znaki.
W praktyce używa się jednego ze strumieni (zwykle dodatniego)

0

0

x

x

q

q

=d

=

+

=

notka o kierunku strumienia ciepła

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

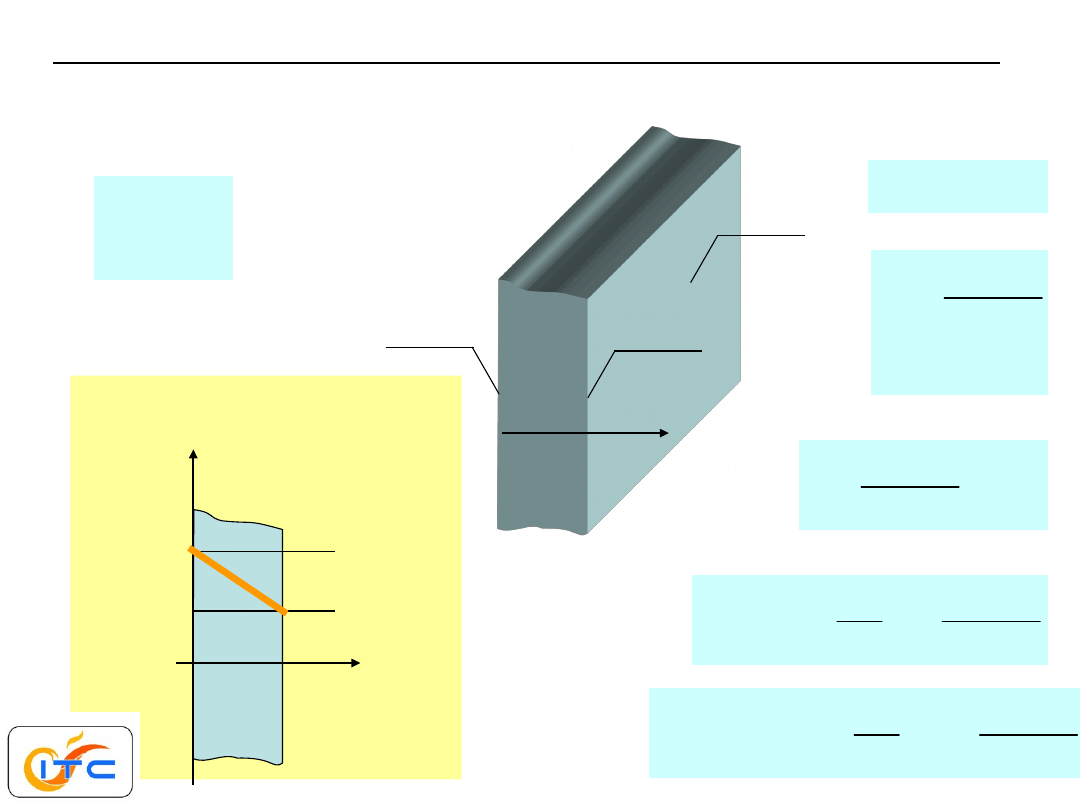
(0)
( )

L

R

T

T

T

T

=

d =

znane obie temperatury skrajne

R

L

L

T T

T

x T

-

=

+

d

( )

L

R

T T

dT

q x

dx

-

=- l

=l

d

x

0

d

L

T

R

T

rozwiązanie

x

0

d

T

R

T

L

T

1

2

R

L

L

T T

C

C

T

-

=

d

=

1

2

T C x C

=

+

przebieg temperatury

l

A

L

R

T T

dT

Q qA

A

A

dx

-

=

=- l

=l

d

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

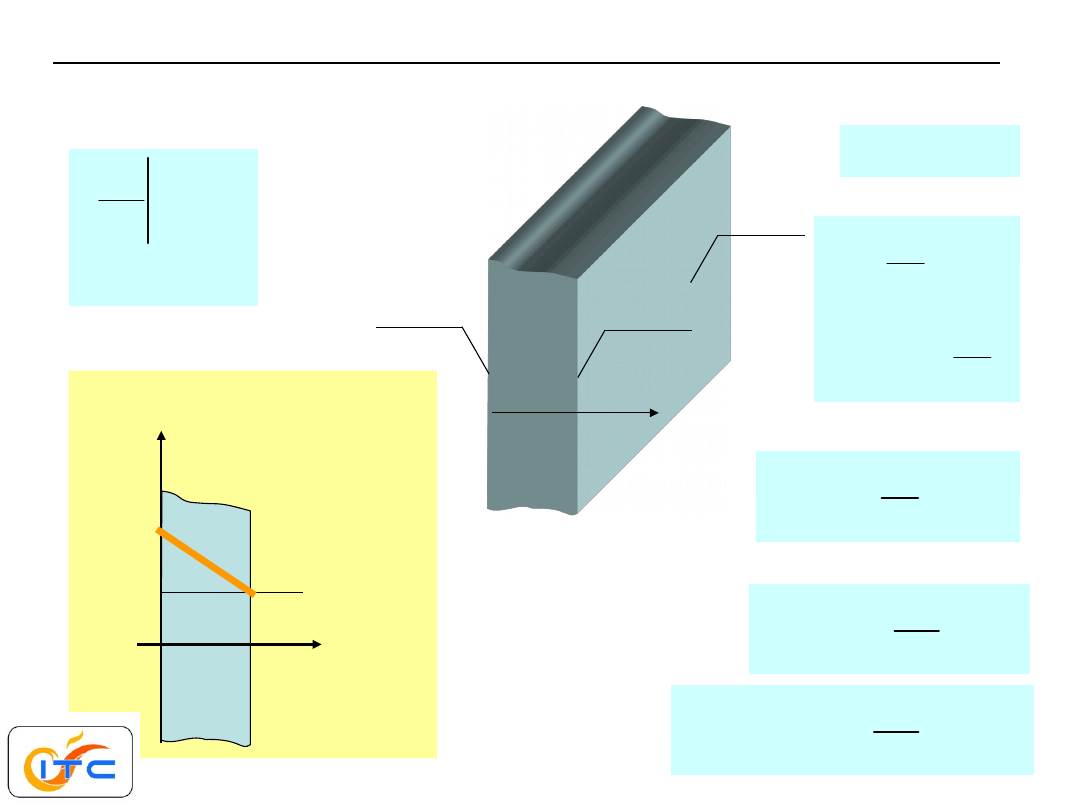
0

( )

L

x

R

dT

q

dx

T

T

=

l

=

d =

znana temperatura i strumień ciepła

(

)

L

R

q

T T

x

= -

d-

l

( )

L

dT

q x

q

dx

=- l

=-

x

0

d

L

q

R

T

x

0

d

T

R

T

1

2

L

L

R

q

C

q

C

T

=

l

= -

d

l

1

2

T C x C

=

+

rozwiązanie

l

przebieg temperatury

A

L

dT

Q qA

A

q A

dx

=

=- l

=-

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

0

(

)

(

)

L

fL

x

R

fR

x

dT

T T

dx

dT

T T

dx

=

=d

+l

=a

-

- l

=a

-

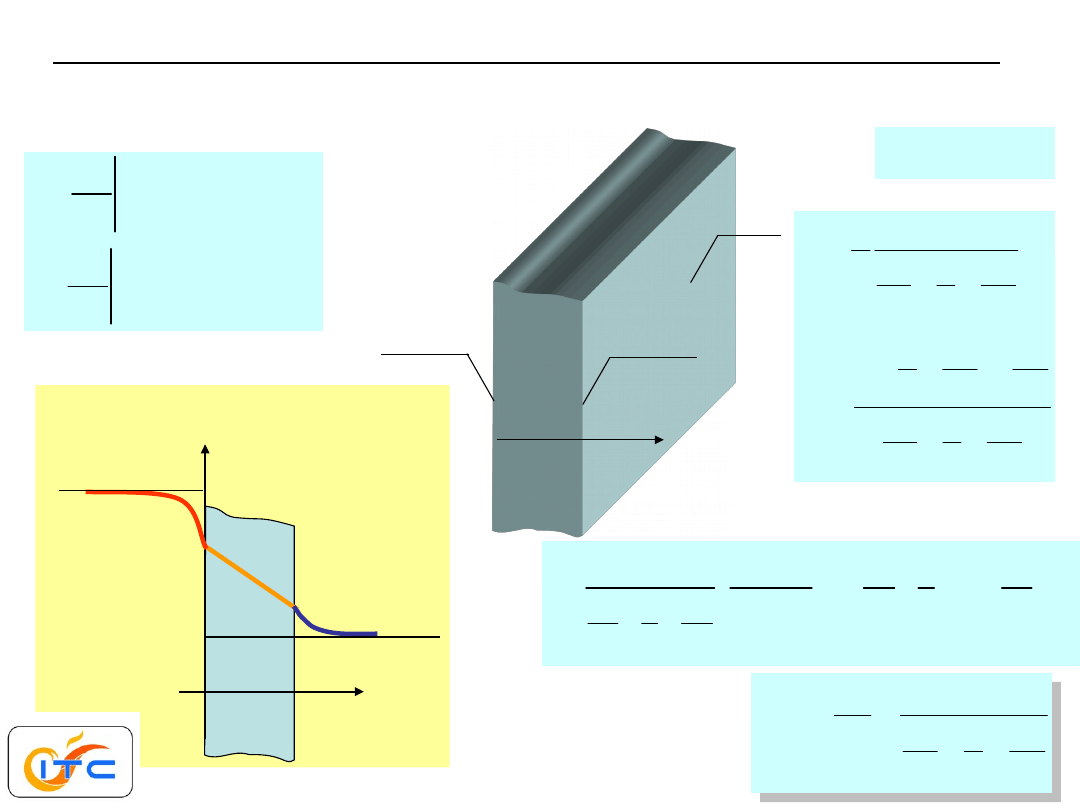
konwekcyjna wymiana ciepła na obu
powierzchniach

x

0

d

,

L

fL

T

a

x

0

d

,

R

fR

T

a

1

2

1

1

1

1

(

)

1

1

fR

fL

L

R

fR

fL

R

L

L

R

T

T

C

T

T

C

-

=

d

l

+ +

a

l

a

d

+

+

l

a

a

=

d

+ +

a

l

a

1

1

1

1

1

fR

fL

fL

fR

R

L

L

R

T

T

T

x

T

T

�

�

-

�

�

d

=

+

+

+

�

�

�

�

d

l

a

l

a

�

�

�

�

+ +

a

l a

1

1

fL

fR

L

R

T

T

dT

q

dx

-

=- l

=

d

+ +

a

l

a

1

1

fL

fR

L

R

T

T

dT

q

dx

-

=- l

=

d

+ +

a

l

a

l

1

2

T C x C

=

+

rozwiązanie

T

fL

T

fR

T

płyn
ciepły

płyn
chłodny

przebieg temperatury

A

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

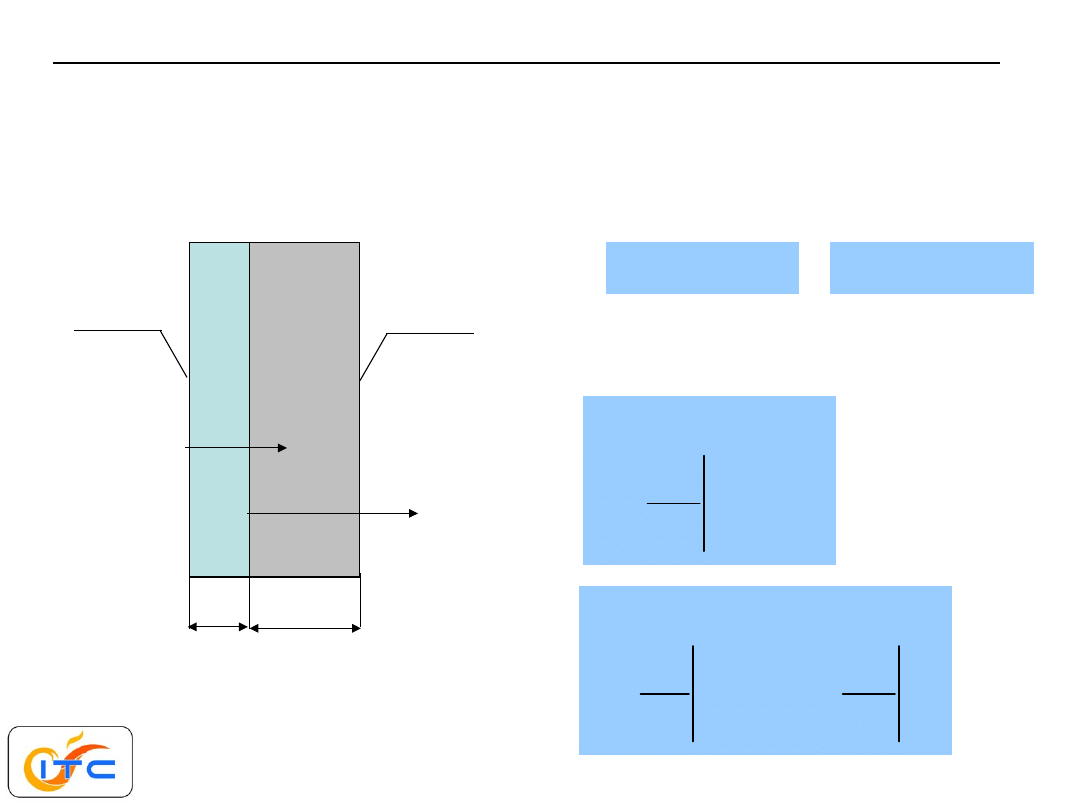
płyta dwuwarstwowa 1

znany strumień ciepła i temperatura na brzegu. Idealny styk warstw

L

T

R

q

1

x

2

x

1

1 1

2

T C x C

=

+

2

3 2

4

T

C x C

=

+

1

l

2

l

1

d

2

d

0

0

2

2

1

1

2

2

2

(

0)

L

R

x

T x

T

dT

q

dx

=d

= =

- l

=

1

1

2

1

1

1

2

2

1

2

1

2

1

2

0

(

)

(

0)

x

x

T x

T x

dT

dT

dx

dx

=d

=

=d =

=

- l

=- l

rozwiązanie w każdej z warstw

nieznane stałe wyznacza się
z warunków brzegowych

brzegi
zewnętrzne

styk

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

płyta dwuwarstwowa 2

podejście uniwersalne, wymaga dość żmudnych
rachunków

1

1

1

2

3

4

1

2

2

;

;

;

R

R

L

R

L

q

q

T

q

C

C

T C

C

l

- d

=

=

=-

=

l

l

l

może być stosowane do zadań o

• dowolnej liczbie warstw,

• dowolnych liniowych warunków brzegowych

• zależnych od współrzędnej źródeł ciepła
lub

•zależnych od temperatury współczynnikach
przewodzenia ciepła

1

1

1

1

2

2

1

2

1

;

R

R

L

R

L

q

q

T

q

T

x T

T

x

l

- d

=

+

=-

+

l

l

l

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

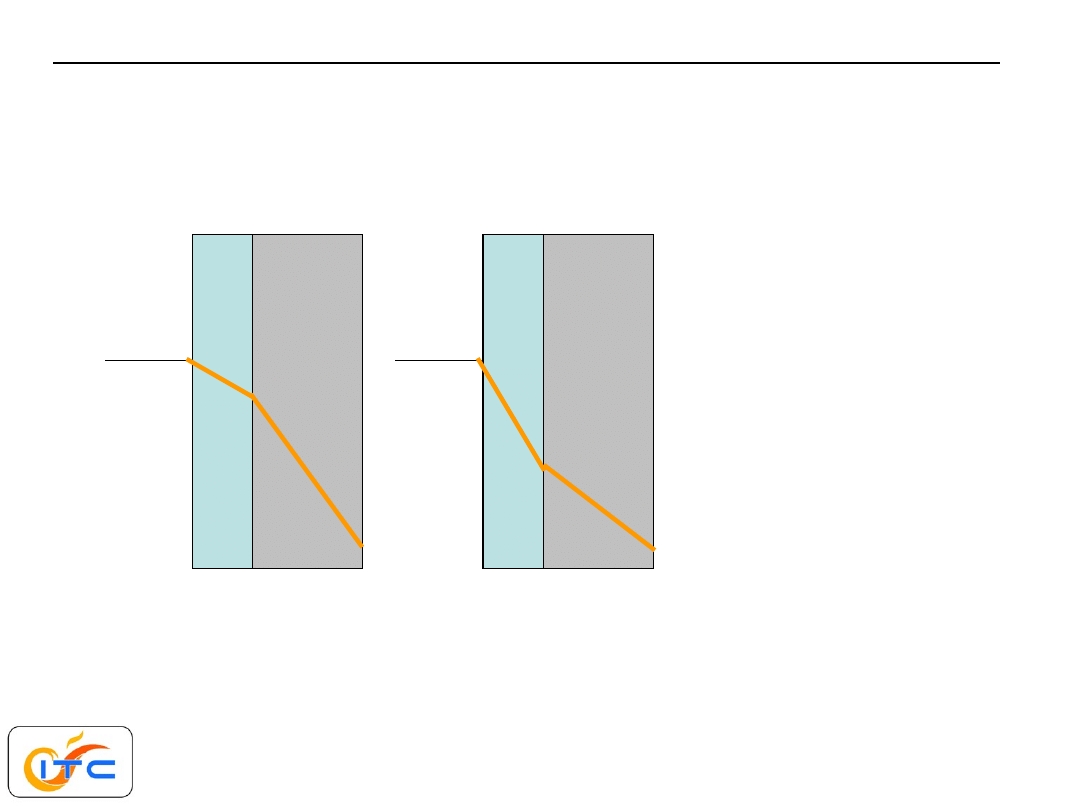
płyta dwuwarstwowa 3

L

T

1

l

2

l

L

T

1

l

2

l

1

2

l <l

1

2

l >l

przebieg temperatury

bardziej strome przebiegi w gorszych przewodnikach ciepła

płaska płyta

płaska płyta

Transport ciepła i masy

©Ryszard A.
Białecki

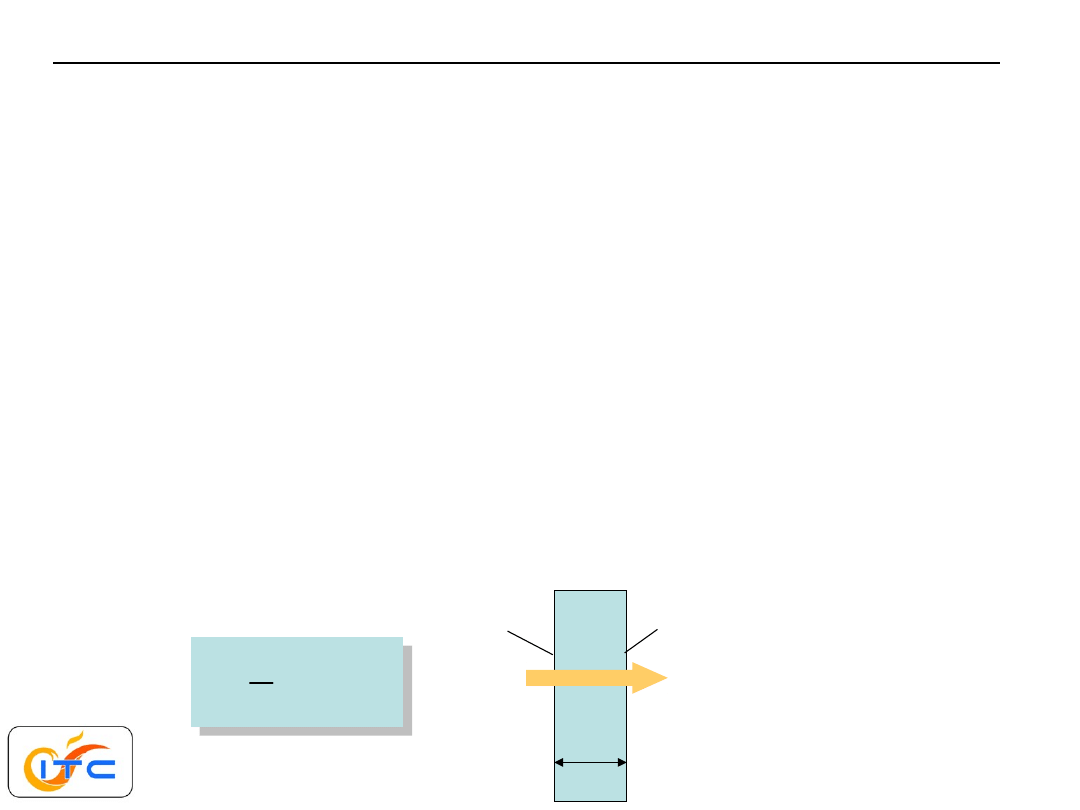
• jednowymiarowych

• ustalonych

• bezźródłowych

• o stałym współczynniku przewodzenia ciepła
Rachunki można znacznie uprościć, jeśli zamiast
wyznaczania
rozkładu temperatury, określa się wpierw strumień
ciepła.

Wykorzystuje się

stałość strumienia ciepła w czasie

(stan ustalony i pole bezźródłowe). Związek między
temperaturami na powierzchni płyty a gęstością
strumienia ciepła (niezależnie od zadanych
warunków brzegowych)

analogia elektryczna.
Szybka metoda rozwiązywania zadań

(

)

L

R

q

T T

l

=

-

d

(

)

L

R

q

T T

l

=

-

d

L

T

d

R

T

l

q

opór cieplny

opór cieplny

Transport ciepła i masy

©Ryszard A.
Białecki

…

…

ścianka płaska, wielowarstwowa, idealny kontakt cieplny

konwekcyjna wymiana ciepła z obu stron ścianki

przenikanie ciepła

Dane:

L

T

1,2

T

2,3

T

1,

i

i

T

-

, 1

i i

T

+

2, 1

n

n

T

-

-

1,

n

n

T

-

R

T

temperatury granic warstw są nieznane

1

d

2

d

i

d

1

n-

d

n

d

,

1,2,...

i

i

n

d =

grubości warstw

1

l

2

l

i

l

1

n-

l

n

l

,

1,2,...

i

i

n

l

=

współczynniki przewodzenia ciepła warstw

,

fL

fR

T T

fL

T

fR

T

temperatury płynów omywających ściankę

L

a

R

a

,

L

R

a a

współczynniki wnikania ciepła

q

opór cieplny

opór cieplny

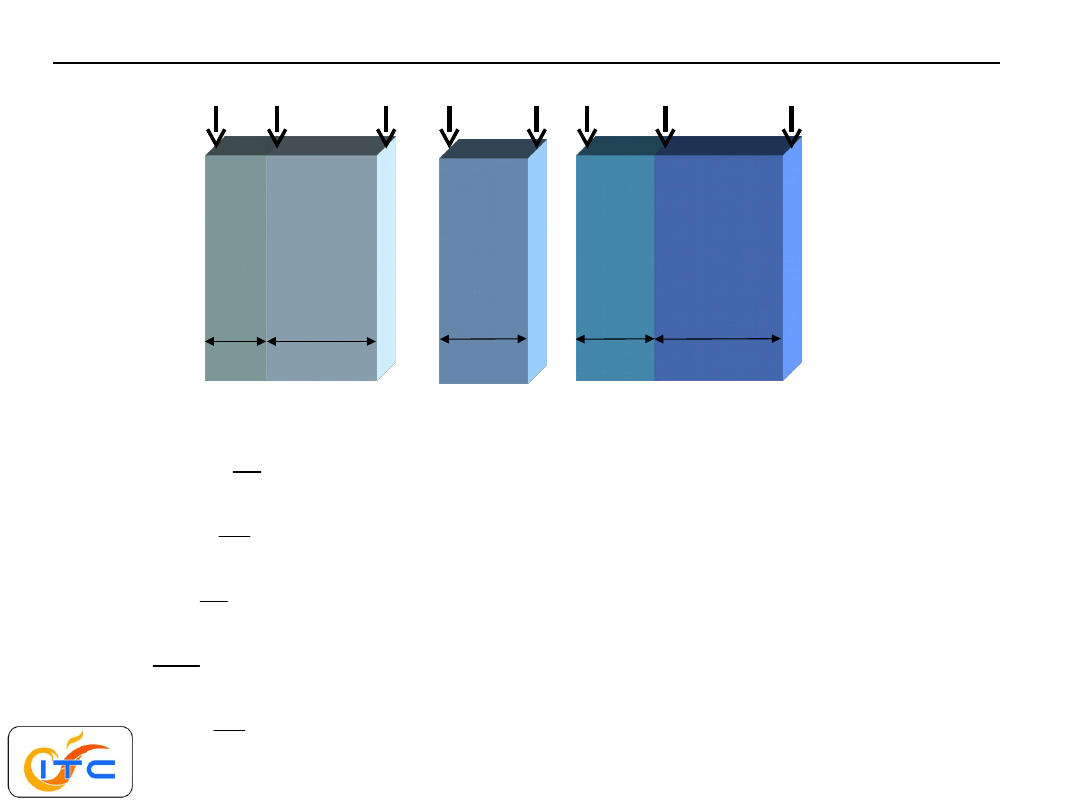
Transport ciepła i masy

©Ryszard A.
Białecki

…

…

1

d

2

d

i

d

1

n-

d

n

d

1

l

2

l

i

l

1

n-

l

n

l

L

a

R

a

L

T

1,2

T

2,3

T

1,

i

i

T

-

, 1

i i

T

+

2, 1

n

n

T

-

-

1,

n

n

T

-

R

T

fL

T

fR

T

(

)

L

fL

L

q

T

T

=a

-

1

1,2

1

(

)

L

q

T T

l

=

-

d

2

1,2

2,3

2

(

)

q

T

T

l

=

-

d

1,

, 1

(

)

i

i

i

i i

i

q

T

T

-

+

l

=

-

d

…

…

1

2, 1

1,

1

(

)

n

n

n

n

n

n

q

T

T

-

-

-

-

-

l

=

-

d

1,

(

)

n

n

n

R

n

q

T

T

-

l

=

-

d

(

)

R

R

fR

q

T T

=a

-

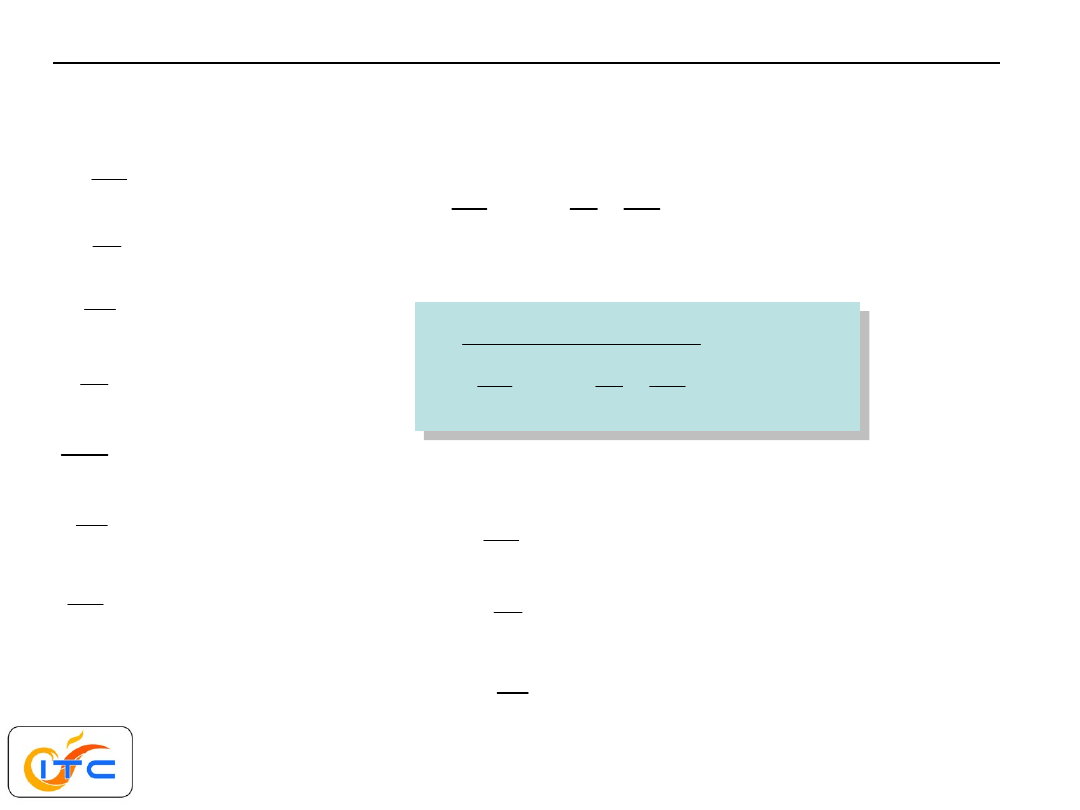
wnikanie do lewej powierzchni

przewodzenie w 1. warstwie

przewodzenie w 2. warstwie

przewodzenie w i-tej warstwie

przewodzenie w n-1-szej warstwie

przewodzenie w n-tej warstwie

wnikanie do prawej powierzchni

opór cieplny

opór cieplny

Transport ciepła i masy

©Ryszard A.
Białecki

1

fL

L

L

q

T

T

=

-

a

1

1,2

1

L

q

T T

d

= -

l

2

1,2

2,3

2

q

T

T

d

=

-

l

1,

, 1

i

i

i

i i

i

q

T

T

-

+

d

=

-

l

1

2, 1

1,

1

n

n

n

n

n

n

q

T

T

-

-

-

-

-

d

=

-

l

1,

n

n

n

R

n

q

T

T

-

d

=

-

l

1

R

fR

R

q

T T

= -

a

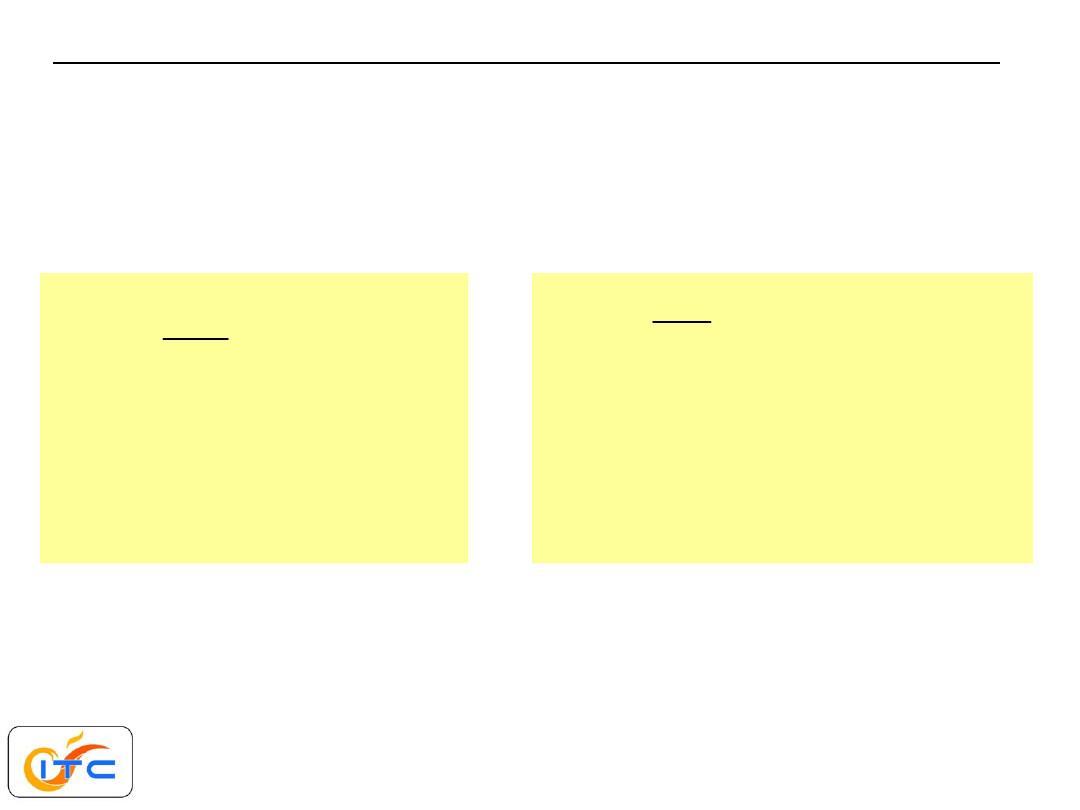
z każdego z równań wyznacza się
różnicę temperatur

dodawanie stronami eliminuje wszystkie (nieznane)
pośrednie temperatury

1

1

1

n

i

fL

fR

i

L

i

R

q

T

T

=

�

�

d

+

+

=

-

�

�

a

l

a

�

�

�

1

(

)

1

1

fL

fR

fL

fR

n

i

i

L

i

R

T

T

q

k T

T

=

-

=

=

-

�

�

d

+

+

�

�

a

l

a

�

�

�

1

(

)

1

1

fL

fR

fL

fR

n

i

i

L

i

R

T

T

q

k T

T

=

-

=

=

-

�

�

d

+

+

�

�

a

l

a

�

�

�

ostatecznie gęstość strumienia ciepła wyznaczyć można ze wzoru

znając gęstość strumienia ciepła, temperatury na stykach
(jeśli są potrzebne) wyznacza się kolejno

1

L

fL

L

T

q

T

=

+

a

1

1,2

1

L

T

q

T

d

=

+

l

2

2,3

1,2

2

T

q

T

d

=

+

l

itd

ponieważ temperatury w warstwach zmieniają się liniowo, wystarcza
to do jednoznacznego wyznaczenia pełnego pola temperatury w przegrodzie

opór cieplny

opór cieplny

Transport ciepła i masy

©Ryszard A.
Białecki

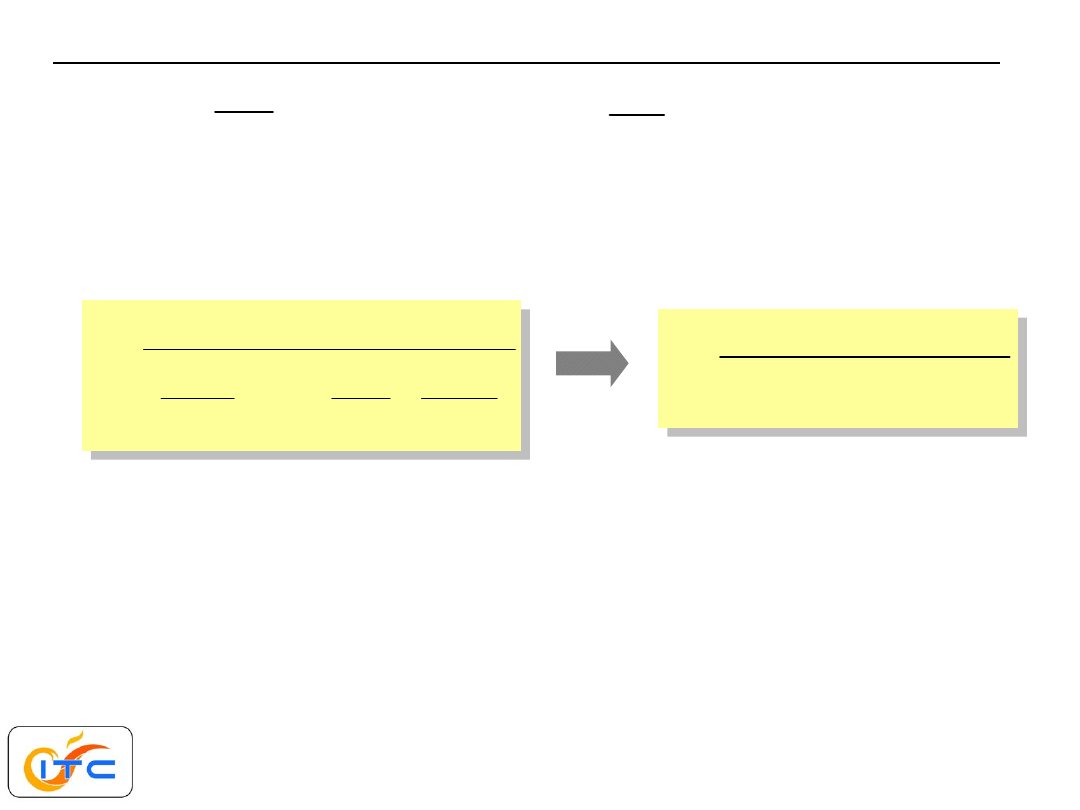
pojęcie oporu cieplnego

U

i

R

D

=

analogia między ustalonym przepływem prądu stałego

a ustalonym, jednowymiarowym przewodzeniem ciepła.

i

natężenie prądu



U

różnica potencjałów

R

opór elektryczny

Q

T

Q

R

D

=

Q

strumień ciepła



T

różnica temperatur

R

Q

opór cieplny

opór cieplny

opór cieplny

Transport ciepła i masy

©Ryszard A.
Białecki

1

1

1

fL

fR

n

i

i

L

L

i i

R R

T

T

Q

A

A

A

=

-

=

�

�

d

+

+

�

�

a

l

a

�

�

�

1

1

1

fL

fR

n

i

i

L

L

i i

R R

T

T

Q

A

A

A

=

-

=

�

�

d

+

+

�

�

a

l

a

�

�

�

1

fL

fR

n

L

i

R

i

T

T

Q

R

R

R

a

l

a

=

-

=

�

�

+

+

�

�

�

1

fL

fR

n

L

i

R

i

T

T

Q

R

R

R

a

l

a

=

-

=

�

�

+

+

�

�

�

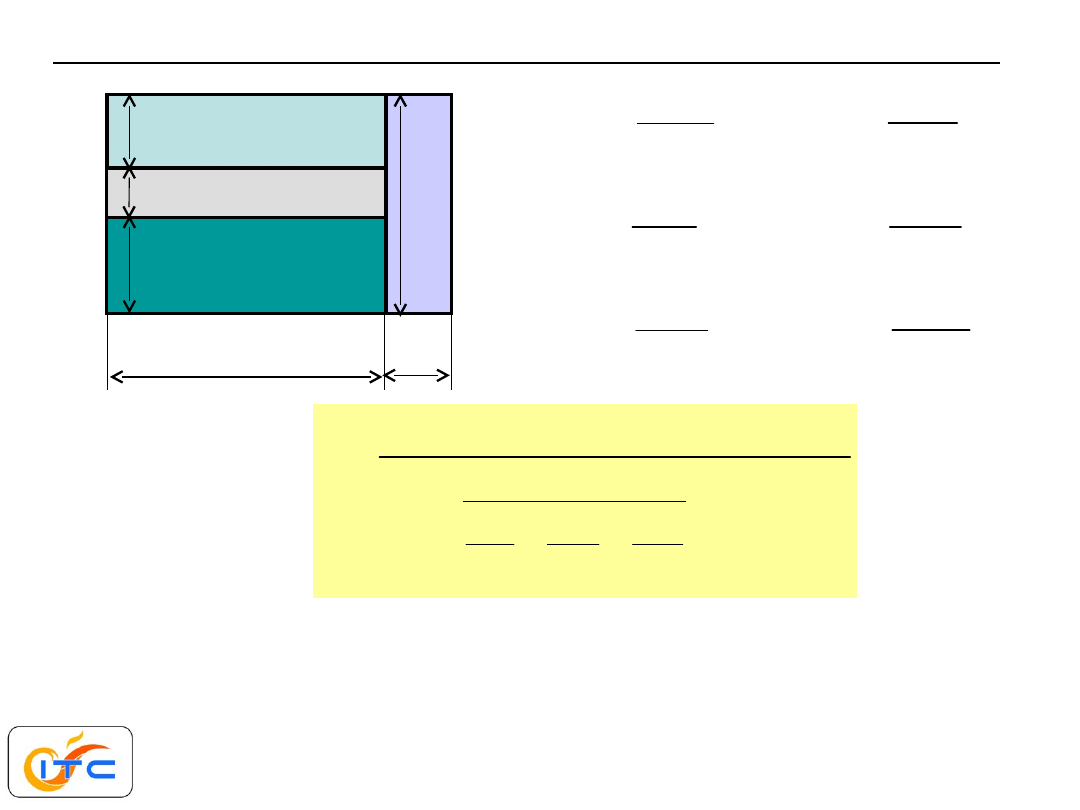
1

R

A

a

=

a

opór wnikania

R

A

l

d

=

l

opór przewodzenia

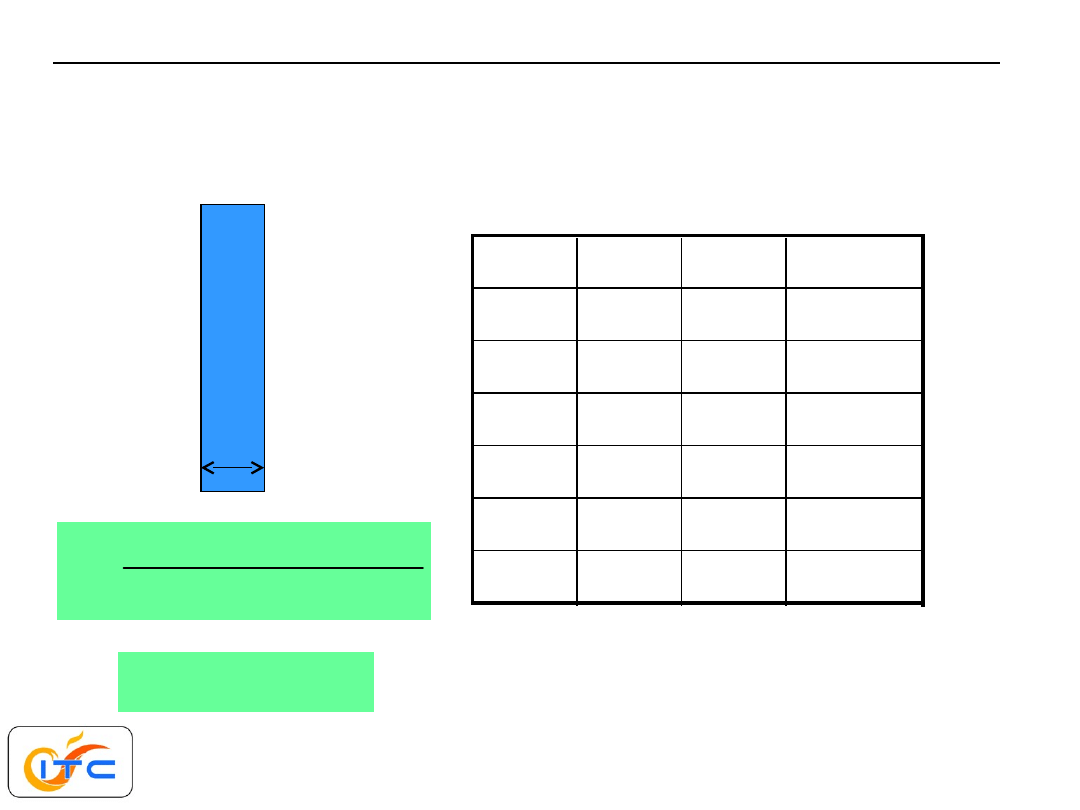
tak zdefiniowane opory cieplne można łączyć tylko szeregowo

jednakże dla pól zbliżonych do jednowymiarowych,
łączenie równoległe i szeregowe oporów jest
dopuszczalne, gdyż prowadzi do niewielkich błędów

opór cieplny

opór cieplny

Transport ciepła i masy

©Ryszard A.
Białecki

L

a

R

a

fL

T

a

d

b

d

R

a

fR

T

1

A

2

A

3

A

1

l

2

l

3

l

4

l

4

A

4

1

1 1

2

2 2

1

L

L

a

a

R

A

R

A

R

A

a

l

l

=

a

d

=

l

d

=

l

3

3 3

4

4 4

4

1

a

b

R

R

R

A

R

A

R

A

l

l

a

d

=

l

d

=

l

=

a

4

1

2

3

1

1

1

1

fL

fR

L

R

T

T

Q

R

R

R

R

R

R

a

l

a

l

l

l

-

=

+

+

+

+

+

współczynniki przewodzenia ciepła powinny być do
siebie zbliżone. W przeciwnym wypadku, założenie
o jednowymiarowości pola temperatury jest
obarczone dużym błędem

opór cieplny

opór cieplny

Transport ciepła i masy

©Ryszard A.
Białecki

opór cieplny

opór cieplny

1

1

,T

a

2

2

,T

a

l

d

1

2

1

1/

/

1/

k

a

d l

a

=

+

+

1

2

(

)

q k T T

=

-

19.5
4

3909

200

0.00
5

30

20

1000

1

a

2

a

l

d

1

2

T T

-

k

q

19.7
4

3947

200

30

20

2000

0.00
5

1000

40

30
0.00
5

200

38.2
2

7643

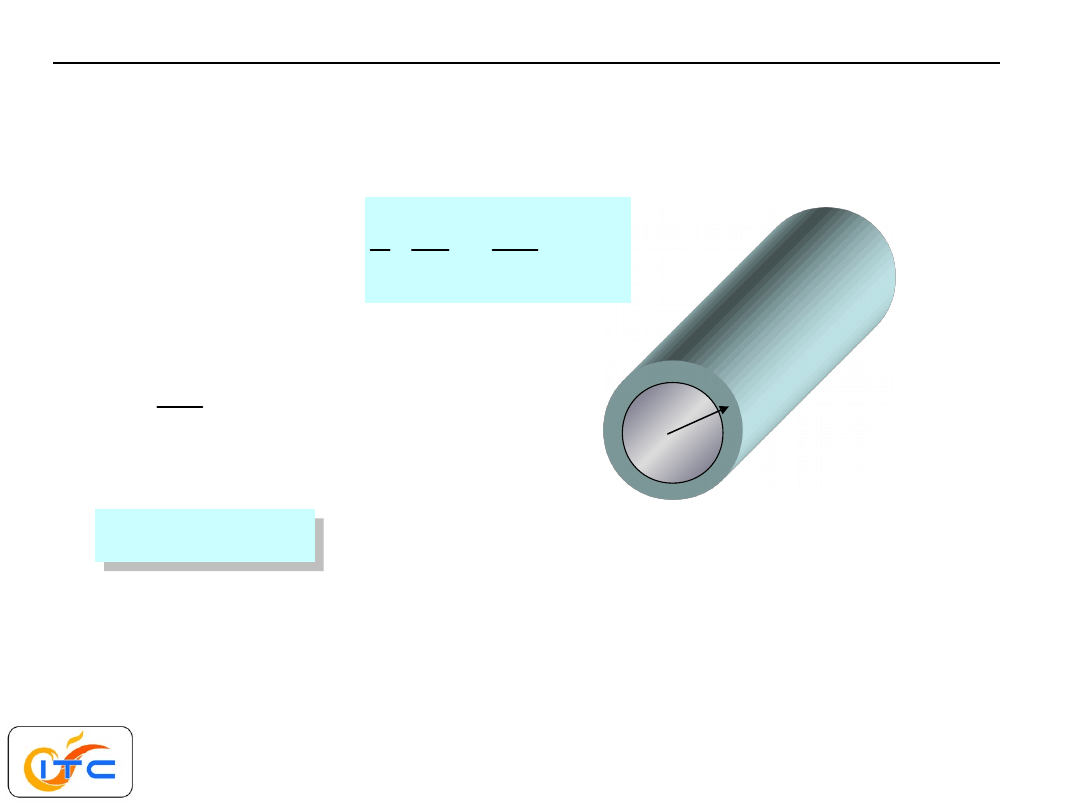
Intensyfikacja wymiany ciepła przy przenikaniu przez
przegrodę

należy zwiększać mniejszy
współczynnik
wnikania ciepła (zmniejszać
większy opór
cieplny)

Transport ciepła i masy

©Ryszard A.
Białecki

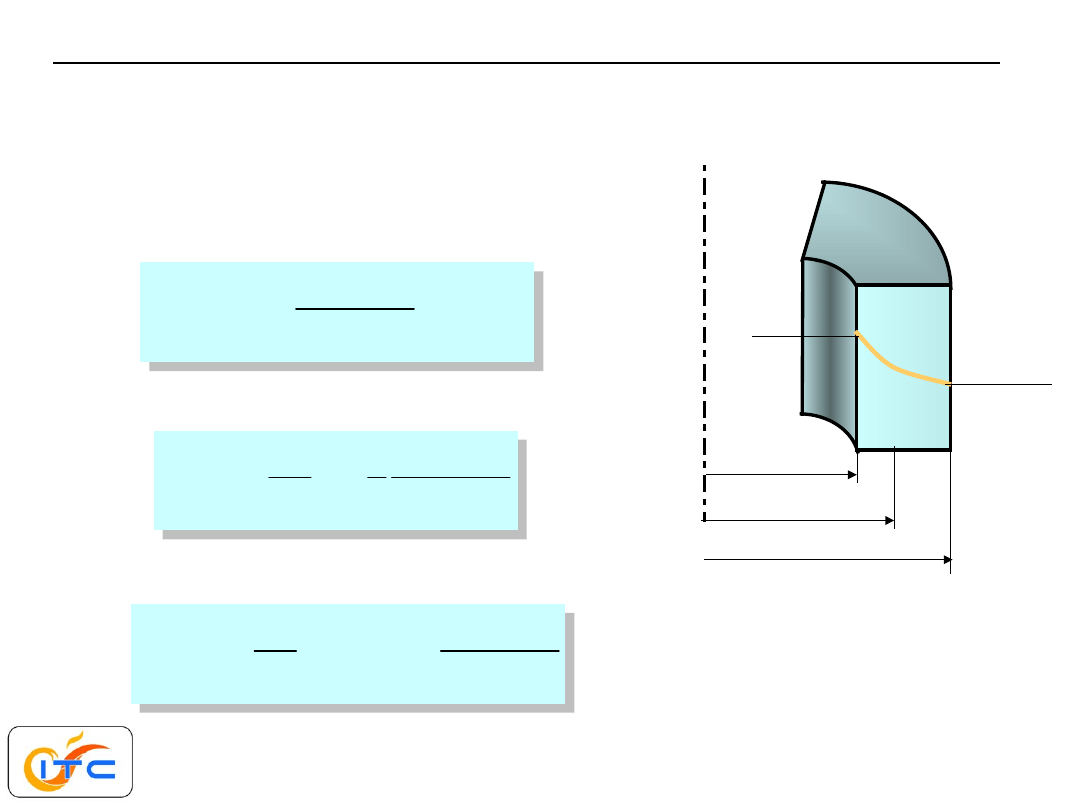
przewodzenie ciepła w układzie cylindrycznym.

Powłoka walcowa, pole bezźródłowe, jednowymiarowe.

Stały współczynnik przewodzenia ciepła

1

0

d

dT

r

r dr

dr

�

�

�

�=

�

�

�

�

�

�

�

�

r

1

dT

r

C

dr

=

jednokrotne całkowanie daje

powtórne całkowanie

1

2

ln

T C

r C

=

+

1

2

ln

T C

r C

=

+

stałe wyznacza się z warunków brzegowych na wewnętrznej
i zewnętrznej powierzchni powłoki.

cylinder

cylinder

Transport ciepła i masy

©Ryszard A.
Białecki

zadane temperatury na obu powierzchniach

( )
( )

w

w

z

z

T r

T

T r

T

=

=

w

T

z

T

w

r

r

z

r

ln( / )

( )

(

)

ln( / )

w

w

z

w

z

w

r r

T r T

T T

r r

= +

-

ln( / )

( )

(

)

ln( / )

w

w

z

w

z

w

r r

T r T

T T

r r

= +

-

rozwiązanie

gęstość strumienia ciepła zależy od promienia

krzywoliniowy przebieg temperatury!

1

( )

ln( / )

z

w

z

w

T T

dT

q r

dr

r

r r

-

=l

=l

1

( )

ln( / )

z

w

z

w

T T

dT

q r

dr

r

r r

-

=l

=l

( )

2

2

ln( / )

z

w

l

z

w

T T

dT

q r

r

dr

r r

-

=l

p = pl

( )

2

2

ln( / )

z

w

l

z

w

T T

dT

q r

r

dr

r r

-

=l

p = pl

strumień jednostkowy

odniesiony do jednostki

długości walca [W/m]

strumień jednostkowy jest stały (nie zależy od promienia)

cylinder

cylinder

Transport ciepła i masy

©Ryszard A.
Białecki

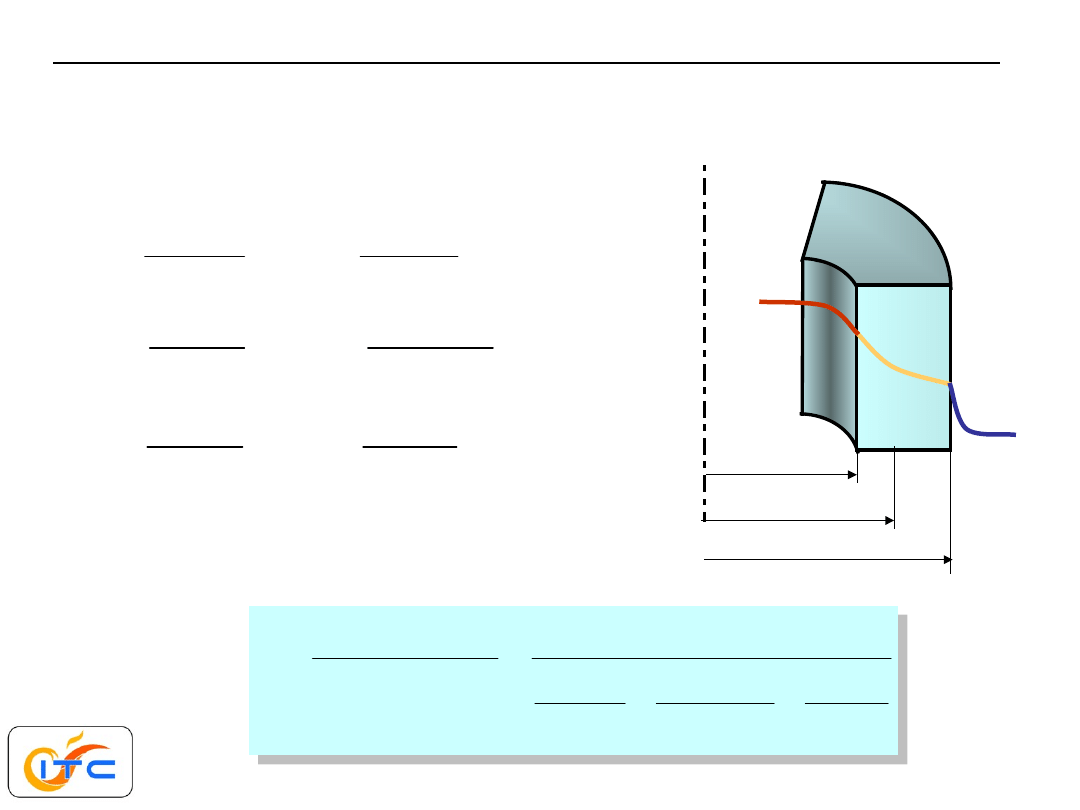
konwekcyjna wymiana ciepła na obu powierzchniach

2

(

)

l

w w

fw

w

q

r

T

T

= p a

-

1

;

2

fw

w

w

l

l

w

l

w w

T

T

q

R

R

r

a

a

-

=

=

p a

rozwiązanie metodą oporu cieplnego

fw

T

fz

T

w

r

r

z

r

2

(

)

lz

z

z

z

fz

q

r

T T

= p a

-

ln( / )

;

2

w

z

z

w

l

l

l

T

T

r r

q

R

R

l

l

-

=

=

pl

1

;

2

z

fz

z

l

l

z

l

z

z

T T

q

R

R

r

a

a

-

=

=

p a

eliminując pośrednie temperatury

ln( / )

1

1

2

fw

fz

fw

fz

l

w

z

z

w

l

l

l

w w

z z

T

T

T

T

q

r r

R

R

R

d

d

a

l

a

-

-

=

=

+

+

+

+

p a

pl

p a

ln( / )

1

1

2

fw

fz

fw

fz

l

w

z

z

w

l

l

l

w w

z z

T

T

T

T

q

r r

R

R

R

d

d

a

l

a

-

-

=

=

+

+

+

+

p a

pl

p a

cylinder

cylinder

Transport ciepła i masy

©Ryszard A.
Białecki

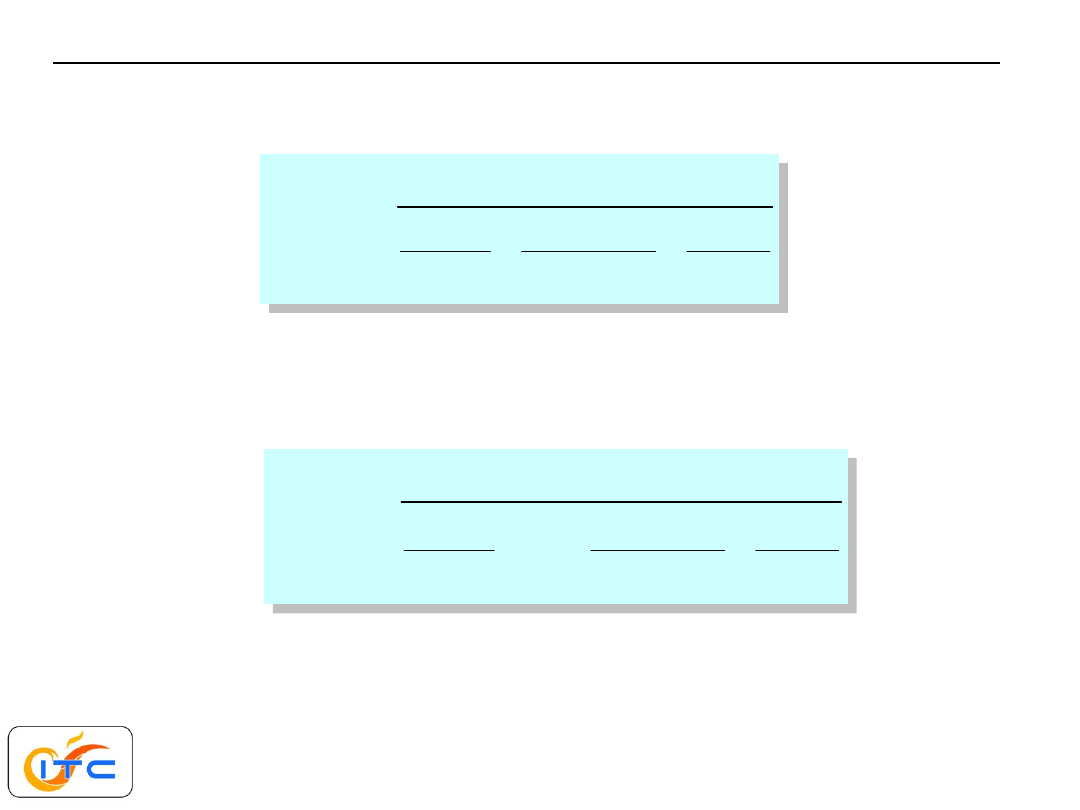
strumień ciepła z rury o długości

L

(

)

ln( / )

1

1

2

fw

fz

l

z

w

w w

z z

T

T L

Q qL

d d

d

d

-

=

=

+

+

p a

pl

p a

(

)

ln( / )

1

1

2

fw

fz

l

z

w

w w

z z

T

T L

Q qL

d d

d

d

-

=

=

+

+

p a

pl

p a

1

(

)

ln( / )

1

1

2

fw

fz

l

i

i

n

z

w

i

i

w w

z z

T

T L

Q qL

d d

d

d

=

-

=

=

+

+

p a

pl

p a

�

1

(

)

ln( / )

1

1

2

fw

fz

l

i

i

n

z

w

i

i

w w

z z

T

T L

Q qL

d d

d

d

=

-

=

=

+

+

p a

pl

p a

�

wielowarstwowa przegroda cylindryczna

,

i

i

w

z

d d

wewnętrzna i zewnętrzna średnica i-tej warstwy

,

w

z

d d

wewnętrzna i zewnętrzna średnica przegrody

cylinder

cylinder