MIKROEKONOMIA 1

Teoria wyboru producenta

Długi okres vs. Krótki okres

Analiza

długookresowa (ang. long-run production analysis)

dotyczy okresu, w

którym mogą się zmieniać wszystkie

nakłady (wszystkie czynniki produkcji są zmienne,
przedsiębiorstwo może inwestować i zmieniać stosowaną
technikę produkcji).

Analiza

krótkookresowa (ang. short-run production

analysis)

– zakłada się w niej, ze niektóre warunki działania

firmy (np. technologia)

są niezmienne. Konsekwencją jest

występowanie stałych i zmiennych czynników produkcji.

Korzyści skali

Efekty skali (ang. economies of scale)

pokazują, w jakim

tempie zmienia

się wielkość produkcji, gdy ilości wszystkich

wykorzystywanych

czynników zmieniają się w tej samej

proporcji. Efekty skali

dotyczą długiego okresu.

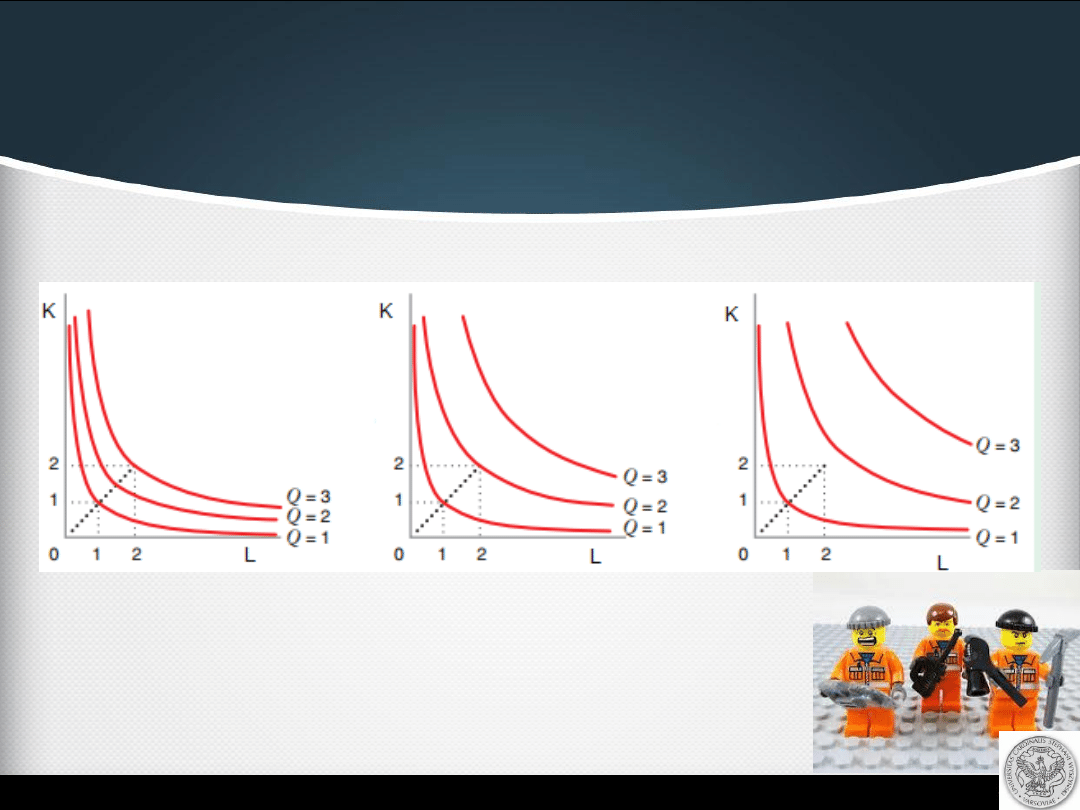
Korzyści skali

Korzyści skali

Rosnące korzyści skali (ang. increasing returns to scale)
występują, gdy a-krotnemu (a>1) zwiększeniu ilości
zastosowanych

czynników wytwórczych towarzyszy ponad

a-krotne

zwiększenie produkcji.

)

,

(

*

)

,

(

K

L

f

a

aK

aL

f



Korzyści skali

Stałe korzyści skali (ang. constans returns to scale)
występują, gdy a-krotnemu (a>1) zwiększeniu ilości
zastosowanych

czynników wytwórczych towarzyszy a-

krotne

zwiększenie produkcji.

)

,

(

*

)

,

(

K

L

f

a

aK

aL

f



Korzyści skali

Malejące korzyści skali (ang. decreasing returns to scale)
występują, jeśli a-krotnemu (a>1) zwiększeniu ilości
zastosowanych

czynników wytwórczych towarzyszy mniej

niż a-krotny przyrost produkcji.

)

,

(

*

)

,

(

K

L

f

a

aK

aL

f



Funkcja produkcji w krótkim

okresie czasu

Założenia analizy funkcji produkcji w krótkim okresie czasu:
- istnieje tylko jeden czynnik zmienny;

- istnieje tylko jeden czynnik

stały;

- technologia produkcji jest dana;

- czynniki produkcji

mogą łączyć się ze sobą w różnych

proporcjach;

- produkt jest jednorodny.

Analiza funkcji produkcji

Produkcyjność przeciętna czynnika produkcji (ang. average
product)

jest

to

średnia produkcyjność jednostki

zatrudnionego czynnika produkcji.

Produkcyjność krańcowa czynnika produkcji (ang. marginal
product)

określa

przyrost

wielkości

produkcji,

odpowiadający zatrudnieniu dodatkowej jednostki czynnika
zmiennego.

L

Q

AP

L



L

Q

MP

L







Analiza funkcji produkcji

Tabela przedstawia dane

dotyczące rocznej produkcji telewizorów w przedsiębiorstwie X. Ustal

przeciętny produkt pracy oraz marginalny produkt pracy dla ilości pracowników dla wielkości produkcji
z

poniższej tabeli (w tys. szt.) . Narysuj krzywe produktu całkowitego, przeciętnego oraz marginalnego.

Liczba

pracowników

Produkcja całkowita

Produkt przeciętny

Produkt marginalny

0

0

-

-

1

10

10

10

2

24

12

14

3

39

13

15

4

52

13

13

5

60

12

8

6

66

11

6

7

63

9

-3

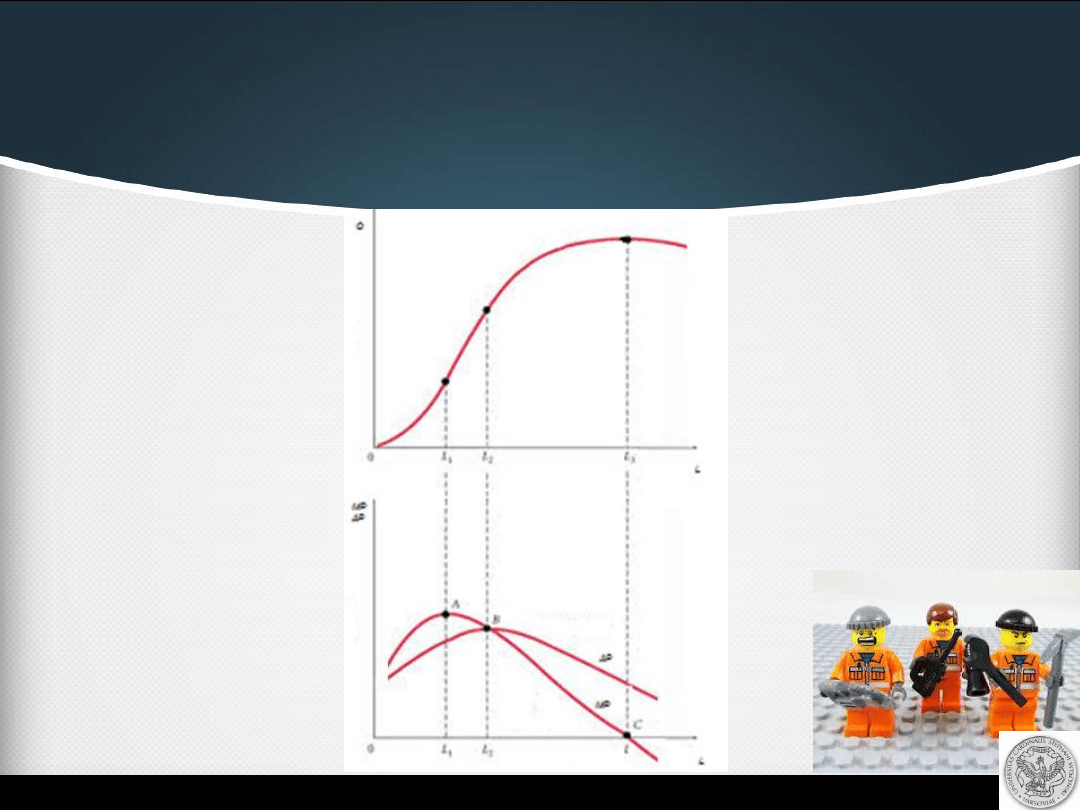
Analiza funkcji produkcji

Etapy produkcji

Etap I:

nakład czynnika zmiennego rośnie od zera do takiej

wielkości, dla której produkt przeciętny jest maksymalny. W
etapie I produkt

przeciętny rośnie.

Etap II:

przedział nakładu czynnika zmiennego, w ramach

którego produkt przeciętny spada. Produkt marginalny
również spada, ale pozostaje ciągle dodatni.

Etap III: produkt

przeciętny ciągle spada.

Produkt marginalny przybiera

wartości ujemne.

Produkt

całkowity spada.

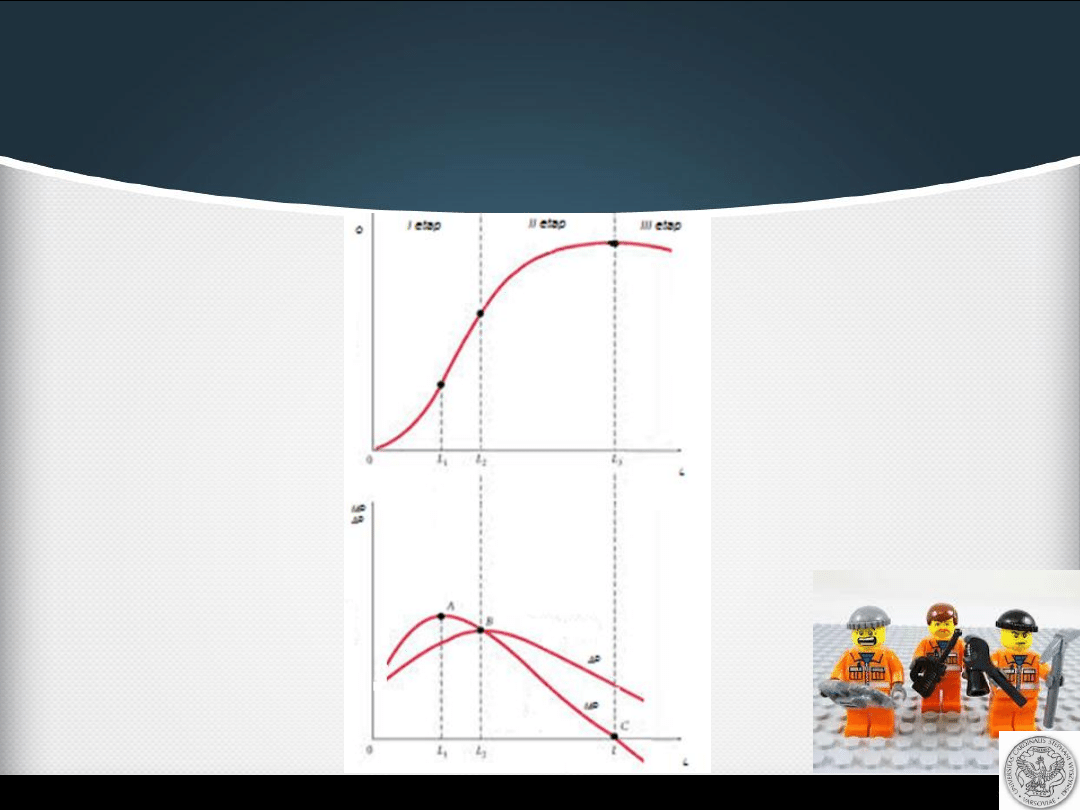
Etapy produkcji

Prawo malejących przychodów

Prawo

malejących przychodów (ang. law of diminishing

return/marginal productivity) dotyczy sytuacji w

której

zwiększając nakłady jednego czynnika o kolejne jednostki i
utrzymując nakłady pozostałych czynników bez zmian,
osiągamy punkt, począwszy od którego dalsze zwiększanie
ilości tego czynnika powoduje mniejsze przyrosty produkcji
(zmniejszanie

krańcowych przyrostów całkowitej produkcji).

3-etapy produkcji -

przykład

Firma wytwarza produkt w

krótkim okresie według

następujące funkcji produkcji: Q(L, K) = -4L

3

+ 240L

2

+ 2700L.

Określ

rozmiary

zatrudnienia

czynnika

pracy

w

poszczególnych etapach produkcji tej firmy. Określ, dla jakich
nakładów pracy (L) produkcja będzie maksymalna oraz
wyznacz

wielkość produkcji przy takim zaangażowaniu

czynnika zmiennego. Ustal

wielkość nakładu pracy, przy

którym zaczyna działać prawo malejących przychodów.
Sytuację zilustruj graficznie.

3-etapy produkcji -

przykład

Funkcja produkcji ma

postać: Q(L,K) = 20KL - K

2

- L

2

.

Określ

rozmiary zatrudnienia czynnika pracy w

poszczególnych

etapach produkcji tej firmy,

jeśli zasób kapitału wynosi K = 4.