MIKROEKONOMIA 1

Teoria wyboru producenta

Koszty produkcji

Podział kosztów w zależności od wielkości produkcji w
krótkim okresie:
- koszty

stałe;

- koszty zmienne.

Koszt

całkowity (ang. total cost) oznacza sumę wydatków

pieniężnych na czynniki wytwórcze zatrudnione w celu
uzyskania

określonej produkcji.

Koszty stałe

Koszty

stałe (ang. fixed costs) obejmują koszty niezależne

od zmian

wielkości produkcji, powstające w pewnych

granicach na jednakowym poziomie.

Koszty zmienne

Koszty zmienne (ang. variable costs)

obejmują koszty,

które reagują na zmianę w rozmiarach produkcji.

Funkcja kosztów produkcji

Funkcja

kosztów (ang. cost curve) jest relacją między

kosztami produkcji i

odpowiednią wielkością produkcji.

Przy

założeniu, że produkcja odbywa się w ramach danej technologii i dotyczy

jednego i tego samego produktu oraz producent nabywa czynniki produkcji po
cenach

obowiązujących.

)

(Q

f

TC



Funkcja kosztów produkcji

Koszt

przeciętny (ang. average cost) średni koszt

wytworzenia jednostki produktu.

Koszt

krańcowy (ang. marginal cost) przyrost kosztów

przypadający na jednostkowy przyrost produkcji.

Q

TC

ATC



Q

TC

MC







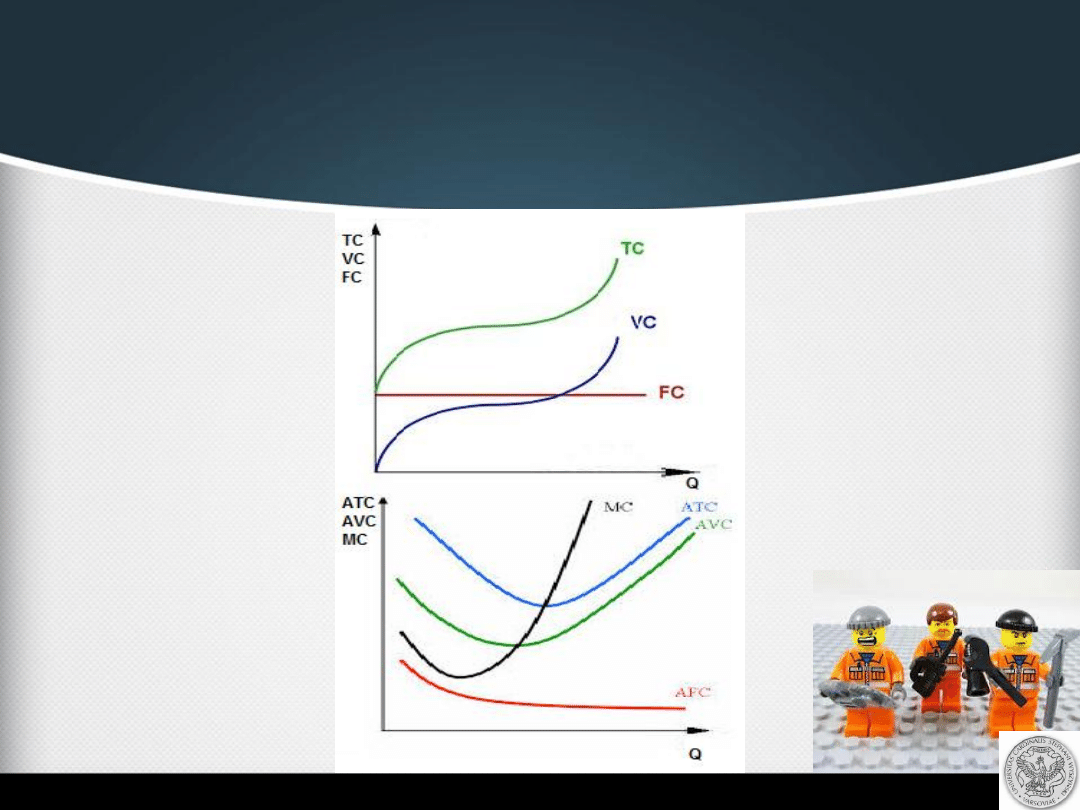
Analiza krótkookresowa

kosztów

Tabela przedstawia dane

dotyczące kosztów produkcji w przedsiębiorstwie X. Ustal wysokość kosztów

całkowitych (TC), kosztu stałego przeciętnego (AFC), kosztu zmiennego przeciętnego (AVC), kosztu
całkowitego przeciętnego (ATC) oraz kosztu marginalnego (MC). Wyniki przedstaw na 2 rysunkach:
wszystkich

kosztów całkowitych oraz wszystkich kosztów przeciętnych wraz z marginalnym.

Wielkość
produkcji

Koszt stały

całkowity

Koszt

zmienny

całkowity

Koszt

całkowity

Koszt stały

przeciętny

Koszt

zmienny

przeciętny

Koszt

całkowity

przeciętny

Koszt

marginalny

0

10

0

10

-

-

-

-

1

10

11

21

10,0

11,0

21,0

11

2

10

18

28

5,0

9,0

14,0

7

3

10

22

32

3,3

7,3

10,7

4

4

10

24

34

2,5

6,0

8,5

2

5

10

25

35

2,0

5,0

7,0

1

6

10

26

36

1,7

4,3

6,0

1

7

10

28

38

1,4

4,0

5,4

2

8

10

32

42

1,3

4,0

5,3

4

9

10

39

49

1,1

4,3

5,4

7

10

10

50

60

1,0

5,0

6,0

11

Analiza krótkookresowa

kosztów

Funkcje kosztów - przykład

Funkcja produkcji jest dana wzorem Q(L,K) = 2L

1/2

K

1/2

.

Wiedząc, że K jest stałe i wynosi 169 jednostek, cena
pracy (w) wynosi 2, a cena

kapitału (r) równa się 4,

wyznacz funkcje TC, ATC, AVC oraz MC.

Koszty vs. Prawo malejących

przychodów

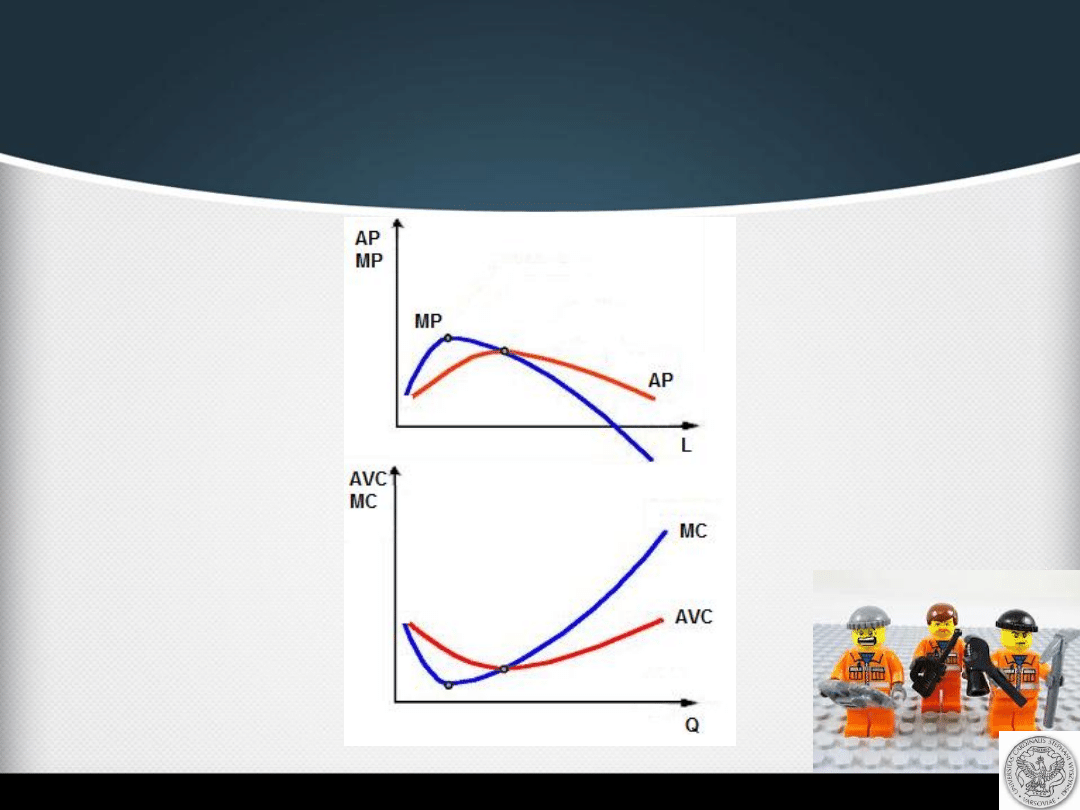
Zależność AVC od AP

Produkt

przeciętny

czynnika

zmiennego

(pracy)

początkowo rośnie a później spada. Dlatego właśnie koszt
zmienny

przeciętny najpierw spada a następnie rośnie,

przy danej cenie czynnika pracy (w).

L

AP

w

AVC



Zależność MC od MP

Przy danej cenie czynnika pracy (w)

rosnącemu produktowi

marginalnemu odpowiada

spadający koszt marginalny. W

punkcie

przegięcia na krzywej produktu całkowitego MP

zaczyna

spadać, MC zaczyna rosnąć.

L

MP

w

MC



Zależności - przykład

Przedsiębiorstwo wytwarza produkt według następującej
funkcji produkcji Q(L) = -3L

3

+ 90L

2

+100L . Wyznacz

minimalną wartość kosztu krańcowego, wiedząc, że cena
pracy wynosi 2000 j.p.

Zależności – przykład 2

Koszt marginalny pewnego

przedsiębiorstwa kształtuje się

zgodnie z

funkcją MC(Q) = 6Q

2

-36Q + 500.

Wiedząc, że

cena pracy i cena

kapitału wynoszą 5 j.p., podaj ilość

czynnika pracy, od

której zaczyna działać prawo

malejących przychodów.

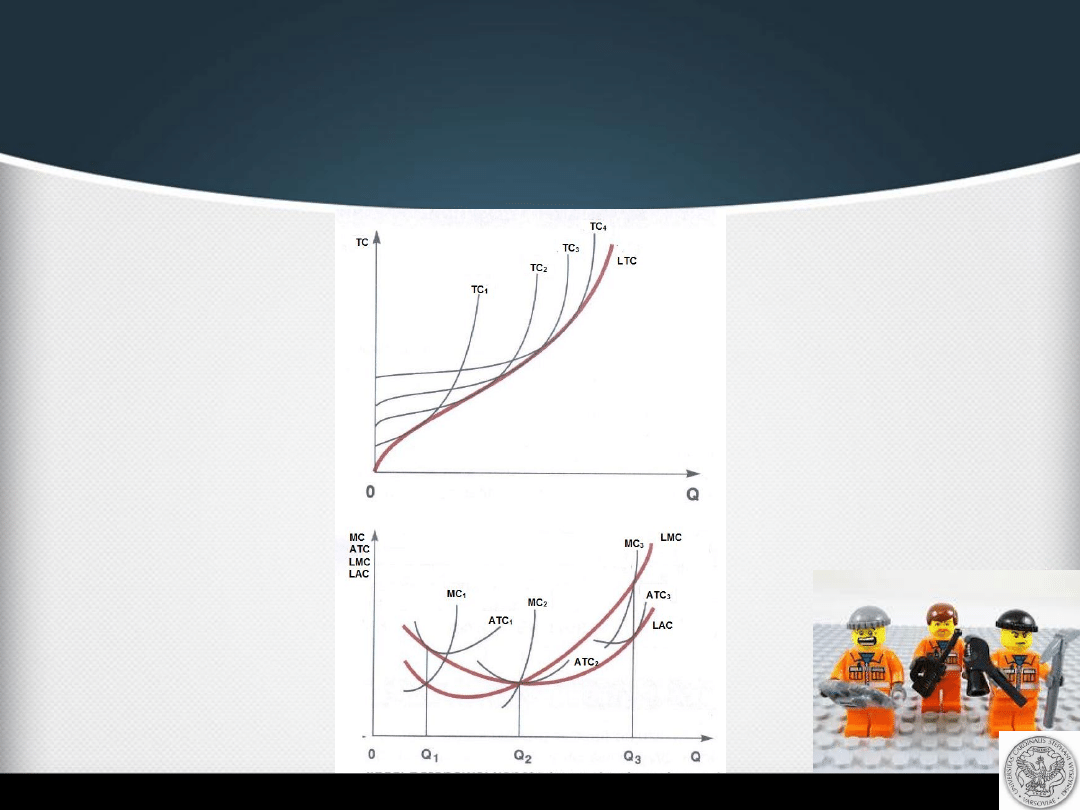
Analiza długookresowa kosztów

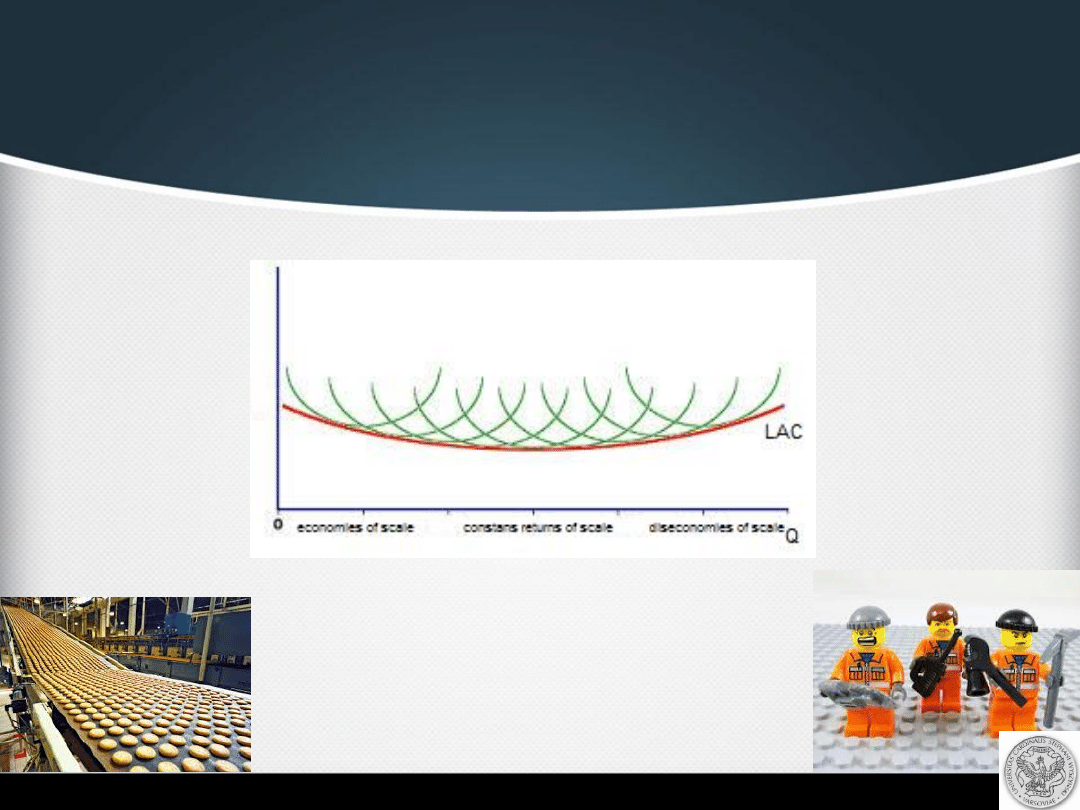
Koszty vs. Korzyści skali

Koszty vs. Korzyści skali

-

przykład

Przedsiębiorstwo produkuje zgodnie z funkcją kosztów
całkowitych: TC(Q) = Q

3

- 8Q

2

+ 60Q.

Określ, dla jakiej

wielkości produkcji występują malejące korzyści skali.

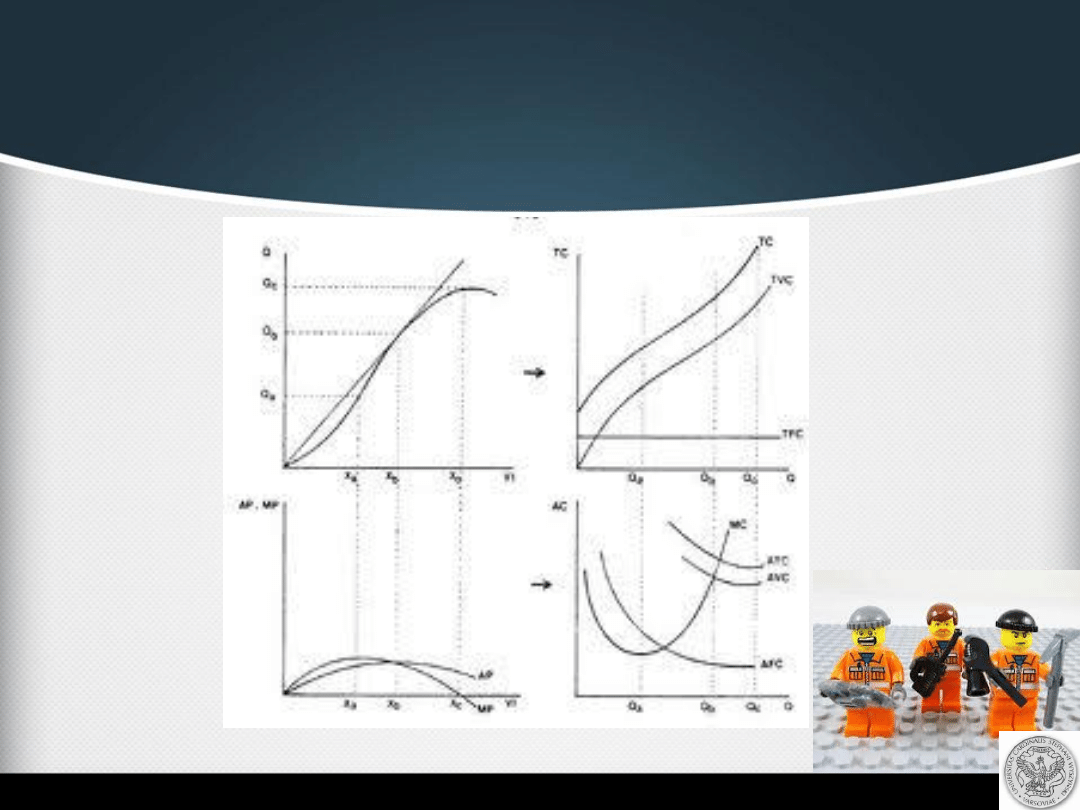
Podsumowanie

Koszty -

przykład

W pewnym

przedsiębiorstwie produkcyjnym funkcja

kosztów marginalnych opisana jest następującą formułą:
MC(Q) = 6Q

2

- 32Q + 50.

Główny ekonomista

przedsiębiorstwa ustalił, że przeciętny koszt stały (AFC) dla
produkcji 25 szt. wynosi 4.

Znajdź optymalną wielkość

produkcji

z

punktu

widzenia

minimalizacji

kosztu

przeciętnego całkowitego.