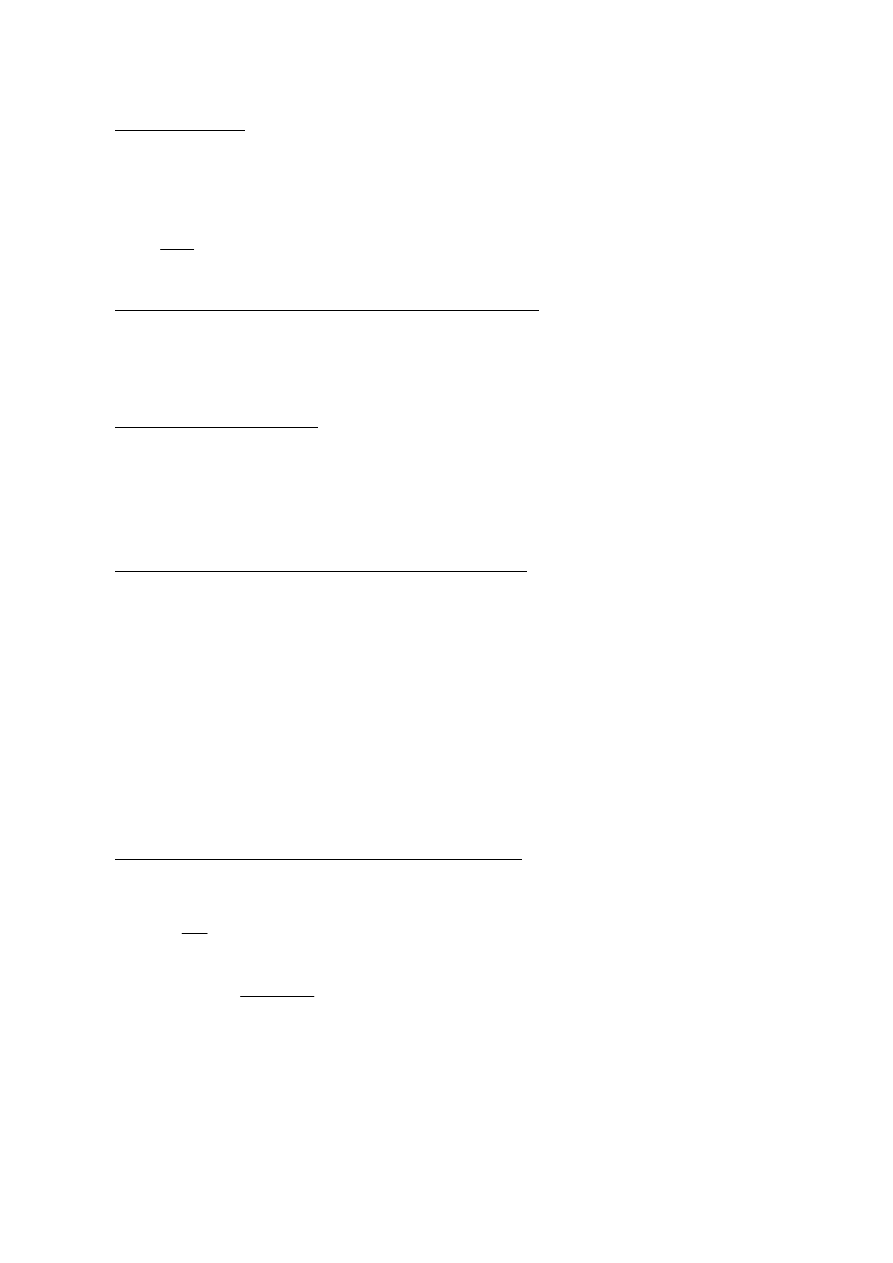
ξ

eff.lim

0.50

=

ξ

eff.lim

0.8

ε

cu

ε

cu

ε

yd

−













⋅

=

ε

yd

fyd

Es

−

=

ε

cu

0.0035

=

Graniczna wartość względnej wysokości strefy ściskanej

Es

200GPa

=

fyd

420MPa

=

STAL PRĘTÓW ZBROJENIA GŁÓWNEGO KLASY A-IIIN O ZNAKU RB 500W

Ecm

31GPa

=

fctm

2.6MPa

=

fck

25MPa

=

fcd

16.70MPa

=

BETON KLASY C20/25

Przyjęto następujące dane materiałowe do wymiarowania

l0

11.610 m

=

długość obliczeniowa słupa

l0

β

lcol

⋅

=

współczynnik wznaczony na podstawie Tablica C.1

β

1.8

=

Długość obliczeniowa słupa

odległość między punktami podparcia

lcol

6.45m

=

h

0.5m

=

b

0.6m

=

Przyjęto następujące dane geometryczne do wymiarowania

ee

0.207 m

=

ee

Msd

Nsd

=

Nsd

156.33kN

=

Msd

32.38kNm

=

Siły wymiarujące:

2.2.1.2 Wymiarowanie słupa żelbetowego estakady po kierunku podłużnym

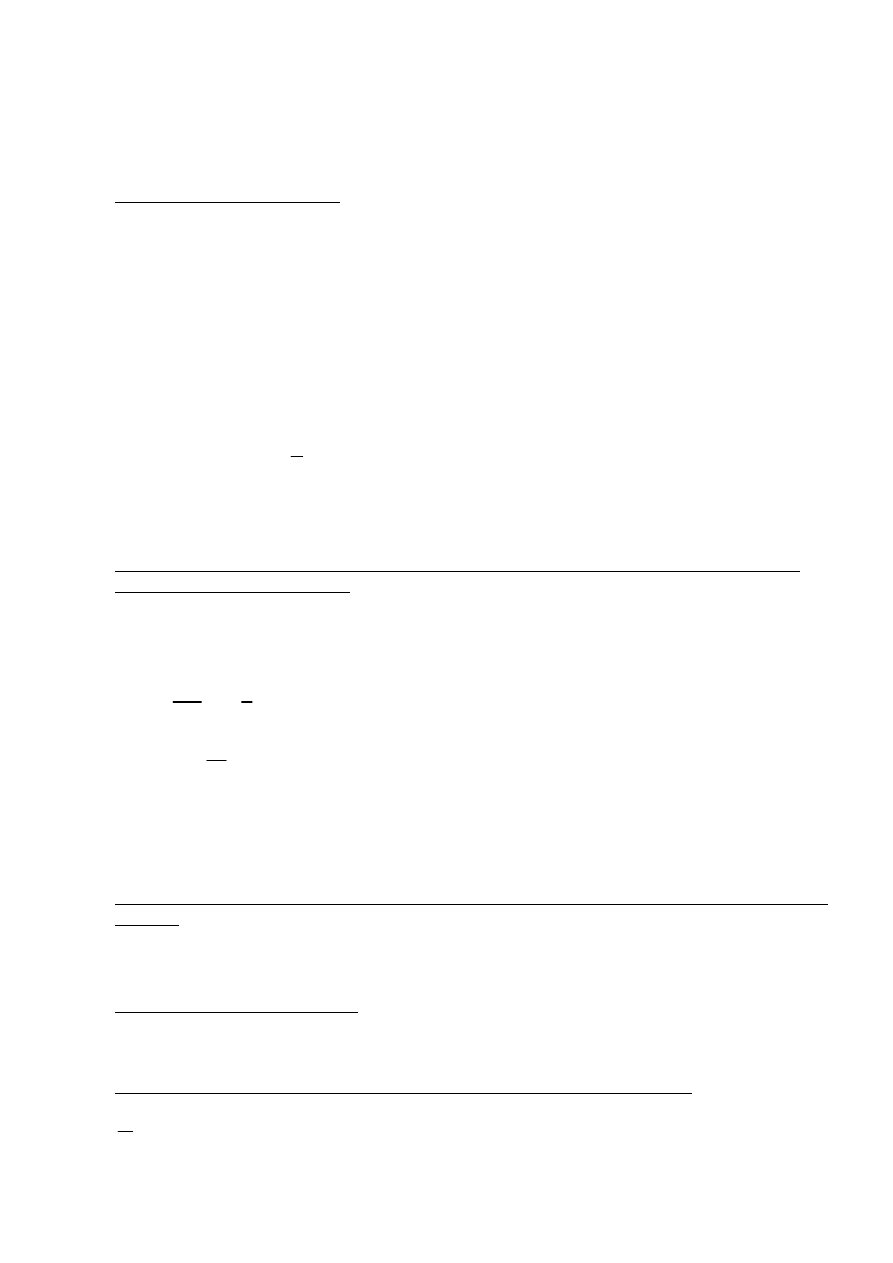
użyteczna wysokość przekroju

Wyznaczenie mimośrodu początkowego oraz sprawdzenie wpływu smukłości słupa i obciążeń
długotrwałych na wymiarowanie

Wyznaczenie wartości niezamierzonego mimośrodu początkowego

n

1

=

ilość kondygnacji licząc od góry

ea

lcol
600

1

1

n

+













h

30

20mm





























=

ea

21.50000

16.66667

20.00000

















mm

=

ea.max

max ea

( )

=

ea.max

21.500 mm

=

Wyznaczenie wartości mimośrodu konstrukcyjnego dla czterech założonych wcześniej schematów
obciążeń

ee

0.207 m

=

Całkowity mimośród początkowy

e0

ee ea.max

+

=

e0

0.229 m

=

Sprawdzenie wpływu smukłości i obciążeń długotrwałych na nośność elementu:

l0

h

23.220

=

>

7.0

Należy więc uwzględnić wpływ smukłosci i obciążeń długotrwałych

STAL PRĘTÓW ZBROJENIA POPRZECZNEGO KLASY A-0 O ZNAKU St0S-b

fyds

190MPa

=

Es

200GPa

=

Wyznaczenie grubości otulenia

Przyjęto pręty o średnicach:

φ

20mm

=

pręty zbrojenia głównego

φ

s

8mm

=

pręty zbrojenia poprzecznego

Przyjęto klasę ekspozycji XC4 dla stali zwykłej

cmin

25mm

=

∆

c

5mm

=

dla elementów prefabrykowanych

Odległość środka ciężkości zbrojenia od krawędzi rozciąganej (ściskanej) jest równa:

a1

cmin

∆

c

+

φ

s

+

φ

2

+

=

a1

48 mm

=

a2

a1

=

a2

48 mm

=

d

h

a1

−

=

d

0.452 m

=

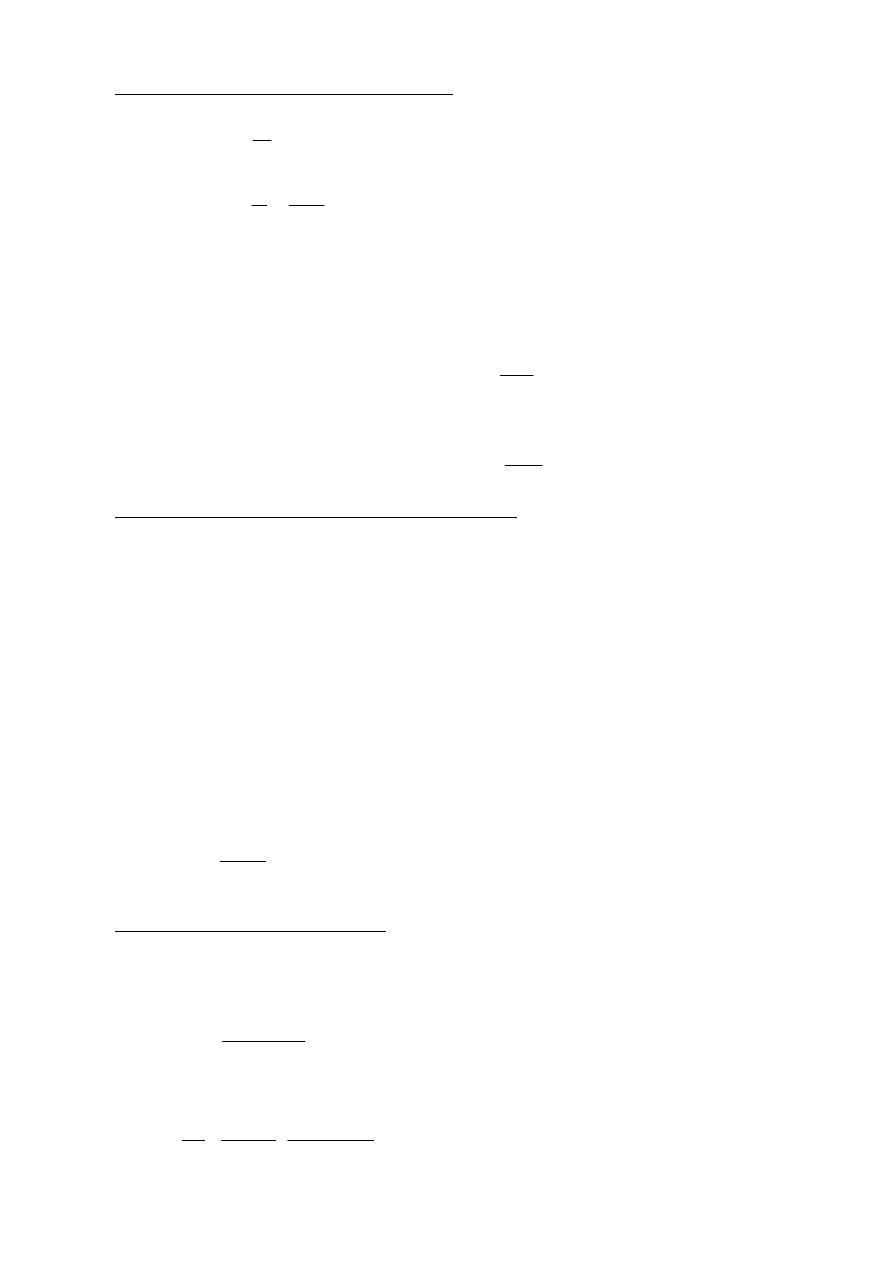
RH

50%

=

- wilgotność względna

φ ∞

t0

,

( )

2.68

=

- wg tabeli A1

Siła podłużna od obciążeń całkowitych:

Nsd.d

Nsd

=

Nsd.d

156.330 kN

=

Siła podłużna wywołana działaniem długotrwałej czści obciążenia obliczeniowego odczytana
z RM-WINa:

Nsd.lt

Nsd

=

Nsd.lt

156.330 kN

=

Wyznaczenie współczynnika wyrażającego wpływ obciążenia długotrwałego, wzór (40):

klt

1

0.5

Nsd.lt
Nsd.d

⋅

φ ∞

t0

,

( )

⋅

+

=

klt

2.340

=

Wyznaczenie wartości siły krytycznej

Zakladam stopień zbrojenia

:

Σρ

0.6%

=

Is

Σρ

b

⋅

d

⋅

h

a1

−

a2

−

2













2

⋅

=

Is

6639.627 cm

4

=

Wartość siły krytycznej

Ncrit

9

l0

2

Ecm Ic

⋅

2 klt

⋅

0.11

0.1

β

max

+

0.1

+













Es Is

⋅

+













⋅

=

Ncrit

1708.723 kN

=

Wyznaczenie wartości współczynnika pełzania

β

s

e0

h

0.5

0.01

l0

h

⋅

−

0.01

MPa

fcd

⋅

−

0.05

































=

β

s

0.457

0.101

0.050

















=

β

max

max

β

s

( )

=

β

max

0.457

=

Pole powierzchni przekroju betonowego

Ac

b h

⋅

=

Ac

3000.000 cm

2

=

Moment bezwładności przekroju betonowego Ic

b h

3

⋅

12

=

Ic

625000.000 cm

4

=

Obwód przekroju betonowego

U

2 b

⋅

2 h

⋅

+

=

U

220.000 cm

=

Miarodajny wymiar przekroju elementu

h0

2 Ac

⋅

U

=

h0

272.727 mm

=

Wartość współczynnika pełzania dla przyjętych danych

t0

28

=

dni - wiek betonu w chwili obciążenia

As1

0.087 cm

2

=

As2

As1

=

As2

0.087 cm

2

=

Minimalne pole przekroju zbrojenia podłużnego w elementach ściskanych nie może byc
mniejsze niż

wzór (25a)

As1.min

0.5 0.15

⋅

Nsd

fyd

⋅

=

As1.min

0.279 cm

2

=

As2.min

As1.min

=

As2.min

0.279 cm

2

=

wzór (25b)

As1.min

0.5 0.003

⋅

Ac

⋅

=

As1.min

4.500 cm

2

=

As2.min

As1.min

=

As2.min

4.500 cm

2

=

Zgodnie z powyższymi obliczeniami przyjęto zbrojenie

liczbapretow

2

=

φ

20 mm

=

Pole zbrojenia wynosi:

As1

6.283 cm

2

=

As2

As1

=

As2

6.283 cm

2

=

η

1

1

Nsd

Ncrit

−

=

η

1.101

=

Wartość mimośrodu całkowitego wymiesie zatem

etot

η

e0

⋅

=

etot

0.252 m

=

Wyznaczenie ilości potrzebnego zbrojenia

xeff.lim

ξ

eff.lim d

⋅

=

xeff.lim

0.226 m

=

α

1.0

=

xeff

Nsd

α

fcd

⋅

b

⋅

=

xeff

0.016 m

=

xeff

0.016 m

=

< xeff.lim

0.226 m

=

DUśY MIMOŚRÓD

xeff

0.016 m

=

<

2 a2

⋅

0.096 m

=

es1

etot 0.5 h

⋅

+

a1

−

=

es1

0.454 m

=

As1

Nsd es1

⋅

fcd xeff

⋅

b

⋅

d

0.5 xeff

⋅

−

(

)

⋅

−

fyd d a2

−

(

)

⋅

=

Stopień zbrojenia wynosi:

Σρ

prov

As1 As2

+

b h

⋅

=

Σρ

prov

0.42 %

=

Σρ

prov

Σρ

−

Σρ

prov

0,38< 10%

OBLICZENIA POPRAWNE. Założony stopień zbrojenia różni się od obliczonego mniej niż o
10%.

Dobrano rozstaw strzemion czterociętych

F

F

F

F8 wzdłuż wysokości słupa: 30 cm. Na końcach słupa

na długości równej większemu wymiarowi słupa strzemiona zagęścić do 1/3 normalnego
rozstawu.