lg 10 m
=
7.3.3 Cały słup
lcol
12.0 m
:=
lo
1.6 lcol
⋅
:=
lo 1.6 12.00
⋅
=
lo 19.2 m
=
7.4 Wymiarowanie cz
ęś
ci podsuwnicowej - pret nr 1
Przekrój słupa.
b
0.5 m
:=
h
0.8 m
:=
Sprawdzenie smukło
ś
ci.
ld
h
16.0
=
ld
h
7
<
16.0 > 7
- nale
ż
y uwzgl
ę
dni
ć
smukło
ść
.
7.4.1 Przekrój dolny słupa
M1,A,w 798.63 kNm
:=
- M
max
V1
129.3
−
kN
:=
N1
1240.0
−
kN
:=
- N
max
Okre
ś
lenie mimo
ś
rodu pocz
ą
tkowego:
•
eo ea ee
+
=
- mimo
ś
ród pocz
ą
tkowy.
7. SŁUP
7.1 Ci
ęż
ar własny słupa.
Gs
1.1 25
⋅
kN
m
3
⋅
0.5
⋅
m 8.80
⋅
m
2
:=
s
7.2 Dobór materiałów.
- Beton C35/45
fcd
25.0 MPa
:=
Ecm
34 GPa
:=
- Stal na zbrojenie główne - A III.
fyd
350MPa
:=
Es
205GPa
:=
- Stal na strzemiona - A I.
fyd
210MPa
:=
Es
205GPa
:=
7.3 Długo
ś
ci wyboczeniowe w płaszczy
ź
nie układu poprzecznego.
7.3.1 Dolny odcinek słupa.
ll
8.0m
:=
ld
1.6 ll
⋅
:=
ld 1.6 8.0
⋅
=
ld 12.8 m
=
7.3.2 Górny odcinek słupa.
lu
4.0 m
:=
lg
2.5 lu
⋅
:=
lg 2.5 4.0
⋅
=
M1,A,z - 729.57 kNm
:=
- M
min
- V
max
G = 121.0 kN

Ι
c
2133333cm
4
=
>
eo
h
0.5
0.01
ld
h
⋅
−
0.01fcd
−
=
0.5
0.01
12.8
0.8
⋅
−
0.01 25.0
⋅
−
=
0.09
=
eo
h
61.24
80
=
0.76
=
>
eo
h
0.05
=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
Φ ∞
t
o
,
( )
- ko
ń
cowy współczynnik pełzania betonu, przy zało
ż
eniu
ż
e ,
ż
e słup b
ę
dzie obci
ąż
ony po
28 dniach w
ś
rodowisku o wilgotno
ś
ci 50%
ho
2Ac
u
:=
- miarodajny wymiar przekroju.
Ac
b h
⋅
:=
Ac 500 800
⋅
=
Ac 400000 mm
2
=
u
2 b
⋅
2 h
⋅
+
:=
u
2 500
⋅
2 800
⋅
+
=
u 2800 mm
=
ho
2 400000
⋅
2800
=
286 mm
=
=>
Φ ∞
t
o
,
( )
2.0
=
ea
max
ll
400
h
30
,
20mm
,
:=
- niezamierzony mimosród przypadkowy.
ea max
800
400
80
30
,
2cm = max (2.0; 2.67; 2.0)
,
=
ea 2 .67 cm
=
ee
M1,A,w
N1
Gs
+
:=
- mimo
ś
ród konstrukcyjny.
ee
798.63
1240.0
−
121.0
+
=
ee 58.57 cm
=
eo
ea ee
+
:=
eo
2.67 + 58.57
=
eo 61.24 cm
=
etot
η
eo
⋅
=
- mimo
ś
ród całkowity.
η
1
1
Nsd
Ncrit
−
=
Nsd
N1
Gs
+
:=
Nsd
1240.0
−
121.0
+
=
Nsd 1361.0 kN
=
Ncrit
9
ld
2
Ecm Ic
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es Is
⋅
+
⋅
=
- siła krytyczna.
Ι
c
b h
3
⋅
12
:=
- moment bezwładno
ś
ci przekroju betonu wzgl
ę
dem jego
ś
rodka ci
ęż
ko
ś
ci.
Ι
c
50 80
3
⋅
12
=
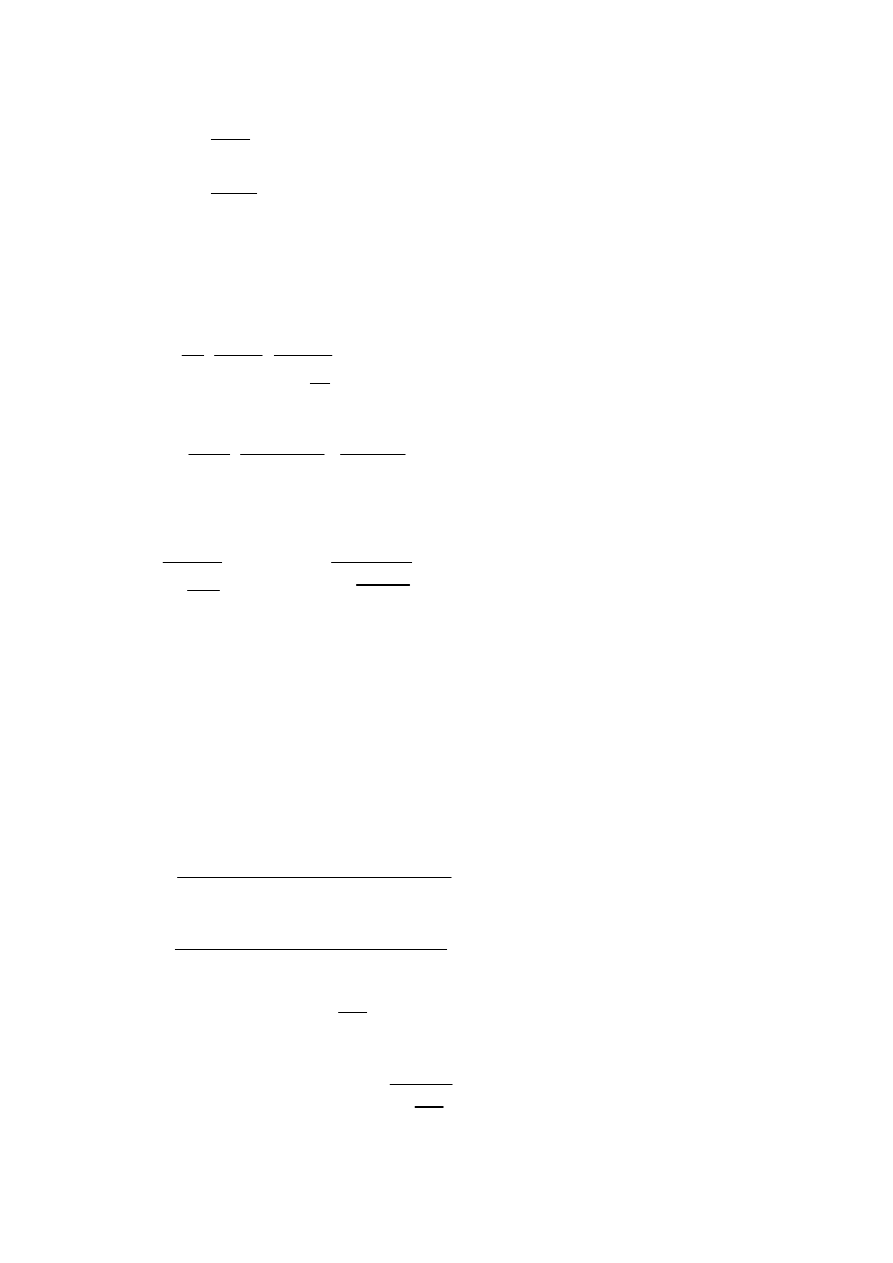
Sprawdzenie mimo
ś
rodu:
es1
etot 0.5 d a1
−
⋅
+
:=
es1 72.9 + 0.5 75 - 5
⋅
=
es1 105.4 cm
=
es1 1.054 m
=
>
d
a1
−
0.75
0.05
−
=
0.70 m
=
- du
ż
y mimo
ś
ród
Zakładam :
ξ
eff
ξ
eff.lim
=
0.53
=
- dla stali A-III
Obliczenie zbrojenia A
s2 :
d
h
a1
−
:=
d
0.75 m
=
As2
Nsd es1
⋅
ξ
eff.lim 1
0.5
ξ
eff.lim
⋅
−
(
)
⋅
d
2
⋅
b
⋅
fcd
⋅
−
d
a1
−
(
)
fyd
⋅
:=
As2
1361.0 110
⋅
0.53 1
0.5 0.53
⋅
−
(
)
⋅
75
2
⋅
50
⋅
2.5
⋅
−
(75 - 5) 35
⋅
=
As2
56.12
−
cm
2
=
As2.min max 0.0020 b
⋅
h
⋅
0.10
NEd
fyd
⋅
,
=
As2.min
max 0.0020 50
⋅
cm 80
⋅
cm 0.10
1240.0kN
35
kN
cm
2
⋅
= max (8.0; 3.54)
,
:=
As2.min 8.0 cm
2
=
Nsd.lt
889,66 kN
Gs
+
:=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
kit 1 0.5
1010.7
1361.0
⋅
2.0
⋅
+
=
kit 1.82
=
Przyj
ę
to:
a1 a2
=
50mm
=
ρ
s
1%
:=
Ι
s
ρ
s b
⋅
h
⋅
0.5 h
⋅
a1
−
(
)
2
⋅
:=
Ι
s
0.01 50
⋅
80 (
⋅
0.5 80
⋅
5)
−
2
⋅
=
Ι
s
4900 cm
4
=
Ncrit
9
ld
2
Ecm
Ι
c
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es
Ι
s
⋅
+
⋅
:=
Ncrit
9
1200
2
3500 2133333
⋅
2 1.82
⋅
0.11
0.1
0.76
+
0.1
+
⋅
20500 4900
⋅
+
⋅
=
Ncrit 8318.2 kN
=
η
1
1
Nsd
Ncrit
−
:=
η
1
1
1361.0
8318.2
−
=
η
1.18
=
etot
η
eo
⋅
:=
etot 1.18 61.24
⋅
=
etot 72.9 cm
=

< 1%
ρ
l
0.52%
=
ρ
l
19.63
50 75
⋅
=
AsL 19.63 cm
2
=
ρ
l
AsL
b d
⋅
:=
k 0.95
:=
k
1.6
d
−
=
1.6
0.75
−
=
b 50 cm
=
d 75 cm
=
VRd1
0.35 k
⋅
fctd
⋅
1.2
40
ρ
l
⋅
+
(
)
⋅
0.15
σ
cp
⋅
+
b
⋅
d
⋅
:=
Sprawdzenie no
ś
no
ś
ci obliczeniowej na
ś
cinanie ze wzgl
ę
du na rozciaganie bez zbrojenia
na
ś
cinanie.
0.9
39.26
40
≤
0.98 1.1
≤
=
0.9
As.obliczone
As.zało
ż
one
≤
1.1
≤
As.obliczone 39.26 cm
2
=
As.obliczone 2 19.63
=
Przyj
ę
to : 2
φ
16 o A
s
= 8.04 cm
2
Określenie
ξ
eff
wg wzoru:
ξ
eff
1
1
2
NEd es1
⋅
As2 d a1
−
(
)
⋅
fyd
⋅
−
⋅
b d
2
⋅
fcd
⋅
−
−
:=
ξ
eff
1
1
2 1240.0kN 110
⋅
cm 8.04cm
2
(75cm
5cm)
−
⋅
35
⋅
kN
cm
2
−
⋅
50cm 75cm
(
)
2
⋅
2.5
⋅
kN
cm
2
−
−
:=
ξ
eff
0.18
=
Obliczenie zbrojenia
As1
As1
fcd b
⋅
d
⋅ ξ
eff
⋅
fyd As2
⋅
+
Nsd
−
fyd
:=
As1
2.50 50
⋅
75
⋅
0.18
⋅
35 8.04
⋅
+
1361.0
−
35
=
As1 17.42 cm
2
=
- przyj
ę
to 4
φ
25 o
As1
19.63 cm
2
:=
Zbrojenia.
As.zało
ż
one
ρ
s Ac
⋅
:=
As.zało
ż
one
0.010 50
⋅
80
⋅
=
As.zało
ż
one
40 cm
2
=
As.obliczone
As2 As1
+
:=
Ze wzgledu na zblizone wartosci momentów po obu stronach słupa przyjeto
As2 As1
=
⋅
cm
2
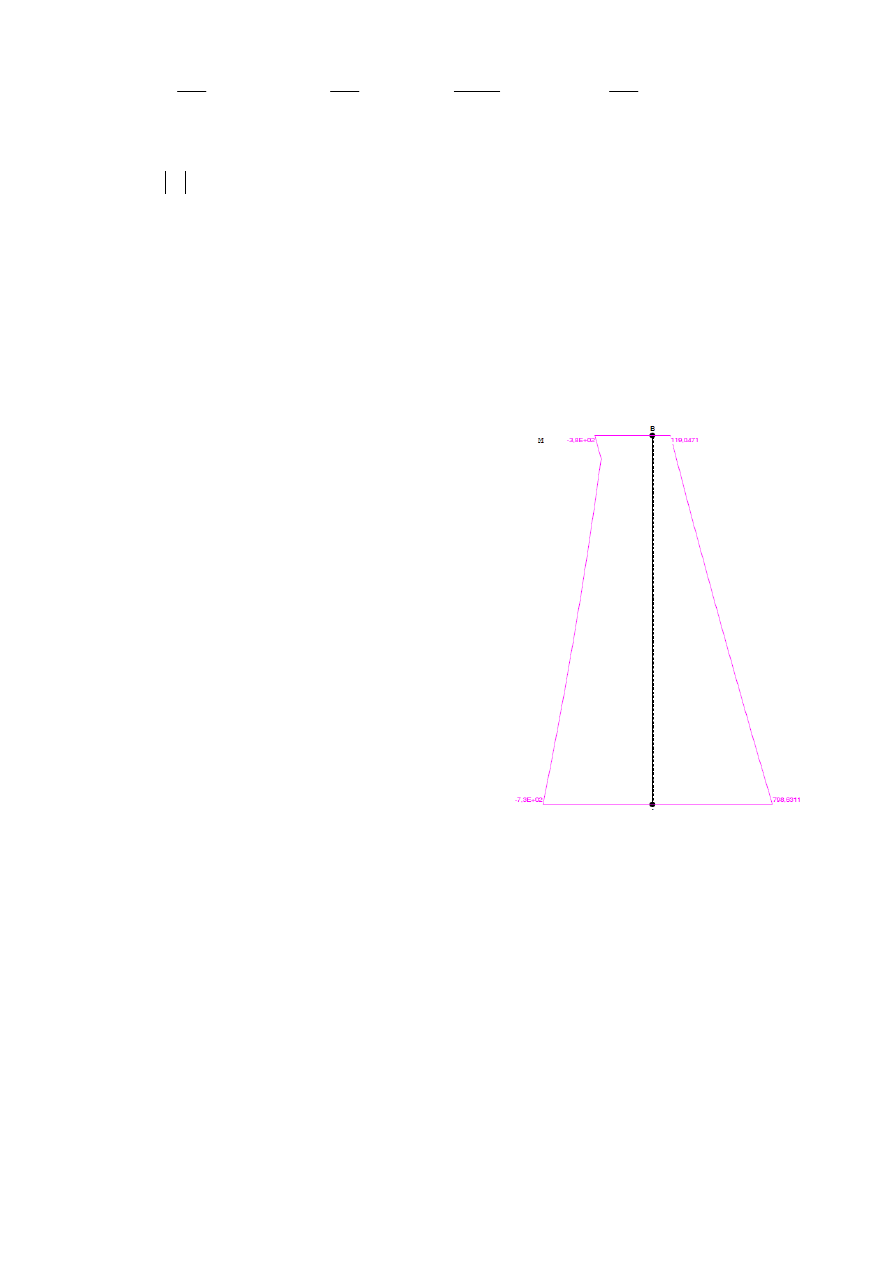
σ
cp
NEd
b h
⋅
:=
<
0.2 fcd
⋅
0.50
kN
cm
2
=
σ
cp
1240.0
50 80
⋅
=
σ
cp
0.31
kN
cm
2
=
VRd1
0.35 0.95
⋅
0.16
⋅
(1.2
40 0.0055)
⋅
+
⋅
0.15 0.31
⋅
+
[
] 50
⋅
75
⋅
=
V1
129.3 kN
=
<
VRd1 457.6 kN
=
Przyjmuj
ę
strzemiona konstrukcyjne, czteroci
ę
te
φ
8.
Rozstaw strzemion.
s
15
φ
⋅
≤
φ
25mm
:=
s
15 25
⋅
mm
≤
375 mm
=
Przyj
ę
to s = 35 cm
Okreslenie mimosrodu pocztkowego:
7.4.2 Przekrój górny słupa
M1,B,w
119.05 kNm
:=
- M
max
V1
118.12
−
kN
:=
N1
1240.0
−
kN
:=
- N
max
M1,B,z
- 354.58 kNm
:=
- M
min
- V
max
o
a
e
e
= e + e
- mimosród pocztkowy.
•
sg
G = 40.5 kN
Ciezar górnej (nadsuwnicowej) czesci słupa
7.4.2.1 Zewnetrzna strona słupa
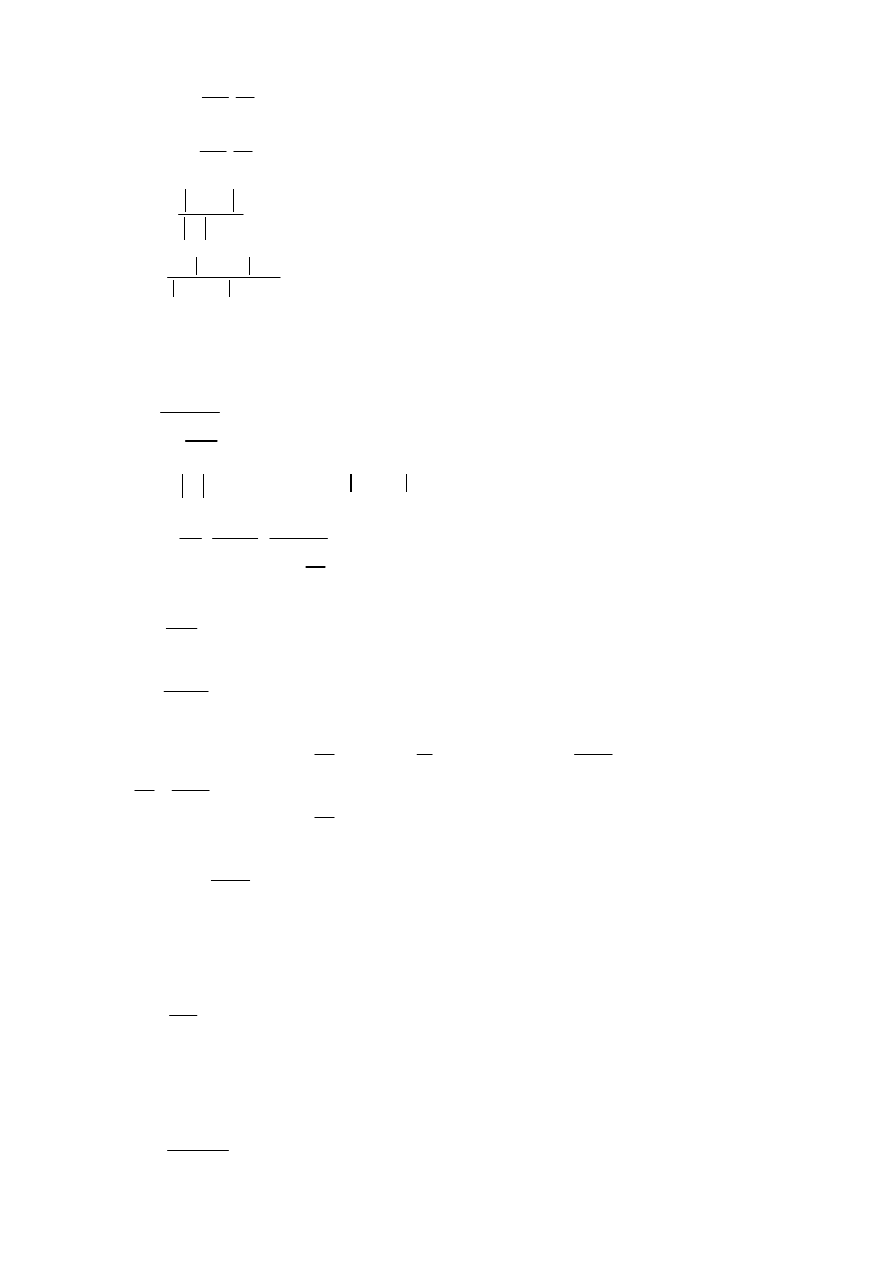
Ι
c
2133333cm
4
=
>
eo
h
0.5
0.01
ld
h
⋅
−
0.01fcd
−
=
0.5
0.01
12.8
0.8
⋅
−
0.01 25.0
⋅
−
=
0.09
=
eo
h
30.37
80
=
0.38
=
>
eo
h
0.05
=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
Φ ∞
t
o
,
( )
- ko
ń
cowy współczynnik pełzania betonu, przy zało
ż
eniu
ż
e ,
ż
e słup b
ę
dzie obci
ąż
ony po
28 dniach w
ś
rodowisku o wilgotno
ś
ci 50%
ho
2Ac
u
:=
- miarodajny wymiar przekroju.
Ac
b h
⋅
:=
Ac 500 800
⋅
=
Ac 400000 mm
2
=
u
2 b
⋅
2 h
⋅
+
:=
u
2 500
⋅
2 800
⋅
+
=
u 2800 mm
=
ho
2 400000
⋅
2800
=
286 mm
=
=>
Φ ∞
t
o
,
( )
2.0
=
ea
max
ll
400
h
30
,
20mm
,
:=
- niezamierzony mimosród przypadkowy.
ea max
800
400
80
30
,
2cm = max (2.0; 2.67; 2.0)
,
=
ea 2 .67 cm
=
ee
M1,B,z
N1
Gsg
+
:=
- mimo
ś
ród konstrukcyjny.
ee
354.58
1240.0
−
40.5
+
=
ee 27.7 cm
=
eo
ea ee
+
:=
eo
2.67 + 27.7
=
eo 30.37 cm
=
etot
η
eo
⋅
=
- mimo
ś
ród całkowity.
η
1
1
Nsd
Ncrit
−
=
Nsd
N1
Gsg
+
:=
Nsd
1240.0
−
40.5
+
=
Nsd 1280.5 kN
=
Ncrit
9
ld
2
Ecm Ic
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es Is
⋅
+
⋅
=
- siła krytyczna.
Ι
c
b h
3
⋅
12
:=
- moment bezwładno
ś
ci przekroju betonu wzgl
ę
dem jego
ś
rodka ci
ęż
ko
ś
ci.
Ι
c
50 80
3
⋅
12
=
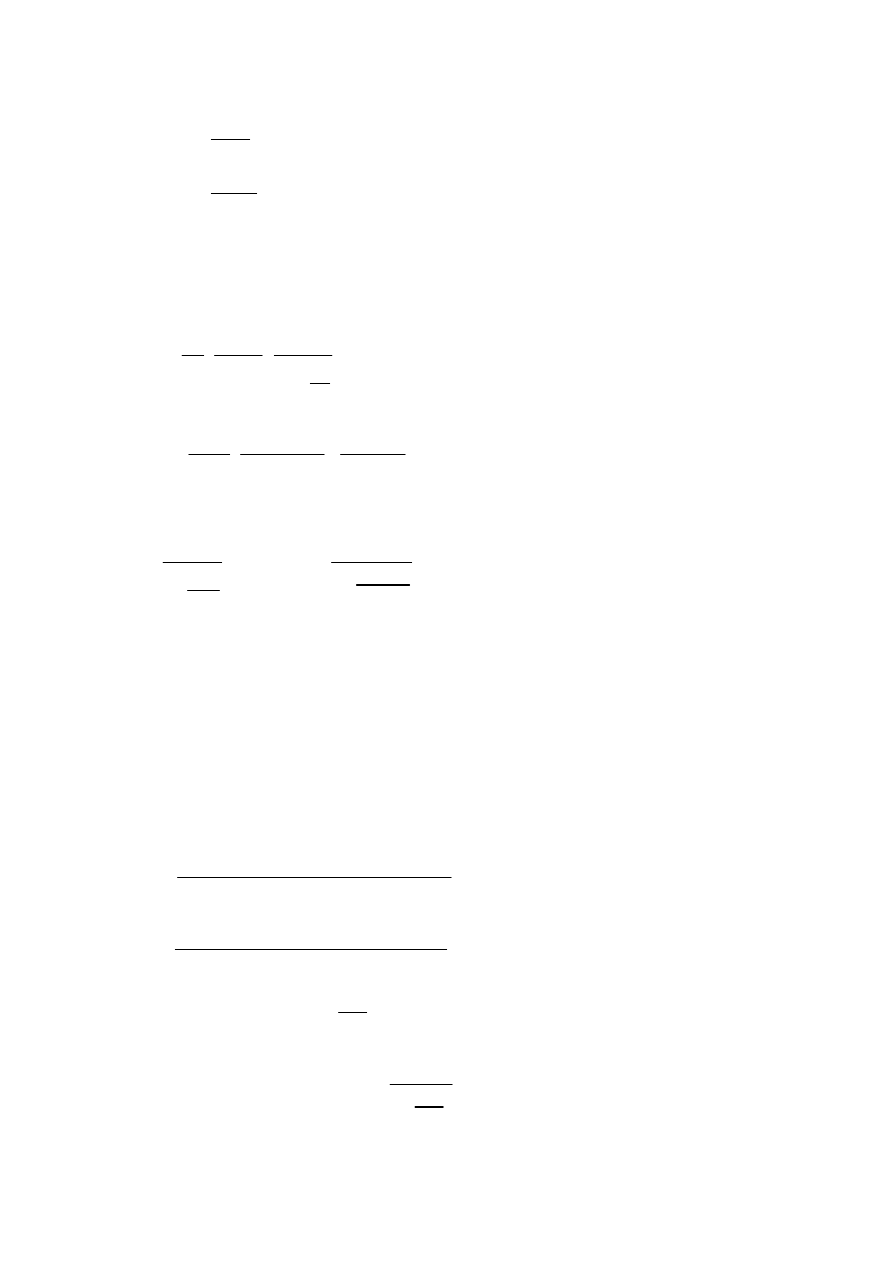
Sprawdzenie mimo
ś
rodu:
es1
etot 0.5 d a1
−
⋅
+
:=
es1 34.62 + 0.5 75 - 5
⋅
=
es1 67.12 cm
=
es1 0.671 m
=
Zakładam :
ξ
eff
ξ
eff.lim
=
0.53
=
- dla stali A-III
Obliczenie zbrojenia A
s2 :
d
h
a1
−
:=
d
0.75 m
=
As2
Nsd es1
⋅
ξ
eff.lim 1
0.5
ξ
eff.lim
⋅
−
(
)
⋅
d
2
⋅
b
⋅
fcd
⋅
−
d
a1
−
(
)
fyd
⋅
:=
As2
1280.0 67
⋅
0.53 1
0.5 0.53
⋅
−
(
)
⋅
75
2
⋅
50
⋅
2.5
⋅
−
(75 - 5) 35
⋅
=
As2
76.79
−
cm
2
=
As2.min max 0.0020 b
⋅
h
⋅
0.10
NEd
fyd
⋅
,
=
As2.min
max 0.0020 50
⋅
cm 80
⋅
cm 0.10
1240.0kN
35
kN
cm
2
⋅
= max (8.0; 3.54)
,
:=
As2.min 8.0 cm
2
=
Nsd.lt
889,66 kN
G = 889.66 + 40.5 = 930.16
sg
+
:=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
kit 1 0.5
930.16
1280.5
⋅
2.0
⋅
+
=
kit 1.72
=
Przyj
ę
to:
a1 a2
=
50mm
=
ρ
s
1%
:=
Ι
s
ρ
s b
⋅
h
⋅
0.5 h
⋅
a1
−
(
)
2
⋅
:=
Ι
s
0.01 50
⋅
80 (
⋅
0.5 80
⋅
5)
−
2
⋅
=
Ι
s
49000 cm
4
=
Ncrit
9
ld
2
Ecm
Ι
c
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es
Ι
s
⋅
+
⋅
:=
Ncrit
9
1200
2
3500 2133333
⋅
2 1.72
⋅
0.11
0.1
0.38
+
0.1
+
⋅
20500 49000
⋅
+
⋅
=
Ncrit 10809 kN
=
η
1
1
Nsd
Ncrit
−
:=
η
1
1
1280.5
10809
−
=
η
1.14
=
etot
η
eo
⋅
:=
etot 1.14 30.37
⋅
=
etot 34.62 cm
=
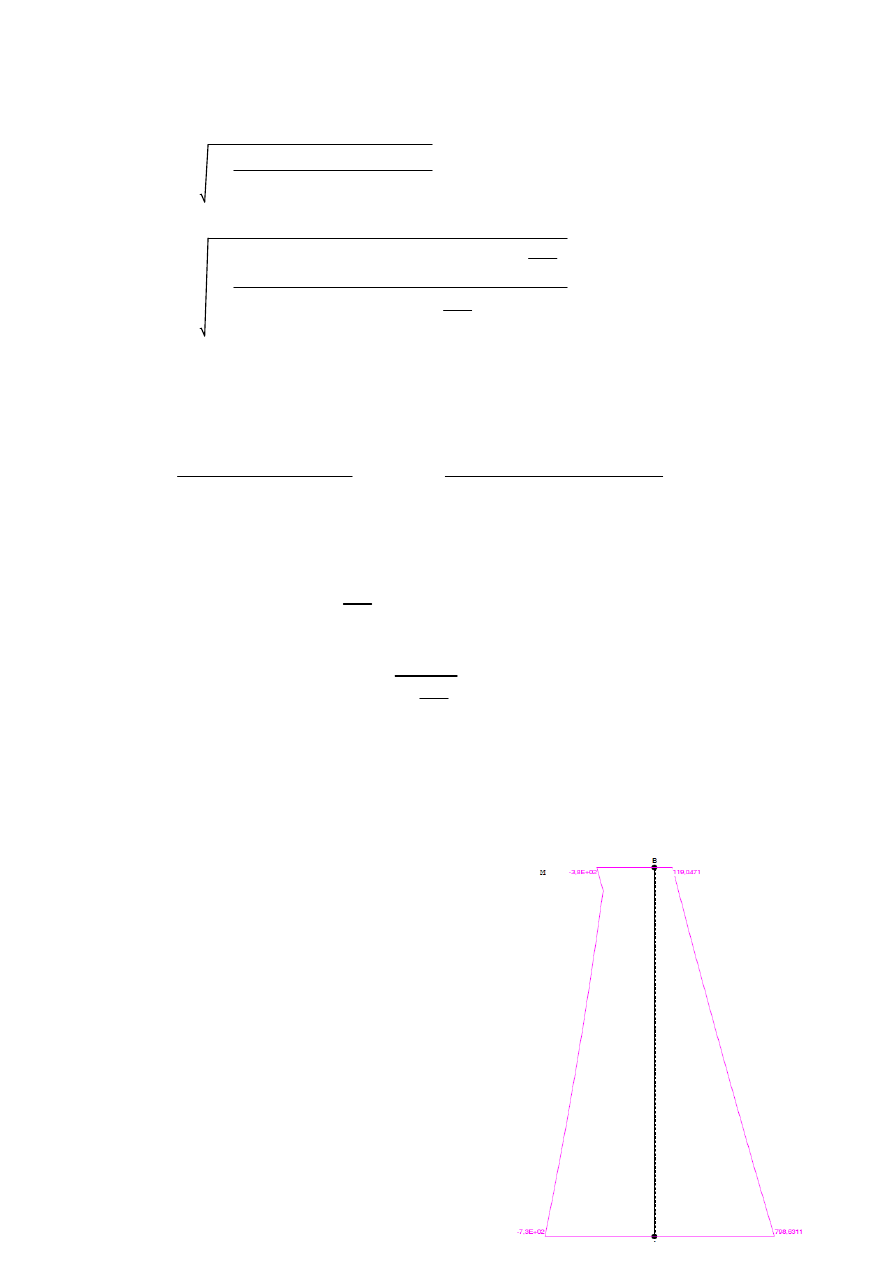
Przyj
ę
to : 4
φ
16 o A
s
= 8.04 cm
2
Określenie
ξ
eff
wg wzoru:
ξ
eff
1
1
2
Nsd es1
⋅
As2 d a1
−
(
)
⋅
fyd
⋅
−
⋅
b d
2
⋅
fcd
⋅
−
−
:=
ξ
eff
1
1
2 1280.0 kN 67
⋅
cm 8.04cm
2
(75cm
5cm)
−
⋅
35
⋅
kN
cm
2
−
⋅
50cm 75cm
(
)
2
⋅
2.5
⋅
kN
cm
2
−
−
:=
ξ
eff
0.1
=
Obliczenie zbrojenia
As1
As1
fcd b
⋅
d
⋅ ξ
eff
⋅
fyd As2
⋅
+
Nsd
−
fyd
:=
As1
2.50 50
⋅
75
⋅
0.10
⋅
35 8.04
⋅
+
1280.0
−
35
=
As1 -1.56 cm
2
=
- przyj
ę
to 2
φ
25 o
As1
9.81 cm
2
:=
As1.min max (0.0020 b
⋅
h
⋅
0.10 )
NEd
fyd
⋅
,
=
As1.min
max (0.0020 50
⋅
cm 80
⋅
cm 0.10 )
1240.0kN
35
kN
cm
2
⋅
= max (8.0; 3.54)
,
:=
As1.min 8.0 cm
2
=
Okreslenie mimosrodu pocztkowego:
o
a
e
e
= e + e
- mimosród pocztkowy.
•
7.4.2.2 Wewnetrzna strona słupa
M 1,B,w
119.05 kNm
:=
- M
max
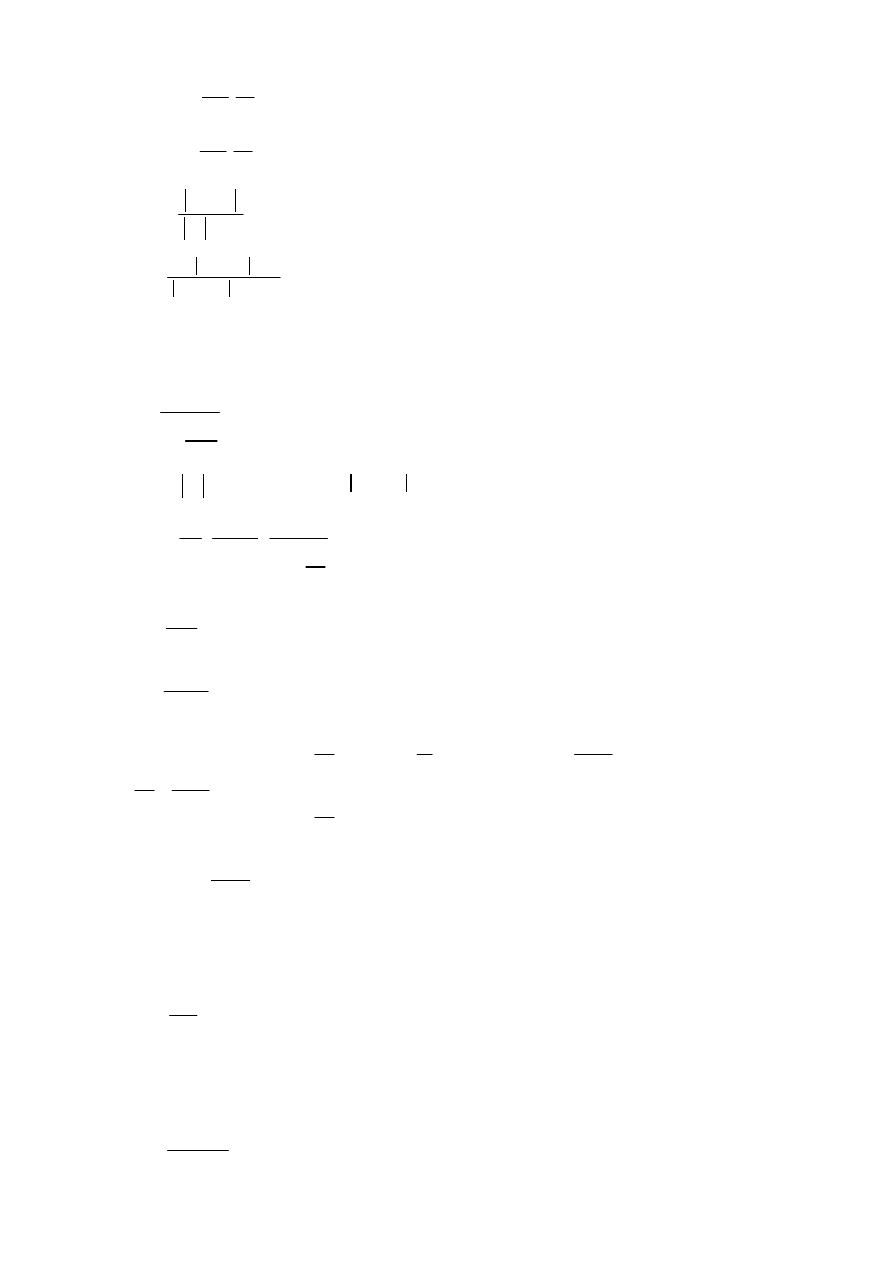
Ι
c
2133333cm
4
=
>
eo
h
0.5
0.01
ld
h
⋅
−
0.01fcd
−
=
0.5
0.01
12.8
0.8
⋅
−
0.01 25.0
⋅
−
=
0.09
=
eo
h
12.36
80
=
0.16
=
>
eo
h
0.05
=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
Φ ∞
t
o
,
( )
- ko
ń
cowy współczynnik pełzania betonu, przy zało
ż
eniu
ż
e ,
ż
e słup b
ę
dzie obci
ąż
ony po
28 dniach w
ś
rodowisku o wilgotno
ś
ci 50%
ho
2Ac
u
:=
- miarodajny wymiar przekroju.
Ac
b h
⋅
:=
Ac 500 800
⋅
=
Ac 400000 mm
2
=
u
2 b
⋅
2 h
⋅
+
:=
u
2 500
⋅
2 800
⋅
+
=
u 2800 mm
=
ho
2 400000
⋅
2800
=
286 mm
=
=>
Φ ∞
t
o
,
( )
2.0
=
ea
max
ll
400
h
30
,
20mm
,
:=
- niezamierzony mimosród przypadkowy.
ea max
800
400
80
30
,
2cm = max (2.0; 2.67; 2.0)
,
=
ea 2 .67 cm
=
ee
M1,B,w
N1
Gsg
+
:=
- mimo
ś
ród konstrukcyjny.
ee
119.05
1240.0
−
40.5
+
=
ee 9.69 cm
=
eo
ea ee
+
:=
eo
2.67 + 9.69
=
eo 12.36 cm
=
etot
η
eo
⋅
=
- mimo
ś
ród całkowity.
η
1
1
Nsd
Ncrit
−
=
Nsd
N1
Gsg
+
:=
Nsd
1240.0
−
40.5
+
=
Nsd 1280.5 kN
=
Ncrit
9
ld
2
Ecm Ic
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es Is
⋅
+
⋅
=
- siła krytyczna.
Ι
c
b h
3
⋅
12
:=
- moment bezwładno
ś
ci przekroju betonu wzgl
ę
dem jego
ś
rodka ci
ęż
ko
ś
ci.
Ι
c
50 80
3
⋅
12
=
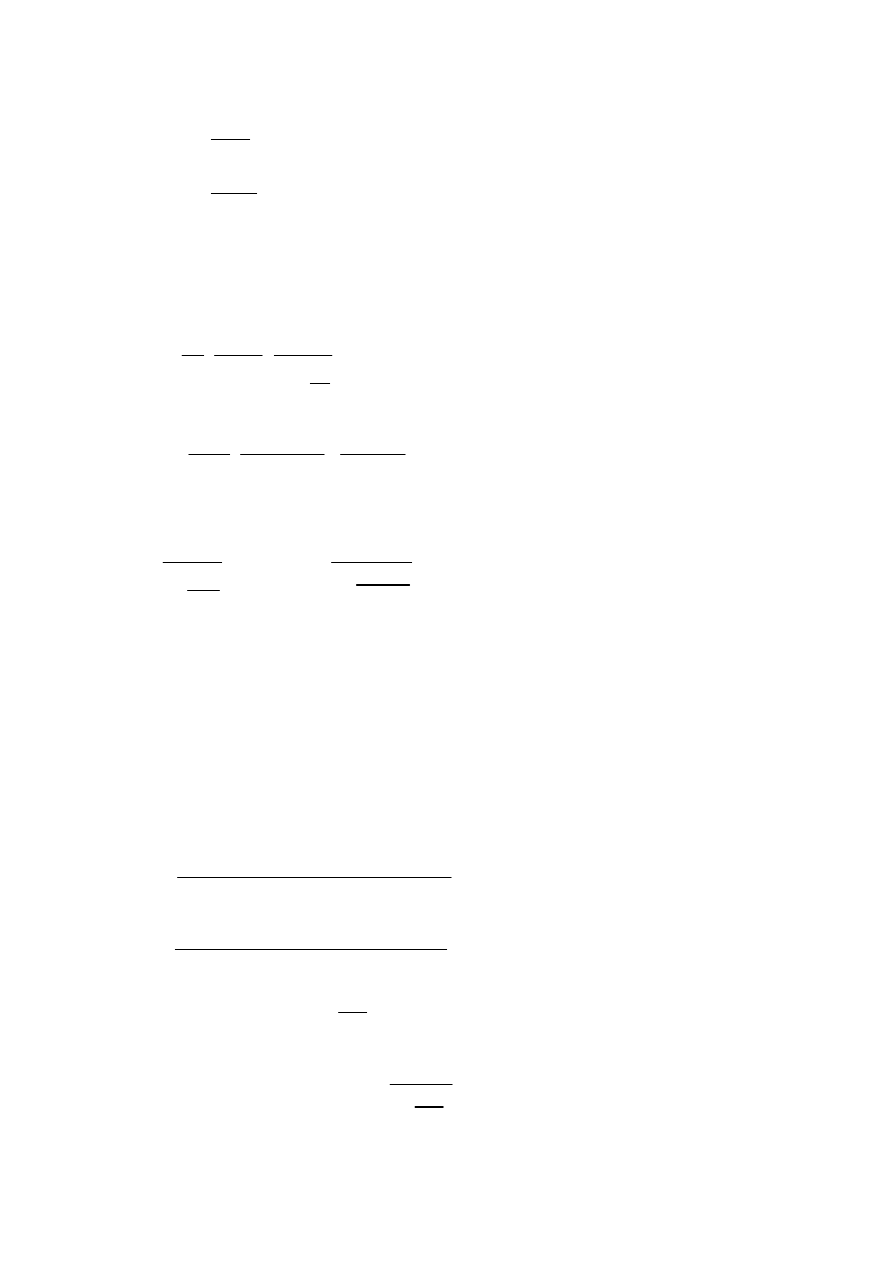
Sprawdzenie mimo
ś
rodu:
es1
etot 0.5 d a1
−
⋅
+
:=
es1 13.72 + 0.5 75 - 5
⋅
=
es1 46.21 cm
=
es1 0.462 m
=
Zakładam :
ξ
eff
ξ
eff.lim
=
0.53
=
- dla stali A-III
Obliczenie zbrojenia A
s2 :
d
h
a1
−
:=
d
0.75 m
=
As2
Nsd es1
⋅
ξ
eff.lim 1
0.5
ξ
eff.lim
⋅
−
(
)
⋅
d
2
⋅
b
⋅
fcd
⋅
−
d
a1
−
(
)
fyd
⋅
:=
As2
1280.5 46
⋅
0.53 1
0.5 0.53
⋅
−
(
)
⋅
75
2
⋅
50
⋅
2.5
⋅
−
(75 - 5) 35
⋅
=
As2
87.76
−
cm
2
=
As2.min max 0.0020 b
⋅
h
⋅
0.10
NEd
fyd
⋅
,
=
As2.min
max 0.0020 50
⋅
cm 80
⋅
cm 0.10
1240.0kN
35
kN
cm
2
⋅
= max (8.0; 3.54)
,
:=
As2.min 8.0 cm
2
=
Nsd.lt
889,66 kN
G = 889.66 + 40.5 = 930.16 kN
sg
+
:=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
kit 1 0.5
930.16
1280.5
⋅
2.0
⋅
+
=
kit 1.72
=
Przyj
ę
to:
a1 a2
=
50mm
=
ρ
s
1%
:=
Ι
s
ρ
s b
⋅
h
⋅
0.5 h
⋅
a1
−
(
)
2
⋅
:=
Ι
s
0.01 50
⋅
80 (
⋅
0.5 80
⋅
5)
−
2
⋅
=
Ι
s
49000 cm
4
=
Ncrit
9
ld
2
Ecm
Ι
c
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es
Ι
s
⋅
+
⋅
:=
Ncrit
9
1200
2
3500 2133333
⋅
2 1.72
⋅
0.11
0.1
0.16
+
0.1
+
⋅
20500 49000
⋅
+
⋅
=
Ncrit 13374 kN
=
η
1
1
Nsd
Ncrit
−
:=
η
1
1
1280.5
13374
−
=
η
1.11
=
etot
η
eo
⋅
:=
etot 1.11 12.36
⋅
=
etot 13.72 cm
=

Przyj
ę
to : 4
φ
16 o A
s
= 8.04 cm
2
Określenie
ξ
eff
wg wzoru:
ξ
eff
1
1
2
NEd es1
⋅
As2 d a1
−
(
)
⋅
fyd
⋅
−
⋅
b d
2
⋅
fcd
⋅
−
−
:=
ξ
eff
1
1
2 1280.5kN 46.2
⋅
8.04cm
2
(75cm
5cm)
−
⋅
35
⋅
kN
cm
2
−
⋅
50cm 75cm
(
)
2
⋅
2.5
⋅
kN
cm
2
−
−
:=
ξ
eff
0.06
=
Obliczenie zbrojenia
As1
As1
fcd b
⋅
d
⋅ ξ
eff
⋅
fyd As2
⋅
+
Nsd
−
fyd
:=
As1
2.50 50
⋅
75
⋅
0.06
⋅
35 8.04
⋅
+
1280.5
−
35
=
As1 -12.5 cm
2
=
- przyj
ę
to 2 25
φ
o
As1
9.81 cm
2
:=
As1.min max (0.0020 b
⋅
h
⋅
0.10 )
NEd
fyd
⋅
,
=
As1.min
max (0.0020 50
⋅
cm 80
⋅
cm 0.10 )
1240.0kN
35
kN
⋅
= max (8.0; 3.54)
,
:=
As1.min 8.0 cm
2
=
k 0.95
:=
k
1.6
d
−
=
1.6
0.75
−
=
b 50 cm
=
d 75 cm
=
VRd1 [ 0.35 k
⋅
fctd
⋅
(1.2
40 )
ρ
l
⋅
+
⋅
0.15
σ ]
cp
⋅
+
b d
⋅
:=
Sprawdzanie nosnosci obliczeniowej na scinanie ze wzgledu na rozciaganie bez zbrojenia na scinanie
ρ
l
AsL
b d
⋅
:=
AsL 8.04 cm
2
=

7.5 Wymiarowanie cz
ęś
ci nadsuwnicowej - pret nr 3
Przekrój słupa.
b
0.5 m
:=
h
0.6 m
:=
Sprawdzenie smukło
ś
ci.
lg
h
16.7
=
ld
h
7
<
16.7 > 7
- nale
ż
y uwzgl
ę
dni
ć
smukło
ść
.
7.5.1 Przekrój dolny słupa
M3,A,w
250.13 kNm
:=
- M
max
V3
79.4
−
kN
:=
N3
683.1
−
kN
:=
- N
max
Okre
ś
lenie mimo
ś
rodu pocz
ą
tkowego:
•
eo ea ee
+
=
- mimo
ś
ród pocz
ą
tkowy.
M3,A,z
- 49.7 kNm
:=
- M
min
- V
max
7.5.1.1 Wewnetrzna strona słupa
sg
G = 40.5 kN
Ciezar górnej (nadsuwnicowej) czesci słupa
s
15 16
⋅
mm
≤
240 mm
=
Przyjeto s = 20 cm
Przyjmuje strzemiona konstrukcyjne, czterociete
φ
8.
Rozstaw strzemion.
s
15
φ
⋅
≤
φ
16mm
:=
< 1%
ρ
l
0.21%
=
ρ
l
8.04
50 75
⋅
=
σ
cp
Nsd
b h
⋅
:=
<
0.2 fcd
⋅
0.50
kN
cm
2
=
σ
cp
1280.0
50 80
⋅
=
σ
cp
0.32
kN
cm
2
=
VRd1
0.35 0.95
⋅
0.16
⋅
(1.2
40 0.0021)
⋅
+
⋅
0.15 0.32
⋅
+
[
] 50
⋅
75
⋅
=
V1
118.12 kN
=
<
VRd1 436.2 kN
=
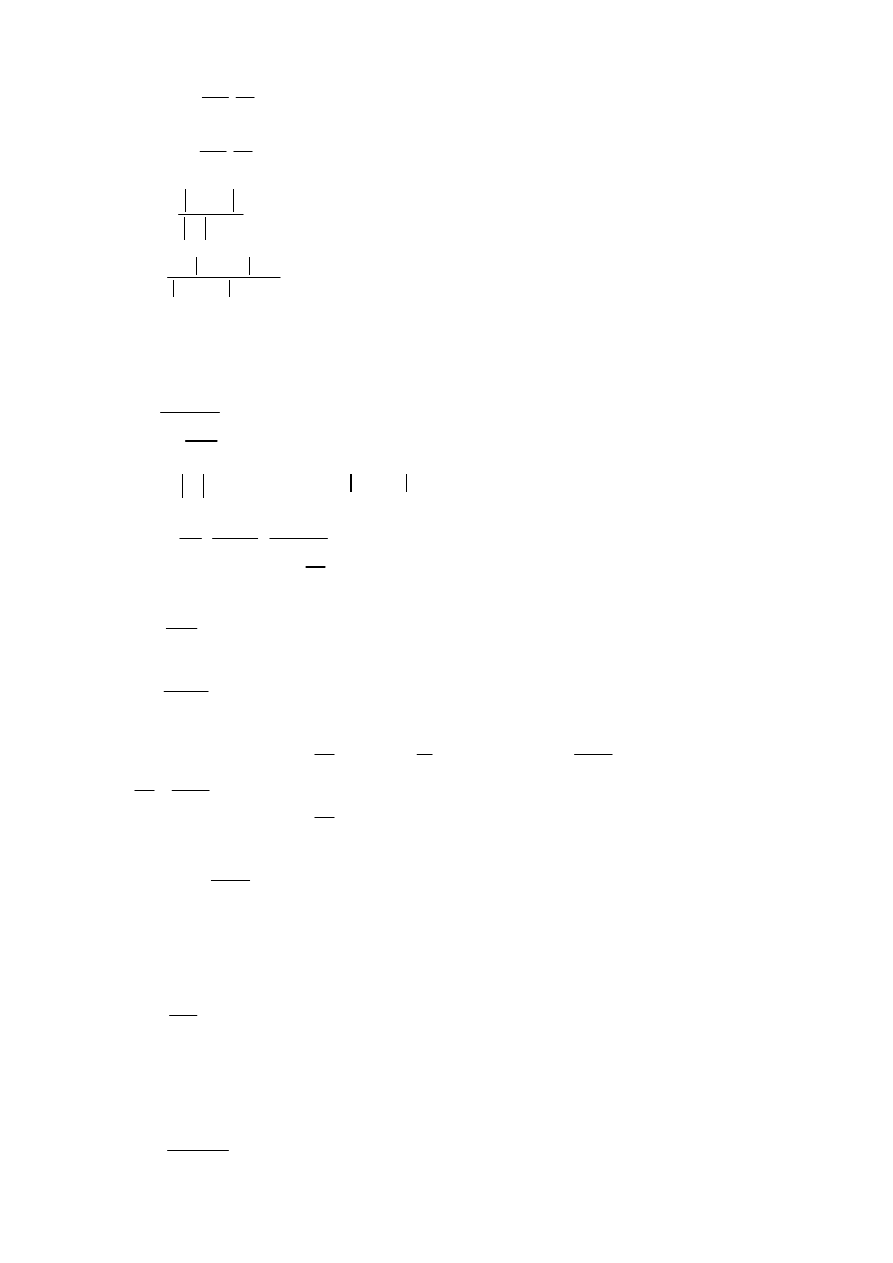
Ι
c
900000 cm
4
=
>
eo
h
0.5
0.01
lg
h
⋅
−
0.01fcd
−
=
0.5
0.01
10.0
0.6
⋅
−
0.01 25.0
⋅
−
=
0.08
=
eo
h
37.1
60
=
0.62
=
>
eo
h
0.05
=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
Φ ∞
t
o
,
( )
- ko
ń
cowy współczynnik pełzania betonu, przy zało
ż
eniu
ż
e ,
ż
e słup b
ę
dzie obci
ąż
ony po
28 dniach w
ś
rodowisku o wilgotno
ś
ci 50%
ho
2Ac
u
:=
- miarodajny wymiar przekroju.
Ac
b h
⋅
:=
Ac 500 600
⋅
=
Ac 300000 mm
2
=
u
2 b
⋅
2 h
⋅
+
:=
u
2 500
⋅
2 600
⋅
+
=
u 2400 mm
=
ho
2 300000
⋅
2400
=
250 mm
=
=>
Φ ∞
t
o
,
( )
2.0
=
ea
max
lg
400
h
30
,
20mm
,
:=
- niezamierzony mimosród przypadkowy.
ea max
1000
400
60
30
,
2cm = max (2.5; 2.0; 2.0)
,
=
ea 2 .5 cm
=
ee
M3,A,w
N3
Gsg
+
:=
- mimo
ś
ród konstrukcyjny.
ee
250.13
683.1
−
40.5
+
=
ee 34.6 cm
=
eo
ea ee
+
:=
eo
2.5 + 34.6
=
eo 37.1 cm
=
etot
η
eo
⋅
=
- mimo
ś
ród całkowity.
η
1
1
Nsd
Ncrit
−
=
Nsd
N3
Gsg
+
:=
Nsd
683.1
−
40.5
+
=
Nsd 723.6 kN
=
Ncrit
9
lg
2
Ecm Ic
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es Is
⋅
+
⋅
=
- siła krytyczna.
Ι
c
b h
3
⋅
12
:=
- moment bezwładno
ś
ci przekroju betonu wzgl
ę
dem jego
ś
rodka ci
ęż
ko
ś
ci.
Ι
c
50 60
3
⋅
12
=
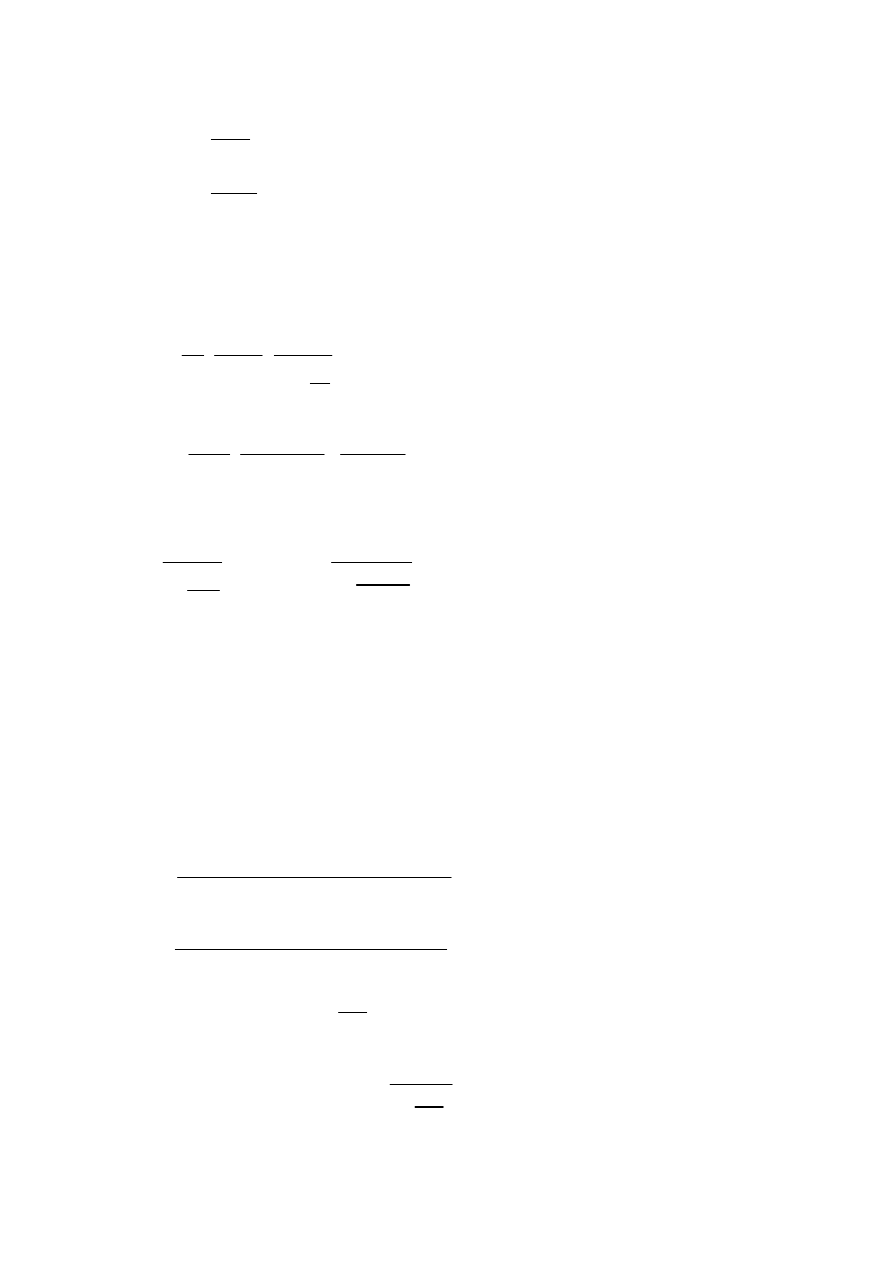
Sprawdzenie mimo
ś
rodu:
es1
etot 0.5 d a1
−
⋅
+
:=
es1 42.7 + 0.5 55 - 5
⋅
=
es1 65.2 cm
=
es1 0.652 m
=
Zakładam :
ξ
eff
ξ
eff.lim
=
0.53
=
- dla stali A-III
Obliczenie zbrojenia A
s2 :
d
h
a1
−
:=
d
0.55 m
=
As2
Nsd es1
⋅
ξ
eff.lim 1
0.5
ξ
eff.lim
⋅
−
(
)
⋅
d
2
⋅
b
⋅
fcd
⋅
−
d
a1
−
(
)
fyd
⋅
:=
As2
723.6 65.2
⋅
0.53 1
0.5 0.53
⋅
−
(
)
⋅
55
2
⋅
50
⋅
2.5
⋅
−
(55 - 5) 35
⋅
=
As2
57.21
−
cm
2
=
As2.min max 0.0020 b
⋅
h
⋅
0.10
Nsd
fyd
⋅
,
=
As2.min
max 0.0020 50
⋅
cm 60
⋅
cm 0.10
723.6kN
35
kN
cm
2
⋅
= max (6.0; 2.06)
,
:=
As2.min 6.0 cm
2
=
Nsd.lt
490.1 kN
G = 490.1 + 40.5 = 530.6 kN
sg
+
:=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
kit 1 0.5
530.6
723.6
⋅
2.0
⋅
+
=
kit 1.73
=
Przyj
ę
to:
a1 a2
=
50mm
=
ρ
s
1%
:=
Ι
s
ρ
s b
⋅
h
⋅
0.5 h
⋅
a1
−
(
)
2
⋅
:=
Ι
s
0.01 50
⋅
60 (
⋅
0.5 60
⋅
5)
−
2
⋅
=
Ι
s
18750 cm
4
=
Ncrit
9
lg
2
Ecm
Ι
c
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es
Ι
s
⋅
+
⋅
:=
Ncrit
9
1000
2
3500 900000
⋅
2 1.73
⋅
0.11
0.1
0.62
+
0.1
+
⋅
20500 18750
⋅
+
⋅
=
Ncrit 5530.1 kN
=
η
1
1
Nsd
Ncrit
−
:=
η
1
1
723.6
5530.1
−
=
η
1.15
=
etot
η
eo
⋅
:=
etot 1.15 37.1
⋅
=
etot 42.7 cm
=
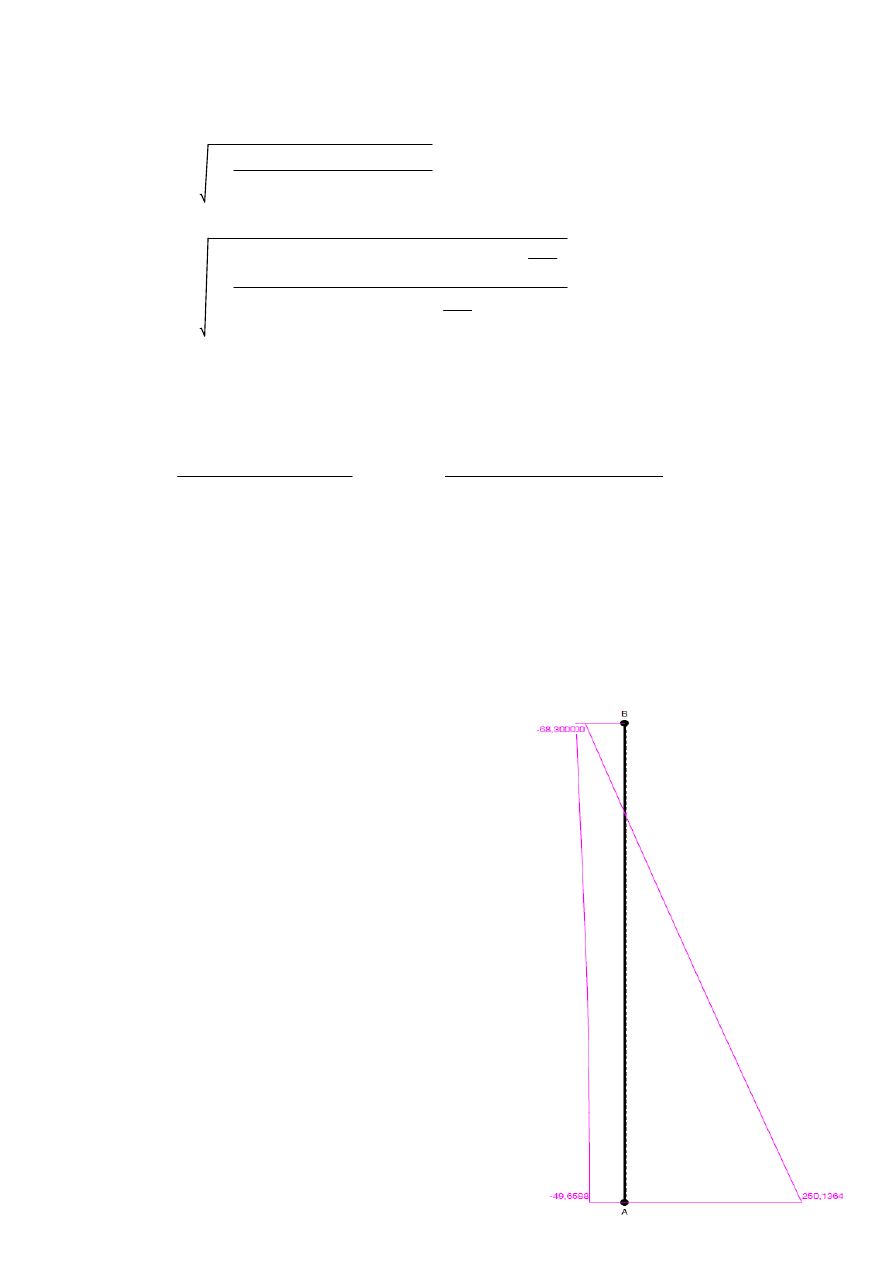
Przyj
ę
to : 2
φ
20 o A
s
= 6.28 cm
2
Określenie
ξ
eff
wg wzoru:
ξ
eff
1
1
2
Nsd es1
⋅
As2 d a1
−
(
)
⋅
fyd
⋅
−
⋅
b d
2
⋅
fcd
⋅
−
−
:=
ξ
eff
1
1
2 723.6 kN 65.2
⋅
cm 6.28cm
2
(55cm
5cm)
−
⋅
35
⋅
kN
cm
2
−
⋅
50cm ( 55cm)
2
⋅
2.5
⋅
kN
cm
2
−
−
:=
ξ
eff
0.1
=
Obliczenie zbrojenia
As1
As1
fcd b
⋅
d
⋅ ξ
eff
⋅
fyd As2
⋅
+
Nsd
−
fyd
:=
As1
2.50 50
⋅
55
⋅
0.10
⋅
35 6.28
⋅
+
723.6
−
35
=
As1 5.25 cm
2
=
- przyj
ę
to 2
φ
20 o
As1
6.28 cm
2
:=
eo ea ee
+
=
7.5.1.2 Zewnetrzna strona słupa
•
Okreslenie mimosrodu poczatkowego
- mimosrod poczatkowy
M3,A,z
- 49.7 kNm
:=
- M
min

Ι
c
900000 cm
4
=
>
eo
h
0.5
0.01
lg
h
⋅
−
0.01fcd
−
=
0.5
0.01
10.0
0.6
⋅
−
0.01 25.0
⋅
−
=
0.08
=
eo
h
9.3
60
=
0.16
=
>
eo
h
0.05
=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
Φ ∞
t
o
,
( )
- ko
ń
cowy współczynnik pełzania betonu, przy zało
ż
eniu
ż
e ,
ż
e słup b
ę
dzie obci
ąż
ony po
28 dniach w
ś
rodowisku o wilgotno
ś
ci 50%
ho
2Ac
u
:=
- miarodajny wymiar przekroju.
Ac
b h
⋅
:=
Ac 500 600
⋅
=
Ac 300000 mm
2
=
u
2 b
⋅
2 h
⋅
+
:=
u
2 500
⋅
2 600
⋅
+
=
u 2400 mm
=
ho
2 300000
⋅
2400
=
250 mm
=
=>
Φ ∞
t
o
,
( )
2.0
=
ea
max
lg
400
h
30
,
20mm
,
:=
- niezamierzony mimosród przypadkowy.
ea max
1000
400
60
30
,
2cm = max (2.5; 2.0; 2.0)
,
=
ea 2 .5 cm
=
ee
M3,A,z
N3
Gsg
+
:=
- mimo
ś
ród konstrukcyjny.
ee
- 49.7
683.1
−
40.5
+
=
ee 6.8 cm
=
eo
ea ee
+
:=
eo
2.5 + 6.8
=
eo 9.3 cm
=
etot
η
eo
⋅
=
- mimo
ś
ród całkowity.
η
1
1
Nsd
Ncrit
−
=
Nsd
N3
Gsg
+
:=
Nsd
683.1
−
40.5
+
=
Nsd 723.6 kN
=
Ncrit
9
lg
2
Ecm Ic
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es Is
⋅
+
⋅
=
- siła krytyczna.
Ι
c
b h
3
⋅
12
:=
- moment bezwładno
ś
ci przekroju betonu wzgl
ę
dem jego
ś
rodka ci
ęż
ko
ś
ci.
Ι
c
50 60
3
⋅
12
=
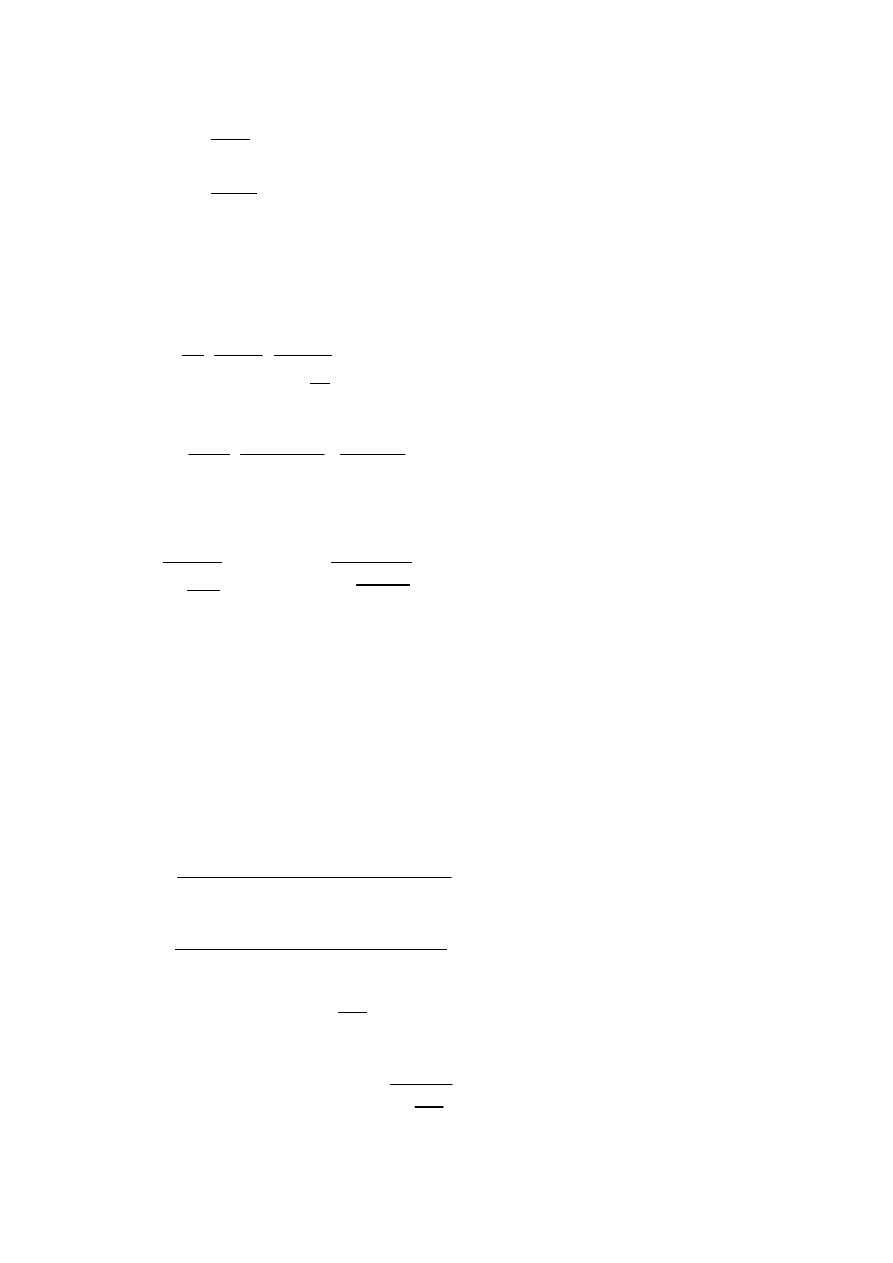
Sprawdzenie mimo
ś
rodu:
es1
etot 0.5 d a1
−
⋅
+
:=
es1 10.3 + 0.5 55 - 5
⋅
=
es1 32.8 cm
=
es1 0.328 m
=
Zakładam :
ξ
eff
ξ
eff.lim
=
0.53
=
- dla stali A-III
Obliczenie zbrojenia A
s2 :
d
h
a1
−
:=
d
0.55 m
=
As2
Nsd es1
⋅
ξ
eff.lim 1
0.5
ξ
eff.lim
⋅
−
(
)
⋅
d
2
⋅
b
⋅
fcd
⋅
−
d
a1
−
(
)
fyd
⋅
:=
As2
723.6 32.8
⋅
0.53 1
0.5 0.53
⋅
−
(
)
⋅
55
2
⋅
50
⋅
2.5
⋅
−
(55 - 5) 35
⋅
=
As2
70.6
−
cm
2
=
As2.min max 0.0020 b
⋅
h
⋅
0.10
Nsd
fyd
⋅
,
=
As2.min
max 0.0020 50
⋅
cm 60
⋅
cm 0.10
723.6kN
35
kN
cm
2
⋅
= max (6.0; 2.06)
,
:=
As2.min 6.0 cm
2
=
Nsd.lt
490.1 kN
G = 490.1 + 40.5 = 530.6 kN
sg
+
:=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
kit 1 0.5
530.6
723.6
⋅
2.0
⋅
+
=
kit 1.73
=
Przyj
ę
to:
a1 a2
=
50mm
=
ρ
s
1%
:=
Ι
s
ρ
s b
⋅
h
⋅
0.5 h
⋅
a1
−
(
)
2
⋅
:=
Ι
s
0.01 50
⋅
60 (
⋅
0.5 60
⋅
5)
−
2
⋅
=
Ι
s
18750 cm
4
=
Ncrit
9
lg
2
Ecm
Ι
c
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es
Ι
s
⋅
+
⋅
:=
Ncrit
9
1000
2
3500 900000
⋅
2 1.73
⋅
0.11
0.1
0.16
+
0.1
+
⋅
20500 18750
⋅
+
⋅
=
Ncrit 7745 kN
=
η
1
1
Nsd
Ncrit
−
:=
η
1
1
723.6
7745.0
−
=
η
1.11
=
etot
η
eo
⋅
:=
etot 1.11 9.3
⋅
=
etot 10.3 cm
=

Przyj
ę
to : 2
φ
20 o A
s
= 6.28 cm
2
Określenie
ξ
eff
wg wzoru:
ξ
eff
1
1
2
Nsd es1
⋅
As2 d a1
−
(
)
⋅
fyd
⋅
−
⋅
b d
2
⋅
fcd
⋅
−
−
:=
ξ
eff
1
1
2 723.6 kN 32.8
⋅
cm 6.28cm
2
(55cm
5cm)
−
⋅
35
⋅
kN
cm
2
−
⋅
50cm ( 55cm)
2
⋅
2.5
⋅
kN
cm
2
−
−
:=
ξ
eff
0.07
=
Obliczenie zbrojenia
As1
As1
fcd b
⋅
d
⋅ ξ
eff
⋅
fyd As2
⋅
+
Nsd
−
fyd
:=
As1
2.50 50
⋅
55
⋅
0.07
⋅
35 6.28
⋅
+
723.6
−
35
=
As1 -0.62 cm
2
=
- przyj
ę
to 2
φ
20 o
As1
6.28 cm
2
:=
As1.min max (0.0020 b
⋅
h
⋅
0.10 )
Nsd
fyd
⋅
,
=
As1.min
max (0.0020 50
⋅
cm 60
⋅
cm 0.10 )
723.6kN
35
kN
cm
2
⋅
= max (6.0; 2.06)
,
:=
As1.min 6.0 cm
2
=
k 1.05
:=
k
1.6
d
−
=
1.6
0.55
−
=
b 50 cm
=
d 55 cm
=
VRd3 [ 0.35 k
⋅
fctd
⋅
(1.2
40 )
ρ
l
⋅
+
⋅
0.15
σ ]
cp
⋅
+
b d
⋅
:=
Sprawdzanie nosnosci obliczeniowej na scinanie ze wzgledu na rozciaganie bez zbrojenia na scinanie
ρ
l
AsL
b d
⋅
:=
AsL 6.28 cm
2
=
< 1%
ρ
l
0.23%
=
ρ
l
6.28
50 55
⋅
=

7.5.2 Przekrój górny słupa
M3,B,w
0.0 kNm
:=
- M
max
V3
73.4
−
kN
:=
N3
683.1
−
kN
:=
- N
max
•
eo ea ee
+
=
M3,B,z
- 68.3 kNm
:=
- M
min
- V
max
7.5.2.1 Zewnetrzna strona słupa
Okreslenie mimosrodu poczatkowego
- mimosród poczatkowy
s
15 20
⋅
mm
≤
300 mm
=
Przyjeto s = 30 cm
Przyjmuje strzemiona konstrukcyjne, czterociete
φ
8.
Rozstaw strzemion.
s
15
φ
⋅
≤
φ
20mm
:=
σ
cp
Nsd
b h
⋅
:=
<
0.2 fcd
⋅
0.50
kN
cm
2
=
σ
cp
723.6
50 60
⋅
=
σ
cp
0.24
kN
cm
2
=
VRd3
0.35 1.05
⋅
0.16
⋅
(1.2 40 0.0024)
⋅
+
⋅
0.15 0.24
⋅
+
[
] 50
⋅
55
⋅
=
V3
73.4 kN
=
<
VRd3 307.9 kN
=

Ι
c
900000 cm
4
=
>
eo
h
0.5
0.01
lg
h
⋅
−
0.01fcd
−
=
0.5
0.01
10.0
0.6
⋅
−
0.01 25.0
⋅
−
=
0.08
=
eo
h
12.5
60
=
0.21
=
>
eo
h
0.05
=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
Φ ∞
t
o
,
( )
- ko
ń
cowy współczynnik pełzania betonu, przy zało
ż
eniu
ż
e ,
ż
e słup b
ę
dzie obci
ąż
ony po
28 dniach w
ś
rodowisku o wilgotno
ś
ci 50%
ho
2Ac
u
:=
- miarodajny wymiar przekroju.
Ac
b h
⋅
:=
Ac 500 600
⋅
=
Ac 300000 mm
2
=
u
2 b
⋅
2 h
⋅
+
:=
u
2 500
⋅
2 600
⋅
+
=
u 2400 mm
=
ho
2 300000
⋅
2400
=
250 mm
=
=>
Φ ∞
t
o
,
( )
2.0
=
ea
max
lg
400
h
30
,
20mm
,
:=
- niezamierzony mimosród przypadkowy.
ea max
1000
400
60
30
,
2cm = max (2.5; 2.0; 2.0)
,
=
ea 2 .5 cm
=
ee
M3,B,z
N3
Gsg
+
:=
- mimo
ś
ród konstrukcyjny.
ee
- 68.3
683.1
−
=
ee 10.0 cm
=
eo
ea ee
+
:=
eo
2.5 + 10.0
=
eo 12.5 cm
=
etot
η
eo
⋅
=
- mimo
ś
ród całkowity.
η
1
1
Nsd
Ncrit
−
=
Nsd
N3
:=
Nsd
683.1
−
=
Nsd 683.1 kN
=
Ncrit
9
lg
2
Ecm Ic
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es Is
⋅
+
⋅
=
- siła krytyczna.
Ι
c
b h
3
⋅
12
:=
- moment bezwładno
ś
ci przekroju betonu wzgl
ę
dem jego
ś
rodka ci
ęż
ko
ś
ci.
Ι
c
50 60
3
⋅
12
=
Sprawdzenie mimo
ś
rodu:
es1
etot 0.5 d a1
−
⋅
+
:=
es1 13.9 + 0.5 55 - 5
⋅
=
es1 36.4 cm
=
es1 0.364 m
=
Zakładam :
ξ
eff
ξ
eff.lim
=
0.53
=
- dla stali A-III
Obliczenie zbrojenia A
s2 :
d
h
a1
−
:=
d
0.55 m
=
As2
Nsd es1
⋅
ξ
eff.lim 1
0.5
ξ
eff.lim
⋅
−
(
)
⋅
d
2
⋅
b
⋅
fcd
⋅
−
d
a1
−
(
)
fyd
⋅
:=
As2
683.1 36.4
⋅
0.53 1
0.5 0.53
⋅
−
(
)
⋅
55
2
⋅
50
⋅
2.5
⋅
−
(55 - 5) 35
⋅
=
As2
67.6
−
cm
2
=
As2.min max 0.0020 b
⋅
h
⋅
0.10
Nsd
fyd
⋅
,
=
As2.min
max 0.0020 50
⋅
cm 60
⋅
cm 0.10
723.6kN
35
kN
cm
2
⋅
= max (6.0; 2.06)
,
:=
As2.min 6.0 cm
2
=
Nsd.lt
490.1 kN
:=
kit 1 0.5
Nsd.lt
Nsd
⋅
Φ ∞
t
o
,
( )
⋅
+
=
kit 1 0.5
490.1
683.1
⋅
2.0
⋅
+
=
kit 1.72
=
Przyj
ę
to:
a1 a2
=
50mm
=
ρ
s
1%
:=
Ι
s
ρ
s b
⋅
h
⋅
0.5 h
⋅
a1
−
(
)
2
⋅
:=
Ι
s
0.01 50
⋅
60 (
⋅
0.5 60
⋅
5)
−
2
⋅
=
Ι
s
18750 cm
4
=
Ncrit
9
lg
2
Ecm
Ι
c
⋅
2 kit
⋅
0.11
0.1
eo
h
+
0.1
+
⋅
Es
Ι
s
⋅
+
⋅
:=
Ncrit
9
1000
2
3500 900000
⋅
2 1.72
⋅
0.11
0.1
0.21
+
0.1
+
⋅
20500 18750
⋅
+
⋅
=
Ncrit 7207 kN
=
η
1
1
Nsd
Ncrit
−
:=
η
1
1
683.1
7207
−
=
η
1.11
=
etot
η
eo
⋅
:=
etot 1.11 12.5
⋅
=
etot 13.9 cm
=
Przyj
ę
to : 2
φ
20 o A
s
= 6.28 cm
2
Określenie
ξ
eff
wg wzoru:
ξ
eff
1
1
2
Nsd es1
⋅
As2 d a1
−
(
)
⋅
fyd
⋅
−
⋅
b d
2
⋅
fcd
⋅
−
−
:=
ξ
eff
1
1
2 683.1 kN 36.4
⋅
cm 6.28cm
2
(55cm
5cm)
−
⋅
35
⋅
kN
cm
2
−
⋅
50cm ( 55cm)
2
⋅
2.5
⋅
kN
cm
2
−
−
:=
ξ
eff
0.04
=
Obliczenie zbrojenia
As1
As1
fcd b
⋅
d
⋅ ξ
eff
⋅
fyd As2
⋅
+
Nsd
−
fyd
:=
As1
2.50 50
⋅
55
⋅
0.04
⋅
35 6.28
⋅
+
683.1
−
35
=
As1 -5.88 cm
2
=
- przyjeto 2
φ
20 o
As1
6.28 cm
2
:=
As1.min max (0.0020 b
⋅
h
⋅
0.10 )
Nsd
fyd
⋅
,
=
As1.min
max (0.0020 50
⋅
cm 60
⋅
cm 0.10 )
683.1 kN
35
kN
cm
2
⋅
= max (6.0; 1.95)
,
:=
As1.min 6.0 cm
2
=
M3,B,w
0.0 kNm
:=
- M
max
7.5.2.1 Zewnetrzna strona słupa
Ze wzgledu na zerowy moment przyjto zbrojenie minimalne równe:
As1
6.28 cm
2
:=
As1.min max (0.0020 b
⋅
h
⋅
0.10 )
Nsd
fyd
⋅
,
=
As1.min
max (0.0020 50
⋅
cm 60
⋅
cm 0.10 )
683.1 kN
35
kN
cm
2
⋅
= max (6.0; 1.95)
,
:=
As1.min 6.0 cm
2
=
- przyjeto 2
φ
20 o
k 1.05
:=
k
1.6
d
−
=
1.6
0.55
−
=
b 50 cm
=
d 55 cm
=
VRd3 [ 0.35 k
⋅
fctd
⋅
(1.2
40 )
ρ
l
⋅
+
⋅
0.15
σ ]
cp
⋅
+
b d
⋅
:=
Sprawdzanie nosnosci obliczeniowej na scinanie ze wzgledu na rozciaganie bez zbrojenia na scinanie
ρ
l
AsL
b d
⋅
:=
AsL 6.28 cm
2
=
< 1%
ρ
l
0.23%
=
ρ
l
6.28
50 55
⋅
=
s
15 20
⋅
mm
≤
300 mm
=
Przyjeto s = 280 cm
Przyjmuje strzemiona konstrukcyjne, czterociete
φ
8.
Rozstaw strzemion.
s
15
φ
⋅
≤
φ
20mm
:=
σ
cp
Nsd
b h
⋅
:=
<
0.2 fcd
⋅
0.50
kN
cm
2
=
σ
cp
683.1
50 60
⋅
=
σ
cp
0.23
kN
cm
2
=
VRd3
0.35 1.05
⋅
0.16
⋅
(1.2 40 0.0023)
⋅
+
⋅
0.15 0.24
⋅
+
[
] 50
⋅
55
⋅
=
V3
73.4 kN
=
<
VRd3 305.8 kN
=
Wyszukiwarka
Podobne podstrony:
Modelowanie w Robocie (płyta słup)(1)
4 Słup jednokier przykład NS ukl o wezl nieprzes
04 HBT Slup EC3
06 slup teoria
słup soli, lektury
Projekt 2 Plyta Slup Guide cz II
Mathcad SŁUP PROJEKT 23 05
K 08 SLUP id 229567 Nieznany
Tajemniczy słup światła nad piramidą Chichen Itza, W ஜ DZIEJE ZIEMI I ŚWIATA, ●txt RZECZY DZIWNE
slup uzwojony
słup
Metale słup
WĘZŁY słup 2, Skrypty, PK - materiały ze studiów, II stopień, pomoc, III semestr, Konstrukcje stalow
wyniki słup srodkowy
Słup żelbetowy poprawiony
projekt cz2 slup
SŁUP DWUTEOWY KLEJONY, SŁUP DWUTEOWY KLEJONY
Instrukcja K1, 53-68, Słup kilometrowy
więcej podobnych podstron