.

Ćwiczenie nr. 5

Wahadło matematyczne

M. Bielewski, E. Rulikowska

.

Krótki opis fizyki ćwiczenia:

Wahadło proste (matematyczne) jest to wyidealizowane ciało o masie punk-
towej m, zawieszone na cienkiej, nierozciągliwej i nieważkiej nici. Takie wahadło,
wyprowadzone z położenia równowagi, wykonuje ruch drgający w płaszczyźnie
pionowej pod wpływem siły ciężkości. Jest to ruch okresowy o okresie T . Na
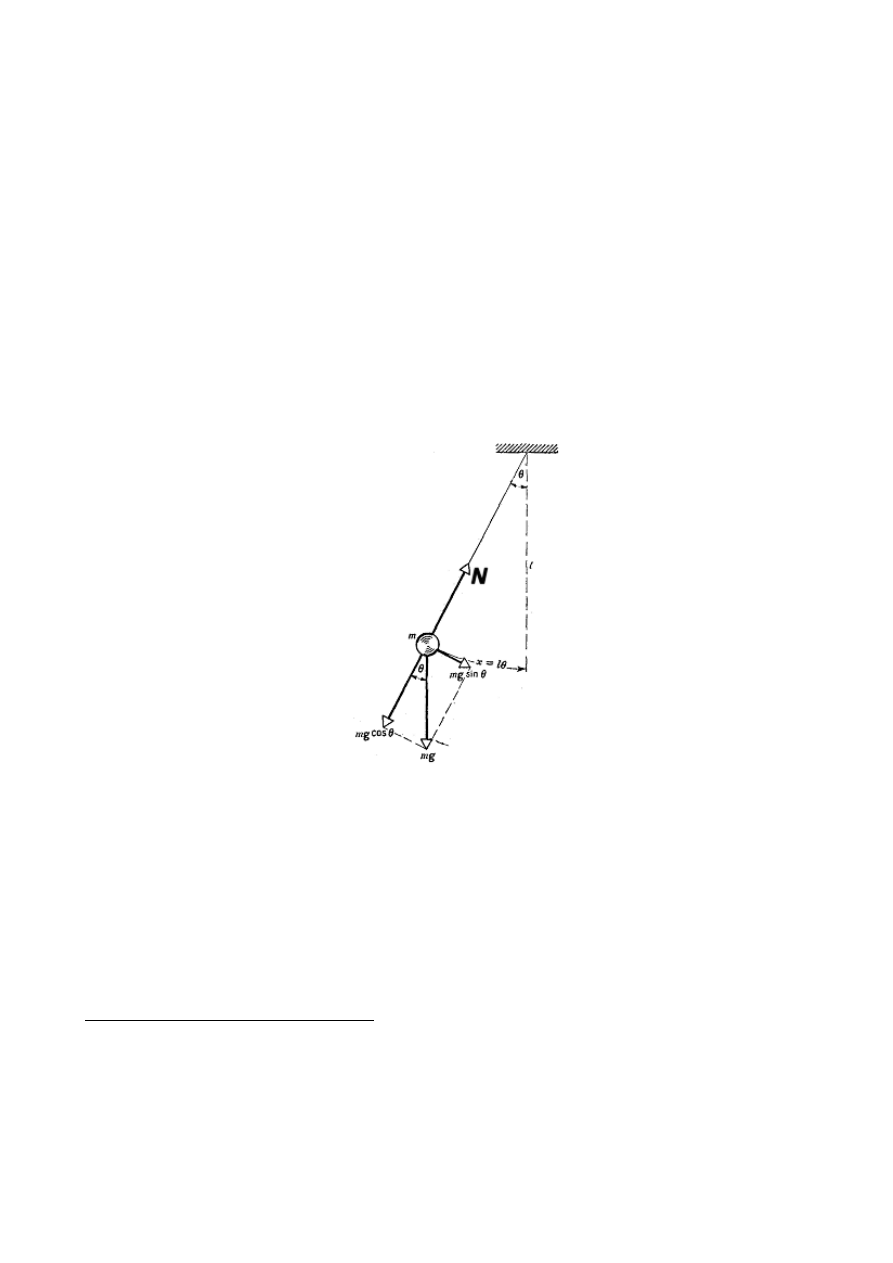
rysunku

5.1

przedstawiono wahadło o długości l i masie m, odchylone od pionu

o kąt θ. Na masę m działa siła ciężkości mg i naprężenie nici N . Jako osie
współrzędnych przyjmujemy styczną do łuku (oś x) i przedłużenie promienia
nici (oś y). Siłę ciężkości mg rozkładamy na współrzędną radialną mg cos θ i
współrzędną styczną mg sin θ. Współrzędna styczna siły ciężkości wynosi

Rysunek 5.1: Wahadło matematyczne.

F = −mg sin θ.

Siła F nie jest więc proporcjonalna do przemieszczenia kątowego θ, ale do sin θ.
Dla małych kątów θ mamy sin θ ≈ θ

1

, przemieszczenie masy m wzdłuż łuku wy-

nosi x = lθ i (znowu dla małych kątów θ) ruch jest w przybliżeniu prostoliniowy,

1

θ[

◦

]

θ[rad]

sin θ

różnica w %

2

◦

0, 03491 rad

0, 03490

0, 03

5

◦

0, 08727 rad

0, 08716

0, 24

10

◦

0, 17453 rad

0, 17356

0, 50

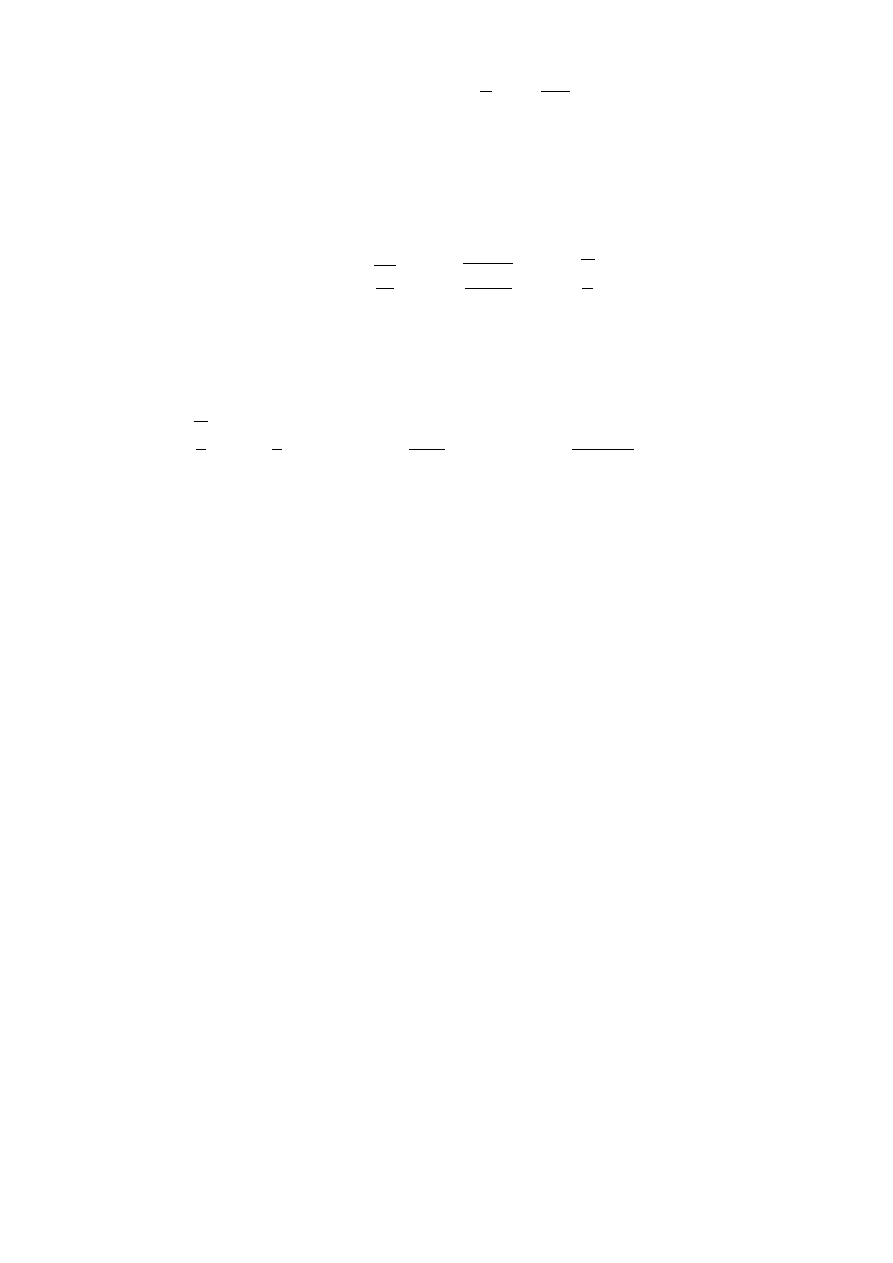
a siłę w nim działająca możemy zapisać jako

F = −mgθ = −mg

x

l

= −

mg

l

x.

Dla małych przemieszczeń siła F jest proporcjonalna do przemieszczenia ze
znakiem przeciwnym, czyli masa m wykonuje drgania harmoniczne proste. Sta-
ła mg/l jest odpowiednikiem stałej k w równaniu F = −kx, opisującym siłę
harmoniczną. Z teorii ruchu harmonicznego prostego, wiemy że okres takiego
ruchu wynosi

T = 2π

s

m

k

= 2π

v
u
u
t

m

mg/l

= 2π

v
u
u
t

l

g

.

(5.1)

Okres drgań wahadła prostego zależy więc jedynie od długości wahadła l oraz
od g (nie zależy od masy m wahadła). Można pokazać , że dla wahań o większej
amplitudzie wzór na okres ma postać

T = 2π

v
u
u
t

l

g





1 +

1

2

!

2

sin

2

θ

m

+

1 · 3

2 · 4

!

2

sin

4

θ

m

+

1 · 3 · 5

2 · 4 · 6

!

2

sin

6

θ

m

+ . . .





(5.2)

W powyższym wzorze θ

m

jest maksymalnym przemieszczeniem kątowym (zwy-

kle wychyleniem początkowym), a kolejne wyrazy wewnątrz nawiasu są coraz
mniejsze. Wzór (

5.1

) dostajemy z powyższego wzoru przy zaniedbaniu wszyst-

kich wyrazów w nawiasie za wyjątkiem jedności.