1

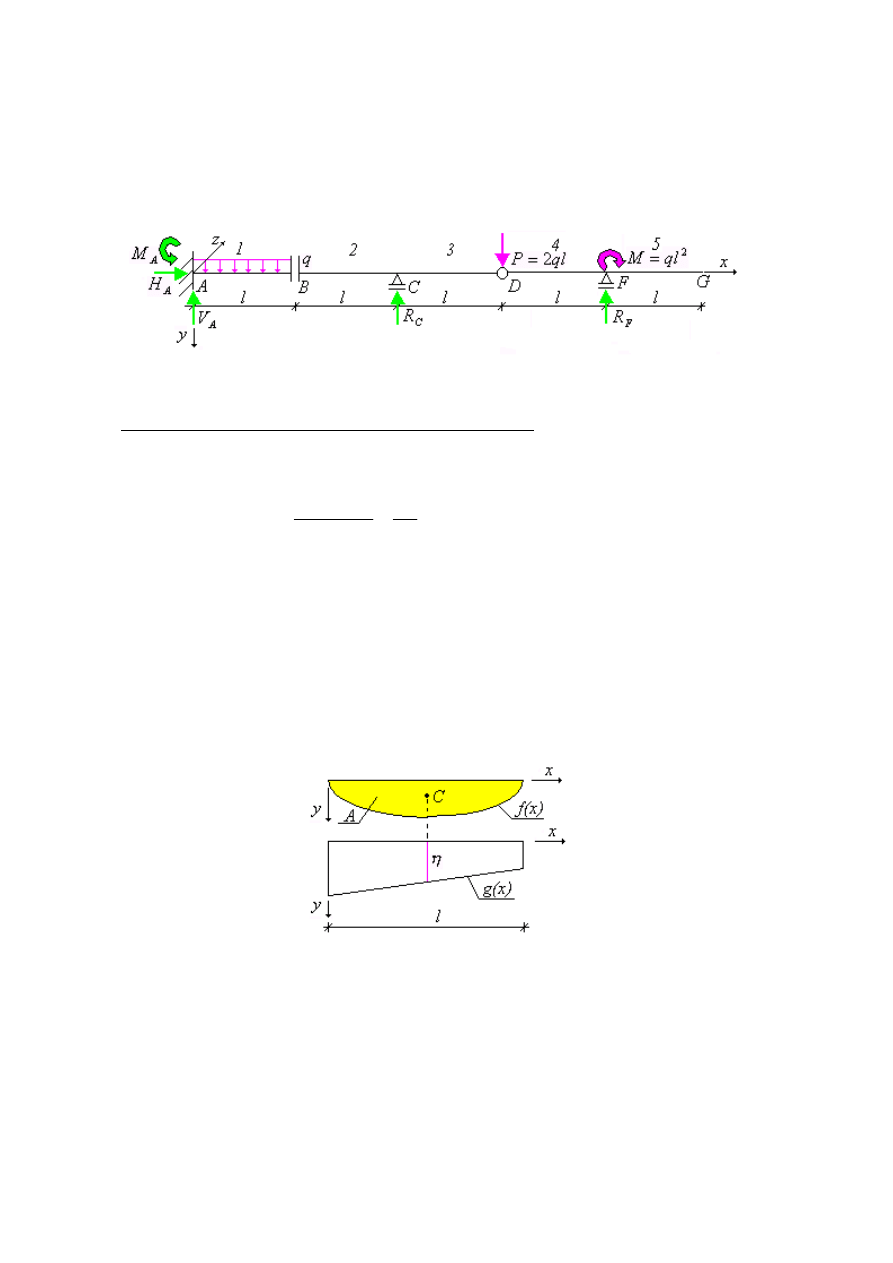
Przykład 2.1 Belka wieloprzęsłowa I.

Dla statycznie wyznaczalnej belki wieloprzęsłowej o stałej sztywności EJ, obciążonej jak

na rysunku poniżej, wyznaczyć ugięcie w punkcie D i kąt ugięcia w punkcie G.

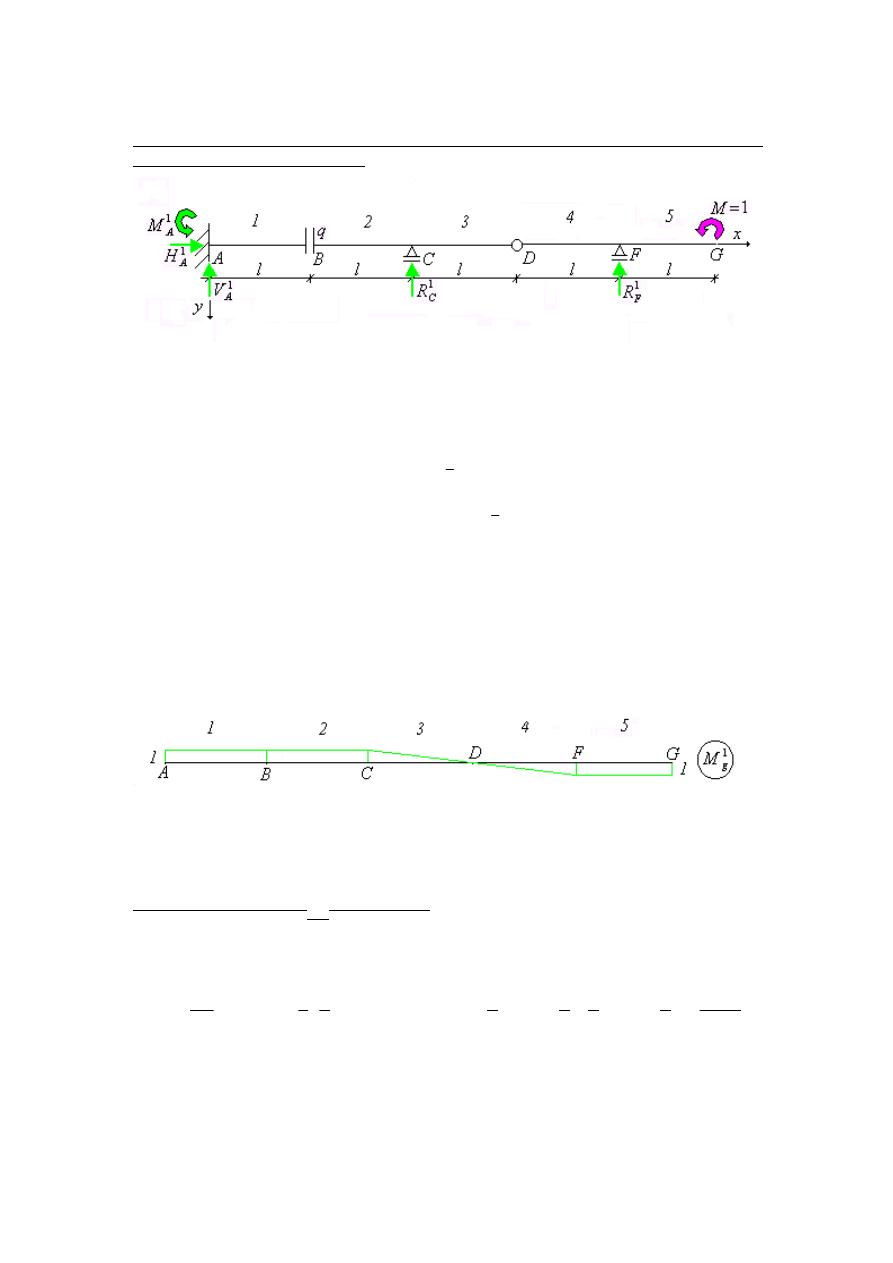
Rys. 1. Schemat statyczny belki

I. Wyznaczenie przemieszczenia pionowego v punktu D.

Przemieszczenie pionowe wyznaczymy stosując metodę Maxwella-Mohra, ze wzoru

v

D

∑∫

∑∫

=

=

=

=

5

1 0

1

5

1 0

1

1

i

l

zi

zi

i

l

zi

i

i

zi

zi

i

i

dx

M

M

EJ

J

E

ds

M

M

(1)

gdzie: v

D

- pionowe przemieszczenie punktu D,

zi

M - moment gnący w i-tym przedziale belki od obciążenia zewnętrznego,

1
zi

M - moment gnący w i-tym przedziale belki od pionowej siły jednostkowej, przy-

łożonej w punkcie D, odpowiadającej poszukiwanemu przemieszczeniu,

i

l - długość i-tego przedziału belki.

Możemy zastąpić całkowanie analityczne metodą całkowania graficznego. Objaśniono to

poniżej.

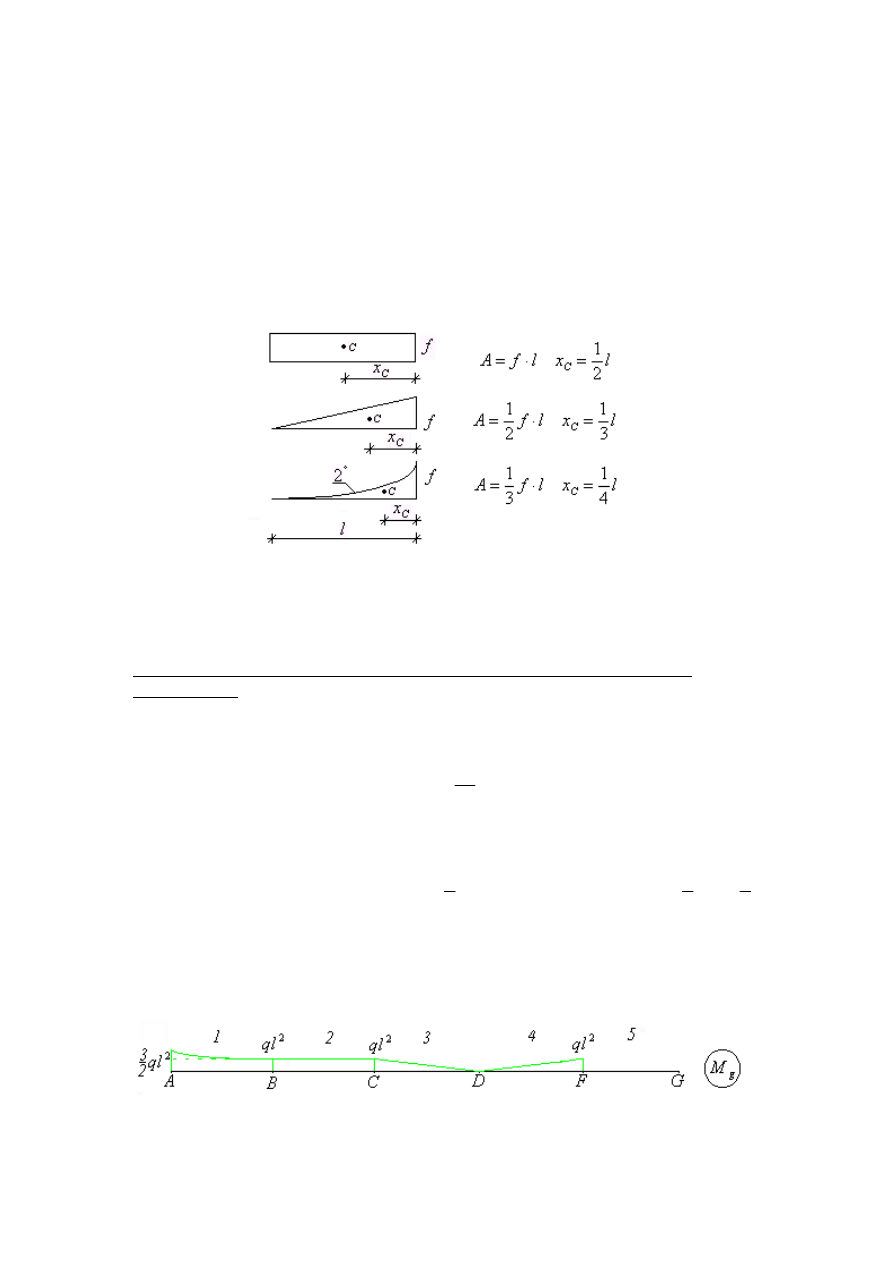
Rys. 2. Wykresy funkcji

( )

x

f

i

( )

x

g

Całkowanie wykonujemy korzystając ze wzoru

( ) ( )

η

⋅

=

⋅

∫

A

dx

x

g

x

f

l

0

(2)

gdzie: A - pole wykresu nieliniowego,

2

η - rzędna wykresu liniowego dla odciętej odpowiadającej środkowi ciężkości figury

pierwszego wykresu.

Uwaga: Bierzemy zawsze pole wykresu krzywoliniowego, jeżeli wykres od obciążenia
zewnętrznego jest nieliniowy.
Na wstępie ustalamy znak iloczynu funkcji

( )

x

f

i

( )

x

g

.

Wzór (2) jest również słuszny, gdy oba wykresy są liniowe.

Jeżeli funkcja momentu jest wielomianem, to każdy składnik wielomianu całkujemy osobno.

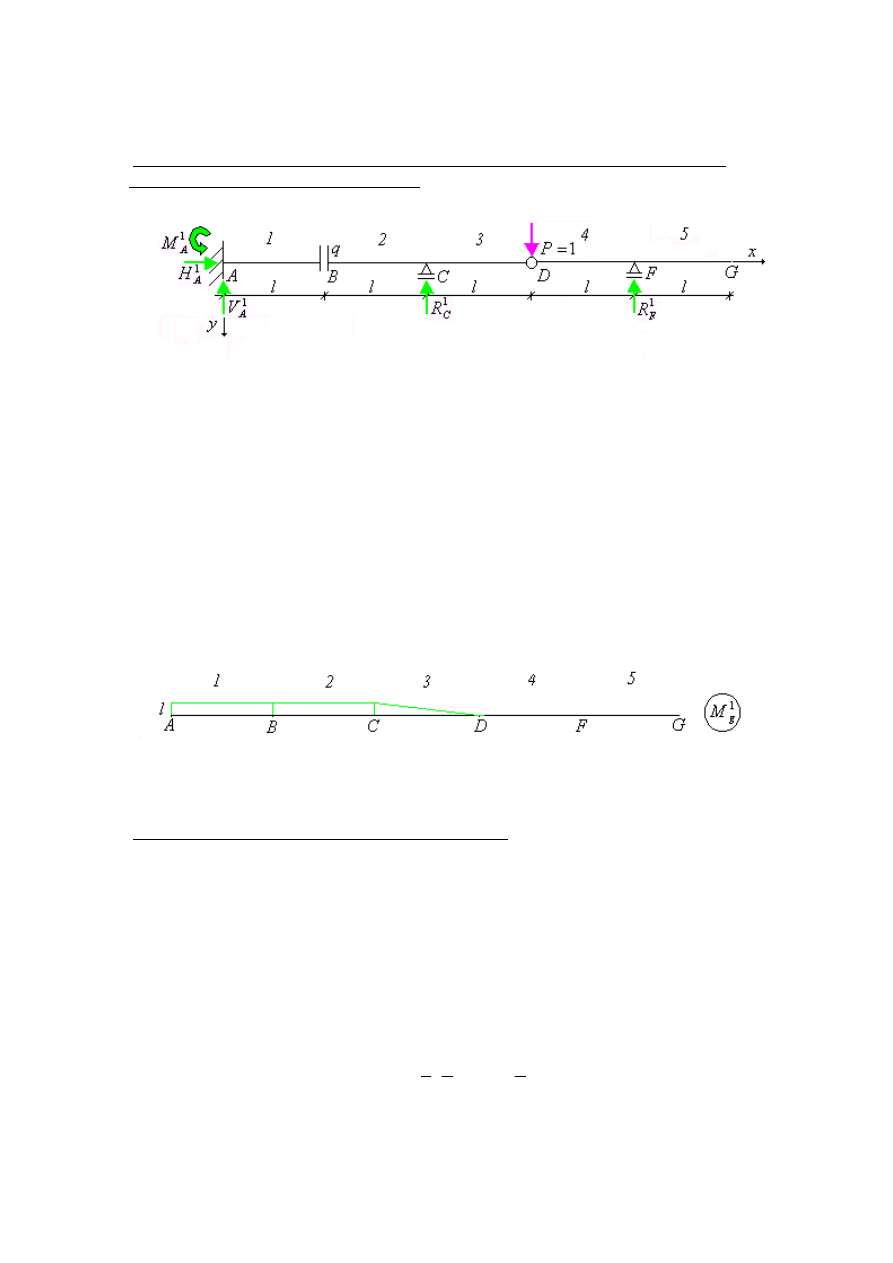
Rys. 3. Pola i środki ciężkości wybranych figur

Można także skorzystać wprost z odpowiednich tablic z wartościami całek.

1. Obliczenie reakcji i sporządzenie wykresu momentów gnących od obciążenia

zewnętrznego.

Z warunków równowagi dla belki wyznaczamy reakcje podpór

ql

l

M

R

l

R

M

M

F

F

DG

D

=

=

→

=

⋅

+

−

→

=

∑

0

0

ql

R

P

R

P

R

R

P

F

C

F

C

BG

iy

=

−

=

→

=

+

−

−

→

=

∑

0

0

ql

V

l

q

V

P

A

A

AB

iy

=

→

=

⋅

+

−

→

=

∑

0

0

2

2

2

3

2

5

3

0

2

5

3

0

ql

ql

l

R

l

V

M

l

ql

l

R

M

l

V

M

C

A

A

C

A

A

AD

D

=

−

+

=

→

=

⋅

+

⋅

−

+

⋅

−

→

=

∑

0

0

=

→

=

∑

A

ix

H

P

Wykorzystując przeprowadzone obliczenia sporządzamy wykres momentów gnących od

obciążenia zewnętrznego.

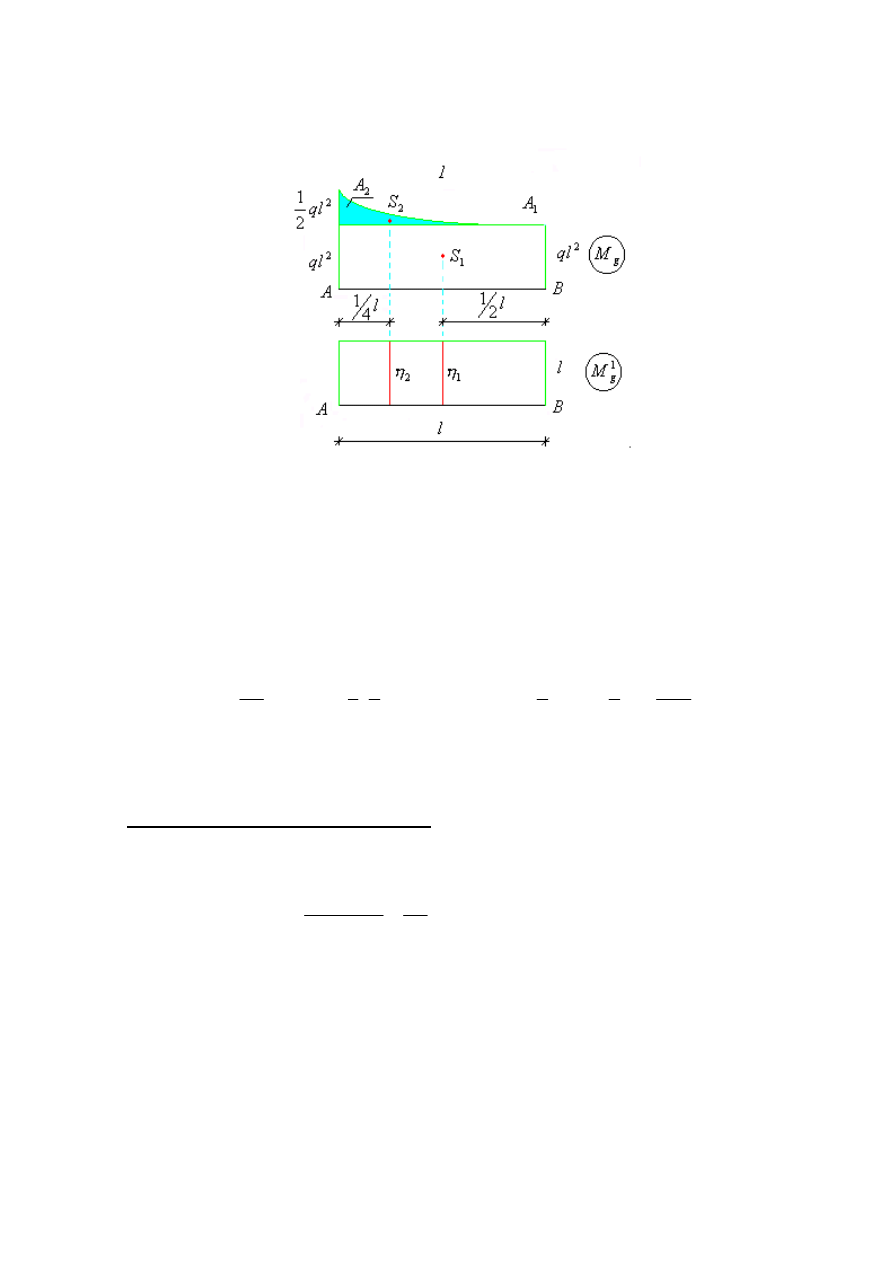
Rys. 4. Wykres momentów gnących od obciążenia zewnętrznego.

3

2. Obliczenie reakcji i sporządzenie wykresu momentów gnących od pionowej siły
jednostkowej przyłożonej w punkcie D.

Rys. 5. Schemat statyczny

Wyznaczamy reakcje podpór

0

0

0

1

1

1

=

→

=

⋅

→

=

∑

F

F

DG

D

R

l

R

M

1

0

1

0

1

1

1

1

=

→

=

+

−

−

→

=

∑

C

F

C

BG

iy

R

R

R

P

0

0

1

1

=

→

=

∑

A

AB

iy

V

P

l

l

R

l

V

M

l

R

M

l

V

M

C

A

A

C

A

A

AD

D

=

+

=

→

=

⋅

−

+

⋅

−

→

=

∑

1

1

1

1

1

1

3

0

3

0

0

0

1

1

=

→

=

∑

A

ix

H

P

Wykorzystując przeprowadzone obliczenia sporządzamy wykres momentów gnących od

obciążenia jednostkowego.

Rys. 6. Wykres momentów gnących od pionowej siły jednostkowej, przyłożonej w punkcie D

3. Obliczenie przemieszczenia pionowego v punktu D.

Zauważmy, że pole figury wykresu

g

M w przedziale 1 można przedstawić jako sumę

prostokąta i pola ograniczonego parabolą, dla których znamy pola powierzchni i położenie
środków ciężkości. Całkę w przedziale 1 obliczymy jako sumę iloczynów pól składowych
figury wykresu

g

M przez rzędne w wykresie

1
g

M odpowiadające środkom ciężkości w

wykresie

g

M . Pola powierzchni i odpowiadające im rzędne drugiego wykresu dla odciętej

odpowiadającej środkowi ciężkości figury pierwszego wykresu przedstawiono poniżej (patrz
rysunek 7).

l

ql

l

ql

A

ql

l

ql

A

=

=

=

⋅

⋅

=

=

⋅

=

2

1

3

2

2

3

2

1

6

1

2

1

3

1

η

η

4

Rys. 7. Wykresy momentów gnących w przedziale 1

W przedziale 2 całkę obliczymy mnożąc pole figury wykresu

g

M w przedziale 2 przez

rzędną w wykresie

1
g

M odpowiadającą środkowi ciężkości figury wykresu

g

M w przedziale

2. Podobnie w przedziale 3. Łatwo dostrzec, że całki w przedziałach 4 i 5 są równe zeru.

Ostatecznie wykorzystując wzór (1) i przeprowadzone obliczenia otrzymujemy

EJ

ql

l

l

ql

l

l

ql

l

l

ql

l

l

ql

EJ

v

D

2

5

3

2

2

1

2

1

3

1

1

4

2

2

2

2

=













⋅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

⋅

⋅

+

⋅

⋅

=

Otrzymany wynik końcowy ze znakiem plus oznacza, że zwrot wektora przemieszczenia

jest zgodny ze zwrotem założonej siły jednostkowej (Rys. 5).

II. Wyznaczenie kąta ugięcia w punkcie G.

Kąt ugięcia wyznaczymy stosując metodę Maxwella-Mohra, ze wzoru

∑∫

∑∫

=

=

=

=

5

1 0

1

5

1 0

1

1

i

l

zi

zi

i

l

zi

i

i

zi

zi

G

i

i

dx

M

M

EJ

J

E

ds

M

M

θ

(3)

gdzie:

G

θ - kąt ugięcia w punkcie G,

zi

M - moment gnący w i-tym przedziale belki od obciążenia zewnętrznego,

1
zi

M - moment gnący w i-tym przedziale belki od momentu jednostkowego, odpo-

wiadającego poszukiwanemu kątowi ugięcia, przyłożonemu w punkcie G,

i

l - długość i-tego przedziału belki.

5

1. Obliczenie reakcji i sporządzenie wykresu momentów gnących od momentu jednostko-
wego, przyłożonego w węźle G.

Rys. 8. Schemat statyczny

Wyznaczamy reakcje podpór

l

R

l

R

M

F

F

DG

D

1

0

1

0

1

1

1

−

=

→

=

+

⋅

→

=

∑

l

R

R

R

R

P

F

C

F

C

BG

iy

1

0

0

1

1

1

1

1

=

−

=

→

=

−

−

→

=

∑

0

0

1

1

=

→

=

∑

A

AB

iy

V

P

1

3

0

3

0

1

1

1

1

1

1

=

+

=

→

=

⋅

−

+

⋅

−

→

=

∑

l

R

l

V

M

l

R

M

l

V

M

C

A

A

C

A

A

AD

D

0

0

1

1

=

→

=

∑

A

ix

H

P

Wykorzystując przeprowadzone obliczenia sporządzamy wykres momentów gnących od

obciążenia jednostkowego.

Rys. 9. Wykres momentów gnących od momentu jednostkowego, przyłożonego w węźle G.

2. Obliczenie kąta ugięcia

G

θ w punkcie G.

Ostatecznie wykorzystując wzór (3) i wyniki przeprowadzonych obliczeń otrzymujemy

EJ

ql

l

ql

l

ql

l

ql

l

ql

l

ql

EJ

G

6

13

3

2

2

1

3

2

2

1

1

1

2

1

3

1

1

1

3

2

2

2

2

2

=













⋅

⋅

⋅

−

⋅

⋅

⋅

+

⋅

⋅

+

⋅

⋅

⋅

⋅

+

⋅

⋅

=

θ

Otrzymany wynik końcowy ze znakiem plus oznacza, że kąt ugięcia jest zgodny z

założonym momentem jednostkowym (Rys. 8).