Rozdział 3

Rozdział 3

Obliczanie płyt krzyżowo-

Obliczanie płyt krzyżowo-

zbrojonych

według

teorii

zbrojonych

według

teorii

sprężystości

i

nośności

sprężystości

i

nośności

granicznej

granicznej

W płytach prostokątnych, których długości boków znacznie się różnią przyjmuje

W płytach prostokątnych, których długości boków znacznie się różnią przyjmuje

się, że pracują one tylko w jednym kierunku (tzn. wzdłuż mniejszej rozpiętości). Na

się, że pracują one tylko w jednym kierunku (tzn. wzdłuż mniejszej rozpiętości). Na

podstawie doświadczeń ustalono, że w płytach prostokątnych opartych na całym

podstawie doświadczeń ustalono, że w płytach prostokątnych opartych na całym

obwodzie należy uwzględnić dwukierunkowe zginanie, gdy stosunek długości

obwodzie należy uwzględnić dwukierunkowe zginanie, gdy stosunek długości

boków płyty

boków płyty

l

l

x

x

i

i

l

l

y

y

zawiera się w granicach

zawiera się w granicach

0.5

2.0

y

x

l

l

Ł

Ł

Płyty oblicza się według teorii sprężystości lub teorii nośności granicznej.

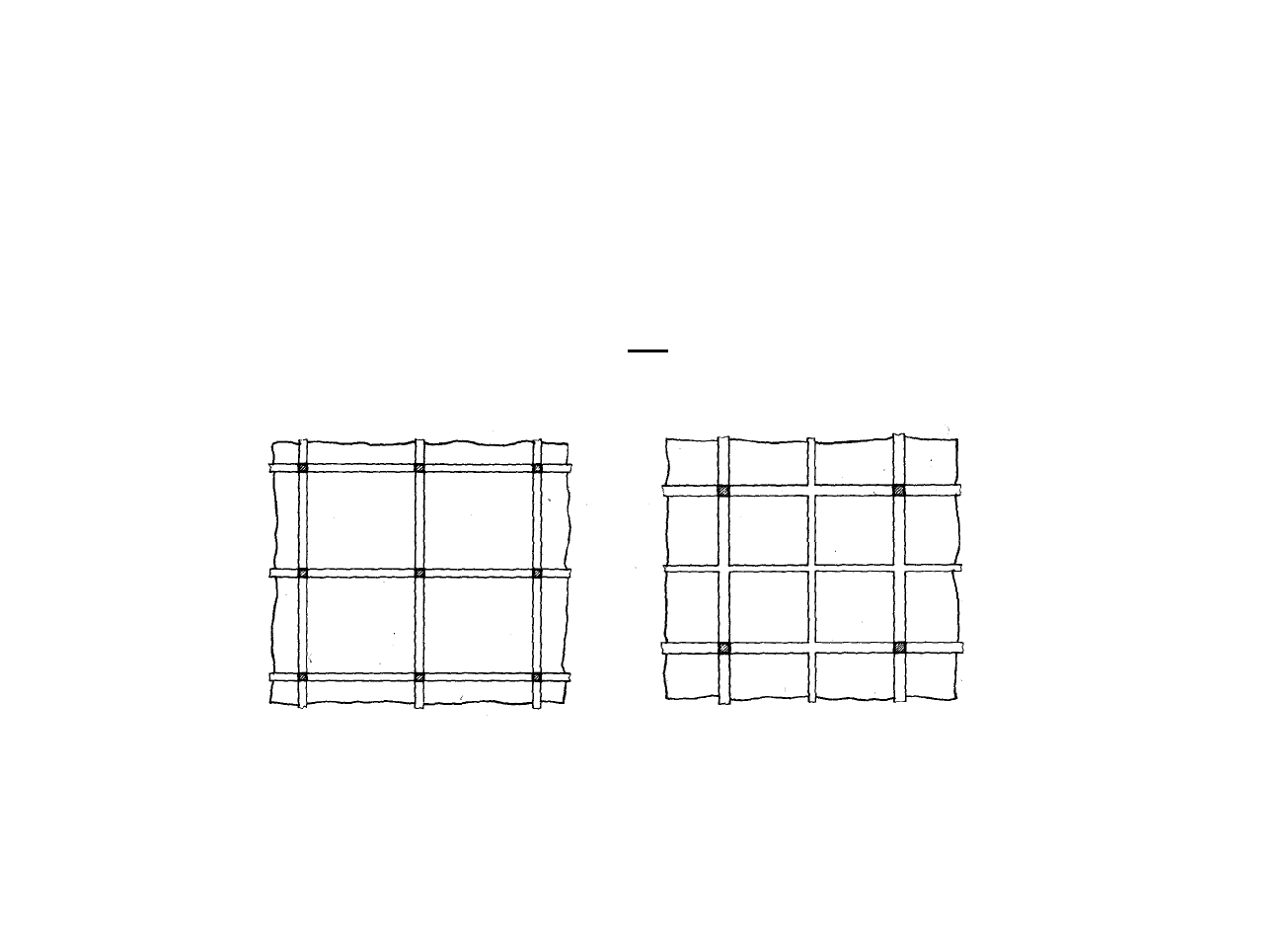
Rys.3.1:

Płyty pracujące dwukierunkowo

Płyty pracujące dwukierunkowo

Obliczanie płyt według teorii

Obliczanie płyt według teorii

sprężystości

sprężystości

Zakłada się, że:

Zakłada się, że:

- grubość jest niewielka w porównaniu z pozostałymi wymiarami,

- grubość jest niewielka w porównaniu z pozostałymi wymiarami,

- punkty leżące na normalnej do powierzchni również po odkształceniu

- punkty leżące na normalnej do powierzchni również po odkształceniu

pozostają na normalnej do odkształconej powierzchni,

pozostają na normalnej do odkształconej powierzchni,

- ugięcia są małe w porównaniu z grubością płyty,

- ugięcia są małe w porównaniu z grubością płyty,

- pomija się wydłużenia i odkształcenia kątowe w płaszczyźnie środkowej.

- pomija się wydłużenia i odkształcenia kątowe w płaszczyźnie środkowej.

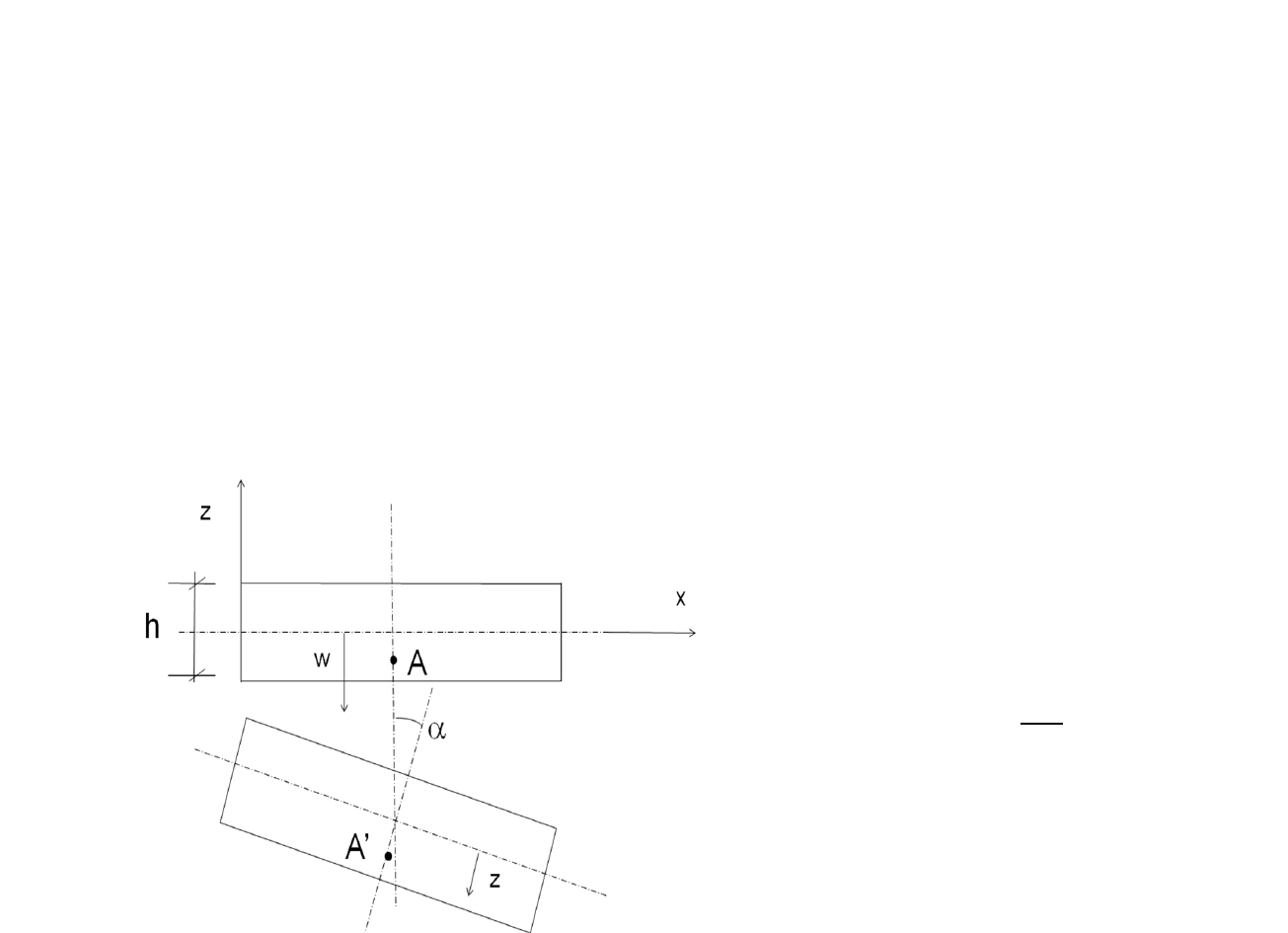
Przemieszczenie płyty

Przemieszczenie płyty

w płaszczyźnie

w płaszczyźnie

zy

zy

w

x

α

∂

=

∂

Wzory na przemieszczenia są następujące

Wzory na przemieszczenia są następujące

:

:

w

u

tg

z

z

x

α

∂

= −

• =

•

∂

w

v

tg

z

z

y

β

∂

= −

• =

•

∂

w w

=

Równanie płyty

Równanie płyty

:

:

4

4

4

2

4

2

2

4

3

2

12(1

)

w

w

w

q

x

x y

y

Eh

ν

∂

∂

∂

−

+

+

=

∂

∂ ∂

∂

h

h

- grubość płyty,

- grubość płyty,

E

E

- moduł sprężystości,

- moduł sprężystości,

q

q

- obciążenie ciągłe,

- obciążenie ciągłe,

ν

ν

- współczynnik Poissona

- współczynnik Poissona

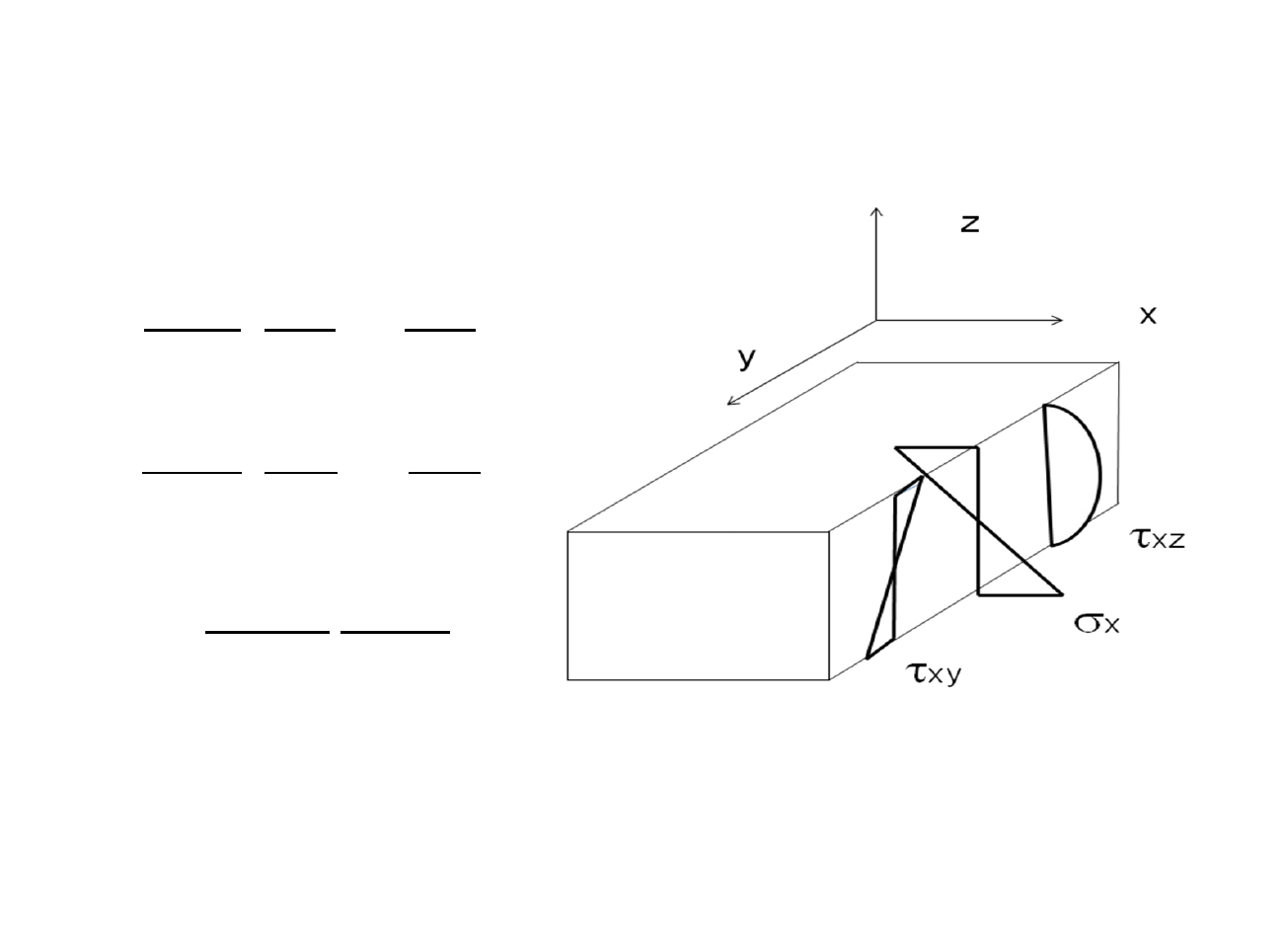
Jeżeli znana jest funkcja

Jeżeli znana jest funkcja

w (x,y

w (x,y

), to naprężenia normalne i styczne są

), to naprężenia normalne i styczne są

równe

równe

2

2

2

2

2

(

)

1

x

Ez

w

w

x

y

σ

ν

ν

∂

∂

=

+

−

∂

∂

2

2

2

2

2

(

)

1

y

Ez

w

w

y

x

σ

ν

ν

∂

∂

=

+

−

∂

∂

2

1

xy

Ez

w

x y

τ

ν

∂

= −

+

∂ ∂

Rys.3.2: Naprężenia na jednym boku

płyty pracującej dwukierunkowo

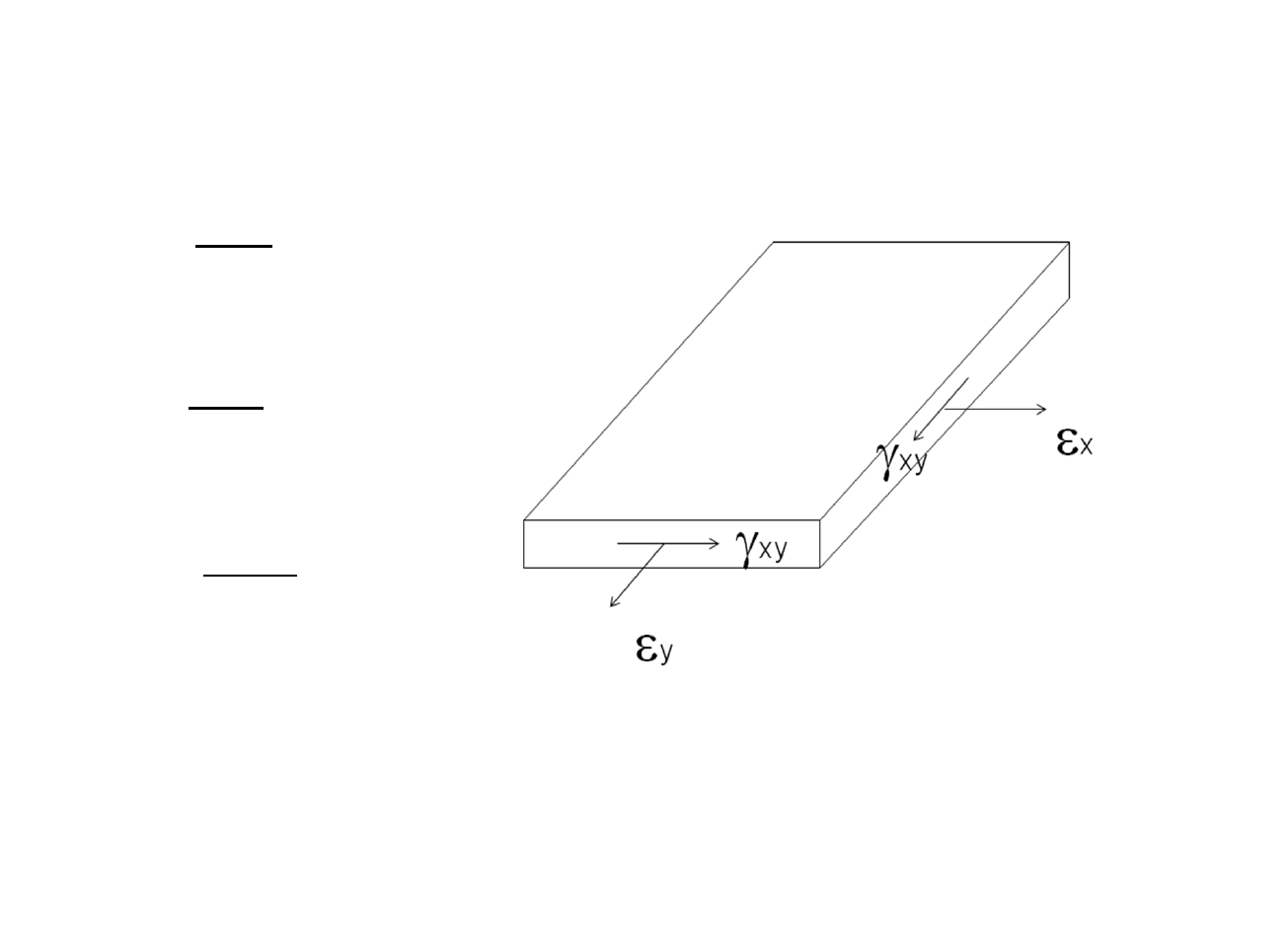
Odkształcenia normalne i styczne są równe (Rys.3.3)

Odkształcenia normalne i styczne są równe (Rys.3.3)

2

2

x

w

z

x

ε

∂

= −

∂

2

2

y

w

z

y

ε

∂

= −

∂

2

xy

w

z

x y

γ

∂

= −

∂ ∂

Rys.3.3: Odkształcenia normalne i
styczne boku na bokach płyty
pracującej dwukierunkowo

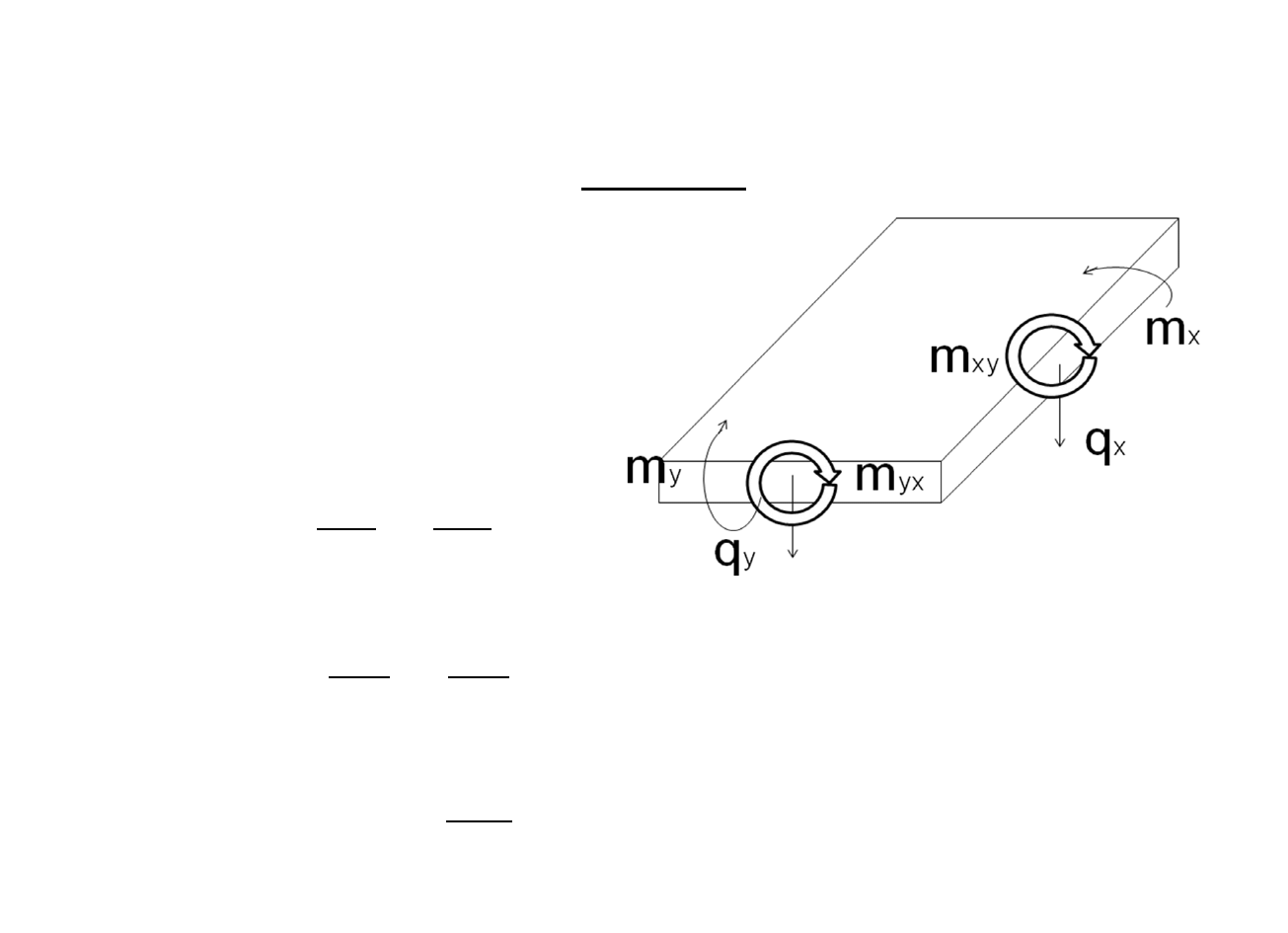
Siły tnące i momenty oblicza się ze wzorów

Siły tnące i momenty oblicza się ze wzorów

( )

( )

3

2

12(1

)

Eh

K

ν

=

−

/ 2

/ 2

h

x

xz

h

q

dz

τ

−

=

ň

/ 2

/ 2

h

y

yz

h

q

dz

τ

−

=

ň

/ 2

2

2

2

2

/ 2

(

)

h

x

x

h

w

w

m

zdz

K

x

y

σ

ν

−

∂

∂

=

= −

+

∂

∂

ň

/ 2

2

2

2

2

/ 2

(

)

h

y

y

h

w

w

m

zdz

K

y

x

σ

ν

−

∂

∂

=

= −

+

∂

∂

ň

/ 2

2

/ 2

(1

)

h

xy

yx

xy

h

w

m

m

dz

K

x y

τ

ν

−

∂

=

=

= − −

∂ ∂

ň

Rys.3.4: Siły tnące i momenty na

Rys.3.4: Siły tnące i momenty na

bokach

płyty

pracującej

bokach

płyty

pracującej

dwukierunkowo

dwukierunkowo

[ ,

,

]

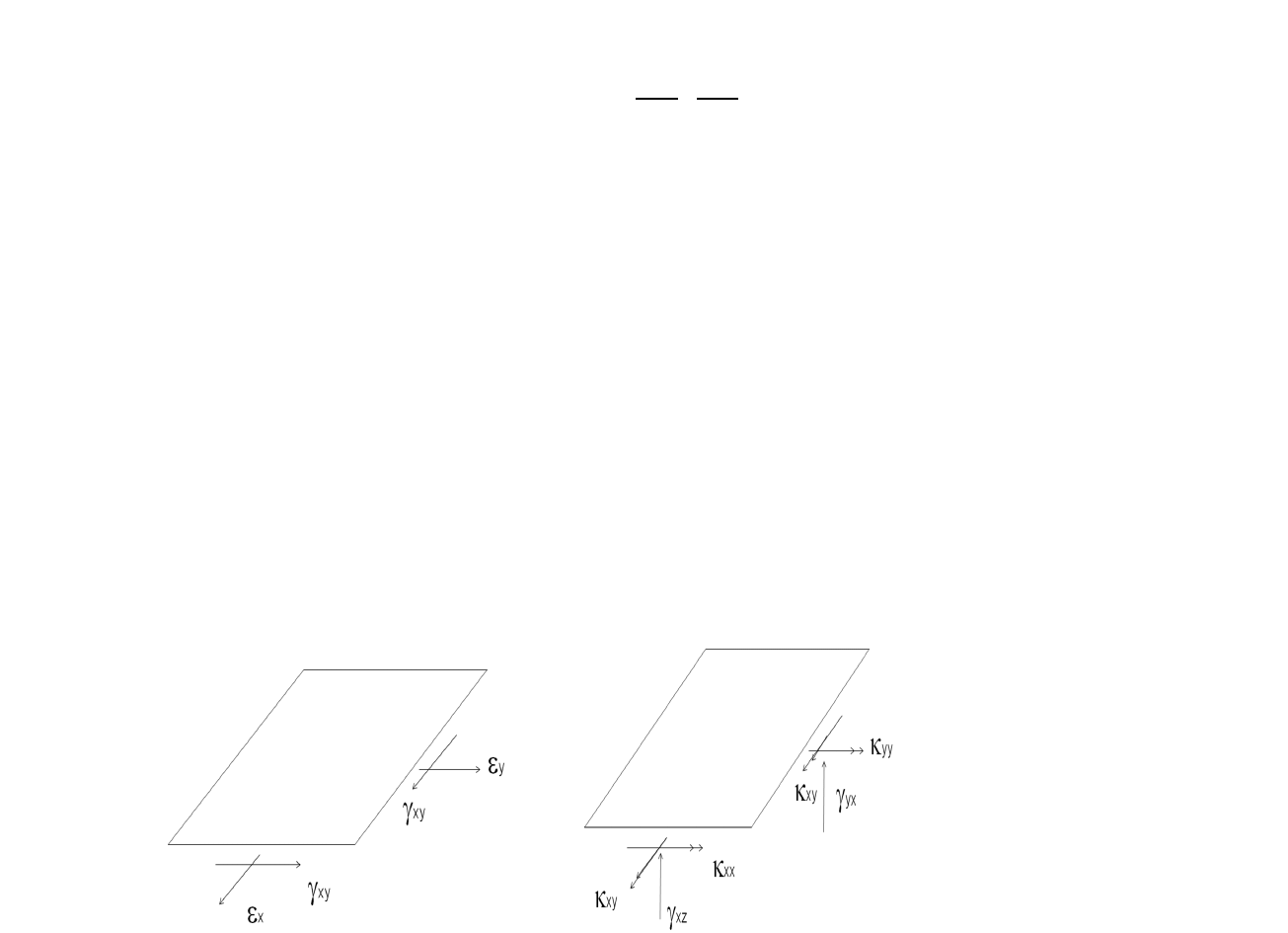
w w

w

y

x

∂

∂

∂

∂

, ,

xx

yy

xy

ε ε γ

Każdy punkt płyty ma 3 stopnie swobody
(przemieszczenie + 2 obroty):

Na podstawie przemieszczeń i obrotów oblicza się odkształcenia

.

Obliczenia płyt można też wykonać w oparciu o teorię sprężystości dla
tzw. płyty Mindlina, która uwzględnia się odkształcenia styczne
(Rys.3.5). Każdy węzeł ma wtedy 5 stopni swobody (3 przemieszczenia i
2 niezależne obroty): u, v, w,

θ

x

i

θ

y

. Na podstawie przemieszczeń i

obrotów wyznacza się odkształcenia i siły wewnętrzne:

[ ,

,

,

,

, ,

]

[ , , , ,

, , ]

xx

yy

xx

yy

xy

xz

yz

x

y

x

y

xy

x

y

n n m m m q q

ε ε κ κ κ γ γ

→

.

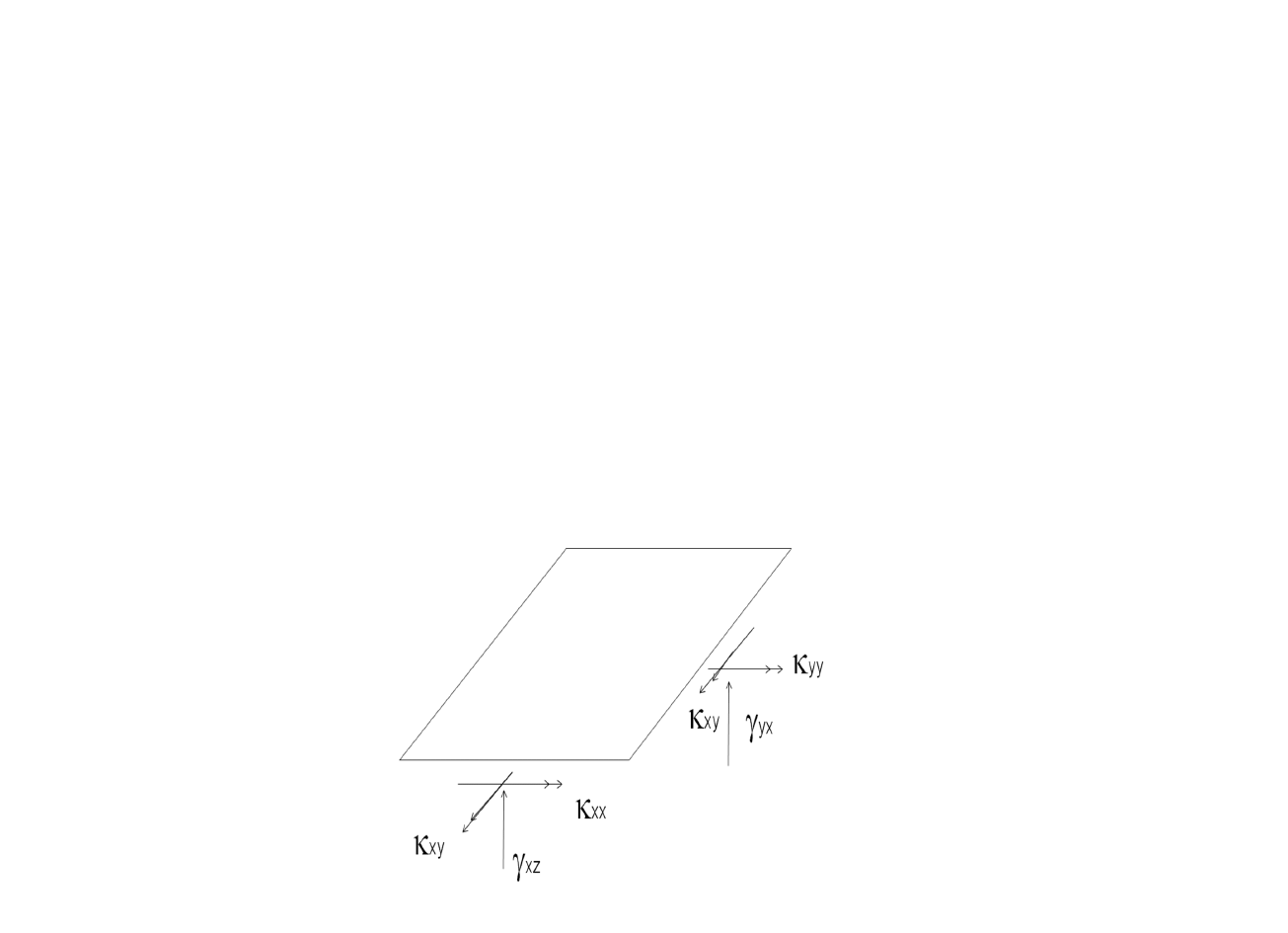
Zakrzywienia oblicza się ze wzorów:

Zakrzywienia oblicza się ze wzorów:

,

x

y x

κ

θ

=

,

y

x y

κ

θ

= −

,

,

xy

x x

y y

κ

θ

θ

= −

+

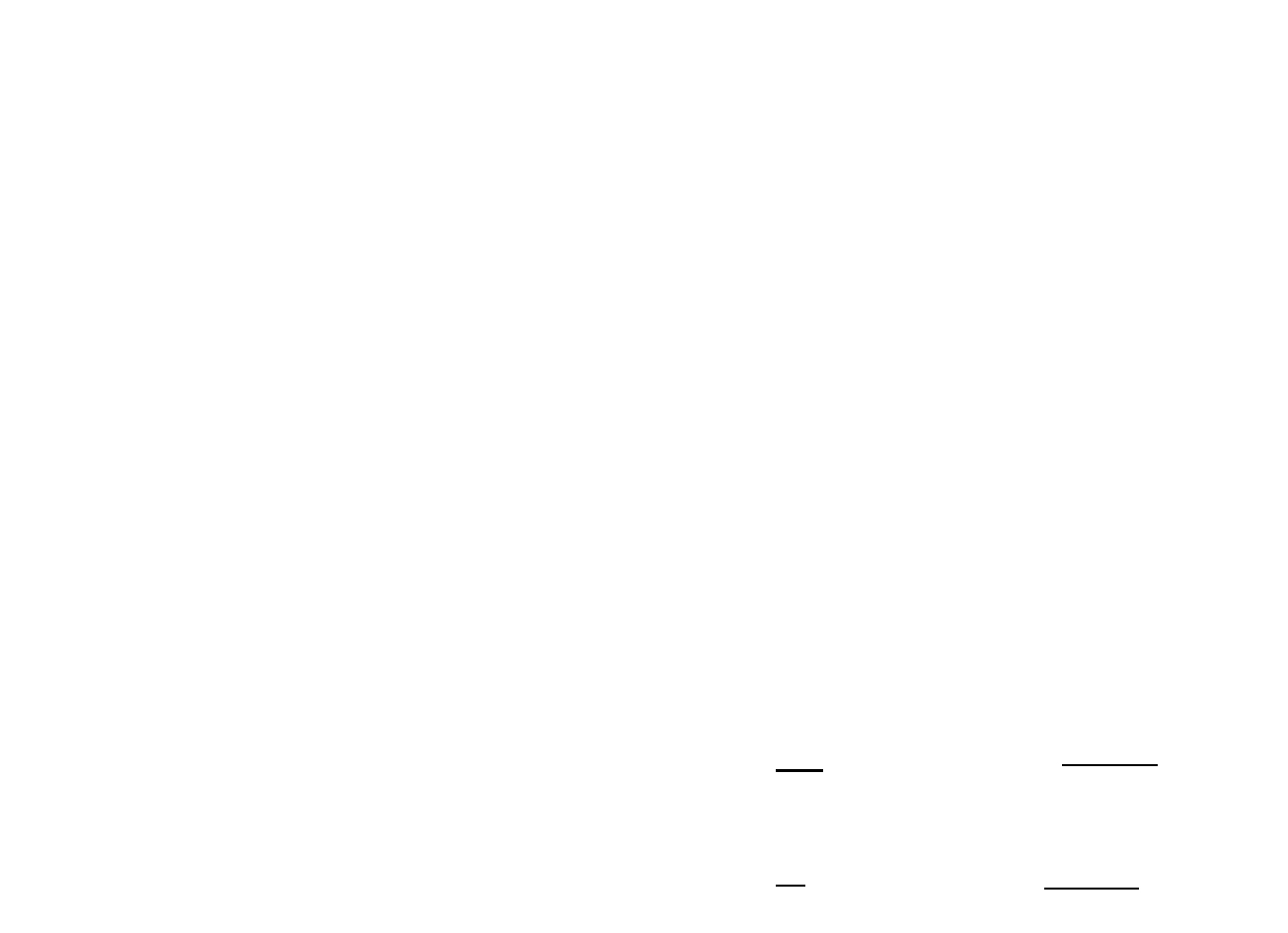
Obliczanie płyt krzyżowo-zbrojonych według teorii sprężystości pod

Obliczanie płyt krzyżowo-zbrojonych według teorii sprężystości pod

obciążeniem równomiernym

obciążeniem równomiernym

Płyty jednoprzęsłowe obciążone równomiernie

Płyty jednoprzęsłowe obciążone równomiernie

Momenty przęsłowe są obliczone ze wzorów:

Momenty przęsłowe są obliczone ze wzorów:

2

x

x

x

M

ql

ϕ

=

2

y

y

y

M

ql

ϕ

=

q

q

– obciążenie równomierne,

– obciążenie równomierne,

l

l

x

x

i

i

l

l

y

y

– wymiary płyty,

– wymiary płyty,

ϕ

ϕ

x

x

i

i

ϕ

ϕ

y

y

–

–

współczynniki

współczynniki

Momenty podporowe są obliczone ze wzorów:

Momenty podporowe są obliczone ze wzorów:

-

płyty obustronne zamocowanie

płyty obustronne zamocowanie

2

12

x

x

M

ql

χ

= −

2

(1

)

12

y

y

M

ql

χ

−

= −

- jednostronne zamocowanie

- jednostronne zamocowanie

2

8

x

x

M

ql

χ

= −

2

(1

)

8

y

y

M

ql

χ

−

= −

Rys.3.6: Schematy płyt prostokątnych podpartych wzdłuż

Rys.3.6: Schematy płyt prostokątnych podpartych wzdłuż

obwodu

obwodu

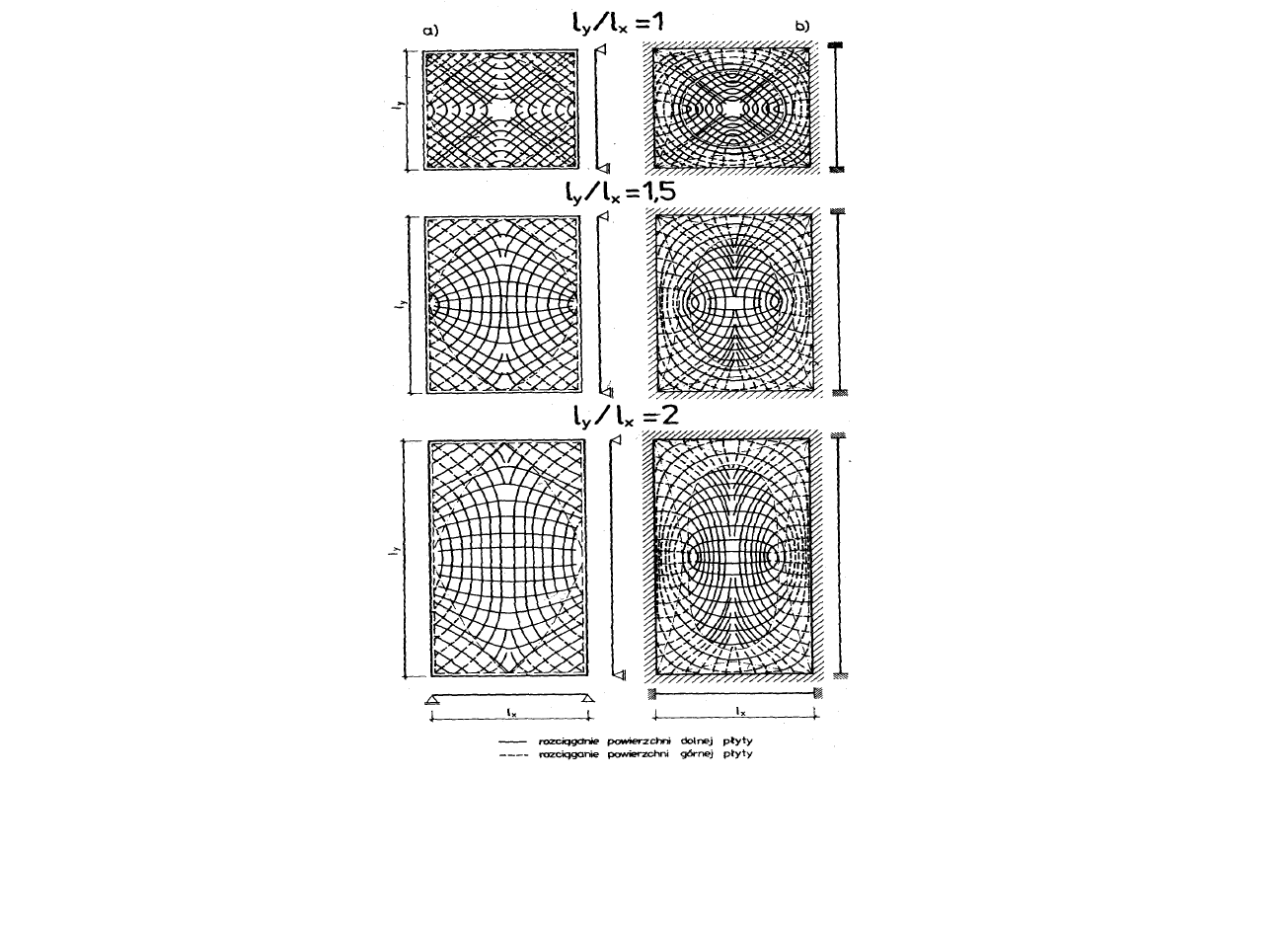
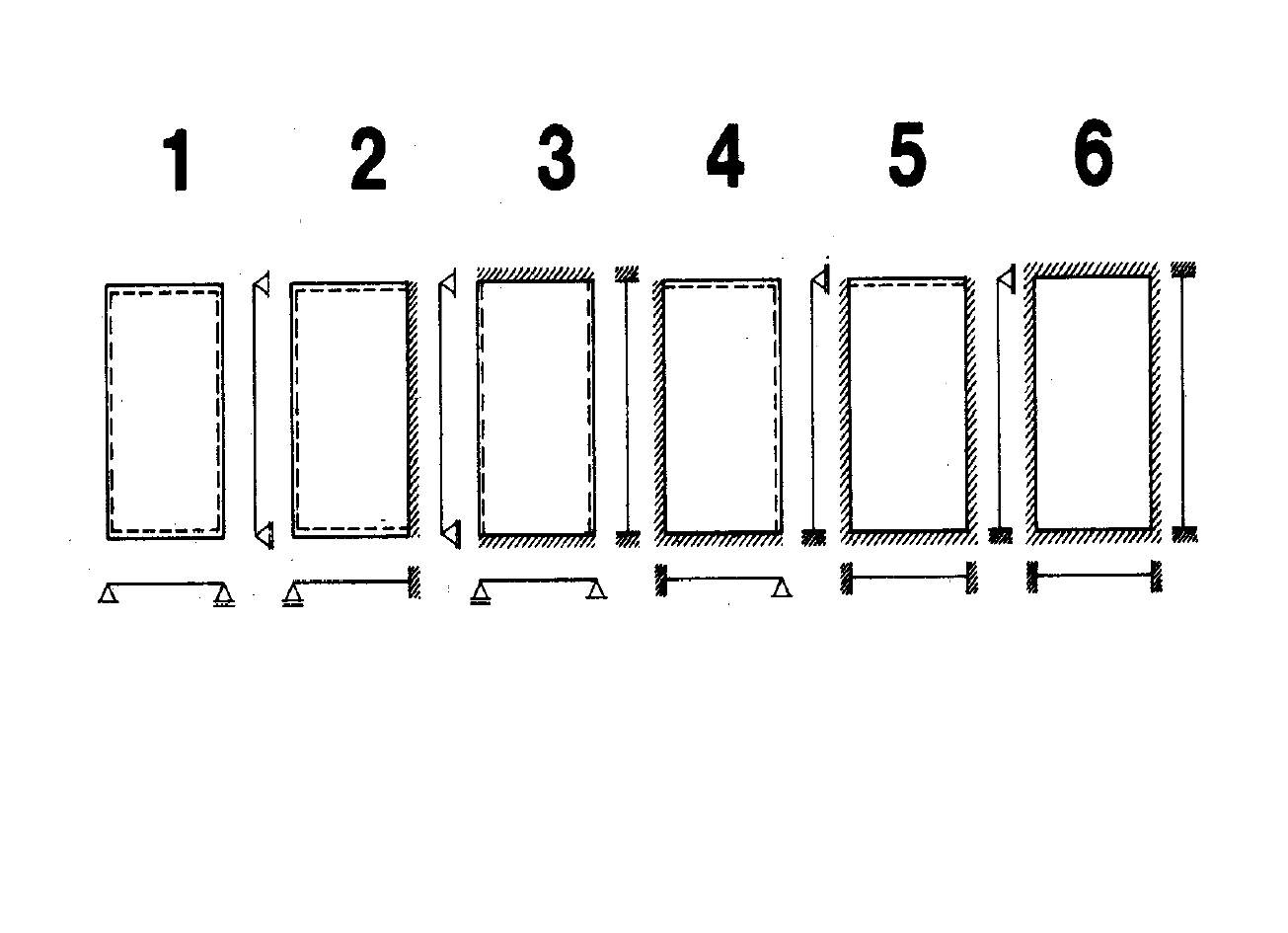
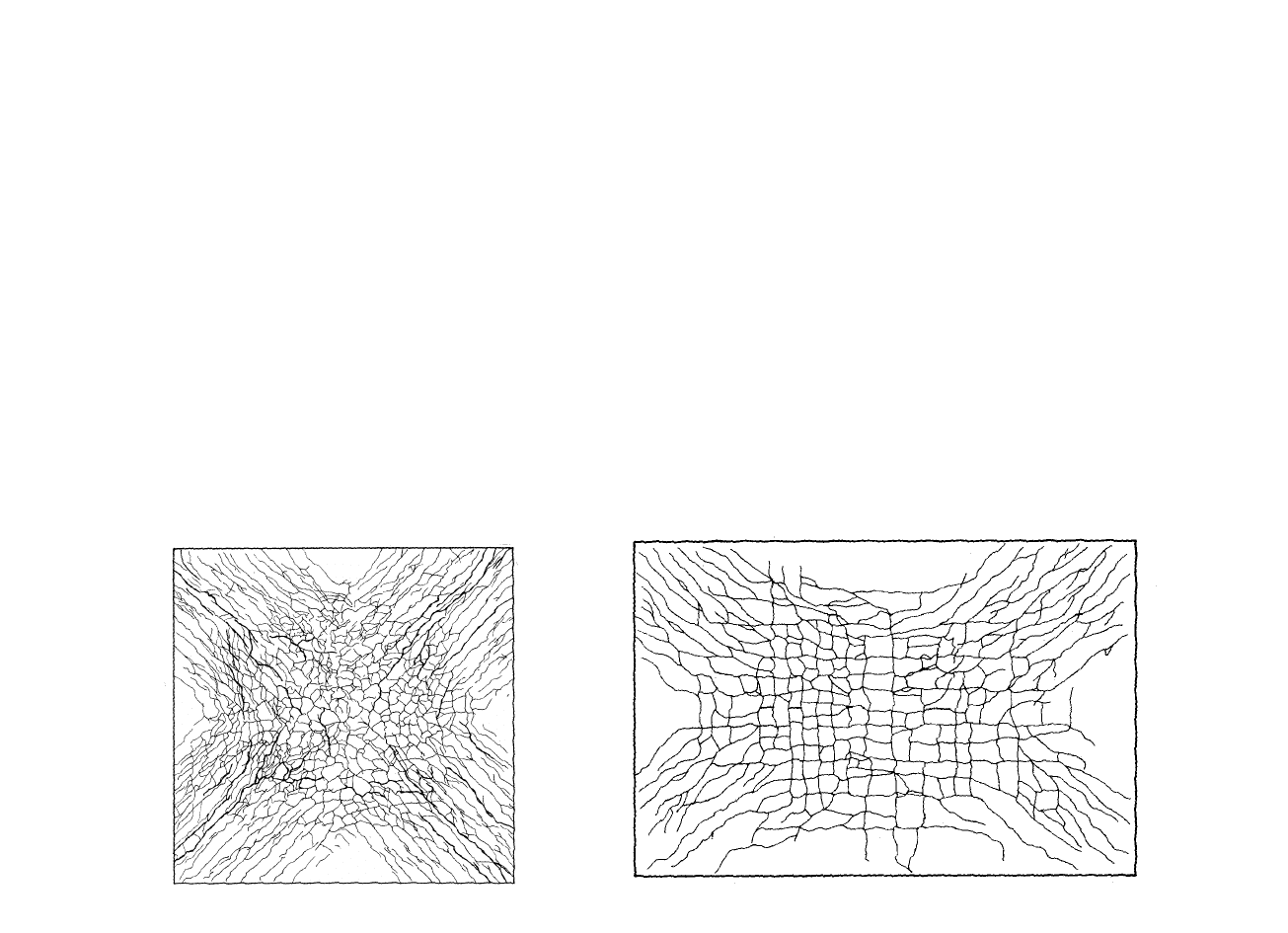
Rys.3.7: Trajektorie momentów głównych dla płyty obciążonej
równomiernie: a) płyta swobodnie podparta na obwodzie, b) płyta
zamocowana na obwodzie

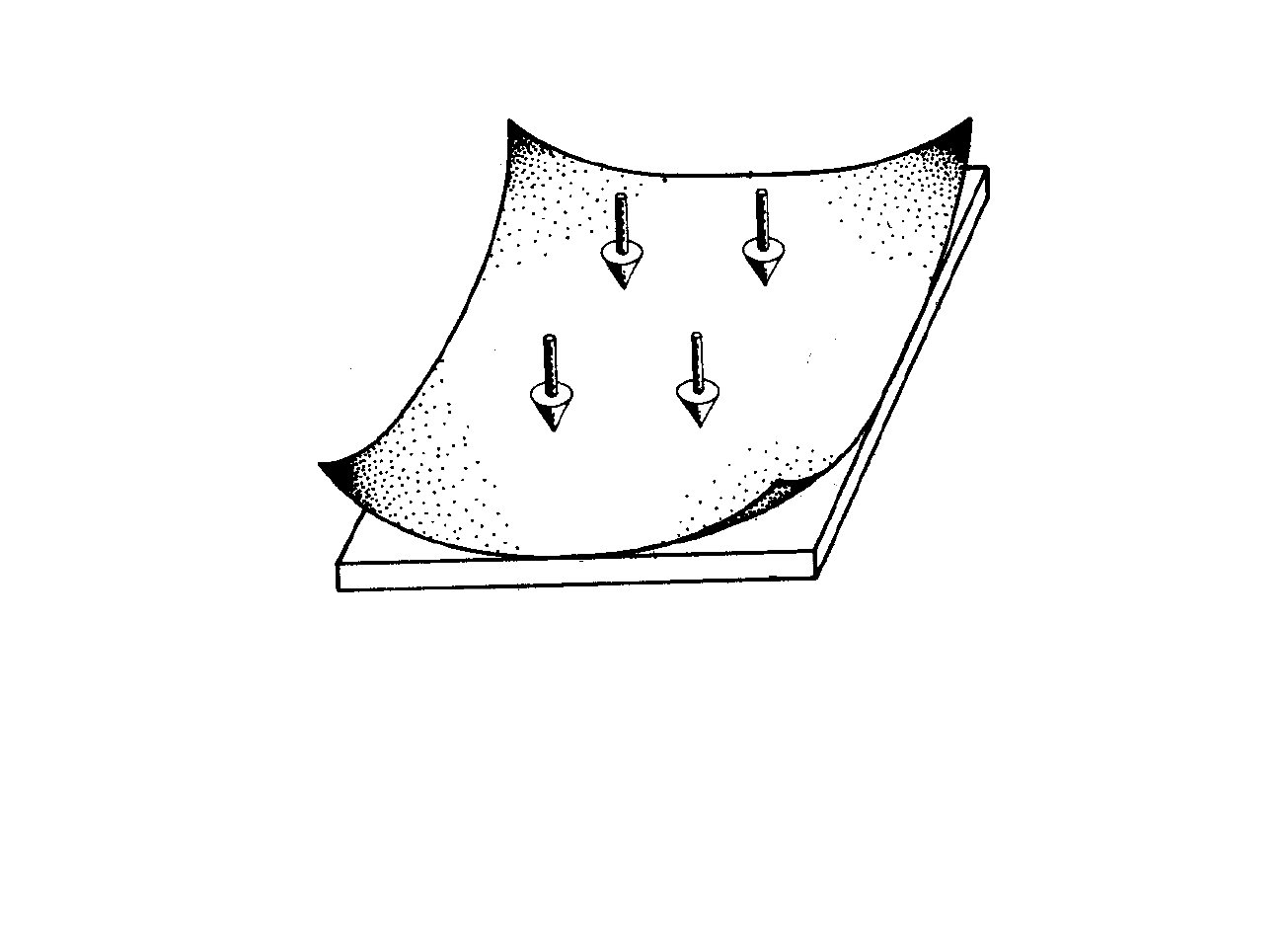
Rys.3.8: Unoszenie naroży płyty podpartej swobodnie wzdłuż obwodu

Rys.3.8: Unoszenie naroży płyty podpartej swobodnie wzdłuż obwodu

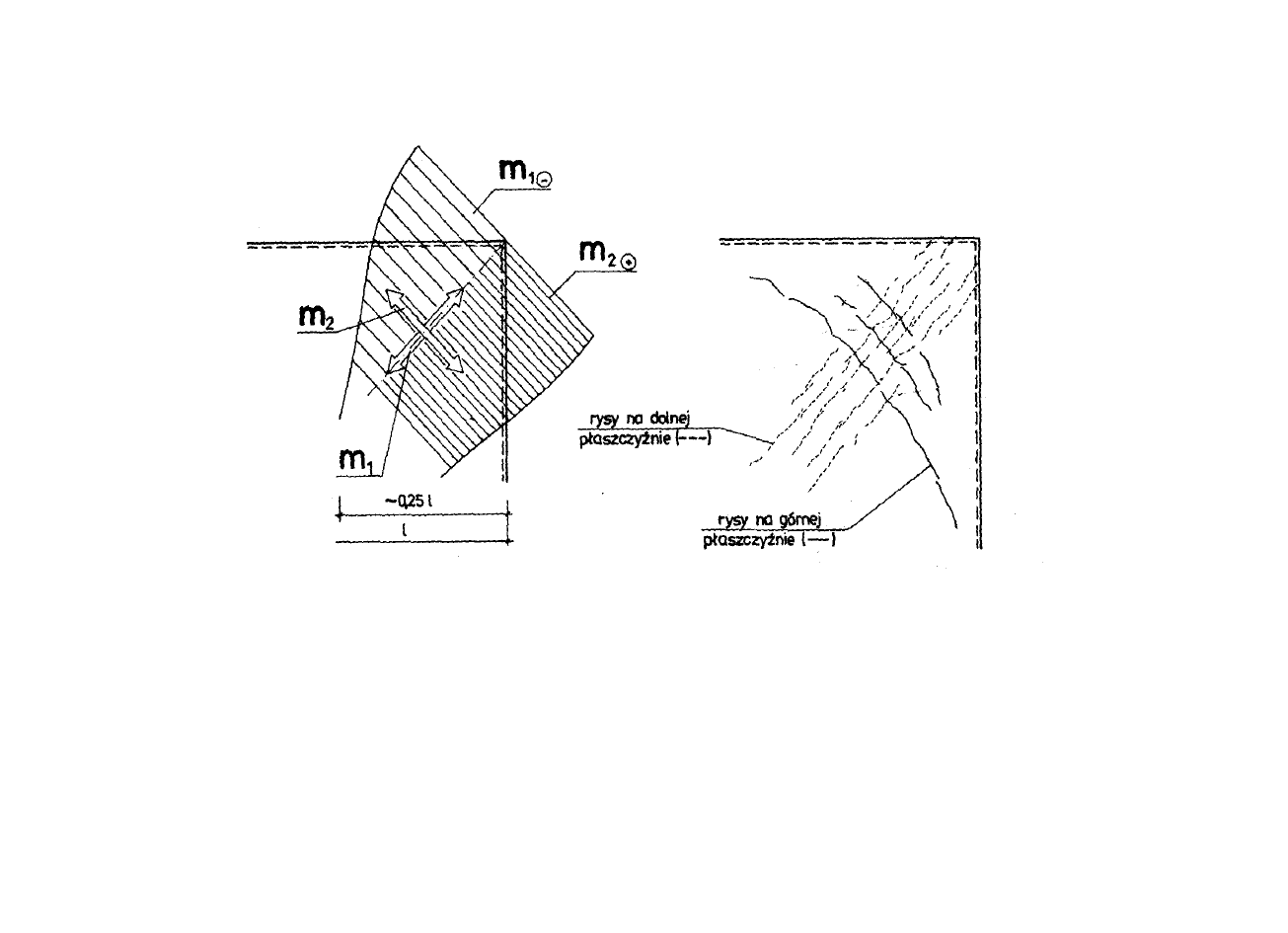
Rys.3.9: Praca części płyty w narożu swobodnie podpartej na

Rys.3.9: Praca części płyty w narożu swobodnie podpartej na

obwodzie: a) główne momenty zginające, b) szkic zarysowania

obwodzie: a) główne momenty zginające, b) szkic zarysowania

a

a

b

b

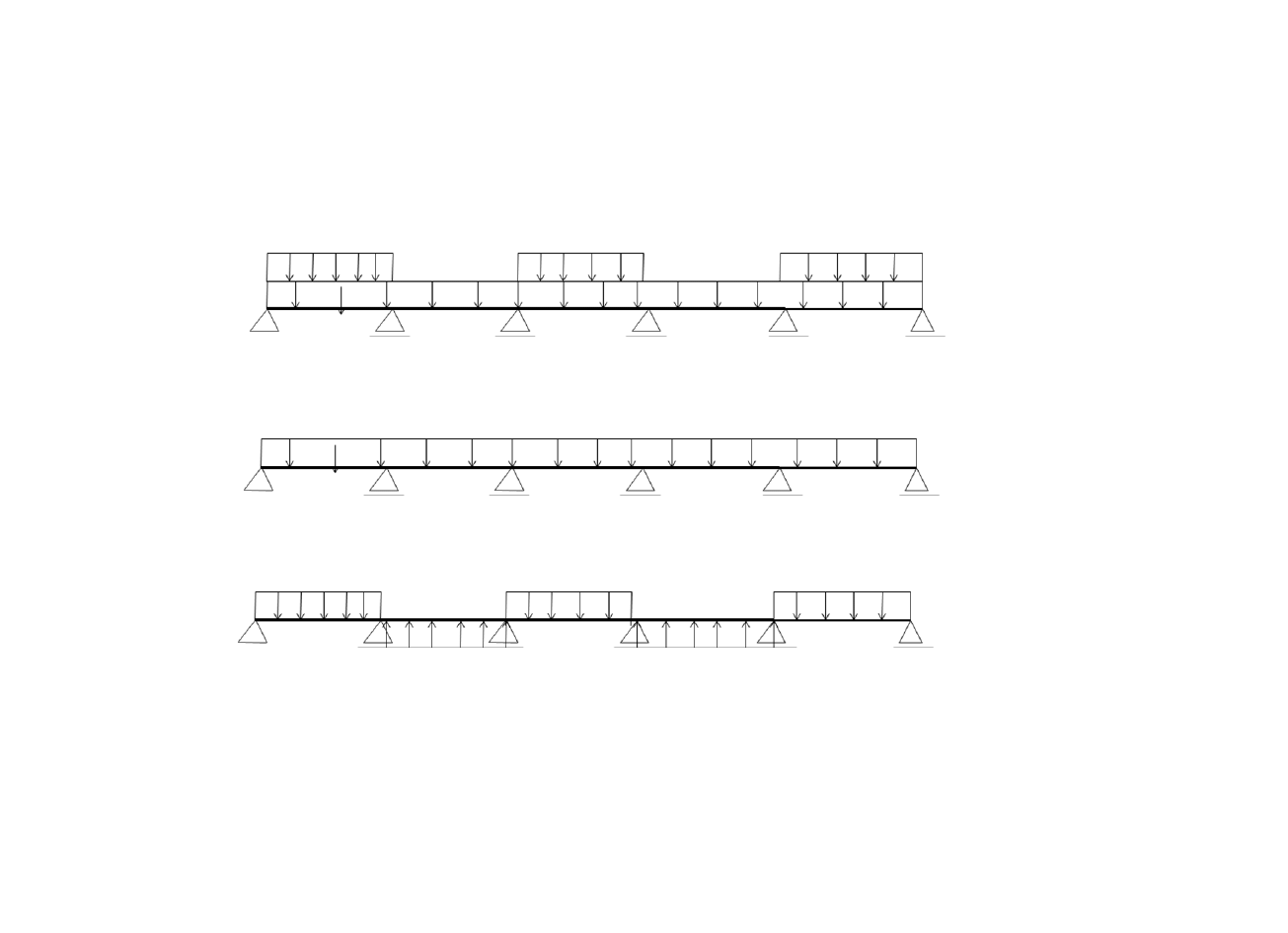
Płyty wieloprzęsłowe obciążone równomiernie

Płyty wieloprzęsłowe obciążone równomiernie

W celu obliczenia maksymalnych momentów przęsłowych schemat

W celu obliczenia maksymalnych momentów przęsłowych schemat

obciążeniowy

obciążeniowy

g

g

i

i

p

p

jest rozłożony na 2 schematy (Rys.3.10).

jest rozłożony na 2 schematy (Rys.3.10).

q’=g+p

q’=g+p

/2

/2

g+p

g+p

q”=p

q”=p

/2

/2

Rys.6.6: Schemat obciążeniowy do wyznaczenia maksymalnych

Rys.6.6: Schemat obciążeniowy do wyznaczenia maksymalnych

momentów przęsłowych w płytach pracujących dwukierunkowo

momentów przęsłowych w płytach pracujących dwukierunkowo

(Starosolski 1985)

(Starosolski 1985)

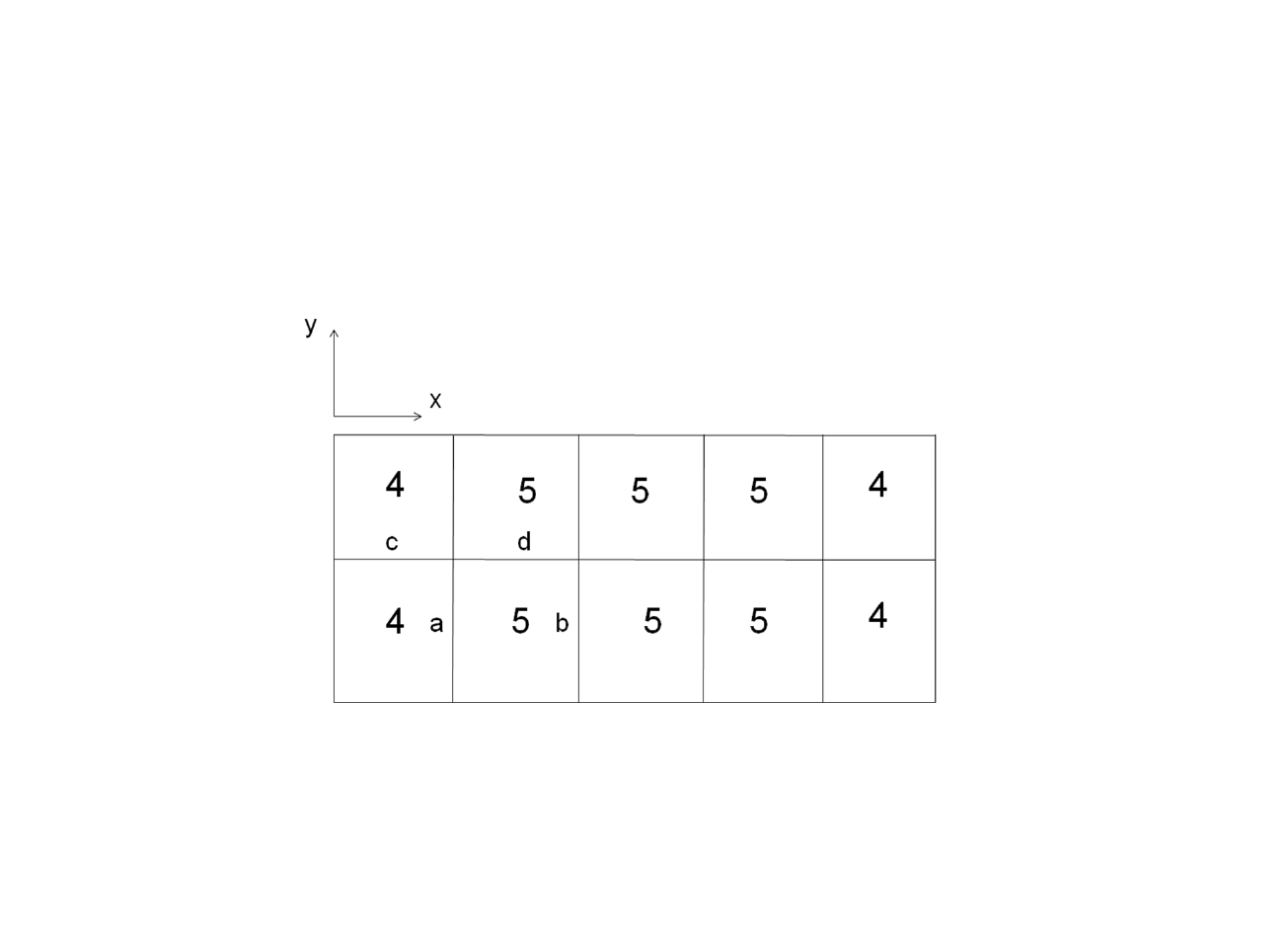
Maksymalne momenty przęsłowe

Maksymalne momenty przęsłowe

(przy szachownicowym obciążeniu

(przy szachownicowym obciążeniu

p)

p)

2

'

''

1

(

)

x

x

x

x

M

l

q

q

ϕ

ϕ

=

+

2

'

''

1

(

)

y

y

y

y

M

l

q

q

ϕ

ϕ

=

+

2

'

''

4

1

(

)

x

x

x

x

M

l

q

q

ϕ

ϕ

=

+

2

'

''

4

1

(

)

y

y

x

y

M

l

q

q

ϕ

ϕ

=

+

2

'

''

5

1

(

)

x

x

x

x

M

l

q

q

ϕ

ϕ

=

+

2

'

''

5

1

(

)

y

y

x

y

M

l

q

q

ϕ

ϕ

=

+

‘

‘

4’

4’

‘

‘

5’

5’

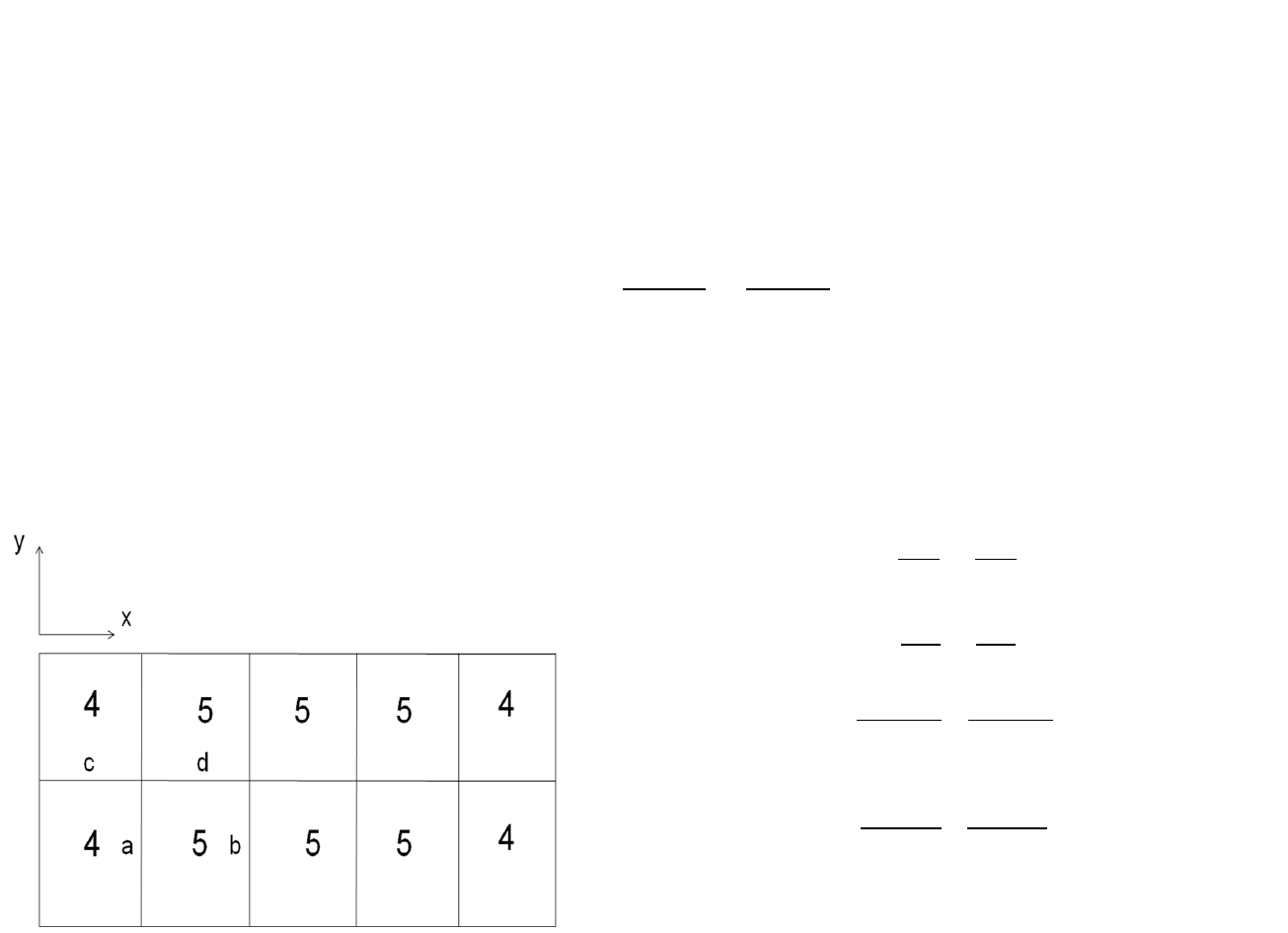
Maksymalne momenty podporowe otrzymuje się

Maksymalne momenty podporowe otrzymuje się

przy obciążeniu wszystkich przęseł (

przy obciążeniu wszystkich przęseł (

q=p+g

q=p+g

)

)

2

2

(

)

pod

i xL

i xP

x

L

P

l

l

M

q

χ

χ

ψ

ψ

= −

−

gdzie (jeżeli przeciwległa podpora jest swobodnie podparta)

gdzie (jeżeli przeciwległa podpora jest swobodnie podparta)

oraz (jeżeli przeciwległa podpora jest utwierdzona).

oraz (jeżeli przeciwległa podpora jest utwierdzona).

,

16

L P

ψ

=

,

24

L P

ψ

=

2

5

4

(

)

16

24

pod

a

x

M

ql

χ

χ

= −

+

2

5

5

(

)

24 24

pod

b

x

M

ql

χ

χ

= −

+

2

4

4

(1

) (1

)

(

)

16

16

pod

c

y

M

ql

χ

χ

−

−

= −

+

‘

‘

a’

a’

‘

‘

b’

b’

‘

‘

c’

c’

2

5

5

(1

) (1

)

(

)

16

16

pod

d

y

M

ql

χ

χ

−

−

= −

+

‘

‘

d’

d’

Momenty krawędziowe oblicza się ze wzorów:

Momenty krawędziowe oblicza się ze wzorów:

2 2

kr

pod

x

x

x

ql b

M

M

χ

=

+

(1

)

2

2

y

kr

pod

y

y

ql b

M

M

χ

−

=

+

gdzie

gdzie

b

b

– szerokość podpory

– szerokość podpory

.

.

3.3 Obliczanie płyt według teorii nośności

3.3 Obliczanie płyt według teorii nośności

granicznej

granicznej

W konstrukcji żelbetowej obliczonej według liniowej teorii

W konstrukcji żelbetowej obliczonej według liniowej teorii

sprężystości tkwią znaczne rezerwy nośności. Analizując stan

sprężystości tkwią znaczne rezerwy nośności. Analizując stan

granicznego zniszczenia można uzyskać około 20-25%

granicznego zniszczenia można uzyskać około 20-25%

oszczędności zbrojenia.

oszczędności zbrojenia.

Obszar zarysowania płyty krzyżowo zbrojonej:

Obszar zarysowania płyty krzyżowo zbrojonej:

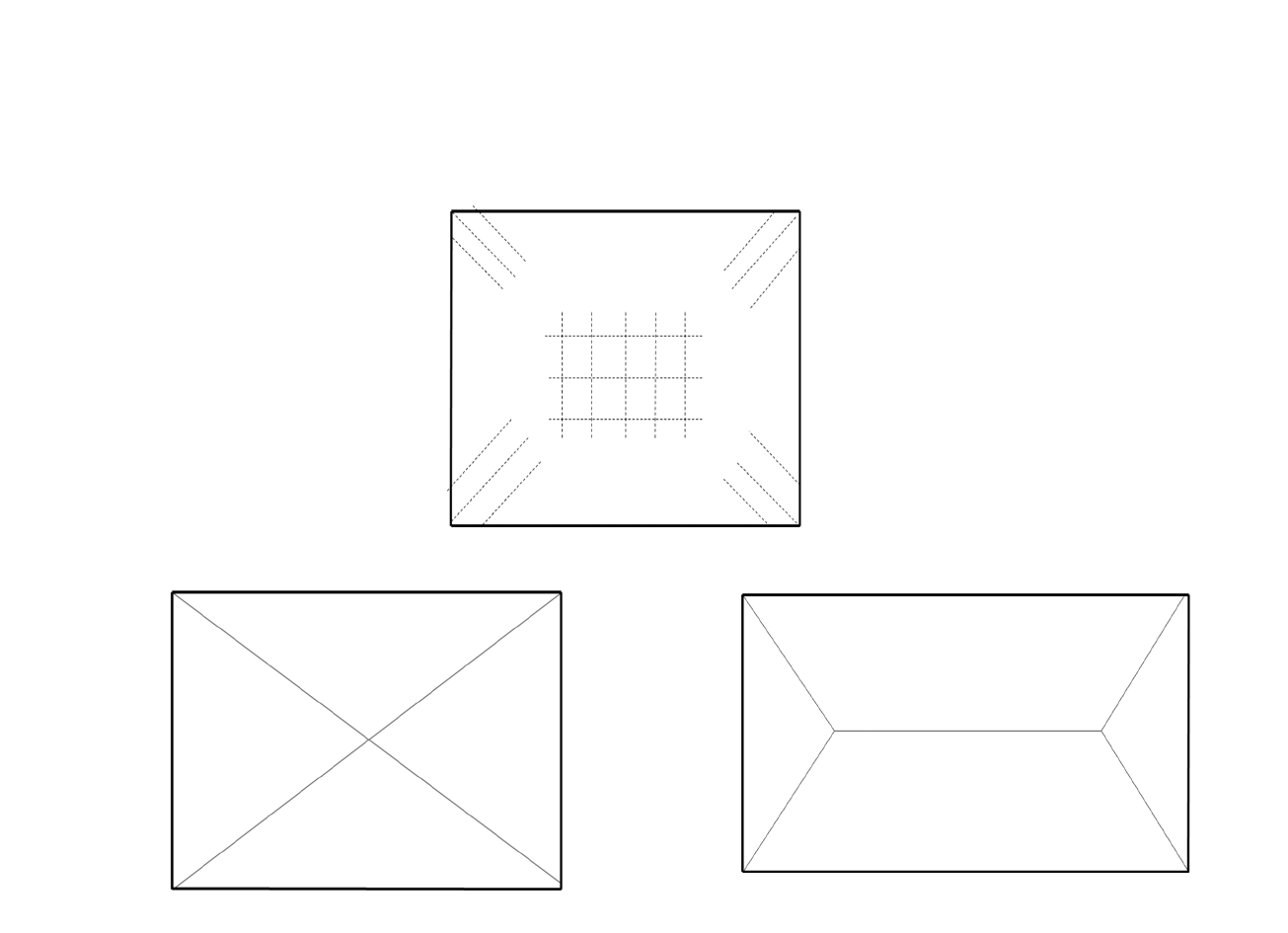
Przyjmuje się, że zarysowanie (uplastycznienie) przekrojów występuje

Przyjmuje się, że zarysowanie (uplastycznienie) przekrojów występuje

wzdłuż pewnych linii zwanych liniami załomów, których przebieg

wzdłuż pewnych linii zwanych liniami załomów, których przebieg

zależy od warunków podparcia, stosunku boków, obciążenia i zbrojenia

zależy od warunków podparcia, stosunku boków, obciążenia i zbrojenia

Warunek nośności płyty określa się metodą kinematyczną

Warunek nośności płyty określa się metodą kinematyczną

przyrównując pracę sił zewnętrznych do pracy sił wewnętrznych.

przyrównując pracę sił zewnętrznych do pracy sił wewnętrznych.

Praca sił zewnętrznych jest pracą obciążeń na przemieszczeniach od

Praca sił zewnętrznych jest pracą obciążeń na przemieszczeniach od

odkształceń

odkształceń

Praca sił zewnętrznych jest pracą obciążeń na przemieszczeniach od

Praca sił zewnętrznych jest pracą obciążeń na przemieszczeniach od

odkształceń

odkształceń

V

L q ydF

qV

δ =

=

ň

gdzie

gdzie

q

q

– obciążenie równomiernie rozłożone,

– obciążenie równomiernie rozłożone,

V

V

–

–

objętość bryły między powierzchnia płyty przed

objętość bryły między powierzchnia płyty przed

obciążeniem i po obciążeniu

obciążeniem i po obciążeniu

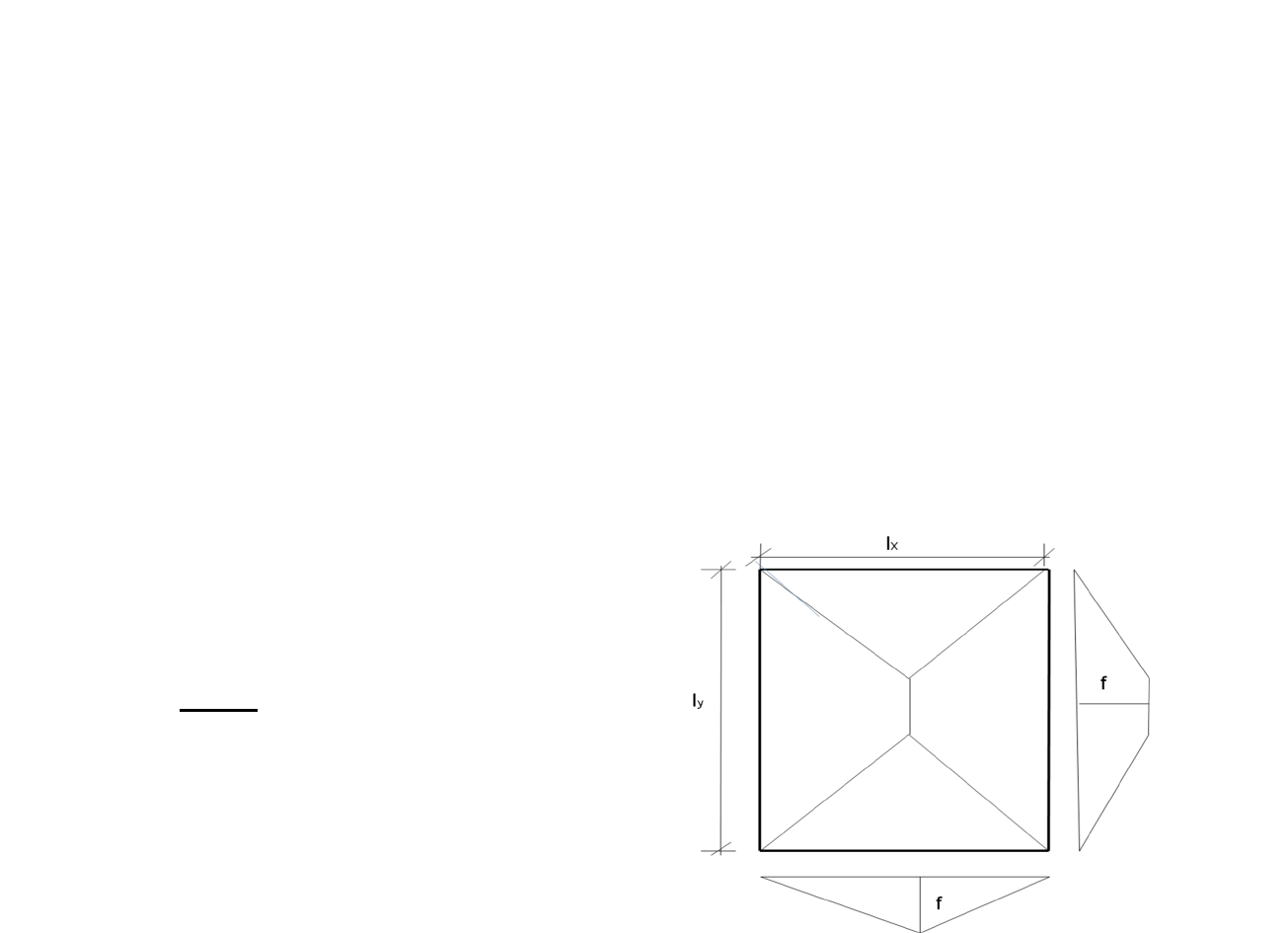
(3

)

6

x

y

x

fl

V

l

l

=

−

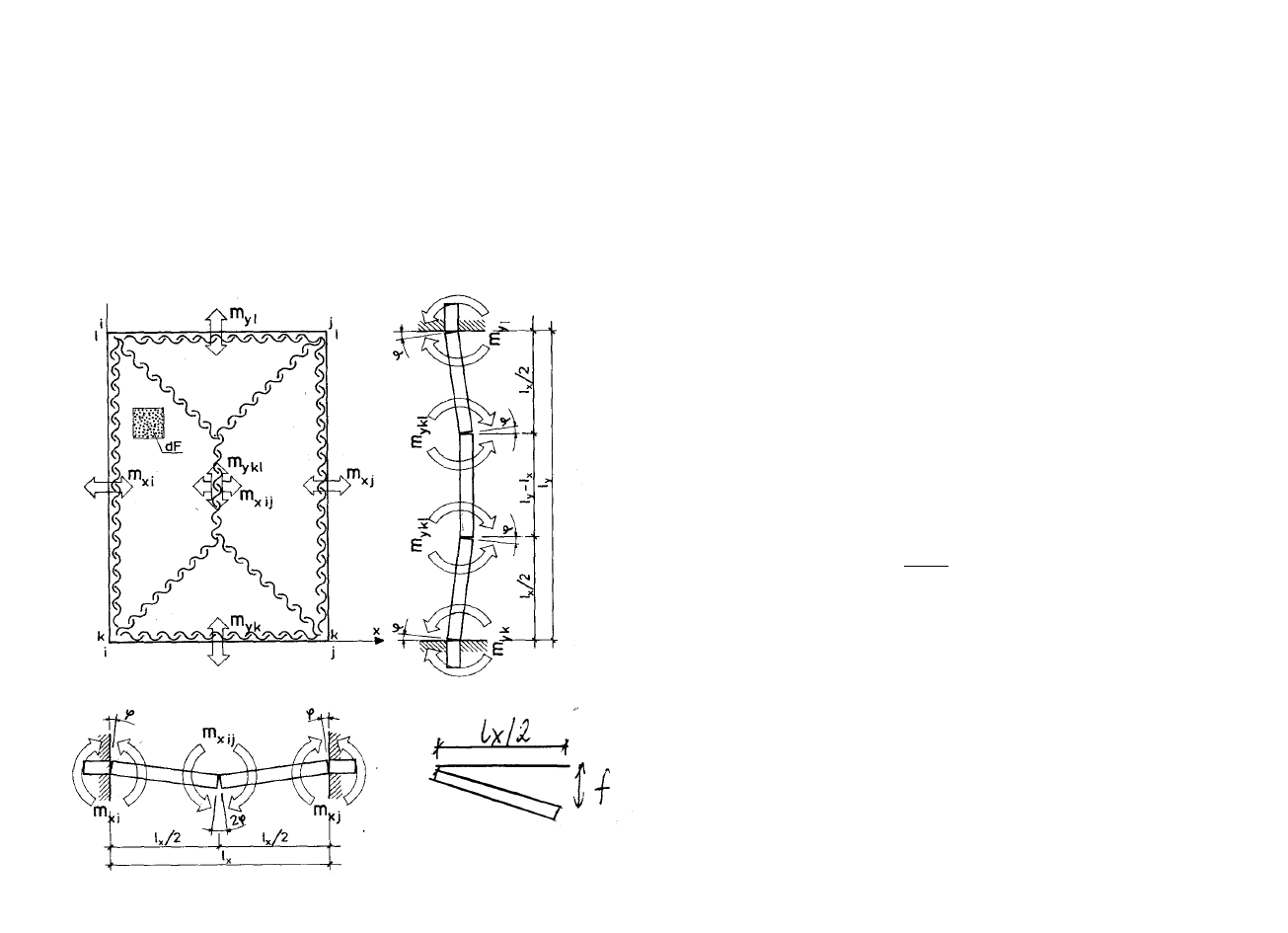
Praca sił wewnętrznych jest pracą momentów zginających na

Praca sił wewnętrznych jest pracą momentów zginających na

odpowiadających im kątach płatów wzdłuż linii załomu. Zakłada

odpowiadających im kątach płatów wzdłuż linii załomu. Zakłada

się, że zbrojenie jest rozłożone równomiernie dla każdego

się, że zbrojenie jest rozłożone równomiernie dla każdego

kierunku.

kierunku.

Praca sił wewnętrznych jest równa

Praca sił wewnętrznych jest równa

U

M

δ

ϕ

=

ĺ

(

2

)

(

2

)

g

d

g

g

d

g

xi

xij

xj

y

yk

ykl

yl

x

U

m

m

m

l

m

m

m

l

δ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

=

+

+

+

+

+

2

(tan

)

f

l

ϕ

ϕ ϕ

=

≅

Z porównania prac

Z porównania prac

2

(

2

)

(

)

(3

)

12

g

d

g

g

d

g

xi

xij

xj

y

yk

ykl

yl

x

x

y

x

q

m

m

m l

m

m

m l

l

l

l

+

+

+

+

+

=

−

Redukcja zbrojenia w pasmach środkowych o 50% w pasmach o

Redukcja zbrojenia w pasmach środkowych o 50% w pasmach o

szerokości 1/5

szerokości 1/5

l

l

uwzględnia się przez redukcję momentu

uwzględnia się przez redukcję momentu

m

m

xij

xij

i

i

m

m

ykl

ykl

.

.

Dla kierunku

Dla kierunku

l

l

y

y

2

8

2

2

2

2 5

5

d

xij

d

d

xij

y

xij y

m

m

l

m l

ϕ

ϕ

ϕ

−

=

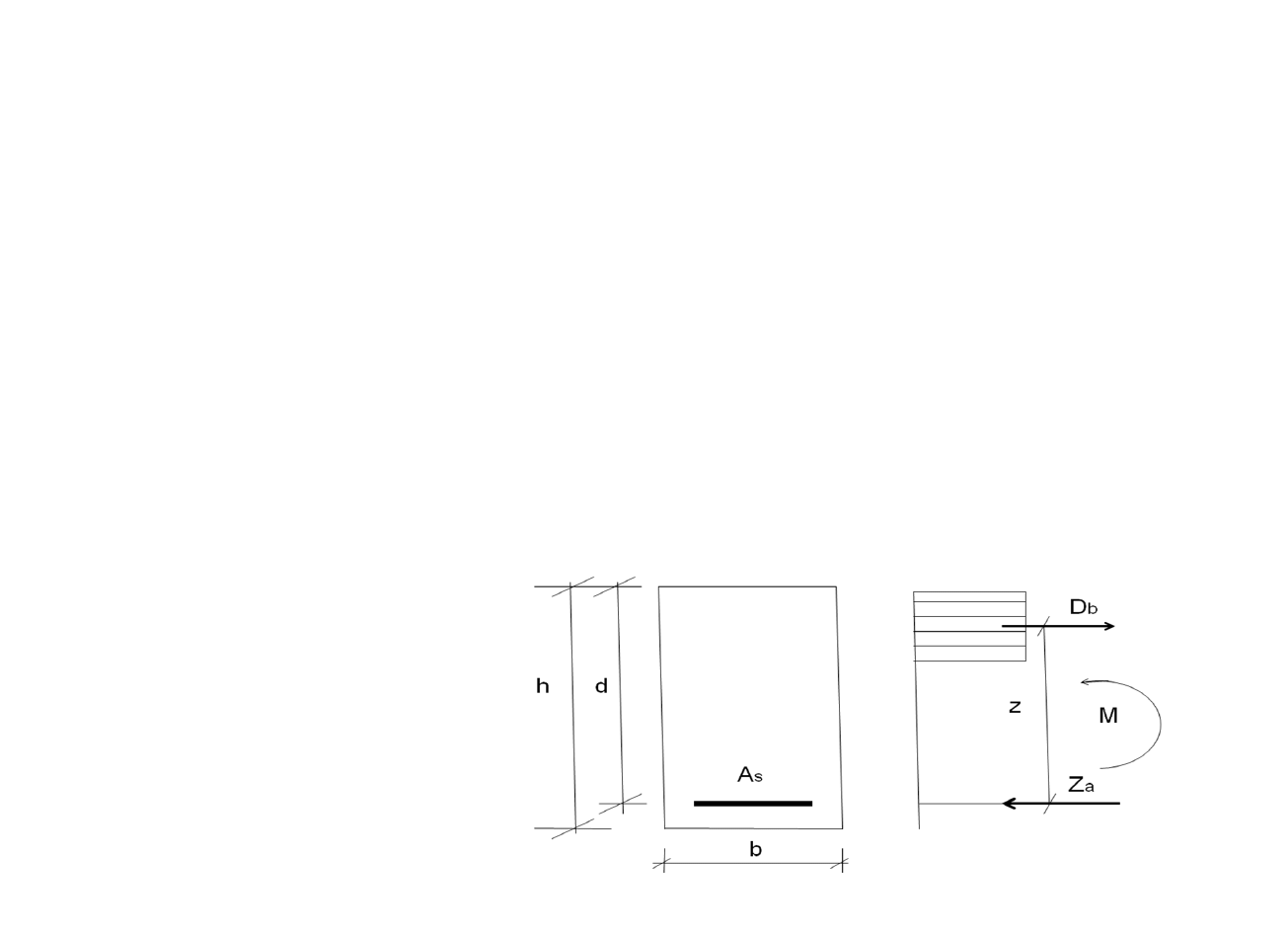
W stanie granicznym momenty są równe

W stanie granicznym momenty są równe

g

xi

si

y

m

A f z

η

=

g

xij

sij y

m

A f z

η

=

g

xi

sj

y

m

A f z

η

=

0.9

z

d

≅

a

s

y

Z

A f

=

Współczynnik redukcyjny jest przyjęty

Współczynnik redukcyjny jest przyjęty

z uwagi na monolityczne połączenie z

z uwagi na monolityczne połączenie z

żebrami i wieńcami:

żebrami i wieńcami:

η

η

=1.25 (dla pól o

=1.25 (dla pól o

podpór wewnętrznych) i

podpór wewnętrznych) i

η

η

=1.10 (dla

=1.10 (dla

pól skrajnych).

pól skrajnych).

xi

xi

xij

m

m

ψ

=

xj

xj

xij

m

m

ψ

=

yk

yk

xij

m

m

ψ

=

yl

yl

xij

m

m

ψ

=

ykl

ykl

xij

m

m

ψ

=

2

[(

2

)

(

) ]

(3

)

12

xij

xi

xi

y

yk

ykl

yl

x

x

y

x

q

m

l

l

l

l

l

ψ

ψ

ψ

ψ

ψ

+ +

+

+

+

=

−

Wprowadza się współczynniki

Wprowadza się współczynniki

ψ

ψ

, które określają stosunek

, które określają stosunek

wszystkich momentów zginających w stosunku do momentu

wszystkich momentów zginających w stosunku do momentu

m

m

xij

xij

Współczynniki

Współczynniki

ψ

ψ

powinny być tak dobrane, aby

powinny być tak dobrane, aby

uzyskane momenty, a co za tym idzie zbrojenie

uzyskane momenty, a co za tym idzie zbrojenie

było proporcjonalne do rozkładu momentów pod

było proporcjonalne do rozkładu momentów pod

obciążeniem eksploatacyjnym.

obciążeniem eksploatacyjnym.

l

x

/l

y

ψ

ykl

ψ

xi ,

ψ

xj

ψ

yk, ,

ψ

yl

1

1.2

1.5

1.8

2.0

0.8-1.0

0.6-0.8

0.35-0.55

0.20-0.40

0.15-0.30

1.3-2.5

1.0-2.0

1.3-2.5

0.2-0.75

Z równania wyznacza się moment zginający

Z równania wyznacza się moment zginający

m

m

xij

xij

,

,

a potem

a potem

pozostałe momenty zginające. Płyty liczymy jako zespół

pozostałe momenty zginające. Płyty liczymy jako zespół

płyt pojedynczych zaczynając od pola wewnętrznego.

płyt pojedynczych zaczynając od pola wewnętrznego.

Obliczając następnie płytę sąsiednią wprowadza się do

Obliczając następnie płytę sąsiednią wprowadza się do

równania momenty podporowe.

równania momenty podporowe.

3.4 Zbrojenie płyt

3.4 Zbrojenie płyt

 

 

Zbrojenie płyty krzyżowo-zbrojonej według teorii

Zbrojenie płyty krzyżowo-zbrojonej według teorii

liniowo-sprężystej

liniowo-sprężystej

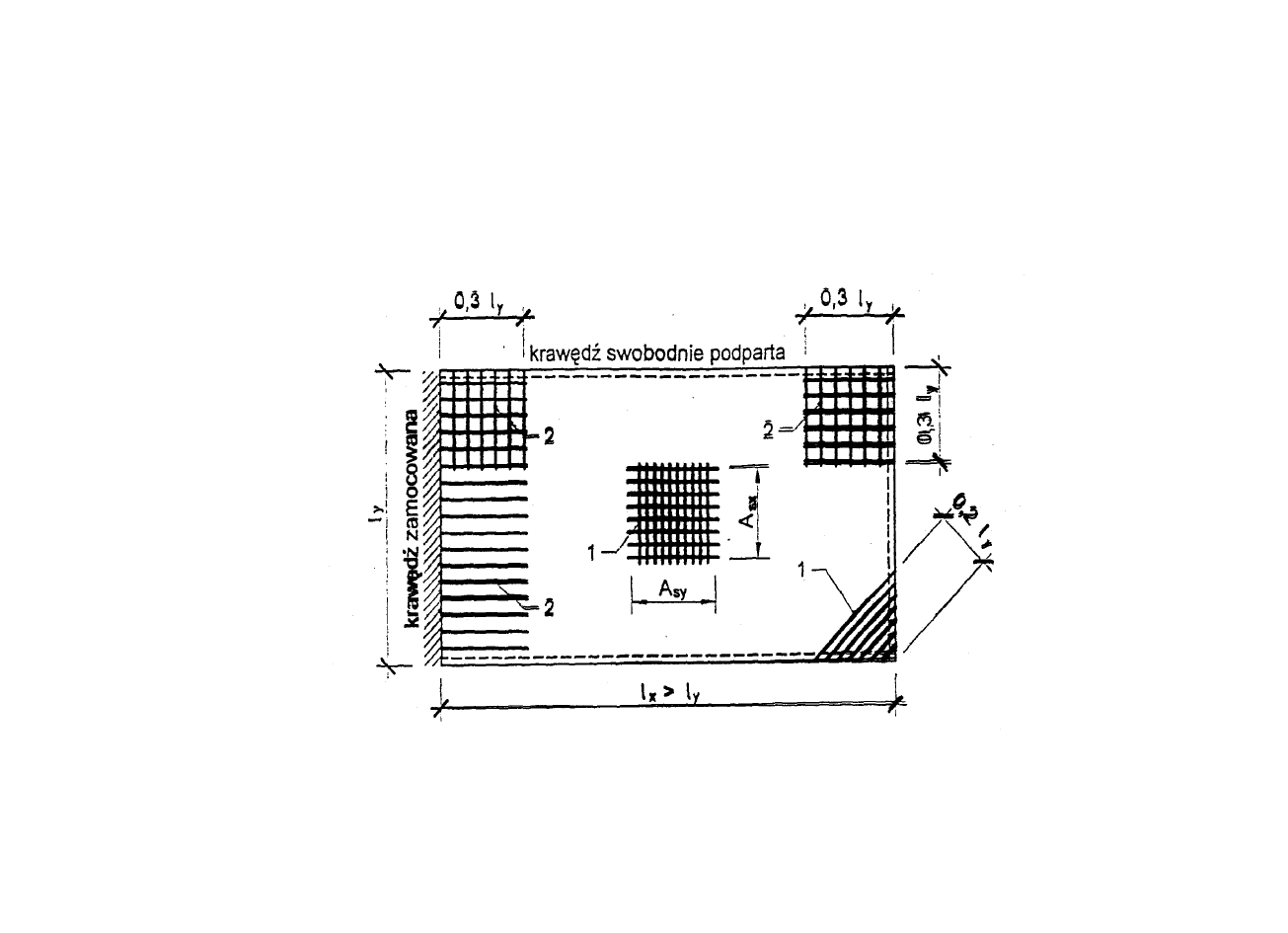
Zbrojenie płyt krzyżowo zbrojonych:

Zbrojenie płyt krzyżowo zbrojonych:

1 – zbrojenie dolne, 2 – zbrojenie górne

1 – zbrojenie dolne, 2 – zbrojenie górne

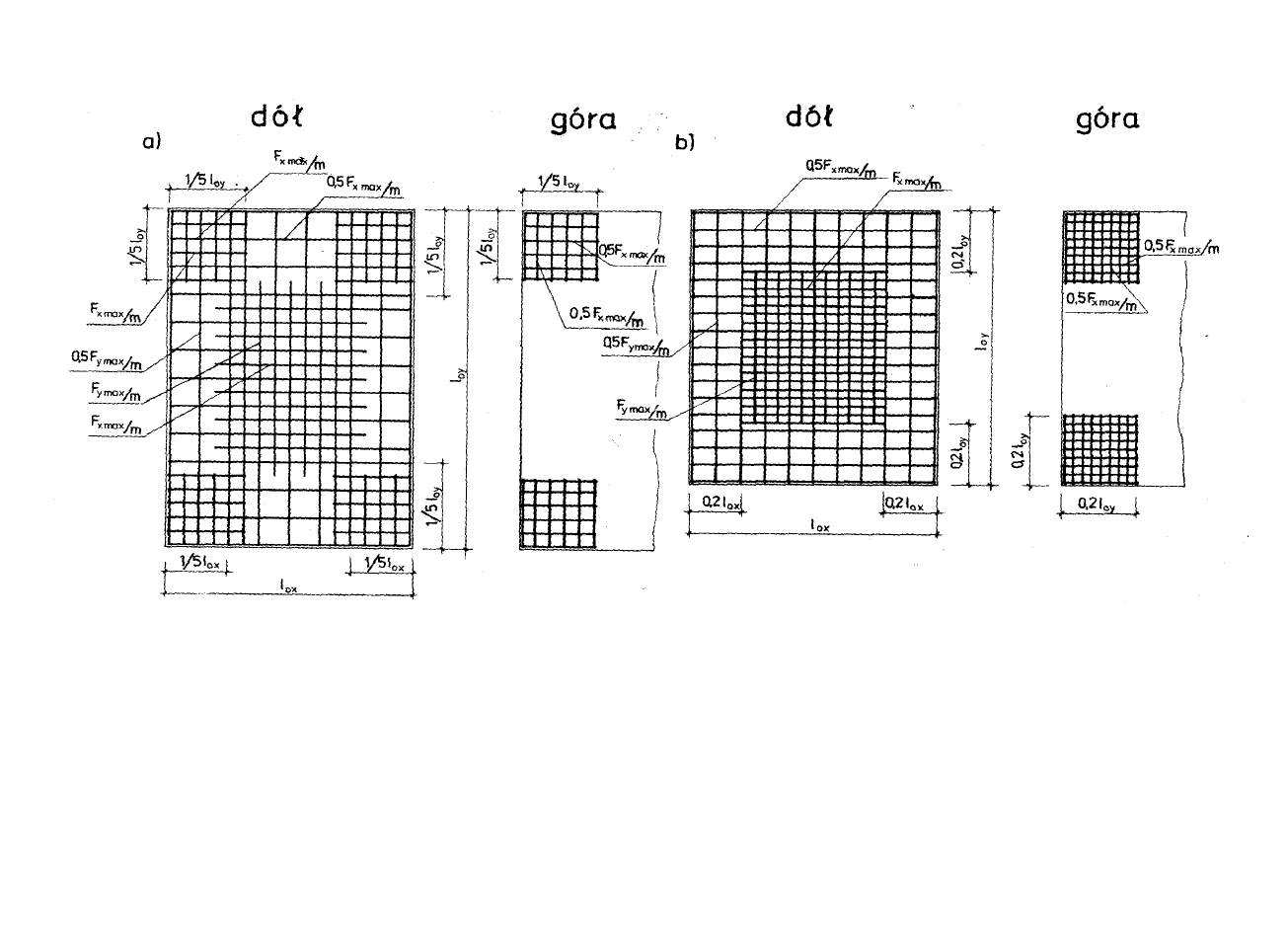
Zbrojenie płyty jednopolowej swobodnie podpartej: a)

Zbrojenie płyty jednopolowej swobodnie podpartej: a)

niezależnymi prętami, b) płaskimi siatkami zgrzewanymi

niezależnymi prętami, b) płaskimi siatkami zgrzewanymi

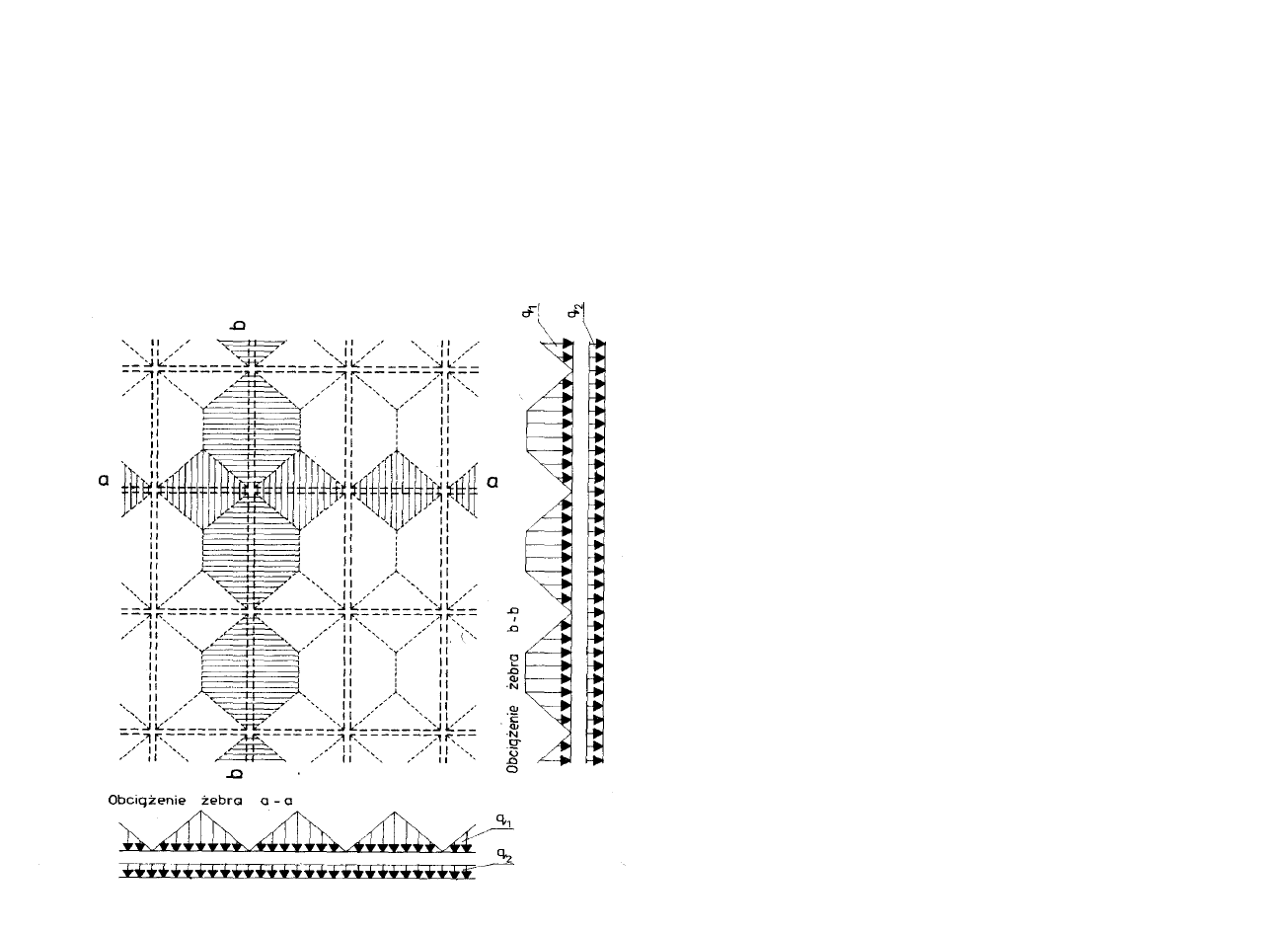
Obliczanie belek podpierających (żeber)

Obliczanie belek podpierających (żeber)

 

 

Do obliczeń żeber przyjmuje się obciążenie trapezowe (żebra

Do obliczeń żeber przyjmuje się obciążenie trapezowe (żebra

dłuższe) i trójkątne (żebra krótsze).

dłuższe) i trójkątne (żebra krótsze).

Obciążenie przenoszące się na

Obciążenie przenoszące się na

żebra

podpierające

płyty

żebra

podpierające

płyty

krzyżowo-zbrojone

krzyżowo-zbrojone

(

(

q

q

1

1

– obciążenie płyty,

– obciążenie płyty,

q

q

2

2

– ciężar

– ciężar

własny żebra)

własny żebra)

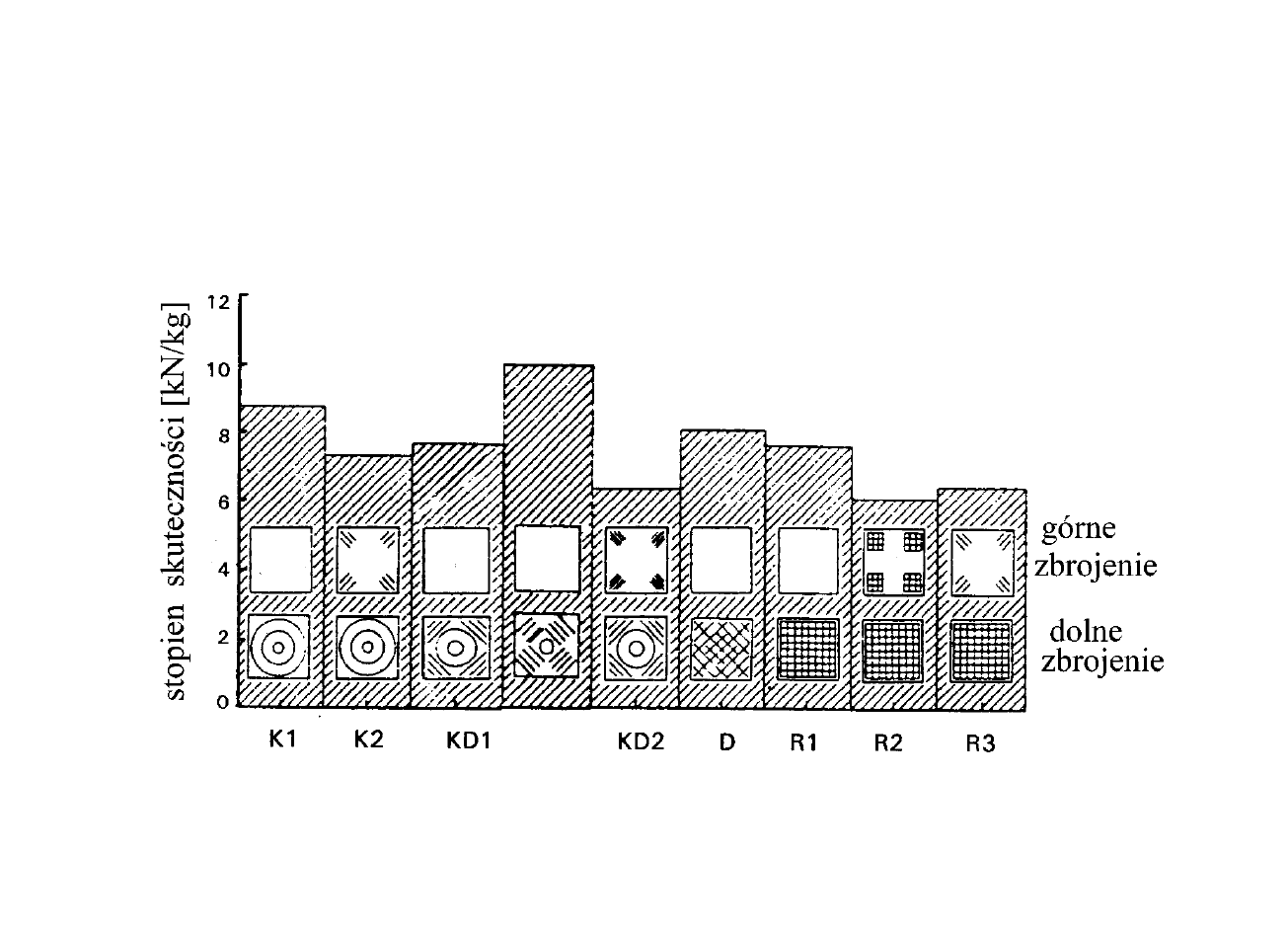
Stopień skuteczności rożnych typów zbrojenia dla płyty

Stopień skuteczności rożnych typów zbrojenia dla płyty

kwadratowej swobodnie podpartej

kwadratowej swobodnie podpartej

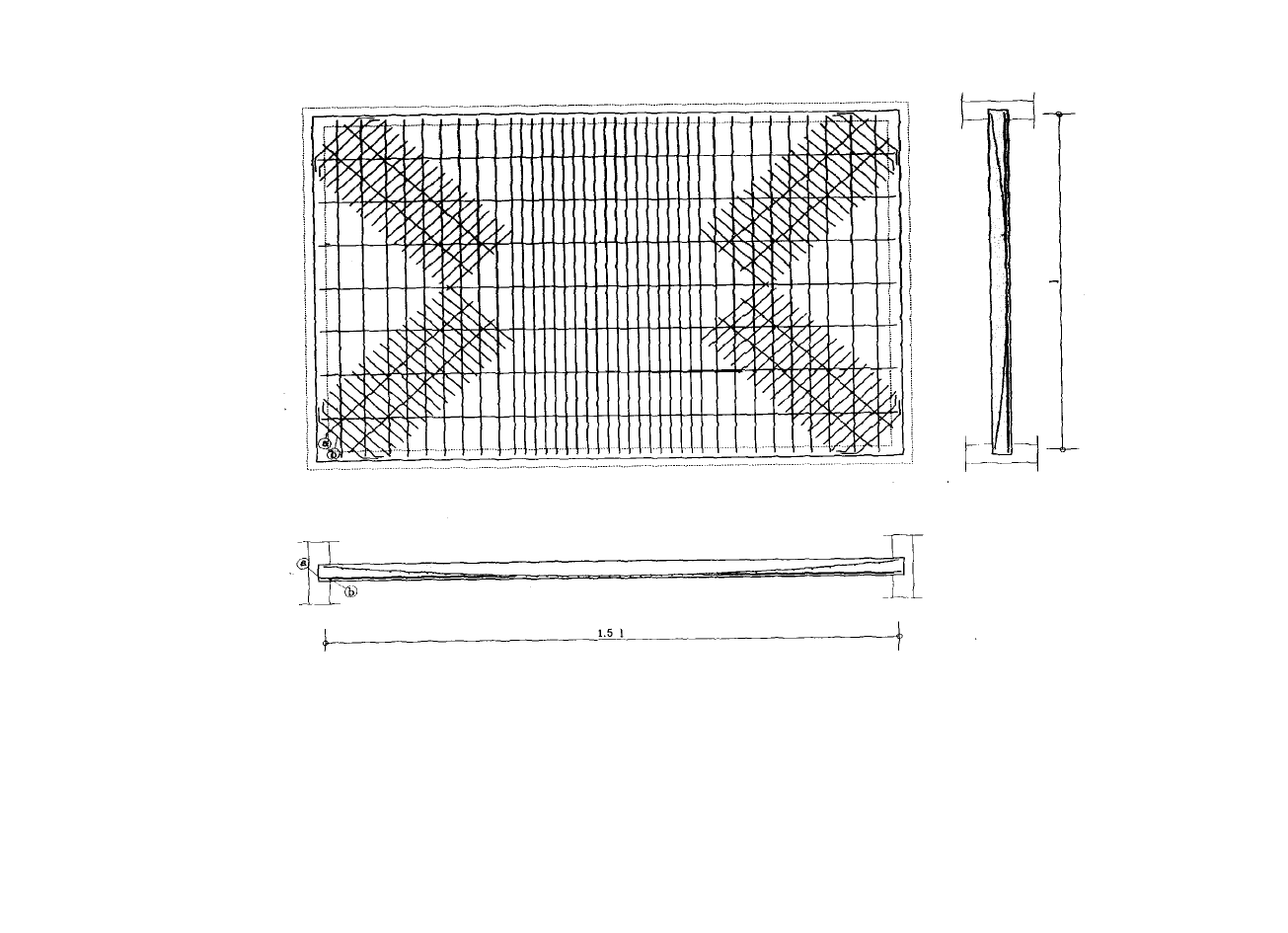
Efektywne zbrojenie płyty prostokątnej (Polonyi 1996)

Efektywne zbrojenie płyty prostokątnej (Polonyi 1996)

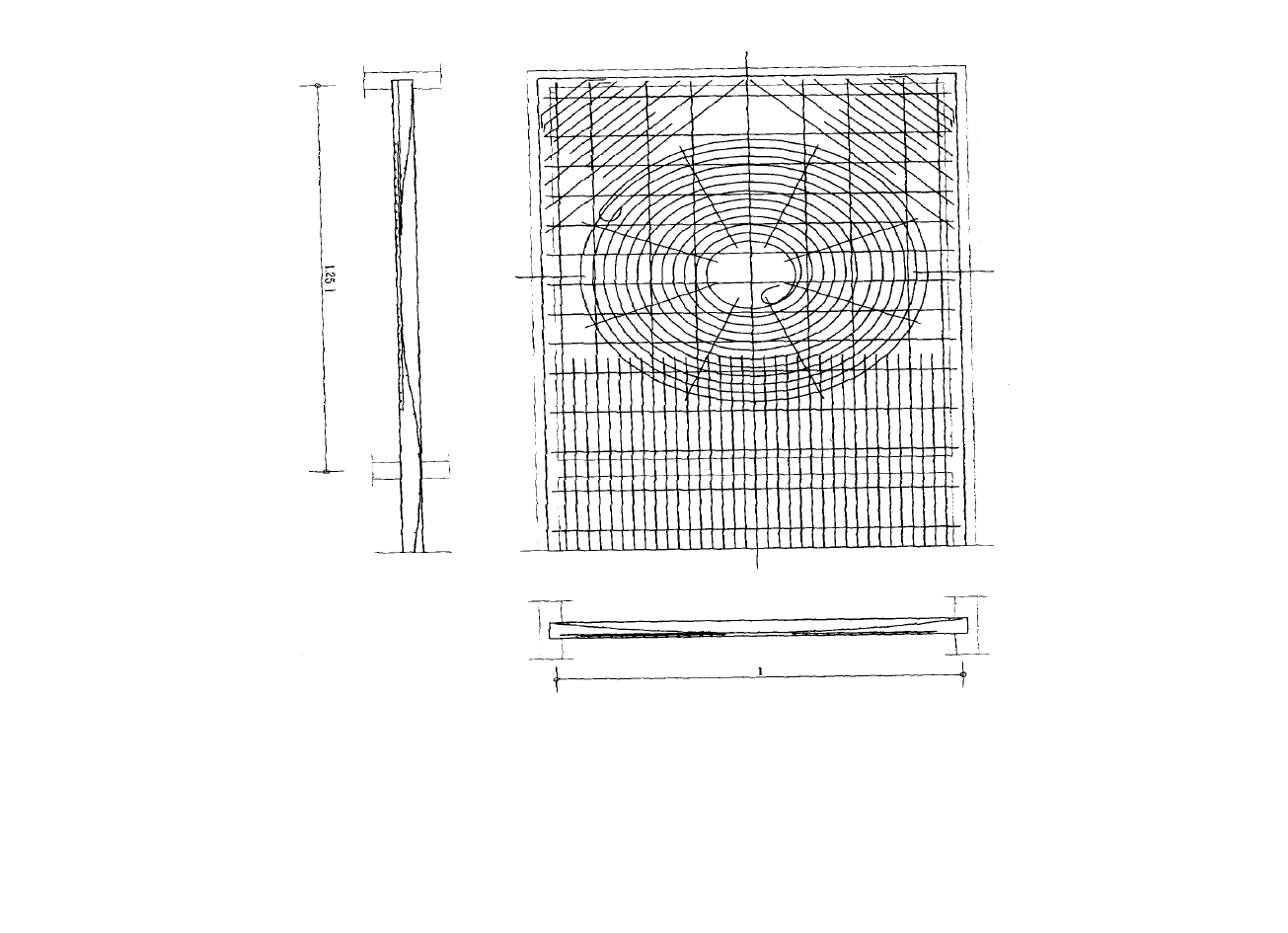
Efektywne zbrojenie płyty ciągłej (Polonyi 1996).

Efektywne zbrojenie płyty ciągłej (Polonyi 1996).