Ćwiczenie 4

Inwertaza (II)

Kinetyka reakcji enzymatycznych

ENZYMOLOGIA

Wydział Nauk o Żywności i Rybactwa

Centrum Bioimmobilizacji

i Innowacyjnych Materiałów

Opakowaniowych

ul. Klemensa Janickiego 35

2

Ćwiczenie 4

Inwertaza (II). Kinetyka reakcji enzymatycznych

Inwertaza (sacharaza, β-fruktofuranozydaza) - enzym należący do grupy hydrolaz, został po

raz pierwszy wyizolowany z ekstraktu drożdży przez Berthelota w 1860 roku. Hydrolizuje

wiązania glikozydowe utworzone z udziałem grupy hydroksylowej w położeniu β, związanej
z węglem anomerycznym (C2) pierścienia fruktofuranozy. Sacharaza powoduje hydrolizę

dwucukru sacharozy do glukozy i fruktozy, trójcukru rafinozy do fruktozy i dwucukru

melibiozy. Głównym, naturalnym substratem β-fruktofuranozydazy jest sacharoza (Rys.1).

Inwertazy występują w bakteriach i innych mikroorganizmach, w roślinach wyższych (w
ścianie komórkowej) i u zwierząt. Przez pszczoły sacharaza wykorzystywana jest do

hydrolizy sacharozy podczas produkcji miodu. U ludzi inwertaza, podobnie jak laktaza,

występuje na wewnętrznej powierzchni komórek nabłonka wyściełającego jelito cienkie.
Bogatym źródłem inwertazy są drożdże. Inwertaza drożdżowa wykazuje optimum działania w

pH 4.0—5.5. Aktywność enzymatyczną inwertazy można oznaczyć różnymi metodami np.

metodą kolorymetryczną lub polarymetryczną.

Rys.1. Sacharoza (α-D-glukopiranozylo-β-D-fruktofuranozyd) z zaznaczonym miejscem działania
inwertazy (Dubin i Turyna, 1999)

Sacharoza to disacharyd zbudowany z α-D-glukozy i β-D-fruktozy połączonych wiązaniem

glikozydowym 1-2. W większych ilościach występuje w burakach cukrowych i trzcinie

cukrowej. Nie posiada właściwości redukujących.

Zastosowanie sacharazy w technologii żywności

Sacharaza otrzymywana jest głównie z drożdży Saccharomyces cerevisiae. Enzym ten może

być stosowany w produkcji cukierniczej, do przygotowania syropów cukru inwertowanego
używanego do wyrobu sztucznego miodu, cukierków, marmolad, konfitur, likierów itp.

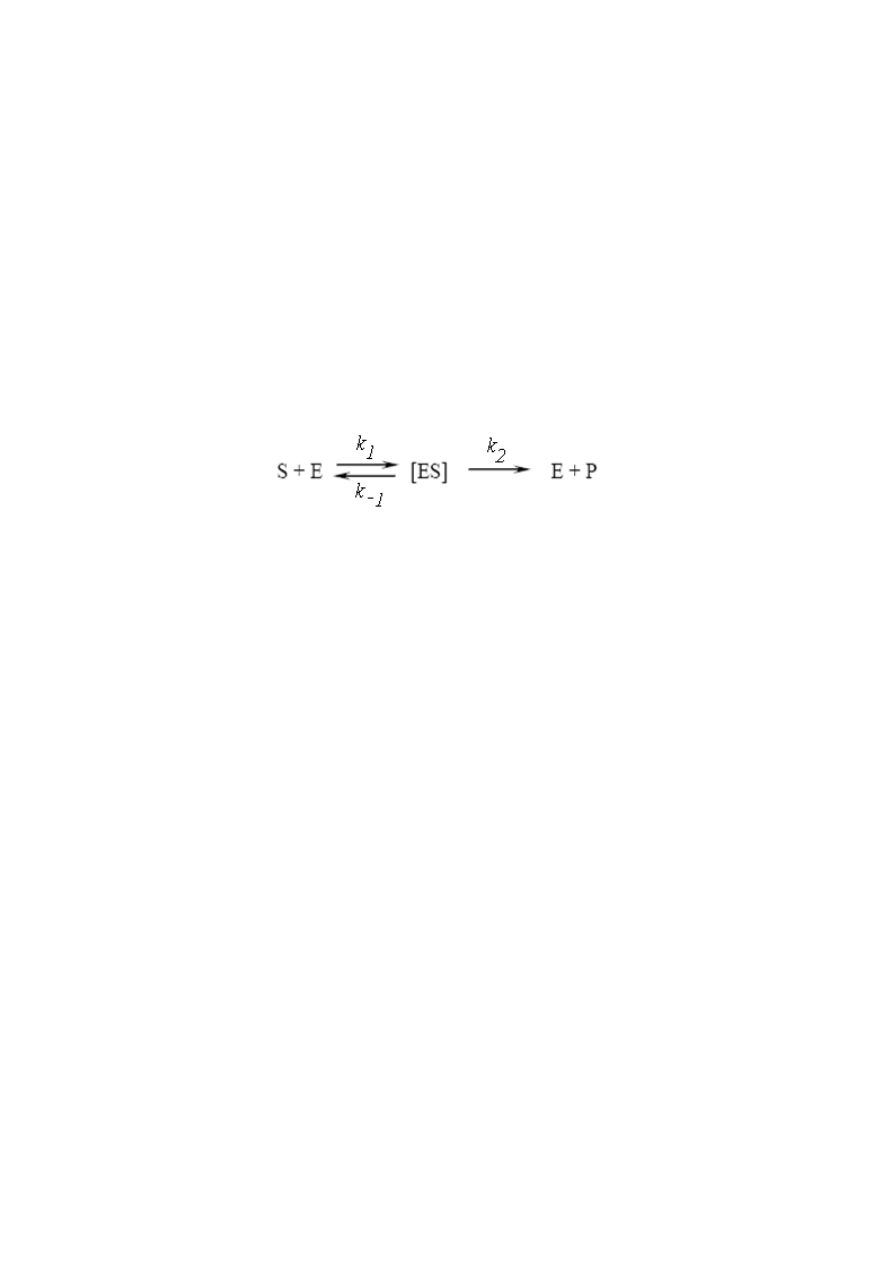
3

Kinetyka reakcji chemicznych zajmuje się badaniem szybkości przebiegu reakcji

w zależności od różnych czynników (stężenia reagujących substancji, temperatury, obecności
aktywatorów i inhibitorów). Zadaniem kinetyki jest ustalenie charakteru reakcji
i matematyczne ujęcie zależności między szybkością reakcji, a czasem jej trwania. Poznanie
tych zależności pozwala na określenie szybkości, z jaką będzie przebiegać reakcja

w dowolnie obranym czasie i dowolnym stężeniu substratu.

Szybkość reakcji enzymatycznej mierzona jest najczęściej przyrostem produktu lub ubytkiem

substratu w jednostce czasu.

Zasadniczym założeniem teorii Michaelisa-Menten, jako podstawy rozważań

kinetycznych, jest konieczność wytworzenia odwracalnego kompleksu między enzymem

i substratem (1)

(1)

S – substrat,
E – enzym,
[ES] – kompleks enzym – substrat,
P – produkt
k – stała szybkości reakcji

Kompleks ten podlega przemianie nieodwracalnej do produktu (lub produktów) P

z uwolnieniem enzymu. Dla pełnego scharakteryzowania kinetyki tych przemian niezbędne są

stałe szybkości reakcji. Ponieważ w porównaniu ze stężeniem substratu i produktu, stężenie
enzymu jest wielokrotnie mniejsze, więc w przybliżeniu można przyjąć, że stężenie

kompleksu ES jest stałe (szybkość jego powstawania jest zrównoważona szybkością

powstawania produktu) i zależy tylko od stężenia enzymu w roztworze. Oczywiście,
im większe jest stężenie kompleksu ES (a więc i enzymu), tym więcej produktu powstanie

w jednostce czasu.

Przy stałym stężeniu enzymu szybkość reakcji enzymatycznej w pewnych granicach

zależy od stężenia substratu (rys. 1). Jak wynika z przedstawionej krzywej, przy małym
stężeniu substratu w stosunku do stężenia enzymu zwiększenie szybkości reakcji wraz ze
zwiększeniem stężenia substratu jest do niego w przybliżeniu wprost proporcjonalne
(zależność liniowa) i odpowiada tzw. kinetyce pierwszego rzędu.

Natomiast przy dużym stężeniu substratu szybkość reakcji ma wartość maksymalną

V

max

i nie zależy od dalszego zwiększania jego stężenia. W tym przypadku reakcja podlega

kinetyce zerowego rzędu. Tego typu kinetykę obserwuje się przy osiągnięciu pełnego
wysycenia cząsteczek enzymu przez substrat. Wtedy dalsze zwiększanie stężenia substratu nie
może już powodować zwiększenia szybkości reakcji, gdy stężenie enzymu pozostaje stałe;

4

reakcja przebiega ze stałą szybkością. Zależność szybkości reakcji od stężenia substratu

przedstawiona na rys. 1 jest zgodna z następującym równaniem Michaelisa-Menten

:

(2)

gdzie:

V

o

– szybkość reakcji, V

max

– szybkość maksymalna, K

m

– stała Michaelisa, [S] – stężenie

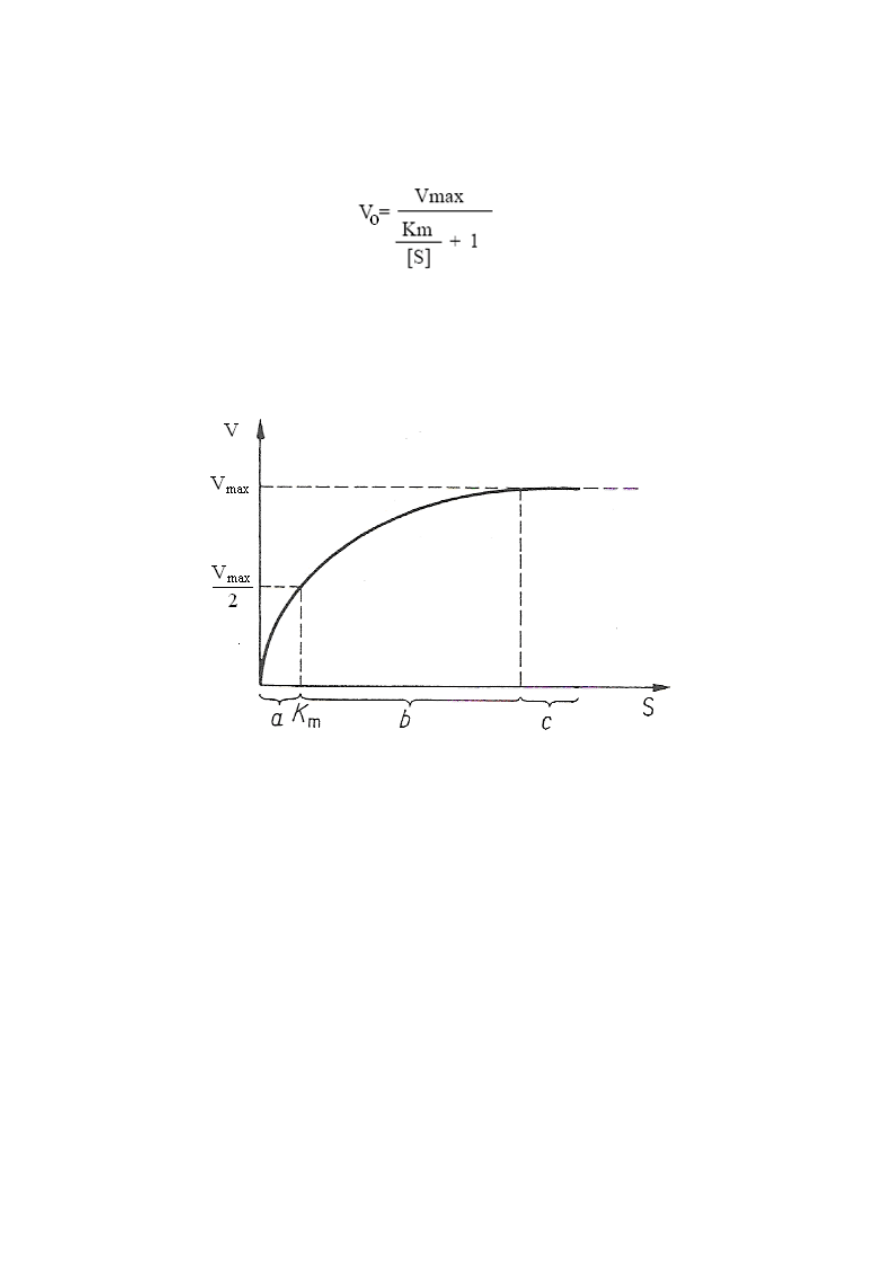
substratu; graficznie równanie to przyjmuje postać hiperboli:

Rys. 1. Wpływ stężenia substratu na szybkość reakcji przy stałym stężeniu enzymu – krzywa
wg Michaelisa-Menten; V

max

-szybkość maksymalna, S-stężenie substratu, K

m

-stała

Michaelisa-Menten, a – reakcja pierwszego rzędu, b – reakcja o mieszanej kinetyce, c –
reakcja zerowego rzędu (Kączkowski 2005)

Jeżeli wartość [S] = K

m,

równanie (2) przybierze postać V = V

max

/2, czyli reakcja osiągnie

połowę szybkości maksymalnej. Takie stężenie substratu, przy którym szybkość reakcji
stanowi połowę szybkości maksymalnej, nosi nazwę stałej Michaelisa (K

m

).

Odwrotność stałej (l/K

m

) jest nazywana powinowactwem enzymu do substratu. Z tej

zależności wynika, że mała wartość K

m

oznacza duże powinowactwo enzymu do danego

substratu i dużą szybkość procesu a duża wartość K

m

oznacza odwrotnie. Wartości stałej

Michaelisa, oznaczone dla wielu enzymów, wynoszą przeważnie od 10

-3

do 10

5־

M.

Wartość K

m

można wyznaczyć graficznie z wykresu, jak podano na wykresie 1. Podana

metoda graficzna jest jednak niezbyt dokładna, nie daje bowiem pewności, czy została
osiągnięta szybkość maksymalna reakcji V

max

. O wiele dogodniejszym sposobem

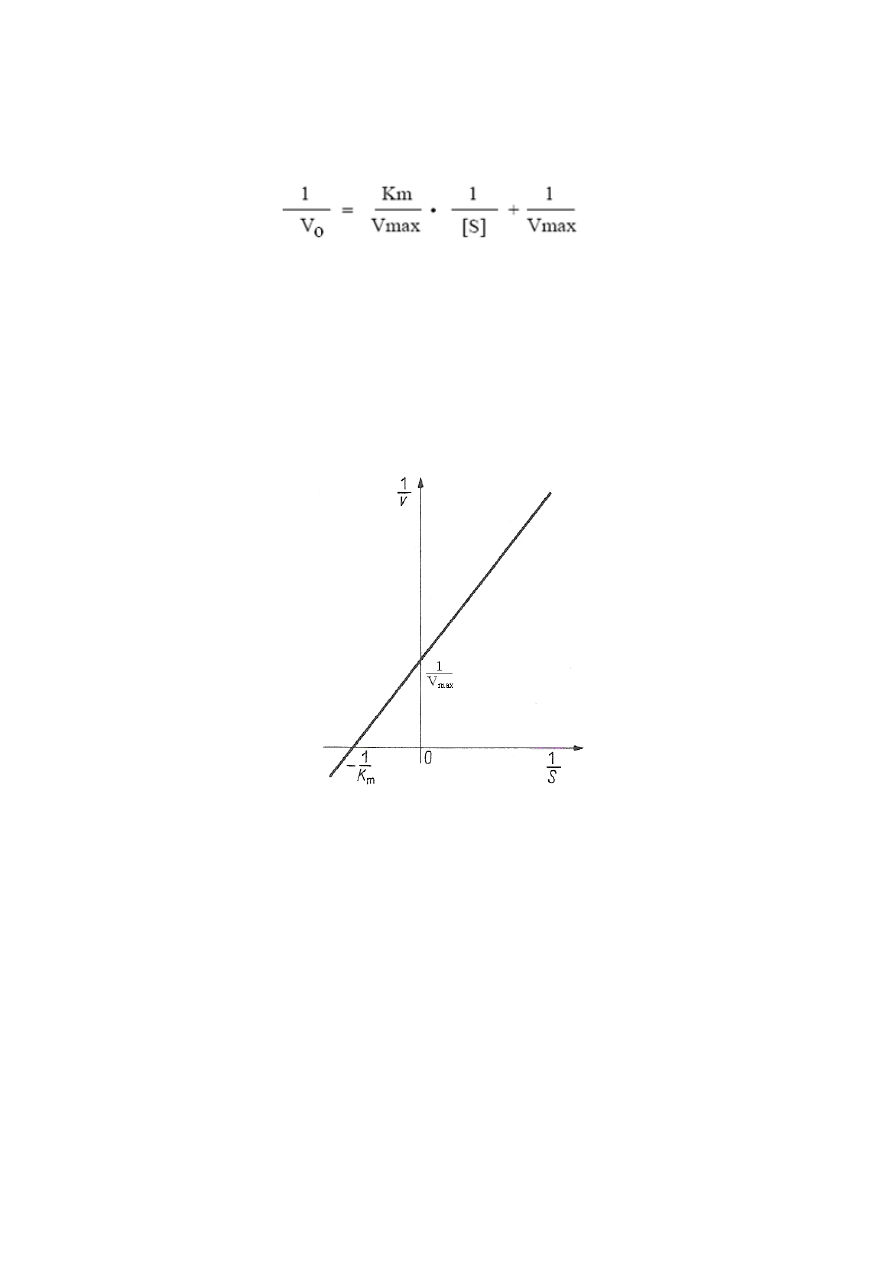
5

wyznaczania wartości Km jest wykorzystanie równania Lineweavera – Burka, które jest

przekształceniem równania Michaelisa – Menten:

(3)

Przekształcenie to ma na celu uzyskanie równania linii prostej (y = ax + b). Wartości K

m

/V

max

(a) i 1/V

max

(b) są wielkościami stałymi, stąd zależność 1/v od 1/[S] jest linią prostą. W

układzie współrzędnych wartości 1/v odkłada się na osi rzędnych a wartości 1/[S] na osi
odciętych. Wówczas równanie (3) daje linię prostą, której nachylenie określa stosunek

K

m

/V

max

(współczynnik regresji a) i która przecina oś rzędnych w punkcie wyznaczającym

1/V

max

(współczynnik regresji b), a oś odciętych w punkcie 1/K

m

(rys. 2). Na podstawie tego

wykresu można jednoznacznie wyznaczyć wartości stałej K

m

i V

max

.

Rys. 2. Graficzne przedstawienie równania Lineweavera – Burka; V

max

-szybkość

maksymalna, S-stężenie substratu, K

m

-stała Michaelisa-Menten (Kączkowski 2005)

Pomiary stałej Michaelisa dokonywane przy użyciu różnych substratów pozwalają
wnioskować o sposobie wiązania enzymu z substratem, a zastosowanie do badań
kinetycznych różnych aktywatorów i inhibitorów pozwala na wyciągnięcie wniosków
dotyczących budowy centrum katalitycznego enzymu oraz warunków powstawania
kompleksów enzym-substrat.

6

Część doświadczalna

Ćwiczenie 4

Inwertaza (II). Kinetyka reakcji enzymatycznych

Zasada: Inwertaza (sacharaza, β-fruktofuranozydaza) należy do hydrolaz rozszczepiających

wiązania β-glikozydowe w sacharozie, hydrolizując ją do glukozy i fruktozy. Optymalne pH

działania enzymu wynosi ok. 4,7; przy pH 10 jest on już zupełnie nieaktywny.

Aktywność inwertazy można mierzyć metodą redukcyjną, ponieważ w miarę postępowania

hydrolizy sacharozy wzrasta stężenie cukrów redukujących. Do oznaczenia ilości cukrów

redukujących, w ćwiczeniu wykorzystano reakcję z kwasem pikrynowym, który przez cukry

redukowany jest do kwasu pikraminowego. Powstający w środowisku alkalicznym

pikraminian sodu daje czerwono-brązowe zabarwienie. W ćwiczeniu ilość cukrów

redukujących oznaczono metodą kolorymetryczną w przeliczeniu na mg glukozy uwolnione

z zastosowanego do analizy enzymatycznej substratu (sacharozy).

Metoda pozwala wyznaczyć szybkości początkowe reakcji przy różnych stężeniach sacharozy

i z wykresu Michaelisa-Menten lub Lineweavera – Burka wyznaczyć stałą Michaelisa.

I. Wykreślanie krzywej kalibracyjnej

1. Przygotować 6 probówek i oznaczyć je numerami od 0 do 5.

2. Do probówek odważyć odpowiednią ilość roztworu wzorcowego (0,25% roztwór

glukozy), a następnie uzupełnić wodą do 1 ml.

Zawartość probówek przygotować według schematu zamieszczonego w tabeli poniżej:

Nr probówki

0

(próbka zerowa)

1

2

3

4

5

0,25% wzorzec glukozy [g]

0

0,2

0,4

0,6

0,8

1,0

Woda destylowana [g]

1,0

0,8

0,6

0,4

0,2

0

Końcowa ilość glukozy [mg]

0

0,5

1

1,5

2

2,5

3. Do probówek dodać po 1,5 ml 10% NaOH oraz 1,5 ml 0,5% roztworu kwasu

pikrynowego, następnie zawartość probówek wymieszać i wstawić na 5 minut do wrzącej

łaźni wodnej.

4. Po wyjęciu probówek z wrzącej łaźni, wstawić je do łaźni lodowej również na 5 minut.

7

5. Po ochłodzeniu oznaczyć wartość absorbancji przy λ = 530 nm wobec próbki zerowej

i wykreślić krzywą zależności wartości absorbancji (A) od ilości glukozy [mg].

Uwaga! Próbki zerowej proszę nie wylewać!

Krzywa wzorcowa (kalibracyjna) przedstawia zależność między absorbancją i stężeniem.

W tym przypadku roztwór stosuje się do prawa Lamberta-Beera, więc ma postać linii prostej

przechodzącej przez punkt przecięcia osi współrzędnych.

W celu przygotowania krzywej na podstawie wykonanych pomiarów absorbancji dla kilku

stężeń roztworu wzorcowego i wykreśla się krzywą odkładając na osi X mg glukozy, a na osi

Y odpowiednie wartości absorbancji. Należy tak dobierać podziałkę na osiach żeby krzywa

była nachylona do osi pod kątem mniej więcej 45°. Ilość glukozy [mg] w próbie badanej

odczytuje się ze sporządzonej krzywej wzorcowej.

II. Wyznaczanie szybkości początkowych przy różnych stężeniach substratu

1. Przygotować dwa zestawy po 5 probówek. Pierwszy zestaw oznaczyć numerami t

0

, t

5

, t

10

,

t

15

, t

20

(probówki w drugim zestawie ponumerować analogicznie dopisując symbol ’ czyli

t

0’,

t

5’,

itd.).

2. Do probówek t

0

, t

0’

, wprowadzić po 1,5 ml 10% NaOH.

3. Następnie przygotować 2 mieszaniny inkubacyjne o różnym stężeniu substratu według

schematu zamieszczonego w tabeli poniżej i natychmiast po wymieszaniu (t = 0) z każdej

probówki pobrać po 1 ml mieszaniny inkubacyjnej i dodać do probówek zawierających

1,5 ml 10% NaOH i włączyć minutnik na 5 minut.

4. W międzyczasie do pozostałych (przygotowanych w pkt. 1) probówek ponalewać

po 1,5 ml 10% NaOH i wprowadzać do nich pobrane po 5, 10, 15, 20 minutach próbki

inkubacyjne o obj. 1 ml. Uwaga! Próbki mieszaniny inkubacyjnej pobrane z probówki nr

1 dodawać kolejno do probówek t

0

, t

5

, t

10

itd., natomiast próbki mieszaniny inkubacyjnej

pobrane z probówki nr 2 dodawać kolejno do probówek t

0’

, t

5’

, t

10’

itd.,

Nr probówki

1

2

0,2 M roztwór sacharozy

w buforze octanowym

6

3

bufor octanowy [ml]

0

3

inwertaza [ml]

6

6

Końcowe stężenie

sacharozy [M]

0,1

0,05

8

5. Po pobraniu ostatniej próbki do wszystkich 10 probówek dodać po 1,5 ml 0,5% roztworu

kwasu pikrynowego, następnie zawartość probówek wymieszać i wstawić na 5 minut do
wrzącej łaźni wodnej. Schemat doświadczenia przedstawiono w tabeli poniżej:

Nr probówki

t

0

(próbka

kontrolna)

t

5

t

10

t

15

t

20

Czas inkubacji [min.]

0

5

10

15

20

NaOH [ml]

1,5

1,5

1,5

1,5

1,5

Próbka mieszaniny

inkubacyjnej [ml]

1

1

1

1

1

0,5% roztwór kwasu

pikrynowego [ml]

1,5

1,5

1,5

1,5

1,5

6. Po wyjęciu probówek z wrzącej łaźni, wstawić je do łaźni lodowej również na 5 minut.

7. Po ochłodzeniu oznaczyć wartość absorbancji przy λ = 530 nm wobec próbki zerowej (tej

samej, której używano przy wyznaczaniu krzywej kalibracyjnej). Uwaga! Próbki zerowej

proszę nie wylewać!

8. Z krzywej kalibracyjnej odczytać ilości mg glukozy odpowiadającym poszczególnym

wartościom absorbancji uzyskanym dla próbek pobieranych po różnych czasach
z mieszanin o różnym stężeniu substratu.

9. Po odjęciu ilości mg glukozy przypadających na próbę kontrolną, wyniki przedstawić

w postaci wykresu zależności między ilością glukozy [mg], a czasem inkubacji (na osi
odciętych – czas w minutach, na osi rzędnych – ilość glukozy w mg). Wykresy
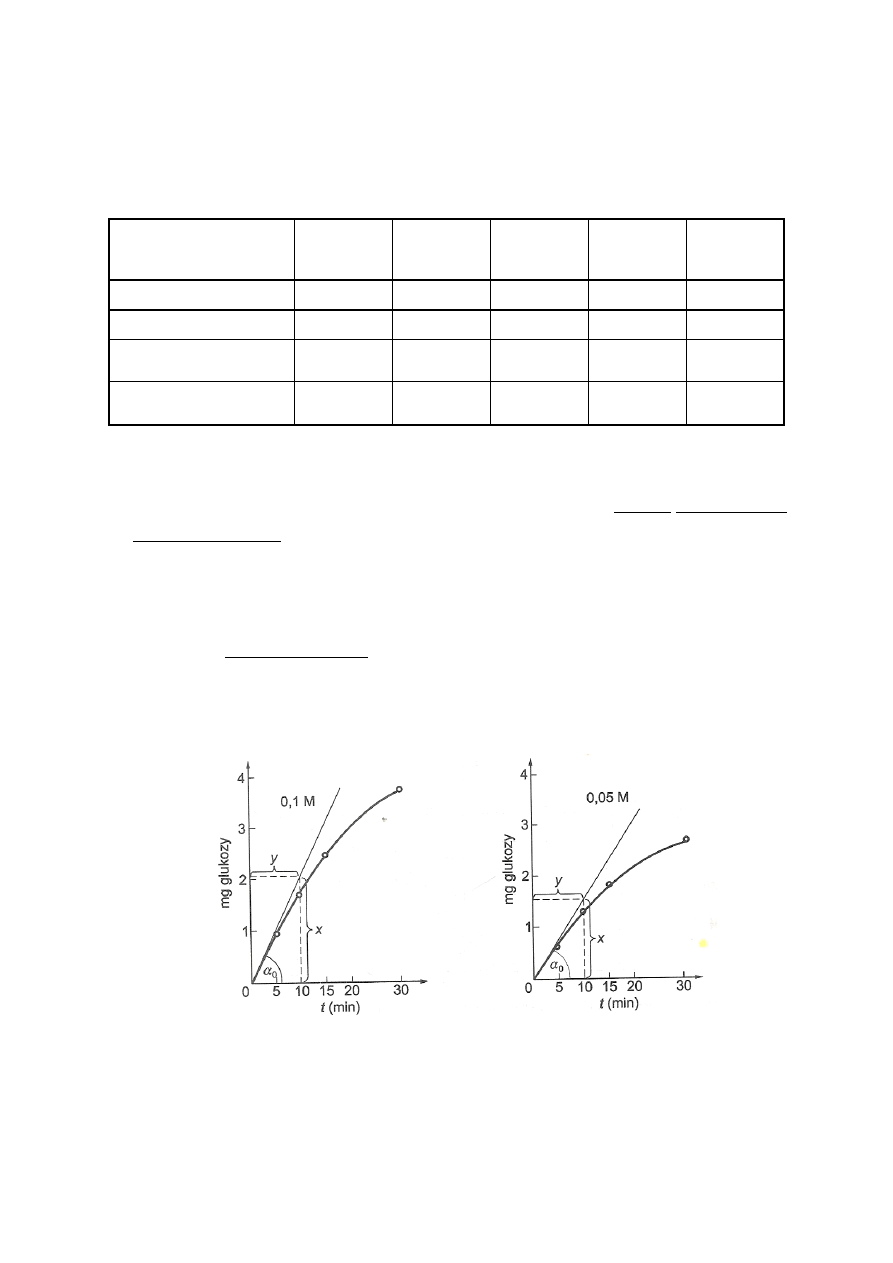
te należy sporządzić dla obydwu stężeń sacharozy (przykład na rys. 3).

Rys. 3. Wyznaczanie szybkości początkowej reakcji przy różnych stężeniach substratu
(Kłyszejko-Stefanowicz 2003)
10. Z wykresów należy wyznaczyć szybkości początkowe (v

o

) reakcji enzymatycznej (przykład

na rys. 3). W tym celu należy przeprowadzić styczną do krzywej w punkcie t = 0. Styczna z

9

osią odciętych utworzy kąt α, którego tangens jest miarą szybkości początkowej (v

o

).

Wartości tg α nie wolno odczytywać z tablic na podstawie wartości kąta w stopniach,

ponieważ nanoszone na osi odciętych i rzędnych wartości nie są tej samej wielkości.

Oblicza się go ze stosunku wielkości przyprostokątnej przeciwległej do kąta α, podanej w

wartościach odkładanych na osi rzędnych (mg glukozy), do przyprostokątnej przyległej do

kąta α, podanej w wartościach odkładanych na osi odciętych (czas w minutach).

11. Z szybkości początkowych v

o

, wyliczonych dla obydwu stężeń substratu, wykreślić

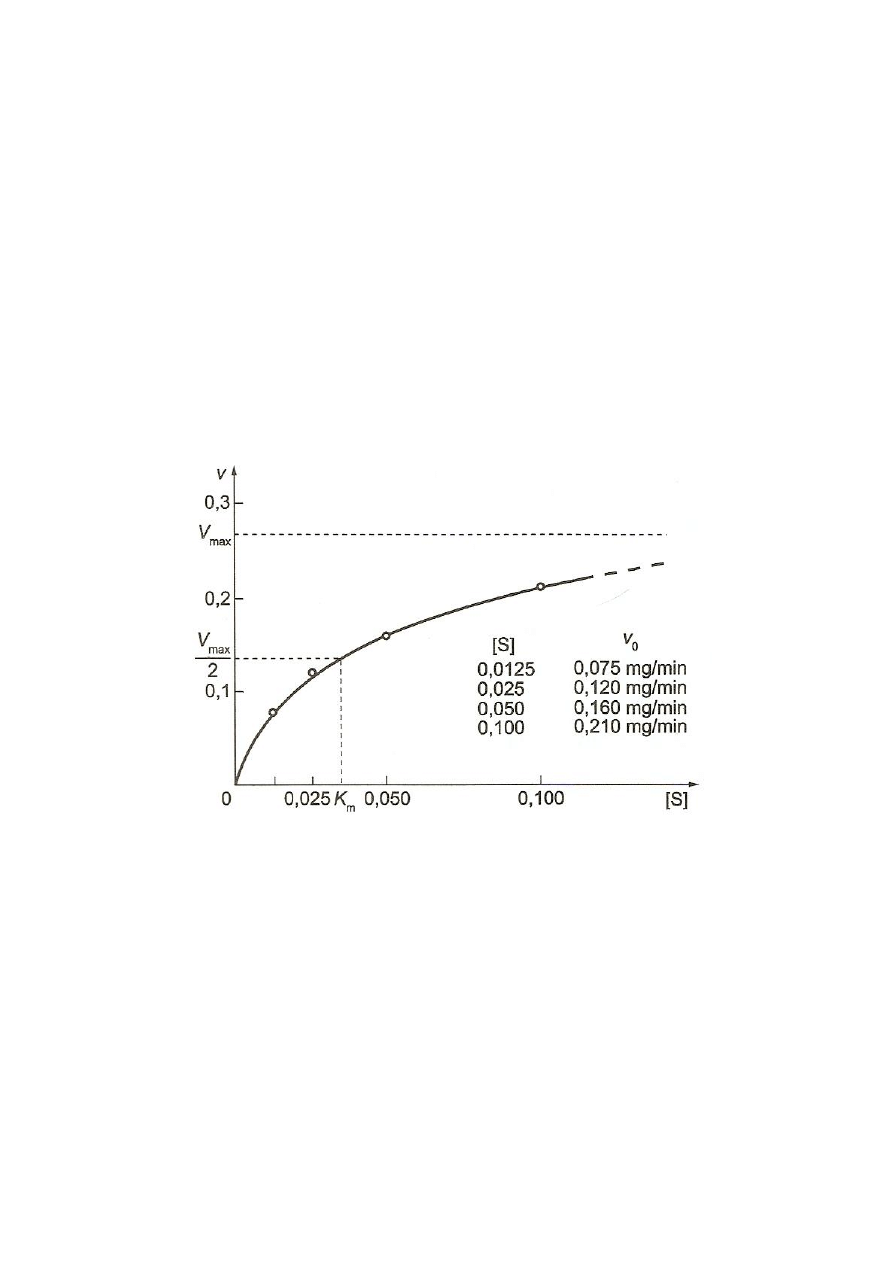
zależność tych szybkości od stężenia substratu (krzywa Michaelisa-Menten) (rys. 4).

Ze względu na ograniczenia czasowe doświadczenie wykonywane jest jedynie dla dwóch

stężeń substratu, co sprawia, że wykreślona krzywa (hiperbola) ma przebieg jedynie

orientacyjny.

Rys. 4. Graficzne przedstawienie równania Michaelisa-Menten (Kłyszejko-

Stefanowicz 2003)

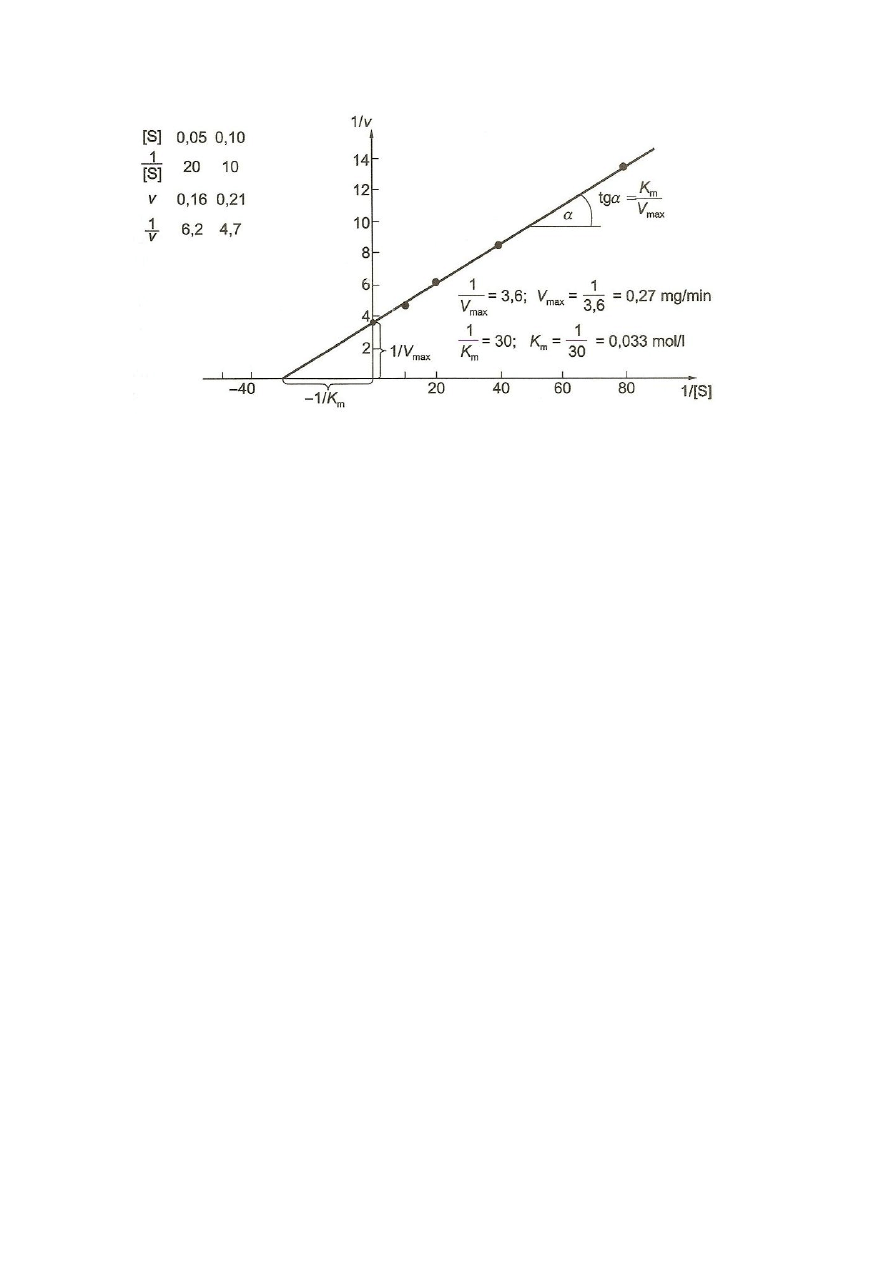
12. Wyznaczyć prostą dla równania Lineweavera – Burka – zależności 1/v od 1/[S] (Rys 5).

Wyznaczyć stałą Michaelisa K

m

oraz szybkość maksymalną V

max.

10

Rys. 5. Graficzne przedstawienie równania

Lineweavera – Burka

(Kłyszejko-

Stefanowicz 2003)

Literatura:

1) Podstawy biochemii. Kączkowski J. Wydawnictwa Naukowo-Techniczne, Warszawa,

2005.

2) Praktikum z biochemii. Praca zbiorowa pod red. Dubina A. i Turyny B. Instytut Biologii

Molekularnej Uniwersytetu Jagiellońskiego, Kraków 1999.

3) Przepisy do ćwiczeń z biochemii. Praca zbiorowa pod red. Stryjeckiej-Zimmer M.

Akademia Medyczna im

.

prof

.

F

.

Skubiszewskiego w Lublinie, Lublin, 2004.

4) Ćwiczenia z biochemii. Praca zbiorowa pod red. Kłyszejko-Stefanowicz L. Wydawnictwo

Naukowe PWN, Warszawa, 2003.

5) Ogólna technologia żywności. Pijanowski E., Dłużewski M., Dłużewska A., Jarczyk A.

Wydawnictwa Naukowo-Techniczne, Warszawa, 2004.