Ćwiczenie 1. Matlab – podstawy (1)

Matlab

firmy MathWorks to uniwersalny pakiet do obliczeń naukowych i inżynierskich, analiz układów statycz-

nych i dynamicznych, symulacji procesów, przekształceń i obliczeń symbolicznych itp.

Środowisko Matlaba składa się z:

- okna Command Window, w którym wpisujemy pojedyncze polecenia,
- okna Command History - historia poleceń,
- okna z zakładkami:

- Workspace - obszar roboczy - lista zainicjowanych przez użytkownika zmiennych i ich wartości,
- Current Directory - zawartość katalogu roboczego.

Dodatkowo można otworzyć okno edytora plików tekstowych (Editor).

Domyślne rozmieszczenie okien uzyskujemy z menu: Desktop/Desktop Layout/Default.

Ćwiczenie

1.

Uruchomić program Matlab.

2.

Zapoznać się ze strukturą okien programu.

Podstawowa praca w środowisku odbywa się sposobami:

•

interakcyjnym, w oknie poleceń (Command Window) wpisujemy polecenia i na bieżąco otrzymuje-
my wyniki.

•

wsadowo – wykonywanie napisanych skryptów (m-plików) zawierających ciągi poleceń.

Najważniejesze polecenie: instrukcja przypisania

zmienna =

wyra

ż

enie

Działanie instrukcji polega na obliczeniu wyrażenia i jego wartość nadawana jest zmiennej o podanej nazwie.

Zmienna

jest inicjowana (można zauważyć jej pojawienie na liście w okienku Workspace) lub, jeśli już taka zmien-

na istnieje, zmieniana jest jej wartość.

Wyrażenie

arytmetyczne budujemy w znany sposób, łącząc stałe, zmienne (uprzednio zainicjowane) oraz funkcje

za pomocą operatorów arytmetycznych.

Nazwy zmiennych

to dowolny ciąg liter, cyfr i znaków _, lecz muszą się zaczynać od litery. W nazwach zmiennych

istotne są duże i małe litery.

Operatory działań jak w Excelu:

- jednoargumentowe: + powielenie znaku, – zmiana znaku
- dwuargumentowe: +, –, *, /, ^(potęgowanie),.

Uwaga: Potęgowanie wykonywane przed zmianą znaku (-2^2= -4 ale 2^-1=0.5).
Stosujemy również nawiasy okrągłe ustalające kolejność operacji.

Ćwiczenie

1.

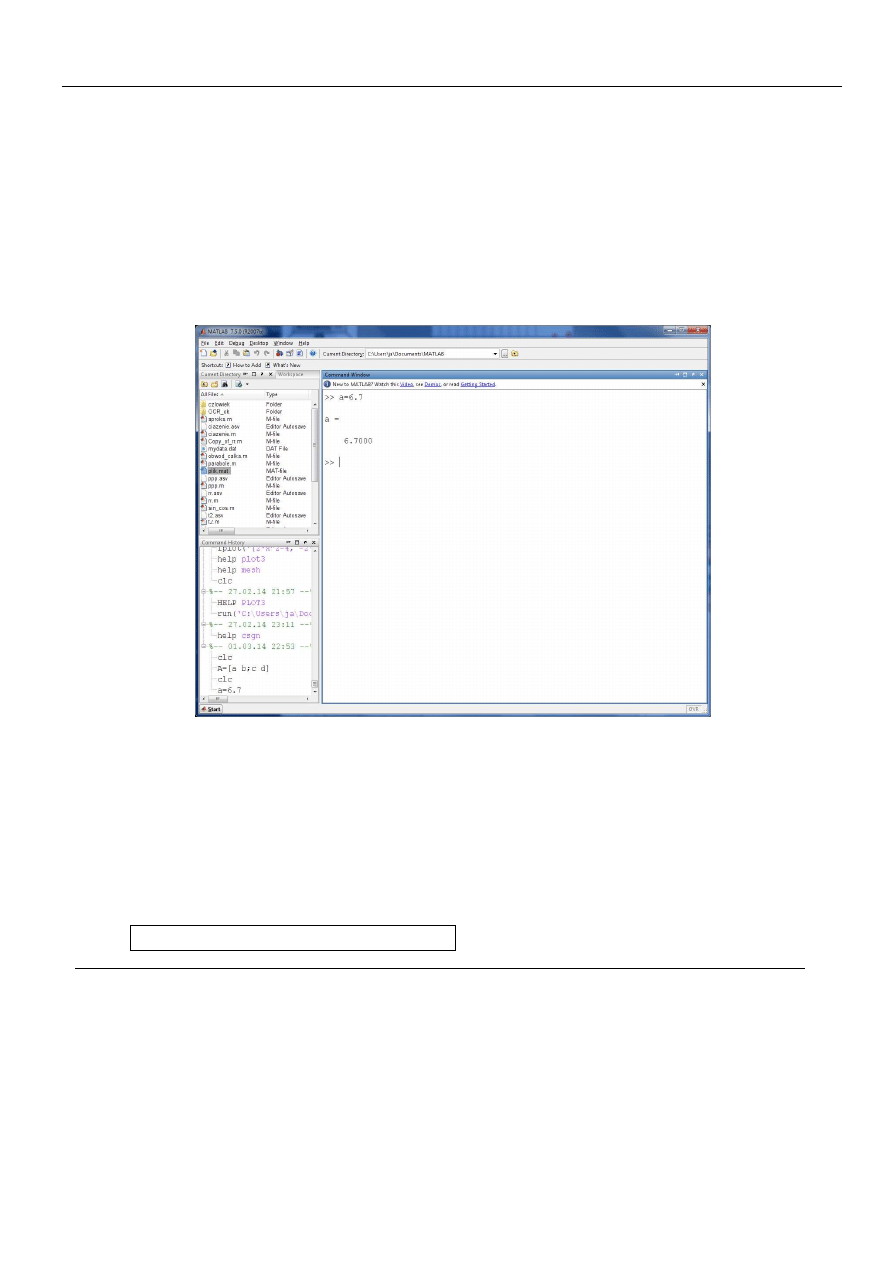
Wpisać w oknie Command Window kolejne polecenia (każde zakończone Enterem):

x1=5.4
x2=x1+1
x1=x1-2

2.

Zrozumieć działanie poleceń. Obserwować pojawienie się informacji o zmiennych i ich wartościach w
oknie Workspace.

M-pliki

W Matlab-ie można zapisać tekst ciągu instrukcji w pliku tekstowym ASCII o rozszerzeniu m. (tzw. m-pliki), a na-

stępnie wykonać te instrukcje kolejno jedna po drugiej. Matlab zawiera własny edytor ASCII.

Ćwiczenie

1.

Utworzyć własny folder.

2.

Zmienić katalog bieżący w Matlabie na utworzony katalog metodami jak na rysunku:

3.

Utworzyć nowy m-plik (menu File/New/M-file lub z menu podręcznego okna Current Directory) w folderze
roboczym, nadając mu nazwę z rozszerzeniem m, np. test1.m,

4.

W oknie edytora Matlaba napisać kolejne instrukcje jako tekst w m-pliku:

a = 1.2;
b = 1.5;
c = 2.5e-3;

%naukowy zapis liczby : 2.5*10

-3

d = a/(b+c);
d = d^(1/3)

%pierwiastek 3-go stopnia!

Uwagi:
- instrukcje piszemy w osobnych wierszach, jeśli w jednym wierszu to oddzielamy je przecinkami,
- średniki na końcu instrukcji powodują brak wyświetlenia echa instrukcji na ekranie,
- nazwy zmiennych muszą być różne od nazwy m-pliku!

5.

Wykonać wsadowo m-plik w Matlabie następującymi sposobami:

- przy pomocy narzędzia Run w oknie edytora m-pliku,
- przeciągając plik z okna Current Directory do Command Window
- wpisując nazwę pliku (bez rozszerzenia!) w linii poleceń Command Window:

>>

test1

6.

Przeanalizować rezultat wykonania skryptu.

Wybrane funkcje arytmetyczne

sin(w), cos(w), tan(w), cot(w) – funkcje trygonometryczne (argument w mierze łukowej)
sind(w), cosd(w), tand(w), cotd(w) – funkcje trygonometryczne (argument w stopniach)
sqrt(w) – pierwiastek kwadratowy
abs(w) – wartość bezwzględna
exp(w) – funkcja wykładnicza (e

w

)

power(a, b) – potęga (a

b

), alternatywnie do operatora ^ (Uwaga: tak liczymy również pierwiastki!)

log(w) – logarytm naturalny!!!

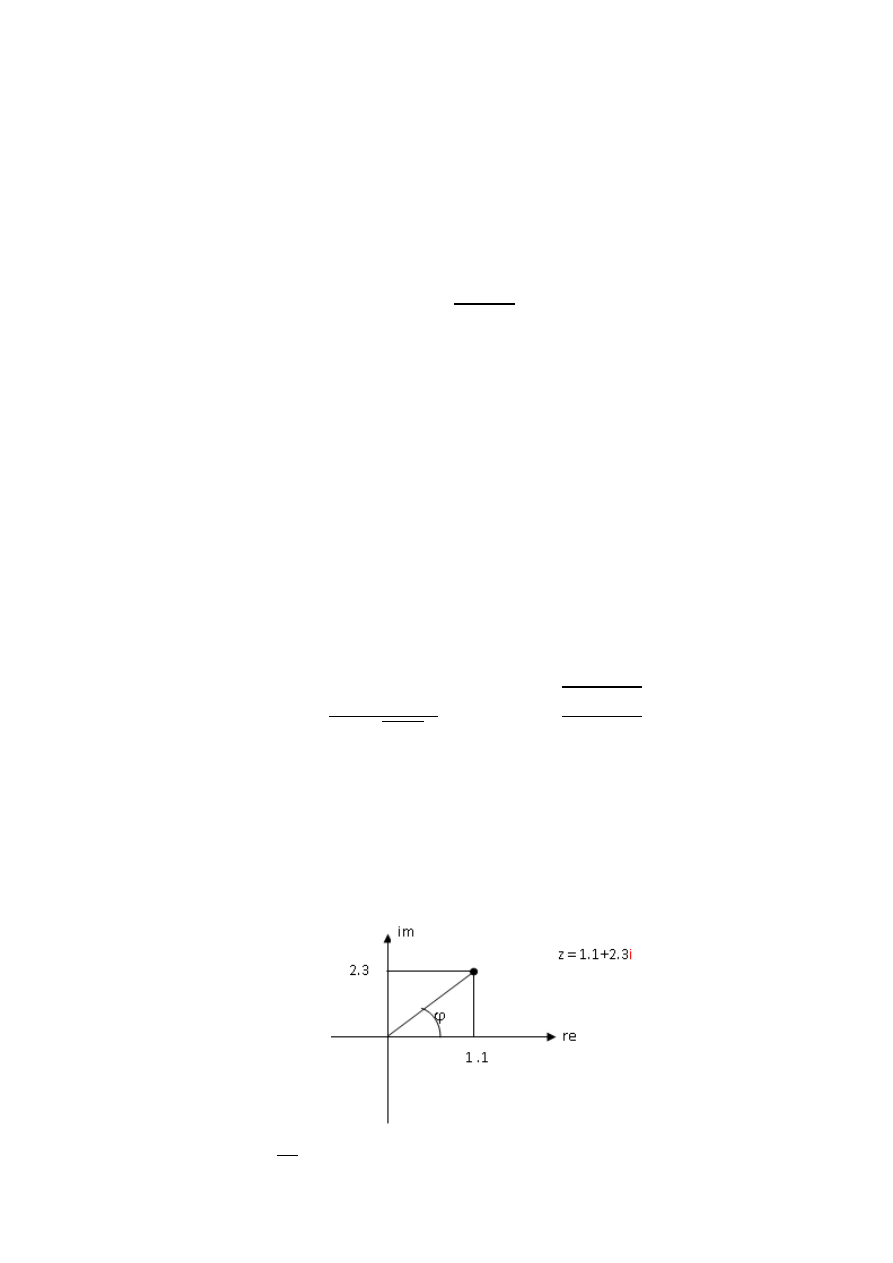
log10(w) – logarytm dziesiętny
rem(x, y) – reszta z dzielenia x/y
round(w) – zaokrąglenie do najbliższej całkowitej,
fix(w) – zaokrąglenie do całkowitej w kierunku 0,
ceil(w) – zaokrąglenie do całkowitej w kierunku +∞
floor(w) – zaokrąglenie do całkowitej w kierunku -∞
pi – stała π

gdzie: w, a, b, x, y – dowolne wyrażenia obliczeniowe.

Przykład

x=3.45

y=(x^3-exp(-2*x))/(power(x,6)-2)

→

Inne użyteczne polecenia:

help

- pomoc globalna

help elfun

- pomoc – spis funkcji elementarnych

help rem

- pomoc na temat wybranej funkcji (tu: rem)

format long

- zwiększona dokładność wyświetlanych wyników

format short

- dokładność podstawowa

clc

- czyszczenie ekranu

clear zmienna - usunięcie zmiennej z obszaru roboczego (Workspace)
clear

- usunięcie wszystkich zmiennych z obszaru roboczego

pause

Zadanie

1.

Sprawdzić algorytm zaokrąglania z dowolną dokładnością:

format long
pi5=round(pi*1E5)/1E5

%zaokrąglenie π do 5-ciu miejsc dziesiętnych

2.

Wykonać przykładowe obliczenia wyrażeń dla wartości x=2.43:

Zmienne zespolone

Zmienna zespolona ma postać:

a + b i

gdzie: a – liczba będąca tzw. częścią rzeczywistą,

b – liczba będąca tzw. częścią urojoną,

i – jednostka urojona: i

2

=–1

Reprezentacja liczby zespolonej:

W Matlab-ie otrzymujemy wyniki w postaci zespolonej dla niektórych działań nieposiadających rozwiązań w dzie-

dzinie liczb rzeczywistych, np.

√−2 , log(-2) itp.

z1 = 5.0 + 5.0i

% zmienna zespolona

z2 = sqrt(-1)

% jednostka urojona (pierwiastek arytmetyczny z –1)

z3 = angle(z1)

% kąt, jak na rysunku

z4 = z3*4

k1 = angle(0+1i)*180/pi

k2 = angle(1+0i)*180/pi

z1o=1/z1
z4=z1*z2
log(0)
log(-1)
exp(1)^log(-1)

%sprawdzenie

Ćwiczenie

1.

Napisać m-plik, w którym:

2.

Zainicjujemy dwie zmienne zespolone o wartościach:

4.5+4.7i

–2.5 –5.6i

3.

Wykonamy i wyświetlimy wynik dodawania i mnożenia obu liczb.

Instrukcja warunkowa

Instrukcja służy do sprawdzenia warunków i alternatywnego wykonywania różnych grup instrukcji gdy dany wa-

runek będzie prawdziwy (true). Postać ogólna

if

warunek1

instrukcje (wykonywane gdy jest spełniony warunek1)

elseif

warunek2

instrukcje

(wykonywane gdy jest spełniony warunek2)

elseif

warunek3

instrukcje (wykonywane gdy jest spełniony warunek3)

…itd

else

instrukcje (wykonywane gdy niespełnione oba warunki)

end

Bloki else i elseif mogą zostać pominięte – wówczas gdy warunek1 nie jest spełniony wykonywana jest kolejna in-

strukcja po instrukcji if. Gdy pierwszy lub kolejny warunek jest prawdziwy, pozostałe warunki nie są już sprawdzane.

Warunek to połączenie dwóch wyrażeń arytmetycznych znakami:
>

<

>=

<=

== (równe)

!= (nie równe)

Dwa warunki można związać:

- koniunkcją warunków, łącząc je operatorem logicznym &&

- alternatywą warunków, łącząc je operatorem logicznym ||

Przykłady warunków:

a == 0

(czy jest równe, UWAGA: 2 znaki ==)

b<c
2*a >= 5
x ~= 5

(różne od)

x>0 && x<100

Ćwiczenie

Przeanalizować poniższe przykłady, tworząc i wykonując odpowiednie m-pliki:

Przykład 1

a = 1
b = 6
c = 3
delta = b^2-4*a*c;
if delta<0
disp ('delta jest ujemne') % wyświetlenie tekstu
else
disp(delta)

% wyświetlenie wartości zmiennej

end;

Przykład 2 . Interakcja z użytkownikiem

a = input('Podaj a:');
b = input('Podaj b:');
c = input('Podaj c:');
delta = b^2-4*a*c;
if delta<0
disp ('delta jest ujemne')
else
disp('delta=');
disp(delta);
end;

Zadanie

Uzupełnić przykład 1 o:

a.

obliczanie niewiadomych x1 i x2.

b.

obliczanie pierwiastków tylko dla delta dodatniego,

c.

obliczanie tylko jednego pierwiastka gdy delta będzie równe 0,

d.

sprawdzenie rozwiązań - podstawić pierwiastki do równania i przekonać się czy da to wynik 0.