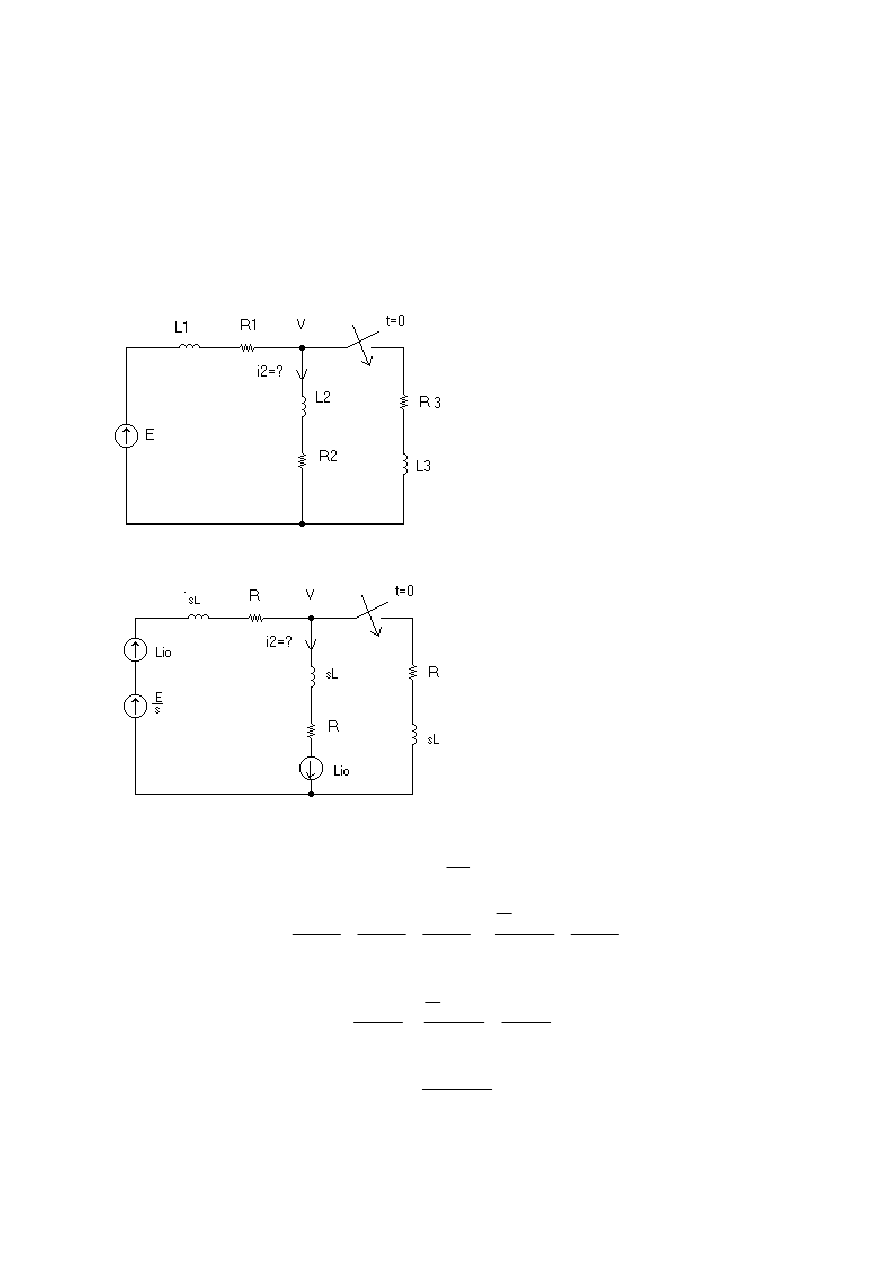
1
Podstawy Elektrotechniki - Stany nieustalone
II. Metoda Operatorowa
Zadanie o.1
Wyznaczyć prąd i
2
(t).
Po zastosowaniu przekształcenia Laplace’a
Io=
R
E
2
V(
sL
R
Lio
sL
R
Lio
s
E
sL
R
sL
R
sL
R
+
−
+
+
=
+
+
+
+
+
)
1
1
1
V
=
+ sL
R
3
sL
R
Lio
sL
R
Lio
s
E
+
−
+
+
V=
)
(
sL
R
s
E
+
2
2
I
(s)=
)
(
3
)
(
3
s
L
R
Ls
E
sL
R
s
E
sL
R
V
+
=
+
=
+
]
3
3
[
3
3
)
(
2
t
L
R
t
L
R
e
R
E
R
E
e
R
E
R
E
t
i
−
−
−
=
−
+
=
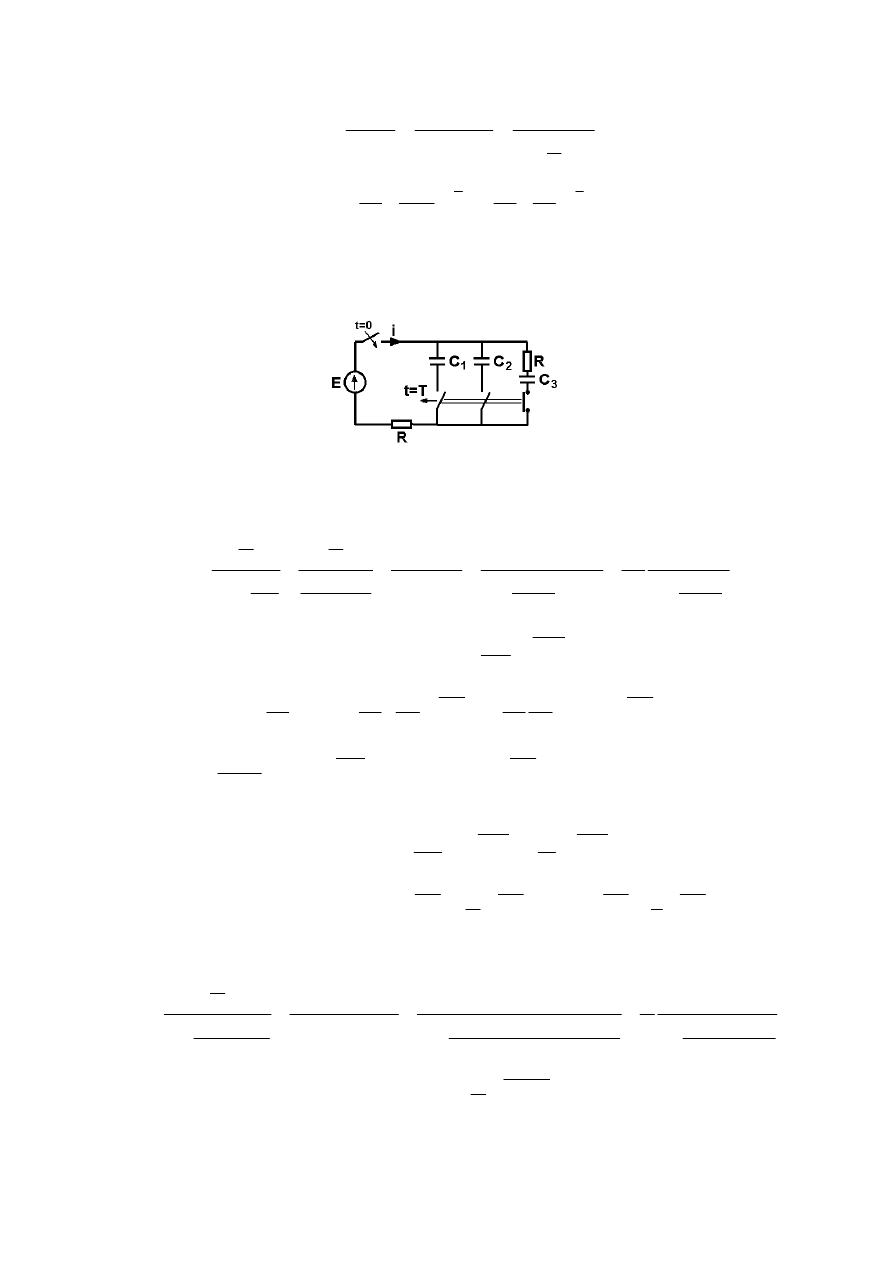
Zadanie o.2
Obliczy
ć
napi
ę
cie na zaciskach wył
ą
cznika w chwili t=0 i napi
ę
cia na C
1
i
C
2
w chwili t=T.
a)
t=0:
)
2
1
(
1
2
2
)
2
1
(
1
2
1
2
1
2
)
(
3
3
3
3
3
3
3
3
3
RC
s
R
E
RC
RC
s
EC
s
RC
EC
s
C
s
RC
s
E
s
C
R
s
E
s
J
+
=
+
=
+
=
+
=
+
=
t
RC
e
R
E
s
J
L
t
i
3
2
1
1
2
)}
(
{
)
(
−
−
=
=
3
3
3
3
2
1
3
2
1
3
3
0
2
1
3
3
0
2
1
3
0
3
3
1
(
]
2
2
[
2
]
2
[
2
1
2
1
)
(
1
)
(
RC
t
RC
t
t
RC
t
t
RC
t
c
e
E
RC
e
RC
R
C
E
e
RC
R
E
C
dt
e
R
E
C
dt
t
i
C
t
U
−
−
−
−
−
=
+
−
=
=
−
=
=
=
∫
∫
t
RC
t
RC
R
e
E
R
E
R
t
i
t
U
3
3
2
1
2
1
2
Re
2
)
(
)
(
−
−
=
=
=
)
2
1
1
(
2
)
1
(
)
(
)
(
)
(
3
3
3
3
2
1
2
1
2
1
2
1
3
t
RC
t
RC
t
RC
RC
R
c
wyl
e
e
E
e
E
e
E
t
U
t
U
t
U
−
−
−
−
+
−
=
+
−
=
+
=
b)
t=T
)
(
1
1
)
(
)
(
1
(
)
(
1
)
(
)
(
)
(
1
)
(
2
1
2
1
2
1
2
1
2
1
2
1
2
1
C
C
RC
s
R
E
C
C
R
C
C
RC
s
C
C
E
C
C
Rs
C
C
E
C
C
s
R
s
E
s
J
+
+
=
+
+
+
+
=
+
+
+
=
+
+
=
t
C
C
R
e
R
E
s
J
L
t
J
)
(
1
1
2
1
)}
(
{
)
(
+
−
−
=
=
Obliczamy napi
ę
cie na C
1
i C
2
pami
ę
taj
ą
c
ż
e: C
z
=C
1
+C
2
3
)
1
(
)
(
)
(
)
(
)
(
]
)
(
[
1
)
(
1
)
(
)
(
)
(
1
2
1
2
1
)
(
1
2
1
2
1
0
)
(
1
2
1
0
)
(
1
0
2
1
2
1
2
1
2
1
2
1
t
C
C
R
t
C
C
R
t
t
C
C
RC
t
z
t
C
C
R
z
t
z
c
c
e
E
C
C
R
C
C
ER
e
C
C
R
C
C
ER
e
C
C
RC
RC
E
dt
e
R
E
C
dt
t
i
C
t
U
t
U
+
−
+
−
+
−
+
−
−
=
+
+
+
+
+
−
=
+
−
=
=
=
=
∫
∫
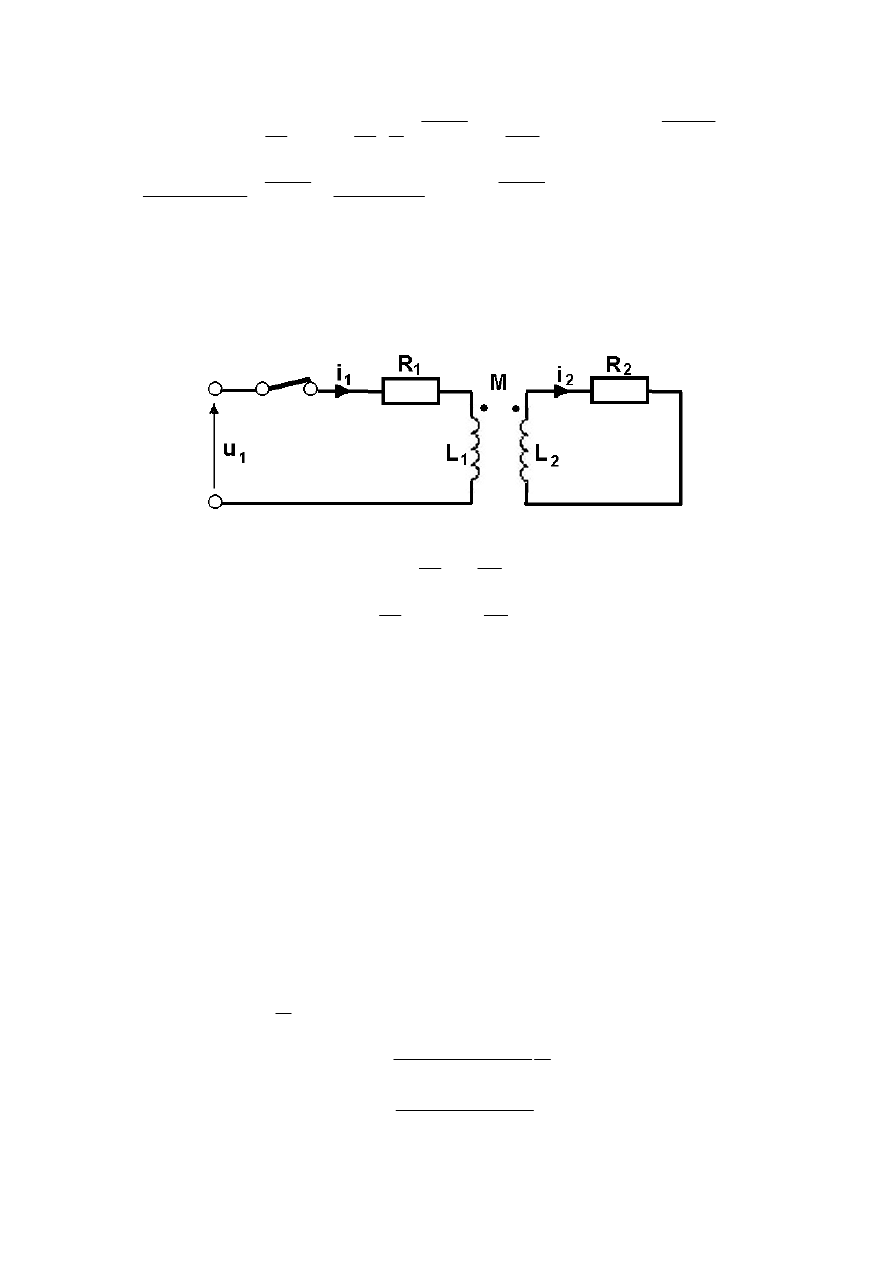
Zadanie o.3
Wyznaczy
ć
rozpływ pr
ą
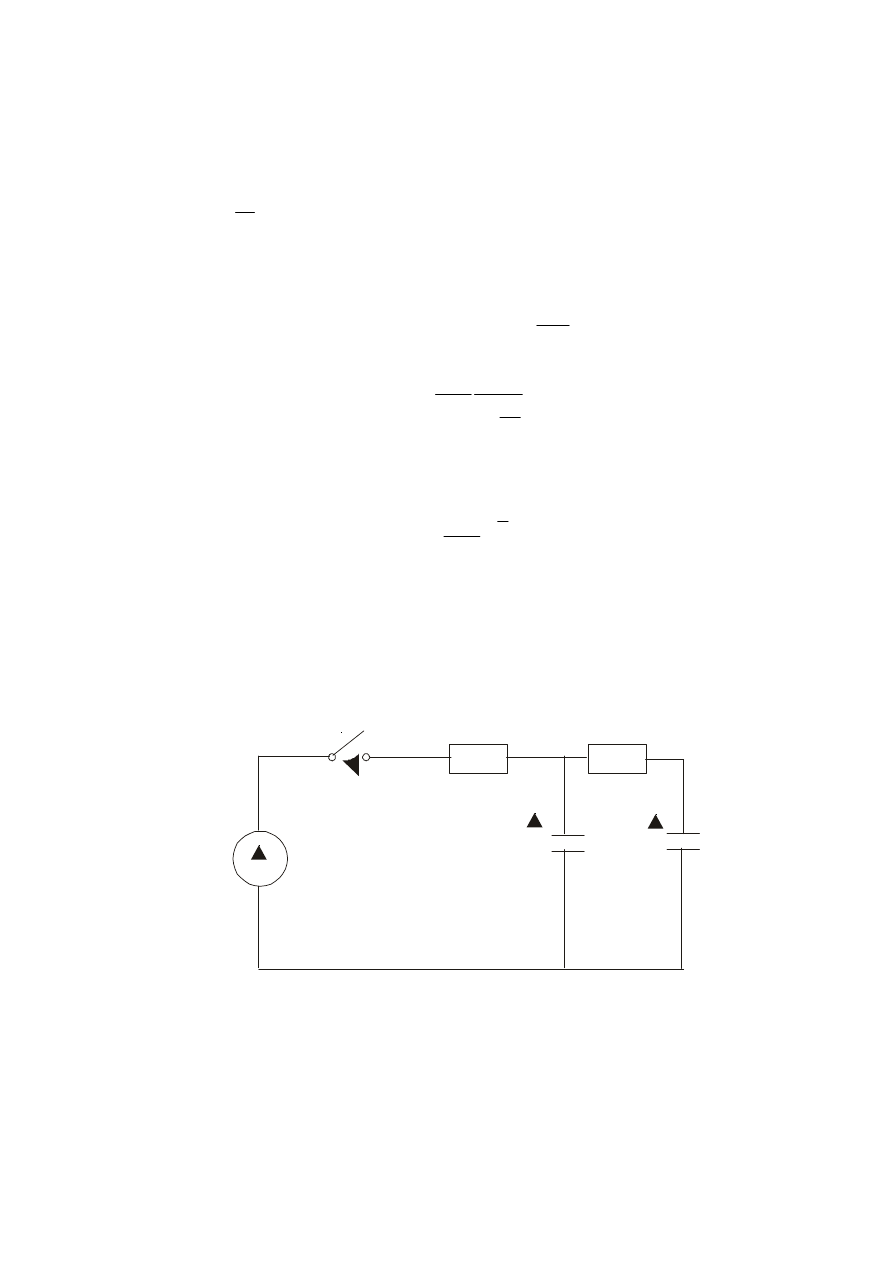
dów w układzie przedstawionym poni
ż
ej dla dwóch przypadków
zamykania i otwierania wył
ą
cznika.
Dla obwodu przedstawionego na rysunku równania ró
ż
niczkowe maj
ą
posta
ć
:
1
2
1
1
1
1
u
dt
di
M
dt
di
L
i
R
=
−
+
0
2
2
2
2
1
=
+
+
−
u
dt
di
L
i
R
dt
di
M
Te same równania w rachunku operatorowym:
(R
1
+sL
1
)I
1
(s)-sMI
2
(s)=U
1
(s)+L
1
i
1
(0)-Mi
2
(0)
-sMI
1
(s)+(R
2
+sL
2
)I
2
(s)=L
2
i
2
(0)-Mi
1
(0)
Przy zerowych warunkach pocz
ą
tkowych równania powy
ż
sze upraszczaj
ą
si
ę
do postaci
Z
1
(s)I
1
(s)-sMI
2
(s)=U
1
(s)
-sMI
1
(s)+Z
2
(s)I
2
(s)=0
przy czym:
Z
1
(s) – impedancja operatorowa obwodu 1;
Z
2
(s) – impedancja operatorowa obwodu 2.
1. Zamykanie wył
ą
cznika.
Z równa
ń
przy
S
U
s
U
=
)
(
otrzymujemy
s
U
M
s
s
Z
s
Z
s
Z
s
I
2
2
2
1
2
1
)
(
)
(
)
(
)
(
−
=
U
M
s
s
Z
s
Z
M
s
I
2
2
2
1
2
)
(
)
(
)
(
−
=
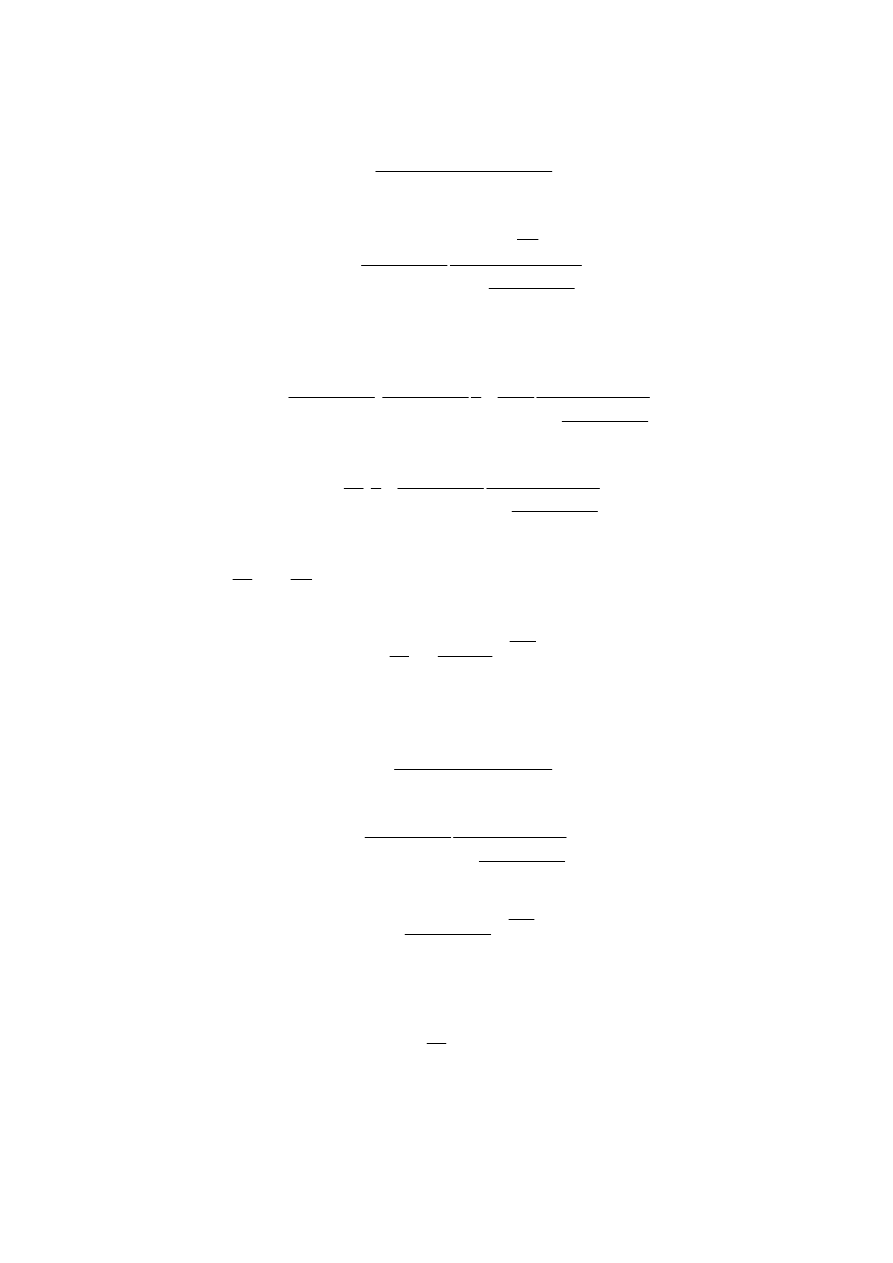
4
Po podstawieniu: Z
1
(s)=R
1
+sL
1
; Z
2
(s)=R
2
+sL
2
; L
1
L
2
=M
2
otrzymujemy
U
R
R
R
L
R
L
s
s
R
sL
s
I
]
)
(
[
)
(
2
1
1
2
2
1
2
2
1
+
+
+
=
]
[
)
(
1
2
2
1
2
1
2
2
1
2
2
1
2
1
R
L
R
L
R
R
s
s
L
R
s
R
L
R
L
UL
s
I
+
+
+
+
=
Rozkładamy na ułamki proste
]
1
1
[
)
(
1
2
2
1
2
1
1
2
2
1
1
2
1
2
2
1
1
2
2
1
2
1
R
L
R
L
R
R
s
R
L
R
L
s
R
L
R
L
R
L
R
L
R
L
UL
s
I
+
+
−
+
+
=
1
2
2
1
2
1
1
2
2
1
2
1
1
1
1
1
[
)
(
R
L
R
L
R
R
s
R
L
R
L
R
L
s
R
U
s
I
+
+
+
−
=
Po podstawieniu
2
2
2
1
1
1
,
τ
τ
=
=
R
L
R
L
otrzymujemy przebieg pr
ą
du
]
1
[
)
(
2
1
2
1
1
1
τ
τ
τ
τ
τ
+
−
+
−
=
t
e
R
U
t
i
Pr
ą
d w obwodzie 2
2
1
1
2
2
1
2
)
(
)
(
R
R
R
L
R
L
s
MU
s
I
+
+
=
1
2
2
1
2
1
1
2
2
1
2
1
)
(
R
L
R
L
R
R
s
R
L
R
L
MU
s
I
+
+
+
=
2
1
1
2
2
1
2
)
(
τ
τ
+
−
+
=
t
e
R
L
R
L
MU
t
i
Pr
ą
dy w stanie ustalonym:
0
;
2
1
1
=
=
u
u
i
R
U
i
2. Otwieranie wył
ą
cznika.
5
Po otwarciu wył
ą
cznika obwód 1 zostaje przerwany, wi
ę
c i
1
=0. Pr
ą
d mo
ż
e płyn
ąć
tylko w
obwodzie
2.
W
celu
jego
obliczenia
podstawimy
w
równaniach:
0
)
0
(
;
)
0
(
;
0
)
(
2
1
1
1
=
−
=
−
=
i
R
U
i
s
I
przyjmuj
ą
c,
ż
e przy zamkni
ę
tym wył
ą
czniku został uprzednio
osi
ą
gni
ę
ty stan ustalony.
1
1
2
2
2
)
0
(
)
)(
(
R
MU
Mi
R
sL
s
I
−
=
−
=
+
2
2
1
2
2
1
)
(
L
R
s
R
L
MU
s
I
+
−
=
st
ą
d
2
1
2
2
)
(
τ
t
e
R
L
MU
t
i
−
−
=
Zadanie o.4
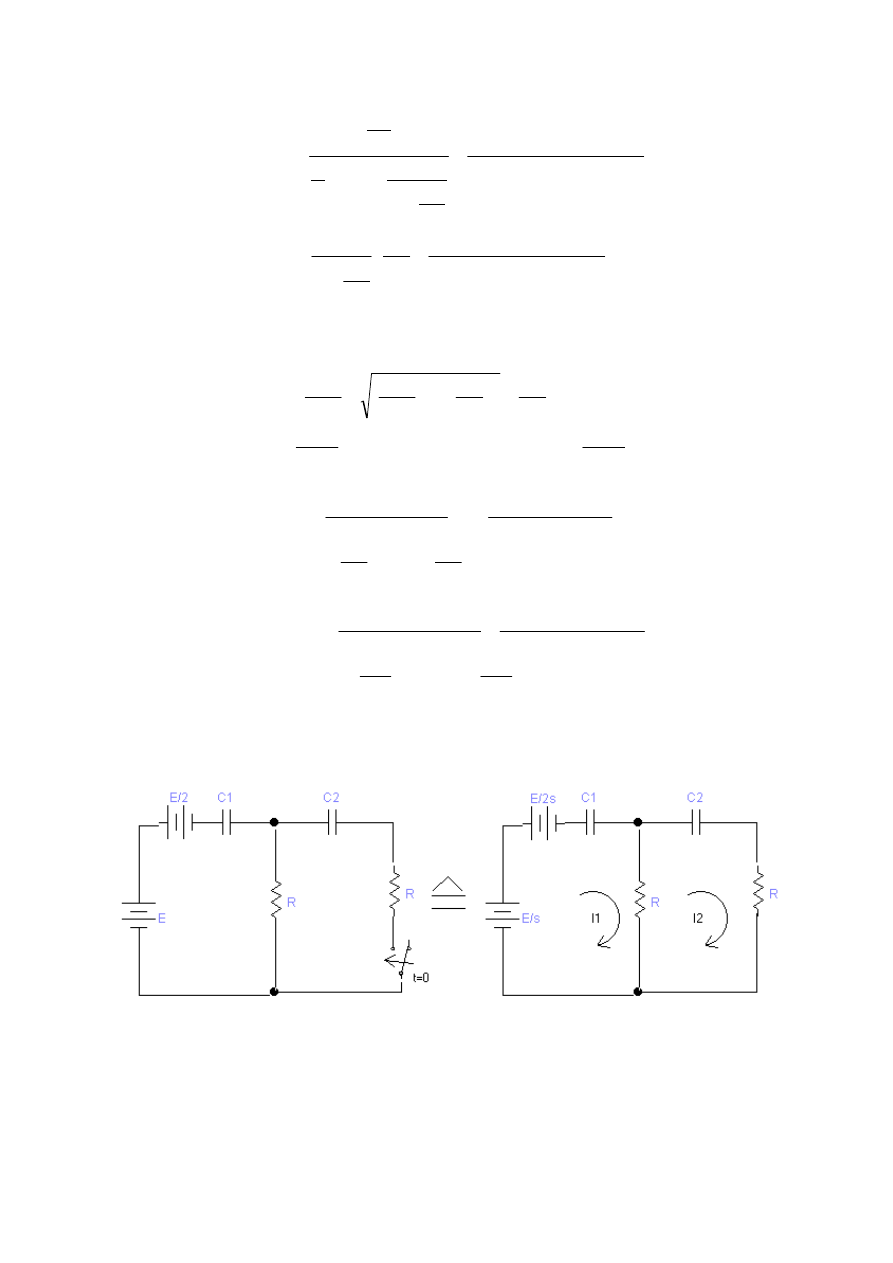
W obwodzie jak na rysunku w chwili t=0 zamkni
ę
to wył
ą
cznik W. Obliczy
ć
przebiegi napi
ęć
na obydwu kondensatorach, je
ż
eli wiemy,
ż
e u
1
(0) = u
2
(0) = 0.
Rozwi
ą
zanie:
Korzystaj
ą
c z metody potencjałów w
ę
złowych otrzymujemy:
R
T=0
W
E=const
R
C
U1(t)
U2(t)
C
6
]
1
3
)
[(
1
1
)
(
)
(
]
1
3
)
[(
)
1
(
1
1
1
)
(
2
2
1
2
2
2
1
+
+
=
⋅
+
=
+
+
+
=
+
+
+
=
RCp
p
RC
p
E
pC
pC
R
p
U
p
U
RCp
p
RC
p
RCp
E
pC
R
pC
R
pR
E
p
U
Przy przej
ś
ciu na posta
ć
czasow
ą
korzystamy z I wzoru Heaviside’a.
Równanie ma posta
ć
: H(p)=(RC)
2
p
2
+3RCp+1=0 posiada dwa nast
ę
puj
ą
ce pierwiastki:
RC
p
RC
p
RC
RC
RC
RC
p
618
,
2
382
,
0
)
118
,
1
5
,
1
(
1
)
1
(
)
2
3
(
2
3
2
1
2
2
2
,
1
−
=
−
=
±
−
=
−
±
−
=
Po obliczeniach mamy:
)
(
1
]
276
,
0
723
,
0
1
[
]
)
(
)
(
1
)
(
)
(
1
1
[
)
(
618
,
2
328
,
0
1
2
2
2
2
2
1
1
2
1
1
2
1
t
e
e
E
e
p
p
p
RC
RCp
e
p
p
p
RC
RCp
E
t
u
RC
t
RC
t
t
p
t
p
⋅
−
−
⋅
=
=
−
+
+
−
+
+
⋅
=
−
−
)
(
1
]
170
,
0
170
,
1
1
[
]
)
(
)
(
)
(
)
(
1
[
)
(
618
,
2
382
,
0
1
2
2
2
2
1
1
2
2
2
1
t
e
e
E
p
p
p
RC
e
p
p
p
RC
e
E
t
u
RC
t
RC
t
t
p
t
p
⋅
⋅
+
⋅
−
⋅
=
=
−
+
−
+
⋅
=
−
−
Zadanie o.5
Wyznaczy
ć
napi
ę
cia na kondensatorze.
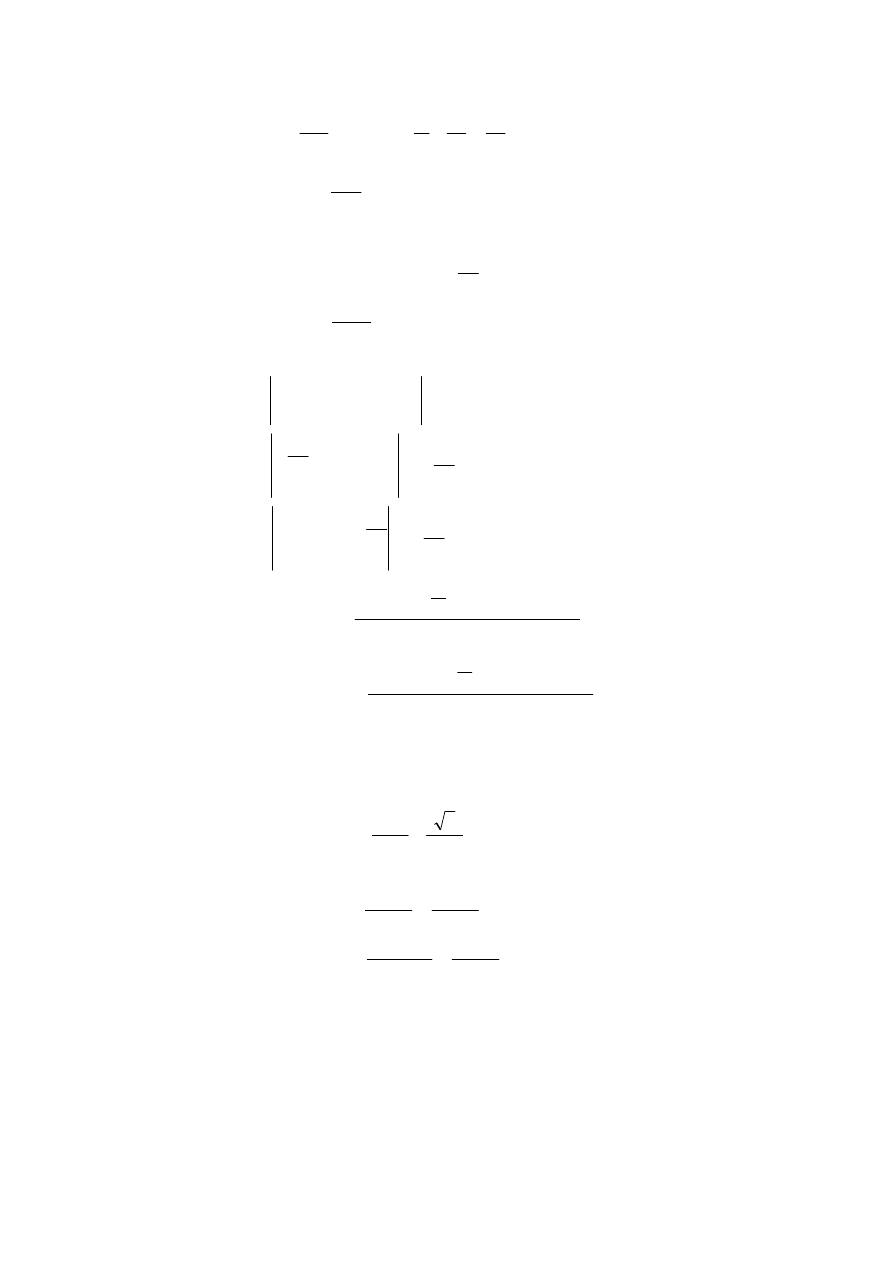
7
(
)
2
1
2
1
1
2
1
2
1
1
2
1
2
2
1
2
2
2
1
1
2
2
2
1
1
1
2
1
1
1
2
2
2
1
1
2
0
2
1
)
1
2
(
2
1
2
0
2
1
)
2
(
1
2
1
0
)
1
2
(
2
)
(
)
(
2
)
(
1
)
(
0
)
(
1
)
(
2
2
)
(
1
)
(
2
1
RsC
C
E
RsC
C
E
RsC
W
RsC
C
E
RsC
RsC
C
E
W
RC
RC
s
s
C
C
R
RsC
RsC
RsC
RsC
Wg
RsC
s
I
RsC
s
I
C
E
RsC
s
I
RsC
s
I
R
I
sC
R
R
s
I
s
E
s
E
s
E
R
I
sC
R
s
I
I
I
=
−
+
=
+
=
+
−
=
+
+
+
=
+
−
−
+
=
=
+
+
−
=
−
+
=
−
+
+
=
−
=
−
+
1
)
2
(
2
)
(
1
)
2
(
2
)
(
2
1
2
2
1
2
1
2
2
1
2
2
1
2
2
1
2
+
+
+
=
+
+
+
=
s
RC
RC
s
C
C
R
R
C
E
s
U
s
RC
RC
s
C
C
R
Rs
C
C
E
s
I
C
RC
RC
s
RC
RC
s
RC
RC
r
RC
R
C
RC
RC
s
R
C
s
s
M
C
C
C
62
.
2
2
24
.
2
3
38
.
0
2
76
.
0
2
5
2
3
)
(
5
4
)
(
9
1
3
)
(
2
1
2
,
1
2
2
2
2
2
2
2
2
1
−
=
⋅
−
=
−
=
−
=
±
−
=
=
−
=
Λ
+
+
=
=
=
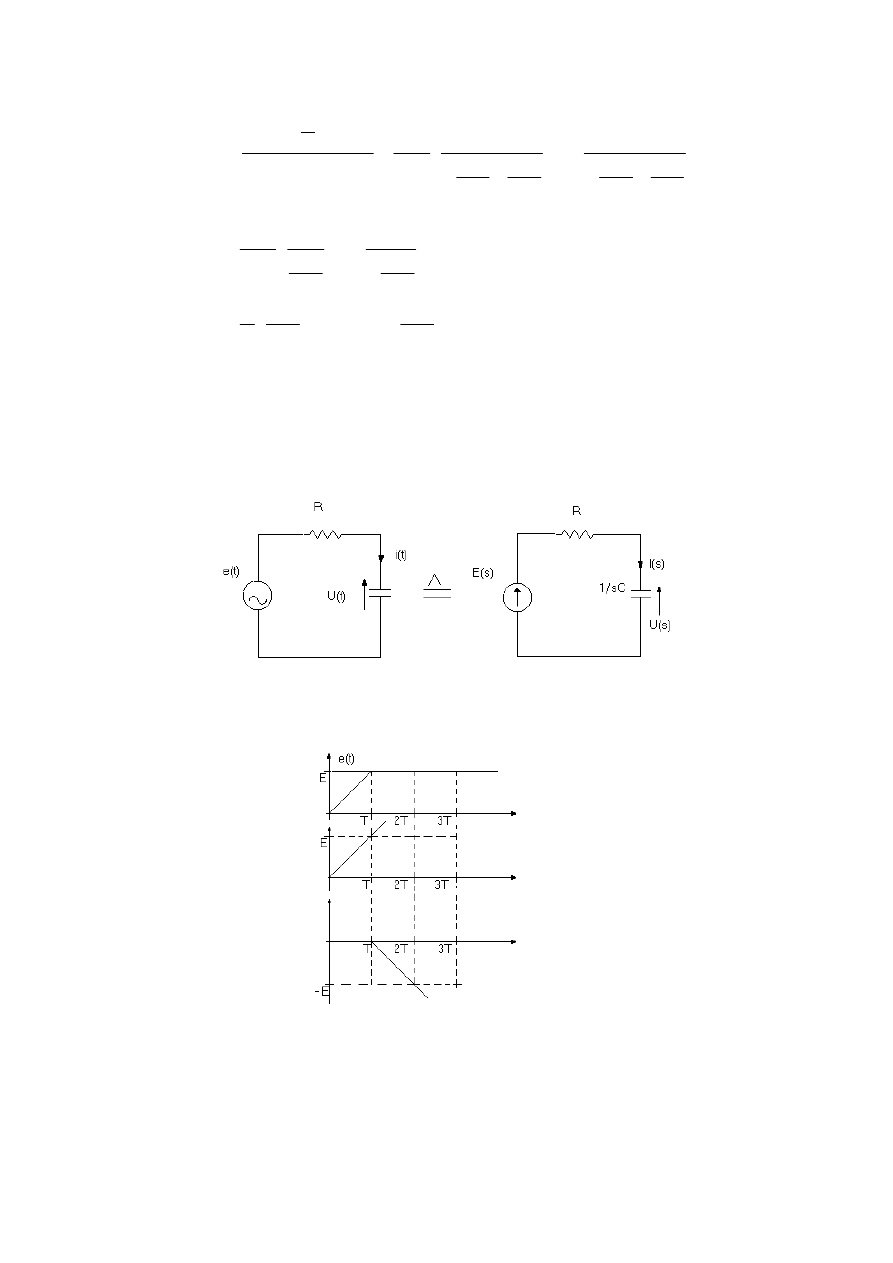
8
(
)
(
)
t
r
t
r
t
r
t
r
C
t
r
t
r
C
t
r
t
r
C
e
e
E
e
e
E
t
U
e
RC
e
RC
RC
E
t
U
e
RC
RC
e
RC
RC
RC
E
s
s
s
s
RC
E
s
U
2
1
2
1
2
1
2
1
48
.
4
24
.
2
1
2
)
(
24
.
2
1
24
.
2
1
2
)
(
38
.
0
62
.
2
1
62
.
2
38
.
0
1
2
)
)(
(
2
)
(
2
2
2
1
2
−
=
−
=
−
+
=
+
−
+
+
−
≅
−
−
=
Zadanie o.6
Wyznaczyć u
c
(t) dla wymuszenia przedstawionego na rys. o.6
Rys. o.6 Przebieg e(t) i jego rozkład na składowe e
1,
e
2.
Przebieg e(t) mo
ż
na przedstawi
ć
jako sum
ę
przebiegów e
1
(t) i e
2
(t).
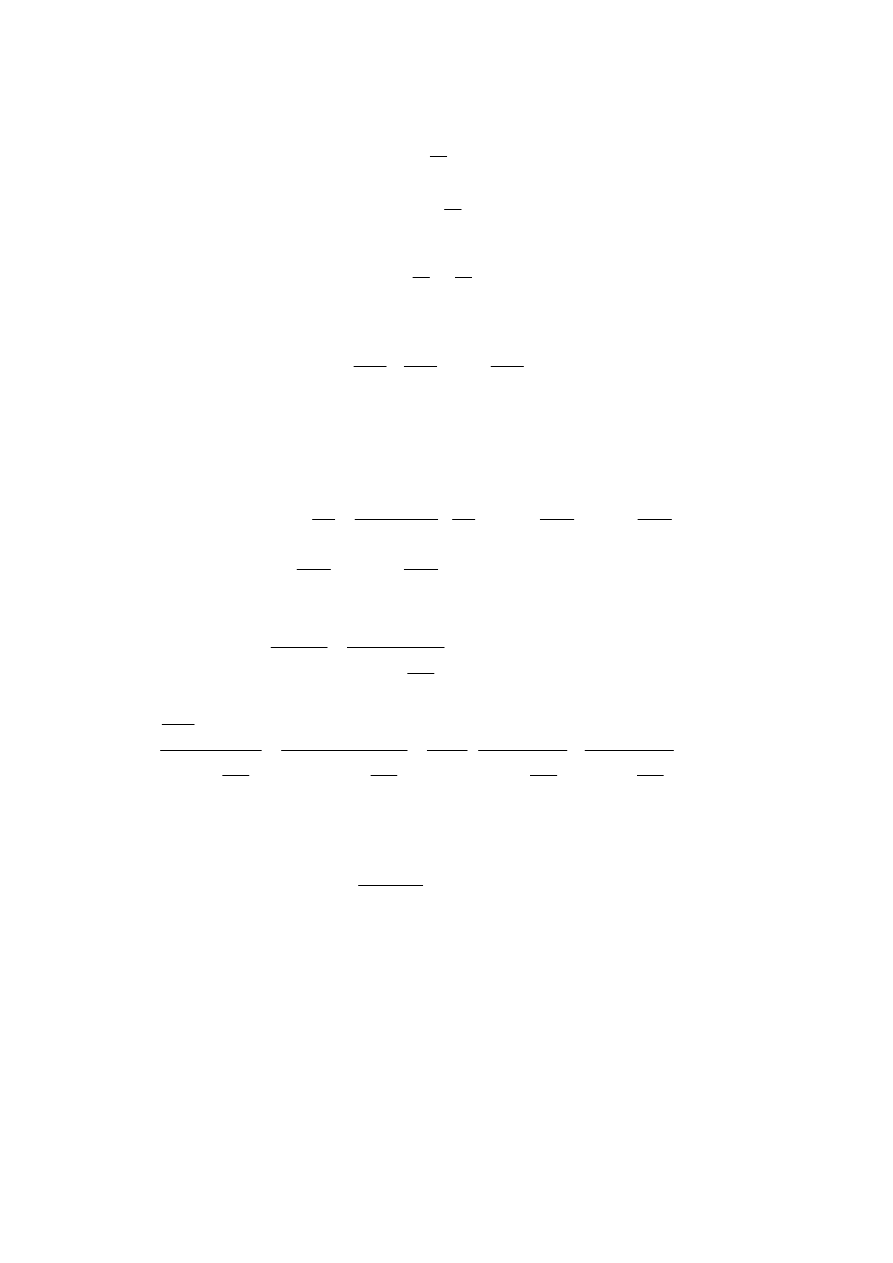
9
( )
( )
(
)
1
1
2
1
1
τ
τ
τ
−
−
=
=
t
E
t
e
t
E
t
e
( )
(
)
1
1
1
τ
τ
τ
−
−
=
t
E
t
E
t
e
Przechodz
ą
c na posta
ć
operatorow
ą
:
( )
[
]
1
1
1
2
1
2
1
2
1
τ
τ
τ
τ
τ
s
s
e
s
E
e
s
E
s
E
s
E
−
−
−
=
−
=
Napi
ę
cie na kondensatorze wyznaczamy nast
ę
puj
ą
co
:
( ) ( )
( )
( )
( ) ( )
R
s
I
s
U
s
E
s
U
R
s
I
s
E
=
−
⇒
+
=
( ) ( )
( )
( )
( )
( )
( )
( )
( ) (
)
( )
( )
( )
( )
+
=
+
=
=
+
=
+
−
=
−
=
=
RC
s
RC
s
E
sRC
s
E
s
U
s
E
sRC
s
U
sRC
s
E
sRC
s
U
sRC
s
U
sRC
s
E
sC
R
s
U
s
E
sC
s
I
s
U
1
1
1
*
1
*
1
1
*
1
*
1
*
1
*
1
*
( )
(
)
(
)
+
−
+
=
+
−
=
+
−
=
−
−
−
1
1
1
1
1
1
1
1
1
1
1
2
2
1
2
1
2
1
τ
τ
τ
τ
τ
τ
s
s
s
e
RC
s
s
RC
s
s
RC
E
RC
s
RC
s
e
E
RC
s
RC
e
s
E
s
U
Opieraj
ą
c si
ę
na zale
ż
no
ś
ci :
(
)
(
)
at
e
at
a
s
s
a
−
−
−
≡
+
1
2
2
Otrzymujemy:
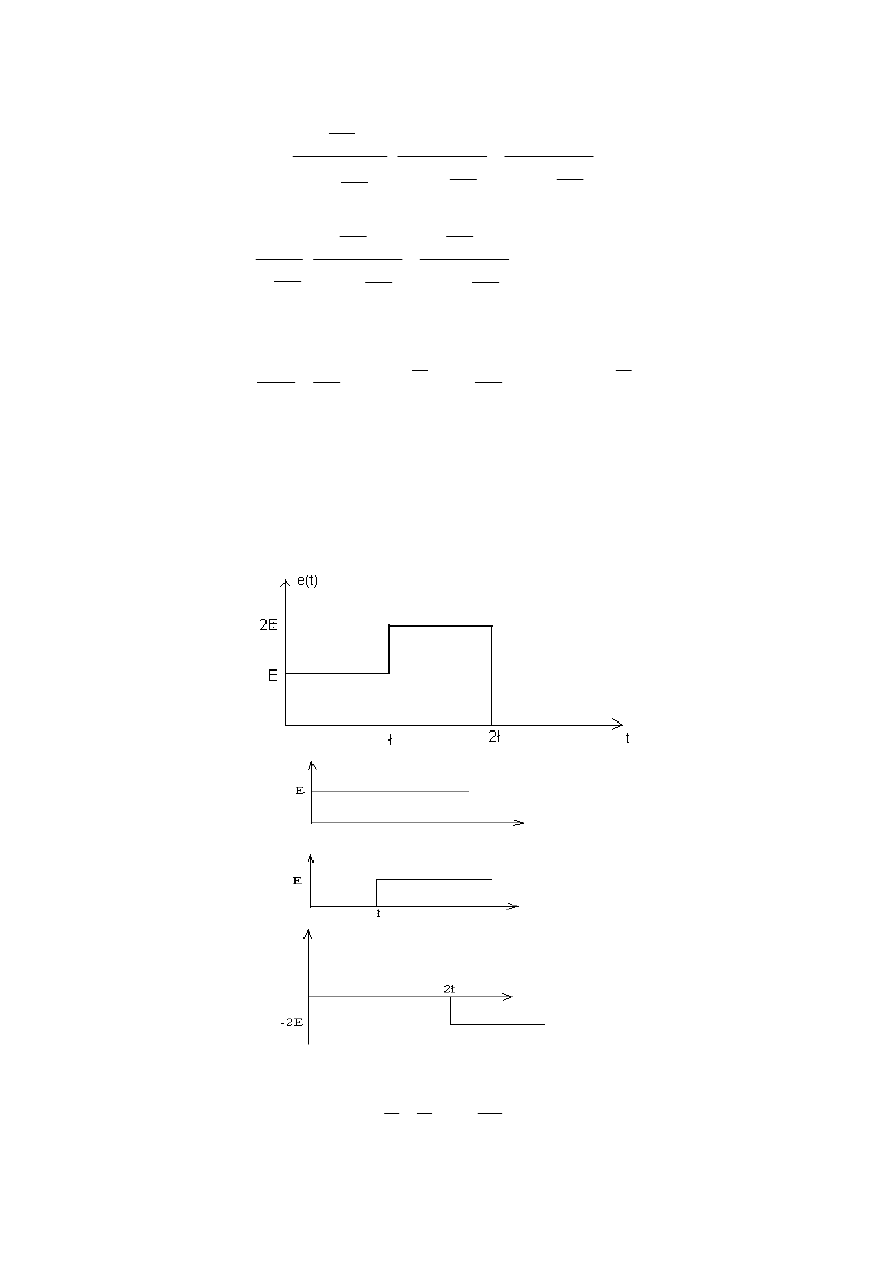
10
( )
+
−
+
=
=
+
−
+
=
−
−
1
1
1
1
1
1
1
1
1
1
1
1
1
2
2
2
2
1
2
2
2
1
2
τ
τ
τ
τ
s
s
e
RC
s
s
RC
RC
s
s
RC
RC
E
e
RC
s
s
RC
s
s
RC
RC
RC
E
s
U
Przechodz
ą
c na posta
ć
czasow
ą
otrzymujemy :
( )
(
)
(
)
−
−
−
−
−
−
=
−
−
−
1
1
1
1
1
1
1
1
1
τ
τ
τ
t
RC
t
RC
e
t
RC
e
t
RC
ERC
t
U
Zadanie o.7
e(t)=E+E(t-
τ
)-2E(t-2
τ
)
E(s)=
s
s
e
s
E
e
s
E
s
E
τ
τ
2
2
−
−
−
+
11
E(s)=I(s)R+I(s)SL
E(s)=I(s)(R+SL)
)
(
)
(
)
(
s
I
S
L
R
L
s
E
=
+
I(s)=
]
)
(
2
)
(
)
(
1
[
]
)
(
2
)
(
1
)
(
1
[
2
2
L
R
S
S
e
L
R
S
S
e
L
R
S
S
L
E
e
S
L
R
S
e
S
L
R
S
S
L
R
S
L
E
s
s
s
s
+
−
+
+
+
=
+
−
+
+
+
−
−
−
−
τ
τ
τ
τ
Korzystaj
ą
c z zasady:
f(t)=
)
(
)
(
2
1
s
F
s
F
=
Σ
st
k
k
e
s
F
s
F
)
(
)
(
'
2
1
otrzymujemy:
i(t)=
L
E
[(
L
R
L
R
e
L
R
L
R
t
L
R
−
+
+
−
+
−
1
1
(
)
1
1
e
]
)
1
1
)
)
2
(
)
(
−
+
−
−
−
−
−
τ
τ
t
L
R
t
L
R
e
L
R
L
R
i(t)=
]
1
[
]
1
(
)
1
(
)
1
[(
)
2
(
)
(
)
2
(
)
(
τ
τ
τ
τ
−
−
−
−
−
−
−
−
−
−
+
−
−
=
−
−
−
+
−
t
L
R
t
L
R
t
L
R
t
L
R
t
L
R
t
L
R
e
e
e
R
E
e
e
e
R
E
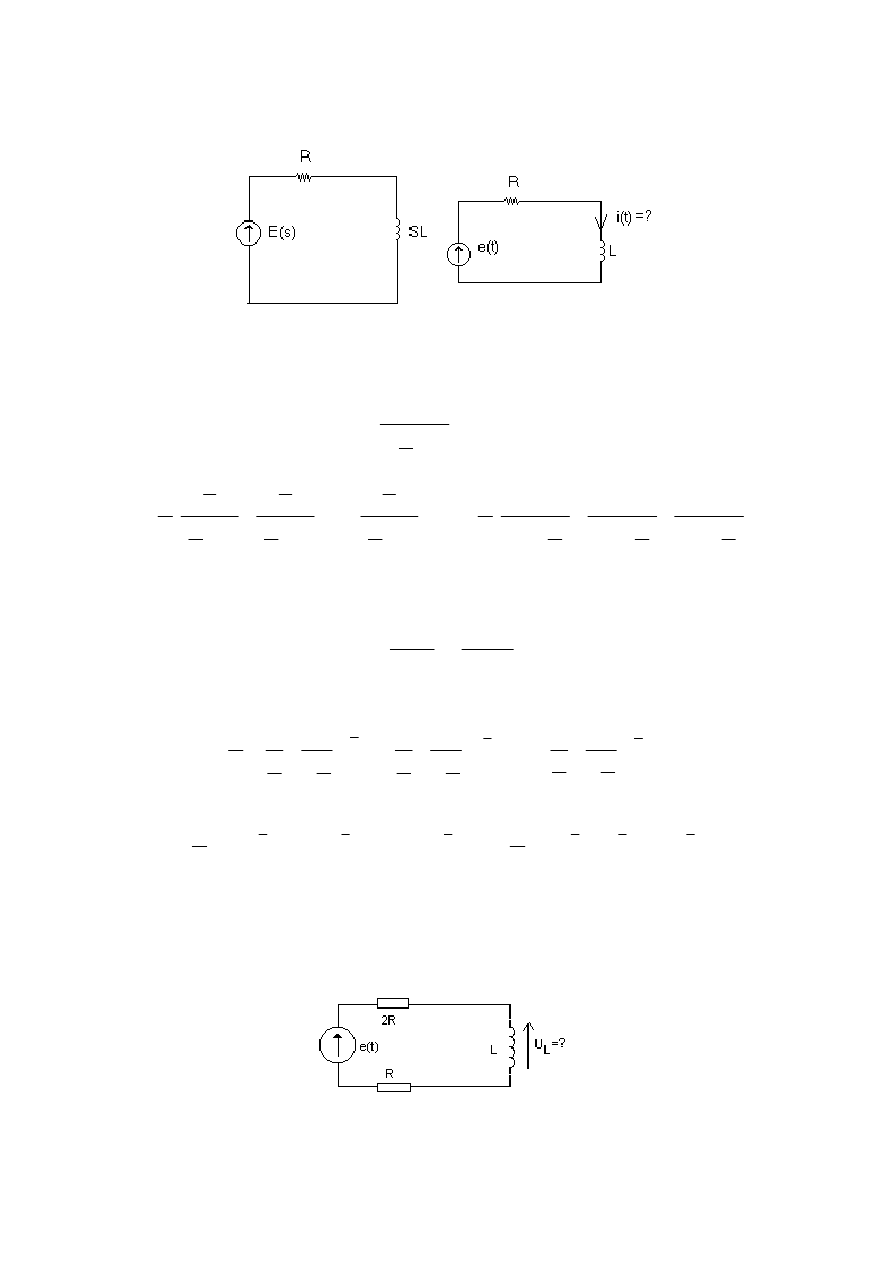
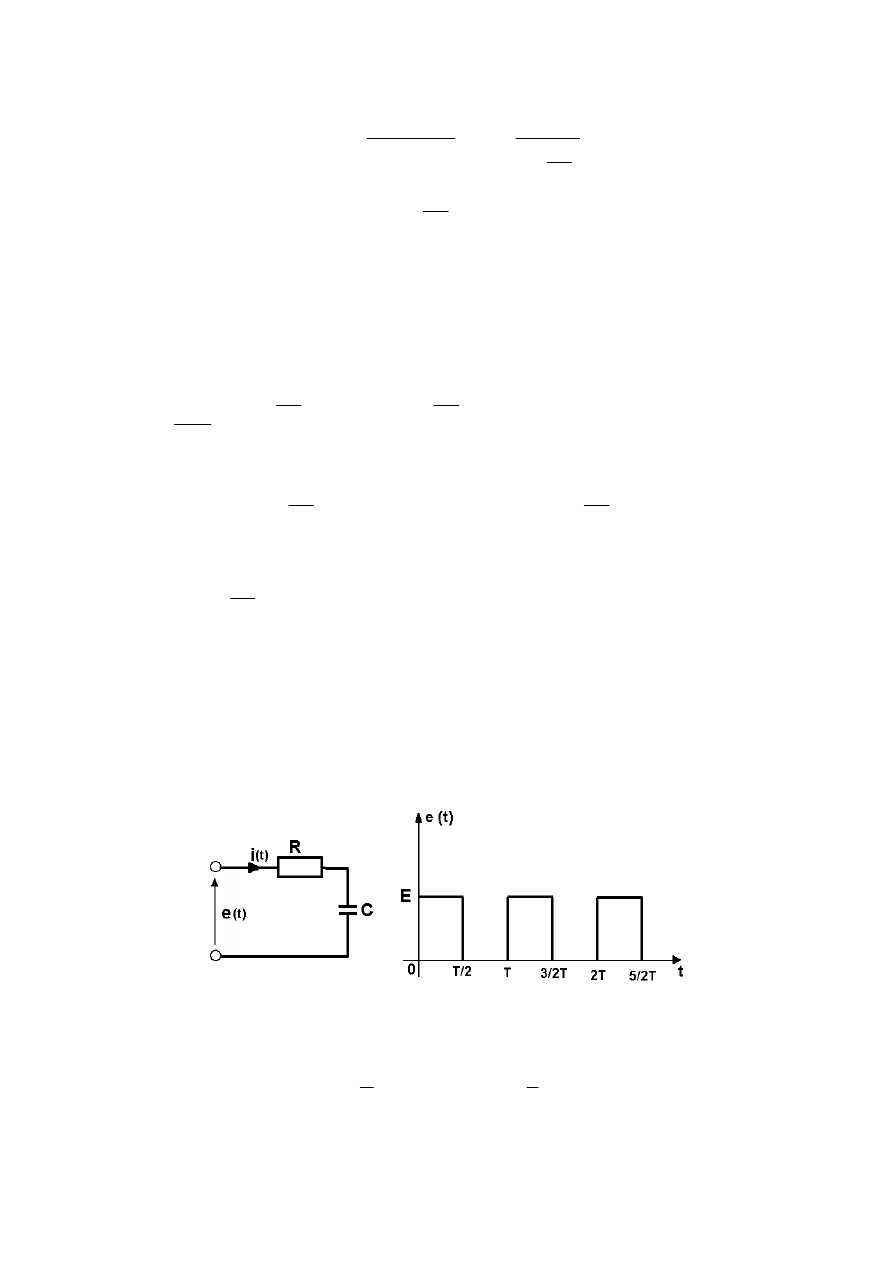
Zadanie o.8
W obwodzie przedstawionym na rysunku obliczy
ć
napi
ę
cie na cewce.
12
Napi
ę
cie zasilaj
ą
ce ma posta
ć
:
Poszczególne przebiegi wynosz
ą
;
4T)
1(t
2E
(t)
5
e
3T)
1(t
t
T
E
(t)
4
e
2T)
1(t
t
T
E
(t)
3
e
T)
1(t
t
T
E
(t)
2
e
1(t)
t
T
E
(t)
1
e
−
⋅
−
=
−
⋅
−
=
−
⋅
=
−
⋅
−
=
⋅
=
Całkowity przebieg napi
ę
cia
s4T
e
s
1
2E
s3T
e
2
s
1
T
E
s2T
e
2
s
1
T
E
sT
e
2
s
1
T
E
2
s
1
T
E
E(s)
czyli
4T)
1(t
2E
3T)
1(t
t
T
E
2T)
1(t
t
T
E
T)
1(t
t
T
E
1(t)
t
T
E
e(t)
(t)
5
e
(t)
4
e
(t)
3
e
(t)
2
e
(t)
1
e
e(t)
−
−
−
⋅
−
−
⋅
+
−
⋅
−
⋅
=
−
⋅
−
−
⋅
−
−
⋅
+
−
⋅
−
⋅
=
+
+
+
+
=
sL)
(3R
E(s)
I(s)
+
=
Tym samym napięcie U
L
:
sL
sL)
(3R
E(s)
(s)
L
U
⋅
+
=
Po podstawieniu do wzoru na napi
ę
cie
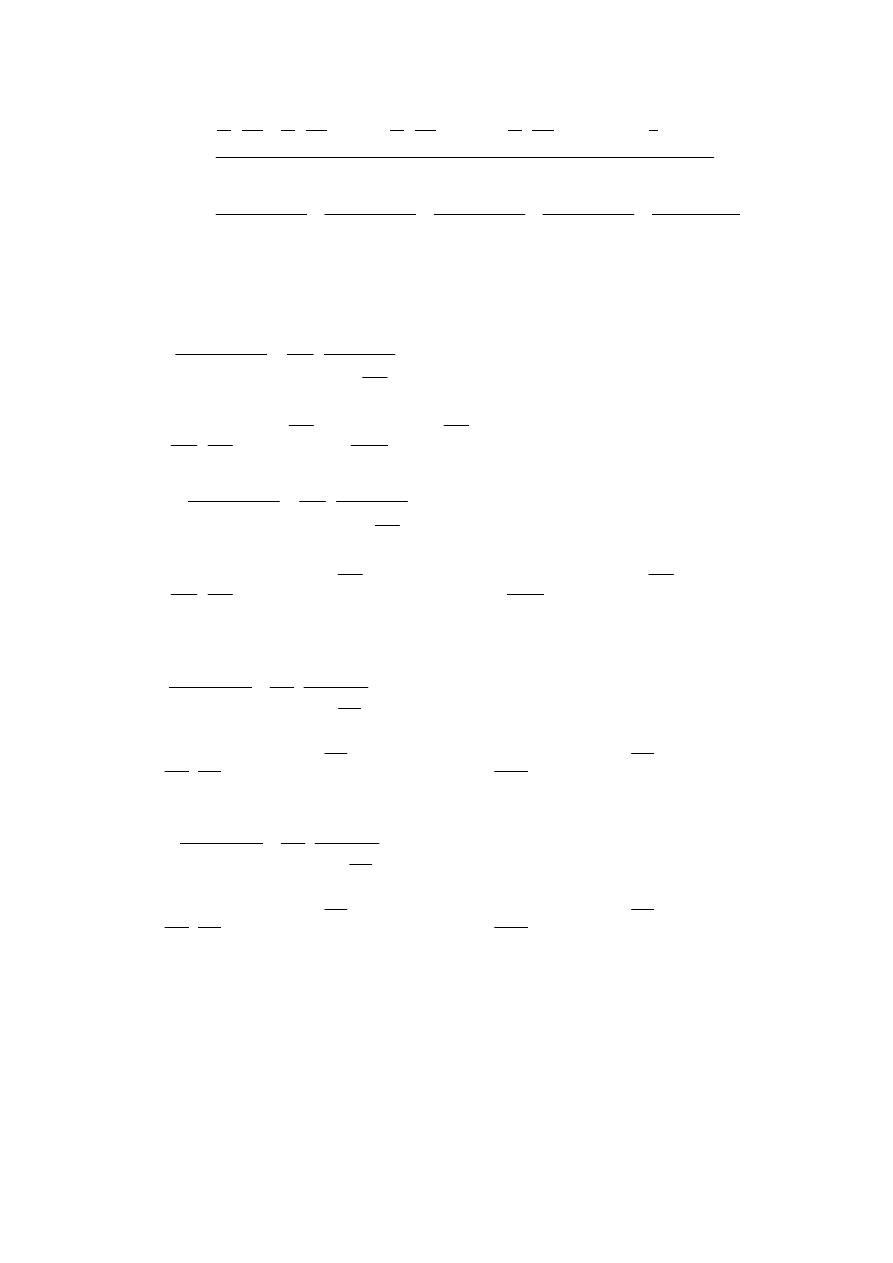
13
sL)
(3R
s4T
2ELe
sL)
Ts(3R
s3T
ELe
sL)
Ts(3R
s2T
ELe
sL)
Ts(3R
sT
ELe
sL)
Ts(3R
EL
(s)
L
U
sL
sL
3R
s4T
e
s
1
2E
s3T
e
2
s
1
T
E
s2T
e
2
s
1
T
E
sT
e
2
s
1
T
E
2
s
1
T
E
(s)
L
U
+
−
+
+
−
−
+
−
+
+
−
−
+
=
⋅
+
−
−
−
⋅
−
−
⋅
+
−
⋅
−
⋅
=
Obliczamy poszczególne człony
−
⋅
−
−
−
−
=
−
⋅
−
−
−
−
⋅
=
+
−
⋅
=
+
−
−
=
−
−
=
−
−
⋅
=
+
⋅
=
+
=
T)
1(t
T)
(t
L
3R
e
T)
1(t
T3R
E
T)
1(t
T)
(t
L
3R
e
T)
1(t
3R
L
TL
E
(t)
2
L
u
)
L
3R
s(s
sT
e
TL
EL
sL)
Ts(3R
sT
ELe
(s)
2
L
U
)
t
L
3R
e
(1
T3R
E
)
t
L
3R
e
(1
3R
L
TL
E
(t)
1
L
u
)
L
3R
s(s
1
TL
EL
sL)
Ts(3R
EL
(s)
1
L
U
−
⋅
−
−
−
−
=
−
⋅
−
−
−
−
⋅
=
+
−
⋅
=
+
−
−
=
−
⋅
−
−
−
−
=
−
⋅
−
−
−
−
⋅
=
+
−
⋅
=
+
−
=
3T)
1(t
3T)
(t
L
3R
e
3T)
1(t
T3R
E
3T)
1(t
3T)
(t
L
3R
e
3T)
1(t
3R
L
TL
E
(t)
4
L
u
)
L
3R
s(s
s3T
e
TL
EL
sL)
Ts(3R
s3T
ELe
(s)
4
L
U
2T)
1(t
2T)
(t
L
3R
e
2T)
1(t
T3R
E
2T)
1(t
2T)
(t
L
3R
e
2T)
1(t
3R
L
TL
E
(t)
3
L
u
)
L
3R
s(s
s2T
e
TL
EL
sL)
Ts(3R
s2T
ELe
(s)
3
L
U
14
−
⋅
−
−
−
=
+
−
⋅
−
=
+
−
=
4T)
1(t
4T)
(t
L
3R
e
2E
(t)
5
L
u
)
L
3R
(s
s4T
e
2E
sL)
(3R
s4T
2ELe
(s)
5
L
U
Napi
ę
cie na cewce wynosi
(t)
5
L
u
(t)
4
L
u
(t)
3
L
u
(t)
2
L
u
(t)
1
L
u
(t)
L
u
+
+
+
+
=
−
⋅
−
−
+
−
⋅
−
−
−
−
−
−
⋅
−
−
−
−
+
+
−
⋅
−
−
−
−
−
−
=
T)
1(t
T)
(t
L
3R
e
2E
-
T)
1(t
T)
(t
L
3R
e
T)
1(t
T)
1(t
T)
(t
L
3R
e
T)
1(t
T)
1(t
T)
(t
L
3R
e
T)
1(t
-
)
t
L
3R
e
(1
T3R
E
4
4
3
3
3
2
2
2
)
(t
u
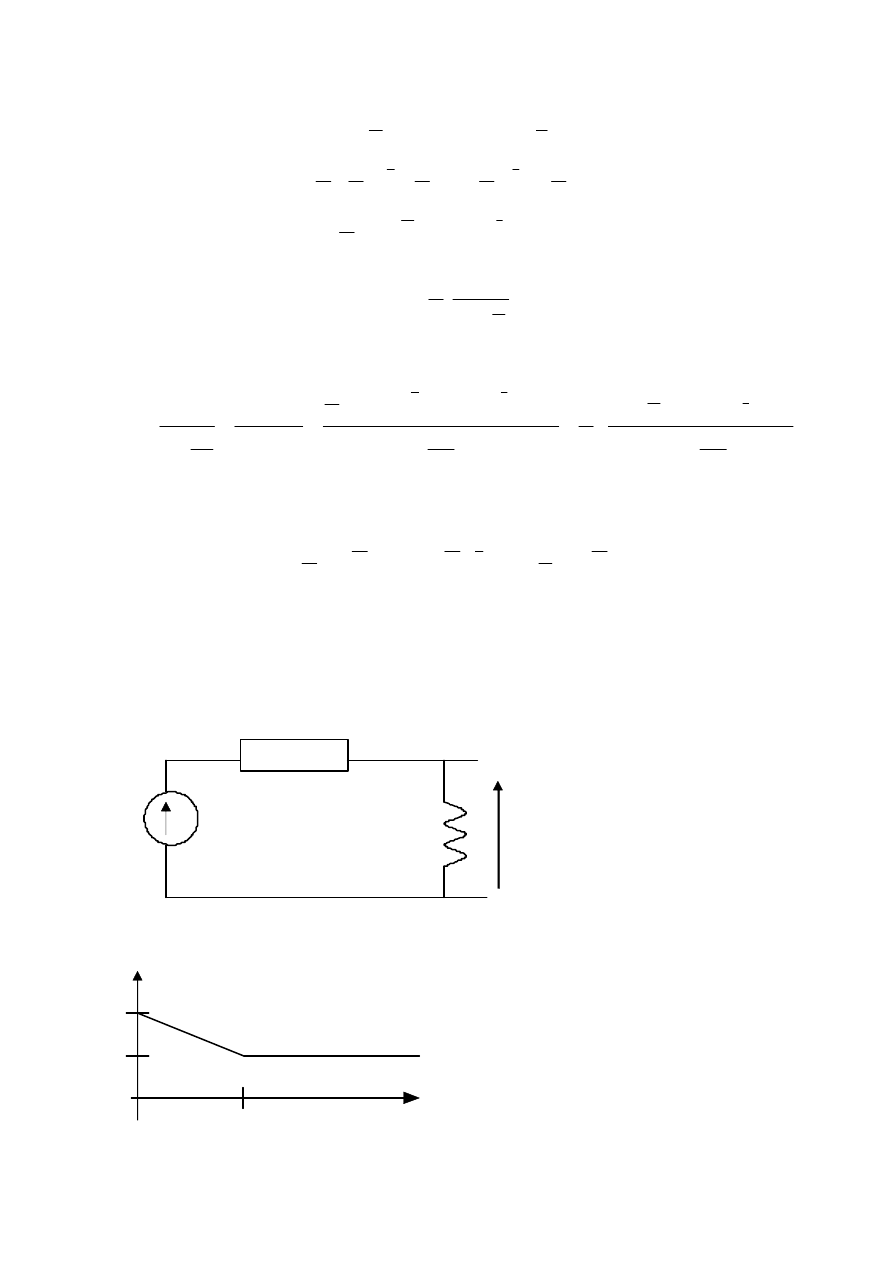
Zadanie o.9
Obliczy
ć
przebieg pr
ą
du w obwodzie je
ż
eli w układzie działa wymuszenie o przebiegu jak na
rysunku:
Rozkładamy podan
ą
funkcj
ę
na składowe:
...
)
2
(
1
)
2
3
(
1
)
(
1
)
2
(
1
)
(
1
)
(
−
−
+
−
−
−
+
−
−
=
T
t
E
T
t
E
T
t
E
T
t
E
t
E
t
e
dokonujemy przekształcenia Laplace’a
15
...]
)
2
(
1
)
2
3
(
1
)
(
1
)
2
(
1
)
(
1
[
)
(
−
−
+
−
−
−
+
−
−
=
T
t
E
T
t
E
T
t
E
T
t
E
t
E
L
s
E
...
)
(
2
2
3
2
−
+
−
+
−
=
−
−
−
−
T
sT
sT
T
s
e
s
E
e
s
E
e
s
E
e
s
E
s
E
s
E
...)
1
(
)
(
2
2
3
2
−
+
−
+
−
=
−
−
−
−
sT
sT
sT
sT
e
e
e
e
s
E
s
E
Wyra
ż
enie w nawiasie jest ci
ą
giem geometrycznym wi
ę
c:
)
1
1
(
)
(
2
sT
e
s
E
s
E
−
+
=
Obliczamy pr
ą
d w obwodzie:
)
1
(
...
1
*
)
1
(
...)
1
(
1
*
)
(
1
)
(
)
(
2
3
2
2
3
2
RC
s
e
e
e
s
E
RC
RC
s
e
e
e
Cs
s
E
RsC
Cs
s
E
sC
R
s
E
s
J
sT
sT
sT
sT
sT
T
s
+
+
−
+
−
=
+
+
−
+
−
=
+
=
+
=
−
−
−
−
−
−
Dokonujemy odwrotnego przekształcenia Laplace’a
)...]
(
1
*
)
2
(
1
*
)
(
1
*
[
*
)}
(
{
)
(
)
(
1
)
2
(
1
1
1
T
t
e
T
t
e
t
e
R
E
s
J
L
t
i
T
t
RC
T
t
RC
t
RC
−
+
−
−
=
=
−
−
−
−
−
−
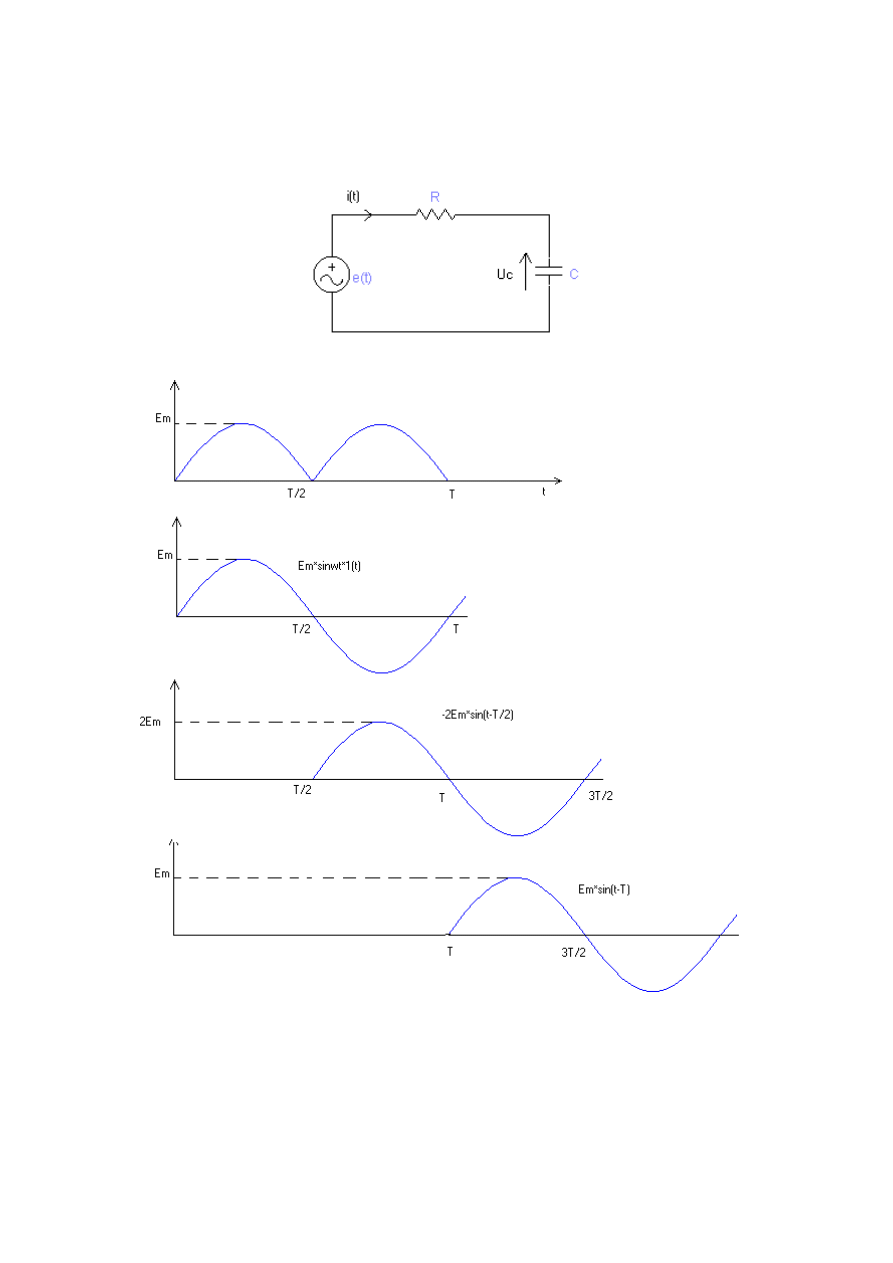
Zadanie o.10
Okre
ś
li
ć
odpowied
ź
u(t) układu RL na napi
ę
cie wymuszaj
ą
ce e(t) jak na rysunku
R
L
U
L
e(t)
2E
E
t
T
e(t)
16
Zadanie o.11
Wyznaczy
ć
napi
ę
cie na kondensatorze dla wymuszenia przedstawionego poni
ż
ej.
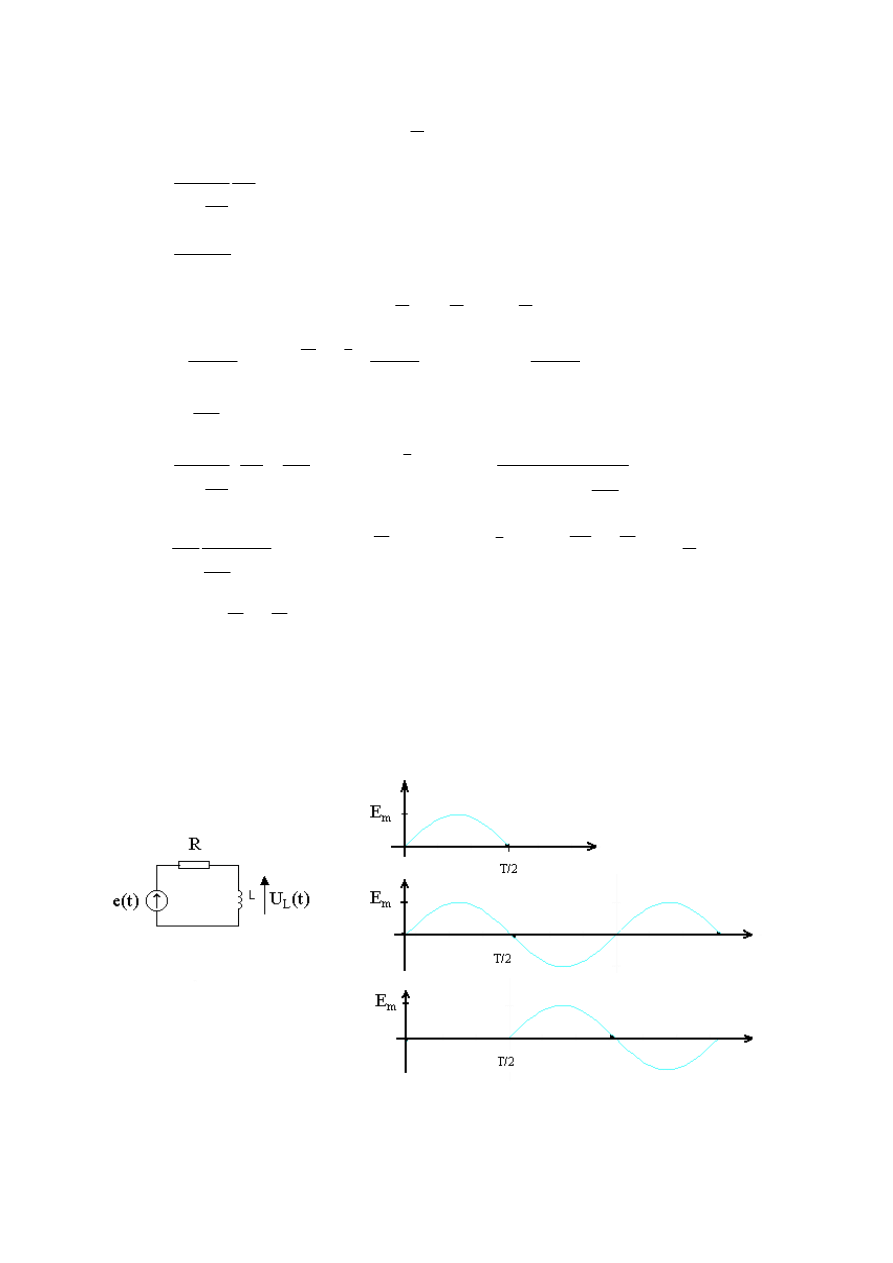
17
(
)
(
)
[
]
)
)
(
1
2
1
2
)
(
1
2
1
1
)
(
1
)
(
1
2
1
1
1
)
(
)
(
2
:
1
1
2
1
)
(
)
(
1
sin
2
1
2
2
sin
2
)
(
1
sin
)
(
1
)
(
)
(
1
1
)
(
)
(
1
sin
2
1
sin
2
)
(
1
sin
)
(
1
1
2
2
1
2
2
2
2
T
t
e
e
e
e
T
t
e
e
e
e
t
e
e
j
RC
RC
E
t
U
RC
s
j
s
e
e
e
RC
E
sC
sC
R
s
E
s
U
T
gdzie
j
s
e
e
E
j
s
e
e
E
j
s
E
s
E
T
t
T
T
t
E
T
t
T
T
t
E
t
t
E
t
e
sRC
s
E
s
U
sC
sC
R
s
E
s
U
T
t
t
E
T
t
t
E
t
t
E
t
e
t
RC
RC
T
t
j
T
j
t
RC
RC
T
t
j
T
j
t
RC
t
j
m
C
Ts
s
T
j
m
C
Ts
T
j
m
s
T
T
j
m
m
m
m
m
C
C
m
m
m
−
⋅
⋅
−
⋅
+
+
⋅
⋅
−
⋅
+
⋅
−
−
+
=
+
−
⋅
+
⋅
−
=
⋅
+
=
Π
=
−
⋅
⋅
+
−
⋅
⋅
−
−
=
−
⋅
+
−
⋅
+
−
⋅
+
−
⋅
−
⋅
⋅
=
+
=
+
=
−
⋅
⋅
+
−
⋅
⋅
−
⋅
⋅
=
−
−
−
−
Π
−
Π
−
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
ω
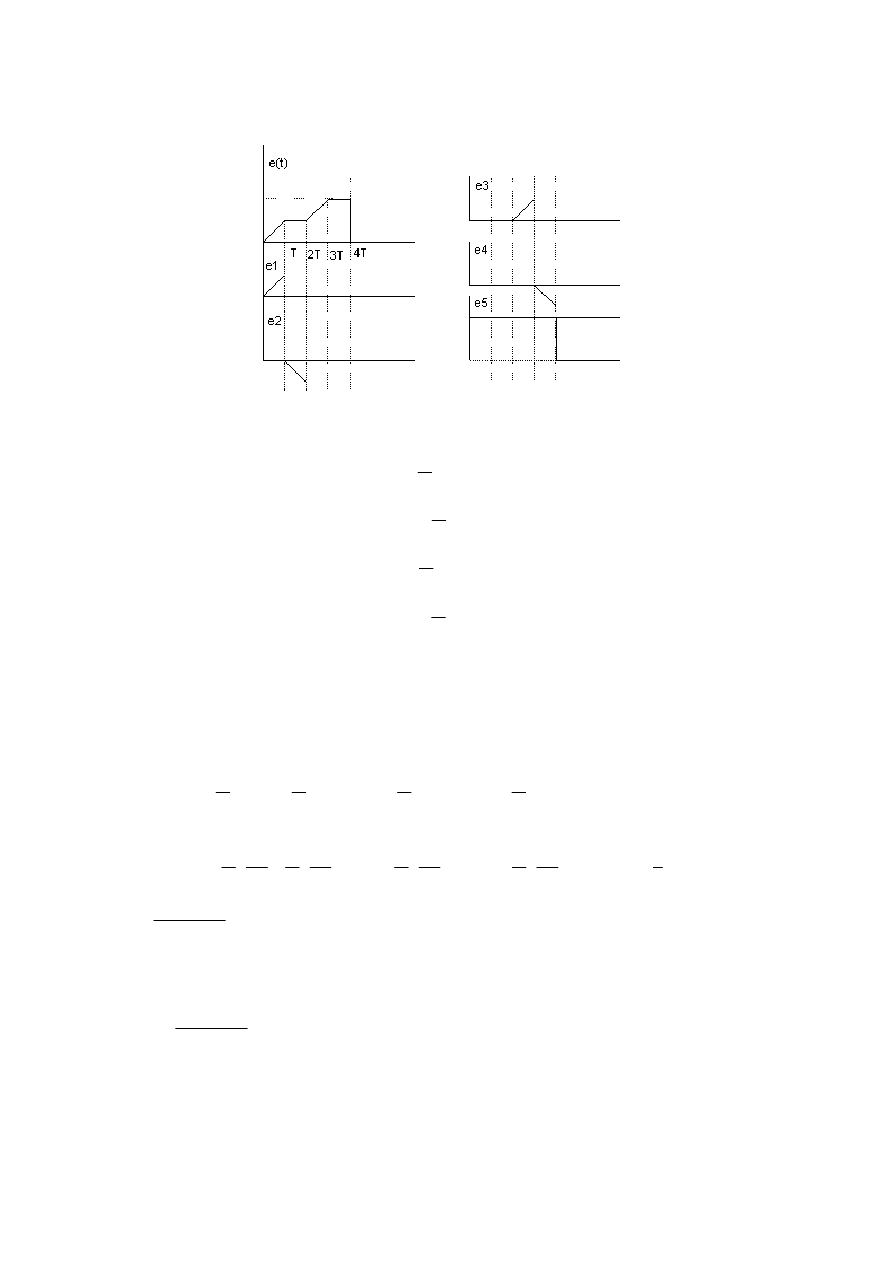
Zadanie o.12
Wyznaczy
ć
U
L
(t) dla napi
ę
cia zasilania e(t) jak na wykresie.
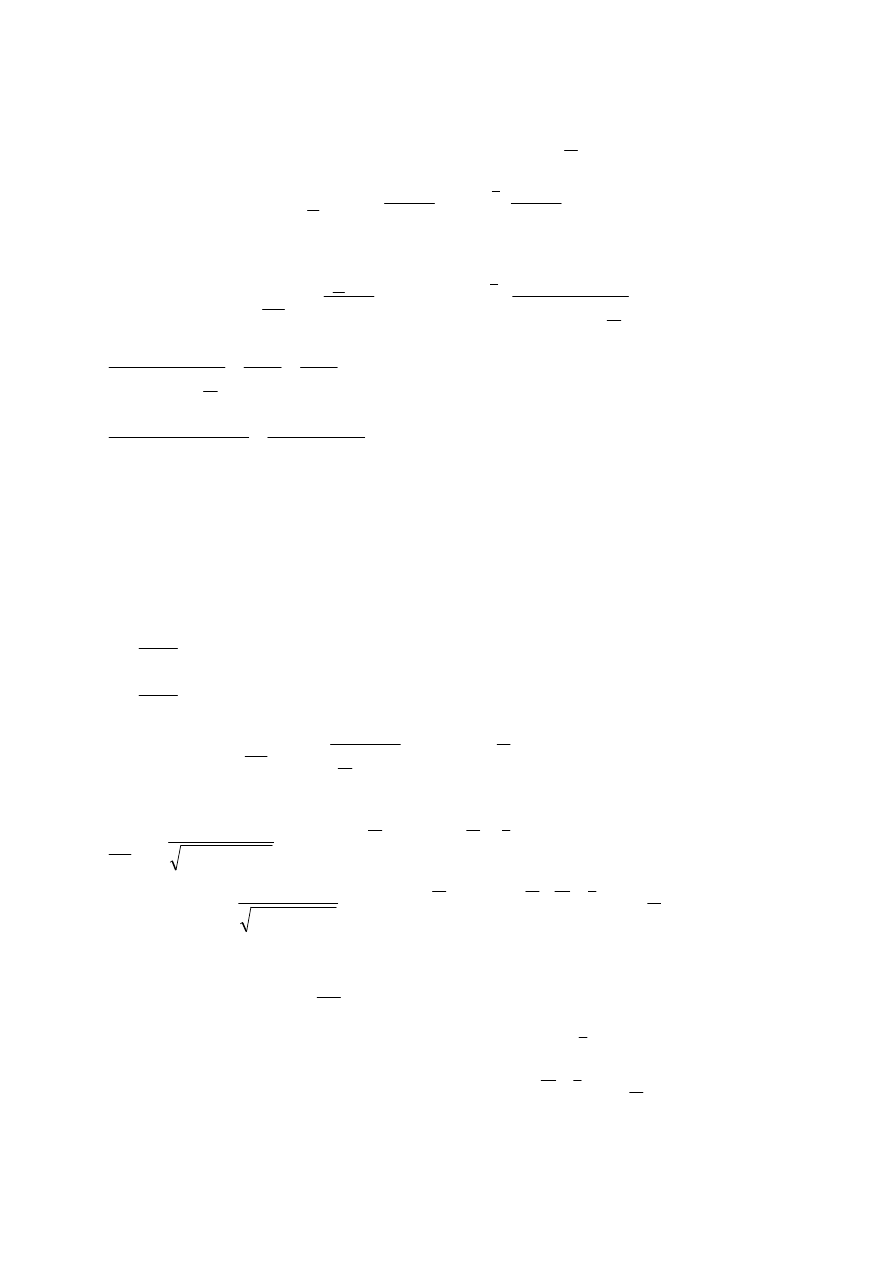
18
Napi
ę
cie wymuszaj
ą
ce:
ω
ω
ω
ω
j
s
e
E
j
s
E
s
E
T
t
t
E
t
t
E
t
e
s
T
m
m
m
m
−
+
−
=
−
+
=
−
1
1
)
(
)
2
(
1
sin
)
(
1
sin
)
(
2
Odpowied
ź
układu:
)
)(
(
1
)
(
)
(
2
L
R
s
j
s
s
e
E
sL
sL
R
s
E
s
U
T
s
m
L
+
−
+
=
+
=
−
ω
b
s
B
a
s
A
L
R
s
j
s
s
+
+
−
=
+
−
)
)(
(
ω
)
)(
(
)
)(
(
)
(
)
(
b
s
a
s
s
b
s
a
s
a
s
B
b
s
A
+
−
=
+
−
−
+
+
s
Ba
Ab
Bs
As
=
−
+
+
=
−
=
+
0
1
Ba
Ab
B
A
B
A
−
= 1
0
)
1
(
=
−
−
Ba
B
b
0
)
(
=
+
−
a
b
B
b
a
b
b
B
+
=
a
b
a
A
+
=
+
⋅
−
+
+
=
−
)
(
)
2
(
1
)
(
1
)
(
1
)
(
bt
at
m
L
Be
Ae
T
t
t
j
L
R
E
t
U
ω
Po podstawieniach otrzymamy:
+
+
+
=
−
−
−
)
(
1
Re
)
(
(
)
(
ctg
)
ctg
(
2
2
t
e
Le
L
R
E
t
U
t
L
R
R
L
jar
R
L
ar
t
j
m
L
ω
ω
ω
ω
ω
)
2
(
1
Re
)
(
2
ctg
)
ctg
(
2
2
T
t
e
e
Le
L
R
E
t
L
R
L
RT
R
L
ar
R
L
ar
t
j
m
−
+
+
+
−
−
−
ω
ω
ω
ω
ω
Przyjmijmy oznaczenie:
)
2
(
1
)
sin
cos
)
cos(
sin
(
)
(
1
)
sin
cos
)
cos(
sin
(
)
(
ctg
2
T
t
e
e
E
t
E
t
e
E
t
E
t
u
R
L
ar
t
L
R
L
RT
m
m
t
L
R
m
m
L
−
−
−
−
+
+
−
−
=
=
−
−
ϕ
ϕ
ϕ
ω
ϕ
ϕ
ϕ
ϕ
ω
ϕ
ω
ϕ
Ostatecznie:

19
>
+
−
<
<
−
−
<
=
−
−
2
)
1
(
2
sin
2
1
2
0
2
sin
2
1
)
cos(
sin
0
0
)
(
2
T
t
dla
e
e
E
T
t
dla
e
E
t
E
t
dla
t
u
t
L
R
L
RT
m
t
L
R
m
m
L
ϕ
ϕ
ϕ
ω
ϕ
Zadanie o.13
Wyznaczy
ć
i(t) dla napi
ę
cia zasilania e(t) jak na wykresie.
Funkcj
ę
napi
ę
cia e(t) mo
ż
na rozło
ż
y
ć
na trzy składowe:
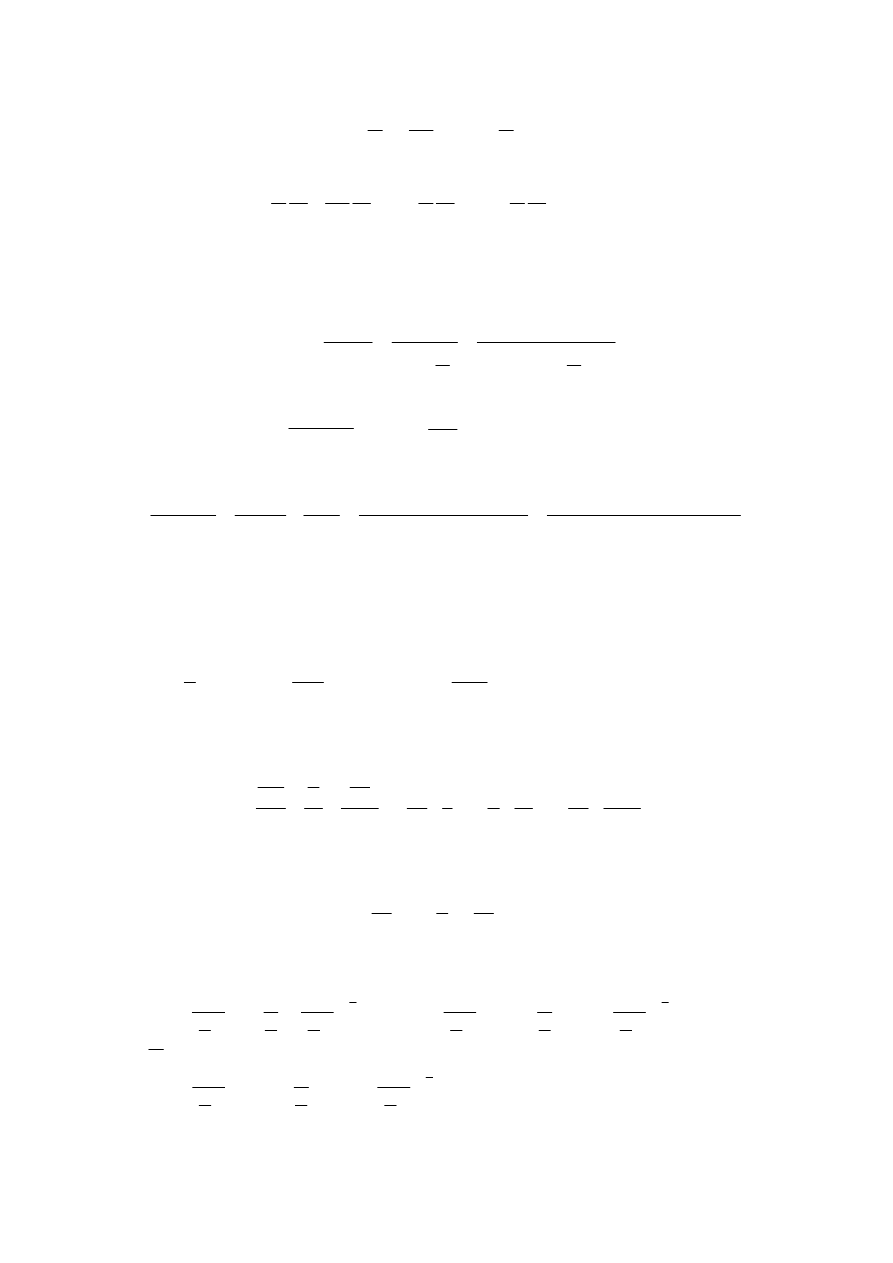
20
)
2
(
)
(
2
)
(
τ
τ
τ
τ
τ
−
+
−
−
=
t
E
t
E
t
E
t
e
[
]
τ
τ
τ
τ
τ
τ
τ
τ
s
s
s
s
e
e
s
E
e
s
E
e
s
E
s
E
s
e
2
2
2
2
2
2
2
1
1
1
1
2
1
)
(
−
−
−
−
+
−
=
+
−
=
Pr
ą
d w obwodzie obliczamy z :
)
(
)
2
1
(
)
(
)
(
)
(
)
(
2
2
L
R
s
L
s
e
e
E
L
R
s
L
s
e
sL
R
s
e
s
I
s
s
+
+
−
=
+
=
+
=
−
−
τ
τ
τ
Szukamy obrazu funkcji
)
(
1
2
a
s
s
+
gdzie a=
L
R
)
(
)
(
)
(
)
)(
(
)
(
1
2
2
2
2
2
2
2
a
s
s
Cs
Ba
Aas
Bs
As
a
s
s
s
C
a
s
B
As
a
s
C
s
B
As
a
s
s
+
+
+
+
+
=
+
+
+
+
=
+
+
+
=
+
Porównujemy współczynniki:
A+C=0
B+Aa=0
aB=1 B=
a
1
A=
2
1
a
−
C=
2
1
a
Podstawiamy A B C
+
+
+
=
+
+
+
−
a
s
a
s
a
s
a
a
s
a
s
a
s
s
a
1
*
1
1
*
1
1
*
1
1
1
1
2
2
2
2
2
2
2
Przechodz
ą
c na posta
ć
czasow
ą
:
at
e
a
t
a
t
a
−
+
+
2
2
1
1
)
(
1
1
Podstawiaj
ą
c
−
+
−
+
−
+
−
+
−
+
−
−
−
+
+
−
=
−
−
−
−
−
)
2
(
1
*
)
(
1
)
2
(
1
1
)
2
(
1
)
(
1
)
(
1
*
)
(
1
)
(
1
1
)
(
1
)
(
1
2
)
(
1
*
)
(
1
1
)
(
1
)
(
1
)
(
)
2
(
2
2
)
(
2
2
2
2
τ
τ
τ
τ
τ
τ
τ
τ
τ
t
e
L
R
t
L
R
t
L
R
t
e
L
R
t
L
R
t
L
R
t
e
L
R
t
L
R
t
L
R
L
E
t
I
t
L
R
t
L
R
t
L
R
Wyszukiwarka
Podobne podstrony:
deren,technika analogowa,zadani Nieznany
08 Stany nieustalone w obwodach RLCid 7512 ppt
SPRAWKO STANY NIEUSTALONE, Elektrotechnika, Elektrotechnika
stany nieustalone w RC, Elektrotechnika-materiały do szkoły, Elektrotechnika
03 stany nieustalone
C7a Stany nieust RLC 2012
planimetria, szkola technikum, matma, matura matma zadania
instrukcja - stany nieustalone, Elektrotechnika AGH, Semestr III zimowy 2013-2014, semestr III, seme
Stany nieustalone w obwodach RL, RC, RLC, ˙wiczenie II-13
stany nieustalone w obwodach z elemetami rc
8 Stany nieustalone w obwodach Nieznany
Stany nieustalone w obwodach elektrycznych o stałych skupionych 2
stany nieustalonerc, Politechnika Lubelska
Cw1 Stany nieustalone RL RC
stany nieustalone 2
wyklad 1 stany nieustalone II rzedu cz1
więcej podobnych podstron