Metody numeryczne

Całkowanie

Janusz Szwabi´nski

[e-mail]

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.1/69

Całkowanie numeryczne

1. Kilka uwag ogólnych
2. Kwadratury Newtona–Cotesa
3. Metoda Romberga
4. Kwadratury Gaussa
5. Trudno´sci i mo˙zliwo´sci w całkowaniu numerycznym
6. Całkowanie metod ˛a Monte Carlo

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.2/69

Kilka uwag ogólnych (1)

Problem:

R

b

a

dxg(x)

(a, b - pewne sko´nczone warto´sci)

Mo˙zliwe

rozwi ˛azanie:

zast ˛ap g(x) przez funkcj˛e interpoluj ˛ac ˛a ϕ(x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.3/69

Kilka uwag ogólnych (2)

Niech

x

k

, k = 0, . . . , n - w˛ezły interpolacji

ϕ(x)

- wielomian interpolacyjny Lagrange’a

ϕ(x) =

n

X

k

=0

g(x

k

)Φ

k

(x)

gdzie

Φ

k

(x) =

(x − x

0

)(x − x

1

) . . . (x − x

k

−

1

)(x − x

k

+1

) . . . (x − x

n

)

(x

k

−

x

0

)(x

k

−

x

1

) . . . (x

k

−

x

k

−

1

)(x

k

−

x

k

+1

) . . . (x

k

−

x

n

)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.4/69

Kilka uwag ogólnych (3)

Z

b

a

dxg(x) '

Z

b

a

dxϕ(x) =

Z

b

a

dx

n

X

k

=0

Φ

k

(x)g(x

k

)

=

n

X

k

=0

g(x

k

)

Z

b

a

dxΦ

k

(x) ≡

n

X

k

=0

A

k

g(x

k

)

Je´sli |g(x) − ϕ(x)| < ² i x ∈ [a, b], to

|

Z

b

a

dxg(x) −

n

X

k

=0

A

k

g(x

k

)| = |

Z

b

a

dx(g(x) − ϕ(x))| ≤ ²(b − a)

⇒ całk˛e mo˙zemy obliczy´c z dowoln ˛a dokładno´sci ˛a, je˙zeli tylko

g(x)

daje si˛e przybli˙zy´c dowolnie dokładnie.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.5/69

Kilka uwag ogólnych (4)

Definicja Wyra˙zenie

Z

b

a

dxg(x) '

n

X

k

=0

A

k

g(x

k

), x ∈ [a, b]

nazywamy kwadratur ˛a. Argumenty x

k

nazywamy w˛ezłami

kwadratury.
Niech

I(g) =

Z

b

a

dxg(x),

S(g) =

n

X

k

=0

A

k

g(x

k

)

Definicja Bł˛edem przybli˙zenia całki I(g) sum ˛a S(g) nazywamy

E(g) = S(g) − I(g)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.6/69

Kilka uwag ogólnych (5)

Definicja Mówimy, ˙ze kwadratura jest rz˛edu r, je˙zeli

(a) I(W ) = S(W ) dla wszystkich wielomianów W (x) stopnia

mniejszego ni˙z r,

(b) istnieje wielomian stopnia r (r ≥ 1) taki, ˙ze

I(W ) 6= S(W ).

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.7/69

Kilka uwag ogólnych (6)

Twierdzenie 1 Kwadratura

Z

b

a

dxg(x) '

n

X

k

=0

A

k

g(x

k

), x ∈ [a, b]

jest zbie˙zna dla ka˙zdej funkcji f(x) ∈ C([a, b]) wtedy i tylko
wtedy, gdy:

1. jest ona zbie˙zna dla ka˙zdego wielomianu,
2. istnieje liczba M niezale˙zna od N taka, ˙ze

N

X

k

=0

|A

k

| ≤ M

dla n = 1, 2, . . ..

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.8/69

Kilka uwag ogólnych (7)

Niech

g(x) = p(x)f (x)

Wówczas (zast˛epuj ˛ac f(x) wielomianem Lagrange’a)

Z

b

a

dxg(x) =

Z

b

a

dxp(x)f (x) =

X

k

=0

A

k

f (x

k

)

gdzie

A

k

=

Z

b

a

dxp(x)Φ

k

(x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.9/69

Kilka uwag ogólnych (8)

Twierdzenie 2 Rz ˛ad kwadratury

Z

b

a

dxp(x)f (x) =

X

k

=0

A

k

f (x

k

)

A

k

=

Z

b

a

dxp(x)Φ

k

(x)

wynosi co najmniej N + 1.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.10/69

Kilka uwag ogólnych (9)

Dowód Niech g(x) - wielomian stopnia co najwy˙zej N. Je˙zeli
wielomian ten zapiszemy w postaci wielomianu interpolacyjnego
Lagrange’a W

N

z w˛ezłami x

0

, . . . x

n

, to

I(g) = I(W

N

) = S(W

N

) = S(g),

czyli rz ˛ad kwadratury rzeczywi´scie wynosi co najmniej N + 1.
Załó˙zmy teraz, ˙ze rz ˛ad kwadratury wynosi N + 1. Jest ona
wtedy dokładna dla wszystkich wielomianów stopnia mniejszego
ni˙z N, a zatem równie˙z dla wielomianów g(x) = Φ

i

(x)

. St ˛ad

I(Φ

i

) =

Z

b

a

dxp(x)Φ

i

(x) =

N

X

k

=0

A

k

Φ

i

(x

k

) = A

i

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.11/69

Kwadratury Newtona–Cotesa

Niech

x

k

= a + kh,

h =

b − a

n

,

k = 0, 1, . . . , n

Zast˛epuj ˛ac funkcj˛e podcałkow ˛a wielomianem interpolacyjnym
otrzymamy

Z

b

a

dxf (x) '

n

X

k

=0

A

k

f (x

k

),

gdzie (x = a + sh)

A

k

=

Z

b

a

dxΦ

k

(x) =

Z

b

a

dx

n

Y

i=0

i

6

=k

x − x

i

x

k

−

x

i

= h

Z

n

0

ds

n

Y

i=0

i

6

=k

s − i

k −

1

≡

hα

k

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.12/69

Wzór trapezów (1)

Dla n = 1 mamy

α

0

=

Z

1

0

ds

s − 1

0 − 1

=

1
2

, α

1

=

Z

1

0

ds

s − 0

1 − 0

=

1
2

⇒ wzór trapezów

Z

b

a

dxf (x) ' h

1

X

k

=0

α

k

f (x

k

) =

h

2

[f

0

+ f

1

]

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.13/69

Wzór trapezów (2)

Je´sli f(x) ∈ C

2

([a, b])

, bł ˛ad interpolacji wielomianem stopnia n

wynosi:

|²(x)| ≤

M

n

+1

(n + 1)!

|ω

n

(x)|,

St ˛ad

|E(f)| =

1

12

h

3

f

(2)

(ξ

1

), ξ

1

∈ (a, b), h = b − a

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.14/69

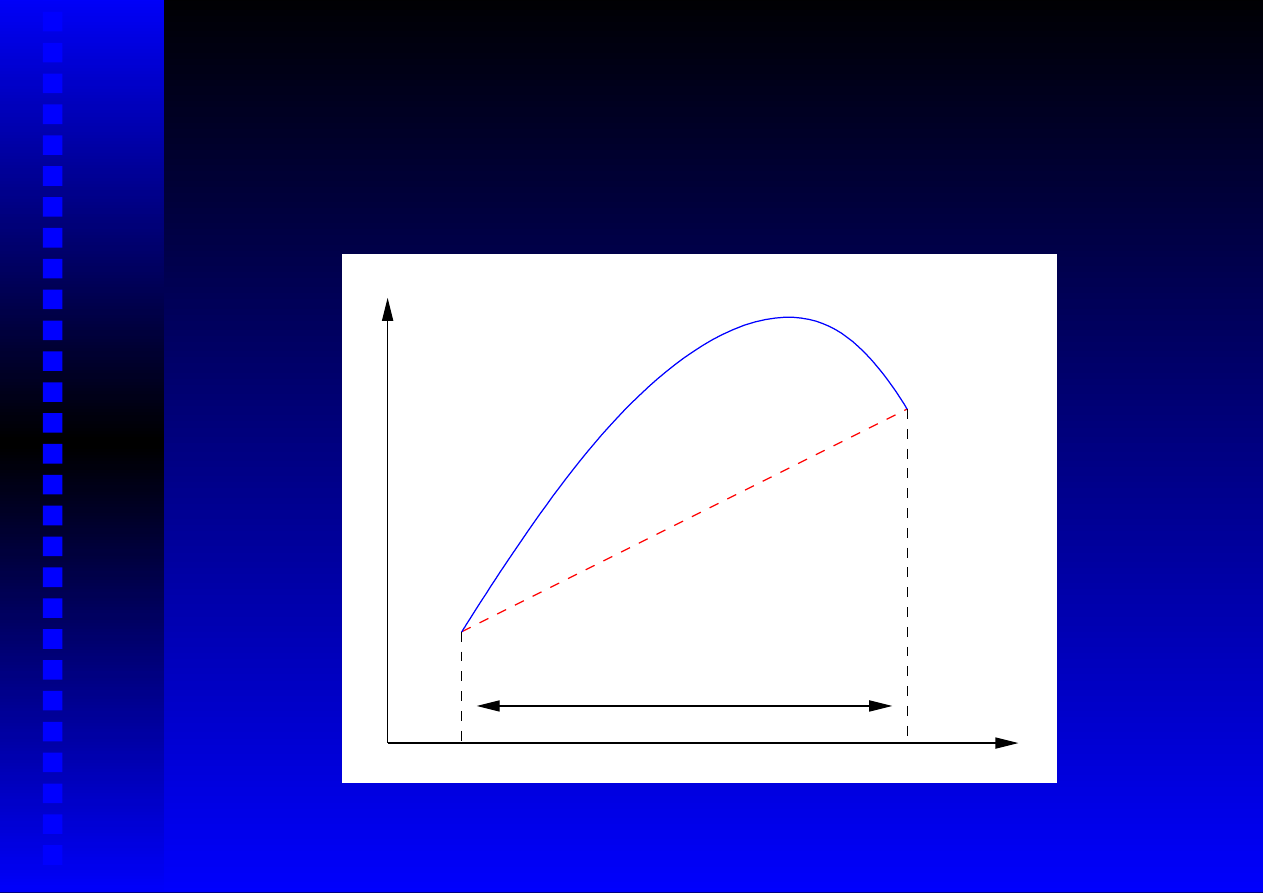
Wzór trapezów (3)

Y

X

b

a

h

f(x)

1

W (x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.15/69

Wzór Simpsona (1)

Dla n = 2 mamy

α

0

=

Z

2

0

ds

s − 1

0 − 1

s − 2

0 − 2

=

1
3

α

1

=

Z

2

0

ds

s − 0

1 − 0

s − 2

1 − 2

=

4
3

α

2

=

Z

2

0

ds

s − 0

2 − 0

s − 1

2 − 1

=

1
3

czyli

Z

b

a

dxf (x) '

h

3

[f

0

+ 4f

1

+ f

2

]

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.16/69

Wzór Simpsona (2)

Bł ˛ad przybli˙zonej warto´sci całki wynosi:

|E(f)| =

1

90

h

5

f

(4)

(ξ

1

),

gdzie ξ

1

∈ (a, b), h =

b−a

2

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.17/69

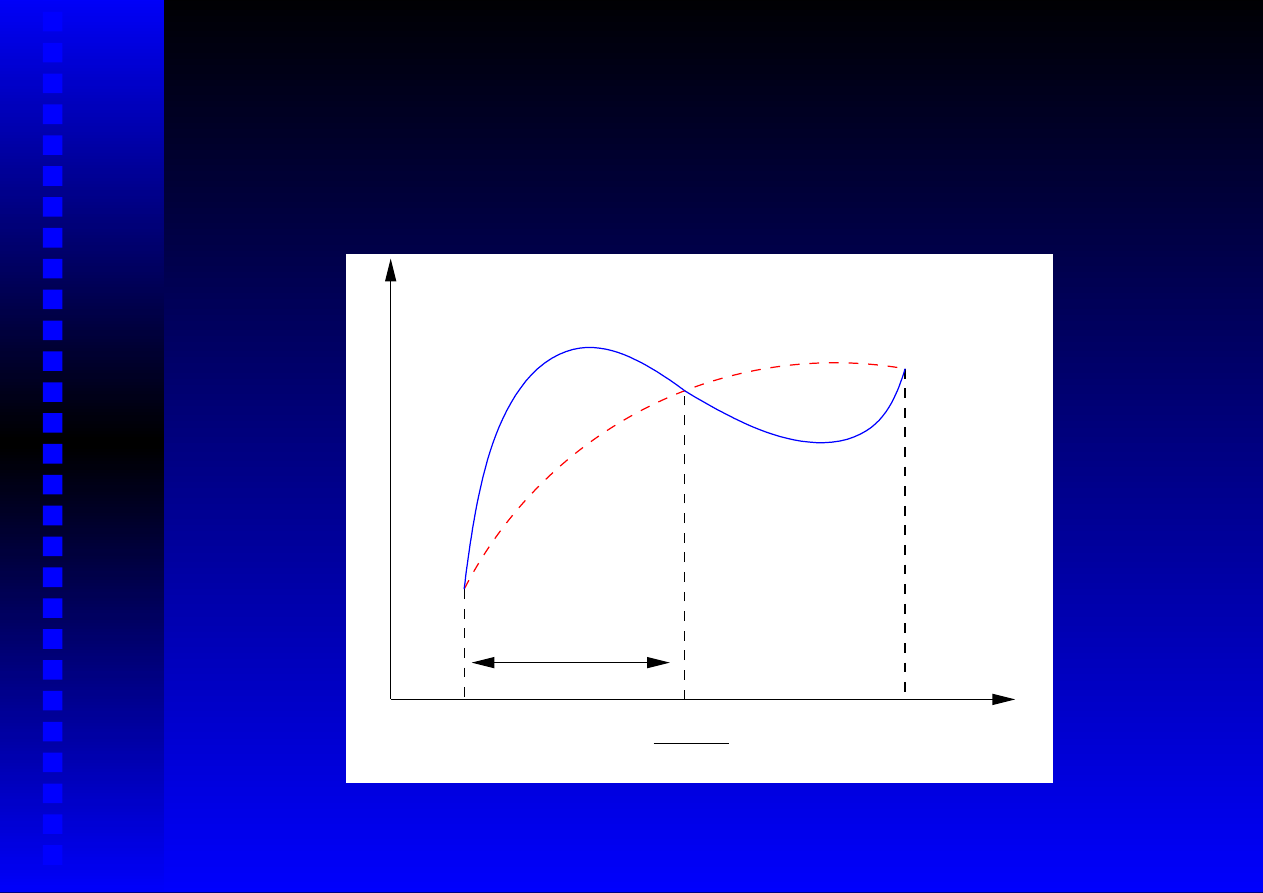
Wzór Simpsona (3)

Y

X

b

a

f(x)

h

a+b

2

W (x)

2

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.18/69

Inne wzory Newtona–Cotesa (1)

Ogólnie dla wszystkich n naturalnych:

Z

b

a

dxf (x) ' f

n

X

k

=0

α

k

f

k

=

b − a

nt

X

k

=0

σ

k

f

k

,

przy czym

•

h =

b−a

n

•

t

jest dobrane tak, aby liczby σ

k

= tα

k

były liczbami

całkowitymi

Dla f ∈ C

∞

([a, b])

:

|E(f)| = h

p

+1

Kf

(p)

(ξ)

gdzie ξ ∈ (a, b), a p i K zale˙z ˛a od n

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.19/69

Inne wzory Newtona–Cotesa (2)

n

σ

k

nt

Bł ˛ad

Nazwa

1

1 1

2

h

3 1

12

f

(2)

(ξ)

wzór trapezów

2

1 4 1

6

h

5 1

90

f

(4)

(ξ)

wzór Simpsona

3

1 3 3 1

8

h

5 3

80

f

(4)

(ξ)

wzór "trzech ósmych"

4

7 32 12 32 7

90

h

7 8

945

f

(6)

(ξ)

wzór Milne’a

5

19 75 50 50 75 19

288

h

7 275

12096

f

(6)

(ξ)

-

6

41 216 27 272 27 216 41

840

h

9

9

1400

f

(8)

(ξ)

wzór Weddle’a

Dla wi˛ekszych warto´sci n pojawiaj ˛a si˛e
współczynniki ujemne

⇒ wzory przestaj ˛a by´c numerycznie u˙zyteczne

(kwadratura nie zawsze jest zbie˙zna)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.20/69

Kwadratury zło˙zone Newtona–Cotesa

Bł ˛ad kwadratur Newtona–Cotesa jest proporcjonalny do pewnej
pot˛egi długo´sci przedziału całkowania

⇒ je˙zeli przedział całkowania jest du˙zy, kwadratura (nawet

niskiego stopnia) mo˙ze nie zapewni´c ˙zadnej dokładno´sci

Wyj´scie:

1. podziel przedział całkowania [a, b] na pewn ˛a liczb˛e

podprzedziałów,

2. w ka˙zdym podprzedziale zastosuj kwadratur˛e niskiego

rz˛edu i zsumuj wyniki.

Definicja Kwadratur˛e b˛ed ˛ac ˛a sum ˛a kwadratur nazywamy
kwadratur ˛a zło˙zon ˛a.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.21/69

Zło˙zony wzór trapezów (1)

Stosuj ˛ac wzór trapezów dla przedziału [x

i

, x

i

+1

]

otrzymujemy

S

i

(f ) =

h

2

[f

i

+ f

i

+1

]

St ˛ad

S(f ) =

n−

1

X

i

=0

S

i

(f ) =

n−

1

X

i

=0

h

2

[f

i

+ f

i

+1

]

= h

µ f

0

2

+ f

1

+ . . . + f

n−

1

+

f

n

2

¶

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.22/69

Zło˙zony wzór trapezów (2)

Je˙zeli f(x) ∈ C

2

([a, b])

, to

|E(f)| =

h

3

12

n−

1

X

i

=0

f

(2)

(ξ

i

) =

(b − a)

3

12n

2

1

n

n−

1

X

i

=0

f

(2)

(ξ

i

)

Czynnik

1

n

P

n−

1

i

=0

f

(2)

(ξ

i

)

jest ´sredni ˛a arytmetyczn ˛a warto´sci

drugiej pochodnej w punktach ξ

i

⇒ |E(f)| =

(b − a)

3

12n

2

f

(2)

(ξ)

⇒ bł ˛ad kwadratury zło˙zonej jest du˙zo mniejszy ni˙z

odpowiedniej kwadratury prostej

⇒ zwi˛ekszaj ˛ac liczb˛e w˛ezłów mo˙zemy dowolnie zmniejsza´c

bł ˛ad

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.23/69

Zło˙zony wzór Simpsona (1)

Niech

h =

b − a

n

, n

parzyste

W ka˙zdym z podprzedziałów [x

2i

, x

2i+2

]

stosujemy wzór

Simpsona:

S

2i

(f ) =

h

3

[f

2i

+ 4f

2i+1

+ f

2i+2

]

St ˛ad wynika:

S(f ) =

n

2

−

1

X

i

=0

S

2i

(f ) =

h

3

[f

0

+ f

n

+ 2(f

2

+ f

4

+ . . . + f

n−

2

) + 4(f

1

+ f

3

+ . . . + f

n−

1

)]

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.24/69

Zło˙zony wzór Simpsona (2)

Bł ˛ad tej kwadratury wynosi

|E(f)| =

(b − a)

5

180n

4

f

(4)

(ξ), ξ ∈ (a, b)

o ile tylko f(x) ∈ C

4

([a, b])

.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.25/69

Zło˙zony wzór Simpsona (3)

Przykład

DOUBLE PRECISION FUNCTION SIMPSON(A,XDEL,N)
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
DIMENSION A(1)
N1=N-1
XINT=A(1)
P=2.D0
PH=-2.D0
DO 10 I=2,N1
PH=-PH
P=P+PH

10

XINT=XINT+A(I)*P
XINT=(XINT+A(N))*XDEL/3.D0
RETURN
END

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.26/69

Zło˙zony wzór Simpsona (4)

Przykład

Z

1

0

dx exp(x)

n

Wzór trapezów Wzór Simpsona

4

1,72722190

1,71831884

8

1,72051859

1,71828415

16

1,71884112

1,71828197

32

1,71842166

1,71828183

64

1,71831678

1,71828182

Dla porównania, dokładny wynik to R

1

0

dxe

x

= 1, 71828182

.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.27/69

Metoda Romberga (1)

Twierdzenie 3 (wzór sumacyjny Eulera-Maclaurina) Je˙zeli
f ∈ C

2m+1

([a, b])

, to zło˙zony wzór trapezów ma rozwini˛ecie:

T (h) =

Z

b

a

dxf (x) + τ

1

h

2

+ . . . + τ

m

h

2m

+ α

m

+1

(h)h

2m+2

,

gdzie τ

i

s ˛a stałymi niezale˙znymi od h, a α

m

+1

(h)

jest funkcj ˛a

ograniczon ˛a zmiennej h, tzn.

|α

m

+1

| ≤ M < ∞

dla ka˙zdego h =

b−a

n

(n całkowite).

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.28/69

Metoda Romberga (2)

Dowód Niech h =

b−a

n

. Zamiast funkcji f(x) rozwa˙zmy

funkcj˛e

g(t) = f (a + th).

Dalej, rozwa˙zmy całk˛e

Z

1

0

dtS

1

(t)g

0

(t)

gdzie S

1

(t)

- funkcja o okresie 1, zło˙zona kawałkami liniowo z

wielomianu Bernoulliego B

1

(x) = x −

1
2

.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.29/69

Metoda Romberga (3)

Dowód (ci ˛ag dalszy)
Poniewa˙z zachodzi

B

0

k

(x) = kB

k−

1

(x), k ≥ 1

B

0

(x) = 1

Z

1

0

dxB

k

(x) = 0

wi˛ec całkuj ˛ac przez cz˛e´sci otrzymamy

Z

1

0

dtS

1

(t)g

0

(t) =

Z

1

0

dtB

1

(t)g

0

(t)

=

1
2

[g(1) + g(0)] −

Z

1

0

dtg(t)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.30/69

Metoda Romberga (4)

Dowód (ci ˛ag dalszy)
Podobnie

Z

i

+1

i

dtS

1

(t)g

0

(t) =

Z

1

0

dtB

1

(t)g

0

(t + i)

=

1
2

[g(i + 1) + g(i)] −

Z

i

+1

i

dtg(t)

dla i = 0, 1, . . . , n − 1. Zatem

g(0)

2

+g(1)+. . .+g(n−1)+

g(n)

2

−

Z

n

0

dtg(t) =

Z

n

0

dtS

1

(t)g

0

(t)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.31/69

Metoda Romberga (5)

Dowód (ci ˛ag dalszy)
Całkuj ˛ac 2m razy przez cz˛e´sci otrzymamy

g(0)

2

+ g(1) + . . . + g(n − 1) +

g(n)

2

−

Z

n

0

dtg(t)

=

m

X

k

=1

(−1)

k

+1

B

k

(2k)!

£g

(2k−1)

(n) − g

(2k−1)

(0)

¤ + R

m

+1

z reszt ˛a

R

m

+1

= −

1

(2m + 2)!

Z

n

0

dt[S

2m+2

(t) − S

2m+2

(0)]g

(2m+2)

(t)

Przy tym B

k

= (−1)

k

+1

B

2k

(0)

to tzw. liczby Bernoulliego.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.32/69

Metoda Romberga (6)

Dowód (ci ˛ag dalszy)
Poniewa˙z g(t) = f(a + th), wi˛ec mamy

Z

n

0

dtg(t) =

1

h

Z

b

a

dxf (x)

g

(k)

(t) = h

k

f

(k)

(a + th), k = 0, 1, . . .

oraz

g(0)

2

+ g(1) + . . . + g(n − 1) +

g(n)

2

=

f (a)

2

+ f (a + h) + . . . + f (b − h) +

f (b)

2

=

T (h)

h

.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.33/69

Metoda Romberga (7)

Dowód (ci ˛ag dalszy)
St ˛ad wynika

T (h) =

Z

b

a

dxf (x) + τ

1

h

2

+ . . . + τ

m

h

2m

+ α

m

+1

(h)h

2m+2

,

gdzie

τ

k

=

(−1)

k

+1

B

k

(2k)!

[f

(2k−1)

(b) − f

(2k−1)

(a)], k = 1, . . . , m,

α

m

+1

(h)

=

−

1

(2m + 2)!

Z

b

a

dxf

(2m+2)

(x)

·

S

2m+2

µ x − a

h

¶

−

S

2m+2

(a)

¸

.

S

2m+2

jest ci ˛agł ˛a funkcj ˛a okresow ˛a, istnieje wi˛ec kres górny dla

|α

m

+1

(h)| niezale˙zny od h. Tym samym twierdzenie jest

udowodnione.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.34/69

Metoda Romberga (8)

Dzielimy [a, b] na 2

i

równych cz˛e´sci (i = 0, 1, . . .):

h

i

=

b − a

2

i

x

i,k

= a + kh

i

f

i,k

= f (x

i,k

)

Zło˙zony wzór trapezów:

T

0,i

= h

i

"

2i

X

k

=0

f

i,k

−

1
2

(f (a) − f(b))

#

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.35/69

Metoda Romberga (9)

Mamy

I(f ) − T

0,i

=

∞

X

k

=1

τ

0,k

h

2k
i

⇒ wyraz wiod ˛acy bł˛edu jest rz˛edu h

2

i

Niech

T

1,i

= T

0,i+1

+

T

0,i+1

− T

0,i

2

2

− 1

Wówczas

I(f ) − T

1,i

=

1
3

∞

X

k

=1

τ

0,k

(2

2

h

2k
i

+1

− h

2k
i

)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.36/69

Metoda Romberga (10)

Wprowad´zmy wielko´s´c

τ

1,k

=

1
3

µ 2

2

2

2k

− 1

¶

τ

0,k

Poniewa˙z τ

1,1

= 0

, otrzymujemy

I(f ) − T

1,i

=

∞

X

k

=2

τ

1,k

h

2k
i

⇒ wiod ˛acy wyraz bł˛edu jest rz˛edu h

4

i

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.37/69

Metoda Romberga (11)

Ogólnie

T

m,i

= T

m−

1,i+1

+

T

m−

1,i+1

− T

m−

1,i

2

2m

− 1

Je˙zeli f(x) ∈ C

2m+2

([a, b])

, to

I(f ) − T

m,i

= Ch

2m+2

f

(2m+2)

(ξ),

gdzie ξ ∈ (a, b), a C jest pewn ˛a stał ˛a.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.38/69

Metoda Romberga (12)

T

m,i

mo˙zna przedstawi´c w postaci kombinacji liniowej

T

0,1

, . . . , T

0,m+i

, a zatem

T

m,i

= h

2

m

+i

X

j

=0

d

m,j

f (a + jh),

h =

b − a

2

m

+i

d

m,j

s ˛a dodatnie dla wszystkich m, j

⇒ T

m,i

s ˛a zbie˙znymi kwadraturami o w˛ezłach równoodległych

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.39/69

Metoda Romberga (13)

T

0,0

T

0,1

T

1,0

T

0,2

T

1,1

T

2,0

T

0,3

T

1,2

T

2,1

T

3,0

T

0,4

T

1,3

T

2,2

T

3,1

T

4,0

T

0,5

T

1,4

T

2,3

T

3,2

T

4,1

T

5,0

..

.

..

.

..

.

..

.

..

.

..

.

· · ·

•

elementy pierwszej kolumny ze zło˙zonego wzoru trapezów

•

po obliczeniu m pierwszych elementów z 1. kolumny
mo˙zemy wyznaczy´c m pierwszych wierszy

•

na ogół zbie˙zno´s´c ci ˛agu T

m,

0

szybsza ni˙z T

0,m

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.40/69

Wielomiany ortogonalne (1)

Niech

{P

n

(x)}

∞

n

=0

- ci ˛ag wielomianów ortogonalnych z wag ˛a p(x)

na przedziale [a, b]

P

n

(x)

- wielomian stopnia n

(P

r

, P

s

) =

Z

b

a

dxp(x)P

r

(x)P

s

(x) = 0, r 6= s

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.41/69

Wielomiany ortogonalne (2)

Twierdzenie 4 Wielomiany ortogonalne na przedziale [a, b]
maj ˛a tylko pierwiastki rzeczywiste, jednokrotne, le˙z ˛ace w (a, b).
Dowód Załó˙zmy, ˙ze pierwiastki wielomianu P

k

(x)

nie spełniaj ˛a

powy˙zszych warunków. Niech ξ

1

, . . . , ξ

m

b˛ed ˛a rzeczywistymi,

ró˙znymi pierwiastkami wielomianu z przedziału (a, b) o
nieparzystych krotno´sciach. Mamy m < k. Niech

W (x) = (x − ξ

1

) . . . (x − ξ

m

)

Przedstawmy W (x) w postaci kombinacji liniowej wielomianów
P

0

(x)

, . . . , P

m

(x)

:

W (x) = a

0

P

0

(x) + . . . + a

m

P

m

(x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.42/69

Wielomiany ortogonalne (3)

Dowód (ci ˛ag dalszy)
Mamy

(W, P

k

) =

m<k

X

i

=0

a

i

(P

i

, P

k

) = 0.

Z drugiej strony W (x)P

k

(x) ≥ 0 w przedziale [a, b], a zatem

(W, P

k

) > 0,

co prowadzi do sprzeczno´sci.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.43/69

Wielomiany ortogonalne (4)

Przykład W przedziale [a, b] = [−1, 1] wielomianami
ortogonalnymi z wag ˛a p(x) = 1 s ˛a wielomiany Legendre’a

P

n

(x) =

1

2

n

n!

d

n

dx

n

(x

2

− 1)

n

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.44/69

Wielomiany ortogonalne (5)

Przykład W przedziale [a, b] = [−1, 1] ci ˛ag wielomianów
ortogonalnych z wag ˛a p(x) = (1 − x)

α

(1 + x)

β

, (α, β > −1)

tworz ˛a wielomiany Jacobiego:

J

n

(x; α, β) =

(−1)

n

2

n

n!

(1−x)

−

α

(1+x)

−

β

d

n

dx

n

[(1−x)

α

+n

(1+x)

β

+n

]

W szczególno´sci, gdy α = β = −

1
2

, mówimy o wielomianach

Czebyszewa pierwszego rodzaju:

T

n

(x) = cos(a arccos x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.45/69

Wielomiany ortogonalne (6)

Przykład Wielomiany Laguerre’a

L

n

(x) = (−1)

n

e

x

d

n

dx

n

(x

n

e

−

x

)

s ˛a wielomianami ortogonalnymi z wag ˛a p(x) = e

−

x

w przedziale

[0, ∞).
Przykład Wielomiany Hermite’a

H

n

(x) = (−1)

n

e

x

2

d

n

dx

n

e

−

x

2

s ˛a wielomianami ortogonalnymi z wag ˛a p(x) = e

−

x

2

na

przedziale (−∞, ∞).

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.46/69

Kwadratury Gaussa (1)

Szukamy kwadratury

S(f ) =

N

X

k

=0

A

k

f (x

k

)

A

k

=

Z

b

a

dxp(x)Φ

k

(x)

o najwy˙zszym mo˙zliwym rz˛edzie

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.47/69

Kwadratury Gaussa (2)

Twierdzenie 5 Nie istnieje kwadratura postaci

S(f ) =

N

X

k

=0

A

k

f (x

k

)

A

k

=

Z

b

a

dxp(x)Φ

k

(x)

rz˛edu wy˙zszego ni˙z 2(N + 1).

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.48/69

Kwadratury Gaussa (3)

Dowód Niech W (x) = ω

2

N

+1

(x)

, gdzie

ω

N

+1

(x) = (x − x

0

) . . . (x − x

N

).

Mamy

I(W ) =

Z

b

a

dxp(x)W (x) > 0

S(W ) =

N

X

k

=0

A

k

W (x

k

) = 0

Istnieje zatem wielomian stopnia 2(N + 1), dla którego
kwadratura nie jest dokładna.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.49/69

Kwadratury Gaussa (4)

Twierdzenie 6 Niech p(x) b˛edzie funkcj ˛a wagow ˛a dodatni ˛a w
przedziale [a, b]. Je˙zeli punkty x

0

, . . . , x

N

s ˛a pierwiastkami

wielomianu P

N

+1

(x)

z ci ˛agu wielomianów ortogonalnych na

[a, b]

z wag ˛a p(x), to kwadratura

S(f ) =

N

X

k

=0

A

k

f (x

k

)

A

k

=

Z

b

a

dxp(x)Φ

k

(x)

jest rz˛edu 2(N + 1).

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.50/69

Kwadratury Gaussa (5)

Dowód Niech

W (x)

- wielomian stopnia 2N + 1

Q(x)

- iloraz z dzielenia W (x)/P

N

+1

(x)

R(x)

- reszta z dzielenia W (x)/P

N

+1

(x)

W (x) = Q(x)P

N

+1

(x) + R(x)

Q(x)

oraz R(x) maj ˛a stopie´n ≤ N, zatem z warunku

ortogonalno´sci otrzymamy

Z

b

a

dxp(x)W (x) =

Z

b

a

dxp(x)Q(x)P

N

+1

(x) +

Z

b

a

dxp(x)R(x)

=

Z

b

a

dxp(x)R(x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.51/69

Kwadratury Gaussa (6)

Dowód (ci ˛ag dalszy)
Ponadto

N

X

i

=0

A

i

f

i

=

N

X

i

=0

A

i

{Q(x

i

)P

N

+1

(x

i

) + R(x

i

)} =

N

X

i

=0

A

i

R(x

i

)

poniewa˙z P

N

+1

(x

i

) = 0

.

Kwadratura jest co rz˛edu co najmniej (N + 1), a wi˛ec jest
dokładna dla R(x),

N

X

i

=0

A

i

R(x

i

) =

Z

b

a

dxp(x)R(x),

co ko´nczy dowód.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.52/69

Kwadratury Gaussa (7)

Twierdzenie 7 Wszystkie współczynniki A

k

w kwadraturach

Gaussa s ˛a dodatnie.
Dowód Rozwa˙zmy wielomian stopnia 2N

R

i

(x) = [(x − x

0

) . . . (x − x

i−

1

)(x − x

i

+1

) . . . (x − x

N

)]

2

gdzie i = 0, 1, . . . , N. Mamy

0 <

Z

b

a

dxp(x)R

i

(x) =

X

k

=0

R

i

(x

k

) = A

i

R

i

(x

i

)

a wi˛ec rzeczywi´scie współczynniki A

i

musz ˛a by´c dodatnie.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.53/69

Kwadratury Gaussa (8)

⇒ kwadratury Gaussa s ˛a zbie˙zne dla ka˙zdej funkcji ci ˛agłej

Je˙zeli f ∈ C

2N +2

([a, b])

, to

|E(f)| =

1

(2N + 2)!

f

(2N +2)

(ξ)

Z

b

a

dxp(x)ω

2

N

+1

(x),

przy czym ξ ∈ (a, b).

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.54/69

Kwadratury Gaussa-Legendre’a (1)

Niech p(x) = 1 oraz [a, b] = [−1, 1]
⇒ wielomianami ortogonalnymi s ˛a wielomiany Legendre’a
Współczynniki i bł ˛ad kwadratury Gaussa–Legendre’a wyra˙zaj ˛a
si˛e wzorami

A

k

= −

2

(N + 2)P

N

+2

(x

k

)P

0

N

+1

(x

k

)

E(f ) =

2

2N +3

[(N + 1)!]

4

(2N + 3)[(2N + 2)!]

3

f

(2N +3)

(ξ)

gdzie −1 < ξ < 1 oraz x

k

- pierwiastki wielomianu P

N

+1

(x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.55/69

Kwadratury Gaussa-Legendre’a (2)

W przypadku dowolnego przedziału całkowania [a, b]:

Z

b

a

dtf (t) =

b − a

2

Z

1

−

1

dxf

µ b − a

2

x +

b + a

2

¶

'

b − a

2

N

X

k

=0

A

k

f (t

k

),

gdzie

t

k

=

b − a

2

x

k

+

b + a

2

i x

k

zdefiniowane jest jak powy˙zej

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.56/69

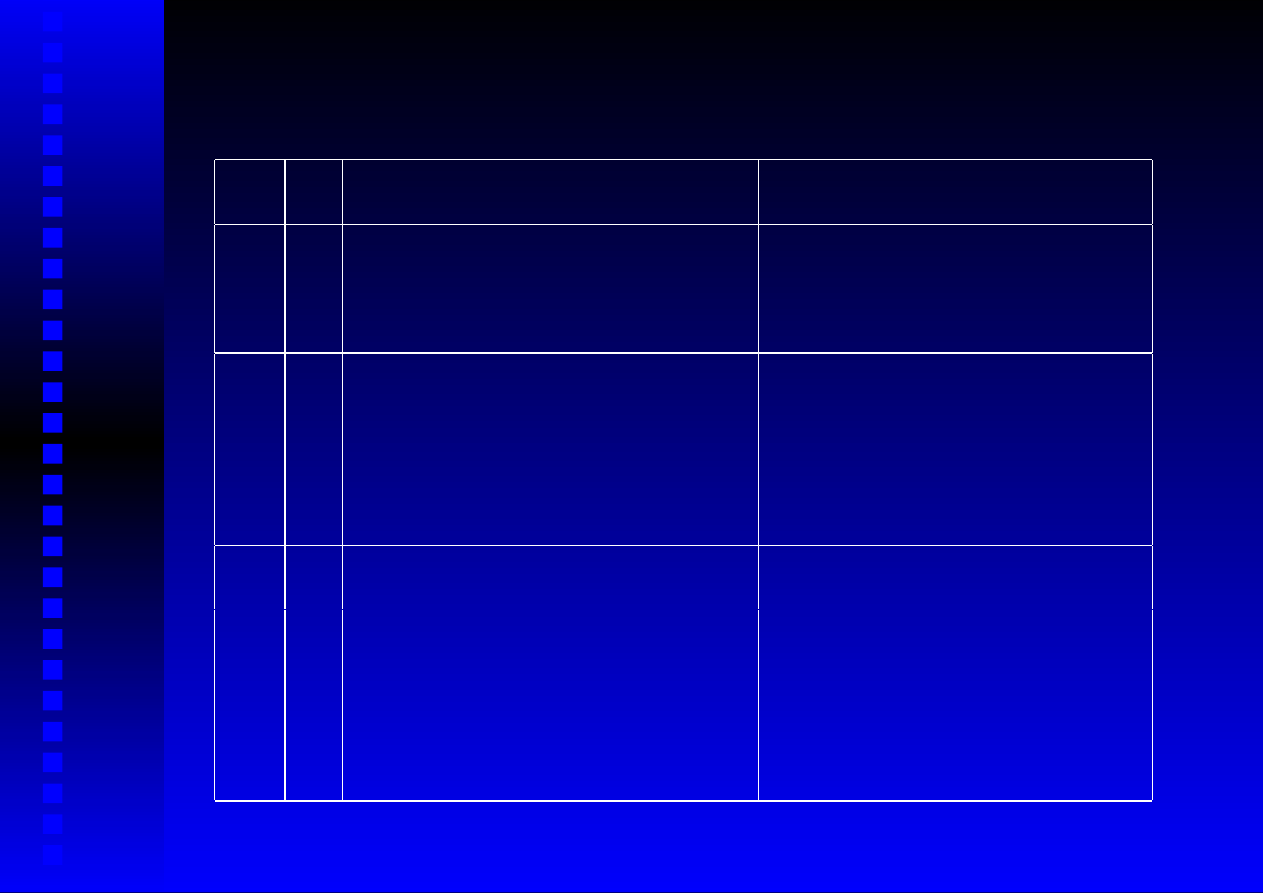
Kwadratury Gaussa-Legendre’a (3)

N

k

W˛ezły x

k

Współczynniki A

k

1

0 x

0

= −0, 5773502692 . . .

A

0

= 1

1

x

1

= 0, 5773502692 . . .

A

1

= 1

2

0 x

0

= −0, 7745966692 . . .

A

0

= 5/9

1

x

1

= 0

A

1

= 8/9

2

x

2

= 0, 7745966692 . . .

A

2

= 5/9

3

0 x

0

= −0, 8611363116 . . . A

0

= 0, 3478548451 . . .

1 x

1

= −0, 3399810436 . . . A

1

= 0, 6521451549 . . .

2

x

2

= 0, 3399810436 . . .

A

2

= 0, 6521451549 . . .

3

x

3

= 0, 8611363116 . . .

A

3

= 0, 3478548451 . . .

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.57/69

Kwadratury Gaussa-Legendre’a (4)

Przykład Obliczy´c całk˛e

Z

0,25

−

0,25

dxe

x

dla N = 1. Mamy

Z

0,25

−

0,25

dxe

x

'

1
4

h

exp

³

x

0

4

´

+ exp

³

x

1

4

´i

=

1
4

[exp(−0, 1443375673) + exp(0, 1443375673)]

= 0, 505217

Dla porównania, wynik dokładny jest równy
2 sinh 0, 25 = 0, 505224

.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.58/69

Kwadratury Gaussa-Legendre’a (5)

Przykład Dla N = 2 mamy

Z

1

0

dxe

x

= 1, 718181104

Ciekawostka Pod adresem

http://www.efunda.com/math/num_integration/findgausslegendre.cfm

mo˙zna obliczy´c w˛ezły i wagi kwadratury Gaussa–Legendre’a
on–line.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.59/69

Trudno´sci i mo˙zliwo´sci w całkowaniu numerycznym (1)

Je´sli funkcja podcałkowa jest osobliwa lub “prawie osobliwa”,
spróbuj zmodyfikowa´c problem.

´Srodki zaradcze:

•

zamiana zmiennych

•

całkowanie przez cz˛e´sci

•

wył ˛aczanie łatwo całkowalnego składnika zawieraj ˛acego
osobliwo´sci (uwaga: mo˙zliwe znoszenie si˛e składników!)

•

specjalne wzory całkowe (konstruowane metod ˛a
czynników nieoznaczonych)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.60/69

Trudno´sci i mo˙zliwo´sci w całkowaniu numerycznym (2)

Przykład Niech

I(f ) =

Z

1

0

dx

√

xe

x

.

Funkcja podcałkowa jest niesko´nczona dla x = 0. Niech x = t

2

.

Wówczas

I(f ) = 2

Z

1

0

dt exp(t

2

)

i całka ta daje si˛e ju˙z łatwo obliczy´c numerycznie.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.61/69

Całkowanie metod ˛a Monte Carlo (1)

f (x)

- funkcja całkowalna w [a, b]

Szukamy całki

Z

b

a

dxf (x) =

Z

b

a

dx

µ f (x)

h(x)

¶

h(x)

Ale

Z

b

a

dx

µ f (x)

h(x)

¶

h(x) =

¿ f (x)

h(x)

À

,

je˙zeli tylko h(x) ma własno´sci g˛esto´sci prawdopodobie´nstwa na
przedziale [a, b], tzn.

Z

b

a

dxh(x) = 1.

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.62/69

Całkowanie metod ˛a Monte Carlo (2)

Metoda Monte Carlo:

•

wybierz losowo M punktów x

i

o rozkładzie h(x)

•

na podstawie tej próbki utwórz warto´s´c ´sredni ˛a funkcji

f

(x)

h

(x)

w przedziale [a, b]

Z

b

a

dx

µ f (x)

h(x)

¶

h(x) '

1

M

M

X

i

=1

µ f (x

i

)

h(x

i

)

¶

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.63/69

Całkowanie metod ˛a Monte Carlo (3)

Twierdzenie 8 (Prawo wielkich liczb) Niech x

1

, . . . , x

M

b˛ed ˛a

zmiennymi losowo wybranymi zgodnie z funkcj ˛a g˛esto´sci
prawdopodobie´nstwa h(x), spełniaj ˛ac ˛a warunek

Z

dxh(x) = 1.

Zakładamy, ˙ze istnieje całka

I =

Z

dxh(x)g(x).

Wówczas dla ka˙zdego ² > 0

lim

M →∞

P

(

I − ² ≤

1

M

M

X

i

=1

g(x

i

) ≤ I + ²

)

= 1

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.64/69

Całkowanie metod ˛a Monte Carlo (4)

Twierdzenie 9 (Mocne prawo wielkich liczb)

P

(

lim

M →∞

1

M

M

X

i

=1

g(x

i

) = I

)

= 1

Twierdzenie 10

|E(f)| ∝

1

√

M

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.65/69

Całkowanie metod ˛a Monte Carlo (5)

Próbkowanie bezpo´srednie (x

i

s ˛a równomiernie rozło˙zone w

całym przedziale [a, b]):

h(x) =

1

b − a

St ˛ad

Z

b

a

dx

µ f (x)

h(x)

¶

h(x) '

b − a

M

M

X

i

=1

µ f (x

i

)

h(x

i

)

¶

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.66/69

Całkowanie metod ˛a Monte Carlo (6)

Przykład Obliczmy całk˛e

Z

1

0

dx exp{−30x

2

}

metod ˛a Monte Carlo, stosuj ˛ac dwie ró˙zne funkcje rozkładu
prawdopodobie´nstwa:

h

1

(x) =

1

b − a

= 1, x ∈ [0, 1]

h

2

(x) =







2, 0 ≤ x ≤

1
2

0, x >

1
2

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.67/69

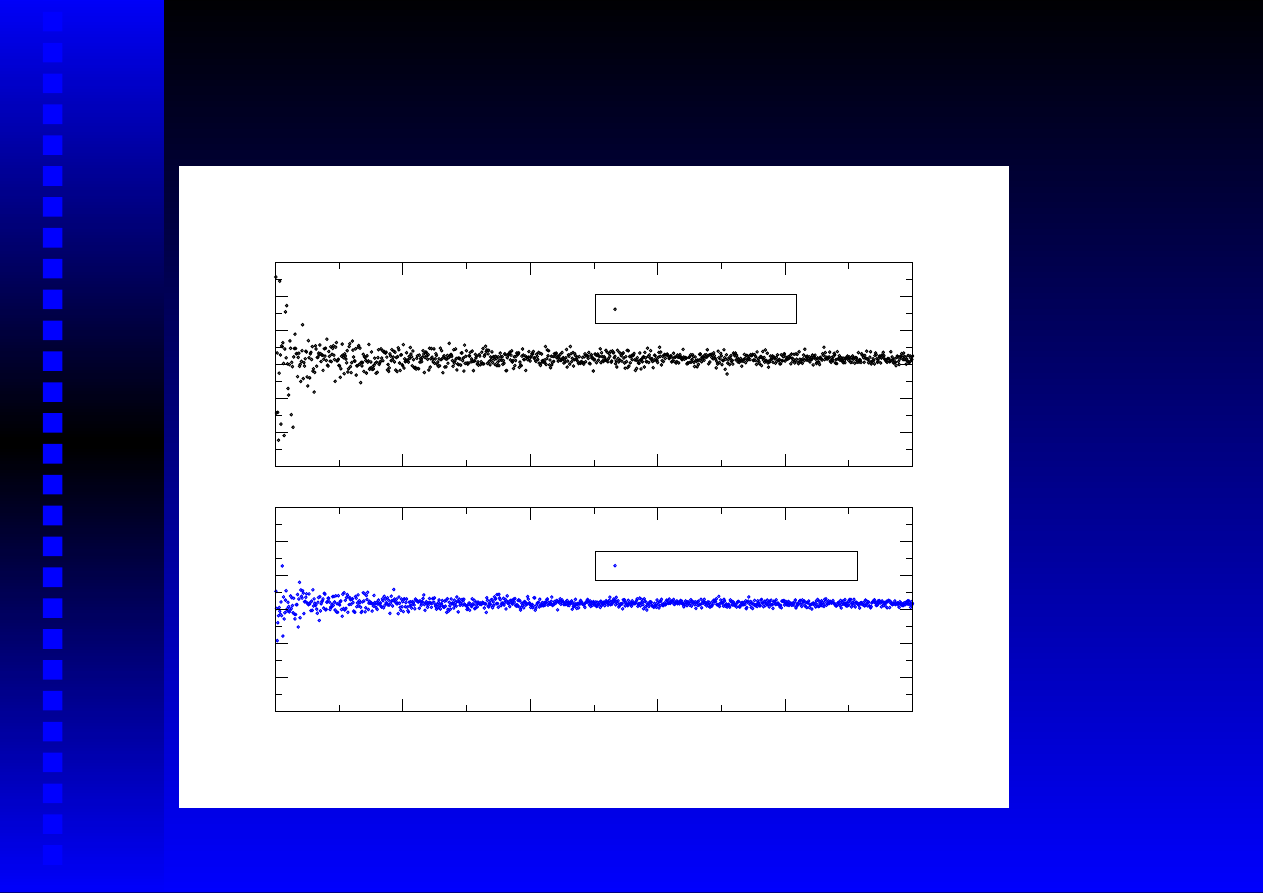
Całkowanie metod ˛a Monte Carlo (7)

0

20000

40000

60000

80000

1e+05

M

0,13

0,14

0,15

0,16

0,17

0,18

0,19

I(f)

rozklad równomierny

0

20000

40000

60000

80000

1e+05

M

0,13

0,14

0,15

0,16

0,17

0,18

0,19

I(f)

rozklad "dopasowany" do f(x)

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.68/69

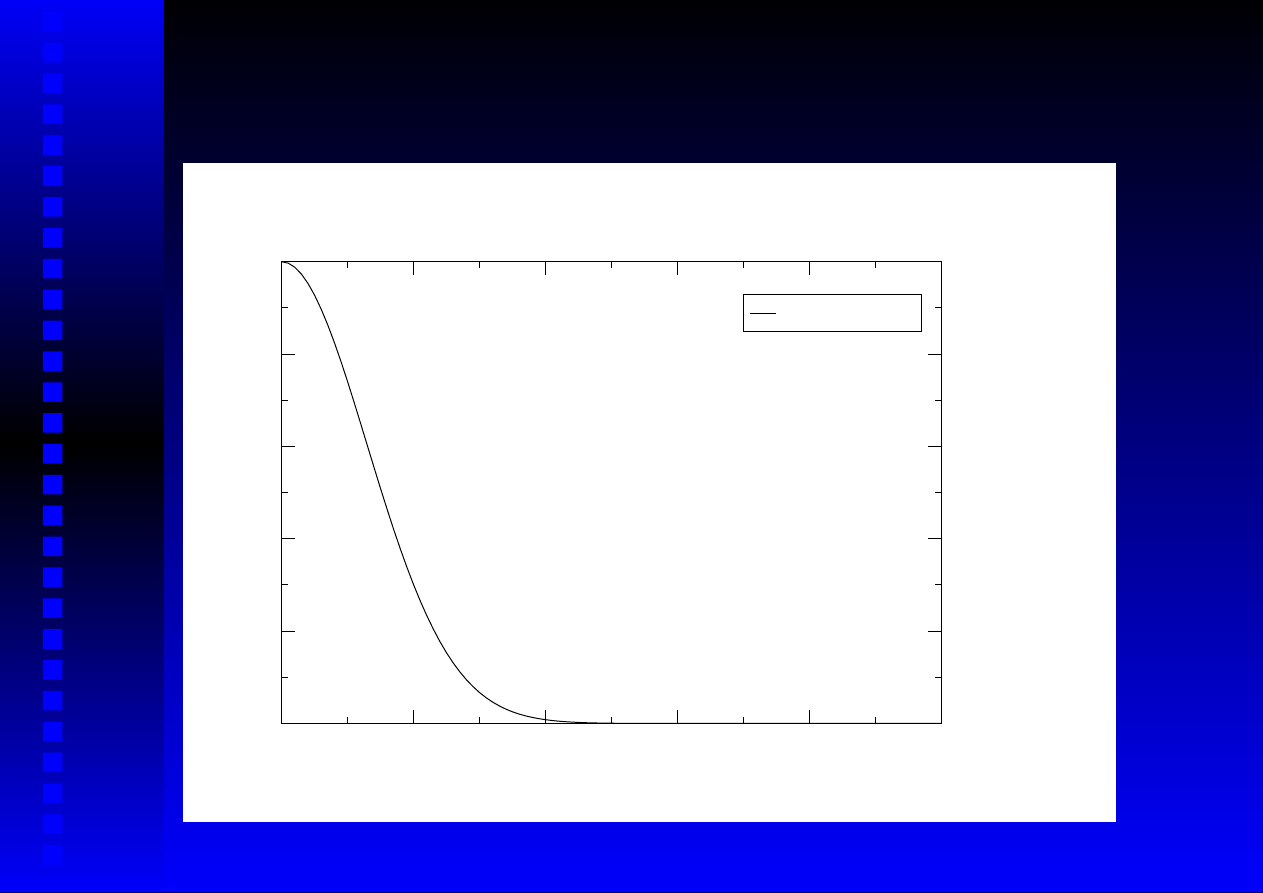
Całkowanie metod ˛a Monte Carlo (8)

0

0,2

0,4

0,6

0,8

1

x

0

0,2

0,4

0,6

0,8

1

f(x)=exp{−30x

2

}

f(x)=exp{−30x

2

}

nm_slides-4.tex – Metody numeryczne – Janusz Szwabi´nski – 23/10/2002 – 10:07 – p.69/69