Zestaw nr 6

Pochodna funkcji jednej zmiennej. Styczna do krzywej.

Elastyczno´s´c funkcji. Regu la de l’Hospitala

November 12, 2009

Przyk ladowe zadania z rozwi¸

azaniami

Zadanie 1. Oblicz pochodne nast¸

epuj¸

acych funkcji:

a) f (x) = x

4

+ 3x

3

+ 2x

2

+ x

Rozwi¸

azanie: Korzystaj¸

ac z wzoru na pochodn¸

a sumy otrzymujemy

(x

4

+ 3x

3

+ 2x

2

+ x)

0

= (x

4

)

0

+ (3x

3

)

0

+ (2x

2

)

0

+ (x)

0

= 4x

3

+ 3 · 3x

2

+ 2 · 2x + 1 = 4x

3

+ 9x

2

+ 4x + 1.

b)f (x) = x

1/2

+ 1/x

Rozwi¸

azanie: Korzystaj¸

ac z wzoru na pochodn¸

a sumy otrzymujemy (

√

x + 1/x)

0

= (

√

x)

0

+

(1/x)

0

=

1

2·

√

x

−

1

x

2

gdy˙z (

√

x)

0

=

1

2·

√

x

oraz (1/x)

0

= −

1

x

2

.

c) f (x) = 3x · log x. Przypominamy, ˙ze logx oznacza logarytm naturalny z liczby x.

Rozwi¸

azanie: Korzystaj¸

ac z wzoru na pochodn¸

a iloczynu funkcji otrzymujemy (3x · log x)

0

=

(3x) · (logx)

0

+ (3x)

0

· logx = 3x ·

1

x

+ 3logx, gdy˙z (logx)

0

= 1/x oraz (3x)

0

= 3.

d) f (x) = 3x · e

x

Rozwi¸

azanie: Korzystaj¸

ac z wzoru na pochodn¸

a iloczynu funkcji otrzymujemy (3x · e

x

)

0

= 3x ·

(e

x

)

0

+ (3x)

0

· e

x

= 3xe

x

+ 3 · e

x

, poniewa˙z (e

x

)

0

= e

x

.

e) f (x) =

3

x−3

Rozwi¸

azanie: Korzystaj¸

ac z wzoru na pochodn¸

a ilorazu funkcji otrzymujemy

(

3

x−3

)

0

=

(3)

0

·(x−3)−3·(x−3)

0

(x−3)

2

=

−3

(x−3)

2

f) f (x) =

x

2

−1

2x

2

+1

Rozwi¸

azanie: Korzystaj¸

ac z wzoru na pochodn¸

a ilorazu funkcji otrzymujemy (

x

2

−1

2x

2

+1

)

0

=

=

(x

2

− 1)

0

· (2x

2

+ 1) − (x

2

− 1)(2x

2

+ 1)

0

(2x

2

+ 1)

2

=

2x(2x

2

+ 1) − 4x(x

2

− 1)

(2x

2

+ 1)

2

=

6x

(2x

2

+ 1)

2

1

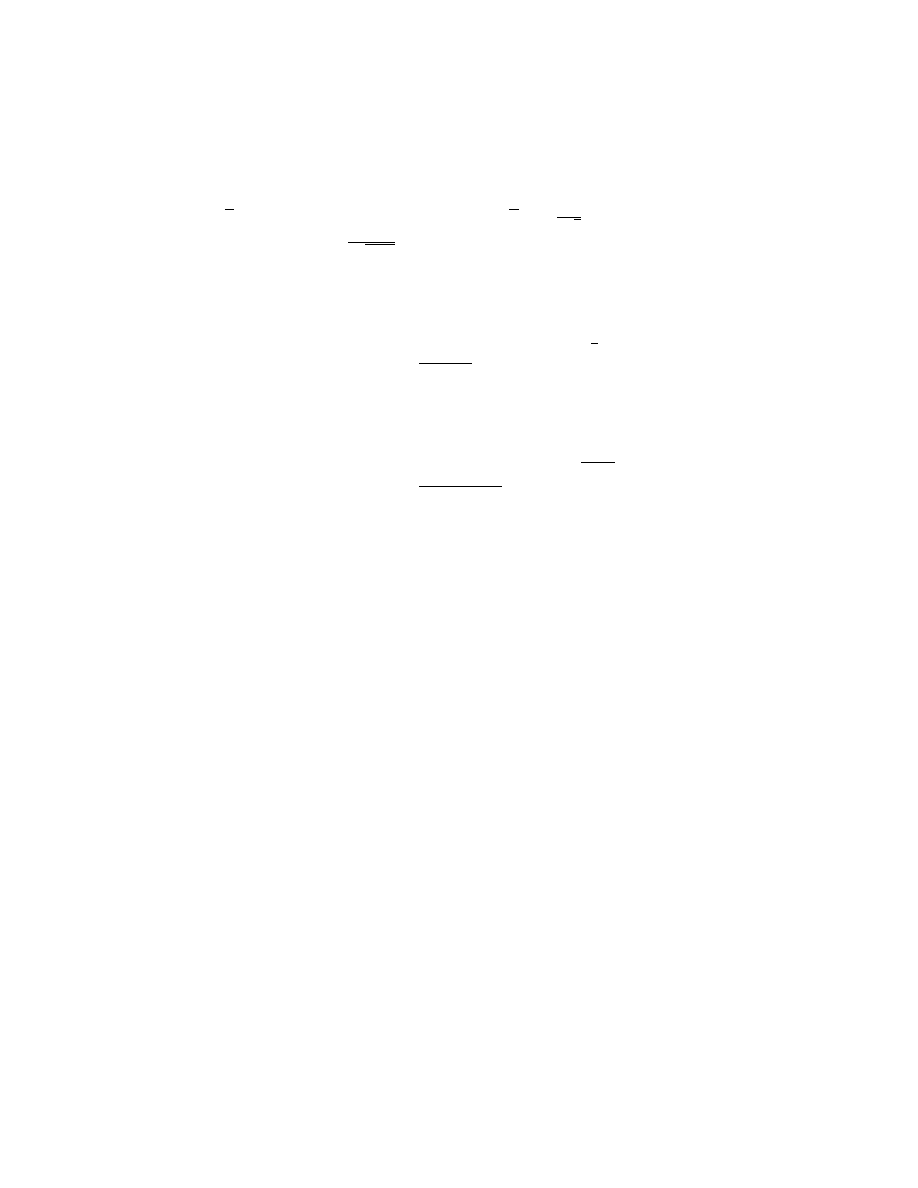
g) f (x) = (x

2

+ 1)

1/2

Rozwi¸

azanie: Korzystamy z wzoru na pochodn¸

a funkcji z lo˙zonej (g(h(x)))

0

= g

0

(h(x)) · h

0

(x).

Niech g(x) =

√

x oraz h(x) = x

2

+ 1 Wiadomo, ˙ze (

√

x)

0

=

1

2

√

x

oraz (x

2

+ 1)

0

= 2x. W´

owczas

f (x) = g(h(x)) oraz (g(h(x)))

0

=

1

2

√

x

2

+1

· 2x.

h) f (x) = ln(3x

2

+ x − 4)

Rozwi¸

azanie: Korzystamy z wzoru na pochodn¸

a funkcji z lo˙zonej (g(h(x)))

0

= g

0

(h(x)) · h

0

(x)

Niech g(x) = log x oraz h(x) = 3x

2

+ x − 4 Wiadomo, ˙ze (log x)

0

=

1
x

oraz (3x

2

+ x − 4)

0

= 6x + 1.

W´

owczas f (x) = g(h(x)) oraz (g(h(x)))

0

=

1

3x

2

+x−4

· (6x + 1).

i) f (x) = log

3

(x

2

+ x + 1)

Rozwi¸

azanie: Korzystamy z wzoru na pochodn¸

a funkcji z lo˙zonej (g(h(x)))

0

= g

0

(h(x)) · h

0

(x)

Niech g(x) = log

3

x oraz h(x) = x

2

+ x + 1 Wiadomo, ˙ze (ln

3

x)

0

=

1

x·log3

oraz (x

2

+ x + 1)

0

= 2x + 1.

W´

owczas f (x) = g(h(x)) oraz (g(h(x)))

0

=

1

(x

2

+x+1)·log3

· (2x + 1).

j) f (x) = (2/3)

1−3x

2

Rozwi¸

azanie: Korzystamy z wzoru na pochodn¸

a funkcji z lo˙zonej (g(h(x)))

0

= g

0

(h(x)) · h

0

(x)

Niech g(x) = (2/3)

x

oraz h(x) = 1 − 3x

2

Wiadomo, ˙ze ((2/3)

x

)

0

= (2/3)

x

· log(2/3) oraz (1 − 3x

2

)

0

=

−6x. W´

owczas f (x) = g(h(x)) oraz (g(h(x)))

0

= (2/3)

1−3x

2

· (−6x) · log(2/3).

k) f (x) = (3x

4

+ x

3

+ x)

5

Rozwi¸

azanie: Korzystamy z wzoru na pochodn¸

a funkcji z lo˙zonej (g(h(x)))

0

= g

0

(h(x)) · h

0

(x)

Niech g(x) = x

5

oraz h(x) = 3x

4

+ x

3

+ x Wiadomo, ˙ze (x

5

)

0

= 5x

4

oraz (3x

4

+ x

3

+ x)

0

=

12x

3

+ 3x

2

+ 1. W´

owczas f (x) = g(h(x)) oraz (g(h(x)))

0

= 5(3x

4

+ x

3

+ x)

4

· (12x

3

+ 3x

2

+ 1).

Zadanie 2. Napisz r´

ownanie stycznej do wykresu funkcji f w punkcie (x

0

, f (x

0

)) je´

sli f (x) =

x

2

− 3x + 2 oraz x

0

= 2

Rozwiazanie: Rownanie prostej l ma postac

y = ax + b

Je´

sli prosta l jest styczna do wykresu funkcji f w punkcie (x

0

, f (x

0

)) to z geometrycznej interpre-

tacji pochodnej otrzymujemy, ˙ze a = f

0

(x

0

). Styczna oraz wykres funkcji f maj¸

a wsp´

olny punkt

(x

0

, f (x

0

)) co daje

f (x

0

) = a · x

0

+ b

czyli

b = f (x

0

) − a · x

0

.

Podstawiajac warto´

sci liczbowe otrzymujemy: f

0

(x) = 2x − 3 czyli f

0

(2) = 1 oraz b = f (2) − 1 · 2 =

−2. R´

ownanie stycznej ma posta´

c

y = x − 2.

2

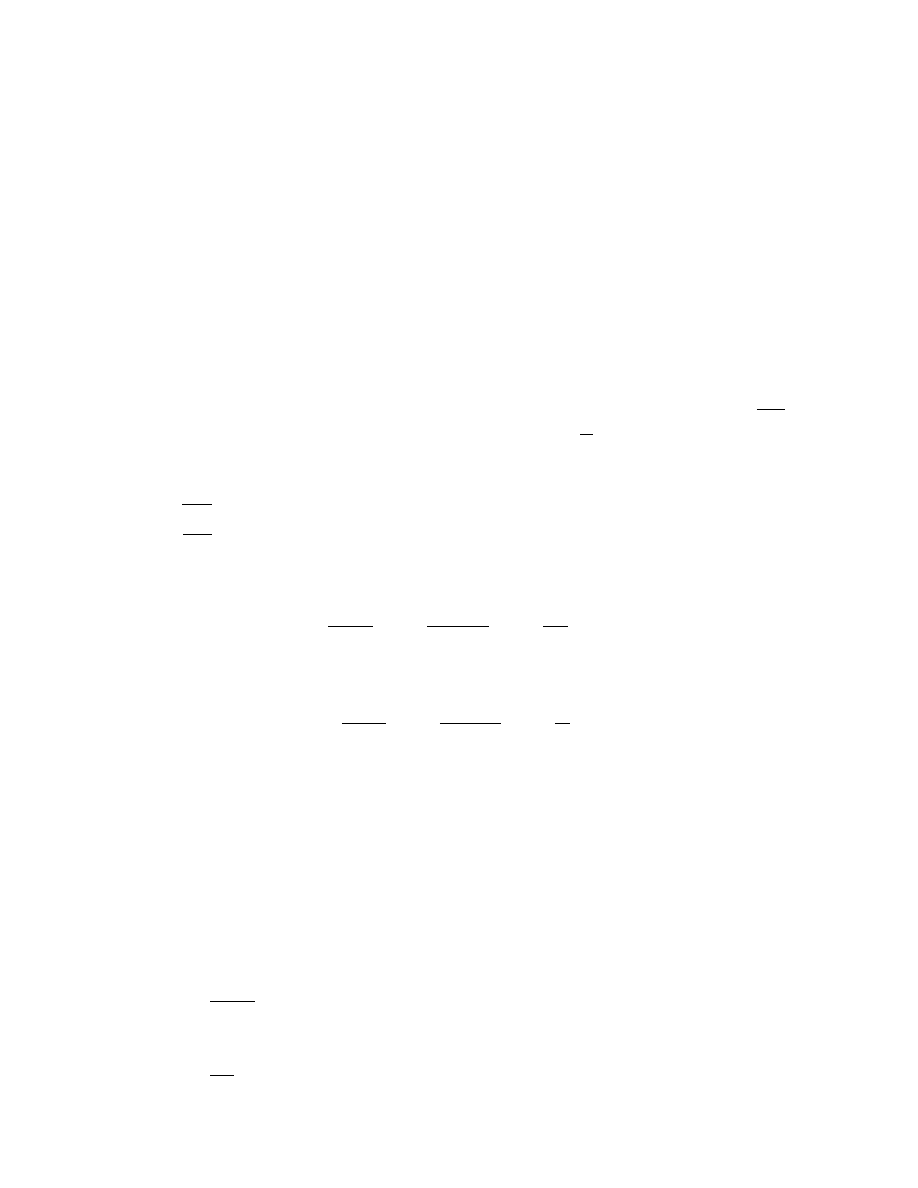
Zadanie 3. Jaki k¸

at z osi¸

a Ox tworzy styczna do paraboli f (x) = x

2

− 3x + 8 w punkcie (2, 6) ?

Rozwiazanie: Z geometrycznej interpretacji pochodnej otrzymujemy, ˙ze tangens k¸

ata α mi¸

edzy

styczn¸

a a osi¸

a Ox wynosi f

0

(2) czyli f

0

(x) = 2x − 3 oraz f

0

(2) = 1 co daje α = 45

0

.

Zadanie 4. W jakim punkcie styczna do wykresu funkcji f (x) = x

3

− 3x

2

− 9x + 2 jest r´

ownoleg la

do osi Ox?

Rozwiazanie: Styczna do wykresu funkcji f w punkcie (x

0

, f (x

0

)) jest r´

ownoleg la do osi Ox gdy

f

0

(x

0

) = 0. Zatem f

0

(x

0

) = 3x

2

0

− 6x

0

− 9 = 0. Rozwi¸azuj¸

ac to r´

ownanie kwadratowe otrzymujemy

odpowiednio ∆ = 144 oraz pierwiastki x

1

= 3 lub x

2

= −1. W punktach (3, f (3)) oraz (−1, f (−1))

styczne s¸

a r´

ownoleg le do osi Ox.

Zadanie 5. Wyznaczy´

c elastyczno´

s´

c funkcji f (x) = x

2

+ 5x + 3 dla x

0

= 3.

Rozwiazanie: Z definicji elastyczno´

s´

c E

x

f funkcji f w punkcie x dana jest wzorem E

x

f =

f

0

(x)

f (x)

· x.

Zatem f

0

(x) = 2x + 5, f

0

(3) = 11 oraz f (3) = 27, co daje E

3

f =

11
27

· 3 = 11/9.

Zadanie 6. Korzystaj¸

ac z regu ly de l’Hospitala oblicz granice:

a) lim

x→1

x

3

−1

x

2

−1

b) lim

x→0

e

x

−1

x

Rozwiazanie: a) Funkcje f (x) = x

3

− 1 oraz g(x) = x

2

− 1 s¸

a okre´

slone na R oraz r´o˙zniczkowalne

w dowolnym punkcie x ∈ R, zatem z regu ly de l’Hospitala otrzymujemy:

lim

x→1

x

3

− 1

x

2

− 1

= lim

x→1

(x

3

− 1)

0

(x

2

− 1)

0

= lim

x→1

3x

2

2x

= 3/2.

b) Funkcje f (x) = e

x

− 1 oraz g(x) = x spe lniaj¸

a za lo˙zenia tw. de l’Hospitala, mamy wi¸

ec:

lim

x→0

e

x

− 1

x

= lim

x→0

(e

x

− 1)

0

(x)

0

= lim

x→0

e

x

1

= 1.

1

Dodatkowe zadania z odpowiedziami

Zadanie 1.1. Oblicz pochodne nastepuj¸

acych funkcji:

a) f (x) = x

4

+ 6x

3

+ 8x

2

+ x

Odp. f

0

(x) = 4x

3

+ 18x

2

+ 16x + 1

b)f (x) = x

1/3

Odp. f

0

(x) =

3

3·(x)

2/3

c) f (x) = 3x · log(x − 1)

Odp. f

0

(x) =

3x

x−1

+ 3 log(x − 1)

3

d) f (x) = 3(x + 2) · e

x−2

Odp. f

0

(x) = 3(x + 2) · e

x−2

+ 3 · e

x−2

e) f (x) =

x+3
x−3

Odp. f

0

(x) =

−6

(x−3)

2

f) f (x) =

x

2

−3

x

2

+2

Odp. f

0

(x) =

10x

(x

2

+2)

2

g) f (x) = (x

2

+ x + 1)

1/2

Odp. f

0

(x) =

2x+1

2

√

x

2

+x+1

h) f (x) = log(3x

2

+ 8)

Odp. f

0

(x) =

6x

3x

2

+8

i) f (x) = log

3

(x

2

+ 4x + 7)

Odp. f

0

(x) =

2x+4

(x

2

+4x+7)log3

j) f (x) = 3

x

4

Odp. f

0

(x) = 4x

3

· 3

x

4

· log3

k) f (x) = 5

x

3

−7x+2

Odp. f

0

(x) = 5

x

3

−7x+2

· (3x

2

− 7) · log5

l) f (x) = (2x

2

+ 2x)(3x

4

+ x)

Odp. f

0

(x) = (2x

2

+ 2x)(12x

3

+ 1) + (4x + 2)(3x

4

+ x)

m) f (x) = (3x

3

+ x

2

+ x)

5

Odp. f

0

(x) = 5(3x

3

+ x

2

+ x)

4

· (9x

2

+ 2x + 1)

Zadanie 2. Napisz r´

ownanie stycznych do wykresu funkcji f w punkcie (x

0

, f (x

0

)) je´

sli

a) f (x) = x

2

− x + 2 oraz x

0

= 2

b) f (x) = x

3

− x

2

+ 2 oraz x

0

= 1

Odpowied´

z: a) y = 3x − 2 b) y=x+1

Zadanie 3. Jaki k¸

at z osi¸

a Ox tworzy styczna do paraboli f (x) = x

2

− 3x + 8 w punkcie x = 1.5 ?

Odpowied´

z: K¸

at 0

0

Zadanie 4. W jakim punkcie styczna do wykresu funkcji f (x) = x

3

− 9x + 2 jest r´

ownoleg la do

osi Ox?

Odpowied´

z: Dla x

0

=

√

3 lub x

0

= −

√

3.

Zadanie 5. Wyznaczy´

c elastyczno´

s´

c funkcji

4

a) f (x) = x

2

+ 5x + 3 dla x

0

= 3.

b) f (x) = e

x

+ 1 dla x

0

= 2

Odpowied´

z: a) 27/17 b)

2e

2

e

2

+1

Zadanie 6. Korzystaj¸

ac z regu ly de l’Hospitala oblicz granice:

a) lim

x→1

x

9

−1

x

2

−1

b) lim

x→∞

e

x

x

c) lim

x→∞

log(x+1)

x

d) lim

x→0

e

x

−x−1

x

2

e) lim

x→∞

5

x

−1

x

2

Odpowied´

z: a) 9/2, b) ∞, c) 0, d) 1/2, e) ∞.

5