Zestaw nr 7
Ekstremum funkcji jednej zmiennej. Punkty przegi¸ecia wykresu.
Asymptoty
November 20, 2009
Przyk ladowe zadania z rozwi¸
azaniami
Zadanie 1. Znajd´
z r´
ownanie asymptot funkcji f je´
sli:
a) f (x) =
2x−3
x+1
Rozwi¸
azanie: Funkcja f jest nieokre´
slona dla x = −1. Liczymy granice jednostronne funkcji f w
x = −1 :
lim
x→−1
−
2x − 3
x + 1
= ∞
lim
x→−1
+
2x − 3
x + 1
= −∞
Wniosek: funkcja f posiada asymptot¸
e pionow¸
a w punkcie x = −1.
Badamy granice funkcji przy x → ∞ oraz x → −∞.
lim
x→∞
2x − 3
x + 1
= 2
lim
x→−∞
2x − 3
x + 1
= 2
Wniosek: funkcja posiada asymptot¸
e poziom¸
a (dwustronn¸
a) o r´
ownaniu y = 2. Sprawdzamy czy
istnieje asymptota uko´
sna, w tym celu liczymy granice
lim
x→∞
2x − 3
x(x + 1)
= 0
lim
x→−∞
2x − 3
x(x + 1)
= 0
Wniosek: brak asymptot uko´
snych.
b)f (x) = x −
4
x
2
1
Rozwi¸
azanie: Funkcja f jest nieokre´
slona dla x = 0. Liczymy granice jednostronne funkcji f w
x = 0 :
lim
x→0
−
x −
4
x
2
= −∞
lim
x→0
+
x −
4
x
2
= −∞
Wniosek: funkcja posiada asymptot¸
e pionow¸
a w punkcie x = 0.
Badamy granice funkcji przy x → ∞ oraz x → −∞.
lim
x→∞
x −
4
x
2
= ∞
lim
x→−∞
x −
4
x
2
= −∞
Wniosek: funkcja nie posiada asymptoty poziomej. Sprawdzamy czy istnieje asymptota uko´
sna, w
tym celu liczymy granice
lim
x→∞
2x − 3
x(x + 1)
= 0
lim
x→−∞
2x − 3
x(x + 1)
= 0
Wniosek: brak asymptot uko´
snych.
c) f (x) =
x
3
(x+1)(x−2)
Rozwi¸
azanie: Funkcja f jest nieokre´
slona dla x = −1 oraz x = 2. Liczymy granice jednostronne
funkcji f w x = −1 :
lim
x→−1
−
x
3
(x + 1)(x − 2)
= −∞
lim
x→−1
+
x
3
(x + 1)(x − 2)
= ∞
oraz w punkcie x = 2
lim
x→2
−
x
3
(x + 1)(x − 2)
= −∞
lim
x→2
+
x
3
(x + 1)(x − 2)
= ∞
Wniosek: funkcja posiada asymptoty pionowe w punktach x = −1 oraz x = 2.
Badamy granice funkcji przy x → ∞ oraz x → −∞.
lim
x→∞
x
3
(x + 1)(x − 2)
= ∞
lim
x→−∞
x
3
(x + 1)(x − 2)
= −∞
Wniosek: funkcja nie posiada asymptot poziomych.
2
Sprawdzamy czy istnieje asymptota uko´
sna, w tym celu liczymy granice
lim
x→∞
x
3
x(x + 1)(x − 2)
= 1
oraz
lim
x→∞
x
3
(x + 1)(x − 2)
− 1 · x = 1
co daje asymptot¸
e uko´
sna y = x + 1 przy x → ∞. Podobnie sprawdzamy czy istnieje asymptota
uko´
sna przy x → −∞. Liczymy granice
lim
x→−∞
x
3
x(x + 1)(x − 2)
= 1
oraz
lim
x→−∞
x
3
(x + 1)(x − 2)
− 1 · x = 1
co daje asymptot¸
e uko´
sn¸
a y = x + 1 przy x → ∞.
Zadanie 2. Wyznacz przedzia ly monotoniczno´
sci nast¸
epuj¸
acych funkcji
a) f (x) = x
3
+ 5x − 9
Rozwiazanie: Liczymy najpierw pochodn¸
a f
0
(x) = 3x
2
+ 5 oraz zauwa˙zamy, ˙ze nier´
owno´
s´
c
3x
2
+ 5 > 0
jest spe lniona dla dowolnego x ∈ R. Czyli f (x) = x
3
+ 5x − 9 lest rosn¸
aca w ca lej swojej dziedzinie.
b) f (x) = 2x
3
+ −9x
2
+ 12x
Rozwiazanie: Liczymy najpierw pochodn¸
a f
0
(x) = 6x
2
+ 18x + 12 oraz rozwi¸
azujemy nier´
owno´
s´
c
6x
2
+ 18x + 12 > 0
lub r´
ownowa˙zn¸
a jej
x
2
+ 3x + 2 > 0.
W tym celu obliczamy pierwiastki r´
ownania
x
2
+ 3x + 2 = 0
∆ = 9 − 4 · 2 = 1 co daje x
1
= −2 lub x
2
= −1. Zatem dla x ∈ (−∞, −2) ∪ (−1, ∞) funkcja jest
rosn¸
aca, natomiast dla x ∈ (−2, −1) jest funkcj¸
a malej¸
ac¸
a.
c) f (x) =
x
2
−3
x
2
+3
Rozwi¸
azanie: Liczymy najpierw pochodn¸
a f
0
(x) =
2x(x
2
+3)−2x(x
2
−3)
(x
2
+3)
2
=
12x
(x
2
+3)
2
oraz rozwi¸
azujemy
nier´
owno´
s´
c f
0
(x) > 0. Mamy wi¸
ec f
0
(x) > 0 wtedy i tylko wtedy gdy 6x > 0. Zatem dla x > 0
funkcja jest rosn¸
aca natomiast dla x < 0 funkcja jest malej¸
aca.
Zadanie 3. Wyznacz ekstrema funkcji f je´
sli:
3
a) f (x) = x
2
− 3x + 8
Rozwi¸
azanie: Liczymy pochodn¸
a f
0
(x) = 2x − 3 i rozwi¸
azujemy r´
ownanie f
0
(x) = 0 co w naszym
przypadku daje 2x − 3 = 0 oraz x
0
= 1.5 Z postaci pochodnej otrzymujemy, ˙ze dla x < 1.5 zachodzi
f
0
(x) < 0 oraz dla x > 1.5 zachodzi f
0
(x) > 0, co daje, ze w punkcie x
0
= 1.5 funkcja f osiaga
minimum lokalne.
b) f (x) = x
4
− 4x
2
+ 4
Rozwi¸
azanie: Liczymy pochodn¸
a f
0
(x) = 4x
3
− 8x i rozwi¸
azujemy r´
ownanie f
0
(x) = 0. Mamy
4x
3
− 8x = 4x(x
2
− 2), co daje nast¸epuj¸
ace rozwi¸
azania x
1
= 0 lub x
2
= −
√
2 lub x
3
=
√
2.
Analizujemy teraz zachowanie pochodnej w otoczeniach tych trzech punkt´
ow korzystaj¸
ac z wykresu
funkcji y = 4x(x
2
− 2).
W lewostronnym otoczeniu punktu x
1
= 0 pochodna f
0
jest dodatnia a w prawostronnym ujemna,
zatem w x
1
= 0 funkcja f przyjmuje lokalne maksimum.
W lewostronnym otoczeniu punktu x
2
= −
√
2 pochodna f
0
jest ujemna a w prawostronnym do-
datnia, zatem w x
2
= −
√
2 funkcja f przyjmuje lokalne minimum.
W lewostronnym otoczeniu punktu x
3
=
√
2 pochodna f
0
jest ujemna a w prawostronnym dodatnia,
zatem w x
2
=
√
2 funkcja f przyjmuje lokalne minimum.
c) f (x) =
x+1
x
2
+4
Rozwi¸
azanie: Obliczamy pochodn¸
a f
0
(x) =
1(x
2
+4)−2x(x+1)
(x
2
+4)
2
=
−x
2
−2x+4
(x
2
+4)
2
oraz rozwi¸
azujemy
r´
ownanie f
0
(x) = 0. Wiadomo, ˙ze f
0
(x) = 0 wtedy i tylko wtedy gdy −x
2
− 2x + 4 = 0. Rozwi¸azuj¸ac
to r´
ownanie otrzymujemy: ∆ = 20 oraz x
1
= −1 −
√
5, x
2
= −1 +
√
5. Pochodna w lewostronnym
otoczeniu punktu x
1
jest ujemna a w prawostronnym otoczeniu dodatnia, zatem w x
1
funkcja f
osi¸
aga minimum lokalne. Podobnie, pochodna w lewostronnym otoczeniu punktu x
2
jest dodatnia
a w prawostronnym otoczeniu ujemna, zatem w x
2
funkcja osi¸
aga maksimum lokalne.
Zadanie 4. Znajd´
z najwi¸
eksze i najmniejsze warto´
sci funkcji na wskazanych przedzia lach
a) f (x) = x
2
+ 2x − 4, dla x ∈ [0, 2]
Rozwi¸
azanie: Liczymy pochodn¸
a f
0
(x) = 2x+2, otrzymujemy miejsce zerowe pochodnej x
0
= −1.
W punkt x
0
= −1 nie nale˙zy do przedzia lu [0, 2]. Funkcja f nie ma lokalnych ekstrem´
ow w przedziale
[0, 2]. Liczymy warto´
sci funkcji w punktach brzegowych. Otrzymujemy f (0) = −4 f (2) = 4 czyli
najwi¸eksza warto´
s´
c funkcji f, w przedziale [0, 2], wynosi 4 a najmniejsza -4.
b) f (x) = x
2
+ 2x − 4, dla x ∈ [−2, 2]
Rozwi¸
azanie: Liczymy pochodn¸
a f
0
(x) = 2x+2, otrzymujemy miejsce zerowe pochodnej x
0
= −1.
W punkcie x
0
= −1 ∈ [−2, 2] funkcja f ma minimum lokalne. Liczymy warto´
sci funkcji w punktach
brzegowych oraz w x
0
, otrzymujemy f (−2) = −4, f (2) = 4 oraz f (−1) = −5. W przedziale [−2, 2]
funkcja osiaga najwi¸
eksz¸
a warto´
s´
c 4 dla x
1
= 2 oraz najmniejsz¸
a warto´
s´
c -5 w punkcie x
0
= −1.
c) f (x) =
2x+5
x+1
dla x ∈ [−3, −1) ∪ (−1, 3]
Rozwi¸
azanie: W punkcie x = −1 funkcja jest nieokre´
slona.
lim
x→−1
−
2x + 5
x + 1
= −∞
lim
x→−1
+
2x + 5
x + 1
= ∞
4
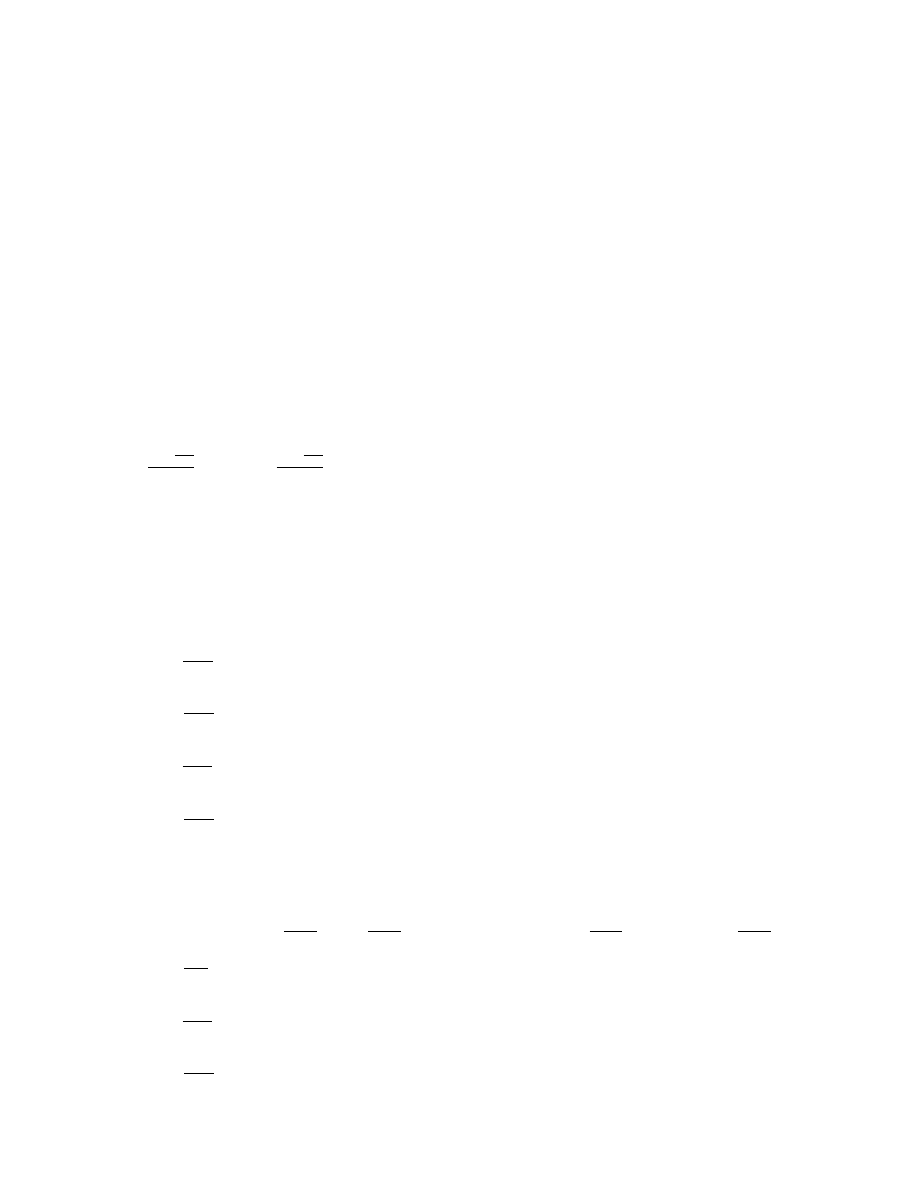
czyli w x = −1 istnieje asymptota pionowa funkcji f. Zatem funkcja f nie osi¸
aga w tym zbiorze ani
sko´
nczonej warto´
sci maksymalnej ani sko´
nczonej minimalnej.
Zadanie 5. Wyznaczy´
c punkty przegi¸
ecia, przedzia ly wypuk lo´
sci oraz wkl¸
es lo´
sci funkcji
a) f (x) = 3x
4
+ 7x + 1 dla x ∈ (0, ∞)
Rozwi¸
azanie: Liczymy pierwsz¸
a pochodn¸
a f
0
(x) = 12x
3
+ 7 oraz drug¸
a f
00
(x) = 36x
2
. Dla
dowolnego x ∈ (0, ∞) zachodzi f
00
(x) > 0 czyli funkcja jest wypuk la w ca lej swojej dziedzinie.
b) f (x) = e
x−1
+ 2
Rozwi¸
azanie: Liczymy pierwsz¸
a pochodn¸
a f
0
(x) = e
x−1
oraz drug¸
a f
00
(x) = e
x−1
. Dla dowolnego
x ∈ (−∞, ∞) zachodzi f
00
(x) > 0 czyli funkcja jest wypuk la w ca lej swojej dziedzinie.
c) f (x) = x
4
− x
3
− x
2
Rozwi¸
azanie: Liczymy pierwsz¸
a pochodn¸
a f
0
(x) = 4x
3
−3x
2
−2x oraz drug¸a f
00
(x) = 12x
2
−6x−2.
Szukamy pierwiastk´
ow r´
ownania 12x
2
− 6x − 2 = 0. Po obliczeniach otrzymujemy pierwiastki
x
1
=
6−
√
132
24
oraz x
2
=
6+
√
132
24
.
Dla x ∈ (−∞, x
1
) mamy f
00
(x) > 0 czyli funkcja f jest wypuk la w tym przedziale. Dla x ∈ (x
2
, ∞)
mamy f
00
(x) > 0 czyli funkcja f jest wypuk la w tym przedziale. Natomiast dla x ∈ (x
1
, x
2
) mamy
f
00
(x) < 0 czyli funkcja f jest wkl¸
es la w tym przedziale. Punkty x
1
oraz x
2
s¸
a punktami przegi¸
ecia.
1
Zadania do samodzielnego rozwi¸
azania
Zadanie 1.1. Znajd´
z r´
ownanie asymptot funkcji f je´
sli:
a) f (x) =
2x−3
x+1
Odp. Asymptota pionowa w x = −1, asymptota pozioma y = 2, brak asymptot uko´
snych.
b) f (x) =
7x+3
x−10
Odp. Asymptota pionowa w x = 10, asymptota pozioma y = 7, brak asymptot uko´
snych.
c) f (x) =
1
x
2
+1
Odp. asymptota pozioma y = 0.
d) f (x) =
1
1−x
2
Odp. Asymptota pionowa w x = 1 lub x = −1, asymptota pozioma y = 0, brak asymptot uko´
snych.
Zadanie 2.1. Wyznacz przedzia ly monotoniczno´
sci nast¸
epuj¸
acych funkcji
a) f (x) = −x
3
+ 3x
2
+ 2x + 2
Odp. Rosn¸
aca w (1 −
p10/6, 1 + p10/6), malej¸aca w (−∞, 1 − p10/6) oraz w (1 + p10/6, ∞).
b) f (x) =
5
1−x
Odp. Malej¸
aca w (−∞, 1), rosn¸
aca w (1, ∞.)
c) f (x) =
7x+3
x−10
Odp. Malej¸
aca w (−∞, 10) oraz w (10, ∞).
d) f (x) =
x
x
2
+4
5
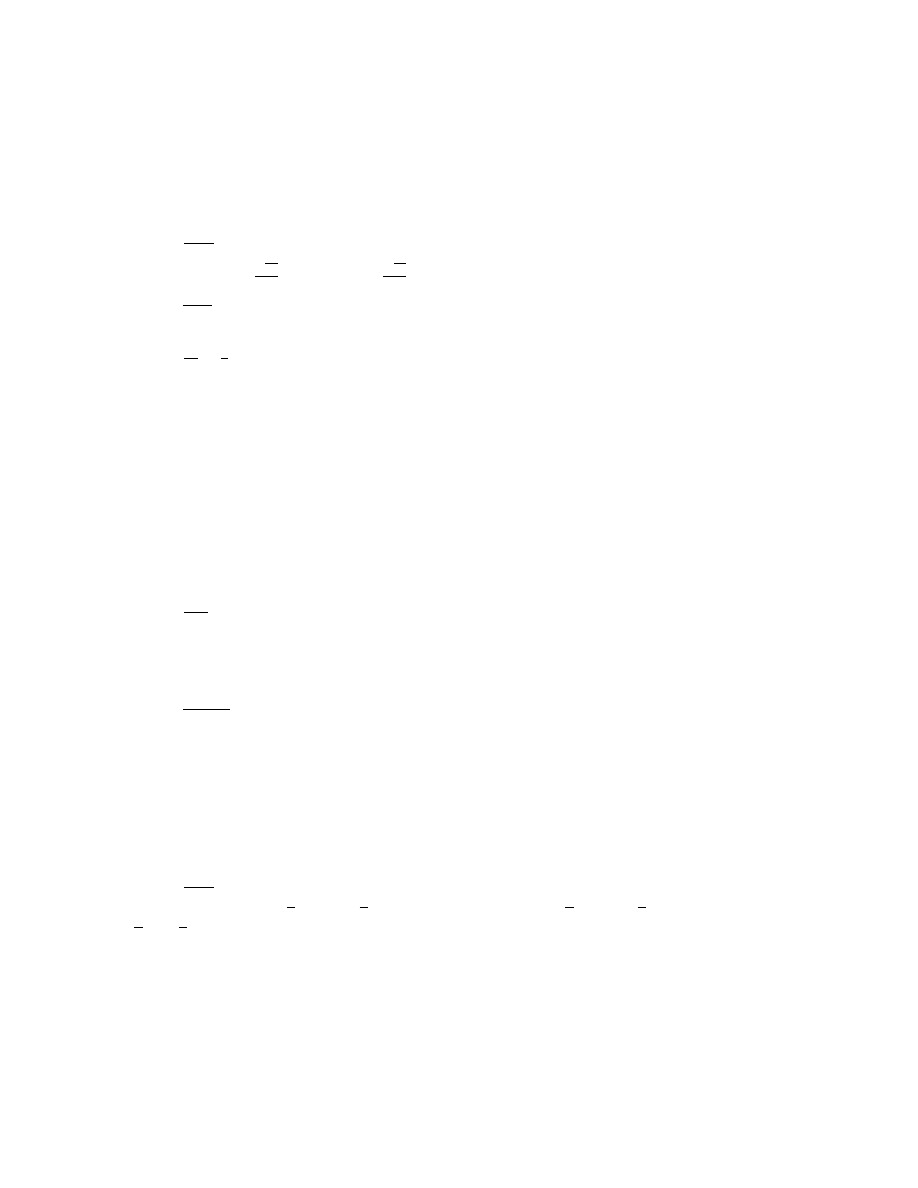
Odp. Malej¸
aca w (−∞, −2) oraz w (2, ∞), rosn¸
aca w (−2, 2).
Zadanie 3.1. Wyznacz ekstrema funkcji f je´
sli:
a) f (x) = −x
3
+ 3x
2
+ 9x + 2
Odp. Min w x
1
= −1, max w x
2
= 3.
b) f (x) =
3x+2
x
2
+1
Odp. Min w x
1
= −
√
13
3
, max w x
2
=
√
13
3
.
c) f (x) =
9−x
2
x+5
Odp. Min w x
1
= −9, max w x
2
= −1.
d) f (x) =
x
2
2
+
1
x
Odp. Min w x
1
= 1.
Zadanie 4.1. Znajd´
z najwi¸
eksze i najmniejsze warto´
sci funkcji na wskazanych przedzia lach
a) f (x) = x
2
+ 2x − 4, dla x ∈ [0, 2]
Odp. Warto´
s´
c min f (0) = −4, warto´
s´
c max f (2) = 4
b) f (x) = 3
x−1
dla x ∈ [0, 2]
Odp. Warto´
s´
c min f (0) = 1/3, warto´
s´
c max f (2) = 1
c) f (x) = −3x
2
+ 6x + 9 dla x ∈ [−4, 2]
Odp. Warto´
s´
c min f (−4) = −63, warto´
s´
c max f (1) = 13.
d) f (x) =
x+1
x−2
dla x ∈ [3, 5]
Odp. Warto´
s´
c min f (5) = 2, max f (3) = 4.
Zadanie 5.1. Wyznaczy´
c punkty przegi¸
ecia, przedzia ly wypuk lo´
sci oraz wkl¸
es lo´
sci funkcji
a) f (x) =
x
2
+x−2
x−2
Odp. f wypuk la dla x > 2, wkl¸
es la dla x < 2. Brak punktu przegi¸
ecia.
b) f (x) = log(1 + x
2
)
Odp. f wypuk la dla x < −1 oraz x > 1, wkl¸
es la dla x ∈ (−1, 1). Punkty przegi¸
ecia dla x = 1 lub
x = −1.
c) f (x) = x
4
+ 2x
3
− 12x
2
− 2x + 1
Odp. Wypuk la w (−∞, −2) oraz (1, ∞). Wkl¸
es la (−2, 1), punkty przegi¸
ecia x = −2 lub x = 1.
d) f (x) =
x
x
2
+1
Odp.
Wypuk la w (−
√
3, 0) ∪ (
√
3, ∞). Wkl¸
es la w (−∞, −
√
3) ∪ (0,
√
3). Punkty przegi¸
ecia :
−
√
3, 0,
√
3.
6