1

Funkcje nieliniowe.
Przykłady

Witold Jurek

W .J. Charakterystyki funkcji

2

Przyrost

Niech będzie dana ciągła i różniczkowalna funkcja y=f(x)

Przyrost zmiennej y dla:



nieskończenie małego przyrostu zmiennej x:



skończonego przyrostu zmiennej x:

Jeżeli x oznacza czas, to w pierwszym przypadku mówimy o
przyroście chwilowym, a w drugim – o okresowym
W zastosowaniach często Δx = 1 i dlatego przyrost zmiennej
y, dla skończonego przyrostu zmiennej x wynosi Δy

dx

dy

x

y





W .J. Charakterystyki funkcji

3

Stopa wzrostu

Zmienna x oznacza czas. Obie stopy (chwilowa, okresowa)
wyrażają stopę wzrostu zmiennej y w czasie



Stopa wzrostu chwilowa:



Stopa wzrostu okresowa:

W zastosowaniach często

Δx = 1 i wówczas okresowa stopa

wzrostu:

y

dx

dy

S

y

:



y

x

y

S

y

:







y

y

S

y





2

W .J. Charakterystyki funkcji

4

Elastyczność

Dana jest funkcja:

Obie zmienne w, z są funkcjami np. czasu.

Elastycznością zmiennej w względem zmiennej z jest
nazywane wyrażenie:

w którym to stopy wzrostu, odpowiednio,
zmiennej w, zmiennej z

))

(

(

)

(

t

z

f

t

w



z

w

z

w

S

S

E

:

,



z

w

S

S ,

W .J. Charakterystyki funkcji

5

Parametry funkcji liniowej

Prosta, funkcja liniowa: y = ax + b

Współczynnik kierunkowy a: przyrost zmiennej y
odpowiadający nieskończenie małemu albo jednostkowemu
przyrostowi zmiennej x

Wyraz wolny b: wartość zmiennej y dla zerowej wartości
zmiennej x. (Współrzędna punktu przecięcia prostej z osią
rzędnych dla x = 0)

W .J. Charakterystyki funkcji

6

Parametry funkcji wykładniczej

Funkcja wykładnicza: albo



Parametr



: stopa wzrostu funkcji (zmiennej y)



Parametr b: wskaźnik wzrostu (zmiennej y)



Parametr a: wartość zmiennej y dla zerowej wartości
zmiennej x.

Zależność między



oraz b:

𝑒

𝛽

= 𝑏 albo



= ln b

Jeżeli stopa



jest liczbą małą (w praktyce



< 0,05), to

1 +





b

x

ae

y





x

ab

y



3

W .J. Charakterystyki funkcji

7

Parametry funkcji potęgowej



Funkcja potęgowa:



Parametr b: elastyczność y względem x.



Parametr a: wartość zmiennej y
dla jednostkowej wartości zmiennej x.

b

ax

y



Przykład interpretacji parametrów

Określić typ i podać interpretację parametrów tzw.
dynamicznej funkcji produkcji Cobba - Douglasa

w której: P – produkcja

M – majątek produkcyjny

Z – zatrudnienie

t – czas

Parametry funkcji:

𝛼

0

, 𝛼

1

, 𝛼

2

, 𝛼

3

W .J. Charakterystyki funkcji

8

Funkcja wykładnicza. Przykład

Nakłady inwestycyjne w gospodarce narodowej pewnego
kraju w kolejnych 6 latach wynosiły

MNK oszacować średnią stopę wzrostu nakładów
inwestycyjnych w tym okresie

W .J. Charakterystyki funkcji

9

lata

1

2

3

4

5

6

inwestycje

227,7

244,8

302,6

378,3

463,7

529,6

4

Funkcja wykładnicza. Przykład



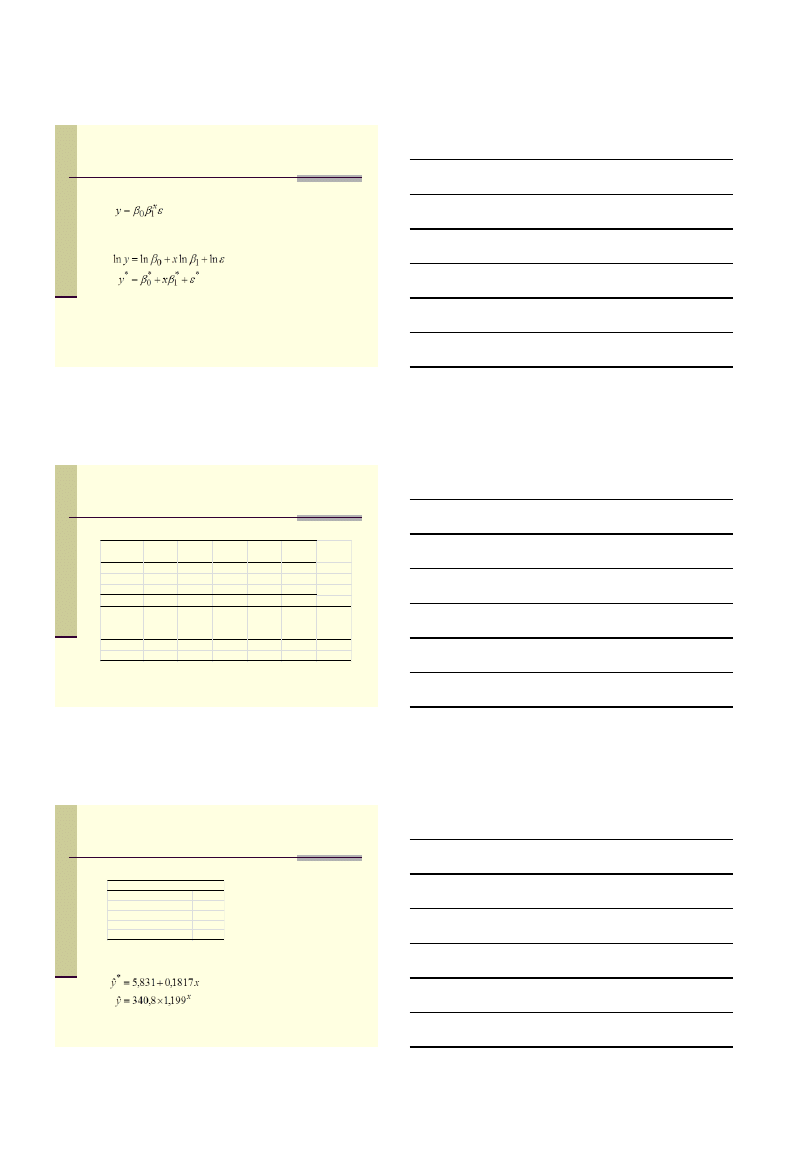
Funkcja wykładnicza poddana oszacowaniu



Funkcja po uliniowieniu



Wartości zmiennej czasowej:
x = -2,5; -1,5; -0,5; 0,5; 1,5; 2,5

W .J. Charakterystyki funkcji

10

Funkcja wykładnicza. Przykład

Oszacowanie

W .J. Charakterystyki funkcji

11

df

SS

MS

F

Istotność

F

Regresja

1 0,577875 0,577875 275,1545 7,74E-05

Resztkowy

4 0,008401

0,0021

Razem

5 0,586276

Współcz

ynniki

Błąd

standard

owy

t Stat

Wartość-

p

Dolne

95%

Górne

95%

Przecięcie

5,831322 0,018709 311,6836 6,36E-10 5,779377 5,883266

Zmienna X 1 0,181718 0,010955 16,58778 7,74E-05 0,151302 0,212134

Funkcja wykładnicza. Przykład



Dopasowanie funkcji uliniowionej do danych



Oszacowanie funkcji wykładniczej

W .J. Charakterystyki funkcji

12

Statystyki regresji

Wielokrotność R

0,99281

R kwadrat

0,98567

Dopasowany R kwadrat

0,98209

Błąd standardowy

0,04583

Obserwacje

6

5

Funkcja wykładnicza. Przykład



Inna postać funkcji wykładniczej



Funkcja wykładnicza, po uliniowieniu



Oszacowanie parametrów funkcji wykładniczej



oszacowanie wyrazu wolnego to samo, co wcześniej



oszacowanie stopy wzrostu: 0,1817



Funkcja uliniowiona:



Oszacowana funkcja wykładnicza:

𝑦 = 340,8 × 𝑒

0,1817𝑥

W .J. Charakterystyki funkcji

13

Funkcja potęgowa. Przykład

W tabeli podano wyposażenie gospodarstw domowych w
motocykle, skutery i motorowery (w szt. na 100 gospodarstw)
oraz przeciętny miesięczny dochód na osobę (w tys. zł) w 7
grupach dochodowych.

Oszacować funkcję wyrażającą potęgową hipotezę o
zależności wyposażenia gospodarstw domowych w
motocykle, skutery i motorowery od dochodu na osobę.

W .J. Charakterystyki funkcji

14

Przychód

1,5

2,0

2,5

3,0

4,0

5,0

6,0

Wyposażenie 14,79 16,6 16,22 15,85 13,49 11,75 9,55

Funkcja potęgowa. Przykład

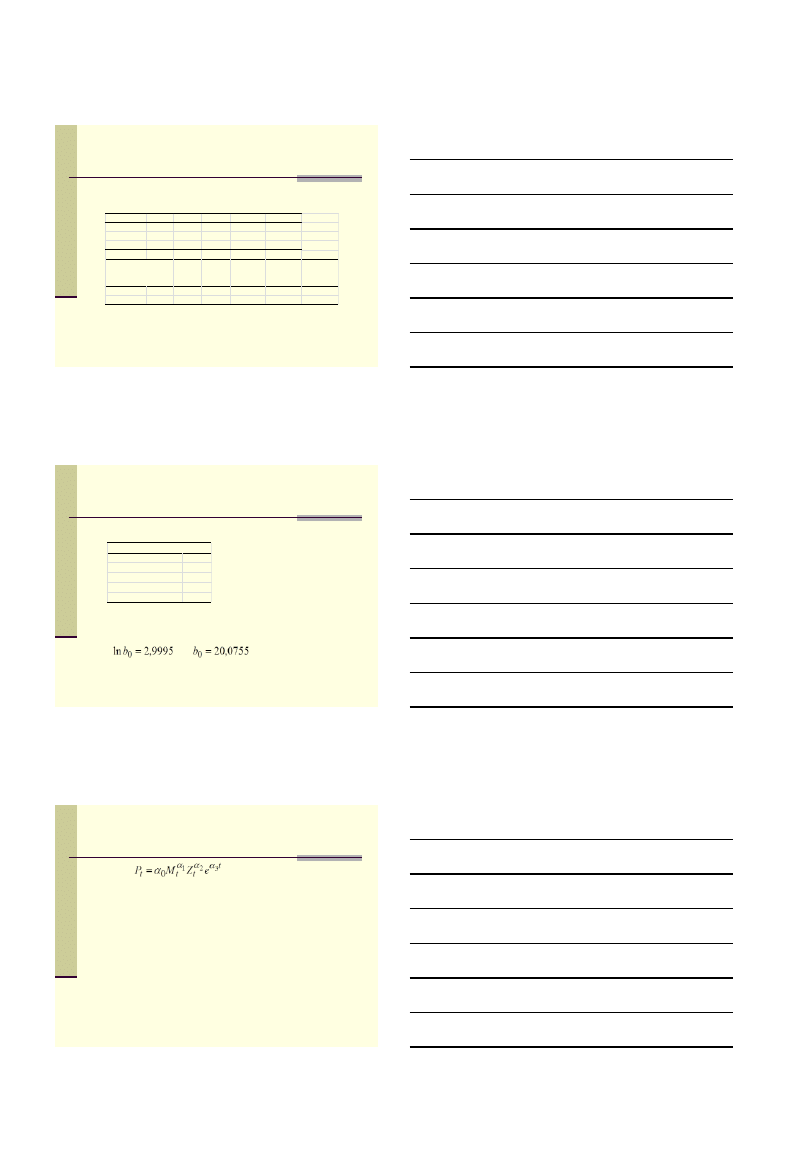
Funkcja potęgowa

Funkcja potęgowa po uliniowieniu

W .J. Charakterystyki funkcji

15

6

Funkcja potęgowa. Przykład

Oszacowanie funkcji uliniowionej

W .J. Charakterystyki funkcji

16

df

SS

MS

F

Istotność F

Regresja

1

0,16466

0,16466

10,10876

0,02455

Resztkowy

5

0,08145

0,01629

Razem

6

0,24611

Współczynniki

Błąd

standard

owy

t Stat

Wartość-p

Dolne 95%

Górne 95%

Przecięcie

2,99950

0,12728 23,56637

0,00000

2,67232

3,32668

Zmienna X 1

-0,33178

0,10435 -3,17943

0,02455

-0,60002

-0,06353

Funkcja potęgowa. Przykład

Dopasowanie

Oszacowanie modelu oryginalnego

- oszacowanie wyrazu wolnego:

- oszacowanie współczynnika kierunkowego (elastyczności) jak
w modelu uliniowionym

W .J. Charakterystyki funkcji

17

Statystyki regresji

Wielokrotność R

0,81796

R kwadrat

0,66907

Dopasowany R kwadrat

0,60288

Błąd standardowy

0,12763

Obserwacje

7

Różniczkowanie iloczynu
Przypomnienie

Funkcja
w której:
traktowana jest jako iloczyn:

y = u

× v × w

Pochodna iloczynu

y’ = u’

× v × w + u × v’ × w + u × v × w’

W .J. Charakterystyki funkcji

18

𝑢 = 𝛼

0

𝑀

𝑡

𝛼

1

𝑣 = 𝑍

𝑡

𝛼

2

𝑤 = 𝑒

𝛼

3

𝑡

7

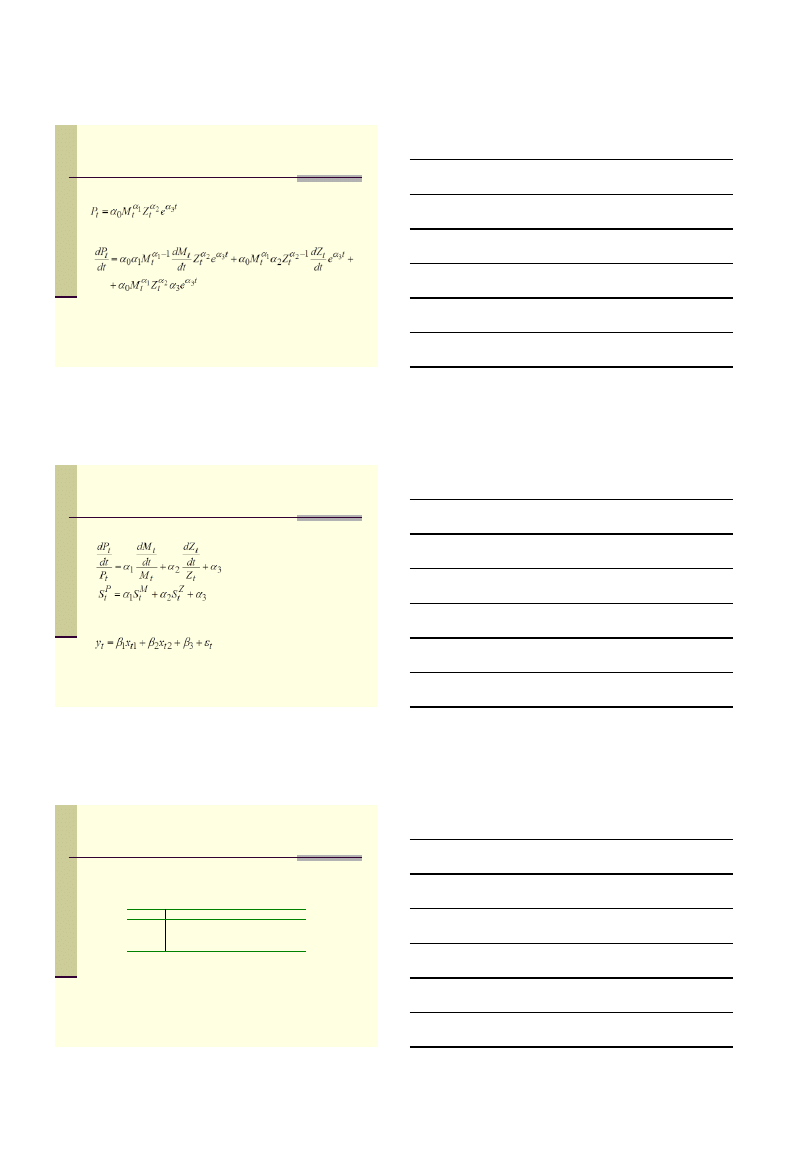
Uliniowienie funkcji produkcji
Cobba - Douglasa

Funkcja produkcji

Pochodna

W .J. Charakterystyki funkcji

19

Uliniowienie funkcji produkcji
Cobba - Douglasa

Stopy wzrostu

Model (liniowy) poddany oszacowaniu

W .J. Charakterystyki funkcji

20

Przykład.
Oszacowanie funkcji Cobba - Douglasa

W 9 kolejnych miesiącach stopa wzrostu nakładów pracy (Z),
majątku produkcyjnego (M) oraz produkcji pewnych
przedsiębiorstw (P) wynosiły

MNK wyznaczyć parametry funkcji produkcji Cobba-
Douglasa

W .J. Uliniowienie_CD

21

Miesiące

1

2

3

4

5

6

7 8 9

M

1

2

3

0

3

2

1 1 1

Z

2

2

1

1

2

1

0 1 2

P

2,2 2,05 1,8 0,85 2,4 1,05 0,3 1,2 1,7

8

Przykład.
Oszacowanie funkcji Cobba - Douglasa



Oszacowanie parametrów funkcji MNK (Excel,
REGLINP)



Oszacowanie modelu liniowego (liniowej transformanty)

W .J. Uliniowienie_CD

22

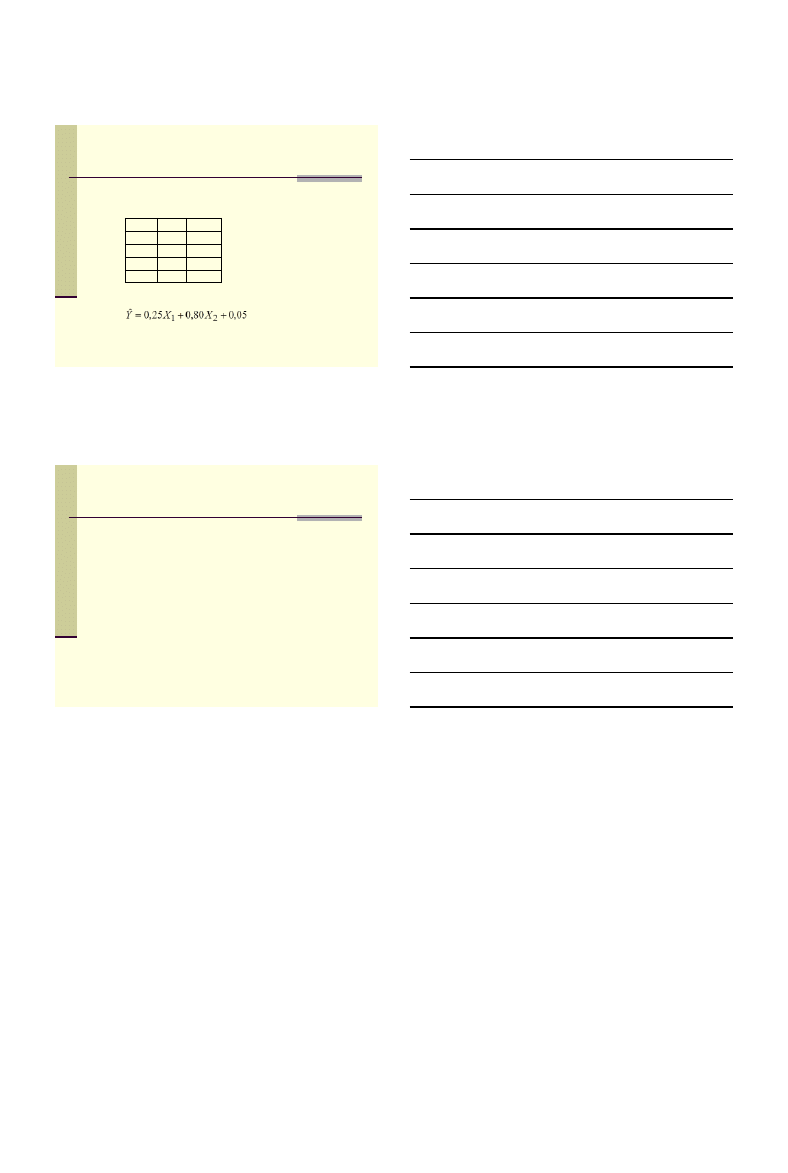
0,800 0,250 0,050 Oceny

0,111 0,078 0,183 Błędy szacunku
0,928 0,216 #N/D! R2

S

38,649

6

#N/D! F

T-K

3,607 0,280 #N/D! RSK

SKO

Przykład.
Oszacowanie funkcji Cobba - Douglasa



Oszacowanie funkcji

𝑃

𝑡

= α

0

𝑀

𝑡

0,25

𝑍

𝑡

0,80

𝑒

0,05𝑡



Uwaga



Na podstawie danych statystycznych w postaci stóp wzrostu
MNK nie zostaje oszacowana stała, α

0

, (wyrażająca

efektywność technologii)



Stałą α

0

należy oszacować na podstawie danych o produkcji

(P), majątku produkcyjnym (M) i nakładach pracy (Z),
po oszacowaniu MNK liniowej transformanty

W .J. Uliniowienie_CD

23