Metody Obliczeniowe 

 

Magdalena Rucka 

Przykład: aproksymacja liniowa 

 

rok akademicki 2012/2013 

Aproksymacja liniowa – metoda najmniejszych kwadratów
Wpasowanie prostej

0

1

y a

a x e







w zbiór danych pomiarowych

( , )

i

i

x y

, i = 1, 2, …, n, gdzie e oznacza błąd między

wartością pomierzonej funkcji a wartością funkcji aproksymującej.

Kryterium błędu: minimum sumy kwadratów

r

S

:





2

2

0

1

1

1

n

n

r

i

i

i

i

i

S

e

y

a

a x

















Cel: wyznaczyć wartości

0

a

oraz

1

a

tak, by zminimalizować

r

S

:

1

1

1

1

2

2

1

1

n

n

n

i i

i

i

i

i

i

n

n

i

i

i

i

n

x y

x

y

a

n

x

x



















 









 





,

0

1

1

1

1

1

1

n

n

i

i

i

i

a

y

x a

y a x

n

n









 





,

gdzie

y

oraz

x

oznaczają wartość średnią:

1

1

n

i

i

y

y

n







,

1

1

n

i

i

x

x

n







.

Ocena dokładności aproksymacji:

 Odchylenie standardowe





2

1

1

1

n

i

t

i

y

y

y

S

s

n

n















,





2

1

n

t

i

i

S

y

y









 Wariancja

2

1

t

y

S

s

n





 Standardowy błąd przybliżenia:

/

2

r

y x

S

s

n





 Współczynnik determinacji

2

t

r

t

S

S

r

S





 Współczynnik korelacji

2

1

1

1

2

2

2

2

1

1

1

1

n

n

n

i i

i

i

t

r

i

i

i

n

n

n

n

t

i

i

i

i

i

i

i

i

n

x y

x

y

S

S

r

r

S

n

x

x

n

y

y























































 









Przykład:
Wykonać aproksymację liniową pomierzonych danych:
xi =[ 0 1 2 3 4 5 6 7]
yi =[ 0.3000 1.3000 1.9000 3.5000 3.9000 5.5000 6.4000 7.0000]
Do rozwiązania wykorzystać funkcję aproksymacja_liniowa.m

[ya,a0,a1,sy,sy2,r2,r]=aproksymacja_liniowa(xi,yi);

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% procedura aproksymacji liniowej

%------------------------------------------------------------------------

% WEJSCIE:

% xi = odciete punktow danych

% yi = rzedne punktow danych

%-------------------------------------------------------------------------

% WYJSCIE:

% ya = funkcja aproksymujaca ya=a0+a1*x

% a0 = wspolczynnik a0 rownania funkcji aproksymujacej ya=a0+a1*x

% a1 = wspolczynnik a1 rownania funkcji aproksymujacej ya=a0+a1*x

% sy = odchylenie standardowe

% sy2 = wariancja
% r2 = wspolczynnik determinacji

% r = wspolczynnik korelacji

%-------------------------------------------------------------------------

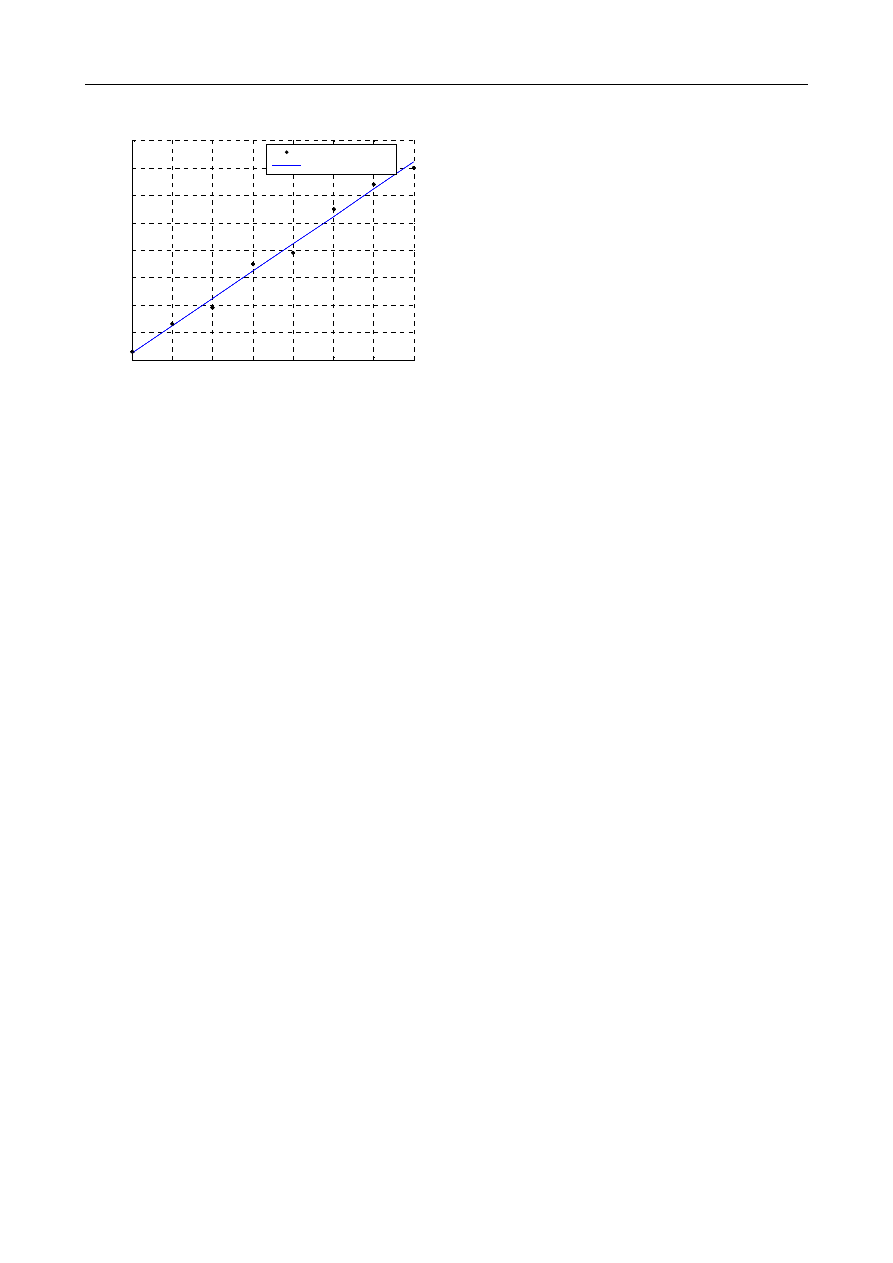
Metody Obliczeniowe 

 

Magdalena Rucka 

Przykład: aproksymacja liniowa 

 

rok akademicki 2012/2013 

Rozwiązanie:

0

1

2

3

4

5

6

7

0

1

2

3

4

5

6

7

8

x

y

r

2

=0.9892

punkty pomiarowe

aproksymacja liniowa

Algorytm w programie MATLAB

% Metody Obliczeniowe

% Przyklad aproksymacja liniowa

% Opracowala: Magdalena Rucka

% Rok.akad. 2012/13

clc;clear;format

short

% odcięte punktow danych

xi=[0 1 2 3 4 5 6 7];

% rzędne punktow danych

yi=[0.3 1.3 1.9 3.5 3.9 5.5 6.4 7];

[ya,a0,a1,sy,sy2,r2,r]=aproksymacja_liniowa(xi,yi);

figure(1);hold

on

;grid

on

plot(xi,yi,

'ko'

,

'MarkerFaceColor'

,

'k'

,

'MarkerSize'

,4)

plot(xi,ya,

'b'

)

xlabel(

'x'

); ylabel(

'y'

);

legend(

'punkty pomiarowe'

,

'aproksymacja liniowa'

)

title([

'r^2='

num2str(r2)])

Wyniki:

a1 =
0.9952

a0 =
0.2417

St =
42.0550

Sr =
0.4540

sy =
2.4511

sy2 =
6.0079

sy_x =
0.2751

aproksymacja poprawna sy_x < sy

r2 =
0.9892

r =
0.9946