MECHANIKA TEORETYCZNA 2

7. Podać zasadę d’Alemberta dla punktu materialnego.

Równanie dynamiczne dowolnego punktu materialnego o masie m

i

należącego do

danego układu ma postać:

′

0

-m

i

p

i

– siła bezwładności punktu materialnego

P

i

– wypadkowa sił zewnętrznych

P’

i

– wypadkowa sił wewnętrznych

Takie równanie można ułożyć dla każdego punktu materialnego. Biorąc to pod uwagę można
sformułować zasadę d’Alemberta:

W czasie ruchu dowolnego układu punktów materialnych siły rzeczywiste działają na punkty
tego układu równoważą się w każdej chwili z odpowiednimi siłami bezwładności.

Zgodnie z tą zasadą siły rzeczywiste działające na punkty materialne rozpatrywanego układu
oraz siły bezwładności muszą spełniać ustalone w statyce ogólne równania równowagi. Także
suma wszystkich sił rzeczywistych i wszystkich sił bezwładności musi być równa zeru i suma
geometryczna ich momentów względem dowolnie obranego punktu O musi także być równa
zeru. Wynikają z tego następujące równania:

′

0

′

0

′

z

x

y

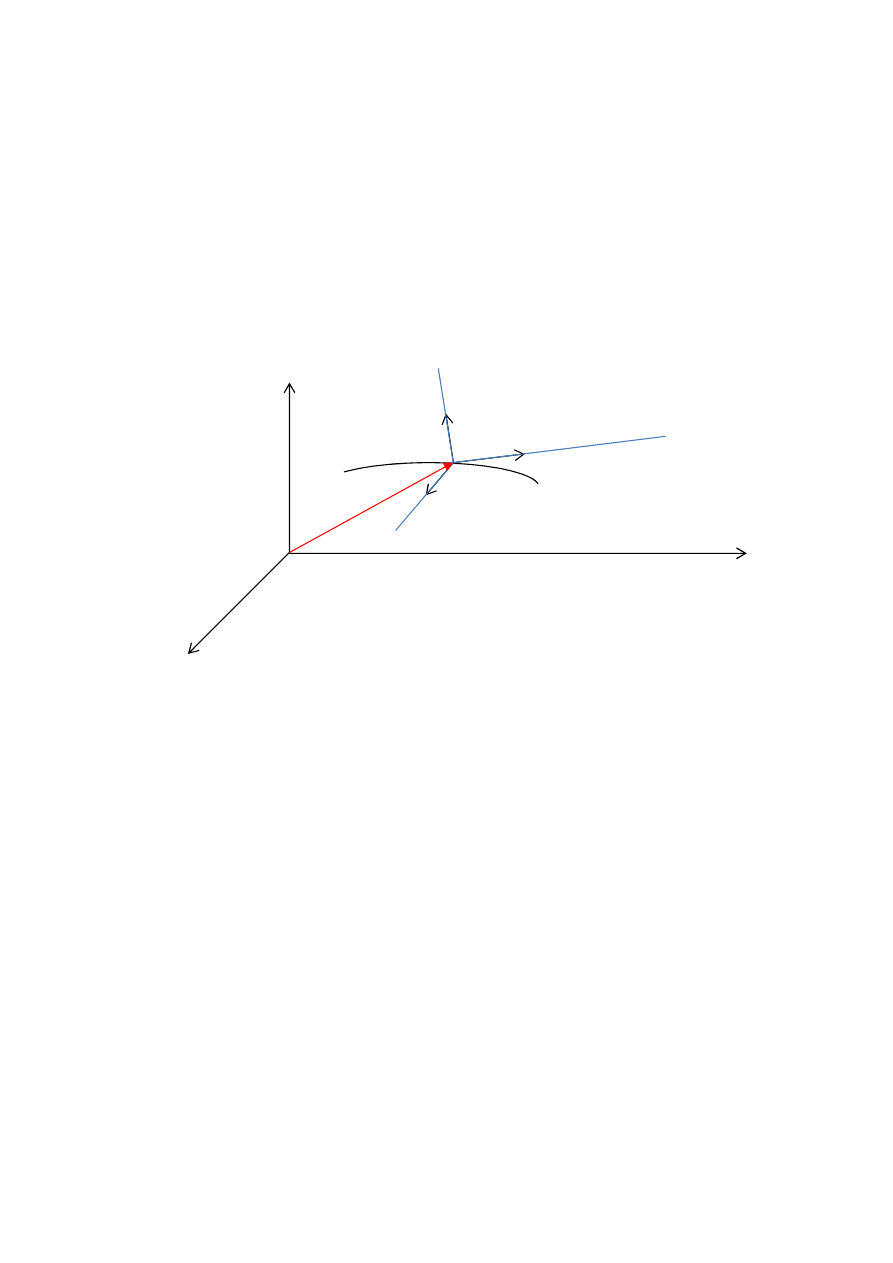
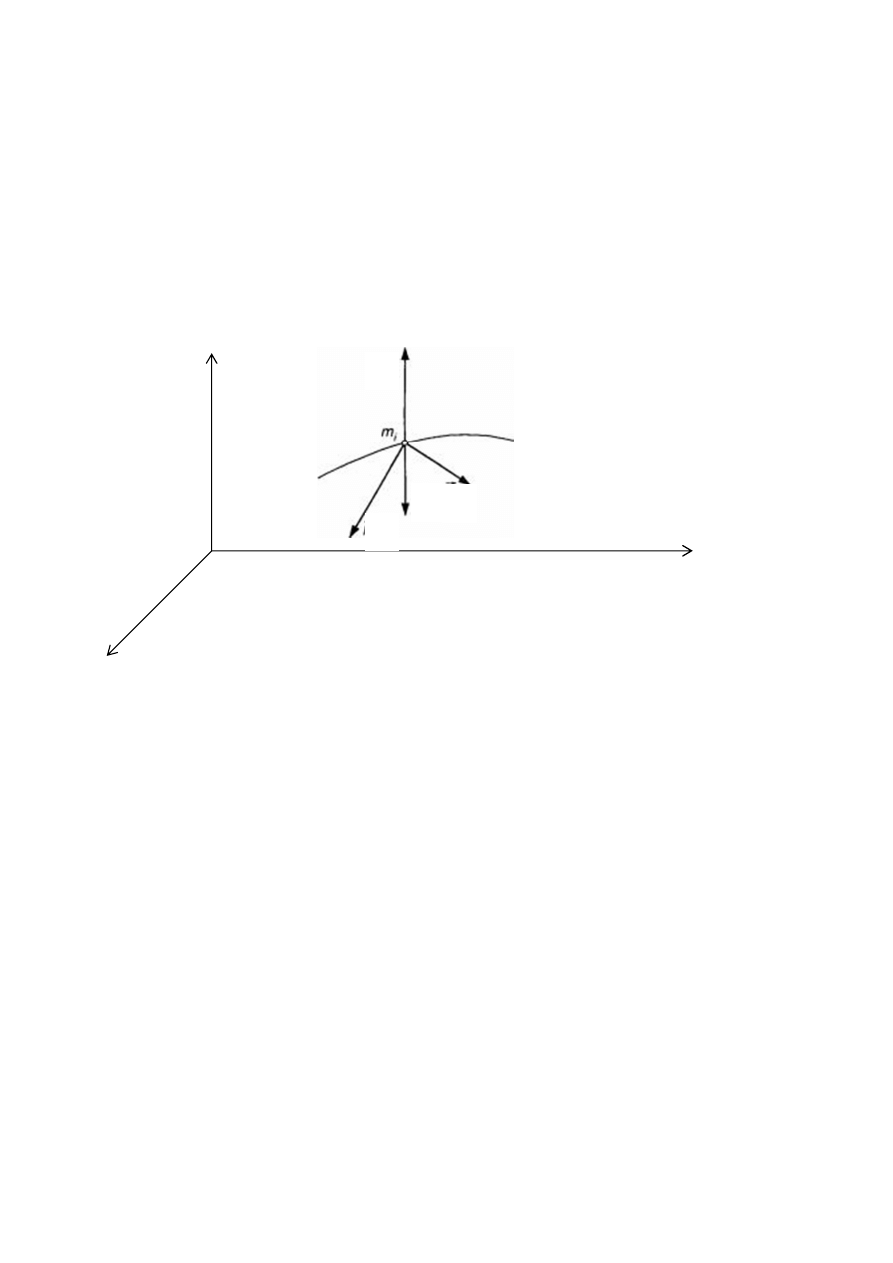
8. Na jakie składowe rozkłada się prędkość punktu, a na jakie przyspieszenie w
trójścianie Freneta.

Przyspieszenie rozkłada się w trójścianie Freneta na składową styczną, normalną i
binormalną. Natomiast prędkość na składową styczną.
przyspieszenie

∙

∙

∙

prędkość

! ! ∙

9. Określić położenie chwilowego środka obrotu dla koła toczącego się bez
poślizgu po prostej.

Na prędkość punktu A okręgu toczącego się bez poślizgu składają się dwa wektory

prędkości: pierwszy to wektor prędkości środka okręgu V

S

oraz drugi to wektor chwilowej

prędkości punktu A wynikający z toczenia się bez poślizgu a więc z ruchu obrotowego tego
okręgu. Dla lepszego zrozumienia na rysunku 107 naniesione zostały oba wektory prędkości
działające na punkt A okręgu.

styczna

normalna

binormalna

płaszczyzna prostująca

płaszczyzna ściśle styczna

płaszczyzna
normalna

"

#

$

z

x

y

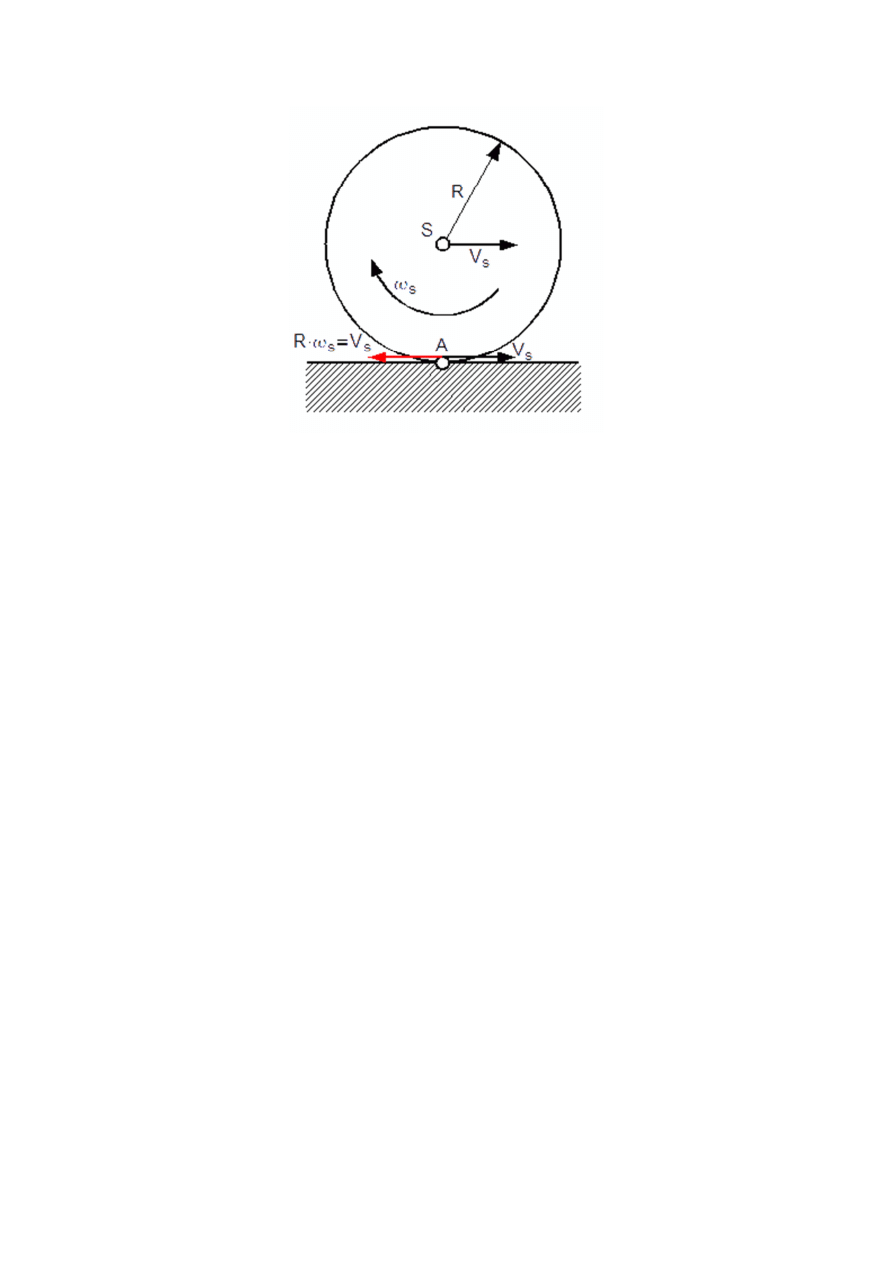
Rys. 4. Uzupełnienie rysunku 3 o wektory prędkości działające na punkt A okręgu toczącego
się bez poślizgu po płaskiej poziomej płaszczyźnie.

Wektor wypadkowy prędkości punktu A stycznego do płaszczyzny poziomej jest wektorem
zerowym. Oczywiście prędkość tego punktu jest prędkością chwilową, co oznacza że punkt A
jest punktem chwilowego środka obrotu i można go wykorzystać do obliczenia chwilowej
prędkości dowolnego punktu okręgu.