- 1 -

Liczby zespolone

Próby formalnego rozwiązywania równań kwadratowych o ujemnych wyróżnikach (delta <0)
doprowadziły matematyków w XVI w. do idei liczb zespolonych sprecyzowanych ostatecznie
pod koniec wieku XVIII. Stąd też by rozwiązać równanie kwadratowe o wyróżniku ujemnym
musimy się zapoznać z definicją i działaniami na liczbach zespolonych.

1. Elementarne pojęcie liczby zespolonej.

Liczbą zespoloną nazywamy zbiór liczb rzeczywistych w postaci z = x + iy, gdzie i

2

= -1.

x = Re(z) - część rzeczywista liczby zespolonej
y = Im(z) - część urojona liczby zespolonej

2. Działania na zbiorze liczb zespolonych.

2.1 Suma liczb zespolonych.

z + z' = (x+iy)

± (x'+iy') = x ± x' + i (y±y')

np. (2-i) + (1+3i) = 3+2i

2.2 Iloczyn liczb zespolonych.

(x+iy)(x'+iy')=xx'-yy' + i(xy'+x'y)

np. (1+i)

2

(1-3i)=(1+2i-1)(1-3i)=6+2i

2.3 Dzielenie liczb zespolonych.

Uwaga: aby podzielić dwie liczby zespolone należy pomnożyć je przez liczbę

sprzężoną (

yi

x

z

−

=

) z dzielną

)

(

yi

x

z

+

=

, wykorzystując zatem

=

z

z *

x

2

+ y

2

:

np.

i

i

i

i

i

i

i

i

2

1

2

)

4

2

(

2

)

3

3

1

(

1

1

)

1

)(

3

1

(

)

1

(

)

3

1

(

−

−

=

−

−

=

−

−

−

=

+

−

−

=

+

−

3.

Interpretacja geometryczna liczby zespolonej.

Dla każdej liczby zespolonej istnieje punkt o współrzędnych (x, y). Obrazem liczby
zespolonej jest wektor

zr = [x, y].

Modułem liczby zespolonej nazywamy długość wektora

zr .

2

2

y

x

z

+

=

Argumentem liczby zespolonej nazywamy kąt

ϕ

zawarty między wektorem

z

r

a osią X.

arg z=

ϕ

-

Π

≤

ϕ

≤

Π

Argumentem liczby z nazywamy

θ

=

ϕ

+ 2k

Π

k

∈

<-

∞

, ... , -2, -1, 0, 1, 2, ... ,

∞

>.

Arg z = arg z + 2k

Π

ϕ

cos

=

z

x

ϕ

cos

z

x

=

- 2 -

ϕ

sin

=

z

y

ϕ

sin

z

y

=

)

sin

(cos

sin

cos

ϕ

ϕ

ϕ

ϕ

⋅

+

=

+

=

i

z

z

i

z

z

4.

Potęga, wzory MOIVRE'a.

4.1

Własności modułu i argumentu liczby zespolonej.

2

1

2

1

z

z

z

z

⋅

=

⋅

2

1

2

1

z

z

z

z

=

(

)

2

1

2

1

arg

arg

arg

z

z

z

z

+

=

⋅

2

1

2

1

arg

arg

arg

z

z

z

z

−

=

)

sin

(cos

1

1

α

α

i

r

z

+

=

1

arg z

=

α

1

1

z

r

=

)

sin

(cos

2

2

β

β i

r

z

+

=

2

arg z

=

β

2

2

z

r

=

(

) (

)

[

]

(

)

(

)

(

)

β

α

β

α

β

α

β

α

β

α

β

α

+

+

+

⋅

=

+

+

−

⋅

=

⋅

sin

cos

cos

sin

sin

cos

sin

sin

cos

cos

2

1

2

1

2

1

i

r

r

i

r

r

z

z

( )

( )

(

)

ϕ

ϕ

n

i

n

z

z

n

n

sin

cos

+

=

ϕ

ϕ

ϕ

2

2

sin

cos

2

cos

−

=

ϕ

ϕ

ϕ

cos

sin

2

2

sin

=

5.

Pierwiastek liczby zespolonej.

Założenie:

( )

( )

(

)

Θ

+

Θ

=

n

i

n

z

z

n

n

sin

cos

C

z

n

=

(

)

(

)

[

]

Π

+

+

Π

+

=

k

i

k

C

2

sin

2

cos

ϕ

ϕ

δ

z=?

n

C

z

=

δ

=

n

z

n

z

δ

=

Π

+

=

Θ

k

n

2

ϕ

n

kΠ

+

=

Θ

2

ϕ

k = 0, 1, 2, ... , n-1.

























Π

+

+













Π

+

=

n

k

i

n

k

z

z

n

n

2

sin

2

cos

ϕ

ϕ

, dla k=0 pierwiastek główny.

6.

Postać wykładnicza liczby zespolonej (EULER'a).

ϕ

ϕ

sin

cos

i

e

iy

+

=

)

sin

(cos

ϕ

ϕ

i

e

e

e

C

x

iy

x

z

+

=

=

=

+

)

sin

(cos

ϕ

ϕ i

C

C

+

=

R

e

C

x

=

=

ϕ

i

e

C

C

=

Π

≤

≤

2

0

ϕ

- postać wykładnicza liczby zespolonej.

ϕ

ni

n

n

e

C

C

=

- 3 -

np.

Korzystając z postaci wykładniczej obliczyć

( )

( )

3

4

3

3

1

i

i

z

−

+

=

.

Zatem:

i

e

i

4

2

1

Π

=

+

oraz

i

e

i

6

2

3

Π

−

=

−

( )

























Π

−

+













Π

−

=

=

=

=

Π

−

Π

−

Π

Π

Π

3

2

sin

3

2

cos

2

1

2

1

8

4

2

2

3

4

3

4

3

3

3

i

e

e

e

e

e

z

i

i

i

i

i













































Π

+

Π

−

+





















Π

+

Π

−

=

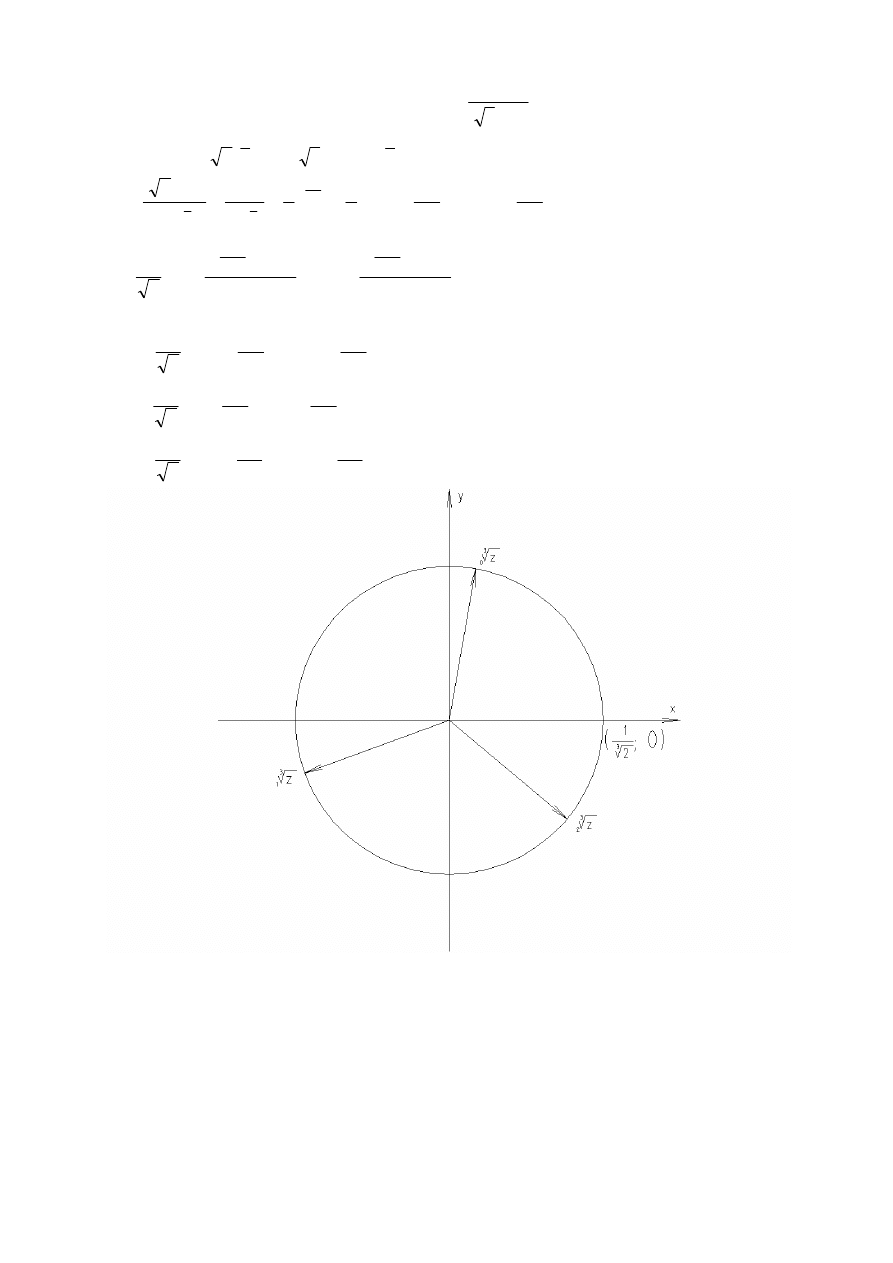
3

2

3

2

sin

3

2

3

2

cos

2

1

3

k

i

k

z

























Π

−

+













Π

−

=

=

9

2

sin

9

2

cos

2

1

3

0

i

z

k























 Π

+











 Π

=

=

9

4

sin

9

4

cos

2

1

3

1

i

z

k

























Π

−

+













Π

−

=

=

9

8

sin

9

8

cos

2

1

3

2

i

z

k

Graficzne rozwiązanie zadania.