Dr inż. Janusz Dębiński

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do

zadań

2. Część 2

2.1. Zadania 1

−

32

Aby przeprowadzić analizę kinematyczną płaskich układów prętowych musimy w pierwszej kolejności

sprawdzić warunek konieczny geometrycznej niezmienności. W przypadku ram płaskich musimy je zamie-
nić na płaski układ tarcz sztywnych, w których tarcze sztywne mają kształt zbliżony do kształtu pręta,
a podpory zbudowane są z odpowiedniego układu prętów podporowych. W konstrukcjach prętowych rozróż-
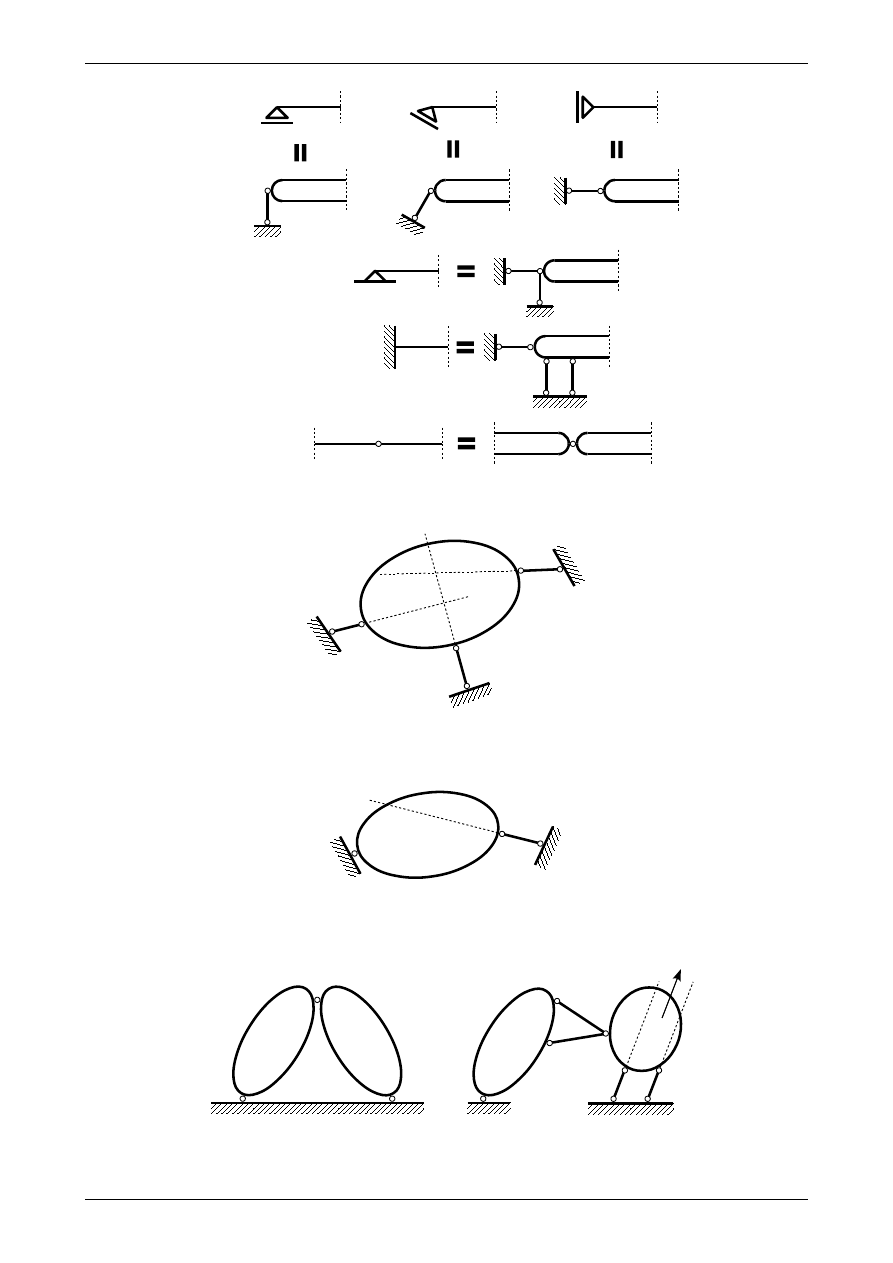
niamy następujące rodzaje podpór:

•

przegubowo-przesuwną

−

rysunek 2.1a

•

przegubowo-nieprzesuwną

−

rysunek 2.1b

•

teleskopową

−

rysunek 2.1c

•

utwierdzenie

−

rysunek 2.1d

•

przegub rzeczywisty nazywany krótko przegubem

−

rysunek 2.1e.

Na rysunku 2.1 widzimy także układy prętów podporowych im odpowiadające. Każdy pręt podporowy od-
biera tarczy sztywnej jeden stopień swobody. Z kolei przegub rzeczywisty odbiera tarczy sztywnej dwa
stopnie swobody. Aby płaski układ tarcz sztywnych był geometrycznie niezmienny oraz statycznie wyzna-
czalny, musi spełniać następujący warunek

3⋅t= p,

(2.1)

gdzie t oznacza liczbę tarcz sztywnych, a p oznacza liczbę stopni swobody odbieranych przez pręty podpo-
rowe i przeguby.

Oprócz warunku koniecznego geometrycznej niezmienności płaski układ tarcz sztywnych musi spełniać

warunki dostateczne geometrycznej niezmienności. Mają one formę:

•

tarcza sztywna połączona z tarczą podporową za pomocą trzech prętów podporowych

−

kierunki

prętów podporowych nie mogą się przecinać w jednym punkcie

−

rysunek 2.2

•

tarcza sztywna połączona z tarczą podporową za pomocą przegubu i pręta podporowego

−

przegub

nie może leżeć na kierunku pręta podporowego

−

rysunek 2.3

•

układ trójprzegubowy

−

przeguby nie mogą leżeć na jednej prostej

−

rysunek 2.4.

Na rysunku 2.4b musimy zwrócić uwagę na dwa typy przegubów złożone z dwóch prętów podporowych:

•

przegub fikcyjny B

−

znajduje się on w punkcie przecięcia kierunków tworzących go prętów podpo-

rowych

•

przegub niewłaściwy C

−

znajduje się w nieskończoności na prostej równoległej do kierunków two-

rzących go prętów podporowych.

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

2

a)

b)

c)

d)

Rys. 2.1. Podpory płaskich układów prętowych. a) przegubowo-przesuwna, b) przegubowo-nieprzesuwna,

c) utwierdzenie, d) przegub

2

1

3

I

TP

TP

TP

Rys. 2.2. Geometrycznie niezmienna tarcza sztywna połączona z tarczą podporową za pomocą trzech prętów

podporowych

1

A

I

TP

T

P

Rys. 2.3. Geometrycznie niezmienna tarcza sztywna połączona z tarczą podporową za pomocą przegubu oraz pręta

podporowego

A

B

C

II

A

B

I

II

C

∞

a)

b)

1

2

3

4

TP

TP

TP

I

Rys. 2.4. Geometrycznie niezmienne układy trójprzegubowe. a) z trzema przegubami rzeczywistymi, b) z przegubem

rzeczywistym A, fikcyjnym B oraz niewłaściwym C

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

3

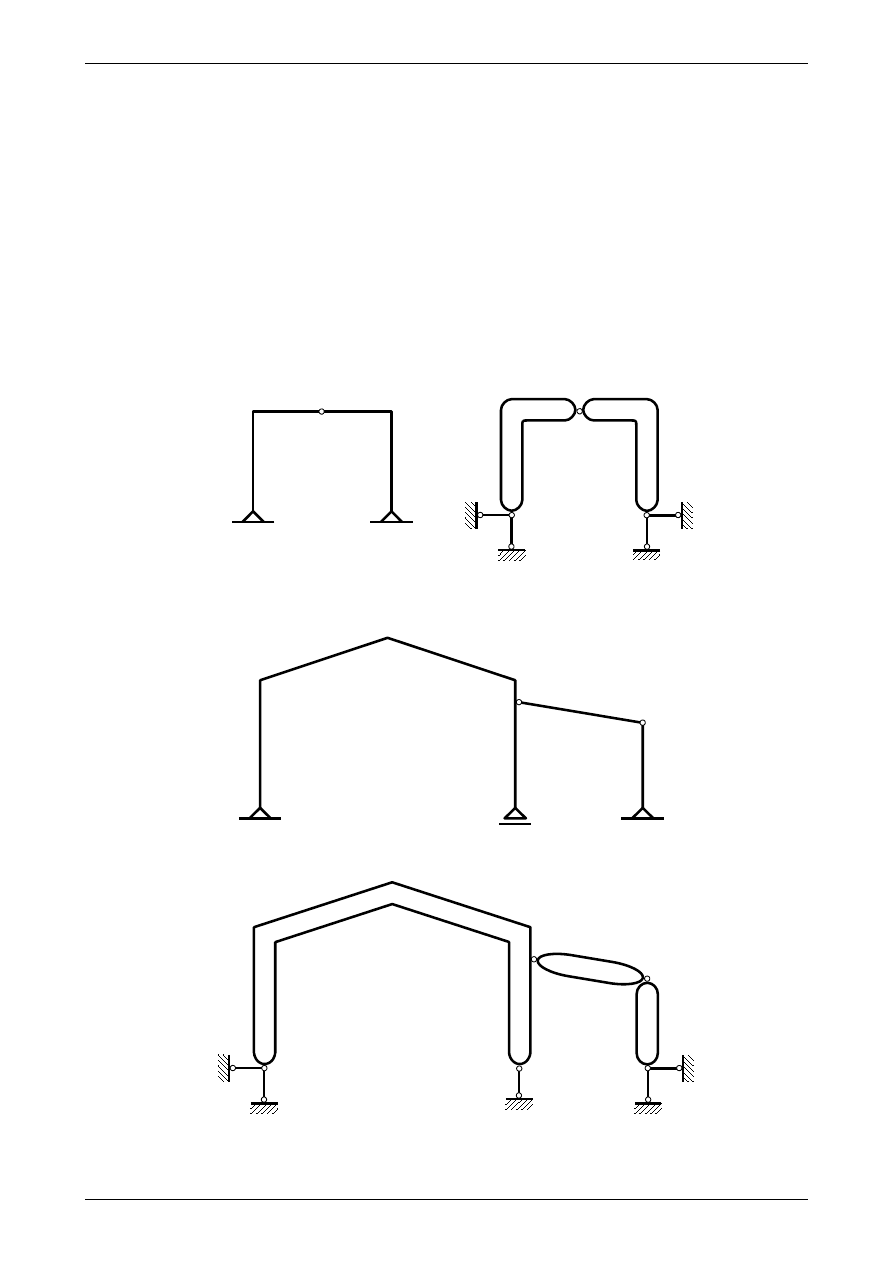
Na rysunku 2.5 możemy zobaczyć ramę płaską zamienioną na płaski układ tarcz sztywnych. Jak łatwo

zauważyć jest to układ trójprzegubowy, w którym przeguby A, B oraz C nie leżą na jednej prostej. Wobec
tego rama ta jest geometrycznie niezmienna i statycznie wyznaczalna. Na rysunku 2.6a widzimy ramę płas-
ką, natomiast na rysunku 2.6b możemy zobaczyć odpowiadający jej płaski układ tarcz sztywnych. Warunek
konieczny geometrycznej niezmienności ma postać

3⋅3=5⋅12⋅2.

(2.2)

Tarcza sztywna numer I połączona jest z tarczą podporową za pomocą trzech prętów podporowych numer 1,
2 oraz 3, których kierunki nie przecinają się w jednym punkcie. Wobec tego jest ona geometrycznie nie-
zmienna i stanowi tarczę podporową dla tarcz sztywnych numer II i III. Pręty podporowe numer 4 i 5 tworzą
przegub fikcyjny C. Tarcze sztywne numer II i III tworzą układ trójprzegubowy z przegubami A, B oraz C.
Przeguby te nie leżą na jednej prostej, więc tarcze sztywne numer II oraz III są także geometrycznie nie-
zmienne. Ostatecznie rama płaska jest układem prętowym geometrycznie niezmiennym oraz statycznie
wyznaczalnym.

1

2

3

4

A

B

C

D

E

C

I

II

A

E

a)

b)

Rys. 2.5. Geometrycznie niezmienna rama trójprzegubowa. a) rama płaska, b) płaski układ tarcz sztywnych

A

B

I

II

III

1

2

4

5

3

a)

b)

C

Rys. 2.6. Geometrycznie niezmienna rama płaska. a) rama płaska, b) płaski układ tarcz sztywnych

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

4

2.2. Zadania 33

−

48

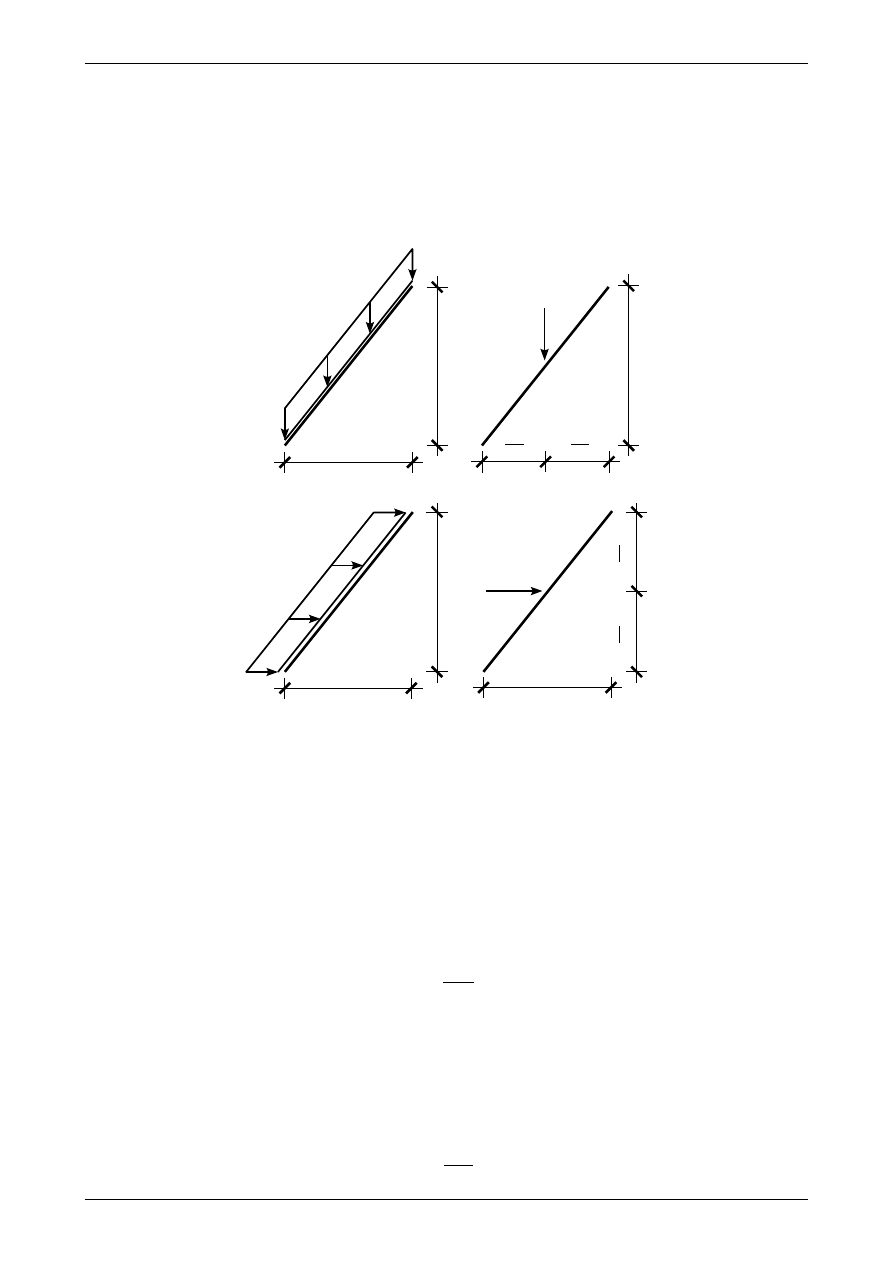
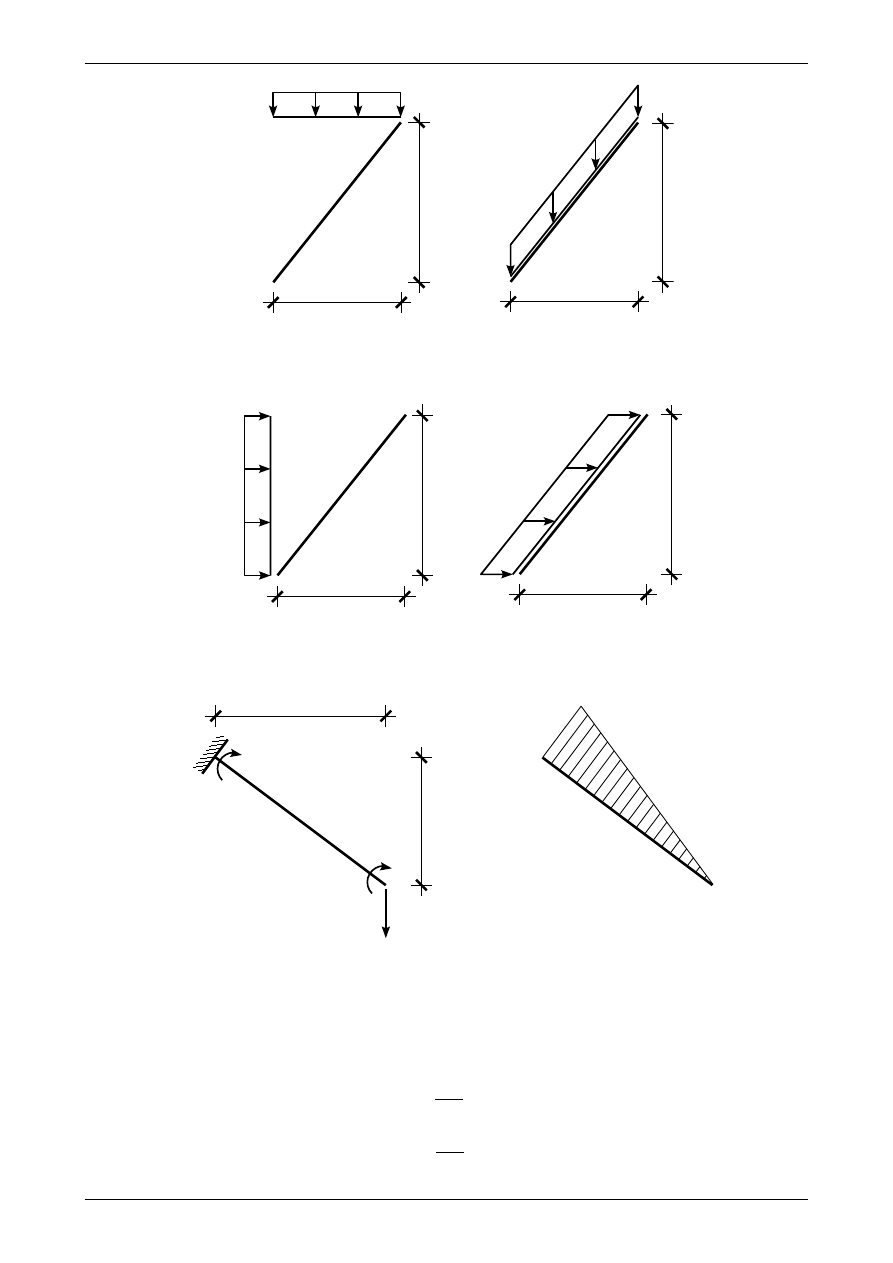
Na rysunku 2.7 możemy zobaczyć pionowe i poziome obciążenia ciągłe równomiernie rozłożone na dłu-

gości pręta ukośnego oraz wartości i położenie sił wypadkowych z tych obciążeń. Jak widać siła wypadkowa
ma zawsze zwrot zgodny z kierunkiem obciążenia ciągłego. Na rysunku 2.8 widzimy pionowe i poziome
obciążenia ciągłe równomiernie rozłożone na długości rzutu pręta ukośnego oraz wartości i położenie sił
wypadkowych z tych obciążeń. Także w tym przypadku siła wypadkowa ma także zwrot zgodny z kierun-
kiem obciążenia ciągłego.

p

L

X

L

Y

- L

-

p∙L

L

Y

- L

-

p

L

X

L

Y

- L

-

- L

-

L

X

p∙L

L

X

2

L

X

2

L

Y

2

L

Y

2

a)

b)

Rys. 2.7. Obciążenia ciągłe równomiernie rozłożone na długości pręta ukośnego. a) obciążenie pionowe, b) obciążenie

poziome

2.3. Zadania 49

−

56

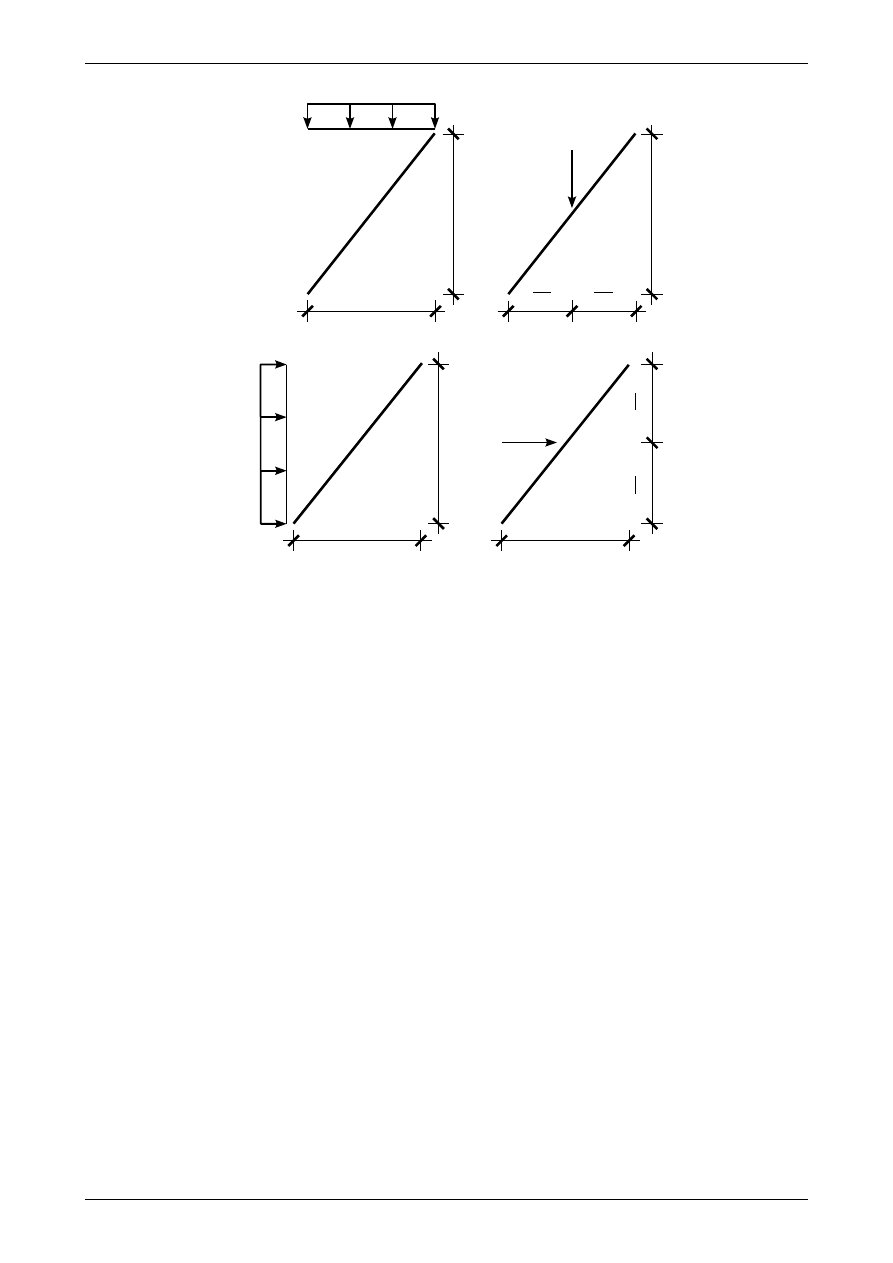
Na rysunku 2.9a widzimy pionowe obciążenie ciągłe równomiernie rozłożone na długości rzutu pręta

ukośnego r, natomiast na rysunku 2.9b możemy zobaczyć pionowe obciążenie ciągłe równomiernie roz-
łożone na długości pręta ukośnego p'. Aby oba te obciążenia były statycznie równoważne, siły wypadkowe
z obu muszą mieć te same wartości, czyli

r⋅L

X

=

p '⋅L ,

(2.3)

p' =

r⋅L

X

L

.

(2.4)

Na rysunku 2.10a możemy zobaczyć poziome obciążenie ciągłe równomiernie rozłożone na długości rzutu
pręta ukośnego r, natomiast na rysunku 2.10b widzimy poziome obciążenie ciągłe równomiernie rozłożone
na długości pręta ukośnego p'. Aby oba te obciążenia były statycznie równoważne, siły wypadkowe z obu
muszą mieć te same wartości, czyli

r⋅L

Y

=

p'⋅L ,

(2.5)

p' =

r⋅L

Y

L

.

(2.6)

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

5

r

L

X

L

Y

- L

-

L

Y

- L

-

r

L

X

L

Y

- L

-

- L

-

L

X

r∙L

X

L

X

2

L

Y

2

L

X

2

L

Y

2

r∙L

Y

a)

b)

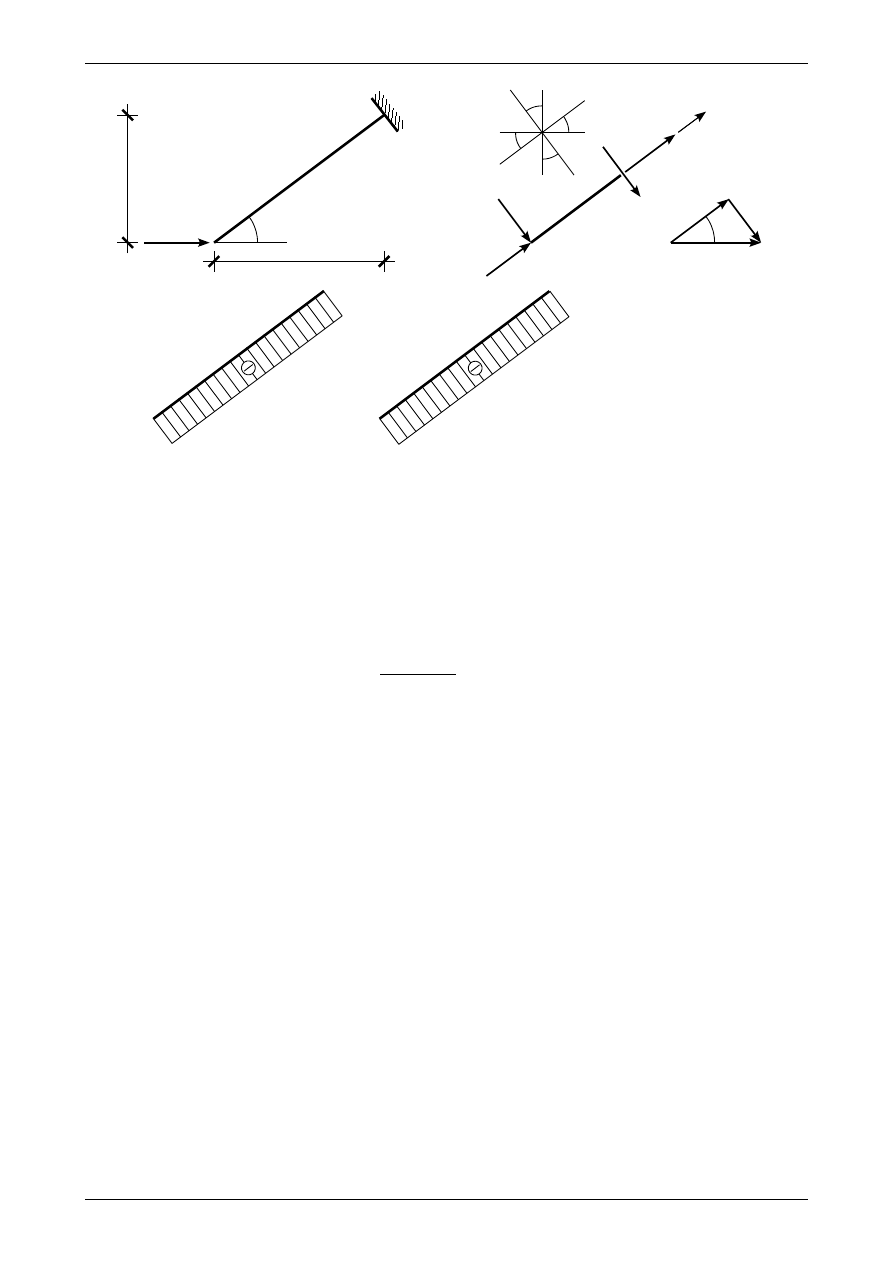
Rys. 2.8. Obciążenia ciągłe równomiernie rozłożone na długości rzutu pręta ukośnego. a) obciążenie pionowe,

b) obciążenie poziome

2.4. Zadania 57

−

120

Aby wyznaczyć wykresy sił normalnej i poprzecznej oraz momentu zginającego w pręcie wspornikowym

nie musimy wyznaczać prawidłowych wartości i zwrotów reakcji w utwierdzeniu. Wystarczy tylko rozpa-
trzyć równowagę odciętej, wolnej części tego pręta. Przy wyznaczaniu wartości sił normalnej i poprzecznej
oraz momentu zginającego stosujemy następujące zasady:

•

siły mające ten sam zwrot co dodatnie siły normalna i poprzeczna zapisujemy z minusem

•

siły mające zwrot przeciwny do dodatnich sił normalnej i poprzecznej zapisujemy z plusem

•

siły kręcące względem danego punktu w tę samą stronę co dodatni moment zginający zapisujemy
z minusem

•

siły kręcące względem danego punktu w przeciwną stronę co dodatni moment zginający zapisujemy
z plusem.

Na rysunku 2.11a możemy zobaczyć pręt wspornikowy obciążony siłą o wartości 20,0 kN na końcu.

Ponieważ w pręcie nie działa obciążenie ciągłe, wykres momentu będzie funkcją liniową. Aby ją jedno -
znacznie narysować musimy wyznaczyć jej wartości na obu końcach pręta wspornikowego. Na rysunku
2.11a możemy zobaczyć założone, dodatnie, momenty zginające w punktach A i B. Momenty te rozciągają
dolną część pręta wspornikowego. Zakrywając pręt i zostawiając widoczny sam punkt A

M

A

=

0,0 kN⋅m .

(2.7)

Zakrywając tylko utwierdzenie

M

B

=−

20,0⋅6,0=−120,0 kN⋅m .

(2.8)

Moment ten jest ujemny, czyli rozciąga on w rzeczywistości górną część pręta wspornikowego. Wykres
momentu zginającego w pręcie wspornikowym widzimy na rysunku 2.11b.

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

6

r

L

X

L

Y

- L

-

a)

p`

L

X

L

Y

- L

-

b)

Rys. 2.9. Statycznie równoważne pionowe obciążenia ciągłe. a) obciążenie ciągłe równomiernie rozłożone na długości

rzutu pręta ukośnego, b) obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego

r

L

X

L

Y

- L

-

a)

p`

L

X

L

Y

- L

-

b)

Rys. 2.10. Statycznie równoważne poziome obciążenia ciągłe. a) obciążenie ciągłe równomiernie rozłożone na długości

rzutu pręta ukośnego, b) obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego

6,0

4,

50

[m]

- 7,5

0 -

20,0 kN

M(x

)

[kN

∙m

]

A

B

M

A

M

B

12

0,

0

0,

0

a)

b)

Rys. 2.11. Pręt wspornikowy obciążony na końcu siłą o wartości 20,0 kN. a) schemat pręta, b) wykres momentu

zginającego w tym pręcie

Na rysunku 2.12a możemy zobaczyć pręt wspornikowy obciążony siłą o wartości 20,0 kN na końcu.

Ponieważ w pręcie tym nie działa żadne obciążenie ciągłe wykresy sił normalnej oraz poprzecznej będą
funkcjami stałymi. Wartości funkcji trygonometrycznych kąta

α

sin



α



=

4,50
7,50

=

0,60 ;

(2.9)

cos



α



=

6,0

7,50

=

0,80 .

(2.10)

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

7

6,0

4,

5

0

[m]

- 7

,50

-

20,0 kN

N(

x)

[kN

]

16

,0

- x

-

N(

x)

X

α

a)

b)

c)

α

α

α

α

20,0 kN

α

12

,0

T(

x)

[kN

]

T(

x)

16

,0

kN

12

,0

kN

12

,0

kN

16

,0

kN

Rys. 2.12. Pręt wspornikowy obciążony na końcu siłą o wartości 20,0 kN. a) pręt wspornikowy, b) odcięta część pręta,

c) wykresy sił normalnej oraz poprzecznej w pręcie wspornikowym

Zgodnie z rysunkiem 2.12b składowe siły 20,0 kN na kierunki sił normalnej i poprzecznej

P

N

=

20,0⋅cos



α



=

20,0⋅0,80=16,0 kN ,

(2.11)

P

T

=

20,0⋅sin



α



=

20,0⋅0,60=12,0 kN .

(2.12)

Jak łatwo sprawdzić



16,0

2



12,0

2

=

20,0 kN .

(2.13)

Siły składowe możemy zobaczyć na rysunku 2.12b. Ostatecznie otrzymamy

N



x



=−

16,0 kN ,

(2.14)

T



x



=−

12,0 kN .

(2.15)

Wykresy sił normalnej i poprzecznej widzimy na rysunku 2.12c.

2.5. Zadania 121

−

320

Aby wyznaczyć wykres momentu zginającego w ramie wspornikowej nie musimy wyznaczać prawi -

dłowych wartości oraz zwrotów reakcji w utwierdzeniu. Wystarczy tylko rozpatrzyć równowagę odciętej,
wolnej części ramy wspornikowej. Przy wyznaczaniu wartości momentu zginającego stosujemy następujące
zasady:

•

siły kręcące względem danego punktu w tę samą stronę co dodatni moment zginający zapisujemy
z minusem

•

siły kręcące względem danego punktu w przeciwną stronę co dodatni moment zginający zapisujemy
z plusem.

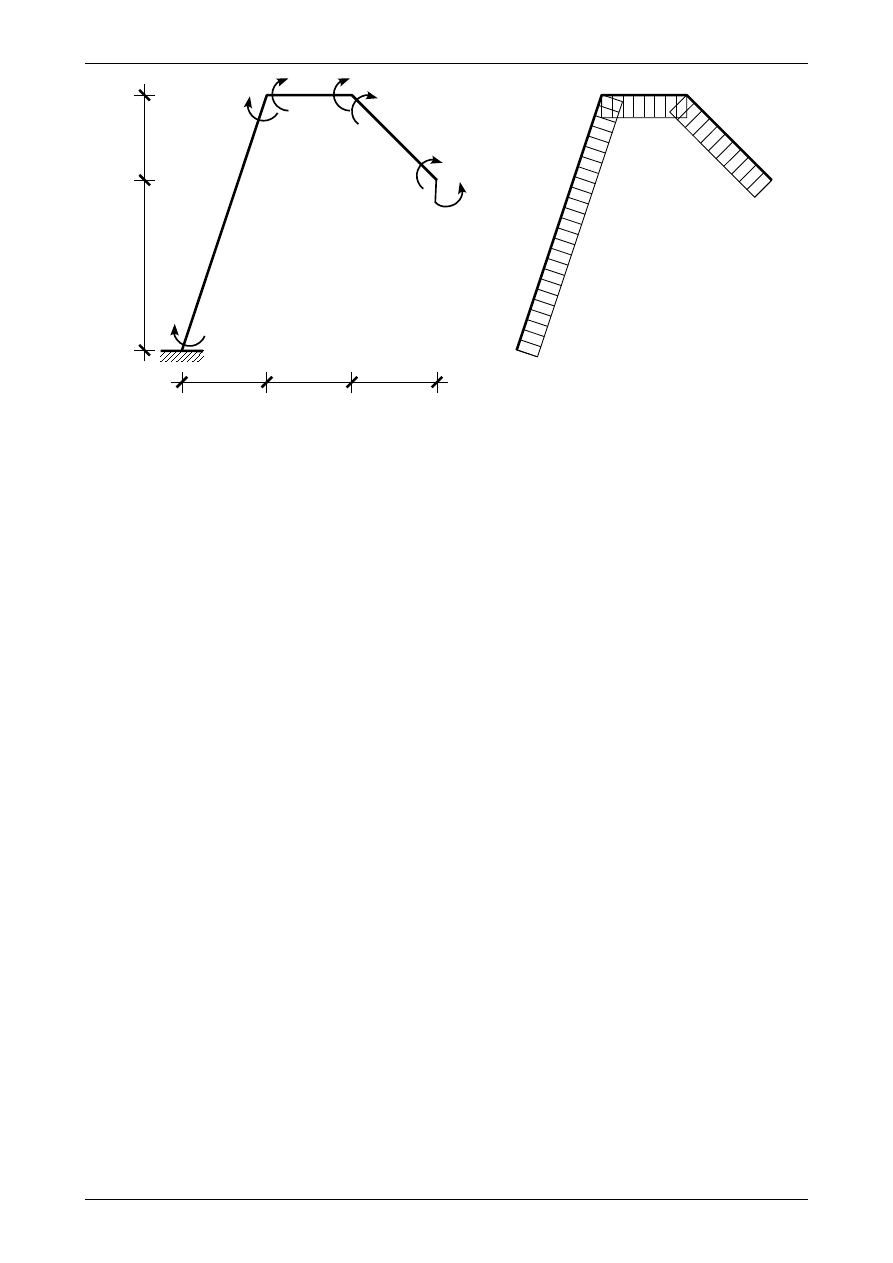
Na rysunku 2.13a możemy zobaczyć ramę wspornikową obciążoną momentem skupionym na końcu.

Ponieważ w żadnym przedziale nie działa obciążenie ciągłe, wykres momentu w każdym z nich będzie funk-
cją liniową. Aby jednoznacznie narysować funkcję liniową, musimy wyznaczyć jej wartości na obu końcach
przedziału. Na rysunku 2.13a widzimy założone, dodatnie, momenty zginające działające na końcach prze-
działów. Momenty te rozciągają dolną część prętów. Zakrywając odpowiednie części pręta wspornikowego
otrzymamy

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

8

18,0 kN∙m

3,0

[m]

6,

0

M(x)

[kN∙m]

3,

0

3,0

3,0

A

B

C

D

M

A

M

B

(AB)

M

B

(BC)

M

C

(BC)

M

C

(CD)

M

D

18,0

18

,0

18

,0

Rys. 2.13. Rama wspornikowa obciążona momentem skupionym na końcu. a) dodatnie momenty zginające na końcach

przedziałów, b) wykres momentu zginającego

M

A

=

M

B



AB 

=

M

B



BC 

=

M

C



BC 

=

M

C



CD 

=

M

D

=

18,0 kN⋅m .

(2.16)

Wykres momentu zginającego widzimy na rysunku 2.13b.

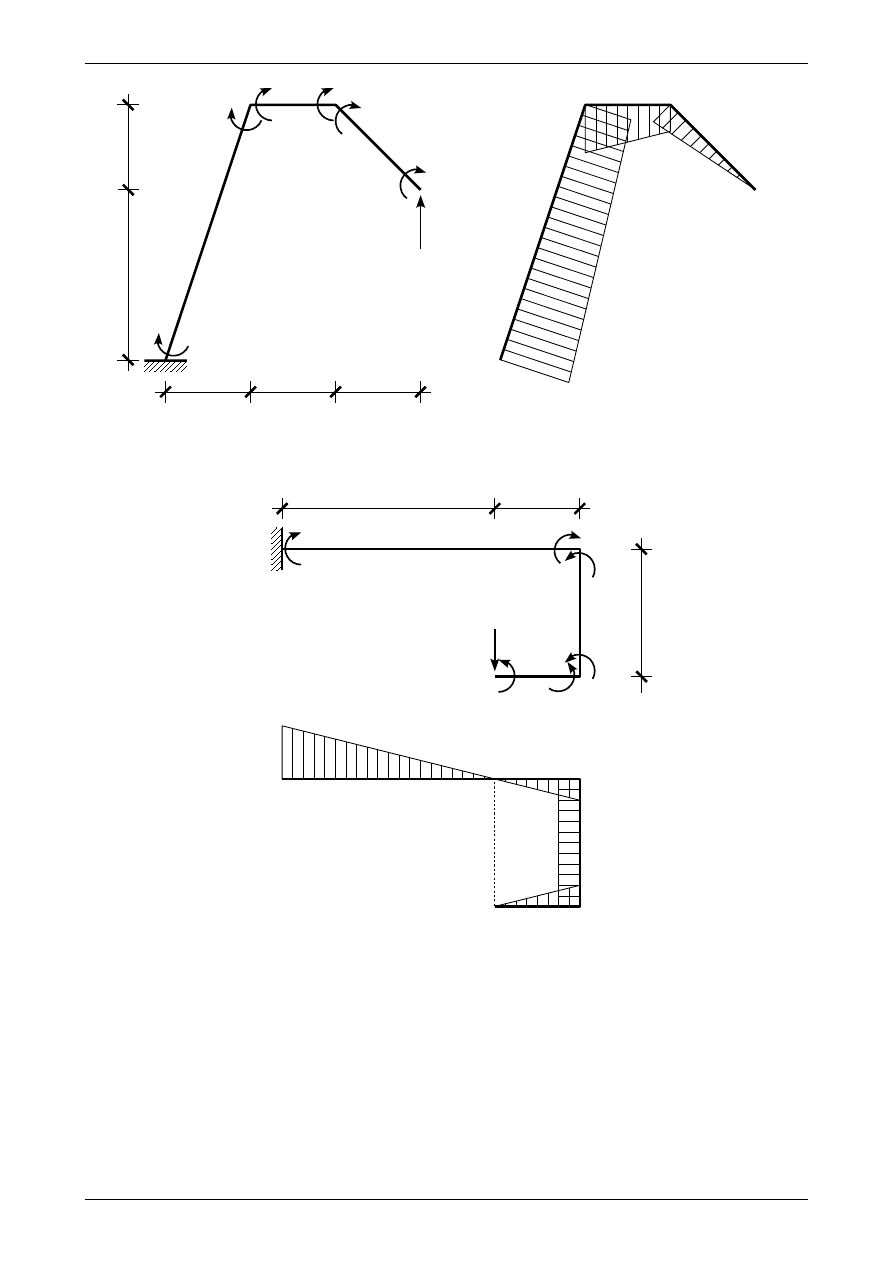
Na rysunku 2.14a możemy zobaczyć ramę płaską obciążoną siłą o wartości 20,0 kN na końcu. Zakrywa-

jąc prawie cały pręt wspornikowy moment zginający w punkcie A

M

A

=

0,0 kN⋅m .

(2.17)

Zakrywając całe przedziały BC i CD

M

B



AB 

=

20,0⋅3,0=60,0 kN⋅m .

(2.18)

Zakrywając cały przedział CD oraz prawie cały przedział BC z wyjątkiem punktu B

M

B



BC 

=

20,0⋅3,0=60,0 kN⋅m .

(2.19)

Zakrywając cały przedział CD

M

C



BC 

=

20,0⋅6,0=120,0 kN⋅m .

(2.20)

Zakrywając prawie cały przedział CD bez punktu C

M

C



CD

=

20,0⋅6,0=120,0 kN⋅m .

(2.21)

Zakrywając tylko utwierdzenie

M

D

=

20,0⋅9,0=180,0 kN⋅m .

(2.22)

Wykres momentu zginającego w ramie wspornikowej możemy zobaczyć na rysunku 2.14b.

W przypadku zadań z prętami pionowymi jako dodanie momenty zginające przyjmiemy te, które rozcią-

gają prawą stronę pręta pionowego. Na rysunku 2.15a widzimy ramę wspornikową obciążoną siłą o wartości
20,0 kN w punkcie A. Zakrywając prawie cały pręt wspornikowy

M

A

=

0,0 kN⋅m .

(2.23)

Zakrywając całe przedziały BC i CD

M

B



AB 

=−

20,0⋅2,0=−40,0 kN⋅m .

(2.24)

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

9

3,0

[m]

6,

0

20,0 kN

3,

0

3,0

3,0

A

B

C

D

M

A

M

B

(AB)

M

B

(BC)

M

C

(BC)

M

C

(CD)

M

D

0,

0

60

,0

120,0

60

,0

120,0

180,0

M(x)

[kN∙m]

Rys. 2.14. Rama wspornikowa obciążona siłą o wartości 20,0 kN na końcu. a) dodatnie momenty zginające na końcach

przedziałów, b) wykres momentu zginającego

5,0

[m]

2,0

3,

0

M

D

A

20,0 kN

B

C

D

M

C

(CD)

M

A

M

C

(BC)

M

B

(BC)

M

B

(AB)

a)

b)

M(x)

[kN∙m]

0

,0

40

,0

4

0,

0

40

,0

10

0

,0

0,

0

Rys. 2.15. Rama wspornikowa obciążona siłą o wartości 20,0 kN w punkcie A. a) dodatnie momenty zginające na

końcach przedziałów, b) wykres momentu zginającego

Zakrywając przedział CD oraz prawie cały przedział BC bez punktu B

M

B



BC 

=−

20,0⋅2,0=−40,0 kN⋅m .

(2.25)

Zakrywając cały przedział CD

M

C



BC 

=−

20,0⋅2,0=−40,0 kN⋅m .

(2.26)

Zakrywając prawie cały przedział CD bez punktu C

Dr inż. Janusz Dębiński

BNS-I

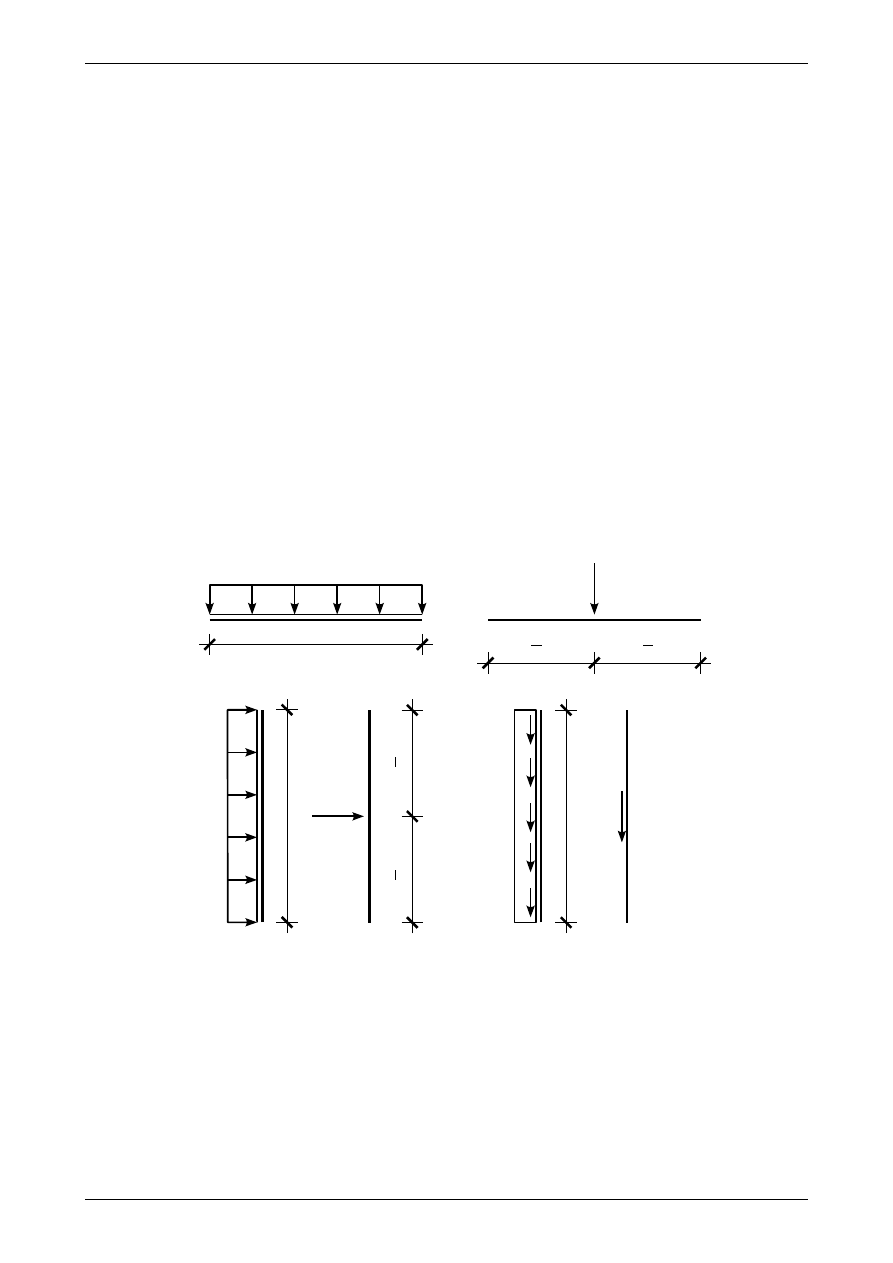
Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

10

M

C

(

CD )

=

20,0⋅2,0=40,0 kN⋅m .

(2.27)

Zakrywając utwierdzenie D

M

D

=−

20,0⋅5,0=−100,0 kN⋅m .

(2.28)

Wykres momentu zginającego w ramie wspornikowej możemy zobaczyć na rysunku 2.15b.

2.6. Zadania 321

−

400

Aby wyznaczyć moment różnych obciążeń pręta względem punktu A musimy wykorzystać zasady poda-

ne w punkcie 1.4 przewodnika dla części 1 pytań sprawdzających z mechaniki teoretycznej. Wszystkie
obciążenia ciągłe sprowadzamy do sił wypadkowych. Siły wypadkowe z obciążeń ciągłych części ukośnej
pręta wyznaczamy według zasad podanych w punkcie 2.2. Siły wypadkowe z obciążeń ciągłych działających
w prętach poziomych i pionowych możemy zobaczyć na rysunku 2.16. W przypadku obciążenia ciągłego
równomiernie rozłożonego prostopadłego do osi pręta widocznego na rysunkach 2.16a oraz 2.16b siła
wypadkowa ma ten sam zwrot co to obciążenie i znajduje się zawsze w połowie długości tego obciążenia.
Siła wypadkowa z obciążenia ciągłego równomiernie rozłożonego równoległego do osi pręta, widoczna jest
na rysunku 2.16c, przyłożona jest w dowolnym punkcie przedziału, w którym działa obciążenie ciągłe i po-
siada ten sam zwrot, co to obciążenie. Przy wyznaczaniu wartości momentu względem punktu A stosujemy
następujące zasady:

•

siły kręcące względem punktu A zgodnie z ruchem wskazówek zegara zapisujemy z minusem

•

siły kręcące względem punktu A przeciwnie do ruchu wskazówek zegara zapisujemy z plusem.

L

q

q∙L

L

2

L

2

a)

L

h

h

∙L

L

q

q∙

L

L

2

L

2

b)

c)

Rys. 2.16. Obciążenia ciągłe. a), b) obciążenie ciągłe równomiernie rozłożone prostopadłe do osi pręta, c) obciążenie

ciągłe równomiernie rozłożone równoległe do osi pręta

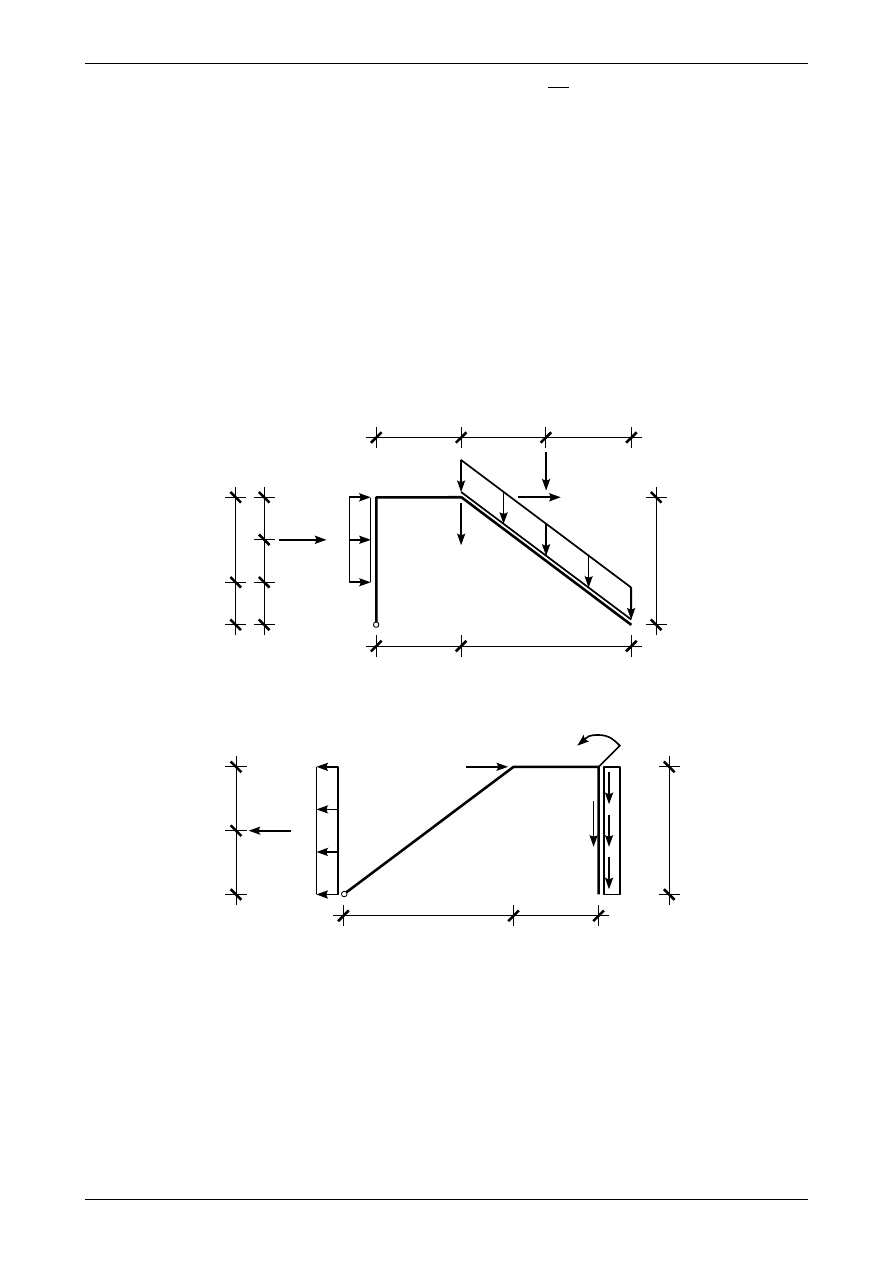
Na rysunku 2.17 możemy zobaczyć obciążony pręt. Siła wypadkowa

W

1

=

11,0⋅2,0 .

(2.29)

Siła wypadkowa

W

2

=

13,0⋅5,0.

(2.30)

Ostatecznie moment wszystkich sił działających na pręt względem punktu A

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

11

M

A

=

11,0⋅2,0⋅2,0+14,0⋅2,0+11,0⋅3,0+13,0⋅5,0⋅

(

2,0+

4,0

2

)

4,0=365,0 kN⋅m .

(2.31)

Na rysunku 2.18 możemy zobaczyć obciążony pręt. Siła wypadkowa

W

1

=

15,0⋅3,0.

(2.32)

Siła wypadkowa

W

2

=

9,0⋅3,0.

(2.33)

Ostatecznie moment wszystkich sił działających na pręt względem punktu A

M

A

=−

9,0⋅3,0⋅1,511,0⋅3,0−7,015,0⋅3,0⋅6,0=255,5 kN⋅m .

(2.34)

Musimy zwrócić uwagę, że momentu obrotowego o wartości 7,0 kN∙m nie wolno mnożyć przez odległość
punktu jego przyłożenia od punktu A. Moment obrotowy jest równoważny parze sił, a moment pary sił
względem dowolnego punktu na płaszczyźnie jest wielkością stałą.

[m]

1,

0

1,

0

1,

0

2,0

4,0

11

,0

k

N

/m

- 5,0

-

14,0 kN

A

3,

0

13,0

kN

/m

11,0 kN

2,

0

1,

0

W

1

W

2

2,0

2,0

2,0

Rys. 2.17. Obciążony pręt

[m]

3,

0

2,0

4,0

9,

0

k

N

/m

- 5

,0

-

11,0 kN

7,0 kN∙m

15

,0

k

N

/m

W

1

1,

5

1,

5

W

2

A

Rys. 2.18. Obciążony pręt

2.7. Zadania 400

−

418

Warunek konieczny geometrycznej niezmienności kratownicy płaskiej ma następującą postać

2⋅w= pr ,

(2.35)

gdzie w oznacza liczbę węzłów (przegubów) kratownicy, p oznacza liczbę prętów kratownicy, a r oznacza
liczbę stopni swobody odbieraną przez podpory. Oprócz warunku (2.35) kratownica płaska musi spełniać
także warunki dostateczne geometrycznej niezmienności. Jeżeli kratownica jest zbudowana z trójkątów,
w wierzchołkach których znajdują się węzły, oraz dwa sąsiednie trójkąty posiadają wspólny jeden bok, to

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

12

kratownicę taką możemy traktować jako tarczę sztywną. Następnie zamieniamy podpory na układ prętów
podporowych zgodnie z punktem 1.2 części pierwszej przewodnika do pytań sprawdzających z mechaniki
teoretycznej. Dalej przeprowadzamy analizę kinematyczną tak jak dla płaskiego układu tarcz sztywnych.

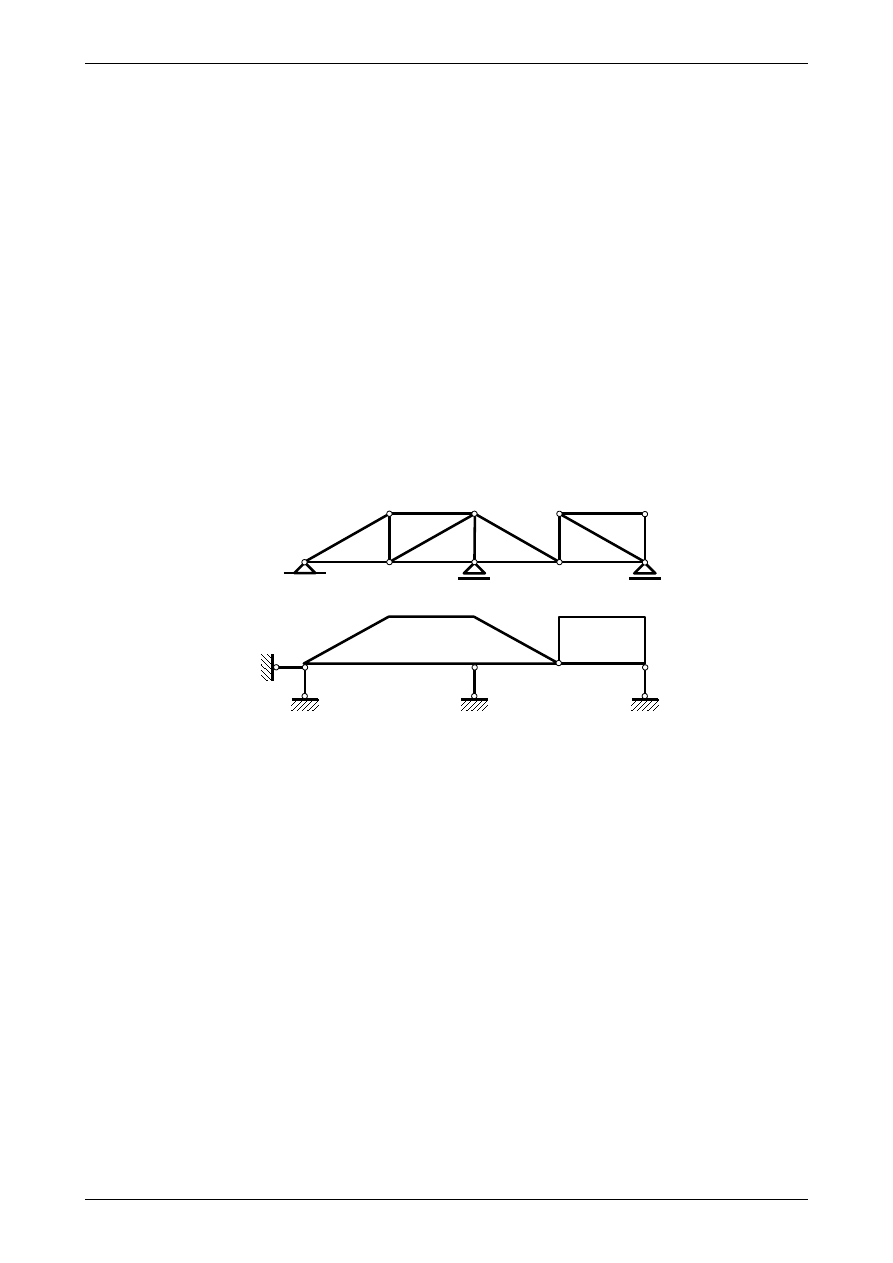
Na rysunku 2.19a widzimy kratownicę płaską. Warunek konieczny geometrycznej niezmienności ma na-

stępującą postać

2⋅9=144.

(2.36)

Warunek ten jest spełniony. W kratownicy płaskiej możemy wyodrębnić dwie tarcze sztywne, ponieważ te
części zbudowane są trójkątów, które w wierzchołkach mają węzły oraz posiadają po jednym wspólnym
boku. Tarcze te widzimy na rysunku 2.19b. Na rysunku tym możemy zobaczyć także podpory zamienione na
układy prętów podporowych. Warunek konieczny dla płaskiego układu tarcz sztywnych

2⋅2=4⋅11⋅2.

(2.37)

Tarcza sztywna numer I jest połączona z tarczą podporową za pomocą trzech prętów podporowych numer 1,
2 i 3, których kierunki nie przecinają się w jednym punkcie. Jest więc ona geometrycznie niezmienna i sta-
nowi tarczę podporową dla tarczy sztywnej numer II. Tarcza sztywna numer II jest połączona z tarczą
podporową za pomocą przegubu A i pręta podporowego numer 4. Przegub A nie leży na kierunku pręta pod-
porowego numer 4. Tarcza ta jest więc także geometrycznie niezmienna. Ostatecznie kratownica płaska jest
geometrycznie niezmienna i statycznie wyznaczalna.

1

2

3

5

6

I

1

2

4

8

3

A

II

4

7

9

a)

b)

1

2

3

4

5

6

7

8

9

10

11 12

13

14

Rys. 2.19. Kratownica płaska. a) schemat kratownicy, b) płaski układ tarcz sztywnych odpowiadający kratownicy

płaskiej

2.8. Zadania 419

−

434

Prętem zerowym w kratownicy płaskiej nazywamy pręt, w którym przy danym obciążeniu siła normalna

wynosi zero. Pręty zerowe występują:

•

jeżeli do nieobciążonego węzła dochodzą dwa pręty, to oba są zerowe

−

rysunek 2.20a

•

jeżeli do nieobciążonego pręta dochodzą trzy pręty oraz dwa z nich leżą na jednej prostej, to trzeci
z nich jest prętem zerowym

−

rysunek 2.20b

•

jeżeli do obciążonego węzła dochodzą dwa pręty i siła działa po kierunku jednego z nich, to drugi
pręt jest prętem zerowym

−

rysunek 2.20c.

Aby znaleźć pręty zerowe musimy przeprowadzić analizę minimum dwa razy. Jeżeli dwie ostatnie analizy
nie zwiększyły liczby prętów zerowych, to poszukiwanie prętów zerowych możemy uznać za zakończone.

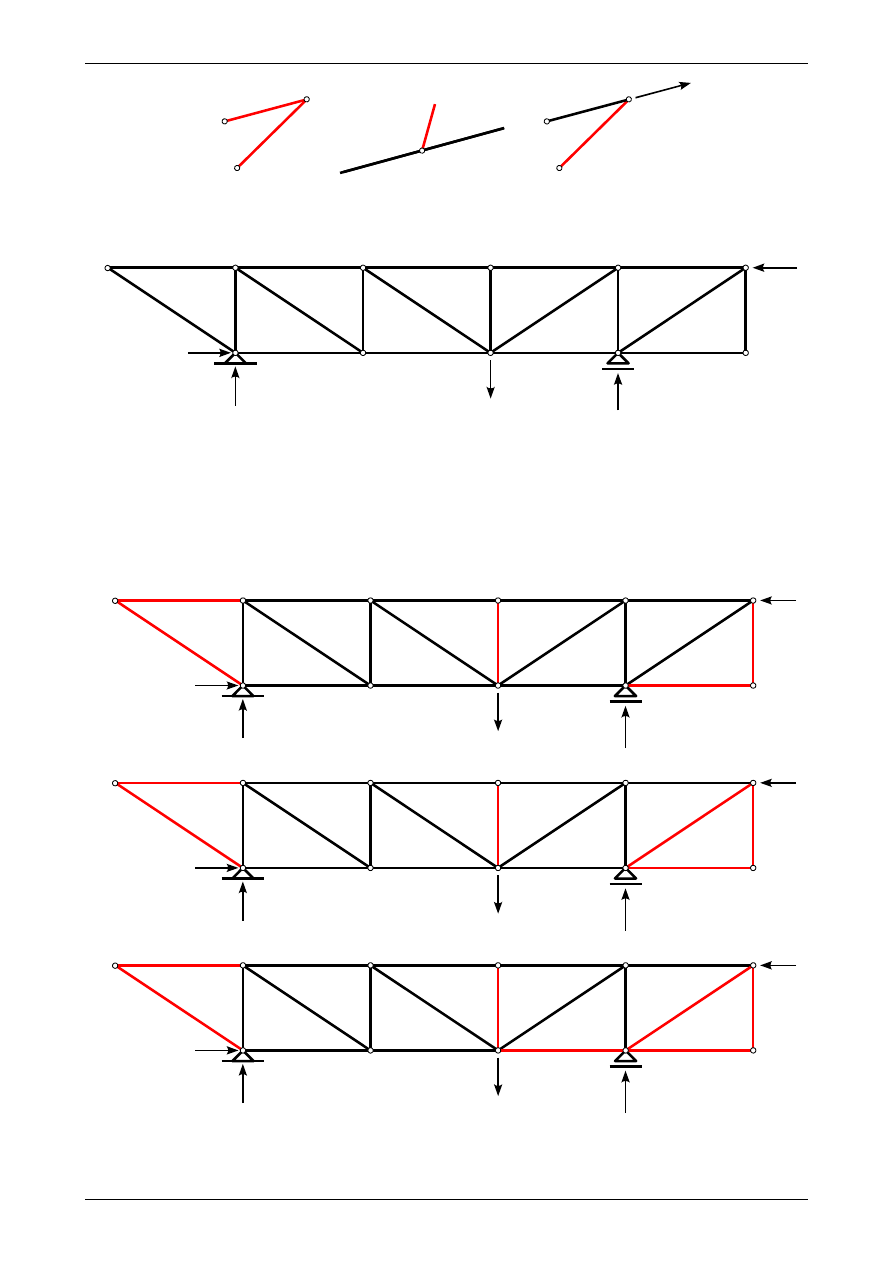
Na rysunku 2.21 widzimy kratownicę płaską obciążoną siłami czynnymi oraz reakcjami. Analizując ją

pierwszy raz możemy stwierdzić że:

•

węzeł numer 1 spełnia pierwszą zasadę

•

węzeł numer 6 spełnia drugą zasadę

•

węzeł numer 11 spełnia pierwszą zasadę.

Dr inż. Janusz Dębiński

BNS-I

Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

13

a)

b)

c)

P

Rys. 2.20. Pręty zerowe. a) nieobciążony węzeł z dwoma prętami, b) nieobciążony węzeł z trzema prętami, c) obciążony

węzeł z dwoma prętami

R

2

R

1

R

3

P

2

P

1

1

2

4

6

8

10

3

5

7

9

11

Rys. 2.21. Kratownica płaska

Pręty zerowe znalezione po pierwszej analizie widzimy na rysunku 2.22a. Analizując kratownicę drugi raz
możemy stwierdzić, że węzeł numer 10 spełnia teraz trzecią zasadę. Widzimy to na rysunku 2.22b. Trzecia
analiza prowadzi do wniosku, że węzeł numer 9 spełnia trzecią zasadę. Następne analizy nie dadzą już no -
wych prętów zerowych w kratownicy płaskiej. Wszystkie pręty zerowe możemy zobaczyć na rysunku 2.22c.

R

2

R

1

R

3

P

2

P

1

1

2

4

6

8

10

3

5

7

9

11

a)

R

2

R

1

R

3

P

2

P

1

1

2

4

6

8

10

3

5

7

9

11

b)

R

2

R

1

R

3

P

2

P

1

1

2

4

6

8

10

3

5

7

9

11

c)

Rys. 2.22. Pręty zerowe w kratownicy płaskiej. a) pręty zerowe po pierwszej analizie, b) pręty zerowe po drugiej

analizie, c) wszystkie pręty zerowe

Dr inż. Janusz Dębiński

BNS-I

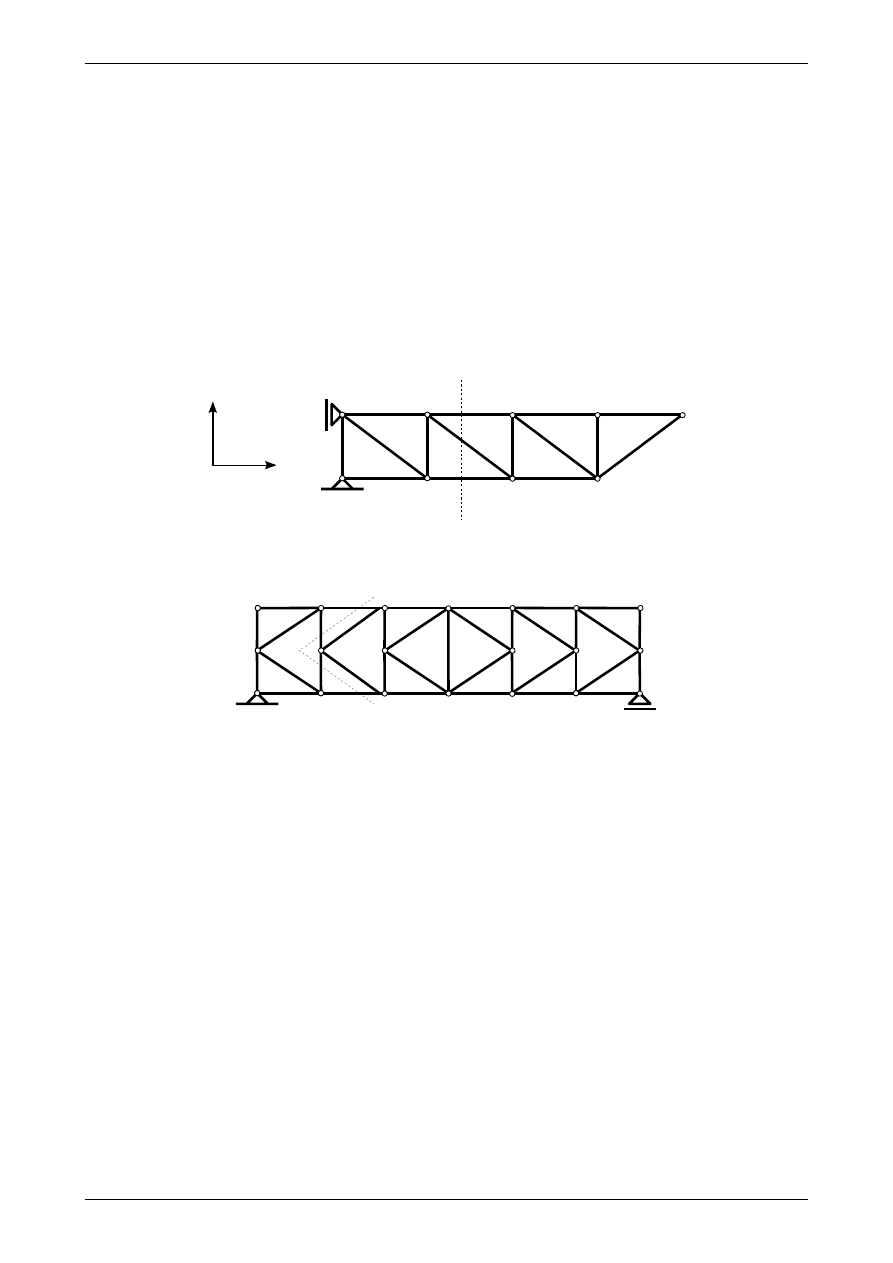
Mechanika teoretyczna

−

zadania sprawdzające

−

przewodnik do zadań

−

Część 2

14

2.9. Zadania 435

−

512

Aby wyznaczyć siłę normalną w zadanym pręcie kratownicy płaskiej musimy wykonać przekrój przez

trzy jej pręty. Następnie rozpatrując równowagę odciętej części kratownicy i z odpowiedniego równania
równowagi wyznaczamy wartość siły normalnej. W większości przypadków tym odpowiednim równaniem
jest równanie sumy momentów wszystkich sił działających na odciętą część kratownicy płaskiej względem
punktu Rittera. Dla zadanego pręta punktem Rittera jest punkt przecięcia się kierunków dwóch pozostałych
prętów w przekroju. Na rysunku 2.23 widzimy kratownicę płaską. Punktem Rittera dla pręta pasa dolnego
jest punkt R

D

, a dla pręta pasa górnego punkt R

G

. W przypadku krzyżulca punkt Rittera ucieka do nie-

skończoności. W takim przypadku należy skorzystać z równania sumy rzutów wszystkich sił działających na
odciętą część kratownicy na oś Y. Na rysunku 2.24 widzimy kratownicę półkrzyżulcową. Jest to szczególny
przypadek, kiedy da się zastosować metodę Rittera pomimo tego, że nie da się tej kratownicy przeciąć tylko
przez trzy pręty. Aby wyznaczyć siłę normalną w pręcie pasa dolnego lub górnego należy wykonać przekrój

α−α

zaznaczony na tym rysunku. Punktem Rittera dla pręta pasa dolnego jest punkt R

D

, natomiast dla pasa

górnego punkt R

G

.

G

X

Y

D

K

R

D

R

G

α

α

Rys. 2.23. Przekrój kratownicy płaskiej oraz punkty Rittera

G

D

R

D

R

G

α

α

Rys. 2.24. Przekrój kratownicy półkrzyżulcowej oraz punkty Rittera

Dr inż. Janusz Dębiński

BNS-I