Dr inż. Janusz Dębiński
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do
zadań
1. Część 1
1.1. Zadania 1
−
8
Funkcje trygonometryczne mają następujące definicje:
•
sinus jest stosunkiem długości przyprostokątnej leżącej naprzeciw kąta do długości przeciwprosto-
kątnej
•
kosinus jest stosunkiem długości przyprostokątnej leżącej przy kącie do długości przeciwprostokąt-
nej
•
tangens jest stosunkiem długości przyprostokątnej leżącej naprzeciw kąta do długości przyprosto -
kątnej leżącej przy kącie
•
kotangens jest stosunkiem długości przyprostokątnej leżącej przy kącie do długości przyprosto-
kątnej leżącej naprzeciw kąta.
1.2. Zadania 9
−
66
Aby przeprowadzić analizę kinematyczną płaskich układów prętowych musimy w pierwszej kolejności
sprawdzić warunek konieczny geometrycznej niezmienności. W przypadku belek musimy je zamienić na
płaski układ tarcz sztywnych, w których tarcze sztywne mają kształt zbliżony do kształtu pręta, a podpory
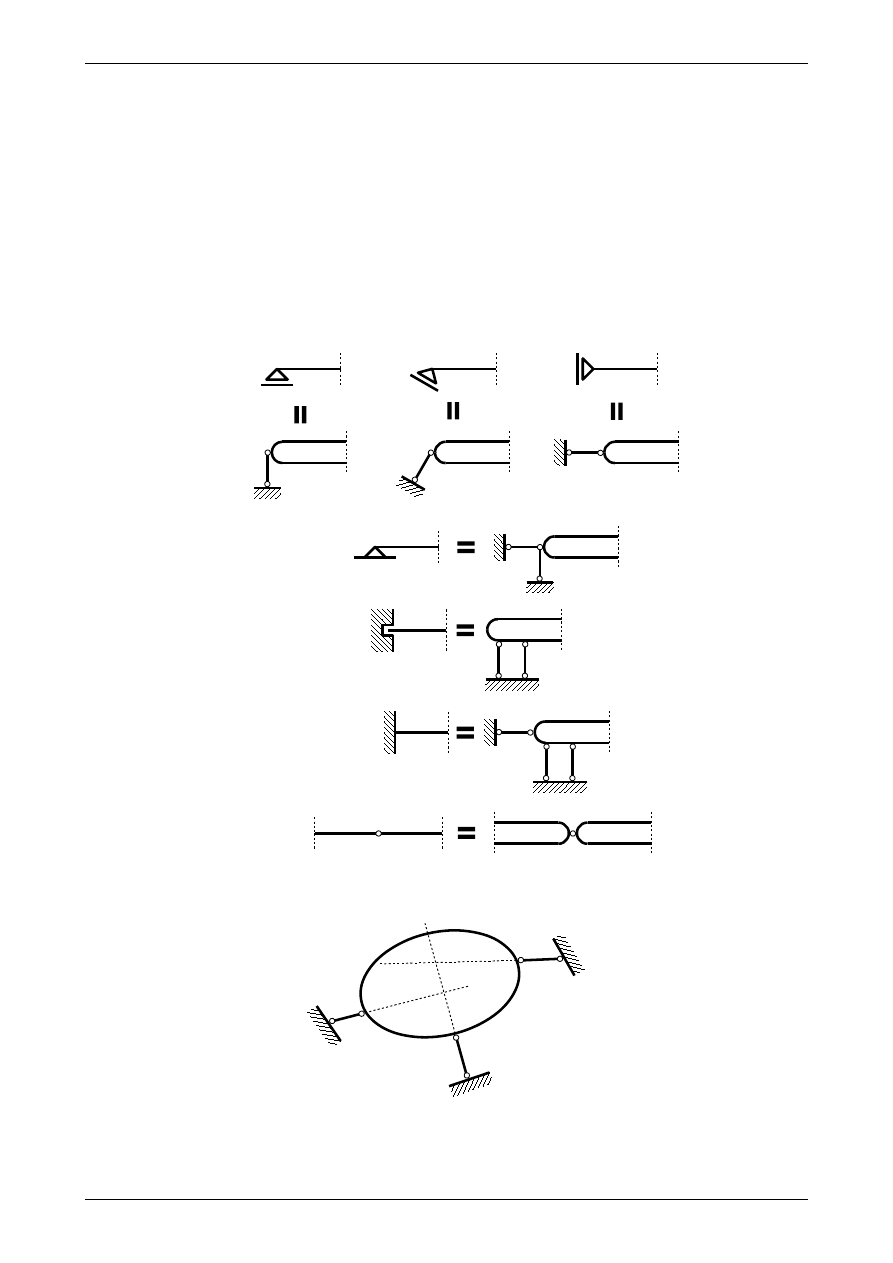
zbudowane są z odpowiedniego układu prętów podporowych. Rozróżniamy następujące rodzaje podpór:
•
przegubowo-przesuwną
−
rysunek 1.1a
•
przegubowo-nieprzesuwną
−
rysunek 1.1b
•
teleskopową
−
rysunek 1.1c
•
utwierdzenie
−
rysunek 1.1d
•
przegub rzeczywisty nazywany krótko przegubem
−
rysunek 1.1e.
Na rysunku 1.1 widzimy także układy prętów podporowych im odpowiadające. Każdy pręt podporowy
odbiera tarczy sztywnej jeden stopień swobody. Z kolei przegub rzeczywisty odbiera tarczy sztywnej dwa
stopnie swobody. Aby płaski układ tarcz sztywnych był geometrycznie niezmienny oraz statycznie wyzna-
czalny, musi spełniać warunek
3⋅t= p,
(1.1)
gdzie t oznacza liczbę tarcz sztywnych, a p oznacza liczbę stopni swobody odbieranych przez pręty podpo-
rowe i przeguby.
Oprócz warunku koniecznego geometrycznej niezmienności płaski układ tarcz sztywnych musi spełniać
warunki dostateczne geometrycznej niezmienności. Mają one formę:
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
2
•
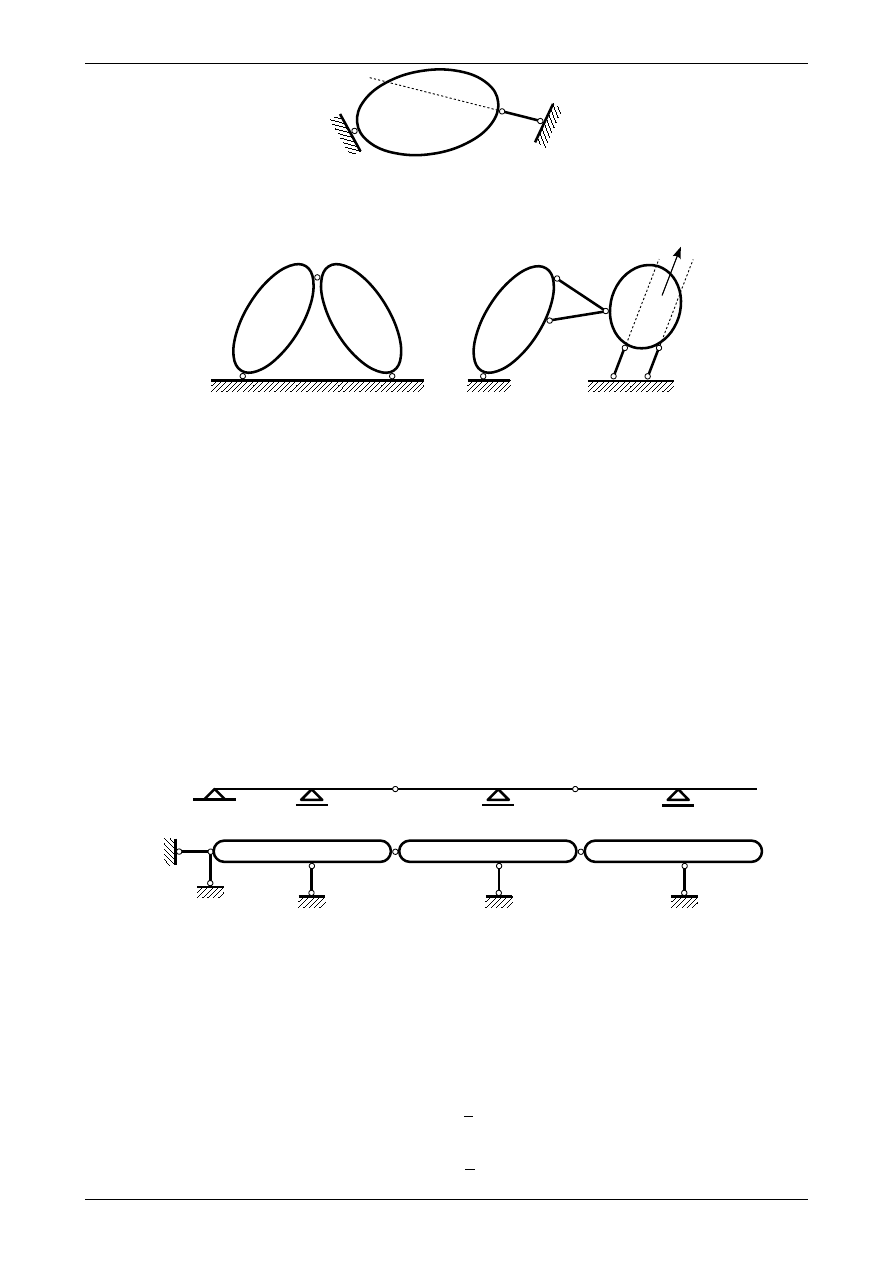
tarcza sztywna połączona z tarczą podporową za pomocą trzech prętów podporowych
−
kierunki
prętów podporowych nie mogą się przecinać w jednym punkcie
−
rysunek 1.2
•
tarcza sztywna połączona z tarczą podporową za pomocą przegubu i pręta podporowego
−
przegub
nie może leżeć na kierunku pręta podporowego
−
rysunek 1.3
•
układ trójprzegubowy
−
przeguby nie mogą leżeć na jednej prostej
−
rysunek 1.4.
Na rysunku 1.4b musimy zwrócić uwagę na dwa typy przegubów złożone z dwóch prętów podporowych:
•
przegub fikcyjny B
−
znajduje się on w punkcie przecięcia kierunków tworzących go prętów podpo-
rowych
•
przegub niewłaściwy C
−
znajduje się w nieskończoności na prostej równoległej do kierunków two-
rzących go prętów podporowych.
a)
b)
d)
e)
c)
Rys. 1.1. Podpory płaskich układów prętowych. a)przegubowo-przesuwna, b) przegubowo-nieprzesuwna,
c) teleskopowa, d) utwierdzenie, e) przegub
2
1
3
I
TP
TP
TP
Rys. 1.2. Geometrycznie niezmienna tarcza sztywna połączona z tarczą podporową za pomocą trzech prętów
podporowych
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
3
1
A
I
TP
T
P
Rys. 1.3. Geometrycznie niezmienna tarcza sztywna połączona z tarczą podporową za pomocą przegubu oraz pręta
podporowego
A
B
C
II
A
B
I
II
C
∞
a)
b)
1
2
3
4
TP
TP
TP
I
Rys. 1.4. Geometrycznie niezmienne układy trójprzegubowe. a) z trzema przegubami rzeczywistymi, b) z przegubami
rzeczywistym A, fikcyjnym B oraz niewłaściwym C
Na rysunku 1.5 przedstawiono belkę złożoną zamienioną na płaski układ tarcz sztywnych. Warunek
konieczny geometrycznej niezmienności ma postać
3⋅3=5⋅12⋅2.
(1.2)
Jak więc widać jest on spełniony. Tarcza sztywna numer I jest połączona z tarczą podporową za pomocą
trzech prętów podporowych numer 1, 2 i 3, których kierunki nie przecinają się w jednym punkcie. Jest więc
ona geometrycznie niezmienna i stanowi tarczę podporową dla tarcz sztywnych numer II i III. Tarcza
sztywna numer II połączona jest z tarczą podporową za pomocą przegubu C i pręta podporowego numer 4.
Przegub C nie leży na kierunku pręta podporowego numer 4, wobec tego tarcza sztywna numer II jest
geometrycznie niezmienna i stanowi tarczę podporową dla tarczy sztywnej numer III. Tarcza sztywna numer
III jest połączona z tarczą podporową za pomocą przegubu E oraz pręta podporowego numer 5. Przegub
E nie leży na kierunku pręta podporowego numer 5, więc tarcza sztywna numer III jest geometrycznie nie-
zmienna. Ostatecznie belka jest geometrycznie niezmienna i statycznie wyznaczalna.
a)
b)
1
2
3
4
5
I
II
III
A
B
C
D
E
F
C
E
Rys. 1.5. Belka złożona. a) schemat belki, b) belka zamieniona na płaski układ tarcz sztywnych
1.3. Zadania 67
−
82
Siła wypadkowa dwóch sił P
x
oraz P
y
znajduje się na przekątnej prostokąta, który tworzą obie siły. Aby
wyznaczyć wartości tych sił musimy wykorzystać trójkąt prostokątny oraz definicję funkcji sinus i kosinus.
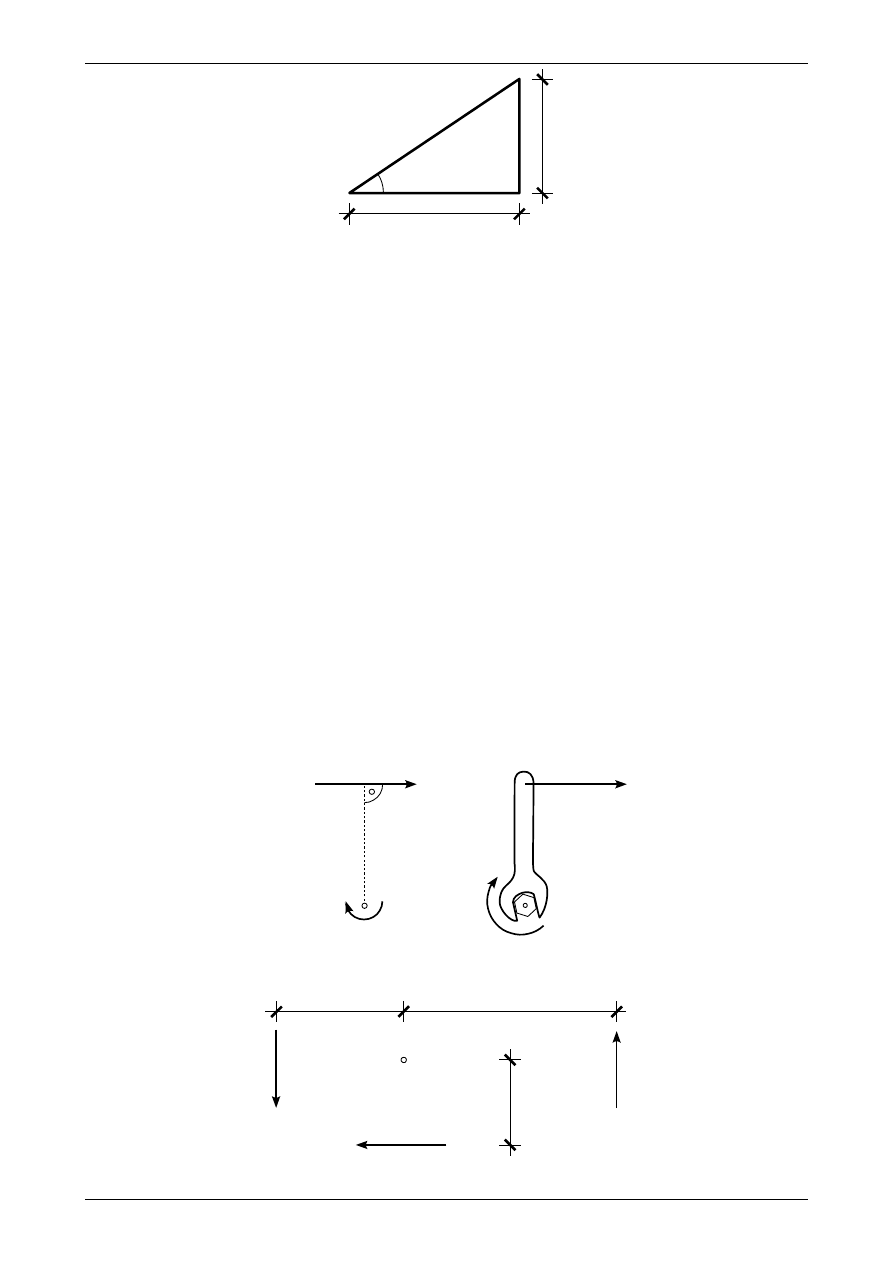
Na rysunku 1.6 widzimy przykładowy trójkąt prostokątny. Na podstawie oznaczeń na tym rysunku
sin
α
=
b
c
,
(1.3)
cos
α
=
a
c
.
(1.4)
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
4
a
b
α
c
Rys. 1.6. Trójkąt prostokątny
Wobec tego
a=c⋅cos
α
,
(1.5)
b=c⋅sin
α
.
(1.6)
1.4. Zadania 83
−
114
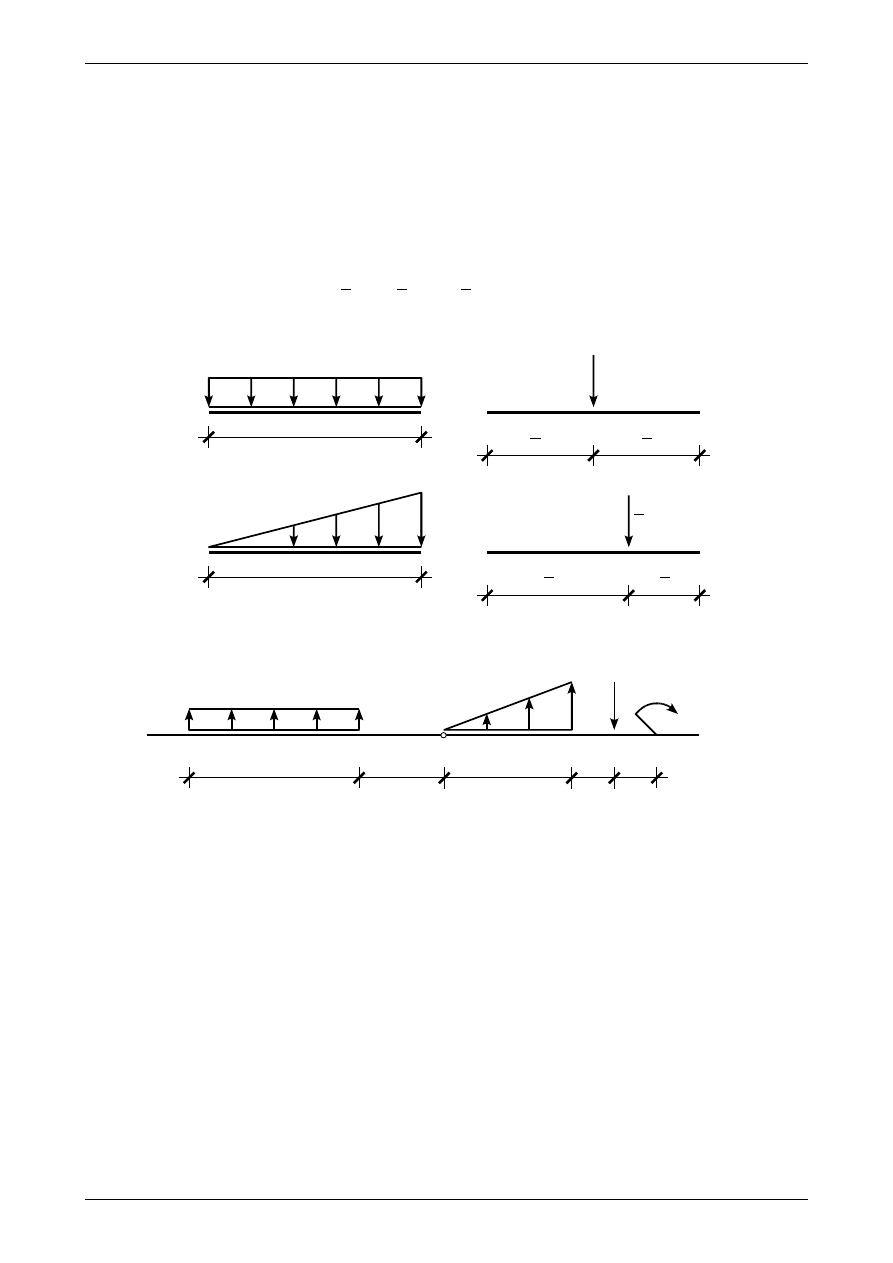
Wartość bezwzględną momentu siły względem dowolnego punktu A wyznaczamy jako iloczyn wartości
tej siły i odległości punktu A od kierunku tej siły, czyli zgodnie z rysunkiem 1.7a
∣
M
A
∣
=
P⋅a,
(1.7)
w którym P oznacza wartość siły, natomiast a oznacza odległość siły od punktu A. Musimy pamiętać o tym,
że odległość a jest zawsze prostopadła do kierunku siły P. Aby określić znak momentu siły możemy zasto-
sować regułę klucza widoczną na rysunku 1.7b. W punkcie A znajduje się śruba, którą obraca klucz. Jeżeli
na końcu tego klucza przyłożymy siłę P, i siła ta powoduje obrót śruby w punkcie A zgodnie z ruchem
wskazówek zegara, to moment taki jest dodatni. Na rysunku 1.7a moment siły P względem punktu A jest
więc dodatni. Jeżeli na płaszczyźnie działa więcej niż jedna siła, to wtedy moment takiego układu względem
punktu A jest sumą momentów względem punktu A od pojedynczych sił. Moment układu sił widocznego na
rysunku 1.8
M
A
=−
8,0⋅1,57,0⋅1,0−10,0⋅2,5=−30,0 kN⋅m .
(1.8)
P
A
M
A
a
M
A
a)
b)
P
Rys. 1.7. Moment siły względem punktu A. a) odległość siły od punktu A, b) reguła klucza
[m]
1,5
2,5
1,
0
8,
0
kN
10
,0
k
N
7,0 kN
A
Rys. 1.8. Płaski układ sił niezbieżnych
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
5
1.5. Zadania 115
−
146
Aby wyznaczyć moment różnych obciążeń pręta względem punktu A musimy wykorzystać zasady poda-
ne w poprzednim punkcie. Wszystkie obciążenia ciągłe należy sprowadzić do sił wypadkowych. Na rysunku
1.9a możemy zobaczyć obciążenie ciągłe równomiernie rozłożone i położenie siły wypadkowej z tego obcią-
żenia, a na rysunku 1.9b widzimy obciążenie ciągłe trójkątne i położenie siły wypadkowej z tego obciążenia.
Musimy pamiętać o tym, że siła wypadkowa z obciążenia ciągłego ma ten sam zwrot co to obciążenie.
Ponadto musimy mieć na uwadze to, że moment skupiony jest statycznie równoważny parze sił, czyli jego
moment względem dowolnego punktu na płaszczyźnie jest stały i równy jego wartości z odpowiednim
znakiem. Moment obciążeń pręta widocznego na rysunku 1.10
M
A
=
8,0⋅5,0⋅
(
4,0+
1
2
⋅
8,0
)
−
1
2
⋅
7,0⋅6,0⋅
2
3
⋅
6,0+9,0⋅8,0+3,0=311,0 kN⋅m .
(1.9)
L
q
q∙L
L
2
L
2
a)
b)
L
q
1
2
⋅
q⋅L
L
3
2
3
⋅
L
Rys. 1.9. Siły wypadkowe. a) z obciążenia ciągłego równomiernie rozłożonego, b) z obciążenia ciągłego trójkątnego
8,0
4,0
6,0
2,0
2,0
5,0 kN/m
7,0 kN/m 9,0 kN
3,0 kN∙m
[m]
A
Rys. 1.10. Obciążenie pręta
1.6. Zadania 147
−
156
Na podporze przegubowo-przesuwnej działa jedna reakcja, której kierunek jest prostopadły do kreski
oznaczającej tę podporę. Reakcje te możemy zobaczyć na rysunku 1.11a. Na podporze przegubowo-nieprze-
suwnej działają dwie reakcje pozioma H oraz pionowa V bez względu na usytuowanie tej podpory. Reakcje
te widzimy na rysunku 1.11b. Na podporze teleskopowej działa reakcja pionowa V oraz moment obrotowy
M. Reakcje te możemy zobaczyć na rysunku 1.11c. W utwierdzeniu działają trzy reakcje: pozioma H, pio-
nowa V oraz moment obrotowy M. Reakcje te są niezależne od usytuowania utwierdzenia, a widzimy je na
rysunku 1.11d.
1.7. Zadania 157
−
164
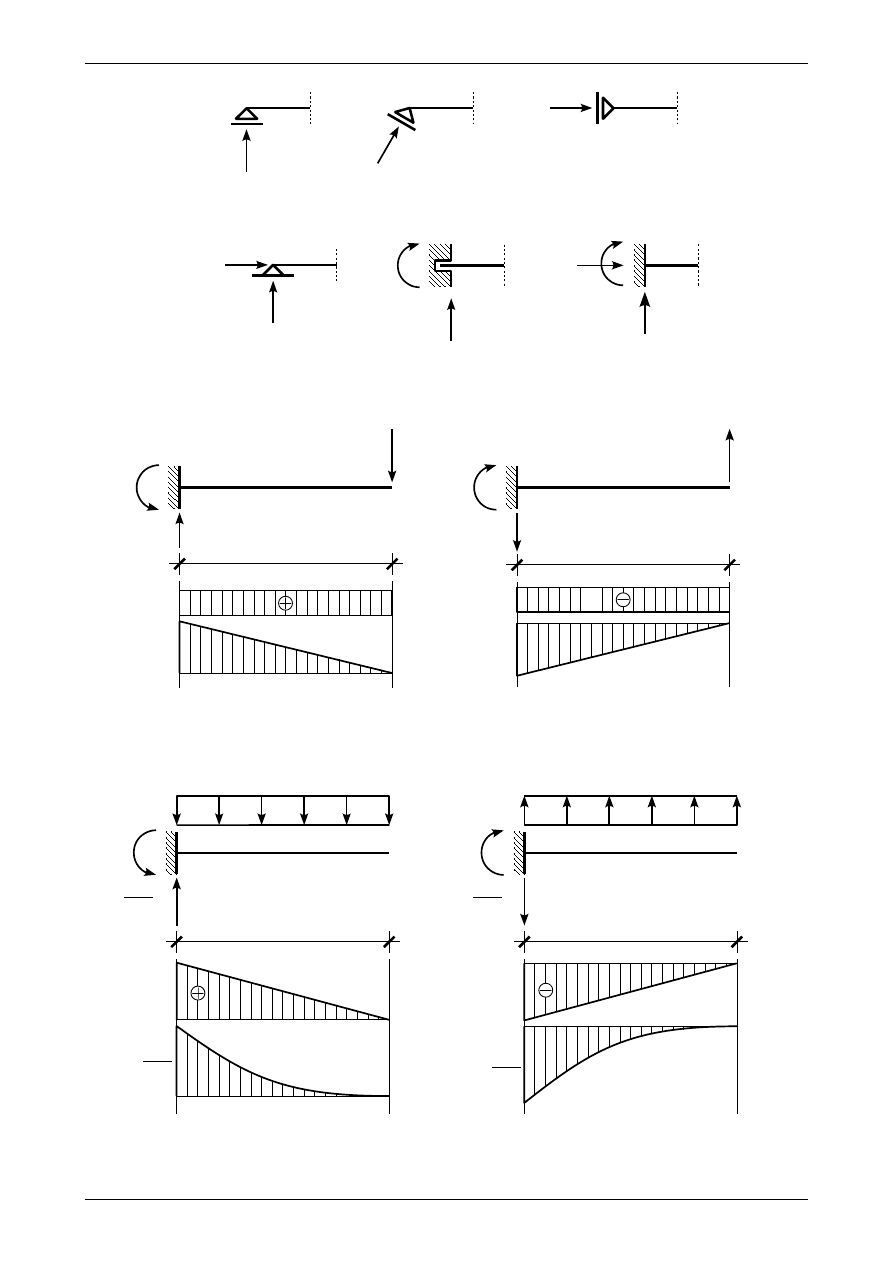
Wykresy siły poprzecznej oraz momentu zginającego do belek wspornikowej oraz swobodnie podpartej
obciążonych siłą skupioną lub obciążeniem ciągłym równomiernie rozłożonym możemy zobaczyć na rysun-
kach 1.12, 1.13, 1.14 oraz 1.15.
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
6
R
R
R
V
H
V
M
V
M
H
a)
b)
c)
d)
Rys. 1.11. Reakcje. a) podpora przegubowo-przesuwna, b) podpora przegubowo-nieprzesuwna, c) podpora
teleskopowa, d) utwierdzenie
L
P
T(x)
P
P∙L
P
P
∙L
0
M(x)
L
P
P
P∙L
P
P
∙L
0
T(x)
M(x)
a)
b)
Rys. 1.12. Wykresy sił przekrojowych dla belki wspornikowej. a) obciążonej siłą skupioną w dół, b) obciążonej siłą
skupioną do góry
L
q
q∙L
q∙
L
0
0
T(x)
M(x)
q⋅L
2
2
q⋅L
2
2
L
q
q∙L
q∙
L
0
0
T(x)
M(x)
q⋅L
2
2
q⋅L
2
2
a)
b)
Rys. 1.13. Wykresy sił przekrojowych dla belki wspornikowej. a) obciążonej obciążeniem ciągłym równomiernie
rozłożonym w dół, b) obciążonej obciążeniem ciągłym równomiernie rozłożonym do góry
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
7
P
P⋅L
4
P
2
L
2
P
2
L
2
P
2
P
2
T(x)
M(x)
P
P⋅L
4
P
2
L
2
P
2
L
2
P
2
P
2
T(x)
M(x)
a)
b)
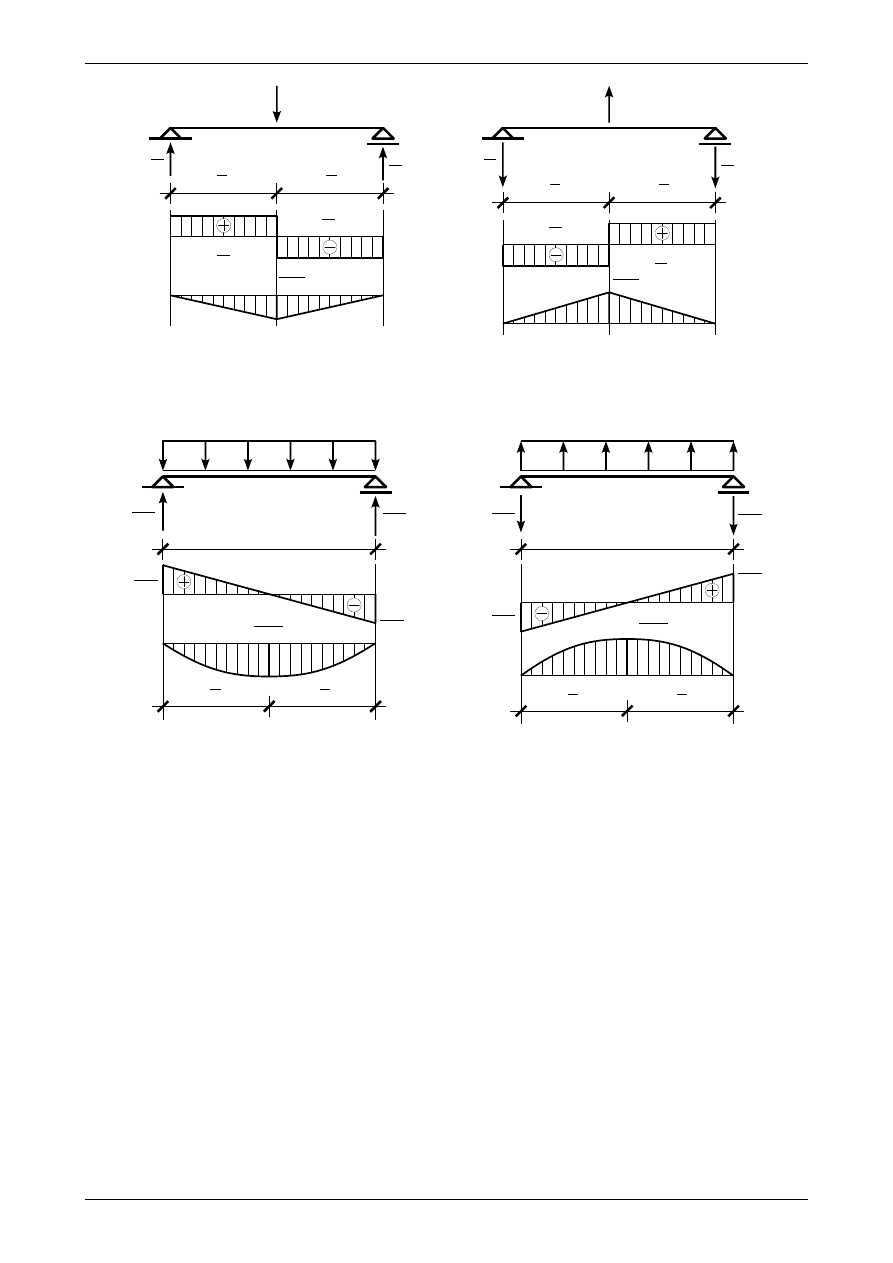
Rys. 1.14. Wykresy sił przekrojowych dla belki swobodnie podpartej. a) obciążonej siłą skupioną w dół, b) obciążonej
siłą skupioną do góry
q
L
T(x)
M(x)
L
2
L
2
q⋅L
2
q⋅L
2
q⋅L
2
q⋅L
2
q⋅L
2
8
0
0
q
L
T(x)
M(x)
L
2
L
2
q⋅L
2
q⋅L
2
q⋅L
2
q⋅L
2
0
0
q⋅L
2
8
a)
b)
Rys. 1.15. Wykresy sił przekrojowych dla belki swobodnie podpartej. a) obciążonej obciążeniem ciągłym równomiernie
rozłożonym w dół, b) obciążonej obciążeniem ciągłym równomiernie rozłożonym do góry
1.8. Zadania 165
−
196
W przedziale, w którym działa obciążenie ciągłe równomiernie rozłożone w dół, wykresy siły poprzecz-
nej oraz momentu zginającego muszą spełniać warunki:
•
liniowy wykres siły poprzecznej musi być malejący
•
brzuszek parabolicznego wykresu momentu zginającego musi być w dół
•
moment zginający ma ekstremum (minimum) w punkcie, w którym siła poprzeczna ma miejsce
zerowe.
Aby wykresy spełniały różniczkowe równania równowagi muszą spełniać wszystkie powyższe warunki.
W przedziale, w którym działa obciążenie ciągłe równomiernie rozłożone do góry, wykresy siły poprzecznej
oraz momentu zginającego muszą spełniać warunki:
•
liniowy wykres siły poprzecznej musi być rosnący
•
brzuszek parabolicznego wykresu momentu zginającego musi być do góry
•
moment zginający ma ekstremum (maksimum) w punkcie, w którym siła poprzeczna ma miejsce
zerowe.
Aby wykresy spełniały różniczkowe równania równowagi muszą spełniać wszystkie powyższe warunki.
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
8
1.9. Zadania 197 - 216
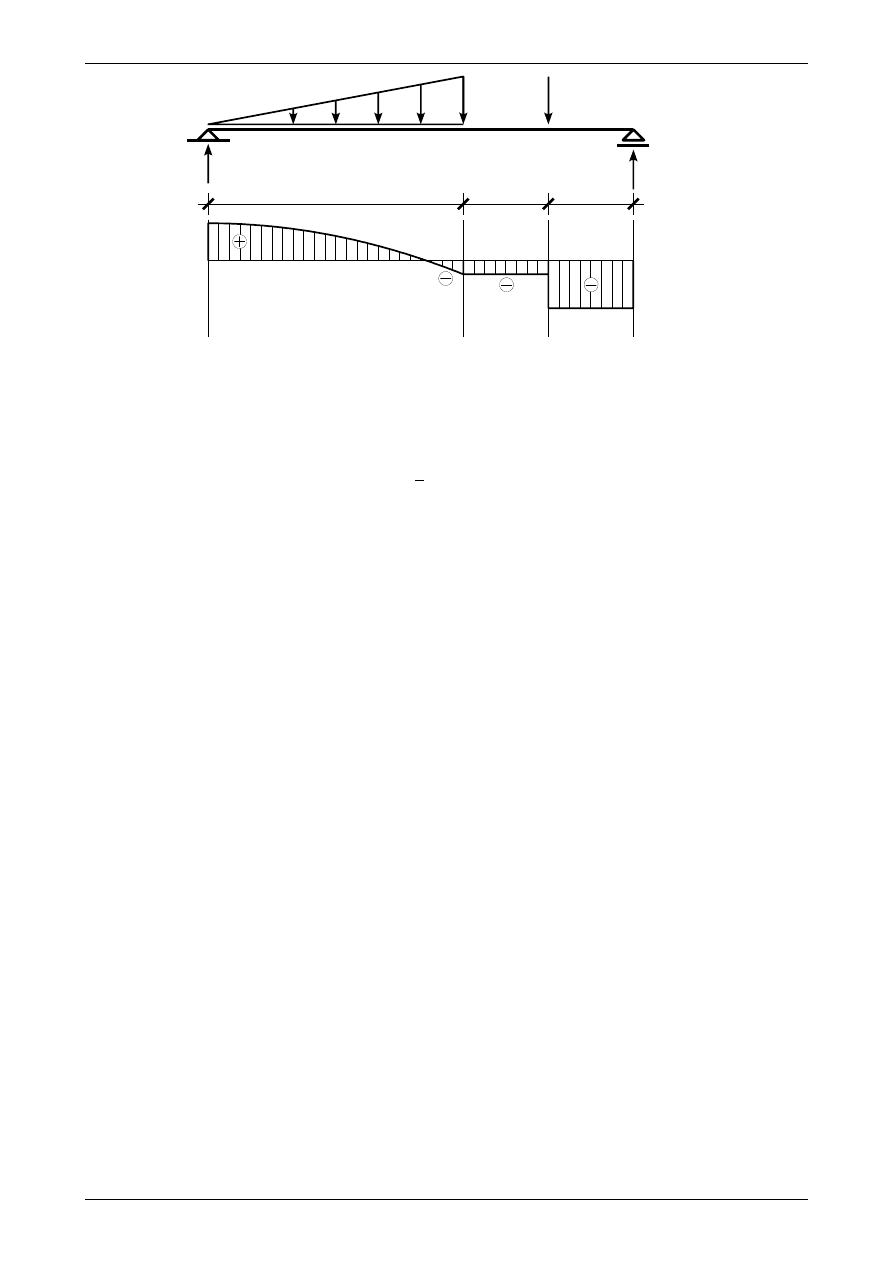
W przedziale, w którym działa obciążenie ciągłe trójkątne w dół, wykresy siły poprzecznej oraz momen-
tu zginającego muszą spełniać warunki:
•
paraboliczny wykres siły poprzecznej musi być malejący
•
wykres siły poprzecznej ma ekstremum w punkcie , w którym obciążenie ciągłe trójkątne ma war-
tość zero
•
brzuszek wykresu momentu zginającego musi być skierowany w dół
•
moment zginający ma ekstremum (minimum) w punkcie, w którym siła poprzeczna ma miejsce ze-
rowe.
Aby wykresy spełniały różniczkowe równania równowagi muszą spełniać wszystkie powyższe warunki.
W przedziale, w którym działa obciążenie ciągłe trójkątne do góry, wykresy siły poprzecznej oraz momentu
zginającego muszą spełniać warunki:
•
paraboliczny wykres siły poprzecznej musi być rosnący
•
wykres siły poprzecznej ma ekstremum w punkcie, w którym obciążenie ciągłe trójkątne ma wartość
zero
•
brzuszek wykresu momentu zginającego musi być skierowany do góry
•
moment zginający ma ekstremum (maksimum) w punkcie, w którym siła poprzeczna ma miejsce
zerowe.
Aby wykresy spełniały różniczkowe równania równowagi muszą spełniać wszystkie powyższe warunki.
1.10. Zadania 217
−
240
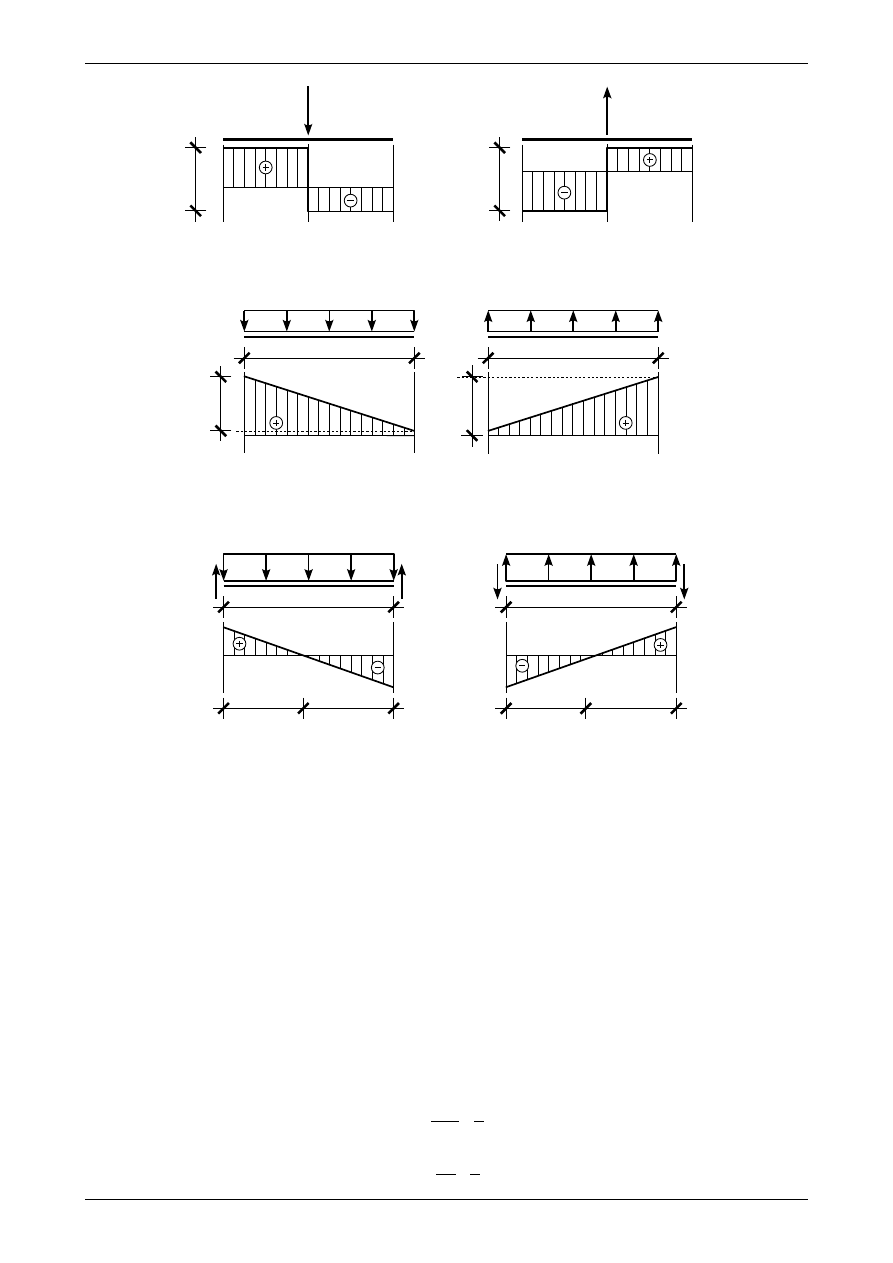
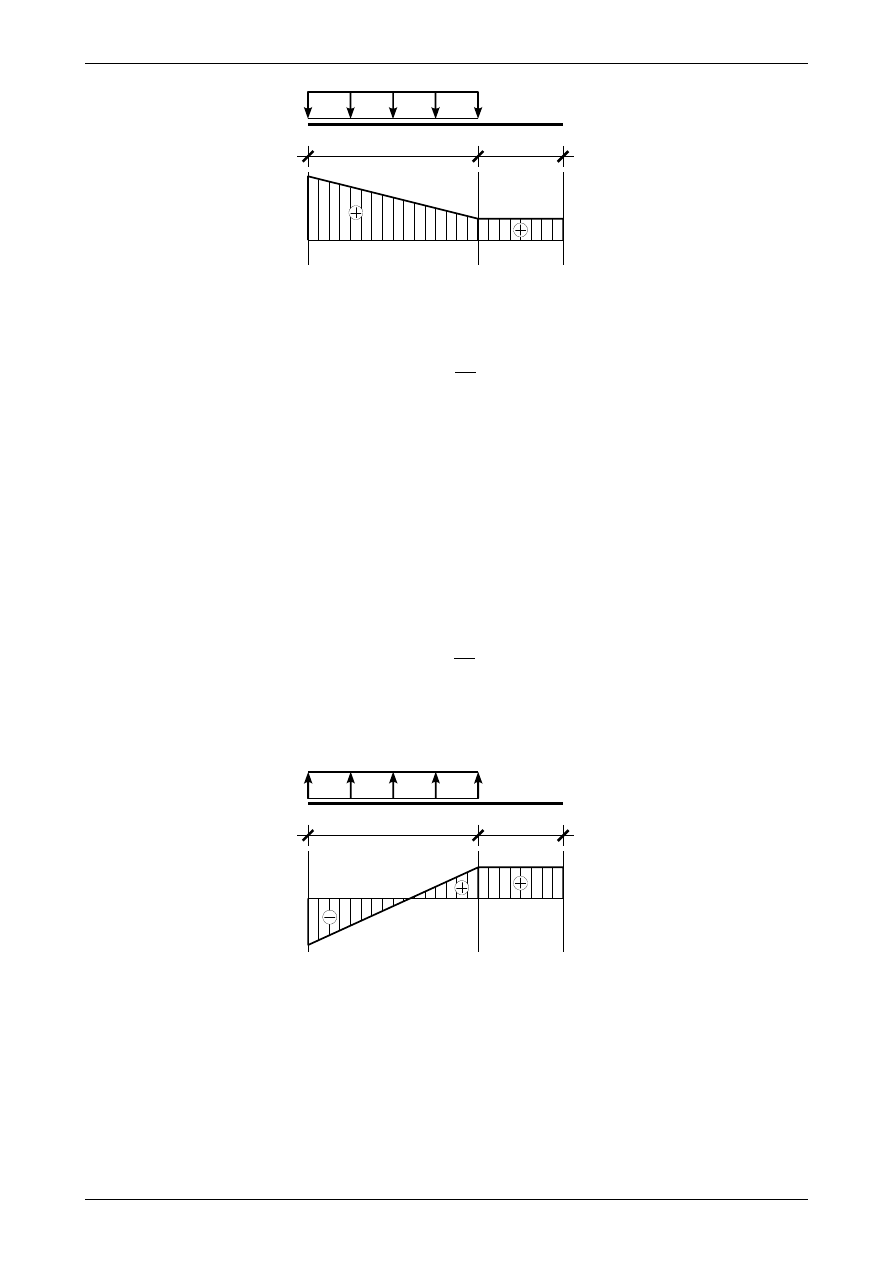
Wyznaczanie wykresu siły poprzecznej zaczynamy na lewym końcu belki swobodnie podpartej. Porusza-
jąc się w prawo musimy stosować następujące zasady:
•
jeżeli w danym punkcie działa siła w dół, to siła poprzeczna zmniejsza się skokowo o wartość tej
siły
−
rysunek 1.16a
•
jeżeli w danym punkcie działa siła do góry, to siła poprzeczna zwiększa się skokowo o wartość tej
siły
−
rysunek 1.16b
•
jeżeli w danym przedziale działa obciążenie ciągłe równomiernie rozłożone w dół, to liniowy wy-
kres siły poprzecznej maleje, a różnica pomiędzy lewym oraz prawym jego końcem równa się sile
wypadkowej z obciążenia ciągłego
−
rysunek 1.17a
•
jeżeli w danym przedziale działa obciążenie ciągłe równomiernie rozłożone do góry, to liniowy wy-
kres siły poprzecznej rośnie, a różnica pomiędzy lewym oraz prawym jego końcem równa się sile
wypadkowej z obciążenia ciągłego
−
rysunek 1.17b.
Jeżeli liniowy wykres siły poprzecznej ma na obu końcach przedziału wartości przeciwnych znaków, to ma
on także w tym przedziale miejsce zerowe. Zgodnie z oznaczeniami widocznymi na rysunku 1.18 znajduje
się ono w odległościach
x
L
=
∣
T
L
∣
∣
q∣
,
(1.10)
x
P
=
∣
T
P
∣
∣
q∣
,
(1.11)
gdzie T
L
i T
P
oznaczają wartości siły poprzecznej odpowiednio z lewej i prawej strony przedziału, a q jest
wartością obciążenia ciągłego równomiernie rozłożonego. W przypadku dziania obciążenia trójkątnego
paraboliczny wykres siły poprzecznej spełnia warunki:
•
jeżeli w danym przedziale działa obciążenie ciągłe trójkątne w dół, to paraboliczny wykres siły
poprzecznej maleje, a różnica pomiędzy lewym oraz prawym jego końcem równa się sile wypad-
kowej z obciążenia ciągłego
−
rysunki 1.19a i 1.19b
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
9
P
P
T(x)
a)
P
P
T(x)
b)
Rys. 1.16. Wykres siły poprzecznej przy działaniu siły. a) siła działająca w dół, b) siła działająca do góry
q
L
a)
q∙
L
T(x)
q
L
b)
q∙
L
T(x)
Rys. 1.17. Wykres siły poprzecznej przy działaniu obciążenia ciągłego równomiernie rozłożonego. a) obciążenie ciągłe
równomiernie rozłożone w dół, b) obciążenie ciągłe równomiernie rozłożone do góry
q
L
T(x)
x
L
x
P
T
L
T
P
q
L
T(x)
x
L
x
P
T
L
T
P
a)
b)
T
L
T
P
T
L
T
P
Rys. 1.18. Położenie miejsca zerowego siły poprzecznej. a) obciążenie ciągłe równomiernie rozłożone w dół,
b) obciążenie ciągłe równomiernie rozłożone do góry
•
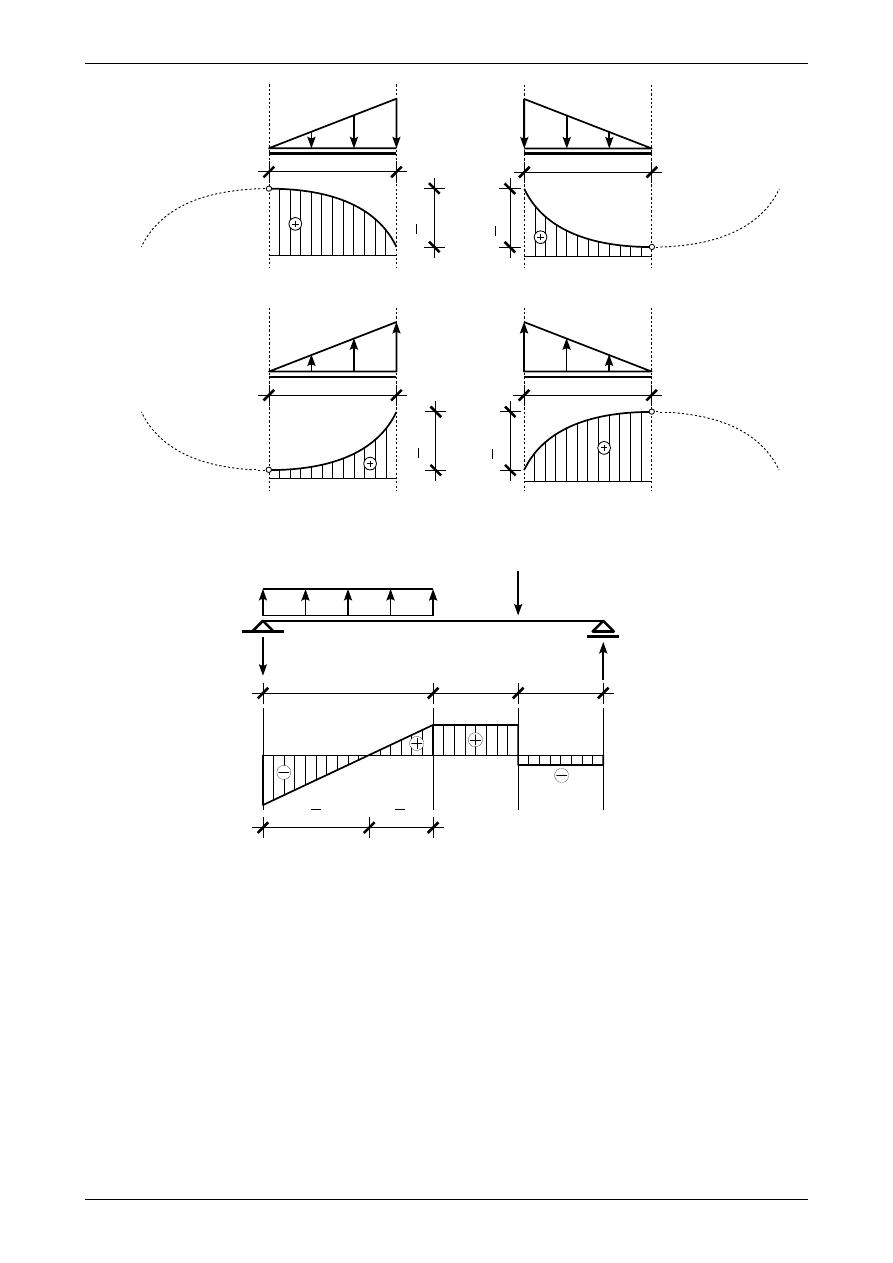
jeżeli w danym przedziale działa obciążenie ciągłe trójkątne do góry, to paraboliczny wykres siły
poprzecznej rośnie, a różnica pomiędzy lewym oraz prawym jego końcem równa się sile wypad-
kowej z obciążenia ciągłego
−
rysunki 1.19c i 1.19d
•
ekstremum wykresu siły poprzecznej (czyli punkt E na rysunku 1.19) znajduje się w punkcie, w któ-
rym obciążenie ciągłe trójkątne ma wartość zero.
Na rysunku 1.20 możemy zobaczyć belkę swobodnie podpartą wraz z obciążeniem czynnym oraz reakcjami.
Siła poprzeczna w punkcie A
T
A
=−
10,0 kN .
(1.12)
Siła poprzeczna z lewej strony punktu B
T
B
L
=−
10,08,0⋅2,0=6,0 kN .
(1.13)
Położenie miejsca zerowego w przedziale AB
x
L
=
10,0
8,0
=
5
4
,
(1.14)
x
P
=
6,0
8,0
=
3
4
.
(1.15)
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
10
q
L
q
L
q
L
q
L
1
2
⋅q
⋅L
1
2
⋅q
⋅L
1
2
⋅q
⋅L
1
2
⋅q
⋅L
T(x)
T(x)
T(x)
T(x)
a)
b)
c)
d)
E
E
E
E
Rys. 1.19. Wykresy siły poprzecznej. a) obciążenie ciągłe trójkątne w dół, b) obciążenie ciągłe trójkątne w dół,
c) obciążenie ciągłe trójkątne do góry, d) obciążenie ciągłe trójkątne do góry
8,0 kN
8,0 kN/m
2,0
1,0
1,0
[m]
10,0 kN
2,0 kN
T(x)
[kN]
5
4
3
4
2,0
6,0
10
,0
A
B
C
D
Rys. 1.20. Wykres siły poprzecznej w belce swobodnie podpartej
Siła poprzeczna z prawej strony punktu B, w przedziale BC oraz z lewej strony punktu C
T
B
P
=
T
BC
=
T
C
L
=
6,0 kN .
(1.16)
Siła poprzeczna z prawej strony punktu C
T
C
P
=
6,0−8,0=−2,0 kN .
(1.17)
Siła poprzeczna w przedziale CD oraz w punkcie D
T
CD
=
T
D
=−
2,0 kN .
(1.18)
W punkcie D działa reakcja 2,0 kN do góry. Jak więc widać wykres siły poprzecznej „zamknie się”. Wykres
siły poprzecznej w belce swobodnie podpartej widzimy na rysunku 1.20. Na rysunku 1.21 możemy zobaczyć
belkę swobodnie podpartą wraz z obciążeniem czynnym i reakcjami. Siła poprzeczna w punkcie A
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
11
6,0
2,0
2,0
[m]
T(x)
[kN]
15,0 kN/m 30,0 kN
33,0 kN
42,0 kN
33
,0
12,0
42,0
A
B
C
D
Rys. 1.21. Wykres siły poprzecznej w belce swobodnie podpartej
T
A
=
33,0 kN .
(1.19)
Siła poprzeczna z lewej strony punktu B
T
B
L
=
33,0−
1
2
⋅
15,0⋅6,0=−12,0kN .
(1.20)
Ekstremum tego wykresu znajduje się w punkcie A, ponieważ w punkcie tym obciążenie trójkątne ma war -
tość zero. Siła poprzeczna z prawej strony punktu B, w przedziale BC oraz z lewej strony punktu C
T
B
P
=
T
BC
=
T
C
L
=−
12,0 kN .
(1.21)
Siła poprzeczna z prawej strony punktu C
T
C
P
=−
12,0−30,0=−42,0 kN .
(1.22)
Siła poprzeczna w przedziale CD oraz w punkcie D
T
CD
=
T
D
=−
42,0 kN .
(1.23)
W punkcie D działa reakcja 42,0 kN do góry. Jak więc widać wykres siły poprzecznej „zamknie się”.Wykres
siły poprzecznej w belce swobodnie podpartej widzimy na rysunku 1.21.
1.11. Zadania 241
−
270
Jeżeli w danym przedziale wykres siły poprzecznej jest funkcją stałą, to w przedziale tym nie działa ob-
ciążenie ciągłe. Kiedy wykres ten jest funkcją liniową, to w przedziale działa obciążenie ciągłe równomier -
nie rozłożone. Ma ono następujące właściwości:
•
jeżeli liniowy wykres siły poprzecznej jest malejący, to obciążenie ciągłe działa w dół
•
jeżeli liniowy wykres siły poprzecznej jest rosnący, to obciążenie ciągłe działa do góry
•
wartość obciążenia ciągłego jest taka, aby siła wypadkowa z niego równa była wartości bezwzględ-
nej różnicy rzędnych pomiędzy prawym a lewym końcem przedziału.
Na rysunku 1.22 widzimy wykres siły poprzecznej. W przedziale AB funkcja liniowa jest malejąca, więc
obciążenie ciągłe równomiernie rozłożone działa w dół. Wartość bezwzględna różnicy rzędnych pomiędzy
prawym i lewym końcem przedziału AB
∣
T
P
−
T
L
∣
=
∣
4,0−12,0∣=8,0 kN .
(1.24)
Wartość obciążenia ciągłego równomiernie rozłożonego wyznaczymy z warunku
q⋅4,0=8,0 kN ,
(1.25)
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
12
[m]
4,0
2,0
1
2,
0
4,0
T(x)
[kN]
2,0 kN/m
0,0
A
C
B
Rys. 1.22. Obciążenie ciągłe oraz wykres siły poprzecznej
czyli
q= 2,0
kN
m
.
(1.26)
W przedziale BC wykres siły poprzecznej jest funkcją stałą, więc obciążenie ciągłe wynosi zero. Obciążenie
ciągłe w obu przedziałach widzimy na rysunku 1.22. Na rysunku 1.23 możemy zobaczyć wykres siły po-
przecznej. W przedziale AB funkcja liniowa jest rosnąca, więc obciążenie ciągłe równomiernie rozłożone
działa do góry. Wartość bezwzględna różnicy rzędnych pomiędzy prawym i lewym końcem przedziału AB
∣
T
P
−
T
L
∣
=
∣
8,0−
−
12,0
∣
=
20,0 kN .
(1.27)
Wartość obciążenia ciągłego równomiernie rozłożonego wyznaczymy z warunku
q⋅4,0=20,0 kN ,
(1.28)
czyli
q=5,0
kN
m
.
(1.29)
W przedziale BC wykres siły poprzecznej jest funkcją stałą, więc obciążenie ciągłe wynosi zero. Obciążenie
ciągłe w obu przedziałach widzimy na rysunku 1.23.
[m]
4,0
2,0
12
,0
8,0
T(x)
[kN]
5,0 kN/m
0,0
A
C
B
Rys. 1.23. Obciążenie ciągłe oraz wykres siły poprzecznej
1.12. Zadania 271
−
300
Jeżeli w danym przedziale moment zginający jest stały, to siła poprzeczna wynosi zero. W przypadku
liniowej funkcji momentu zginającego funkcja siły poprzecznej jest stała, a jej wartość wyznaczymy z na -
stępującej zależności
T =tg
α
,
(1.30)
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
13
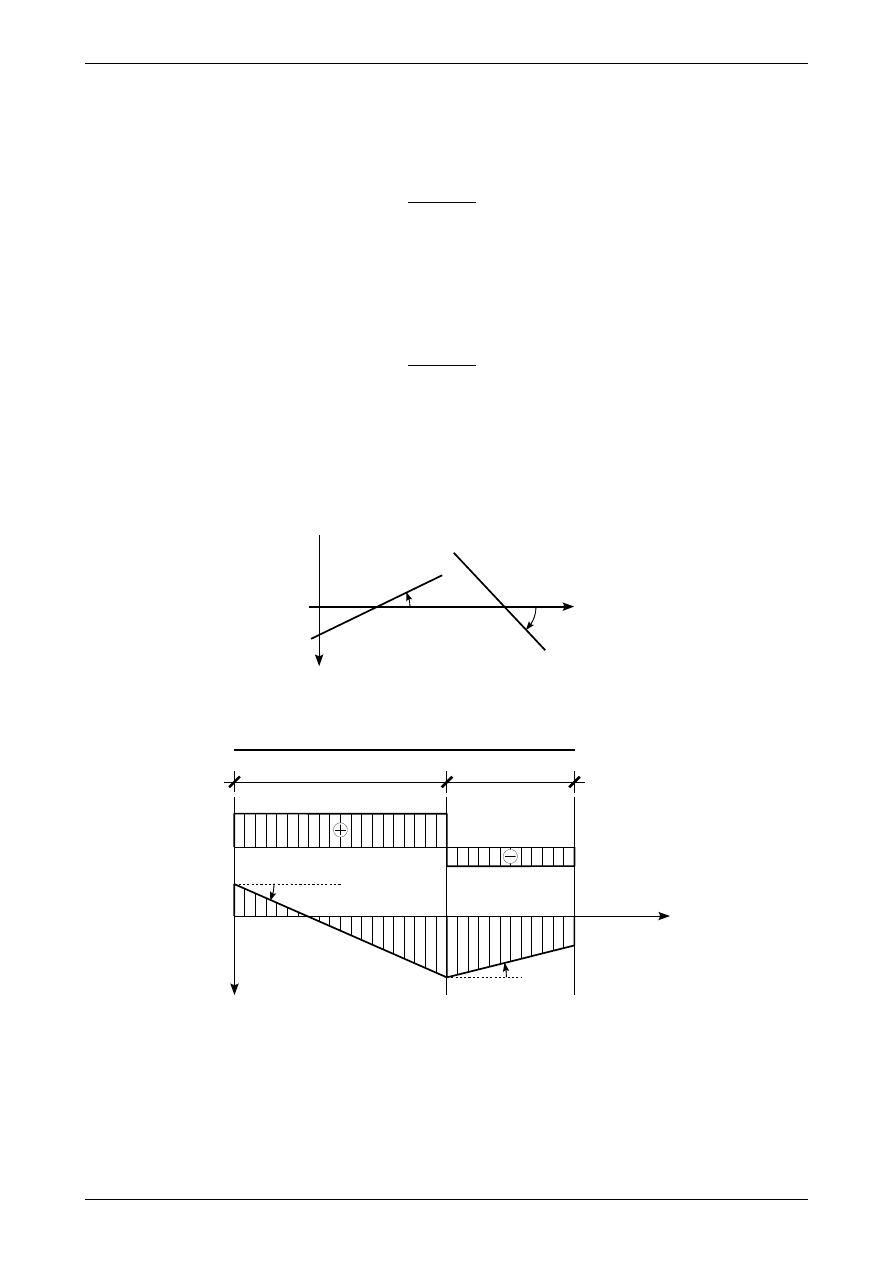
gdzie
α
jest kątem nachylenia liniowego wykresu momentu zginającego. Kąt ten jest dodatni, jeżeli obraca
osią X w kierunku osi Y, ujemny kąt
α
obraca się w przeciwnym kierunku. Widzimy to na rysunku 1.24. Oś
Y na tym rysunku skierowana jest w dół, ponieważ dodatni moment zginający w belkach rozciąga dolną
część belki. Na rysunku 1.25 możemy zobaczyć wykres momentu zginającego w dwóch przedziałach pręta.
Kąt
α
jest dodatni, a kąt
β
ujemny. Wartość bezwzględna tangensa kąta
α
∣
tg
α
∣
=
23,012,0
5,0
=
7,0 kN .
(1.31)
Siła poprzeczna w przedziale AB
T
AB
=
7,0 kN .
(1.32)
Wartość bezwzględna tangensa kąta
β
∣
tg
β
∣
=
23,0−11,0
3,0
=
4,0 kN .
(1.33)
Siła poprzeczna w przedziale BC
T
BC
=−
4,0kN .
(1.34)
Znak minus wynika z tego, że kąt
β
jest ujemny, a tangens ujemnego kąta jest także ujemny. Wykres siły po-
przecznej w pręcie widzimy na rysunku 1.25.
Y=M(x)
X
α
< 0
α
> 0
Rys. 1.24. Kąt nachylenia prostej
[m]
5,0
3,0
11
,0
2
3,
0
12
,0
T(x)
[kN]
M(x)
[kN∙m]
X
Y=M(x)
A
B
C
α
β
7,0
4,0
Rys. 1.25. Wykresy siły poprzecznej oraz momentu zginającego
1.13. Zadania 301
−
468
W przypadku, kiedy w przedziale wykres siły poprzecznej jest stały lub liniowy należy zastosować
metody przedstawione w punkcie 1.11. Jeżeli w danym przedziale wykres siły poprzecznej jest parabolicz-
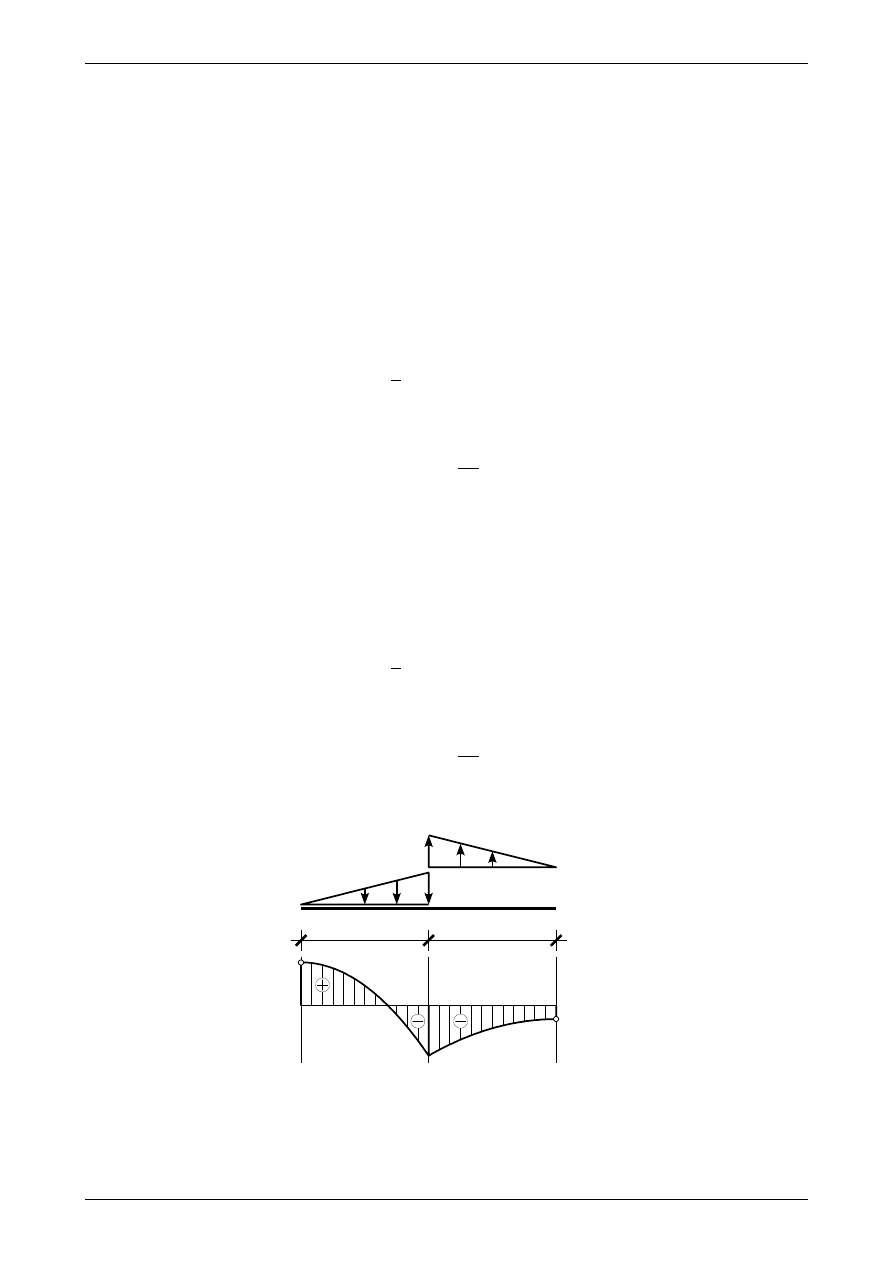
ny, to obciążenie ciągłe jest trójkątne. Ma ono następujące właściwości:
Dr inż. Janusz Dębiński
BNS-I
Mechanika teoretyczna
−
zadania sprawdzające
−
przewodnik do zadań
−
Część 1
14
•
jeżeli paraboliczny wykres siły poprzecznej jest malejący, to działa ono w dół
•
jeżeli paraboliczny wykres siły poprzecznej jest rosnący, to działa ono do góry
•
miejsce zerowe tego obciążenia znajduje się w punkcie, w którym paraboliczny wykres siły po -
przecznej ma ekstremum
•
wartość obciążenia ciągłego trójkątnego jest taka, aby siła wypadkowa z niego równa była wartości
bezwzględnej różnicy rzędnych pomiędzy prawym a lewym końcem przedziału.
Na rysunku 1.26 widzimy wykres siły poprzecznej. W przedziale AB funkcja kwadratowa jest malejąca,
więc obciążenie ciągłe trójkątne działa w dół. Miejsce zerowe tego obciążenia znajduje się w punkcie A.
Wartość bezwzględna różnicy rzędnych pomiędzy prawym i lewym końcem przedziału AB
∣
T
P
−
T
L
∣
=
∣−
37,0−32,0∣=69,0 kN .
(1.35)
Wartość obciążenia ciągłego trójkątnego wyznaczymy z zależności
1
2
⋅
q⋅3,0=69,0kN ,
(1.36)
czyli
q=46,0
kN
m
.
(1.37)
W przedziale BC funkcja kwadratowa jest rosnąca, więc obciążenie ciągłe trójkątne działa do góry. Miejsce
zerowe tego obciążenia znajduje się w punkcie C. Wartość bezwzględna różnicy rzędnych pomiędzy pra-
wym i lewym końcem przedziału BC
∣
T
P
−
T
L
∣
=
∣
−
10,0−
−
37,0
∣
=
27,0 kN .
(1.38)
Wartość obciążenia ciągłego trójkątnego wyznaczymy z zależności
1
2
⋅
q⋅3,0=27,0 kN ,
(1.39)
czyli
q=18,0
kN
m
.
(1.40)
Oba obciążenia ciągłe trójkątne możemy zobaczyć na rysunku 1.26.
18,0 kN/m
46,0 kN/m
3,0
3,0
32
,0
10
,0
[m]
37
,0
E
1
E
2
T(x)
[kN]
A
C
B
Rys. 1.26. Obciążenia ciągłe trójkątne oraz wykres siły poprzecznej
Dr inż. Janusz Dębiński
BNS-I