1
Część I
1. Przenikanie ciepła przez ścianę jednowarstwową.
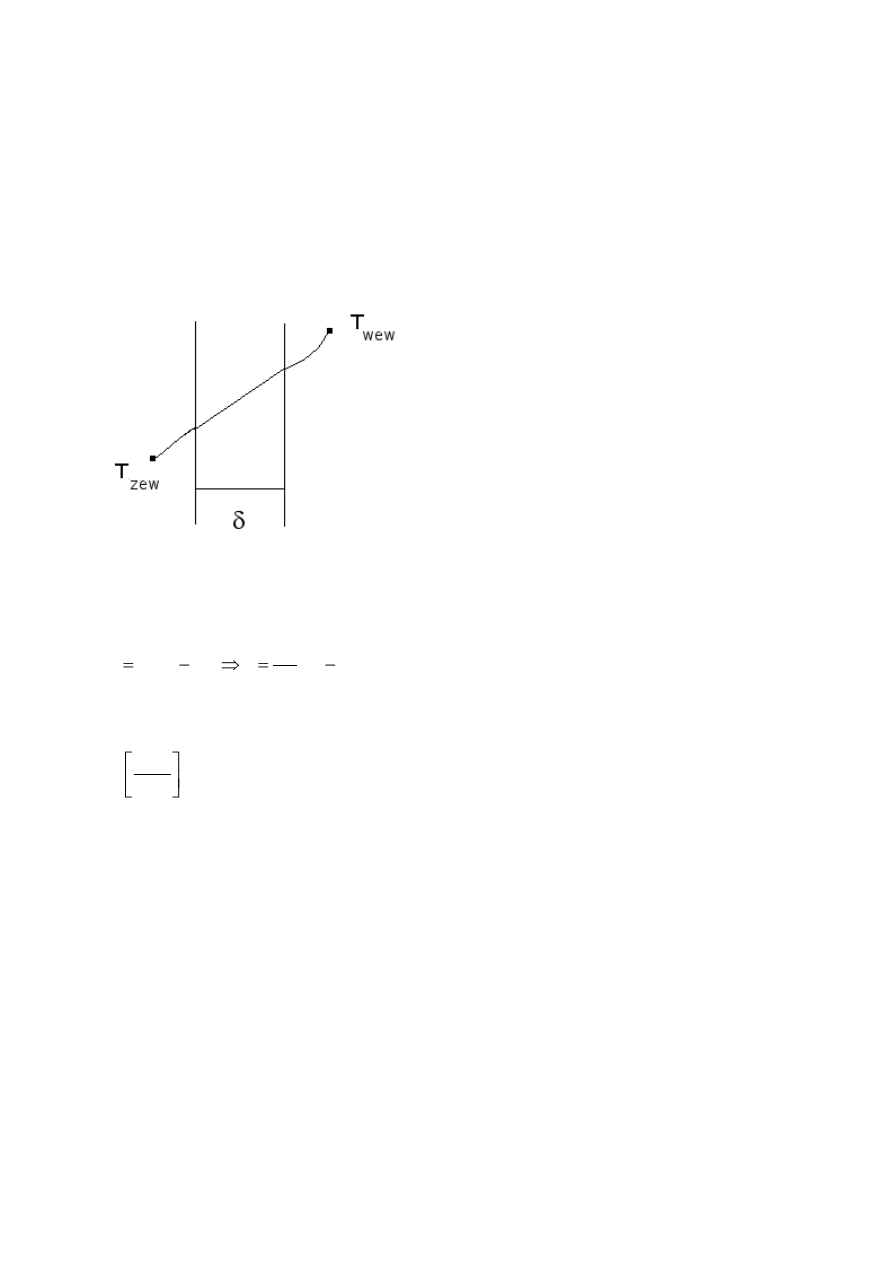
Przenikanie ciepła składa się z dwóch procesów przewodzenia ciepła i przejmowania ciepła.
Na powierzchniach ściany zachodzi przejmowanie ciepła z powietrza a w materiale ściany
odbywa się przewodzenie. Wokół ściany w powietrzu zachodzi wymiana ciepła przez
konwekcje.
1.1 Przejmowanie ciepła
Wzór Newtona
)
(
)
(
f
s
C
f
s
s
T
T
R
q
T
T
h
q
1
Gdzie:
K
m
W
h
s
2
- współczynnik przejmowania ciepła
T
s
- temperatura powierzchni przegrody
T
f
– temperatura powietrza w pewnej odległości od ściany. Jest to odległość w której
obecność ściany nie wpływa już na wartość temperatury.
Ze względu na inne warunki współczynnik przejmowania ciepła na zewnętrznej i
wewnętrznej powierzchni ściany ma inne wartości.
h
z
- współczynnik przejowania od strony środowiska zewnętrznego
h
w
– współczynnik przejmowania od strony środowiska wewnetrznego
Opory przejmowania ciepła sa odwrotnościami współczynników.
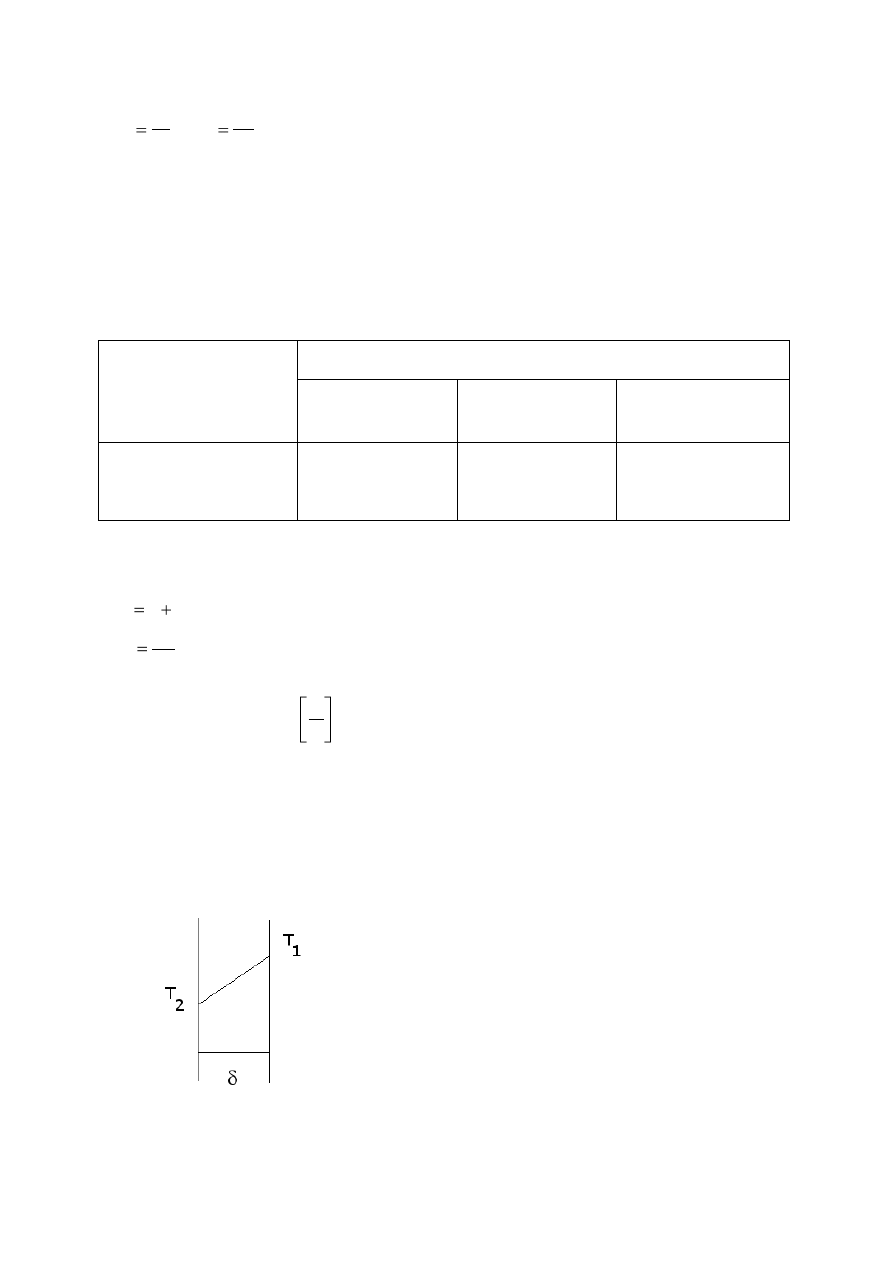
2
w
cw
z
cz
h
R
h
R
1
1
W projektach stosuje się oznaczenia (internal- wewnętrzne) R
ci
=R
cw
i (extrenal- zewnętrzne)
R
ce
=R
cz
Określenie współczynników oporów R
ci
i R
ce
w praktyce jest trudne. Będziemy posługiwać
się wartościami z normalizowanymi.
Tablica . Opory przejmowania ciepła wg. PN-EN ISO 6946
Opór przejmowania
ciepła
(m
2
K)/W
Kierunek strumienia cieplnego
w górę
poziomo
w dół
R
ci
R
ce
0,10
0,04
0,13
0,04
0,17
0,04
Korekta na wiatr za PN-EN ISO 6946
ce
ce
ce
h
R
v
h
1
4
4
Gdzie v- prędkość wiatru
s
m
1.2 Przewodzenie ciepła przez przegrodę jednowarstwową
T
1
,T
2
– temperatury powierzchni ściany
λ – współczynnik przewodzenia ciepła [W/(mK)]
3
Rys 1. Profil temperatury w przegrodzie jednowarstwowej
dx
dT
q
2
1
0
T
T
dT
dxq
1
2
1
2
T
T
q
T
T
q
W
K
m
mK
W
m
R
U
2
*
A zatem strumień przewodzonego ciepła mając dany opór będzie
2
m
W
R
t
q
Współczynnik przenikania ciepła U bierze pod uwagę zarówno przenikanie jak i
przewodzenie. Wzór na strumień ciepła przenikającego przez ścinkę można wyprowadzić.
Procesy przejmowania i przewodzenia ciepła można przedstawić jako procesy w kolejnych
warstwach. Warstwy odnoszące się do przejmowania będą leżały całkowicie w powietrzu
przy powierzchni ściany.
Dla każdej warstwy z osobna obowiązuje:
2
m
W
R
t
q
i
i
Całkowity spadek temperatury na wszystkich warstwach
ce
I
ci
t
t
t
t
(a)
4
Strumień ciepła przez wszystkie warstwy jest jednakowy
ce
ce
I
I
ci
ci
ce
ce
I
I
ci
ci
R
t
q
R
t
q
R
t
q
R
t
R
t
R
t
q
,
,
ce
ce
I
I
ci
ci
qR
t
qR
t
qR
t
,
,
Z (a) mamy
R
t
q
R
q
t
qR
qR
qR
t
ce
I
ci
Suma w mianowniku jest oporem przenikania który jest sumą oporów przejmowania i
przewodzenia
ce
ci
R
R
R
Współczynnik U jest odwrotnością tego oporu.
R
U
1
Zad. Dana jest ściana betonowa o λ=0,5 grubość ściany wynosi δ=0,2m. Obliczyć
współczynnik przenikania ciepła i strumień ciepła przez ściankę jeśli temperatura powietrza
wewnątrz wynosi 20
o
C a zewnątrz 5
o
C .
2
31
26
57
0
5
20
57
0
04
0
5
0
2
0
13
0
m
W
q
R
,
,
,
,
,
,
,
K
m
W
U
2
7
1,
Zad. Obliczyć strumień przez ściankę o δ=0,2m wykonana ze styropianu o λ=0,042.
Temperatura powietrza wewnątrz wynosi 20
o
C a zewnątrz 5
o
C .
K
m
W
U
m
W
q
R
2
2
2
0
04
3
93
4
5
20
93
4
04
0
042
0
2
0
13
0
,
,
,
,
,
,
,
,`
2. Przenikanie ciepła przez przegrodę wielowarstwową
Przejmowanie na brzegach ściany bez zmian. Przewodzenie ciepła polega na przewodzeniu
przez kolejne warstwy. Wzór na przewodzoną ilość ciepła można wyprowadzić tak samo jak
dla ściany jednowarstwowej z przejmowaniem. Jedyną różnicą jest większa liczba warstw.
5
Rys 2. Przemowanie i przewodzenie ciepła
Podsumowywując na rysunku mamy:
h
z
- współczynnik przejmowania od strony środowiska zewnętrznego
h
w
– współczynnik przejmowania od strony środowiska wewnetrznego
II
II
II
I
I
I
w
ce
z
ci
R
R
h
R
h
R
1
1
Strumienie ciepła przejmowane i przewodzone przez przegrodę są równe
ce
z
ce
R
t
q
q
Δt
z
– róznica temperatury między powietrzem w pewnej odległości od ściany po stronie
zewnętrznej a powierzchnią ściany po stronie zewnętrznej. Strumienie ciepła w warstwach I i
II to ten sam strumień q co przy przejmowaniu.
I
I
R
t
q
II
II
R
t
q
Ten sam strumień jest przejmowany od strony wewnętrznej:
ci
w
ci
R
t
q
q
Δt
z
– róznica temperatury między powietrzem w pewnej odległości od ściany po stronie
wewnętrznej a powierzchnią ściany po stronie wewnętrznej
Całkowity spadek temperatury:
w
II
I
z
t
t
t
t
t
ci
II
I
ce
qR
qR
qR
qR
t
6
R
t
q
Δt – różnica temperatur między powietrzem zewnętrznym a wewnętrznym
Zad. Obliczyć strumień ciepła przenikający przez ściankę dwuwarstwową λ
I
=0,042
mK
W
,
δ
1
=0,5 m, λ
II
=0,5
mK
W
,δ
II
=0,2 m, temperatura powietrza zewnętrznego wynosi 1
0
C,
Temperatura powietrza wewnętrznego 20
o
C.
K
m
W
U
m
W
q
W
K
m
R
2
2
2
08
0
52
1
47
12
1
20
47
12
13
0
5
0
2
0
042
0
5
0
04
0
,
,
,
,
,
,
,
,
,
,
,
Zad Ściana o grubości δ=0,25m składa się z warstwy izolacji cieplnej w postaci płyt
styropianowych o λ=0,042 i δ=0,05m i warstwy betonu o λ=0,5 i δ=0,2m. Temperatura
powietrza wewnątrz wynosi 20
o
C a zewnątrz 5
o
C .
K
m
W
U
m
W
q
R
2
2
57
0
52
8
76
1
5
20
76
1
04
0
5
0
2
0
042
0
05
0
13
0
,
,
,
,
,
,
,
,
,
,
4. Współczynnik strat ciepła
Aby odnieść straty ciepła do całej ściany lub wszystkich ścian wprowadzono współczynnik
strat ciepła. Jest to iloczyn współczynnika U i powierzchni ściany. Dodatkowo mnoży się go
przez tak zwany współczynnik korekty temperatury. Wynosi on 1 jeśli po zewnętrznej stronie
ściany jest temperatura zewnętrzna i jest mniejszy od 1 jeśli po zewnętrznej stronie jest
pomieszczenie nieogrzewane. Można obliczyć sumę tych współczynników dla kolejnych
ścian i otrzymujemy współczynnik dla całego budynku.
bUA
H
Zad. Oblicz całkowity współczynnik start ciepła dla dwóch przegród.
przegroda 1
1 warstwa
1
=0,042 W/(mK),
1
=0,2 m
2 warstwa
2
=0,5 W/(mK),
1
=0,45
Współczynnik korekty temperaturowej dla przegrody b=0,6, powierzchnia A
1
=100 m
2
przegroda 2
1 warstwa
1
=0,03 W/(mK),
1
=0,15
2 warstwa
2
=0,7 W/(mK) ,
2
=0,6
7
Współczynnik korekty temperaturowej dla przegrody b=1, powierzchnia A
2
=150 m
2
Opory cieplne i współczynniki przenikania
K
m
W
U
R
2
1
17
0
83
5
13
0
5
0
45
0
042
0
2
0
04
0
,
,
,
,
,
,
,
,
K
m
W
U
R
2
2
16
0
027
6
13
0
7
0
6
0
03
0
15
0
04
0
,
,
,
,
,
,
,
,
K
W
H
2
34
150
16
0
1
100
17
0
6
0
,
*
,
*
*
,
*
,
5. Obliczanie profilu temperatury w ścianie
Mając obliczony strumień ciepła przez ścianę i zakładając że jest on taki sam w każdej
warstwie można obliczyć temperatury w przekroju ściany. Obliczymy temperatury na
granicach warstw. Dla każdej warstwy n można napisać
n
n
n
n
n
R
T
T
R
t
q
1
(b)
Gdzie q jest strumieniem ciepła przez całą ściane i równocześnie strumieniem przez
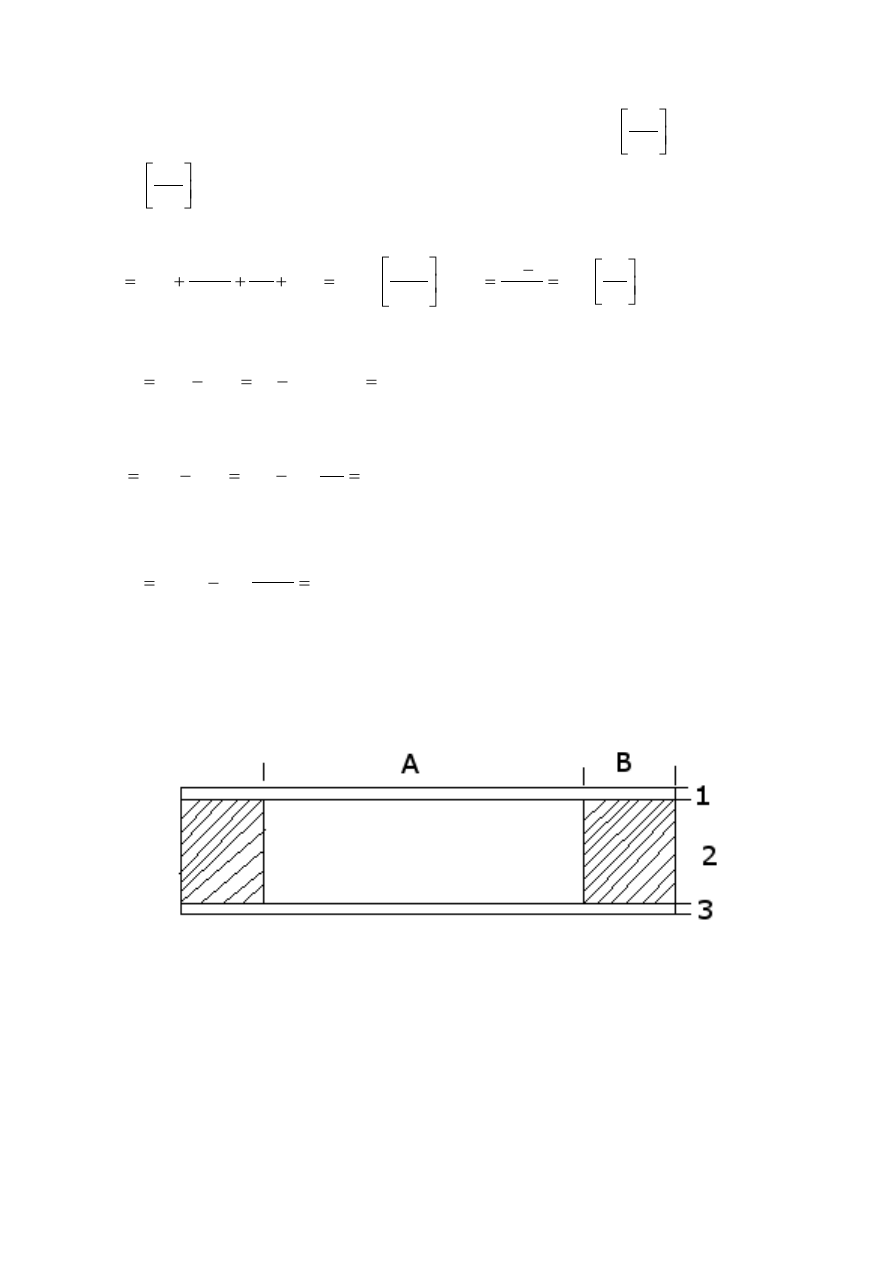
poszczególne warstwy. A T
n
i T
n-1
są temperaturami na stykach warstw jak pokazuje rysunek
4.
Rysunek 3 Obliczanie profilu temperatury w ścianie
Z równania (b) możemy wyznaczyć temperaturę T
n-1
w funkcji strumienia ciepła i oporu
termicznego warstwy leżącj miedzy temperaturami T
n
i T
n-1
)
,
(
1
1
n
n
n
n
qR
T
T
Analogicznie możemy postąpić ze wszystkimi warstwami. Można tez wyznaczyć temperaturę
powierzchni ściany podstawiając jako T
n
temperaturę zewnętrzną a jako R opór przejmowania
ciepła.
8
Zad. Obliczyć profil temperatury w ściance dwuwarstwowej λ
I
=0,042
mK
W
, δ
1
=0,5 m, λ
II
=0,5
mK
W
,δ
II
=0,2 m, temperatura powietrza zewnętrznego wynosi 1
0
C, Temperatura
powietrza wewnętrznego 20
o
C.
,
,
,
,
,
,
,
,
,
,
2
2
52
1
47
12
1
20
47
12
13
0
5
0
2
0
042
0
5
0
04
0
m
W
q
W
K
m
R
Temperatura powierzchni wewnętrznej ściany
C
qR
T
T
O
ci
wew
swew
8
19
13
0
52
1
20
,
,
*
,
Temperatura na styku warstw
C
qR
T
T
O
II
swew
192
19
5
0
2
0
52
1
8
19
1
,
,
,
,
,
Temperatura powierzchni zewnętrznej ściany
C
T
o
szew
1
1
042
0
5
0
52
1
192
19
,
,
,
,
,
6. Obliczenie ścian niejednorodnych cieplnie.
Załóżmy, że mamy element niejednorodny pod względem cieplnym jak na rysunku. Element
dzielimy na tzw wycinki obejmujące przekroje elementów jednorodne termicznie, oraz
warstwy które zawierają części o różnych parametrach termicznych ale zmienność następuje
w całym przekroju warstwy. Widok z góry takiej przegrody pokazuje rysunek 5.
Rys.4 Wycinki (A i B) i warstwy (1,2 i3) elementu niejednorodnego termicznie
Analizując przegrodę (rys.4) pociętą na wycinki i warstwy.
Każdy wycinek m
j
(m=A,B) ma względne pole powierzchni f
m.
Suma względnych pól powierzchni wycinków jest równa jedności.
9
1
B
A
f
f
(6)
gdzie
A
A
f
m
m
.
W przypadku elementów (ścian ) niejednorodnych termicznie opory obliczamy dwoma
sposobami:
a) Kres górny całkowitego oporu cieplnego R
g
,
b) Kres dolny całkowitego oporu cieplnego R
d
.
Kres górny całkowitego oporu cieplnego R
g
, obliczamy w następujący sposób:
Każdy wycinek m
j
stanowi przegrodę jednorodną wielowarstwową i możemy obliczyć opór
cieplny R
mj
Obliczamy opory całkowite każdego wycinka (m=A,B) od powietrza zewnętrznego do
wewnętrznego według wyrażenia (7):
ci
m
m
m
ce
m
R
R
R
R
R
R
3
2
1
(7)
Gdzie R
mi
to opory kolejnych warstw w wycinku
Mając opory wszystkich wycinków (R
A
, R
B
) obliczamy kres górny oporu elementu z
sumowania udziałów współczynnika przenikania każdego wycinka m z zależności:
B
B
A
A
g
R
f
R
f
R
1
(8)
Kres dolny całkowitego oporu cieplnego R
d
, obliczamy następująco:
W przypadku warstw niejednorodnych termicznie (tu warstwa 2) obliczamy opory warstwy z
zależności:
2
2
2
1
B
B
A
A
R
f
R
f
R
(9)
Gdzie R
A2
i R
B2
to opory cieplne w poszczególnych częściach jednorodnych warstwy 2
Obliczamy kres dolny całkowitego oporu cieplnego ze wzoru dla elementu warstwowego
ce
ci
d
R
R
R
R
R
2
1
(12)
Po obliczeniu kresu górnego i dolnego opór elementu obliczamy ze wzoru na średnią
arytmetyczną:
2
g
d
R
R
R
(13)
Zad Dana jest ściana szkieletowa jak na rysunku 6.
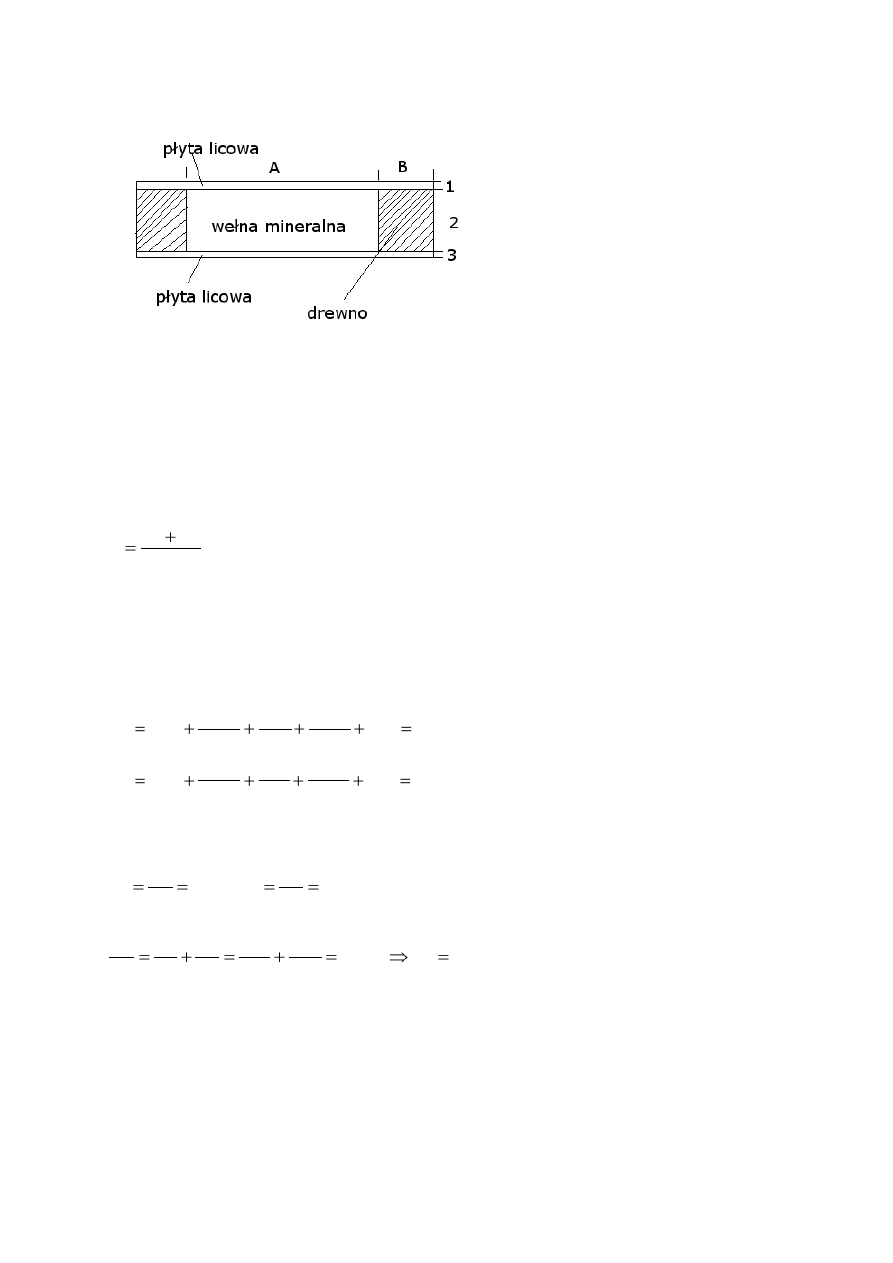
10
Rys 5. Schemat zadania
Zad. Ściana składa się ze szkieletu drewnianego i wypełnienia z wełny mineralnej (rys 5).
Wełna mineralna ma parametry λ=0,04 i grubość δ=0,17m, drewno λ=0,16 i δ=0,17m, płyty
licowe zewnętrzna λ=0,15 i δ=0,012m i wewnętrzna λ=0,14 i δ=0,013m. Długości A=0,6
B=0,1 m Obliczyć strumień ciepła przez tą ścianę. Temperatura zewnętrzna 2
o
C. Temperatura
wewnętrzna 20
o
C.
Opór cieplny:
2
g
d
R
R
R
Gdzie:
Kres górny:
Opory wycinków
40
1
13
0
14
0
013
0
16
0
17
0
15
0
012
0
04
0
59
4
13
0
14
0
013
0
04
0
17
0
15
0
012
0
04
0
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
B
A
R
R
Udziały wycinków
14
0
7
0
1
0
85
0
7
0
6
0
,
,
,
,
,
,
B
A
f
f
44
3
29
0
59
4
85
0
40
1
14
0
1
,
,
,
,
,
,
g
B
B
A
A
g
R
R
f
R
f
R
Kres dolny:
Opór przewodzenia ciepła warstwy 2
11
94
2
34
0
2
0
14
0
25
4
85
0
0628
1
15
0
04
0
17
0
85
0
16
0
17
0
15
0
1
,
,
,
,
,
,
,
,
,
,
,
,
,
,
z
z
R
R
ce
ci
d
R
R
R
R
R
R
3
2
1
282
3
04
0
15
0
12
0
94
2
14
0
013
0
013
0
,
,
,
,
,
,
,
,
d
R
Całkowity opór cieplny ściany:
W
K
m
R
R
R
d
g
2
363
3
2
282
3
444
3
2
,
,
,
Strumień ciepła:
K
m
W
m
W
q
2
2
3
0
35
5
363
3
2
20
,
,
,
Obliczamy trzy cyfry znaczące wyniki zaokrąglamy do dwóch cyfr.