
Wyznaczanie naprężeń stycznych
wywołanych siłą tnącą
9
Wprowadzenie
Naprężenia styczne wywołane siłą tnącą wyznaczamy w oparciu o wzór Żurawskiego.
)
(z
b
I
S
T
τ
y
y
z
z
⋅
⋅
=
gdzie:
z
T –
siła tnąca (styczna do przekroju),
y
S
– moment statyczny względem głównej osi bezwładności
y,
części pola przekroju poprzecznego, odciętej linią przechodzącą
przez punkt dla którego liczymy naprężenia styczne,
y
I
–
moment
bezwładności przekroju poprzecznego,
względem głównej osi bezwładności
y,
)
(z
b
– szerokość przekroju poprzecznego na poziomie punktu,
dla którego liczymy naprężenia styczne.
Przykład
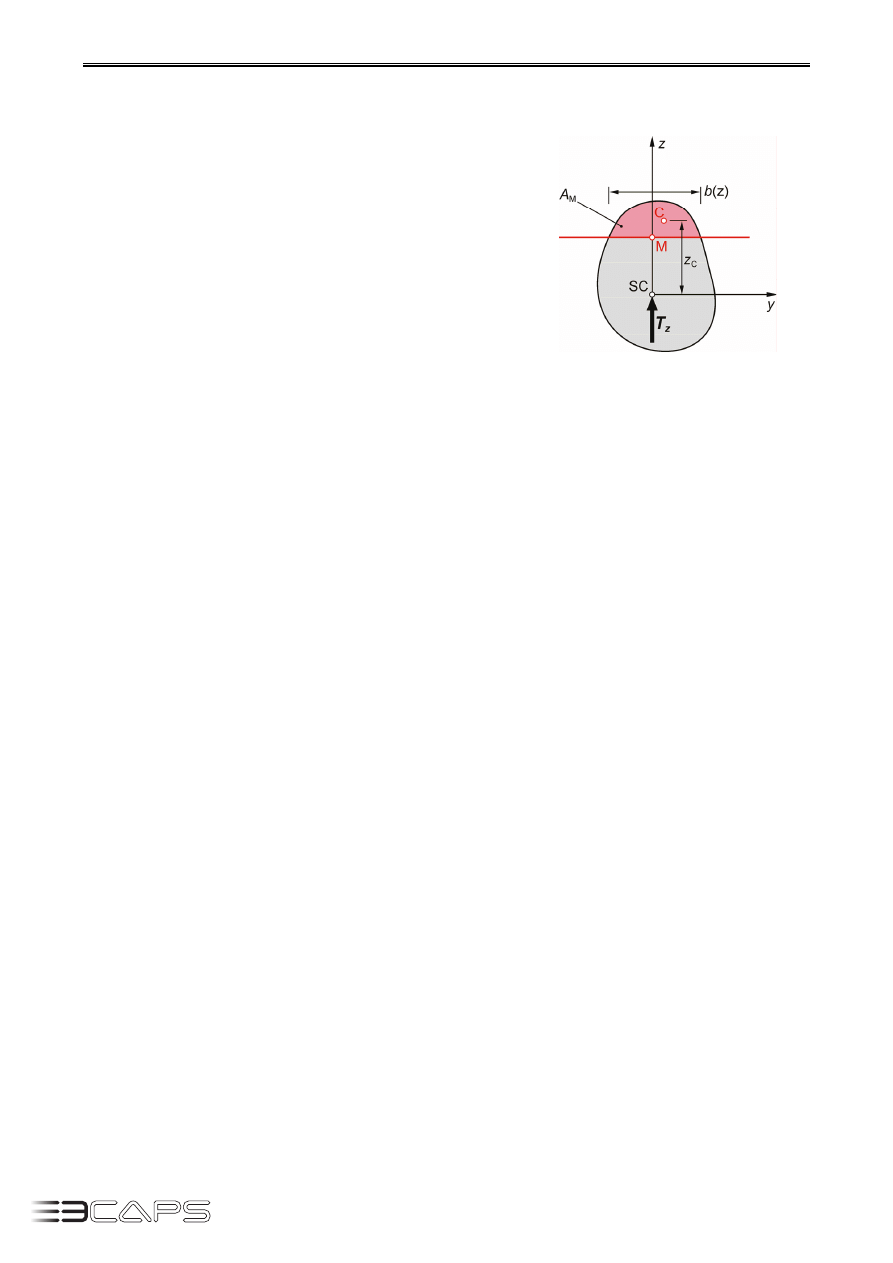
Dla dowolnego przekroju pokazanego na rys. 9.1, chcemy policzyć naprężenia styczne
w punkcie M, wywołane siłą tnącą
z
T . Środek ciężkości rozpatrywanego przekroju
znajduje się w punkcie SC. Osie y i z są głównymi osiami bezwładności przekroju.
Dla tychże osi wyznaczamy momenty bezwładności przekroju (w naszym przypadku
jedynie moment
y
I
). Przez interesujący nas punkt prowadzimy równolegle do osi y
linię prostą, która odcina część pola przekroju poprzecznego. Moment statyczny odcię-
tego fragmentu, którego pole powierzchni jest równe A
M
, a środek ciężkości znajduje
się w punkcie C, wynosi
C
M
M
z
A
S
y
⋅
=
gdzie
C
z
jest odległością środka ciężkości odciętej części przekroju poprzecznego od
głównej osi bezwładności.
Na poziomie punktu M szerokość przekroju poprzecznego jest równa
)
(z
b
, a zatem
zależność na naprężenia styczne przyjmie postać
)
(
M
M
z
b
I
S
T
τ
y
y
z
z
⋅
⋅
=
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.2
Naprężenia o tej wartości występują w każdym
punkcie przekroju poprzecznego leżącym na
poziomie punktu M.
Maksymalne wartości naprężeń stycznych wy-
stępować będą zawsze w warstwie leżącej na
poziomie środka ciężkości przekroju – odcięte
części pola przekroju (górna i dolna) są sobie
równe i osiągają wartości ekstremalne.
Rys. 9.1.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.3
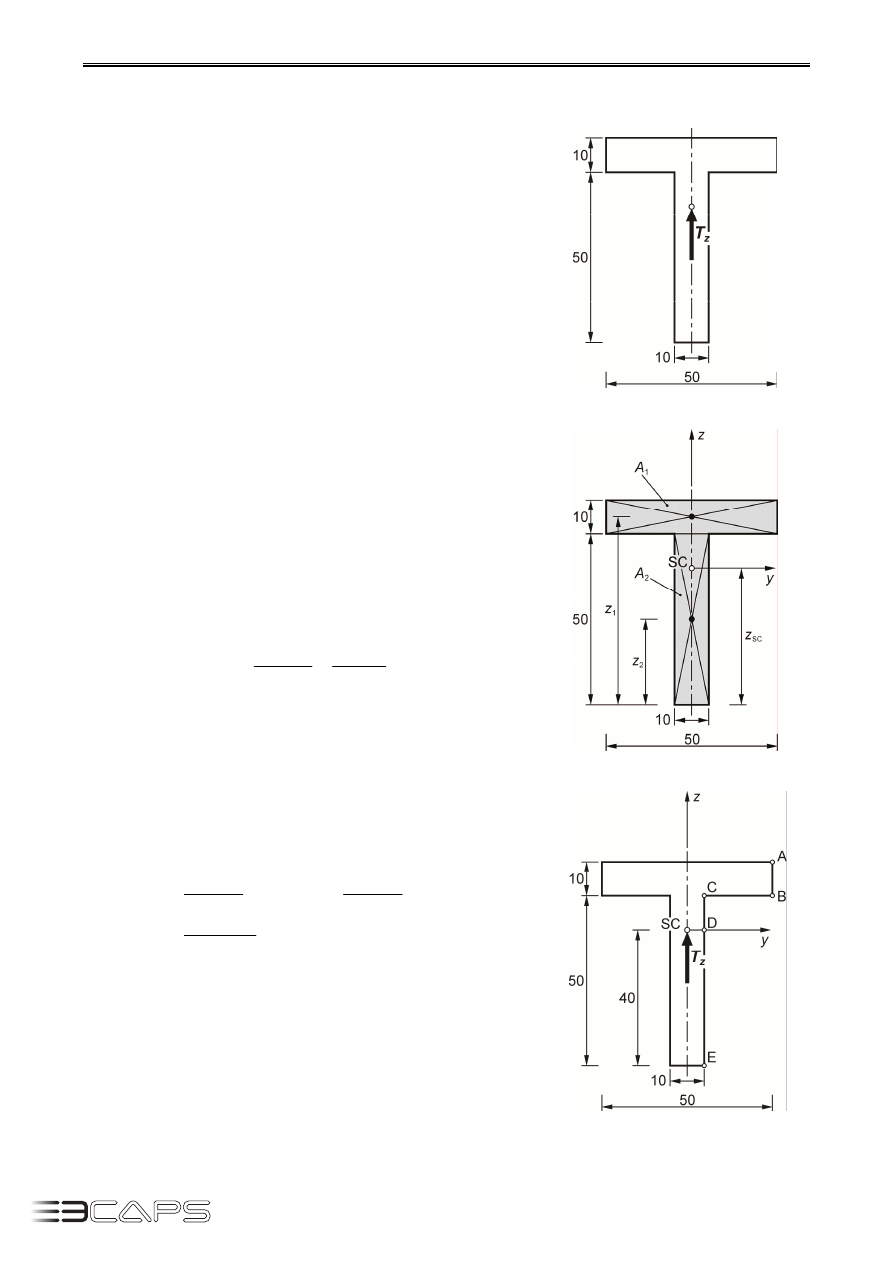
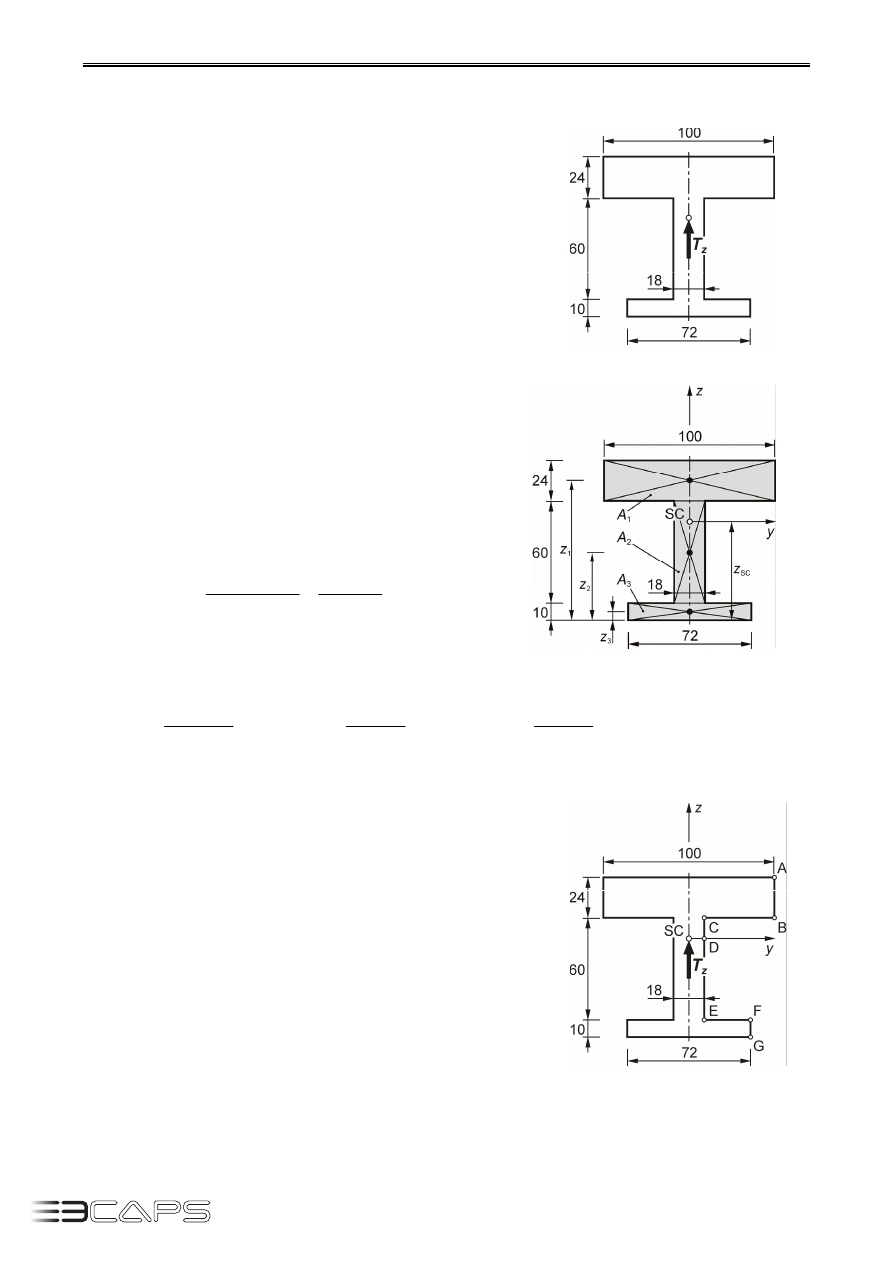
Zadanie 9.1.
Dla przekroju teowego (rys. 9.2) obciążonego siłą tnącą
kN
10
=
z
T
wyznaczyć rozkład naprężeń stycznych
z
τ
.
Wymiary przekroju podano w [mm].
Rozwiązanie
Wyznaczamy środek ciężkości rozpatrywanego przekroju.
W tym celu obliczymy statyczny moment względem pod-
stawy teownika Przekrój składa się z dwu prostokątów
o polach powierzchni
1
A
i
2
A
(rys. 9.3). Moment statyczny
jest równy
3
2
2
1
1
mm
000
40
25
50
10
55
10
50
=
⋅
⋅
+
⋅
⋅
=
=
+
=
z
A
z
A
S
Współrzędna środka ciężkości
SC
z wynosi
mm
40
1000
000
40
2
1
SC
=
=
+
=
A
A
S
z
Określamy główny centralny moment bezwładności
y
I .
W tym celu wyznaczamy główne centralne momenty bez-
władności poszczególnych prostokątów, a następnie, wy-
korzystując twierdzenie Steinera, określamy moment dla
całego przekroju
4
2
3
2
3
2
SC
2
2
2
2
SC
1
1
1
mm
3
1000000
)
15
(
500
12
50
10
15
500
12
10
50
)
(
)
(
=
=
−
⋅
+
⋅
+
⋅
+
⋅
=
=
−
+
+
−
+
=
z
z
A
I
z
z
A
I
I
y
y
y
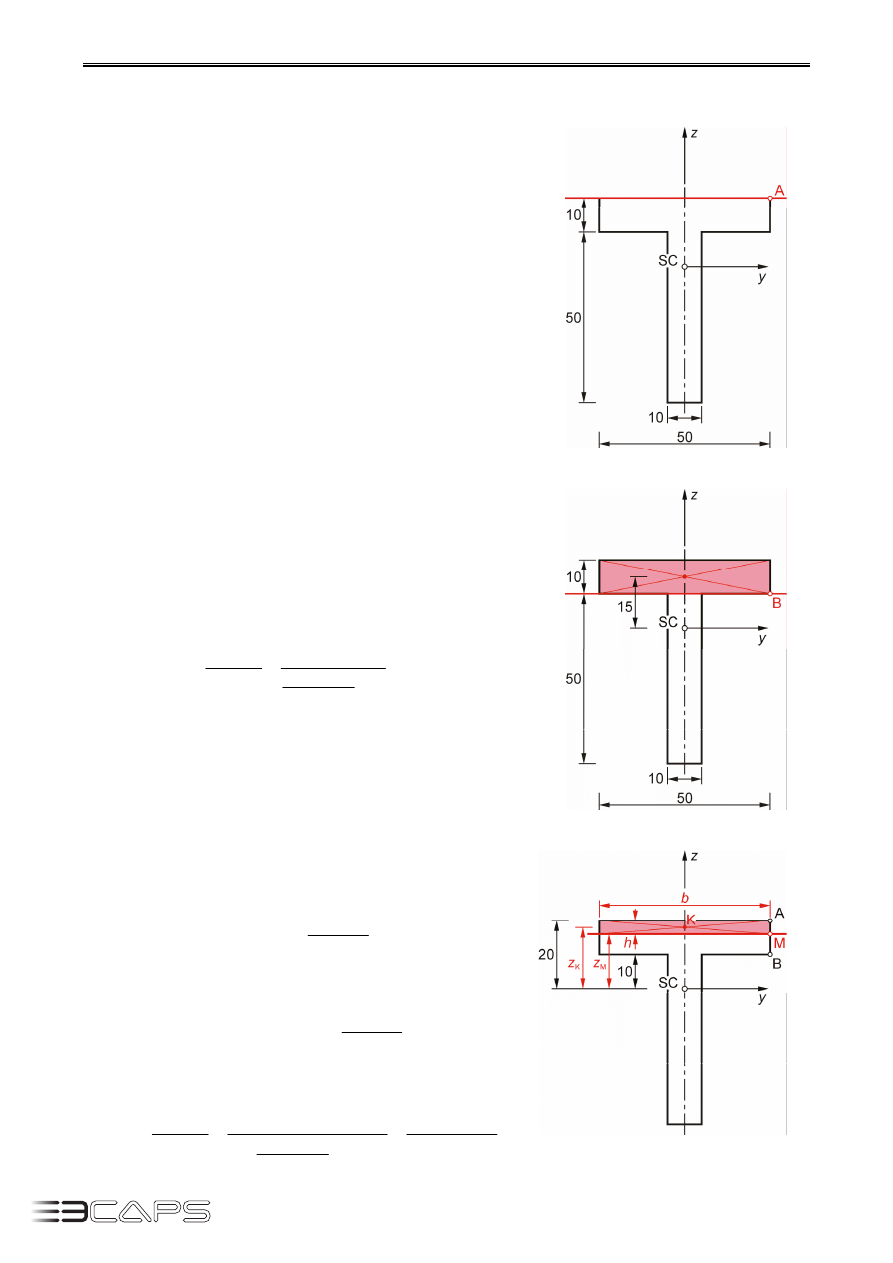
Wyznaczamy rozkład naprężeń stycznych. Musimy okreś-
lić wartości naprężeń w punktach A, B, C, D i E (rys. 9.4).
Rys. 9.2.
Rys. 9.3.
Rys. 9.4.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.4
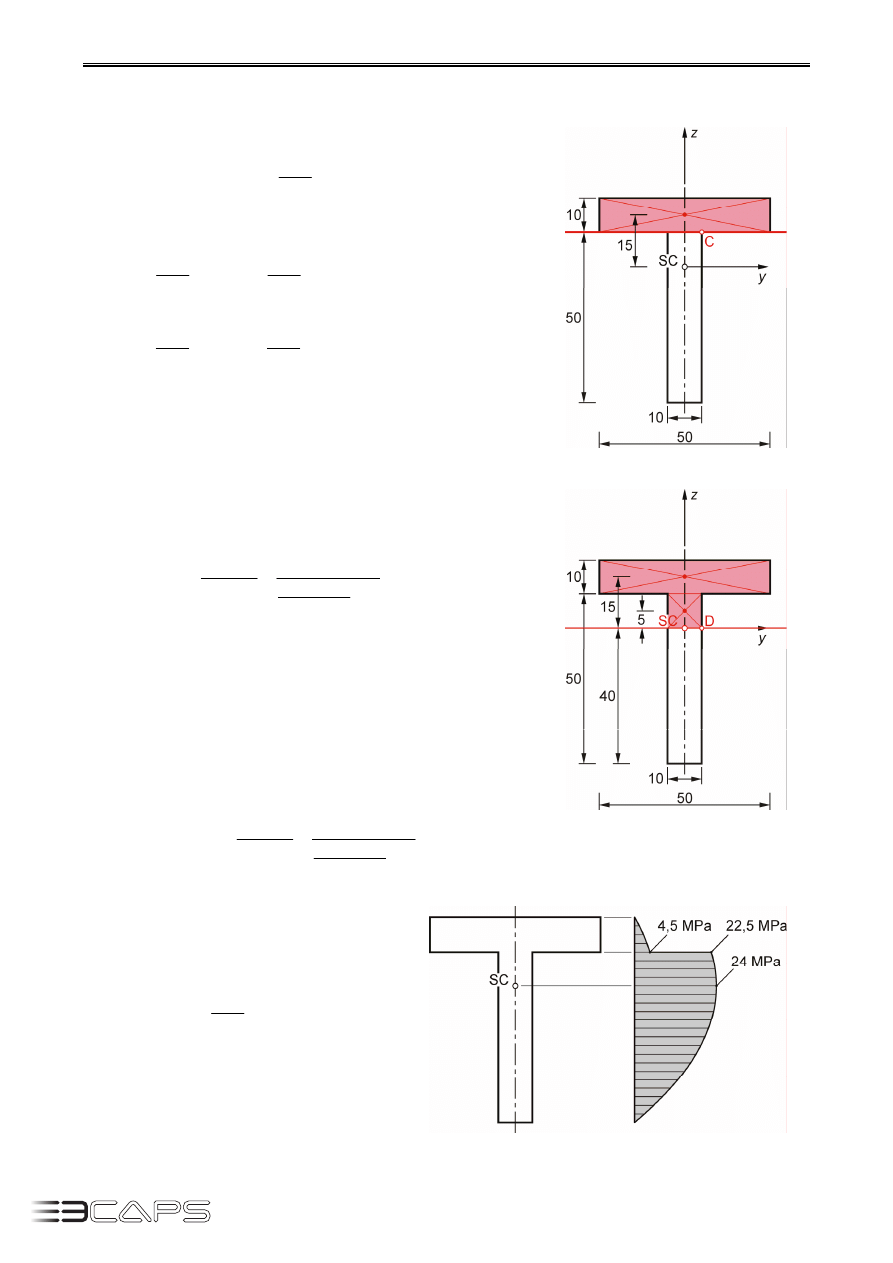
Punkt A (rys. 9.5)
Przez punkt A prowadzimy prostą. Jak widać nie od-
cina ona żadnej części pola przekroju, a zatem mo-
ment statyczny
A
y
S będzie równy zero. Naprężenia dla
punktu A wynoszą
0
A
=
z
τ
Podobna sytuacja wystąpi w przypadku punktu E –
stąd wniosek, że w skrajnych warstwach przekroju
poprzecznego naprężenia styczne przyjmują wartość
zerową.
Punkt B (rys. 9.6)
Prosta poprowadzona przez punkt B odcina prostokąt
o wymiarach
mm
10
50 ×
. Jego moment statyczny
B
y
S
jest równy
3
B
mm
7500
15
10
50
=
⋅
⋅
=
y
S
Szerokość przekroju poprzecznego na poziomie punk-
tu B wynosi
mm
50
)
( =
z
b
Wyznaczamy naprężenia styczne
B
z
τ
MPa
5
,
4
50
3
1000000
7500
10000
)
(
B
B
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
Rozkład naprężeń pomiędzy punktami A i B wyzna-
czymy w oparciu o rysunek 9.7. Prosta poprowa-
dzona przez dowolny punkt M, oddalony od osi y
o wartość
M
z
, odcina prostokąt, którego szerokość b
jest stała, równa 50 mm, a wysokość h wynosi
M
20 z
h
−
=
Odległość środka ciężkości odciętej części (punkt K)
od osi y jest równa
2
20
M
K
z
z
+
=
Zatem moment statyczny odciętej części możemy za-
pisać w sposób następujący
)
400
(
25
2
20
)
20
(
50
2
M
M
M
K
M
z
z
z
z
h
b
S
y
−
=
+
⋅
−
⋅
=
⋅
⋅
=
Ogólna zależność na naprężenia styczne dla odcinka
AB ma postać
200
)
(400
3
50
3
1000000
)
(400
25
10000
)
(
2
M
2
M
M
AB
z
z
z
b
I
S
T
τ
y
y
z
z
−
=
⋅
−
⋅
=
⋅
⋅
=
Rys. 9.5.
Rys. 9.6.
Rys. 9.7.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.5
Wyprowadzona zależność jest parabolą
[MPa]
6
200
3
2
M
AB
+
−
=
z
τ
z
Dokonajmy sprawdzenia powyższej zależności.
Dla punktu A:
mm
20
A
=
z
0
6
20
200
3
6
200
3
2
2
A
A
=
+
⋅
−
=
+
−
=
z
τ
z
Dla punktu B:
mm
10
B
=
z
MPa
5
,
4
6
10
200
3
6
200
3
2
2
B
B
=
+
⋅
−
=
+
−
=
z
τ
z
Punkt C (rys. 9.8)
W przypadku punktu C sytuacja wygląda podobnie
jak w punkcie B (
B
C
y
y
S
S =
) – zmienia się jedynie szero-
kość przekroju poprzecznego
mm
10
)
( =
z
b
Naprężenia styczne
C
z
τ
są równe
MPa
5
,
22
10
3
1000000
7500
10000
)
(
C
C
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
Punkt D (rys. 9.9)
Moment statyczny odciętej części przekroju jest równy
3
D
mm
8000
5
10
10
15
10
50
=
⋅
⋅
+
⋅
⋅
=
y
S
a szerokość przekroju poprzecznego
mm
10
)
( =
z
b
Naprężenia styczne
D
z
τ wynoszą
MPa
24
10
3
1000000
8000
10000
)
(
D
max
D
=
⋅
⋅
=
⋅
⋅
=
=
z
b
I
S
T
τ
τ
y
y
z
z
z
Rys. 9.8.
Rys. 9.9.
Podobnie jak w przypadku odcinka
AB, również na odcinku DE rozkład
naprężeń jest opisany parabolą.
Jej równanie ma postać
[MPa]
24
200
3
2
CE
+
−
=
z
τ
z
Wynik końcowy przedstawiono
na rysunku 9.10.
Rys. 9.10.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.6
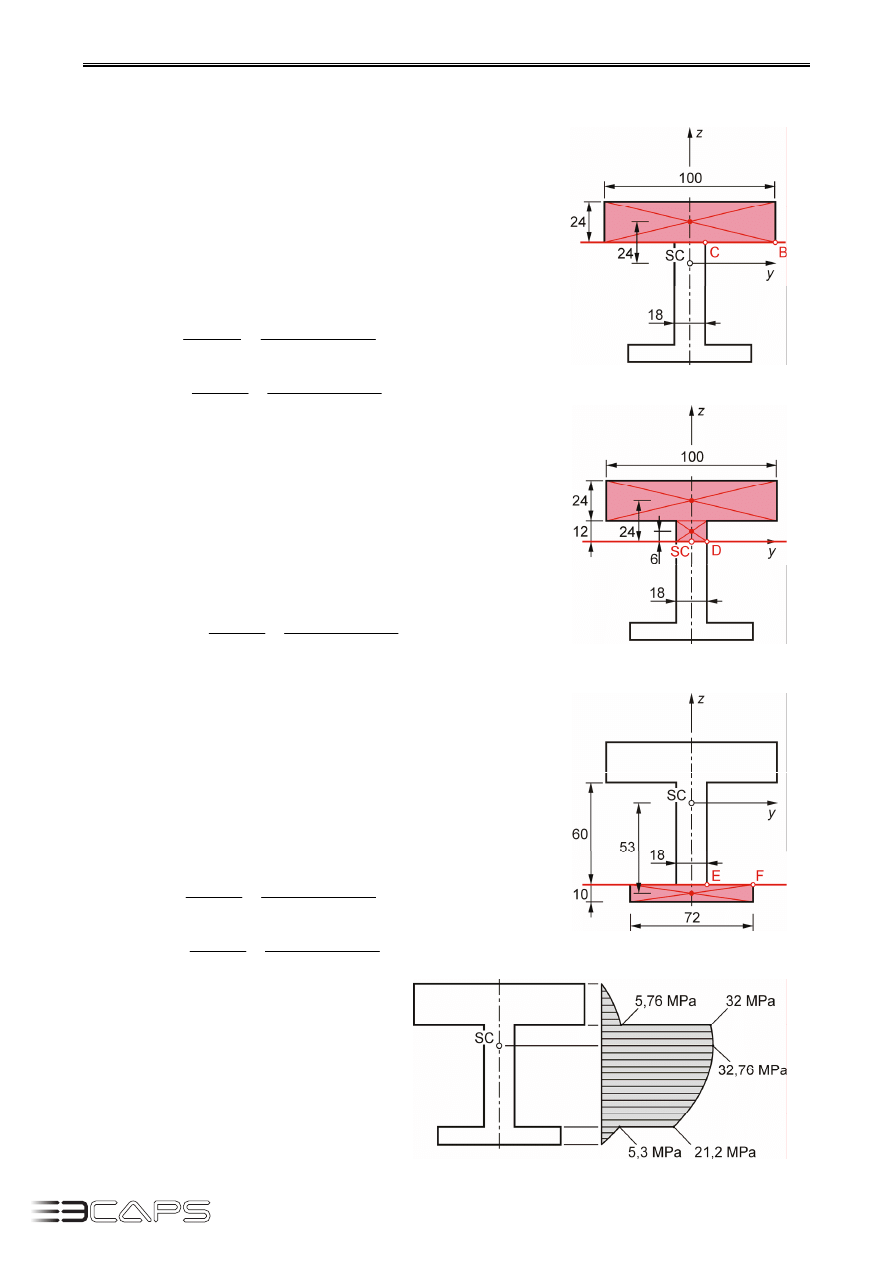
Zadanie 9.2.
Dla przekroju dwuteowego (rys. 9.11) obciążonego
siłą tnącą kN
42
=
z
T
wyznaczyć rozkład naprę-
żeń stycznych
z
τ . Wymiary w [mm].
Rozwiązanie
Wyznaczamy środek ciężkości rozpatrywanego
przekroju (rys. 9.12). Moment statyczny względem
podstawy jest równy
3
3
3
2
2
1
1
mm
00
2436
5
10
72
40
60
18
82
24
100
=
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
=
+
+
=
z
A
z
A
z
A
S
Współrzędna środka ciężkości
SC
z wynosi
mm
58
4200
43600
2
3
2
1
SC
=
=
+
+
=
A
A
A
S
z
Określamy główny centralny moment
bezwładności przekroju
y
I .
Rys. 9.11.
Rys. 9.12.
4
2
3
2
3
2
3
2
SC
3
3
3
2
SC
2
2
2
2
SC
1
1
1
mm
4200000
)
53
(
720
12
10
72
)
18
(
1080
12
60
18
24
2400
12
24
100
)
(
)
(
)
(
=
=
−
⋅
+
⋅
+
−
⋅
+
⋅
+
⋅
+
⋅
=
=
−
+
+
−
+
+
−
+
=
z
z
A
I
z
z
A
I
z
z
A
I
I
y
y
y
y
Określamy wartości naprężeń w punktach A, B, C, D, E,
F i G (rys. 9.13). W skrajnych warstwach, tj. dla punk-
tów A i G, naprężenia są równe
0
G
A
=
=
z
z
τ
τ
Rys. 9.13.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.7
Punkty B i C (rys. 9.14)
Moment statyczny części odciętej wynosi
3
C
B
mm
57600
24
24
100
=
⋅
⋅
=
=
y
y
S
S
Szerokość przekroju jest równa
mm
100
)
(
=
z
b
dla punktu B
mm
18
)
( =
z
b
dla punktu C
Wyznaczamy naprężenia styczne
MPa
76
,
5
100
4200000
57600
42000
)
(
B
B
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
MPa
32
18
4200000
57600
42000
)
(
C
C
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
Punkt D (rys. 9.15)
Moment statyczny części odciętej wynosi
3
D
mm
58896
6
12
18
24
24
100
=
⋅
⋅
+
⋅
⋅
=
y
S
Szerokość przekroju jest równa
mm
18
)
( =
z
b
Wyznaczamy naprężenia styczne
MPa
72
,
32
18
4200000
58896
42000
)
(
D
max
D
=
⋅
⋅
=
⋅
⋅
=
=
z
b
I
S
T
τ
τ
y
y
z
z
z
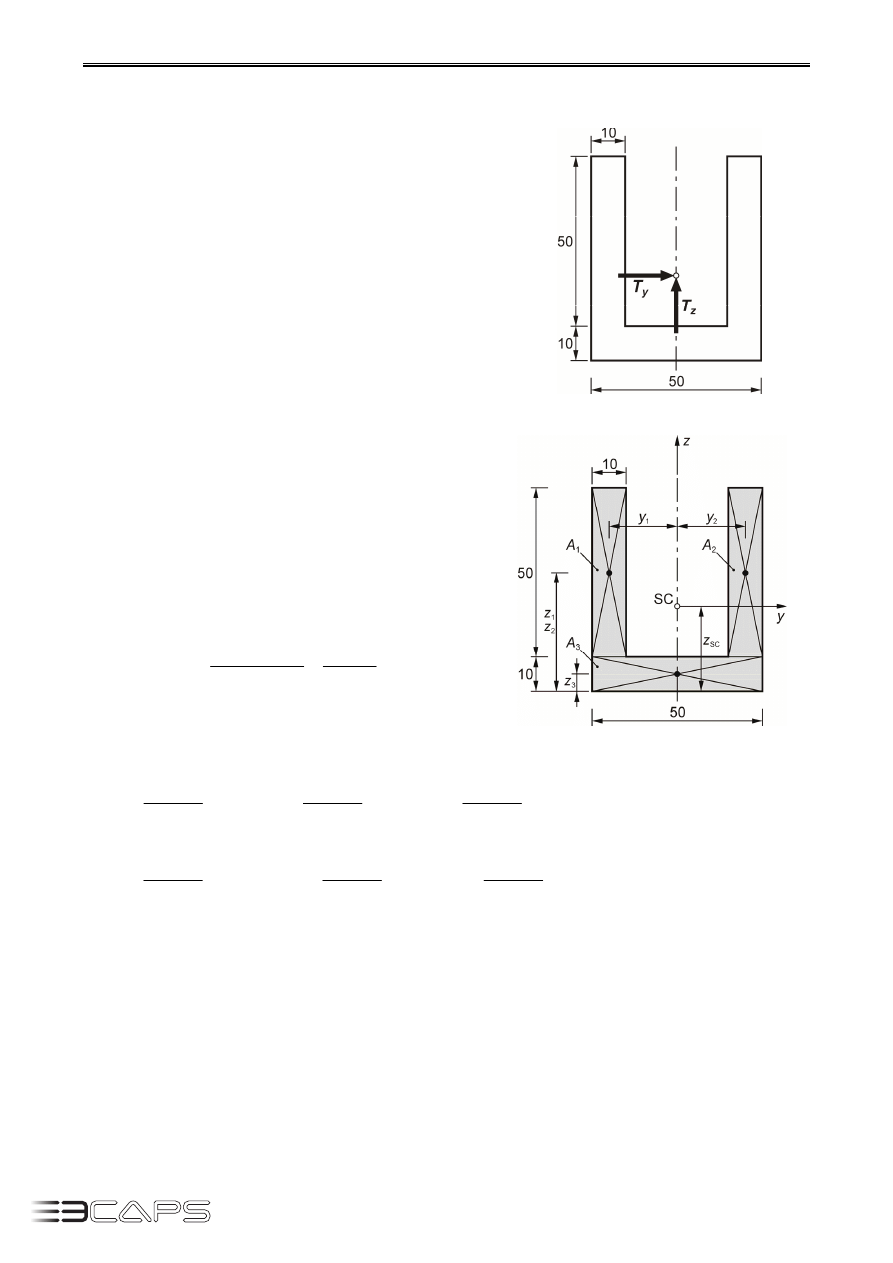
Punkt E i F (rys. 9.16)
Moment statyczny części odciętej wynosi
3
F
E
mm
38160
53
10
72
=
⋅
⋅
=
=
y
y
S
S
Szerokość przekroju jest równa
mm
18
)
( =
z
b
dla punktu E
mm
72
)
( =
z
b
dla punktu F
Wyznaczamy naprężenia styczne
MPa
2
,
21
18
4200000
38160
42000
)
(
E
E
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
MPa
3
,
5
72
4200000
38160
42000
)
(
F
F
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
Rys. 9.14.
Rys. 9.15.
Rys. 9.16.
Rozwiązanie końcowe przedstawiono
na rysunku 9.17.
Rys. 9.17.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.8
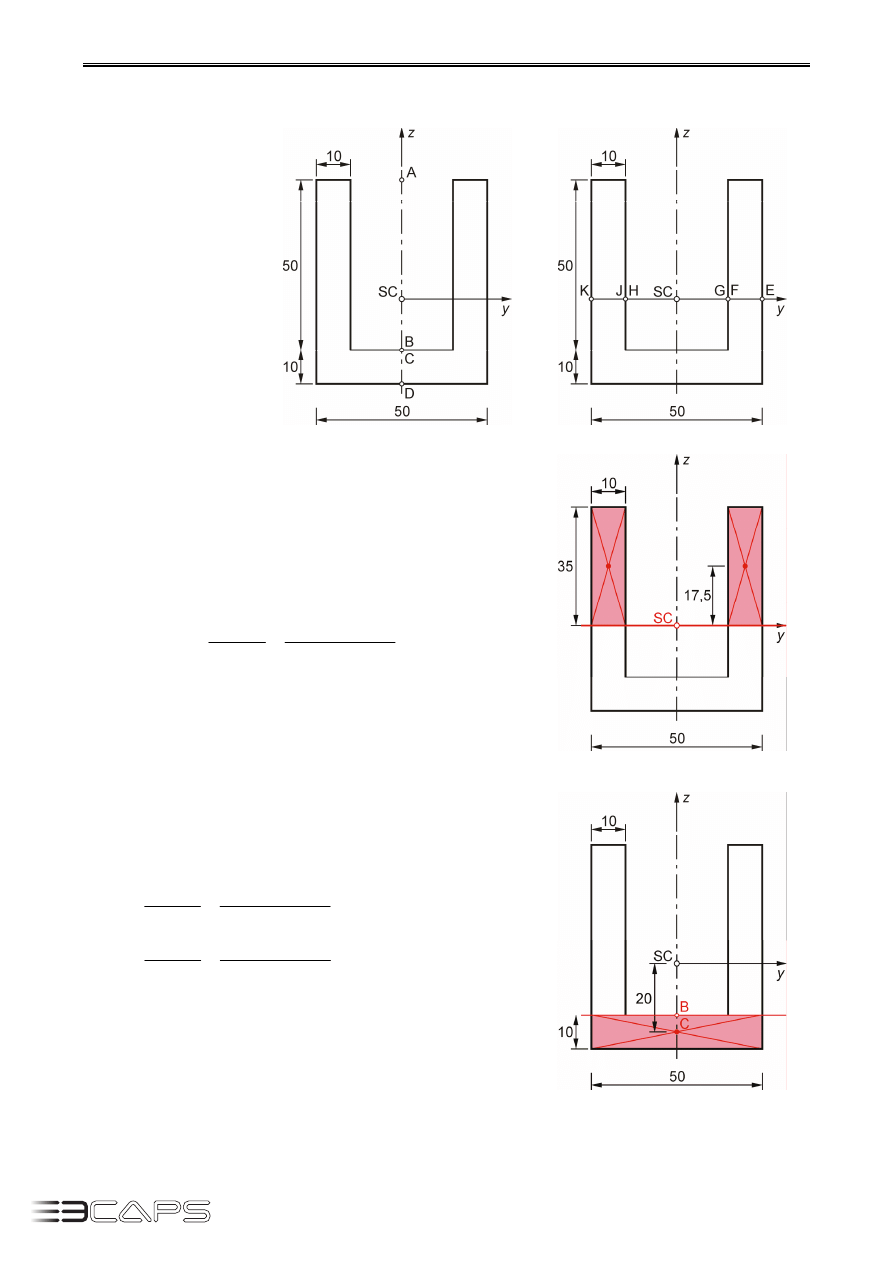
Zadanie 9.3.
Przekrój ceownik o wymiarach jak na rysunku 9.18
obciążony jest siłami tnącymi
kN
10
=
=
z
y
T
T
.
Wyznaczyć rozkłady naprężeń stycznych
y
τ i
z
τ .
Wymiary przekroju w [mm].
Rozwiązanie
Wyznaczamy środek ciężkości rozpatrywanego
przekroju (rys. 9.19). Moment statyczny względem
podstawy jest równy
3
3
3
2
2
1
1
mm
00
375
5
10
50
35
50
10
35
50
10
=
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
=
+
+
=
z
A
z
A
z
A
S
Współrzędna środka ciężkości
SC
z wynosi
mm
25
1500
37500
3
2
1
SC
=
=
+
+
=
A
A
A
S
z
Określamy główne centralne momenty
bezwładności przekroju
y
I oraz
z
I .
Rys. 9.18.
Rys. 9.19.
4
2
3
2
3
2
3
2
SC
3
3
3
2
SC
2
2
2
2
SC
1
1
1
mm
512500
)
20
(
500
12
10
50
10
500
12
50
10
10
500
12
50
10
)
(
)
(
)
(
=
−
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
=
−
+
+
−
+
+
−
+
=
z
z
A
I
z
z
A
I
z
z
A
I
I
y
y
y
y
4
3
2
3
2
3
3
2
2
2
2
2
1
1
1
mm
512500
12
50
10
20
500
12
10
50
)
20
(
500
12
10
50
=
⋅
+
⋅
+
⋅
+
−
⋅
+
⋅
=
=
+
+
+
+
=
y
y
z
z
I
y
A
I
y
A
I
I
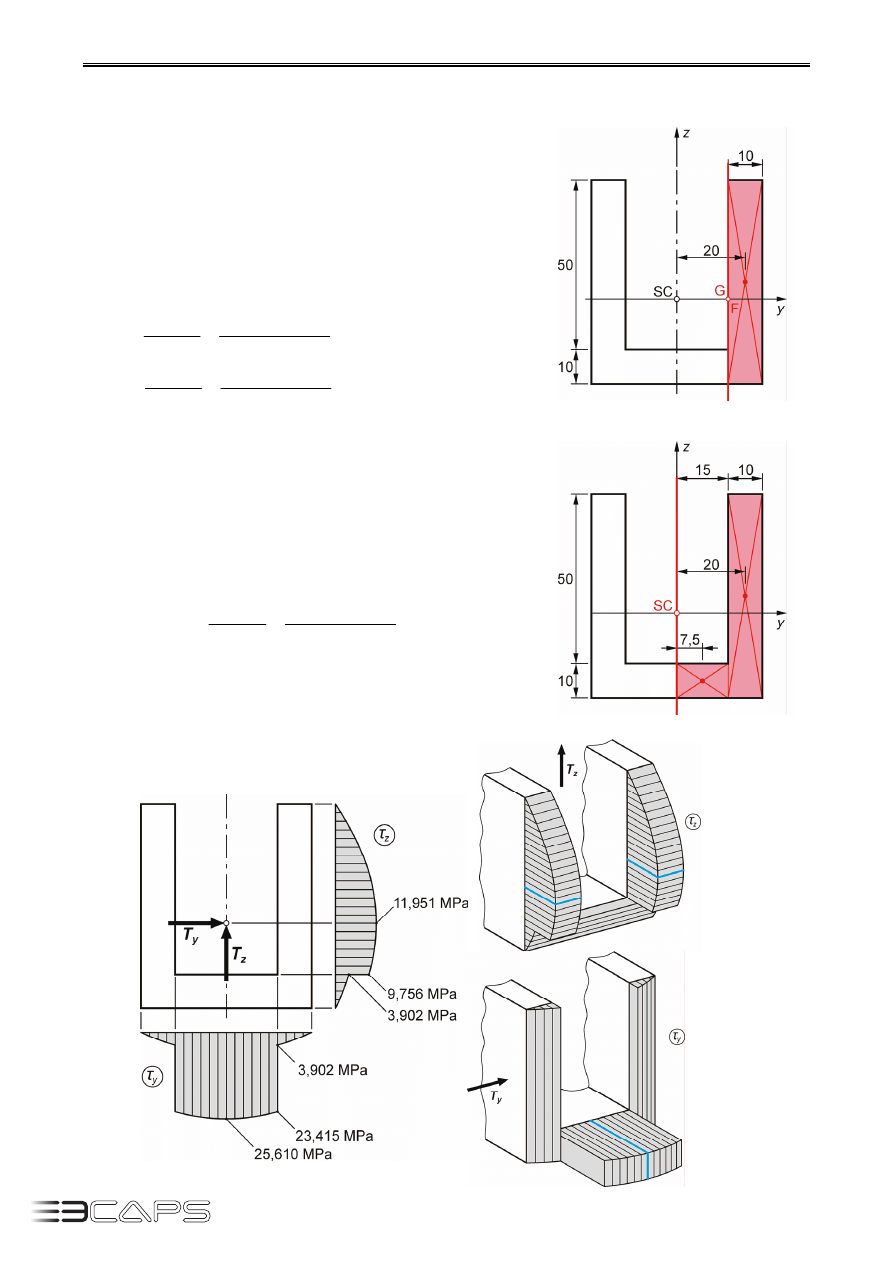
Określamy wartości naprężeń w punktach A, SC, B, C, D – dla siły tnącej
z
T
oraz w punktach E, F, G, SC – dla siły tnącej
y
T
(rys. 9.20).
W skrajnych warstwach naprężenia są równe zeru
0
D
A
=
=
z
z
τ
τ
0
K
E
=
=
y
y
τ
τ
Ponadto, dla obciążenia siłą tnącą
y
T mamy
F
J
y
y
τ
τ =
G
H
y
y
τ
τ =
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.9
Rys. 9.20.
Punkt SC (rys. 9.21)
Moment statyczny części odciętej wynosi
3
SC
mm
12250
)
5
,
17
35
10
(
2
=
⋅
⋅
⋅
=
y
S
Szerokość przekroju jest równa
mm
20
10
2
)
(
=
⋅
=
z
b
Wyznaczamy naprężenia styczne
MPa
951
,
11
20
512500
12250
10000
)
(
SC
max
SC
=
⋅
⋅
=
⋅
⋅
=
=
z
b
I
S
T
τ
τ
y
y
z
z
z
Punkty B i C (rys. 9.22)
Moment statyczny części odciętej wynosi
3
C
B
mm
10000
20
10
50
=
⋅
⋅
=
=
y
y
S
S
Szerokość przekroju jest równa
mm
20
)
( =
z
b
dla punktu B
mm
50
)
( =
z
b
dla punktu C
Wyznaczamy naprężenia styczne
MPa
756
,
9
20
512500
10000
10000
)
(
B
B
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
MPa
902
,
3
50
512500
10000
10000
)
(
C
C
=
⋅
⋅
=
⋅
⋅
=
z
b
I
S
T
τ
y
y
z
z
Rys. 9.21.
Rys. 9.22.
9. Obliczanie naprężeń stycznych wywołanych siłą tnącą
9.10
Punkty F i G (rys. 9.23)
Moment statyczny części odciętej wynosi
3
G
F
mm
12000
20
60
10
=
⋅
⋅
=
=
z
z
S
S
Szerokość przekroju jest równa
mm
60
)
(
=
y
b
dla punktu F
mm
50
)
(
=
y
b
dla punktu G
Wyznaczamy naprężenia styczne
MPa
902
,
3
60
512500
12000
10000
)
(
F
F
=
⋅
⋅
=
⋅
⋅
=
y
b
I
S
T
τ
z
z
y
y
MPa
415
,
23
10
512500
12000
10000
)
(
G
G
=
⋅
⋅
=
⋅
⋅
=
y
b
I
S
T
τ
z
z
y
y
Punkt SC (rys. 9.24)
Moment statyczny części odciętej wynosi
3
SC
mm
13125
5
,
7
10
15
20
60
10
=
⋅
⋅
+
⋅
⋅
=
z
S
Szerokość przekroju jest równa
mm
10
)
(
=
y
b
Wyznaczamy naprężenia styczne
MPa
610
,
25
10
512500
13125
10000
)
(
SC
max
SC
=
⋅
⋅
=
⋅
⋅
=
=
y
b
I
S
T
τ
τ
z
z
y
y
y
Rozwiązanie końcowe przedstawiono na rysunku 9.25.
Rys. 9.23.
Rys. 9.24.
Rys. 9.25.
Wyszukiwarka
Podobne podstrony:
67 Sposoby obliczania sił kształtowania plastycznego ppt
67 Sposoby obliczania sił kształtowania plastycznego ppt
Prezentacja JMichalska PSP w obliczu zagrozen cywilizacyjn 10 2007
3 ANALITYCZNE METODY OBLICZANIA PŁYWÓW
Kształcenie ruchowe i metodyka naucznia ruchu
p 43 ZASADY PROJEKTOWANIA I KSZTAŁTOWANIA FUNDAMENTÓW POD MASZYNY
koncepcja kształcenia wielostronnego
Obliczanie masy cząsteczkowej
reforma ksztalcenia zawodowego(1)
Obliczanie powierzchni
2 Podstawy obliczania
3 2 Ćwiczenie Obliczanie siatki kartograficznej Merkatora
WYKL 5b zmiana kształtu odlewu
Logistyka Zaopatrywania Metody ksztaltowania zapasow
GEOMETRIA OBLICZENIOWA I
TREŚĆ KSZTAŁCENIA2
więcej podobnych podstron