Filtracja - teoria

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

1

Filtracja to zjawisko przepływu płynu przez ośrodek porowaty (np. wody przez grunt). W większości

przypadków przepływ odbywa się ruchem laminarnym, wyjątkiem może być przepływ przez pokłady

grubego żwiru lub kamieni. Aby uprościć obliczenia wprowadzono pojęcie prędkości filtracji, czyli takiej

prędkości, podczas której ciecz płynęłaby pełnym przekrojem ośrodka porowatego:

= /

Q – strumień objętości,

A – przekrój całkowity,

Przedstawiona zależność, zwana prawem filtracji, została podana przez Darcy’ego w postaci

równania:

=

∙

J – spadek linii ciśnień (spadek hydrauliczny),

k – współczynnik filtracji, zależny od średnicy ziaren, porowatości gruntu oraz lepkości cieczy

Wartość liczbowa współczynnika filtracji wyznaczyć można doświadczalnie na podstawie pomiaru

różnicy zwierciadeł cieczy w dwu przekrojach oddzielonych od siebie warstwą ośrodka porowatego. W

praktyce w przybliżeniu można obliczyć wartość współczynnika filtracji dla drobnego żwiru lub piasku z

następującej formuły:

= 40 ∙

δ – przeciętna grubość ziaren w cm

Orientacyjne

wartość

współczynnika

przepuszczalności

zestawia

się

tabelarycznie

dla

poszczególnych rodzajów gruntów.

Praktyczne obliczenia dotyczące wydajność złóż, przepływu przez nasyp, dopływu wody do rowów lub

studzien oparte są na równaniu krzywej dopływu. Jest to linia, według której układa się swobodne

zwierciadło cieczy na gruncie. Obliczenia polegają przede wszystkim na wyznaczeniu prędkości i

strumienia objętości dopływu wód oraz zasięgu depresji.

Najbardziej typowe zagadnienia dotyczące filtracji wód gruntowych:

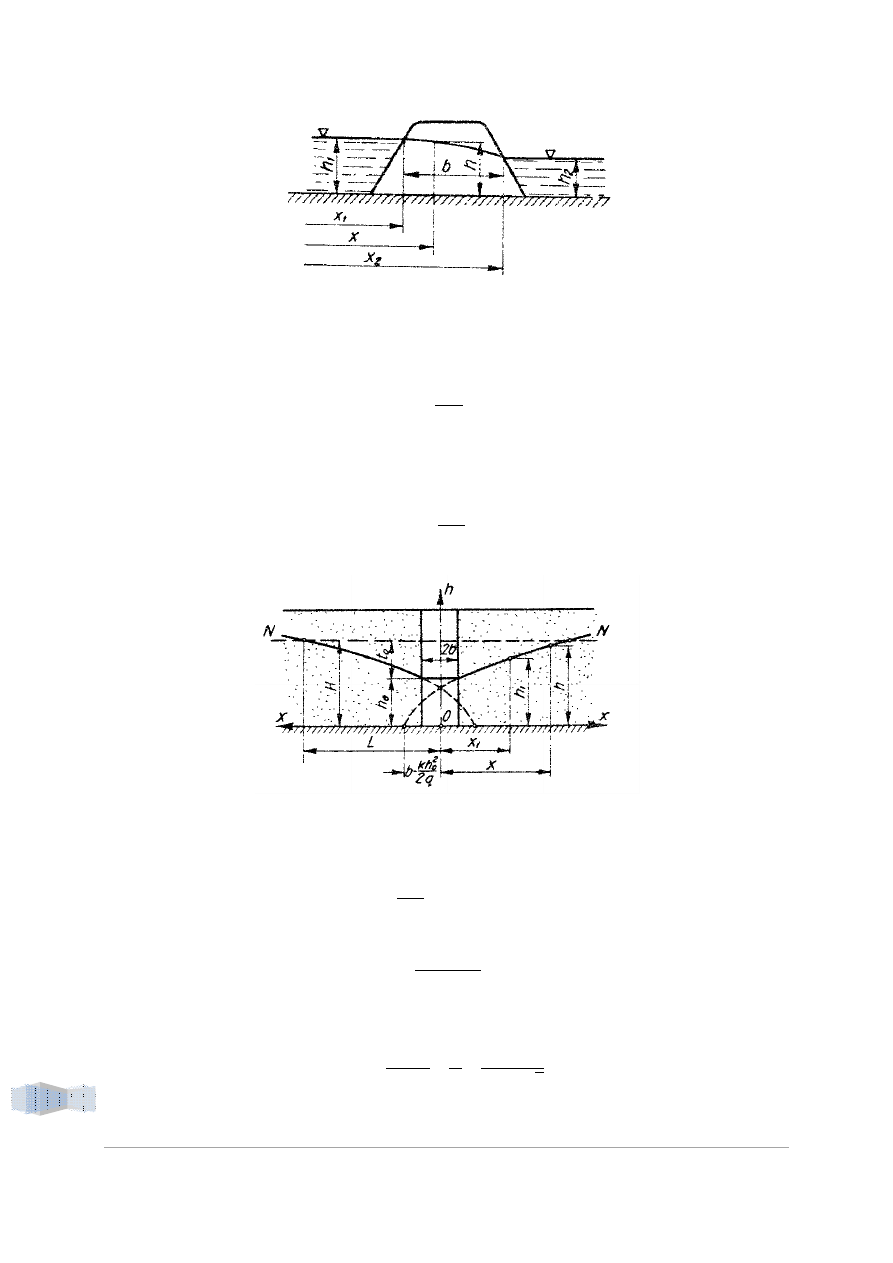
1. Przepływ przez nasyp

Podczas przepływu wody przez nasyp (stanowiący warstwę przepuszczalną na poziomym

nieprzepuszczalnym podłożu) następuje obniżenie się powierzchni swobodnej strugi wzdłuż krzywej,

którą określa równanie:

ℎ +

ℎ − ℎ

∙

=

ℎ ∙

− ℎ ∙

Gdzie jednostkowy strumień objętości:

=

2 ∙

∙ (ℎ − ℎ )

Dla długości nasypu B, strumień objętości:

=

∙

2 ∙

∙ (ℎ − ℎ )

Filtracja - teoria

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

2

Rysunek 1. Przepływ przez nasyp

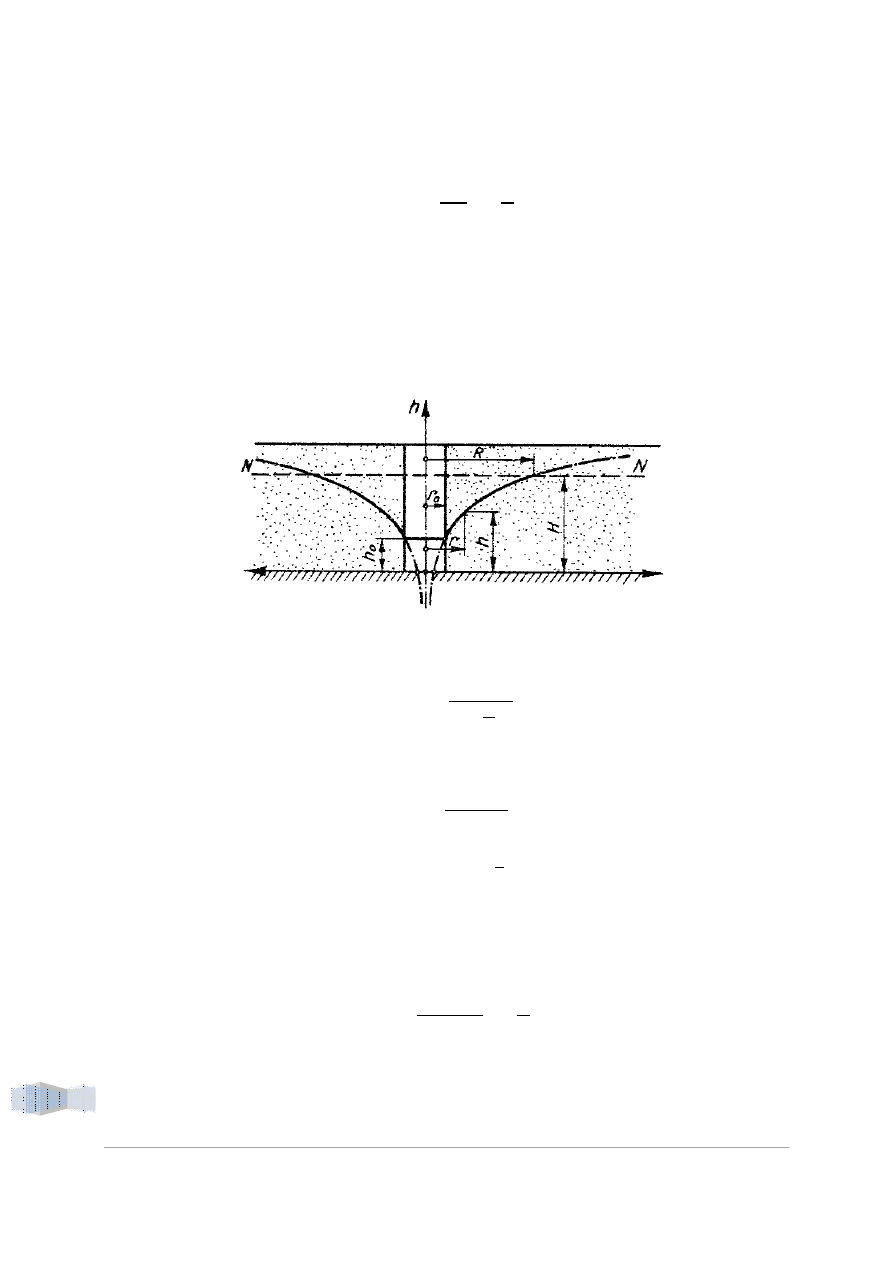
2. Dopływ wody do rowu

Powierzchnia depresji określona jest równaniem:

ℎ − ℎ =

2 ∙

∙ ( −

)

h i h

1

– rzędne krzywej depresji w odległościach x i x

1

od osi rowu,

q – jednostkowy strumień objętości,

Gdy x

1

= b, h

1

= h

0

, wówczas wzór określający krzywą depresji przyjmuje postać:

ℎ − ℎ =

2 ∙

∙ ( − )

Rysunek 2. Dopływ wody do rowu

Zasięg depresji jest określony zależnością:

=

2 ∙

∙ (

− ℎ ) +

Jednostronny strumień dopływu do rowu szerokości B:

−

∙

=

∙

2 ∙ ( − )

∙ (

− ℎ )

W obliczeniach praktycznych wprowadza się pojęcie średniego spadku hydraulicznego, określonego

formułą Sichardta:

=

− ℎ

=

=

1

3000 ∙ √

Współczynnik filtracji k wyrażony jest w m/s.

Filtracja - teoria

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

3

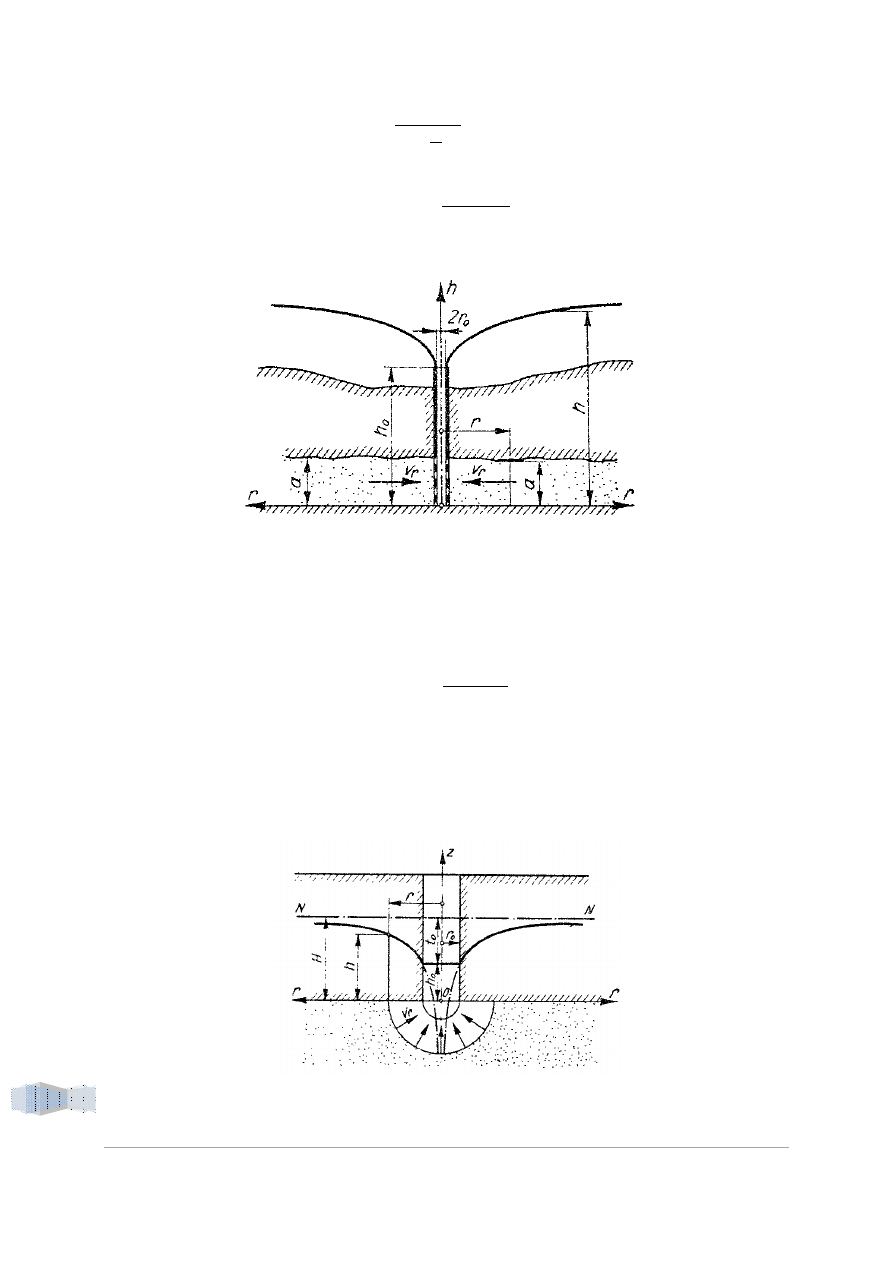
3. Studnia zwykła

Do studni zwykłej o swobodnym zwierciadle cieczy w gruncie, opuszczonej do poziomej warstwy

nieprzepuszczalnej, równanie krzywej depresji ma postać:

ℎ − ℎ =

∙

∙

Gdzie:

r0 – promień studni,

h0 – głębokość wody w studni,

h, r – współrzędna dowolnego punktu krzywej depresji,

Q – strumień dopływu do studni,

Rysunek 3. Studnia zwykła

Strumień dopływu:

=

∙

∙

(

− ℎ )

Gdzie: R – promień zasięgu depresji, gdy h = H tj. pierwotnej wysokości wody.

Promień zasięgu depresji:

=

∙

∙ ∙

Do wyznaczenia promienia zasięgu depresji, używana jest formuła Sichardta:

= 3000 ∙

∙ √

W której R i t

0

= H - h

0

wyrażone są w m, współczynnik k w m/s.

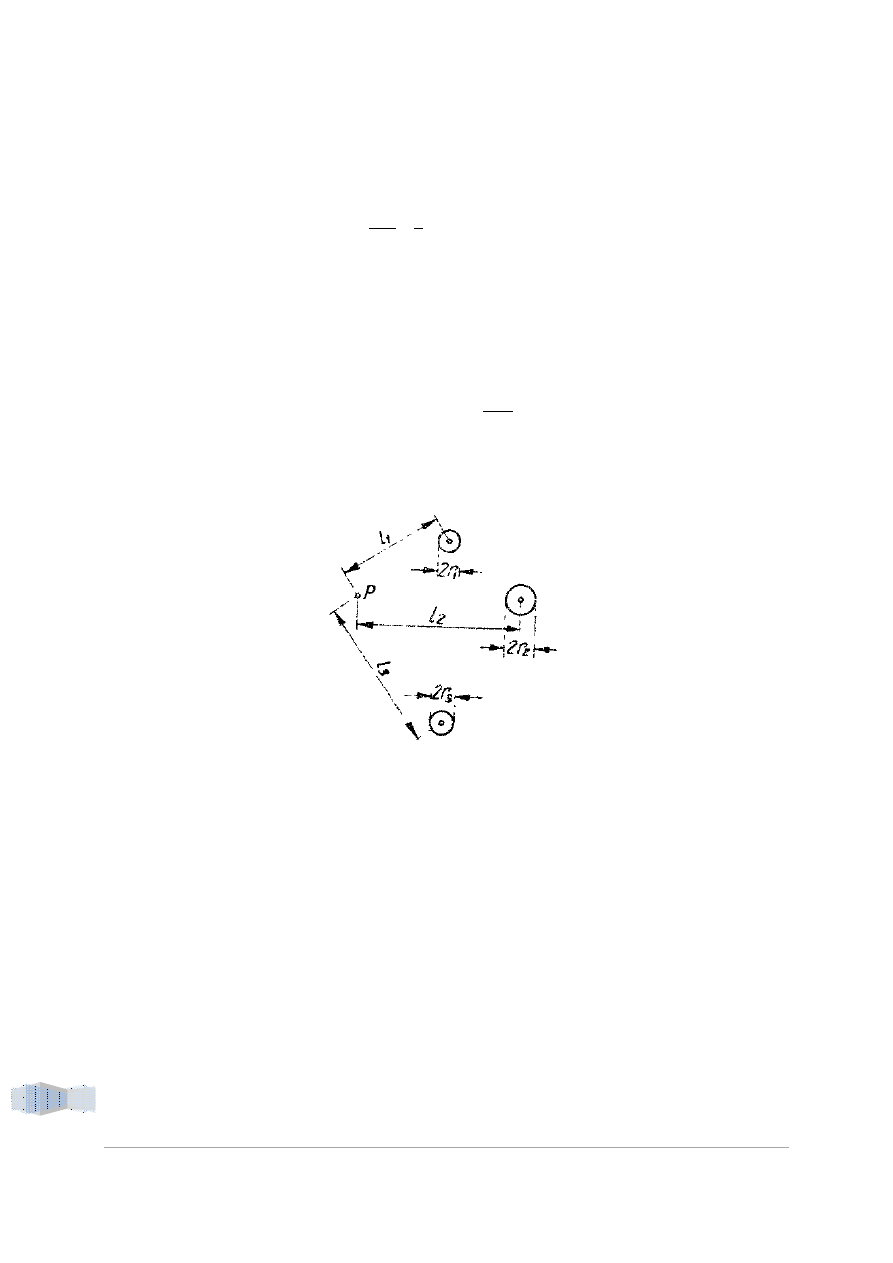
4. Studnia artezyjska

Wysokość rozporządzalna w dowolnym przekroju walcowym o promieniu r:

ℎ = ℎ +

2 ∙

∙

∙

∙

gdzie:

a – grubość warstwy wodonośnej,

h

0

– wysokość strugi wytryskującej ze studni o promieniu r

0

,

Strumień dopływu:

Filtracja - teoria

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

4

=

2 ∙

∙

∙

∙ ( − ℎ )

Zasięg depresji:

=

∙

∙ ∙ ∙ ∙(

)

Rysunek 4. Studnia artezyjska

5. Studnia górnicza

Równanie krzywej depresji studni wywierconej w gruncie nieprzepuszczalnym, stanowiącym powałę

warstwy wodonośnej, ma postać:

ℎ =

−

2 ∙

∙

∙

w którym zasięg depresji:

→ ∞

Strumień dopływu:

= 2 ∙

∙

∙

∙ ( − ℎ )

Rysunek 5. Studnia górnicza

Filtracja - teoria

Notatki w Internecie| Podstawy mechaniki płynów – materiały do ćwiczeń

5

6. Grupy studzien

Podczas jednoczesnej pracy zespołu studzien położonych dostatecznie blisko siebie następuje ich

wzajemne oddziaływanie na siebie. Znając łączny strumień dopływu wszystkich studzien można

wyznaczyć głębokość wody gruntowej (np. w studniach zwykłych) w dowolnym punkcie z zależności:

ℎ =

+

∙

∙

1

∙ ln( ∙

∙ … ∙

) − ln ( )

Gdzie:

l

i

– odległości od rozpatrywanego punktu,

n – liczba studzien,

R – promień zasięgu działania grupy studzien, gdy H = h

Promień zasięgu działania grupy studzien z formuły Kusakina:

= 575 ∙

∙ √ ∙

t

0s

– depresja w środku ciężkości grupy studzien w m, k w m/s.

Rysunek 6. Grupa studzien