Zagadnienie naturalnej stopy procentowej

Michał Brzoza-Brzezina

1

Streszczenie

W artykule przeanalizowane zostało, zyskujące coraz większą popularność w literaturze

ekonomicznej, zagadnienie naturalnej stopy procentowej (NSP), przedstawiono tło

historyczne oraz dyskusję najważniejszych kwestii teoretycznych, związanych z NSP.

Szczególna uwaga poświęcona została dwóm sposobom zdefiniowania stopy naturalnej, w

odniesieniu do inflacji bądź w odniesieniu do krańcowej produktywności kapitału.

Naturalna stopa procentowa, definiowana jako stopa realna prowadząca do stabilizacji

inflacji, ma kluczowe znaczenie dla polityki pieniężnej prowadzonej w ramach strategii

bezpośredniego celu inflacyjnego. Z kolei modele równowagi ogólnej, utożsamiające

naturalną stopę procentową z krańcowej produktywności kapitału pozwalają na określenie

determinantów stopy naturalnej. Artykuł przygotowuje grunt pod analizę empiryczną,

pozwalającą oszacować poziom NSP w Polsce.

Słowa kluczowe: naturalna stopa procentowa, model Ramseya, inflacja

Klasyfikacja JEL: E43, E52, E58

1

Autor jest pracownikiem Departamentu Analiz Makroekonomicznych i Strukturalnych NBP oraz Katedry

Polityki Pieniężnej SGH. Wyrażone poglądy niekoniecznie odpowiadają poglądom Banku. Pragnę złożyć
serdeczne podziękowania osobom, które przyczyniły się do podniesienia jakości opracowania: Jakubowi
Borowskiemu, Tomaszowi Chmielewskiemu, Stanisławowi Gomułce, Rafałowi Kierzenkowskiemu,
Zbigniewowi Polańskiemu, Piotrowi Szpunarowi, Cezaremu Wójcikowi i Jerzemu Żyżyńskiemu oraz
uczestnikom seminarium naukowego w NBP. Uwagi mile widziane: [e-mail]

2

Wstęp

Zagadnienie naturalnej stopy procentowej (NSP) przewija się w literaturze ekonomicznej od

niemal 200 lat. Pierwsze opracowania na zbliżone tematy publikowali już na początku XIX w.

T.Joplin i H.Thornton, jednak jak dotychczas najwięcej dla popularyzacji idei NSP uczynił,

żyjący na przełomie XIX i XX wieku szwedzki ekonomista K.Wicksell.

W ostatnich latach ponownie wzrosło zainteresowanie kwestią NSP. Można przypuszczać, że

podstawową przyczyną jest przechodzenie coraz większej liczby banków centralnych na

strategię bezpośredniego celu inflacyjnego (BCI) lub strategie pokrewne. Do podstawowych

elementów strategii należy sterowanie przez bank centralny krótkoterminowymi stopami

procentowymi rynku pieniężnego, tak aby wpłynąć na realne oprocentowanie kredytów i

depozytów w bankach. Zmiana realnych stóp procentowych na rynku powinna wpływać na

decyzje konsumpcyjne i inwestycyjne podmiotów gospodarujących i - w konsekwencji - na

stopę inflacji.

Bank centralny, wykorzystujący strategię BCI musi wiedzieć, jak realizować politykę

pieniężną prowadzącą odpowiednio do wzrostu, stabilizacji bądź spadku stopy inflacji

(polityka taka będzie nazywana odpowiednio luźną, neutralną i restrykcyjną). Ponieważ, jak

to zostało zaznaczone w poprzednim akapicie, o kształtowaniu się składników

zagregowanego popytu, a w konsekwencji stopy inflacji, decydują (z punktu widzenia

instrumentów dostępnych bankowi centralnemu) realne stopy procentowe (ex ante), władze

monetarne powinny zdawać sobie sprawę z tego, jaki ich poziom skutkuje określonym

stopniem restrykcyjności polityki pieniężnej. Szczególnie interesujący wydaje się w tym

kontekście prowadzący do neutralnego nastawienia w polityce pieniężnej naturalny poziom

stóp procentowych. Wiedza, jaka wysokość realnych stóp zapewnia stabilną inflację, pozwala

ustalić, że stopy wyższe skutkowały będą polityką restrykcyjną (i spadkiem inflacji), zaś

stopy niższe od NSP będą oznaczały politykę luźną, która doprowadzi do wzrostu stopy

inflacji.

Warto również zwrócić uwagę na istotne walory dydaktyczne takiego podejścia do

objaśniania polityki pieniężnej. Praktyka akademicka prowadzi często do nadmiernego

upraszczania zagadnień związanych z bankiem centralnym i procesami inflacyjnymi. Często

spotykanym sposobem tłumaczenia procesu wpływania władz monetarnych na stopę inflacji

3

jest domniemane sterowanie przez bank centralny podażą pieniądza. Tymczasem w praktyce

czynność taka nie ma miejsca, o czym studenci dowiadują się, poznając zasady sterowania

krótkoterminowymi stopami procentowymi w ramach operacji otwartego rynku. Tak więc

powstaje rozbieżność intelektualna pomiędzy znajomością instrumentu banku centralnego a

informacjami o wpływie polityki pieniężnej na inflację. Upowszechnienie koncepcji

naturalnej stopy procentowej pozwoliłoby w zgrabny sposób domknąć opisaną lukę

poznawczą, poprzez wprowadzenie jasnego opisu transmisji monetarnej: bank centralny

wpływa na nominalne stopy procentowe, te wpływają na poziom stóp realnych w bankach

komercyjnych, jeżeli stopy te rosną powyżej NSP popyt maleje i inflacja spada, jeżeli stopy

realne spadają poniżej NSP, popyt i inflacja rosną.

Zagadnienie naturalnej stopy procentowej nie było, jak dotychczas, szczególnie popularne w

polskiej myśli ekonomicznej. Dlatego też w dwóch artykułach pragnę przybliżyć je polskim

ekonomistom. Pierwsze, poniżej przedstawione opracowanie, zawiera omówienie

teoretycznych podstaw stopy naturalnej. W pierwszym rozdziale przedstawione zostanie tło

historyczne oraz najnowsze osiągnięcia w dziedzinie NSP. Rozdział drugi zawiera analizę

dwóch podstawowych podejść do kwestii NSP. W pierwszej kolejności, omówione zostaną

teoretyczne podstawy istnienia NSP zdefiniowanej, jako stopa realna stabilizująca inflację. W

dalszej kolejności przedstawione zostanie alternatywne podejście, utożsamiające stopę

naturalną z realną stopą równowagi modelu równowagi ogólnej. W końcowej części rozdziału

przedstawiona zostanie krótka dyskusja, dotycząca kształtowania się NSP w gospodarce

otwartej.

Jak zaznaczono, posiadanie wiarygodnego oszacowania NSP jest warunkiem koniecznym

prowadzenia odpowiedzialnej polityki pieniężnej przez bank centralny, stosujący strategię

BCI. Kwestia ta dodatkowo zyskuje na znaczeniu, kiedy bank centralny kończy proces

obniżania inflacji i wchodzi w fazę jej stabilizowania. Oba powyższe warunki spełnia w

obecnej chwili Narodowy Bank Polski i dlatego oszacowanie poziomu NSP w Polsce wydaje

się absolutnym priorytetem. W przeciwnym wypadku grozi nam bowiem niewłaściwe

ustawienie stóp procentowych, co może doprowadzić albo do ponownego odbicia inflacji albo

do wpadnięcia w spiralę deflacyjną. Z tych powodów, w drugim opracowaniu,

zatytułowanym „Rola naturalnej stopy procentowej w polskiej polityce pieniężnej”, na

podstawie omawianych poniżej wniosków teoretycznych dotyczących NSP, oszacowany

zostanie jej poziom w Polsce.

4

1 Współczesna wiedza o NSP

1.1 Tło historyczne

Tradycyjnie za ojca koncepcji naturalnej stopy procentowej uznaje się szwedzkiego

ekonomistę Knuta Wicksella (1851-1926). Bez wątpienia Wicksell jest autorem pojęcia

naturalnej stopy procentowej, jednak już niemal 100 lat przed nim zagadnieniem tym

zajmowali się ekonomiści klasyczni (Laidler 1991, s. 129).

Nieodłącznym elementem klasycznej myśli ekonomicznej było traktowanie stopy

procentowej, jako zmiennej zdeterminowanej przez realną sferę gospodarki (dokładnie przez

produktywność kapitału i stopę preferencji czasowych gospodarstw domowych) i tym samym

nie podlegającej wpływowi polityki pieniężnej. Warto przy tym zauważyć, że ekonomiści ci

nie rozróżniali stopy realnej od nominalnej (przynajmniej w sferze werbalnej). Być może

przyczyną był fakt, że w XVIII i XIX wieku inflacja była zjawiskiem równie częstym jak

deflacja, co sprawiało, że ogólny poziom cen w dłuższym okresie był stabilny. W takiej

rzeczywistości gospodarczej zdejmowanie komponentu inflacyjnego ze stóp procentowych

wydaje się zdecydowanie mniej istotne, niż w znanym nam świecie permanentnej i często

wysokiej inflacji.

Jednak, pomimo przekonania o determinowaniu stopy równowagi w realnej sferze

gospodarki, ekonomiści klasyczni dopuszczali możliwość czasowego odchylenia stopy

rynkowej od stopy równowagi. W tym zakresie zbliżone stanowisko zajmowali wszyscy

klasycy, począwszy od D.Hume’a a skończywszy na J.S.Millu (Humphrey 1983).

Fakt, że ekonomiści klasyczni określali determinanty realnych stóp procentowych nie jest

szczególnie zaskakujący. Bardziej interesujące jest natomiast, że szczegółowy opis procesów

inflacyjnych, zachodzących w gospodarce po obniżeniu (podniesieniu) rynkowych stóp

procentowych poniżej (powyżej) stopy naturalnej nie w całości jest dziełem Wicksella. Model

reakcji gospodarki na otwarcie luki stóp procentowych, zwany modelem procesu

kumulacyjnego, jest bowiem najczęściej kojarzony właśnie z tym szwedzkim ekonomistą

(Jonung 1979, s. 461). Tymczasem zręby modelu można znaleźć w pracach dwóch

brytyjskich ekonomistów, H.Thorntona (1760-1815) i T.Joplina (ok. 1790-1847), niemal 100

5

lat wcześniej

2

. Model procesu kumulacyjnego, będący pierwszą próbą opisania związku

pomiędzy luką stóp procentowych i poziomem cen zostanie przytoczony w całości

(Humphrey, 1993).

Model można zapisać za pomocą pięciu równań. Pierwsze należy traktować, w duchu

tradycji wicksellowskiej, jako definicję naturalnej stopy procentowej. Zgodnie z nim, realne

inwestycje (I) różnią się od oszczędności (S) wtedy, gdy rynkowa stopa procentowa (r)

odbiega od stopy naturalnej (r*)

3

.

(1) I-S=a(r*-r)

a>0

NSP wyznacza zatem taki poziom (realnej) stopy procentowej, który zrównuje (oczywiście ex

ante) oszczędności z inwestycjami. Kolejne równanie modelu opisuje fakt, że ewentualne

niezbilansowanie oszczędności i inwestycji skutkuje dodatkową kreacją kredytu, a co za tym

idzie, emisją pieniądza

4

:

(2) I-S=dM/dt,

Dzieje się tak, ponieważ inwestycje są utożsamiane z kredytami, natomiast oszczędności z

depozytami. Ewentualny niedobór depozytów musi zatem skutkować kreacją nowego

kredytu. Równanie (3) przyrównuje nadwyżkę inwestycji nad oszczędnościami do nadwyżki

(E) zagregowanego popytu nad zagregowaną podażą:

(3) I-S=E,

natomiast równanie (4) opisuje działanie mechanizmu cenowego, zgodnie z którym

nierównowaga na rynku dóbr jest przyczyną proporcjonalnej zmiany cen. Nadwyżka popytu

nad podażą powinna prowadzić do wzrostu ogólnego poziomu cen, jak w modelu AD-AS:

2

Wicksell nie zdawał sobie sprawy z wkładu Thorntona i Joplina w budowę modelu procesu kumulacyjnego i

opierał się głównie na na opracowaniach Ricarda i Tooke’a (Laidler 1991, s. 150).

3

Jak zostało wcześniej zauważone, klasycy nie dokonywali rozróżnienia stóp realnych i nominalnych. Model

procesu kumulacyjnego został jednak zapisany w postaci współczesnej z uwzględnieniem stóp realnych. Warto
zauważyć, że ponieważ dochodzi w nim wyłącznie do zmiany poziomu cen, a nie stopy inflacji, rozróżnienie
takie nie zmienia jego charakteru, a jedynie zwiększa spójność z dalszymi rozważaniami.

4

Przez dX/dt oznaczana będzie pochodna zmiennej X względem czasu.

6

(4)

dP/dt=kE

k>0

Dotychczas przedstawione równania w przybliżeniu opisują zarówno model Wicksella, jak i

jego poprzedników, Thorntona i Joplina. To, czego brakuje do jego domknięcia,

zawdzięczamy jednak zdecydowanie Wicksellowi (Humphrey, 1993). Trzeba bowiem

zauważyć, że w dotychczasowej postaci model nie posiada mechanizmu stabilizacyjnego,

który zapewniałby powrót do stanu równowagi. Aby to zobaczyć, należy podstawić równania

(1) oraz (3) do (4), aby otrzymać

5

:

(5) dP/dt=ak(r*-r),

co oznacza, że przyczyną zmian poziomu cen jest rozbieżność pomiędzy realną i naturalną

stopą procentową. Zgodnie z powyższym modelem, gdyby raz doszło do takiej sytuacji, ceny

rosły lub spadałyby w nieskończoność, ponieważ nie ma mechanizmu, przywracającego stopę

realną do poziomu naturalnego.

Wicksell argumentował następująco: jeżeli zaczyna rosnąć poziom cen, nominalne wydatki

ludności również rosną, co implikuje wzrost popytu na gotówkę (Myhrman 1991). Banki

komercyjne (również bank centralny) będą zmuszone chronić swoje zasoby złota przed

wypłynięciem do obiegu, w związku z czym zaczną podnosić stopy procentowe

proporcjonalnie do wzrostu poziomu cen, co usprawiedliwia zapisanie równania:

(6) dr/dt=b

⋅

dP/dt.

b>0

Oczywiście, takie wytłumaczenie nie wydaje się sensowne z punktu widzenia dzisiejszego

systemu finansowego, w którym emisja pieniądza nie posiada pokrycia w złocie. Warto

natomiast zauważyć pewne podobieństwo równania (6) do współczesnych funkcji reakcji

banku centralnego, opisującej sposób ustalania poziomu stóp procentowych przez bank

centralny (Taylor 1993). We współczesnym systemie podnoszenie lub obniżanie stóp

procentowych, zapewniające domknięcie i stabilność modelu, jest związane z misją banku

centralnego, dbającego o stabilność poziomu cen.

5

Ani klasycy ani Wicksell nie zajmowali się szczegółowo rolą oczekiwań w procesie kumulacyjnym. Dlatego

otwarcie luki stóp procentowych prowadziło co najwyżej do stałej, wysokiej inflacji, nie zaś, co podkreślał sam
Wicksell, do „efektu lawiny” czyli niekontrolowanego wybuchu hiperinflacji (Honohan 1981, Uhr 1951, s. 856).

7

Powracając do modelu wicksellowskiego, podstawienie dP/dt z równania (6) do (5) pozwala

wykazać, że jeżeli nastąpi otwarcie luki stóp procentowych, to z upływem czasu, realna stopa

procentowa powracać będzie do swojego naturalnego poziomu:

(7) dr/dt=abk(r*-r).

Na podstawie modelu procesu kumulacyjnego Wicksell uważał, że naturalna stopa

procentowa może odgrywać istotną rolę w prowadzeniu polityki pieniężnej. Sformułował

nawet prostą zasadę, którą powinny kierować się banki centralne: poziom cen powinien być

utrzymywany na stałym poziomie poprzez ciągłe dostosowywanie stóp rynkowych do

poziomu naturalnego. W przypadku wzrostu cen, należało podnieść stopy procentowe

powyżej r*, w przeciwnym wypadku obniżyć poniżej r*, aż do ponownego osiągnięcia

wyjściowego poziomu cen. Zasadę Wicksella próbował w latach 30-tych wcielać w życie

Riksbank, centralny bank Szwecji (Jonung 1979).

Omawiając wicksellowską teorię stóp procentowych, nie można nie odnieść się do jej

związku z ilościową teorią pieniądza. Ta ostatnia była podstawowym narzędziem analizy

monetarnej ekonomistów klasycznych i neoklasycznych i służyła do formułowania zaleceń

dla banków centralnych, wiążących poziom cen z podażą pieniądza. W tym sensie teoria

procesu kumulacyjnego i wynikające z niego zalecenia dla polityki pieniężnej można uznać

za wyzwanie rzucone teorii ilościowej. Niemniej, sam Wicksell traktował swoje rozważania

raczej jako uzupełnienie ilościowej teorii pieniądza, pozwalające przystosować ją dla potrzeb

gospodarki kredytowej niż jako jasno zarysowaną alternatywę. Krytykę teorii ilościowej na

bazie modelu Wicksella rozpoczęli dopiero w latach 30-tych XX w. ekonomiści szkoły

sztockholmskiej (Laidler 1991, s. 119, Myhrman 1991, s. 272).

Warto w tej sytuacji zastanowić się, jak Wicksell wyobrażał sobie determinanty NSP. Otóż z

jego punktu widzenia sprawa była prosta: naturalna stopa procentowa powinna być równa

krańcowej produktywności kapitału (Wicksell 1898, 1907). Krańcowa produktywność

kapitału powinna bowiem stanowić punkt odniesienia, jeśli chodzi o proces inwestycyjny w

przedsiębiorstwach. Jeżeli realna stopa procentowa przekracza produktywność krańcową,

racjonalnie postępujące przedsiębiorstwo powinno ograniczać inwestycje, w przeciwnej

sytuacji powinno je zwiększać. Tak więc w pracach Wicksella można wyróżnić co najmniej

8

trzy definicje stopy naturalnej, jedną związaną ze zrównaniem oszczędności z inwestycjami,

drugą ze stabilizacją ogólnego poziomu cen i wreszcie trzecią, zrównującą stopę naturalną z

krańcową produktywnością kapitału. Dla Wicksella wszystkie trzy definicje opisywały ten

sam obiekt, na gruncie współczesnej ekonomii nie sposób jednak wykazać ich równości i

trzeba uznać że są to trzy odrębne definicje (Laidler 1991, s. 130).

Przez większą część XX wieku wicksellowska teoria stóp procentowych nie budziła

szczególnego zainteresowania ekonomistów, którzy, choć z reguły świadomi jej istnienia, nie

przywiązywali do niej większej wagi. Keynes argumentował jeszcze w duchu koncepcji

wicksellowskiej w „A Treatise of Money” w 1930, jednak koncepcję naturalnej stopy

procentowej odrzucił całkowicie kilka lat później w „Ogólnej teorii zatrudnienia, procentu i

pieniądza” (por. J.M.Keynes 1936 s. 269-270, J.R.Hicks, 1988 s. 121). Do nielicznych

wyjątków zaliczyć można szwedzkich ekonomistów E.Lindahla i G.Myrdala, którzy

zajmowali się w latach 30-tych rozwijaniem koncepcji Wicksella. (por. A.Leijonhufvud,

1989). Również po drugiej wojnie, teoria Wicksella nie znalazła się w centrum

zainteresowania ekonomistów. Zapewne jedną z przyczyn, był obowiązujący do początku lat

70-tych system sztywnych kursów walutowych, który w znacznym stopniu zmniejszał rolę

niezależnej polityki pieniężnej, opartej o sterowanie stopami procentowymi.

1.2 Współczesna analiza NSP

Sytuacja uległa zdecydowanej zmianie w ostatniej dekadzie wieku, kiedy to liczba artykułów,

poświęconych temu zagadnieniu zaczęła gwałtownie rosnąć. Do dyskusji na temat naturalnej

stopy procentowej włączyli się zarówno ekonomiści akademiccy, jak i związani z bankami

centralnymi. Poniżej przedstawione zostały wybrane, współczesne przykłady analizy NSP.

John Taylor (1993) zaproponował tłumaczenie decyzji banku centralnego za pomocą prostej

reguły, wiążącej poziom nominalnej stopy procentowej z warunkami makroekonomicznymi

(inflacją i luką popytową). Integralną częścią reguły stał się od tego czasu neutralny poziom

stóp procentowych, gwarantujący utrzymanie stabilnej inflacji. W latach 90-tych reguły

polityki pieniężnej zaczęły być powszechnie wykorzystywane w pracach teoretycznych i w

modelowaniu ekonometrycznym, przy czym większość z nich odwołuje się do naturalnej

stopy procentowej. Warto jednak zauważyć, że w większości reguł naturalna stopa

procentowa jest stała (por. ECB 2001, L.C.Plantier i D.Scrimgeour 2002).

9

J.C.Fuhrer i G.R.Moore (1995) zaproponowali zbudowanie prostego modelu, opisującego

działanie polityki pieniężnej, który mógłby zastąpić model IS-LM. Również w tym

przypadku, do podstawowych elementów modelu należała stała naturalna stopa procentowa,

gwarantująca stabilną inflację. Niestety, autorzy konkludują, że stabilny model można

otrzymać wyłącznie na podstawie układu trzech równań różniczkowych, co znacząco utrudnia

prezentację graficzną i tym samym nie rokuje najlepiej dla zastąpienia modelu IS-LM.

Od założenia stałej stopy procentowej odeszli natomiast K.Neiss i E.Nelson (2001) z Banku

Anglii, którzy wykorzystali model równowagi ogólnej z nominalnymi sztywnościami,

kalibrowany dla gospodarki brytyjskiej do oszacowania szeregu czasowego NSP w latach

1980-2000. W tym podejściu stopa naturalna została zdefiniowana jako taki poziom stopy

realnej, który wystąpiłby po usunięciu z modelu wszystkich nominalnych sztywności.

Zgodnie z wynikami, uzyskanymi przez autorów, stopa naturalna jest znacząco mniej

zmienna od obserwowanej stopy realnej, a luka pomiędzy stopą realną i naturalną jest

przydatna do prognozowania dynamiki inflacji.

W nurt modelowania mikroekonomicznego wpisują się również prace M.Woodforda (1999,

2000), który na podstawie rozbudowanych modeli równowagi ogólnej określał determinanty

naturalnej stopy procentowej. Najistotniejsze wiążą się z preferencjami gospodarstw

domowych, tempem wzrostu produktywności oraz szokami popytowymi (np. wydatkami

rządowymi). M.Woodford przedstawia również symulacje, pokazujące reakcję gospodarki na

szok stopy naturalnej, nie podejmuje jednak w żadnym z artykułów próby oszacowania stopy

naturalnej. Ważnym wnioskiem, wyraźnie zaakcentowanym w pracach Woodforda, jest

konieczność podążania przez bank centralny ze zmianami realnych stóp krótkoterminowych

za obserwowanymi zmianami stopy naturalnej.

W bardzo wpływowym opracowaniu, omawiającym zasady rządzące współczesną polityka

pieniężną, A.Blinder (2001) wykorzystuje naturalną stopę do objaśnienia podstawowych reguł

transmisji monetarnej i wpływania przez bank centralny na stopę inflacji.

T.Laubach i J.C.Williams (2001) z Rezerwy Federalnej podeszli do zagadnienia NSP od

strony analizy szeregów czasowych. Autorzy oszacowali za pomocą filtru Kalmana szereg

NSP, definiowanej jako taki poziom stopy realnej, który nie przyspiesza inflacji. Na tej

10

podstawie doszli do wniosku, że stopa naturalna jest dodatnio skorelowana z tempem wzrostu

produktywności; wynik taki sugerowały opisane wcześniej opracowania, oparte na analizie

modeli równowagi ogólnej.

M.Brzoza-Brzezina (2003) wykorzystał strukturalny model wektorowej autoregresji (VAR)

do oszacowania stopy naturalnej w Stanach Zjednoczonych w latach 1960-2002. Otrzymane

wyniki wskazują na znaczną zmienność neutralnego poziomu krótkookresowej stopy

procentowej, zbliżoną do zmienności realnego oprocentowania funduszy federalnych.

Istotnym wnioskiem jest znaczna procykliczność stopy naturalnej.

Wydaje się, że obserwowany wzrost zainteresowania zagadnieniem NSP należy wiązać z

powszechnym w ostatnich latach przechodzeniem banków centralnych na strategię

bezpośredniego celu inflacyjnego bądź strategie pokrewne. W pewnym uproszczeniu można

powiedzieć, że banki centralne coraz częściej sterują inflacją poprzez kontrolę

krótkoterminowych stóp procentowych przy płynnym kursie walutowym. Zakładając, że

władze monetarne potrafią rozróżnić stopy realne od nominalnych i zdają sobie sprawę z

podstawowych zasad rządzących mechanizmem transmisji, można oczekiwać, że będą starały

się tak sterować stopą nominalną, aby realizować pewną założoną ścieżkę zmian stóp

realnych, pozwalającą, w ich mniemaniu, osiągnąć cel inflacyjny. Okazuje się zatem, że

strategia bezpośredniego celu inflacyjnego opiera się na bardzo podobnych podstawach, co

teoria naturalnej stopy procentowej. Skuteczny bank centralny musi bowiem próbować ustalić

jaki jest poziom realnych stóp procentowych, który zapewni ustabilizowanie stopy inflacji.

W konsekwencji, stosowane współcześnie definicje NSP odbiegają z reguły od definicji

wicksellowskiej. Wśród nich, stosunkowo często wykorzystywana jest ta, która utożsamia

naturalną stopę procentową z takim poziomem stopy realnej, przy którym inflacja jest

stabilna. Idąc dalej, podniesienie stóp realnych powyżej NSP prowadziło będzie do spadku

inflacji, zaś obniżenie stóp poniżej NSP do wzrostu inflacji

6

. Analogicznie można przy okazji

zdefiniować nastawienie polityki pieniężnej – neutralne, odpowiadające naturalnej stopie

procentowej, prowadzi do stabilizacji inflacji, restrykcyjne (stopa procentowa powyżej NSP)

prowadzi do spadku inflacji, a ekspansywne (stopa procentowa poniżej NSP) – do jej wzrostu.

6

Taką definicją posługują się m.in. A.Blinder (2001), J.C.Fuhrer i G.R.Moore (1995), T.Henckel, A.Ize i

A.Kovanen (1999), T.Laubach i J.C.Williams (2001), M.Brzoza-Brzezina (2003 a, 2003 b) oraz J.Andres,
R.Mestre i J.Valles (1997).

11

Oszacowanie tak zdefiniowanej stopy naturalnej z oczywistych przyczyn wydaje się pożądane

z punktu widzenia banków centralnych, sterujących stopami procentowymi. Powyższą

definicję można zapisać w postaci równania:

(8)

)

*

(

r

r

−

≡

∆

α

π

,

gdzie

∆

jest operatorem różnicowania,

π

oznacza stopę inflacji, zaś r* i r odpowiednio

naturalną i realną stopę procentową. Biorąc pod uwagę kwestię użyteczności powyższej

definicji, w dalszej części artykułu oraz w opracowaniu empirycznym, tak określona

stopa naturalna będzie utożsamiana ze stopą krótkookresową, którą steruje bank

centralny

7

. Jej oszacowanie powinno udostępnić władzom monetarnym dodatkowy

wskaźnik, ułatwiający prowadzenie strategii bezpośredniego celu inflacyjnego.

Definiując naturalną stopę procentową nie można jednak abstrahować od faktu, że znaczna

część współczesnych modeli makroekonomicznych oparta jest na podstawach mikro. W

takich modelach NSP utożsamiana jest z krańcową produktywnością kapitału lub poziomem

stopy realnej po usunięciu wszystkich sztywności

8

. Poważną zaletą tego podejścia jest

możliwość ustalenia na podstawie modelu czynników determinujących stopę równowagi.

Należy przy tym zauważyć, że stopa naturalna, określona na podstawie krańcowej

produktywności kapitału ma z założenia charakter średnio- i długookresowy. Nie należy

zatem utożsamiać powyższych definicji, co zostanie omówione szczegółowo w rozdziale 2.2.

Spośród współczesnych podejść do NSP zostały zatem wyróżnione dwie grupy: definicje

związane ze stopą inflacji oraz te, utożsamiające NSP z realną stopą równowagi modelu

gospodarki o podstawach mikroekonomicznych. Te definicje wydają się stosunkowo

najbardziej użyteczne z punktu widzenia banku centralnego. Pierwsza, pozwala na

oszacowanie krótkookresowej stopy procentowej, która stabilizuje inflację, druga

pomaga poznać determinanty stopy równowagi. W następnym rozdziale przeanalizowane

zostaną oba podejścia do NSP. Należy jednak pamiętać, że jest to z natury rzeczy podejście

uproszczone i nie ukazuje całego bogactwa definicji stopy naturalnej.

7

Zarówno przy opisie modelu procesu kumulacyjnego, jak i w przypadku inflacyjnej definicji NSP dla

uproszczenia pominięte zostały indeksy czasowe. Należy jednak pamiętać, że proces transmisji monetarnej jest
rozłożony w czasie i że inflacja zależy w praktyce od całego ciągu luk stóp procentowych.

8

W ten nurt wpisują się m.in. modele M.Woodforda (1999, 2000), K.Neiss i E.Nelsona (2000), J.S.Chadha i

C.Nolana (2001) oraz R.Gali i T.Monacelliego (2002).

12

2 Teoretyczne podstawy naturalnej stopy procentowej

W pierwszej kolejności przeanalizowana zostanie definicja, wiążąca NSP ze stopą inflacji. W

drugiej części rozdziału omówione zostaną podstawy modelowania równowagi ogólnej i

wynikające stąd wnioski dla analizy NSP.

2.1 Związek stóp procentowych i inflacji a NSP

W pierwszej kolejności przedstawione zostanie uzasadnienie istnienia NSP, zdefiniowanej w

równaniu (8). Dowód przeprowadzony zostanie w oparciu o znajomość mechanizmu

transmisji monetarnej

9

.

W dużym uproszczeniu mechanizm transmisji działa następująco: bank centralny zmienia

(załóżmy, że podnosi) stopy procentowe, celem zaostrzenia polityki pieniężnej. Jeżeli uda mu

się na tyle zdecydowanie podnieść stopy nominalne, że doprowadzi do wzrostu stóp realnych,

jego polityka zaczyna w następujący sposób oddziaływać na gospodarkę. Wzrost realnego

oprocentowania kredytów i depozytów zniechęca przedsiębiorstwa do rozpoczynania

kolejnych projektów inwestycyjnych, jednocześnie efekt substytucji międzyokresowej

zachęca gospodarstwa domowe do odłożenia części dzisiejszej konsumpcji na przyszłe

okresy

10

. Jeżeli dodatkowo zaostrzenie polityki pieniężnej doprowadzi do aprecjacji kursu

walutowego, w procesie transmisji zaczyna również odgrywać istotną rolę handel zagraniczny

– spada popyt zagranicy na towary krajowe oraz ceny towarów importowanych. Spadek

podstawowych składników zagregowanego popytu, inwestycji, konsumpcji i eksportu netto

prowadzi w pierwszej kolejności do spowolnienia dynamiki gospodarki i wzrostu bezrobocia.

Z upływem czasu, zaostrzona sytuacja na rynku pracy prowadzi do obniżenia dynamiki płac,

dzięki czemu przedsiębiorstwa wolniej podnoszą ceny. Ostatecznie produkcja zaczyna

powracać do potencjału, trwałym skutkiem zaostrzenia polityki pieniężnej jest natomiast

niższa stopa inflacji. Można zatem stwierdzić, że wysokie stopy procentowe prowadzą, po

9

Szerzej o mechanizmie transmisji piszą m. in. F.S.Mishkin (1995), A.Blinder (2001) oraz R.Kokoszczyński i.in

(2002).

13

zajściu wszystkich procesów dostosowawczych (co może trwać nawet kilka lat), do spadku

stopy inflacji. Argumentując analogicznie, można pokazać, że niskie, realne stopy procentowe

doprowadzą z czasem do wzrostu inflacji.

Jeżeli zatem przyjmiemy (jak powyżej), że istnieje taki (wysoki) poziom stóp realnych,

któremu odpowiada ujemna dynamika inflacji (

∆π

<0) i taki (niski) poziom stóp realnych,

któremu odpowiada dynamika dodatnia (

∆π

>0), oraz że funkcja

Φ

, zależności dynamiki

inflacji (

∆π

) od stopy realnej (r):

(9)

)

(r

Φ

=

∆

π

jest ciągła i ściśle monotoniczna, możemy na mocy twierdzenia o przyjmowaniu wartości

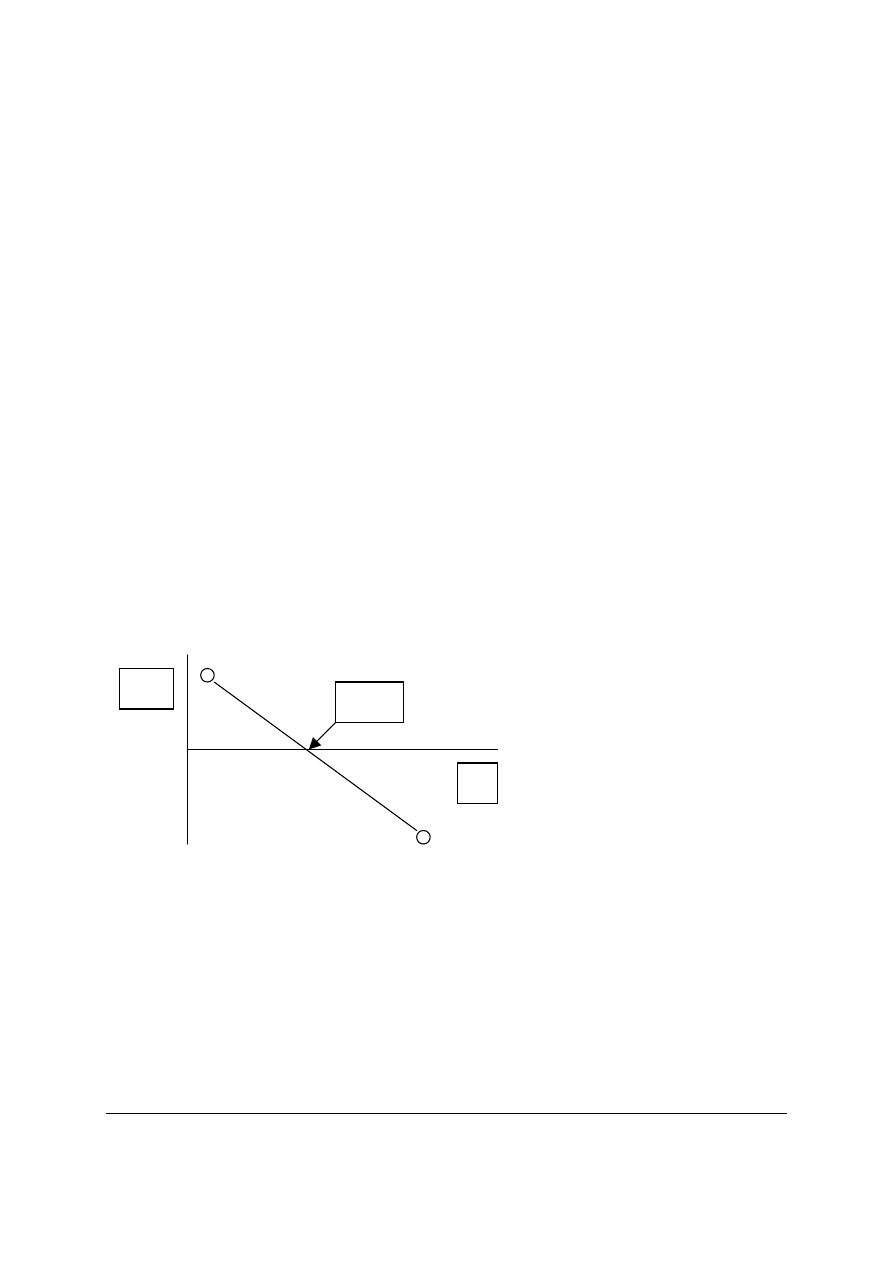
pośrednich przez funkcje ciągłe stwierdzić, że istnieje takie r, dla którego

∆π

=0 (Wyk. 1).

Ponieważ dokładnie w ten sposób definiowana była w równaniu (8) naturalna stopa

procentowa, należy uznać, że z teoretycznego punktu widzenia można wykazać jej istnienie.

Wyk. 1: Związek stóp procentowych i inflacji a istnienie NSP

2.2 Modele równowagi ogólnej a NSP

Jak to zostanie przedstawione w artykule „Rola naturalnej stopy procentowej w polskiej

polityce pieniężnej”, powyższa definicja NSP może być podstawą do ekonometrycznego

oszacowania stopy naturalnej. Niemniej warto również wykorzystać inne narzędzia,

10

Choć teoretycznie możliwe jest wystąpienie przeciwnego skutku, w związku z pojawieniem się efektu

majątkowego, w praktyce prawie zawsze efekt substytucyjny przeważa.

∆π

r

NSP

14

pozwalające na określenie determinantów stopy równowagi. Stosunkowo najlepiej

predestynowane do tego celu wydają się modele równowagi ogólnej, powszechnie

wykorzystywane od ponad 20 lat w analizach makroekonomicznych.

Przekonanie o wyższości modeli opartych o zasadę mikroekonomicznej maksymalizacji

zysku i użyteczności nad układami równań „postulowanych” przez badacza (np. krzywe IS-

LM), wynika przede wszystkim z ich teoretycznego braku podatności na krytykę Lucasa

(zmiana parametrów polityki gospodarczej może wpływać na zachowania ludzi, lecz nie

powinna na podstawowe zasady ich działania, związane np. z kształtem funkcji użyteczności).

W dalszej części rozdziału, do analizy determinantów stopy równowagi, wykorzystany

zostanie model wzrostu Ramseya (1928). Jest to model wyłącznie realnej sfery gospodarki

11

,

co wprawdzie uniemożliwia opisanie wpływu stóp procentowych na inflacje, pozwala jednak

w wiarygodny sposób modelować zachowanie zmiennych realnych w stanie równowagi,

między innymi realnej stopy procentowej. Ponadto, należy zauważyć, że model Ramseya

dotyczy gospodarki zamkniętej. Dyskusja determinantów stopy równowagi w gospodarce

otwartej przeprowadzona zostanie w podrozdziale 2.3. Standardowe obliczenia,

przedstawione w Aneksie 1, pozwalają na określenie determinantów realnej stopy równowagi

w stanie ustalonym modelu Ramseya:

(10)

ρ

δ

+

Θ

=

−

=

x

k

f

r

)

ˆ

(

'

,

gdzie r oznacza realną stopę równowagi,

)

ˆ

(

' k

f

krańcową produktywność kapitału,

δ

stopę

deprecjacji kapitału,

Θ

jest parametrem z funkcji użyteczności (por. równanie 18), x

oznacza stopę wzrostu postępu technicznego zaś

ρ

stopę preferencji czasowych gospodarstw

domowych.

Z równania (10) wynika, że realna stopa równowagi powinna być równa krańcowej

produktywności kapitału pomniejszonej o stopę deprecjacji. Przy danej, neoklasycznej funkcji

produkcji, oznacza to, że większy zasób kapitału per capita oznacza niższy poziom stopy

równowagi.

11

Wnioski dla NSP wyciągane na podstawie Nowych Keynesowskich modeli, uwzględniających występowanie

nominalnych sztywności omawia szczegółowo J.Amato (2001).

15

Z drugiej części równania wynika natomiast, że przyczyną wyższej stopy równowagi może

być również wyższa stopa preferencji czasowych. Wzrost współczynnika

ρ

oznacza, że

gospodarstwa domowe, zaczynają bardziej cenić konsumpcję bieżącą, a w mniejszym stopniu

zainteresowane są tym, co się będzie działo w przyszłości. Takie zachowanie podmiotów

oznacza zmniejszenie oszczędności i, co za tym idzie, wzrost stopy procentowej

równoważącej rynek.

Z kolei wysoki współczynnik

Θ

oznacza, że gospodarstwa domowe są zainteresowane

wygładzaniem poziomu konsumpcji w czasie. W sytuacji, kiedy oczekiwany jest w

przyszłości wzrost dochodu, gospodarstwa takie będą zainteresowane zwiększaniem

konsumpcji dzisiejszej kosztem konsumpcji jutrzejszej, tak aby maksymalnie wygładzić jej

poziom w dłuższym horyzoncie czasowym. Zachowanie takie działa dokładnie tak, jak wzrost

stopy preferencji czasowych, prowadzi do spadku oszczędności i wzrostu stopy procentowej.

O oczekiwanym wzroście dochodu w przyszłości decyduje tempo wzrostu produktywności

(x). Im wyższe x, tym większa jest różnica pomiędzy dochodem bieżącym i oczekiwanym w

przyszłości, co w sytuacji, gdy gospodarstwa domowe mają skłonność do wygładzania

konsumpcji w czasie, będzie prowadziło do podniesienia realnej stopy równowagi. Jak już

wspominano, zależność ta została wykorzystana do zbadania związku pomiędzy stopą

równowagi a NSP przez Laubacha i Williamsa. Uzyskane wyniki potwierdziły istotną,

dodatnią korelację pomiędzy tempem wzrostu produktywności a naturalną stopą procentową.

Modele równowagi ogólnej rozwiązywane są najczęściej w okolicach stanu ustalonego

(stacjonarnego). Dzieje się tak z dwóch przyczyn. Po pierwsze, rozwiązanie układu równań

różniczkowych jest zdecydowanie prostsze właśnie w otoczeniu stanu ustalonego. Po drugie,

o gospodarkach rozwiniętych zakłada się zwykle, że znajdują się w otoczeniu stanu

ustalonego, jeśli więc ktoś nie pragnie zajmować się teorią konwergencji, nie ma powodów,

by rozpatrywać zachowanie się modelu z dala od stanu stacjonarnego.

Model Ramseya pozwala jednak również na porównanie stóp równowagi w dwóch

gospodarkach, z których jedna znajduje się w stanie stacjonarnym, druga zaś, charakteryzuje

się zbliżoną strukturą mikroekonomiczną, ale do stanu ustalonego dopiero zmierza w procesie

konwergencji. Na podstawie równania (24) z Aneksu 1 można wywnioskować, że poza

stanem ustalonym, realna stopa równowagi wynosi:

16

(11)

ρ

γ

δ

+

Θ

+

Θ

=

−

=

x

k

f

r

cˆ

)

ˆ

(

'

,

co oznacza, że zależy dodatkowo od stopy wzrostu konsumpcji na efektywnego pracownika

12

cˆ

γ

. A zatem stopa równowagi poza stanem ustalonym jest wyższa niż w stanie

stacjonarnym

, ponieważ dynamika konsumpcji maleje asymptotycznie do zera w miarę

zbliżania się do stanu ustalonego. Tak więc, jeżeli porównujemy dwie gospodarki, z których

jedna jest w stanie stacjonarnym a druga dopiero do niego zmierza, możemy stwierdzić, że w

tej drugiej stopa procentowa równowagi będzie wyższa.

Do tego samego wniosku można dojść porównując krańcową produktywność kapitału w obu

gospodarkach. Ponieważ w gospodarce znajdującej się w stanie ustalonym zasób kapitału na

efektywnego pracownika jest wyższy niż w gospodarce do stanu ustalonego zmierzającej,

jego krańcowa produktywność musi być niższa. A zatem również stopa procentowa

równowagi musi być niższa w stanie ustalonym.

Otrzymane wyniki można uzasadnić intuicyjnie. Wyższa stopa zwrotu z kapitału sprawia, że

potrzebne są wyższe realne stopy, aby ustabilizować inwestycje. Również szybkie tempo

wzrostu konsumpcji, poza stanem ustalonym, prowadziło będzie do wolniejszego przyrostu

oszczędności i do wzrostu stopy realnej, równoważącej rynek.

Na tym nie kończą się jednak wnioski, jakie model Ramseya pozwala wyciągnąć dla realnej

stopy równowagi w gospodarce zamkniętej. Szczególnie istotne wydaje się porównanie stopy

procentowej ze stopą wzrostu gospodarczego. Otóż okazuje się, że w stanie ustalonym,

stopa równowagi jest zawsze większa bądź równa stopie wzrostu gospodarki (Barro,

Sala-i-Martin 1994, s.72). Przy dość ogólnych założeniach można pokazać, że zasada ta

obowiązuje również na ścieżce dojścia do stanu ustalonego

(dowód w Aneksie 2).

Reasumując, model Ramseya daje nam kilka cennych wskazówek odnośnie zasad rządzących

kształtowaniem się realnej stopy równowagi w gospodarce zamkniętej. Po pierwsze, stopa ta

12

Konsumpcja na efektywnego pracownika to

L

t

A

C

c

⋅

≡

)

(

ˆ

, gdzie C oznacza zagregowaną konsumpcję, L

podaż pracy, zaś A(t) stopień zaawansowania technologicznego (będący w modelu Ramsey’a funkcją czasu).

17

jest niższa w stanie ustalonym niż w drodze do niego i powinna się obniżać w miarę

zachodzenia procesu konwergencji.

Po drugie jest ona zawsze wyższa bądź równa stopie

wzrostu gospodarczego. Po trzecie, zmiana stopy wzrostu produktywności, stopy

preferencji czasowych gospodarstw domowych bądź współczynnika „wygładzania”

profilu konsumpcji powinna prowadzić do zmiany realnych stóp procentowych w tym

samym kierunku.

Przygotowanie gruntu dla analizy empirycznej wymaga poruszenia jeszcze jednego

zagadnienia. Powyżej omówione zostały dwa alternatywne podejścia do zagadnienia

naturalnej stopy procentowej, jedno oparte na inflacyjnej definicji NSP, drugie związane z

pojęciem stopy równowagi w modelu równowagi ogólnej. Nie uprawnia to do przyjęcia

milczącego założenia o bezwzględnej równości omówionych powyżej stóp naturalnych.

Poniżej przedstawiona zostanie krótka dyskusja tego problemu.

Należy na samym wstępie zaznaczyć, że NSP definiowana na podstawie związku z inflacją i

realna stopa równowagi z modelu równowagi ogólnej to dwie różne zmienne. Nietrudno

znaleźć przykłady, pokazujące, że wielkości te nie są sobie równe:

- racjonalnie

postępujące podmioty (a takie zaludniają modele równowagi ogólnej),

podejmując decyzje wpływające na poziom cen (np. w trakcie negocjacji płacowych)

nie będą ograniczać się do analizy dzisiejszej luki stóp procentowych, lecz wezmą pod

uwagę również przewidywania dotyczące wszystkich przyszłych luk. Tymczasem

„inflacyjna” definicja NSP obejmuje wyłącznie wpływ dzisiejszej luki na inflację.

- w modelach równowagi ogólnej stopa równowagi uzależniona jest od parametrów

modelu (takich jak stopa preferencji czasowych gospodarstw domowych). Tak więc

nie należy oczekiwać, że stopa procentowa równowagi (przynajmniej ta z modelu

Ramseya) będzie podlegała krótkookresowym wahaniom, związanym np. z

występowaniem szoków podażowych czy wpływem oczekiwań inflacyjnych.

Mimo to wydaje się, że należy wykorzystywać modele teoretyczne i wyznaczoną na ich

podstawie stopę równowagi do tłumaczenia determinantów stopy naturalnej. W kontekście

pierwszego przykładu, należy bowiem zauważyć, iż podobne zarzuty można postawić choćby

wykorzystywaniu bieżącej podaży pieniądza do modelowania inflacji. Racjonalne podmioty

18

powinny wpływać na poziom cen również na podstawie oczekiwanej w przyszłości ekspansji

monetarnej. Niemniej, w praktyce, w wielu krajach wykorzystanie wyłącznie przeszłych

wartości agregatów pieniężnych do prognozowania inflacji przynosiło i przynosi dobre

rezultaty.

Trudniej zmierzyć się z drugim argumentem. Można natomiast, na podstawie historycznych

szeregów czasowych badać, czy NSP podlegała wahaniom sugerowanym przez modele

równowagi ogólnej. Przykładem udanych badań może być praca Laubacha i Williamsa,

którzy pokazali, że NSP była w przeszłości silnie, dodatnio skorelowana ze stopą wzrostu

produktywności. Taka mieszana analiza teoretyczno-empiryczna może zatem być pomocna w

ustalaniu podobieństw pomiędzy stopą równowagi i NSP. Udało się również pokazać (Neiss,

Nelson 2000), że luka stóp procentowych, wyprowadzona z modelu równowagi ogólnej,

wykalibrowanego dla gospodarki brytyjskiej, posiada dobre własności prognostyczne

odnośnie przyszłej inflacji.

Można zatem powiedzieć, że choć istnieją jednoznaczne dowody, pokazujące że realna stopa

równowagi i NSP muszą się różnić, są również podstawy aby podejrzewać u nich wspólne

cechy. Tak więc, wykorzystywanie modeli równowagi ogólnej do objaśniania właściwości

NSP znajduje uzasadnienie w wynikach prac empirycznych. Przedmiotem dalszych dociekań

powinno być między innymi bardziej szczegółowe opisanie podobieństw i różnic pomiędzy

tymi dwoma kategoriami.

2.3 NSP w gospodarce otwartej

Powyższa analiza determinantów stopy równowagi dotyczyła gospodarki zamkniętej.

Naturalne wydaje się zadanie pytania o kształtowanie się stopy równowagi w gospodarce

otwartej. Standardowy zarzut, z którym trzeba się w tej sytuacji zmierzyć, brzmi następująco:

w gospodarce otwartej, ze swobodą przepływów kapitałowych, wyższa krańcowa

produktywność kapitału spowoduje napływ finansowania zewnętrznego, który doprowadzi do

natychmiastowego wzrostu zasobu kapitału i spadku jego krańcowej produktywności do

poziomu gospodarki światowej. Podobny proces powinien dotyczyć aktywów finansowych,

których wyższe oprocentowanie powinno generować napływ inwestycji portfelowych tak

długo, aż rentowność obniży się do poziomu światowego.

19

Jeżeliby zgodzić się z tymi postulatami, należałoby oczekiwać, że realna stopa równowagi

powinna być równa na całym świecie, a jej krajowe determinanty, opisane powyżej nie

odgrywają istotnej roli. Taki stan rzeczy znacząco ułatwiałby empiryczne szacowanie NSP w

Polsce, ponieważ pozwalałby na skorzystanie z danych zagranicznych. Jest jednak kilka

poważnych argumentów, pozwalających sądzić, iż naturalna stopa procentowa różni się

pomiędzy krajami.

Patrząc na NSP od podażowej strony modelu równowagi ogólnej, należy zauważyć, że

międzynarodowe przepływy kapitału, które powinny prowadzić do wyrównania krańcowych

produktywności, są ograniczone przez kilka czynników. W pierwszej kolejności wyróżnia się

z reguły tzw. koszt instalacji kapitału (J.Tobin 1969). Proces inwestycyjny ma charakter

czasochłonny, a jego przyspieszanie wiąże się z ponoszeniem dodatkowych obciążeń, co

niekoniecznie musi być optymalne z punktu widzenia przedsiębiorstwa. W literaturze

wyróżnia się także zjawisko, zwane home bias. Choć z reguły terminem tym oznacza się

zwiększoną skłonność inwestorów do nabywania aktywów finansowych we własnym kraju, z

powodzeniem można to zjawisko przenieść na problem inwestowania w kapitał fizyczny.

Znajomość reguł, rządzących inwestowaniem na rynku krajowym sprawia, że niewielka

nadwyżka krańcowej produktywności kapitału za granicą może nie być wystarczającą zachętą

do rozpoczynania tam inwestycji. Widać zatem, że istnieją obiektywne powody, dla których

nie należy oczekiwać zrównania krańcowej produktywności kapitału na skalę

międzynarodową.

Nietrudno obronić również tezę o możliwej rozbieżności rentowności papierów

wartościowych w kraju i zagranicą. Przy płynnym kursie walutowym inwestorzy, oceniając

oczekiwany przychód muszą brać pod uwagę nie tylko bezwzględny dysparytet stóp, ale

również oczekiwane wahania kursu. Ponadto nie można zapominać o występowaniu

wspomnianego już zjawiska home bias oraz premii za ryzyko, która z reguły jest wyższa w

przypadku gospodarek rozwijających się (jak Polska) niż w gospodarkach rozwiniętych.

Powyższe spostrzeżenia znajdują potwierdzenie w wynikach modeli równowagi ogólnej,

budowanych dla małych, otwartych gospodarek (MOG). Ponieważ przedstawienie takiego

modelu w całości kwalifikuje się na osobne opracowanie, poniżej zaprezentowane zostaną

20

tylko podstawowe spostrzeżenia, dokonane na podstawie standardowego modelu, opisującego

zachowanie małej otwartej gospodarki, według opracowania J.Gali i T.Monacelli (2002)

13

.

Istotne wydają się przede wszystkim dwa spostrzeżenia. Po pierwsze, realne stopy równowagi

w MOG i w reszcie świata różnią się o składnik, zależny między innymi od stopy wzrostu

gospodarki światowej i stopnia otwartości małej gospodarki. Model nie zawiera elementu

ryzyka, co tłumaczy, dlaczego opisywany wcześniej czynnik nie wpływa w nim na

zróżnicowanie stóp równowagi. Po drugie, zarówno w gospodarce światowej, jak i w

MOG, podstawowe determinanty stopy równowagi pozostają takie same, jak w modelu

Ramseya. Są to tempo wzrostu produktywności, stopa preferencji czasowych

gospodarstw domowych oraz współczynnik z funkcji użyteczności, jak w równaniu (10).

Wydaje się tedy, że model Ramseya może być, w kontekście opisywania własności stopy

równowagi, wykorzystywany szerzej, niż tylko do analizy gospodarki zamkniętej. Niemniej,

właśnie zachowanie stopy naturalnej w gospodarce otwartej powinno w najbliższych latach

stać się podstawowym tematem dociekań naukowych, skupiających się na analizie NSP.

3 Podsumowanie

W artykule przeanalizowane zostało od strony teoretycznej zagadnienie naturalnej stopy

procentowej. W pierwszej kolejności przedstawiona została syntetycznie historia myśli

ekonomicznej w dziedzinie naturalnej stopy procentowej.

W dalszej części opracowania, szczególna uwaga poświęcona została dwóm alternatywnym

sposobom zdefiniowania stopy naturalnej, w odniesieniu do inflacji bądź w odniesieniu do

krańcowej produktywności kapitału. Definicja, utożsamiająca stopę naturalną z takim

poziomem realnej stopy procentowej, który stabilizuje inflację wydaje się bardzo przydatna z

punktu widzenia banku centralnego. Władze monetarne muszą bowiem zdawać sobie sprawę

na jakim poziomie ustawić stopy realne, aby obniżać, stabilizować, bądź podnosić stopę

inflacji. Problem ten w całej okazałości odnosi się do obecnej sytuacji Narodowego Banku

Polskiego, który zakończył obniżanie inflacji i jest w trakcie poszukiwania naturalnego

poziomu stóp procentowych, który zapewni stabilną inflację.

13

Kompleksowy przegląd modeli gospodarek otwartych przedstawia P.R.Lane (1999).

21

Ponieważ definicja, wiążąca NSP ze stopą inflacji nie dostarcza żadnych wskazówek na temat

determinantów stopy naturalnej, w dalszej kolejności przeanalizowany został model

równowagi ogólnej, w którym NSP utożsamiona została z realną stopą równowagi. Stopa ta

jest równa krańcowej produktywności kapitału i w stanie ustalonym zależy między innymi od

stopy wzrostu produktywności oraz od stopy preferencji czasowych gospodarstw domowych.

Dalsza analiza modelu pozwoliła ustalić, że przy spełnieniu dość prawdopodobnych założeń,

stopa równowagi jest zawsze większa bądź równa realnej stopie wzrostu gospodarki. Ponadto,

w gospodarce podlegającej procesowi konwergencji stopa równowagi jest wyższa niż w

stanie ustalonym i maleje asymptotycznie w miarę zbliżania się do stanu stacjonarnego.

Determinanty stopy równowagi są podobne w gospodarce zamkniętej i otwartej.

Choć nie jest możliwe wykazanie równości NSP otrzymanej na podstawie definicji inflacyjnej

i realnej stopy równowagi, można zwrócić uwagę na teoretyczne i empiryczne podobieństwa

obu stóp. Opisane wnioski zostaną wykorzystane w drugiej części opracowania,

zatytułowanej „Rola naturalnej stopy procentowej w polskiej polityce pieniężnej”, do

oszacowania przybliżonego poziomu naturalnej stopy procentowej w Polsce.

22

Bibliografia:

1. Amato, J. 2001. “Wicksell, New Keynesian Models and the Natural Rate of Interest”,

mimeo, Bank for International Settlements, Basel.

2. Andres, J., Mestre, R., Valles, J. 1997. „A Structural Model for the Analysis of the

Impact of Monetary Policy an Output and Inflation”, w: Monetary Policy and the

Inflation Process, BIS Conference Papers Vol.4.

3. Barro, R., Sala-i-Martin, X. 1994. „Economic Growth”, Mc-Graw Hill, New York.

4. Blanchard, O.J., Fischer, S. 1989. “Lectures on Macroeconomics”, Cambridge, MIT

Press.

5. Blinder, A. 2001. „Bankowość centralna w teorii i praktyce”, CeDeWu, Warszawa.

6. BoE 2001. “The Transmission Mechanism of Monetary Policy”, materiał na

sympozjum Prezesów Banków Centralnych, CCBS, Bank of England.

7. Brzoza-Brzezina, M. 2003 a. „Estimating the Natural Rate of Interest: A SVAR

Approach”, Working Paper NBP nr 27.

8. Brzoza-Brzezina, M. 2003 b. „Rola naturalnej stopy procentowej w polityce

pieniężnej”, praca doktorska w przygotowaniu, Szkoła Główna Handlowa.

9. Chadha, J.S., Nolan, C. 2001. “Supply Shocks and the Natural Rate of Interest: an

Exploration”, manuscript.

10. ECB 2001. “Monthly Bulletin”, European Central Bank, Frankfurt, October 2001.

11. Fuhrer, J.C., Moore, G.R. 1995. „Forward-Looking Behavior and the Stability of a

Conventional Monetary Policy Rule“, Journal of Money, Credit and Banking, vol. 27,

No. 4.

12. Gali, J., Monacelli, T. 2002. “Monetary Policy and Exchange Rate Volatility in a

Small Open Economy”, mimeo, Pompeu Fabra.

13. Henckel, T., Ize, A., Kovanen, A. 1999. „Central Banking Without Central Bank

Money“, IMF WP/99/92.

14. Hicks, J.R. 1988. “Perspektywy ekonomii: szkice z teorii pieniądza i teorii wzrostu”,

PWN, Warszawa.

15. Honohan, 1981. „A New Look at Wiksell’s Inflationary Process”, Manchester School

of Economic and Social Studies, vol. 49, grudzień.

16. Humphrey, T.M. 1983. “Can the Central Bank Peg Real Interest Rates? A Survey of

Classical and Neoclassical Opinion”, Federal Reserve Bank of Richmond Economic

Review, September/October, s. 12-21.

23

17. Humphrey, T.M. 1993. “Cumulative Process Models from Thornton to Wicksell”, w

Money, Banking and Inflation: Essays in the History of Monetary Thought, Aldershot,

Brookfield.

18. Inada, K. 1963. “On a Two-sector Model of Economic Growth: Comments and a

Generalization”, Review of Economic Studies 30, s. 119-127.

19. Jonung, L. 1979. „Knut Wicksell’s Norm of Price Stabilization and Swedish Monetary

Policy in the 1930’s”, Journal of Monetary Economics 5, s. 459-496.

20. Keynes, J.M. 1936. “Ogólna teoria zatrudnienia, procentu i pieniądza”, PWN,

Warszawa 1985.

21. Kokoszczyński, R., Łyziak, T., Pawłowska, M., Przystupa, J., Wróbel, E. 2002.

“Mechanizm transmisji polityki pieniężnej-współczesne ramy teoretyczne, nowe

wyniki empiryczne”, mimeo, NBP.

22. Laidler, D. 1991. „The Golden Age of the Quantity Theory”, Harvester Wheatsheaf,

New York.

23. Lane, P.R. 1999. “The New Open Economy Macroeconomics: A Survey”, Journal of

International Economics, vol. 54, s. 235-266.

24. Laubach, T., Williams, J.C. 2001. „Measuring the Natural Rate of Interest”, Board of

Governors of the Federal Reserve System, November.

25. Leijonhufvud, A. 1989. “Natural Rate and Market Rate”, w: The new Palgrave Money,

Macmillan, New York.

26. Mishkin, F.S. 1995. „Symposium on the Monetary Transmission Mechanism”, The

Journal of Economic Perspectives, Vol. 9, No. 4.

27. Myhrman, J. 1991. “The Monetary Economics of the Stockholm School”, w The

Stockholm School of Economics Revisited, ed. L.Jonung, Cambridge University Press,

Cambridge.

28. Neiss, K.S., Nelson, E. 2001. “The Real Interest Rate Gap as an Inflation Indicator”,

Bank of England WP 130.

29. Plantier, L.C., Scrimgeour, D. 2002. “Estimating a Taylor Rule for New Zealand with

a Time – varying Neutral Real Rate”, DP2002/06, Reserve Bank of New Zealand.

30. Ramsey, F. 1928. “A Mathematical Theory of Saving”, Economic Journal 38, s. 543-

559.

31. Taylor, J.B. 1993. “Discretion Versus Policy Rules in Practice”, Carnegie

RochesterConference Series on Public Policy39, s. 195-214.

24

32. Tobin, J. 1969. „A General Equilibrium Approach to Monetary Theory”, Journal of

Money, Credit and Banking 1, s. 15-29.

33. Uhr, C.G. 1951. “Knut Wicksell - A Centennial Evaluation”, American Economic

Review 16, s. 829-860.

34. Wicksell, K. 1898. “Interest and Prices”, tłumaczenie R.F.Kahn, MacMillan, New

York, 1936.

35. Wicksell, K. 1907. “The Influence of the Rate of Interest on Prices”, The Economic

Journal, June, s. 213-220.

36. Woodford, M. 1999. “Interest and Prices”. Plik pdf: www.princeton.edu/~woodford.

Princeton.

37. Woodford, M. 2000. „A Neo-Wicksellian Framework for the Analysis of Monetary

Policy“, plik pdf: www.princeton.edu/~woodford. Princeton.

25

Aneks 1: Stopa równowagi w stanie ustalonym modelu
Ramseya

Poniżej przedstawione zostanie wyprowadzenie równania, pozwalającego określić

determinanty realnej stopy równowagi w modelu Ramseya. W związku z powszechną

znajomością, lub przynajmniej dostępnością

14

modelu, wyprowadzenie równań modelu

ograniczone zostanie do podstawowych przekształceń, interesujących z punktu widzenia

analizy determinantów realnej stopy procentowej. Szczególna uwaga zostanie poświęcona

zagadnieniom, które mogą okazać się przydatne przy szacowaniu poziomu NSP w Polsce.

Modelowa gospodarka zaludniona jest przez nieskończoną ilość gospodarstw domowych,

maksymalizujących międzyokresową funkcję użyteczności:

(12)

∫

∞

−

⋅

⋅

=

0

)]

(

[

max

dt

e

e

t

c

u

U

nt

t

ρ

gdzie U oznacza użyteczność, c konsumpcję, n stopę wzrostu populacji, zaś

ρ

stopę

preferencji czasowej gospodarstw domowych. Rosnąca i wypukła funkcja użyteczności u(c)

spełnia warunki Inady (1963). Gospodarstwa domowe podlegają ograniczeniu budżetowemu:

(13)

na

c

ra

w

a

−

−

+

=

&

gdzie a oznacza realny zasób aktywów per capita, utrzymywanych przez gospodarstwa

domowe w postaci kapitału, bądź pożyczek, zaś r realną stopę procentową. Przez z&

oznaczana będzie pierwsza pochodna zmiennej z po czasie,

dt

dz

z

=

&

, zaś przez

z

γ

stopa

wzrostu zmiennej z,

z

z

z

&

=

γ

.

Rozwiązanie problemu optymalizacji konsumenta wymaga zapisania hamiltonianu:

(14)

)

(

)]

(

[

na

c

ra

w

e

e

t

c

u

H

nt

t

−

−

+

⋅

+

⋅

⋅

=

−

µ

ρ

,

14

Szczegółowy opis modelu zawierają m.in. O.J.Blanchard, S.Fischer (1989) i R.Barro, X.Sala-i-Martin (1994).

26

wraz warunkiem transwersalności, wykluczającym nieskończone wielkie pożyczki (tzw.

schematy Ponziego):

(15)

0

)]

(

)

(

[

lim

=

⋅

∞

→

t

a

t

t

µ

i wyznaczenia warunków pierwszego rzędu:

(16)

0

=

∂

∂

c

H

,

(17)

µ

−

=

∂

∂

a

H

.

Przyjęcie konkretnej postaci funkcji użyteczności:

(18)

Θ

−

−

=

Θ

−

1

1

)

(

1

c

c

u

,

umożliwia otrzymanie rozwiązania dla problemu optymalizacji, postaci:

(19)

)

(

1

ρ

γ

−

Θ

=

r

c

.

Drugi filar gospodarki stanowią przedsiębiorstwa, które produkują zgodnie z neoklasyczną

funkcją produkcji:

(20)

)

,

,

(

t

L

K

F

Y

=

,

gdzie Y oznacza produkcję, K kapitał fizyczny, L nakłady pracy, zaś t obrazuje postęp

techniczny, o którym zakładamy, że pojawia się w gospodarce egzogenicznie, wraz z

upływem czasu.

Funkcję produkcji można również przedstawić w postaci:

27

(21)

)

ˆ

,

(

L

K

F

Y

=

,

gdzie

)

(

ˆ

t

A

L

L

⋅

≡

oznacza nakład efektywnej podaży pracy, zaś technologia A(t) przyrasta w

tempie x. Następnie można przekształcić funkcję produkcji do postaci:

(22)

)

ˆ

(

ˆ

k

f

y

=

,

produktu na efektywnego pracownika, gdzie

L

K

k

ˆ

ˆ

≡

.

Rozwiązanie problemu maksymalizacji zysku, przez reprezentatywnego producenta, pozwala

otrzymać znany wynik, zrównujący krańcową produktywność kapitału netto (czyli

pomniejszoną o deprecjację

δ

) z realną stopą procentową r:

(23)

δ

+

=

r

k

f

)

ˆ

(

'

.

Przekształcenie równania (19) do postaci na efektywnego pracownika:

(24)

x

r

x

c

c

−

−

Θ

=

−

=

)

(

1

ˆ

ρ

γ

γ

,

pozwala na uzyskanie determinantów realnej stopy równowagi w stanie ustalonym (gdzie

0

ˆ

=

c

γ

):

(25)

ρ

δ

+

Θ

=

−

=

x

k

f

r

)

ˆ

(

'

.

Aneks 2: Porównanie realnej stopy równowagi i stopy
wzrostu gospodarki w modelu Ramseya

Załóżmy, że gospodarka charakteryzuje się funkcją produkcji typu Cobba-Douglassa postaci:

(26)

α

k

y

ˆ

ˆ

=

.

28

Jak pokazują Barro i Sala-i-Martin (1994, s.90), w szczególnym przypadku, gdy

Θ

=

α

,

funkcja taka generuje następującą zależność pomiędzy konsumpcją i zasobami kapitału:

(27)

)]

(

/

)

[(

ˆ

ˆ

n

k

c

+

−

Θ

+

=

δ

ρ

δ

.

W tym przypadku istnieje prosta możliwość porównania realnej stopy procentowej ze stopą

wzrostu gospodarki. Ta ostatnia wynosi:

(28)

n

x

k

k

n

x

k

f

k

k

f

n

x

y

Y

+

+

=

+

+

⋅

=

+

+

=

⋅

⋅

ˆ

ˆ

)

ˆ

(

ˆ

)

ˆ

(

'

ˆ

α

γ

γ

,

i po podstawieniu z równania ruchu dla kapitału (Barro, Sala-i-Martin 1994, s. 70):

(29)

k

n

x

c

k

f

k

ˆ

)

(

ˆ

)

ˆ

(

ˆ

⋅

+

+

−

−

=

⋅

δ

może zostać zapisana jako:

(30)

n

x

k

n

x

c

k

k

Y

+

+

⋅

+

+

−

−

=

]

ˆ

)

(

ˆ

ˆ

[

ˆ

1

δ

α

γ

α

.

Teraz podstawiając za

)

ˆ

(

'

ˆ

1

k

f

k

=

−

α

α

z równania (23) otrzymamy:

(31)

)

)(

1

(

ˆ

ˆ

)

)(

1

(

ˆ

ˆ

δ

α

α

α

αδ

α

δ

γ

+

+

−

+

−

=

+

−

+

−

−

+

=

n

x

k

c

r

n

x

k

c

r

Y

.

Następnie, podstawiając z równania (27) otrzymamy:

(32)

ρ

α

δ

α

δ

α

ρ

δ

α

γ

−

+

−

+

=

+

+

−

+













+

−

+

−

=

n

x

r

n

x

n

r

Y

)

1

(

)

)(

1

(

)

(

Ponieważ w stanie ustalonym stopa procentowa jest większa bądź równa stopie wzrostu

gospodarki (Barro, Sala-i-Martin 1994, s.72), wyrażenie

ρ

α

−

+

−

n

x

)

1

(

jest mniejsze bądź

29

równe zeru. Ponieważ nie jest ono funkcją czasu, można przyjąć, że warunek ten zachodzi

również poza stanem ustalonym. A zatem z równania (32) wynika, że dla

α

=

Θ

na całej

ścieżce dojścia do stanu ustalonego

r

Y

≤

γ

.

Jak pokazuje równanie (27),

α

=

Θ

generuje liniową postać zależności pomiędzy kapitałem i

konsumpcją i liniową ścieżkę dojścia do stanu ustalonego. Jednak w rzeczywistości sytuacja

równości powyższych parametrów jest mało prawdopodobna, ponieważ

α

przyjmuje z reguły

wartości w okolicach 0,3, natomiast

Θ

, choć trudniejsze do oszacowania, powyżej jedności.

Dlatego zdecydowanie bardziej prawdopodobny wydaje się przypadek

Θ

<

α

. Odpowiada

mu wklęsła ścieżka dojścia do stanu ustalonego (Wyk. 2).

Należy zauważyć, że dla każdego poziomu kapitału, na wklęsłej ścieżce realizowana jest

większa konsumpcja niż w przypadku

α

=

Θ

, a to, zgodnie z równaniem (30) oznacza

wolniejszy wzrost gospodarczy. Wniosek taki wydaje się uzasadniony intuicyjnie, ponieważ

wyższa konsumpcja oznacza niższe inwestycje i wolniejszy przyrost potencjału

produkcyjnego. Oznacza to, że skoro nierówność

r

Y

≤

γ

jest spełniona dla

α

=

Θ

, tym

bardziej musi być spełniona dla

Θ

<

α

.

Wyk. 2: Ścieżki dojścia do stanu stacjonarnego w modelu Ramseya

Tak więc, przy założeniu funkcji produkcji typu Cobba-Douglasa, można pokazać, że dla

najbardziej prawdopodobnego przypadku

α

>

Θ

, stopa procentowa równowagi jest zawsze

większa od stopy wzrostu gospodarki.

c

ˆ

Θ

=

α

Θ

<

α

0

ˆ

=

•

k

0

ˆ

=

•

c

kˆ

Stan stacjonarny

Ścieżki
dojścia do
stanu
stacjonarnego