TEORIA DO ĆWICZENIA 2
Model neuronu
Sztuczna sieć neuronowa (SSN) to model obliczeniowy, złożony z elementów
naśladujących działania komórek nerwowych zwanych neuronami. Sztuczne neurony nie są
dokładnymi kopiami oryginalnych neuronów, są raczej ich bardzo uproszczonymi
odpowiednikami matematycznymi, mającymi podobne właściwości i działającymi w zbliżony
sposób jak ich pierwowzory. Neuron w SSN charakteryzuje się występowaniem wielu wejść i
jednego wyjścia. W modelu sztucznego neuronu, każdemu połączeniu między neuronami
przypisuje się odpowiednią wagę (siłę powiązania między elementami). Waga (odpowiednik
efektywności synapsy w neuronie biologicznym) to pewna stała, przez którą przemnożony
jest każdy sygnał przechodzący między dwoma konkretnymi neuronami, dzięki czemu,
impulsy od jednych neuronów są ważniejsze od innych. Waga może mieć charakter
pobudzający (dodatnia waga) lub hamujący (ujemna waga). Jeżeli nie ma połączenia między
neuronami to waga jest równa zero. W ten sposób odrzucane są nieistotne informacje
wejściowe.
W praktyce każdy neuron pobiera sygnały od wszystkich połączonych ze sobą
elementów, przemnaża je przez odpowiednią wagę, otrzymane wartości sumuje i to łączne
pobudzenie neuronu jest z kolei przekształcane przez ustaloną funkcję aktywacji (zwaną też
funkcją przejścia) – rys.1. Wartość funkcji aktywacji jest ostatecznie wartością wyjściową
neuronu. Funkcja przejścia może być funkcją liniową, skokową, sigmoidalną, tangensoidalną
etc.. Wybór funkcji należy do projektanta sieci i zależy od problemu, który ma ona
rozwiązywać.
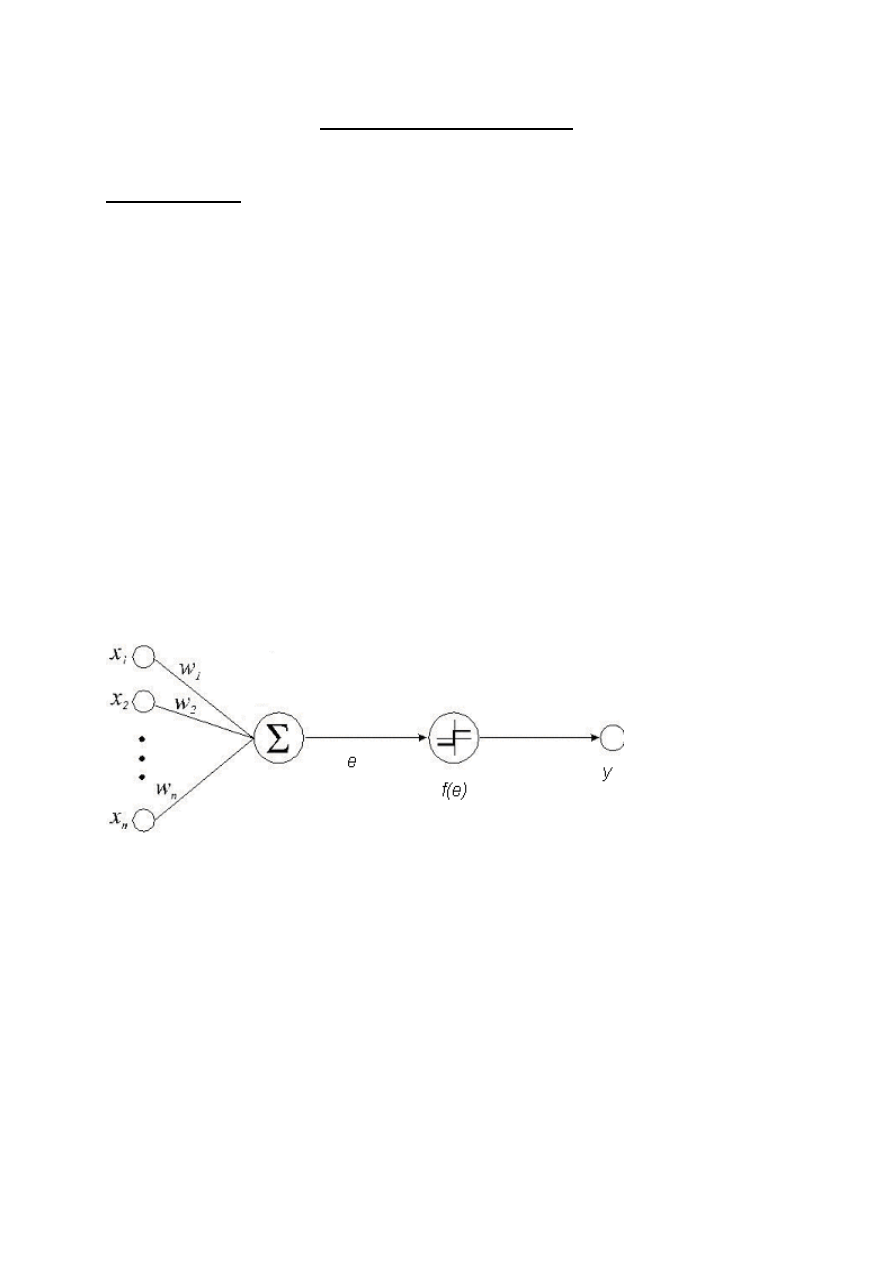
Rys. 1: Model sztucznego neuronu
Do każdego neuronu o numerze i przesyłana jest wartość rzeczywistą x
i
z wagą w
i
.
Informacja wejściowa x
i
jest przemnażana przez odpowiadającą jej wagę w
i
. Przekazana
informacja jest integrowana w neuronie (zwykle przez zsumowanie wszystkich sygnałów) i to
tzw. łączne pobudzenie neuronu e jest przekazywane jako argument do funkcji aktywacji f i
następnie jest wyliczana wartość sygnału wyjściowego.
Model opisujący działanie neuronu może być zapisany w postaci:
)
(
1
n
i
i
i
x
w
f
y
gdzie
x
1
, ... ,x
n
– sygnały wejściowe danego neuronu;
w
1
, ... ,w
n
– wagi synaptyczne;
y – sygnał wyjściowy.
Przykładowe funkcje aktywacji używane przy konstrukcji sieci:
Progowa (skokowa) funkcja aktywacji stosowana w sieciach liniowych
(podstawowa postać)
n
i
i
i
n
i
i
i
x
w
x
w
gdy
gdy
x
f
1
1
,
,
0
1
)
(
gdzie
– wartość progowa.
Funkcja sigmoidalna
x
x
f
exp
1
1
)
(
,
0
Uczenie neuronu
Jedną z najważniejszych cech sieci neuronowych jest ich zdolność uczenia się, czyli
zdolność do samodzielnego dostosowywania współczynników wagowych. Dzięki temu mają
one charakter sztucznej inteligencji, potrafią samodzielnie przystosowywać się do
zmieniających się warunków. Celem uczenia jest taki dobór wag w poszczególnych
neuronach aby sieć mogła rozwiązywać stawiane przed nią problemy.
W naszym przypadku sieć uczy się metodą wstecznej propagacji błędów - jest to
uczenie z nadzorem lub inaczej– z nauczycielem.
Pierwszą czynnością w procesie uczenia jest przygotowanie dwóch ciągów danych:
uczącego i weryfikującego. Ciąg uczący jest to zbiór takich danych, które w miarę dokładnie
charakteryzują dany problem. Jednorazowa porcja danych nazywana jest wektorem uczącym.
W jego skład wchodzi wektor wejściowy czyli te dane wejściowe, które podawane są na
wejścia sieci i wektor wyjściowy czyli takie dane oczekiwane, jakie sieć powinna
wygenerować na swoich wyjściach. Po przetworzeniu wektora wejściowego, porównywane są
wartości otrzymane z wartościami oczekiwanymi i sieć jest informowana, czy odpowiedź jest
poprawna, a jeżeli nie, to jaki powstał błąd odpowiedzi. Błąd ten jest następnie propagowany
do sieci ale w odwrotnej niż wektor wejściowy kolejności (od warstwy wyjściowej do
wejściowej) i na jego podstawie następuje taka korekcja wag w każdym neuronie, aby
ponowne przetworzenie tego samego wektora wejściowego spowodowało zmniejszenie błędu
odpowiedzi. Procedurę taką powtarza się do momentu wygenerowania przez sieć błędu
mniejszego niż założony. Wtedy na wejście sieci podaje się kolejny wektor wejściowy i
powtarza te czynności. Po przetworzeniu całego ciągu uczącego (proces ten nazywany jest
epoką) oblicza się błąd dla epoki i cały cykl powtarzany jest do momentu, aż błąd ten spadnie
poniżej dopuszczalnego. Sieci wykazują tolerancję na nieciągłości, przypadkowe zaburzenia
lub wręcz niewielkie braki w zbiorze uczącym.
Jeżeli mamy już nauczoną sieć, musimy zweryfikować jej działanie. W tym momencie ważne
jest podanie na wejście sieci wzorców z poza zbioru treningowego w celu zbadania czy sieć
może efektywnie generalizować zadanie, którego się nauczyła. Do tego używamy ciągu
weryfikującego, który ma te same cechy co ciąg uczący tzn. dane dokładnie charakteryzują
problem i znamy dokładne odpowiedzi. Ważne jest jednak, aby dane te nie były używane
uprzednio do uczenia. Dokonujemy zatem prezentacji ciągu weryfikującego z tą różnicą, że w
tym procesie nie rzutujemy błędów wstecz a jedynie rejestrujemy ilość odpowiedzi
poprawnych i na tej podstawie orzekamy, czy sieć spełnia nasze wymagania, czyli jak została
nauczona.
Algorytm propagacji wstecznej jest jednym z najskuteczniejszych algorytmów uczenia sieci
wielowarstwowej. Jego nazwa pochodzi od sposobu obliczania błędu w poszczególnych
warstwach sieci. Najpierw obliczane są błędy w warstwie ostatniej na podstawie porównania
aktualnych i wzorcowych sygnałów wyjściowych i na tej podstawie dokonywane są zmiany
wag połączeń, następnie w warstwie ją poprzedzającej i tak dalej aż do warstwy wejściowej.
W algorytmie propagacji wstecznej można wyróżnić trzy fazy:
podanie na wejście sygnału uczącego x i wyliczenie aktualnych wyjść y.
porównujemy sygnał wyjściowy y z sygnałem wzorcowym d, a następnie wyliczamy
lokalne błędy dla wszystkich warstw sieci,
adaptacja wag.
Działanie pojedynczego neuronu
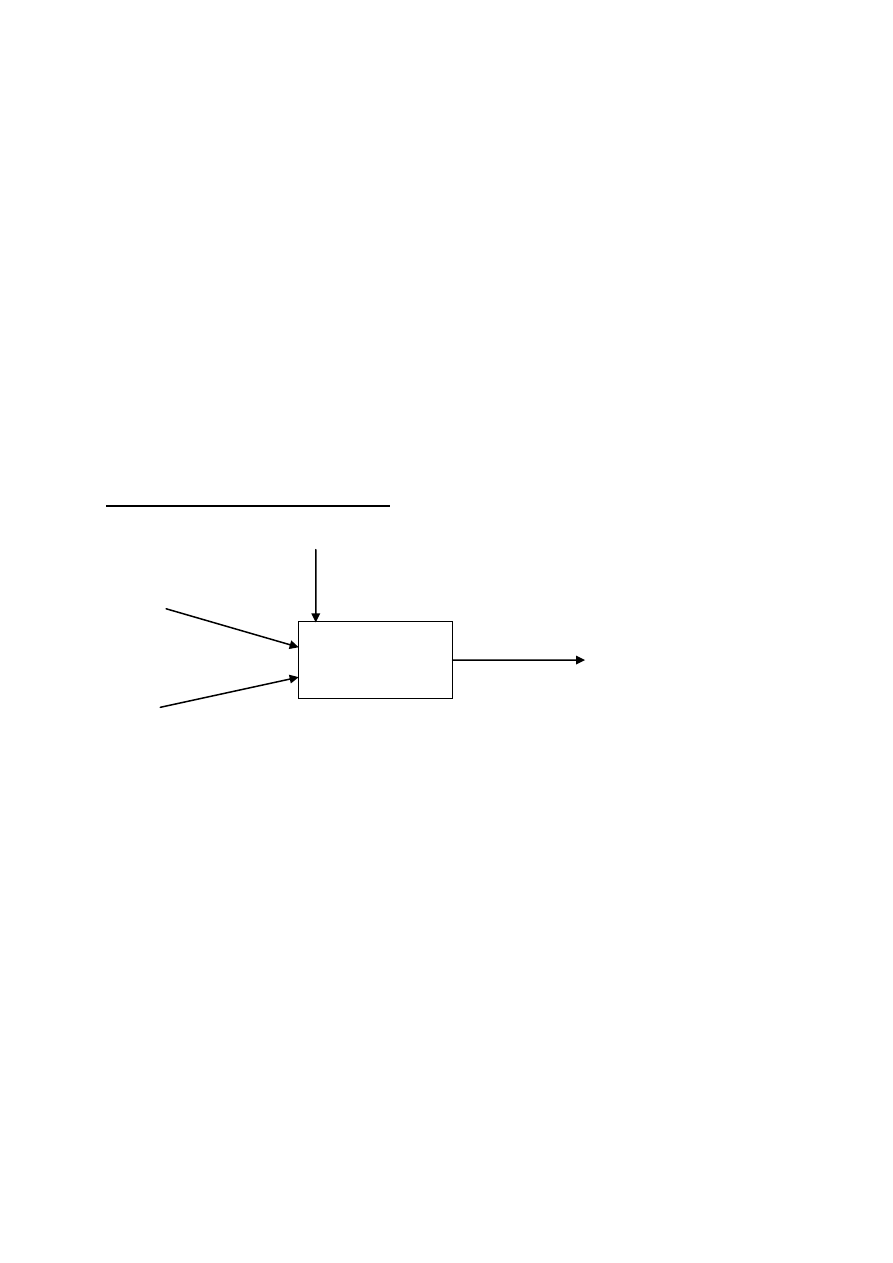
Model pojedynczego neuronu (perceptronu) można przedstawić następująco:
gdzie:
w
1
, w
2
, b – to wartości wag połączeń odpowiednio wejść x
1
, x
2
i biasu
b
x
w
x
w
e
2
2
1
1
jest to łączne pobudzenie neuronu e
Kolejne etapy w jednym kroku uczenia dla przedstawionego neuronu przy skokowej
funkcji aktywacji:
1) dla danego wektora uczącego (x
1
, x
2
, d) wyliczenie łącznego pobudzenia
b
x
w
x
w
e
2
2
1
1
2) wyliczenie aktualnego wyjścia sieci
0
0
,
,
0
1
e
e
gdy
gdy
y
założyliśmy, że wartość progowa
= 0
3) w przypadku błędnej odpowiedzi sieci tzn. y≠d modyfikacja wag według następujących
wzorów:
1
1
1
)
(
'
x
y
d
w
w
2
2
2
)
(
'
x
y
d
w
w
1
)
(
'
y
d
b
b
gdzie
- współczynnik szybkości uczenia
x
1
w
1
x
2
w
2
e = w
1
·x
1
+ w
2
·x
2
+ b
y = f(e)
bias = 1
b
Przy liniowej separowalności sygnałów wejściowych sieć jest w stanie się nauczyć
poprawnych odpowiedzi. Po zakończeniu procesu uczenia granica decyzyjna jest dana
wzorem:
0
2
2
1
1
b
x
w
x
w
. Perceptron poprawnie klasyfikuje sygnały z ciągu uczącego,
jak i te które do ciągu nie należą, ale również spełniają warunek liniowej separowalności.
Na sieci tej możliwa jest realizacja funkcji logicznych AND i OR, ale już nie jest możliwa
realizacja funkcji XOR (nie spełnia warunku liniowej separowalności). „Siła” sieci
neuronowych tkwi w połączeniach, w związku z tym sieci składające się z wielu neuronów
będą miały o wiele więcej zastosowań.
Kolejne etapy w jednym kroku uczenia dla przedstawionego neuronu przy sigmoidalnej
funkcji aktywacji
x
x
f
exp
1
1
)
(
,
1
1) dla danego wektora uczącego (x
1
, x
2
, d) wyliczenie łącznego pobudzenia
b
x
w
x
w
e
2
2
1
1
2) wyliczenie aktualnego wyjścia sieci
e
y
exp
1
1
3) w przypadku błędnej odpowiedzi sieci tzn. y≠d modyfikujemy wagi
Stosujemy tutaj regułę Delta:
i
i
x
e
f
y
d
w
)
(
'
)
(
Warto zauważyć, że dla funkcji sigmoidalnej o wzorze
x
x
f
exp
1
1
)
(
))
(
1
(
)
(
)
(
'
x
f
x
f
x
f
Modyfikacja wag przebiega następująco:
1
1
1
))
(
1
(
)
(
)
(
'
x
e
f
e
f
y
d
w
w
2
2
2
))
(
1
(
)
(
)
(
'
x
e
f
e
f
y
d
w
w
1
))
(
1
(
)
(
)
(
'
e
f
e
f
y
d
b
b
Sieć wielowarstwowa
Sieć wielowarstwowa posiada warstwę wejściową, wyjściową oraz jedną lub więcej
warstw ukrytych. Zadaniem elementów w warstwie wejściowej jest wstępne przetwarzanie
impulsu wejściowego x=[x
1
, x
2
, x
3
, ..., x
N
]. Zasadnicze przetwarzanie neuronowe impulsu
wejściowego odbywa się w warstwach ukrytych oraz w warstwie wyjściowej. Warstwy te
zbudowane są z elementów przetwarzających, które stanowią modele sztucznych neuronów.
Połączenia pomiędzy poszczególnymi warstwami są zaprojektowane tak, że każdy element
warstwy poprzedniej jest połączony z każdym elementem warstwy następnej. Połączeniom
tym są przypisane odpowiednie współczynniki wag, które w zależności od zadania, jakie dana
sieć powinna rozwiązywać, są wyznaczane dla każdego przypadku z osobna. Na wyjściu sieci
generowany jest impuls wyjściowy y=[y
1
, ..., y
M
].
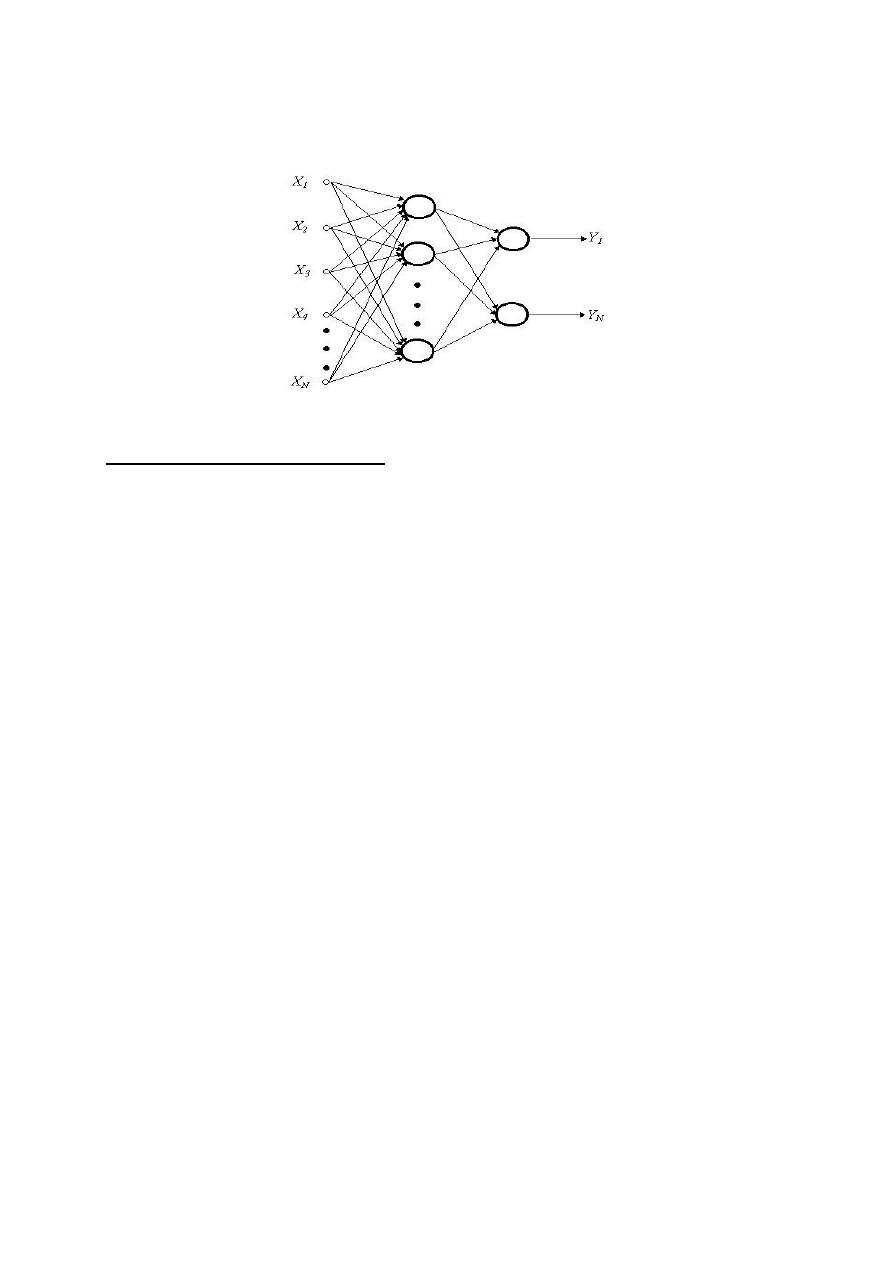
Model sieci wielowarstwowej:
Uczenie sieci wielowarstwowych
W sieciach tego typu najistotniejszym problemem jest dobór wag w warstwach
ukrytych. Jednak istnieją algorytmy umożliwiające efektywne uczenie takich sieci.
Dla dużych sieci i ciągów uczących składających się z wielu tysięcy wektorów uczących ilość
obliczeń wykonywanych podczas całego cyklu uczenia jest gigantyczna a więc i
czasochłonna. Nie zdarza się także aby sieć została dobrze zbudowana od razu. Zawsze jest
ona efektem wielu prób i błędów. Ponadto nigdy nie mamy gwarancji, że nawet prawidłowa
sieć nie utknie w minimum lokalnym podczas gdy interesuje nas znalezienie minimum
globalnego. Dlatego algorytmy realizujące SSN wyposaża się mechanizmy dające
nauczycielowi możliwość regulacji szybkości i jakości uczenia. Są to tzw współczynniki:
uczenia i momentum. Wpływają one na stromość funkcji aktywacji i regulują szybkość
wpływu zmiany wag na proces uczenia.
Przy pojedynczym współczynniku uczenia
, do uczenia sieci wielowymiarowych
stosujemy regułę Delta, przy czym definiujemy sygnał błędu dla każdego neuronu z warstw
ukrytych. Doprowadza nas to do następującego wzoru na zmianę wagi między j- tym
neuronem w warstwie k a i- tym w warstwie k-1:
i
j
k
j
k
ij
x
e
f
w
)
(
'
)
(
)
(
gdzie:
)
(k
ij
w
- zmiana wartości wagi połączenia między neuronem j w warstwie k, a
neuronem i w warstwie k-1,
- współczynnik szybkości uczenia,
)
(k
j
- błąd neuronu j w warstwie k,
f’(e
j
) – pochodna funkcji aktywacji,
x
i
– sygnał wejściowy pochodzący od neuronu j.
Aby przyspieszyć proces uczenia, a jednocześnie uniknąć niebezpieczeństwa oscylacji
w sieci (czyli wpadania algorytmu w minima lokalne funkcji błędu) wprowadza się
modyfikację do algorytmu, zwaną Uogólnioną Regułą Delty, zawierającą czynnik
bezwładności
)
(
2
k
ji
m
:
)
(
2
)
(
1
)
(
)
(
'
k
ji
i
j
k
j
k
ij
m
x
e
f
w
gdzie:
1
- współczynnik szybkości uczenia,
2
– momentum,
)
(k
ji
m
- poprzednia zmiana wag.