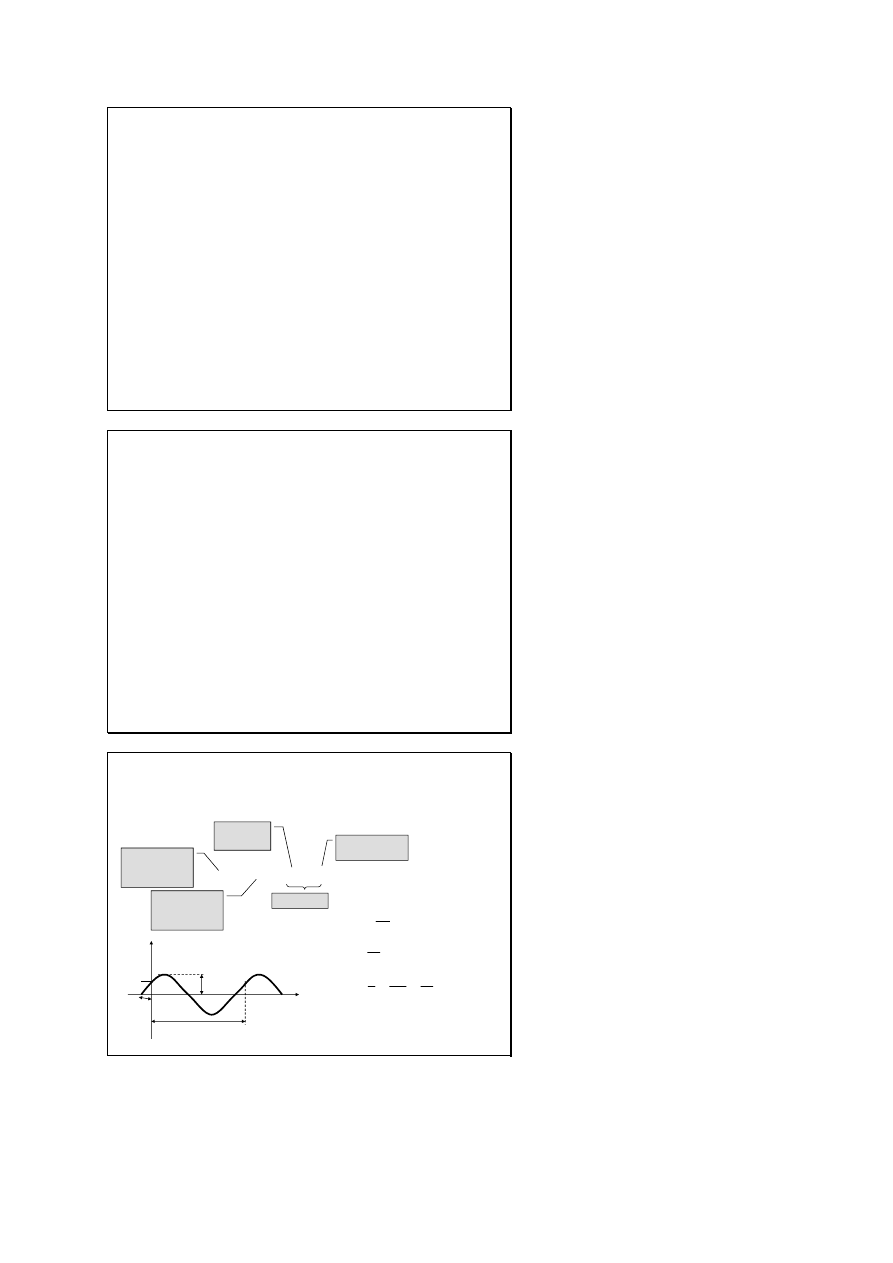
RUCH DRGAJĄCY
Swobodne drgania
harmoniczne
Drgania tłumione
Drgania wymuszone
Podstawowe definicje
– procesy, w których dana wielkość fizyczna na
przemian rośnie i maleje
drgania
– gdy układ, na który nie działają
zmienne siły zewnętrzne, zostanie wyprowadzony z
położenia równowagi
ruch drgający (periodyczny) – jeżeli wartości
wielkości fizycznych zmieniające się podczas drgań,
powtarzają się w pewnych odstępach czasu
drgania
– drgania opisane funkcją
harmoniczną (sin
ωt lub cosωt)
– układ wykonujący drgania
harmoniczne np. wahadło, obwód LC
drgania
swobodne
okresowy
harmoniczne
oscylator harmoniczny
Swobodny oscylator harmoniczny
)
sin(
)
(
ϕ
+
ω
=
t
A
t
s
o
wychylenie z
położenia
równowagi
amplituda -
maksymalne
wychylenie
częstość
kątowa
faza drgań
faza
początkowa
s(t)
t
A
T
o
=2π/ω
o
s(0)
0
π
ϕ
ω
ϕ
ω
2
+
+
=
+
+
)
(
)
(
t
T
t
o
o
o
o
o
T
ω
π
2
=
definicja okresu drgań
częstotliwość (częstość) drgań –
liczba drgań w jednostce czasu
ν
π
ω
2
=
o
(1Hz)
)
sin(
)
(
ϕ
= A
s 0
o
T
t
n =
- liczba drgań w czasie t
o
o
T
t
T
t
t
n
1
=
=
=
ν
- czas 1 drgania
Circular2SHM.swf
częstotliwość kołowa -
ϕ
S – x, ϕ, I
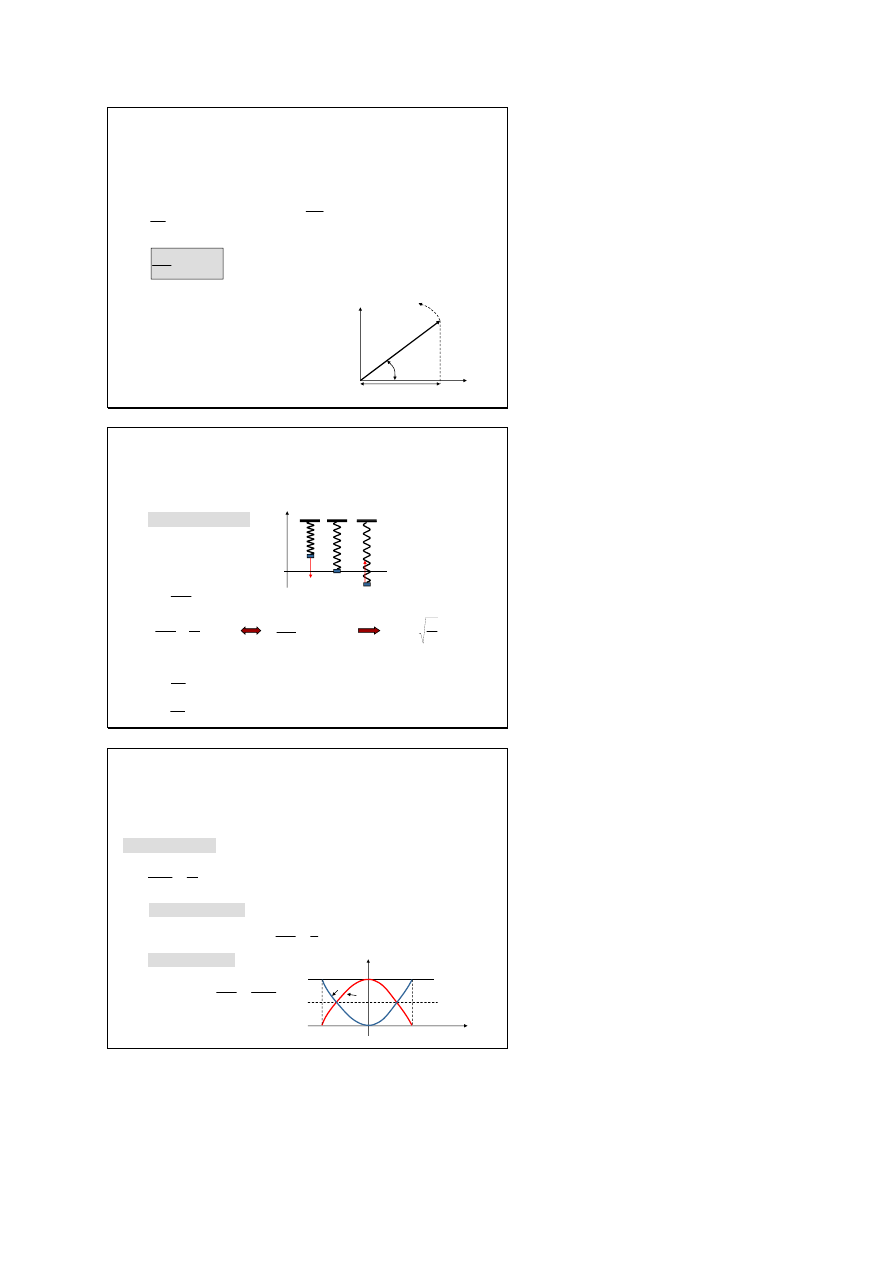
Równanie różniczkowe drgań
harmonicznych
)
sin(
)
(
ϕ
+
ω
=
t
A
t
s
o
)
cos(
ϕ
ω
ω
+
=
t
A
dt
ds
o
o
s
t
A
dt
s
d
o
o
o
2
2
2
2
)
sin(
ω
ϕ
ω
ω
−
=
+
−
=
ω
o
t+ϕ
x
y
A
s(t)
ω
o
Metoda wykresów fazowych
(
)
ϕ
+
ω
=
t
i
o
Ae
z
)
cos(
Re
ϕ
+
ω
=
=
t
A
z
s
o
[
]
)
sin(
)
cos(
ϕ
+
ω
−
ϕ
+
ω
=
t
i
t
A
z
o
o
Opis przy pomocy liczb zespolonych
0
2
2
2
=
ω
+
s
dt
s
d
o
- równanie drgań
Przykład 1:
Mechaniczne drgania harmoniczne
Wahadło sprężynowe
x
k
F
r
r
−
=
x
k
F
r
r
−
=
x
o
=0
x
k – stała sprężystości
x
o
- położenie równowagi
(
)
o
x
x
k
F
−
−
=
x
k
F
−
=
x
k
t
d
x
d
m
−
=
2
2
0
2
2
=
+
x
m
k
dt
x
d
0
2
2
2
=
ω
+
s
dt
s
d
o
m
k
o
=
ω
)
cos(
ϕ
+
ω
=
t
A
x
o
)
sin(
ϕ
+
ω
ω
−
=
=
t
A
dt
dx
v
o
o
)
cos(
ϕ
+
ω
ω
−
=
=
t
A
dt
dv
a
o
o
2
stałe A, ϕ wyznaczamy z warunków
początkowych np.
0
0
)
0
(
)
0
(
v
t
v
x
t
x
=
=
=
=
Energia oscylatora harmonicznego
Energia kinetyczna
)
(
sin
ϕ
+
ω
ω
=
=
t
A
m
mv
E
o
o
k
2
2
2
2
2
2
Energia potencjalna
)
(
cos
ϕ
+
ω
=
=
∫
=
∫
−
=
t
A
k
kx
dx
kx
dx
F
U
o
x
x
2
2
2
0
0
2
2
Energia całkowita
2
2
2
2
2
A
m
kA
U
E
E
o
k
ω
=
=
+
=
E=E
k
+U
E
x
U
E
k
E/2
x
o
-x
o
0
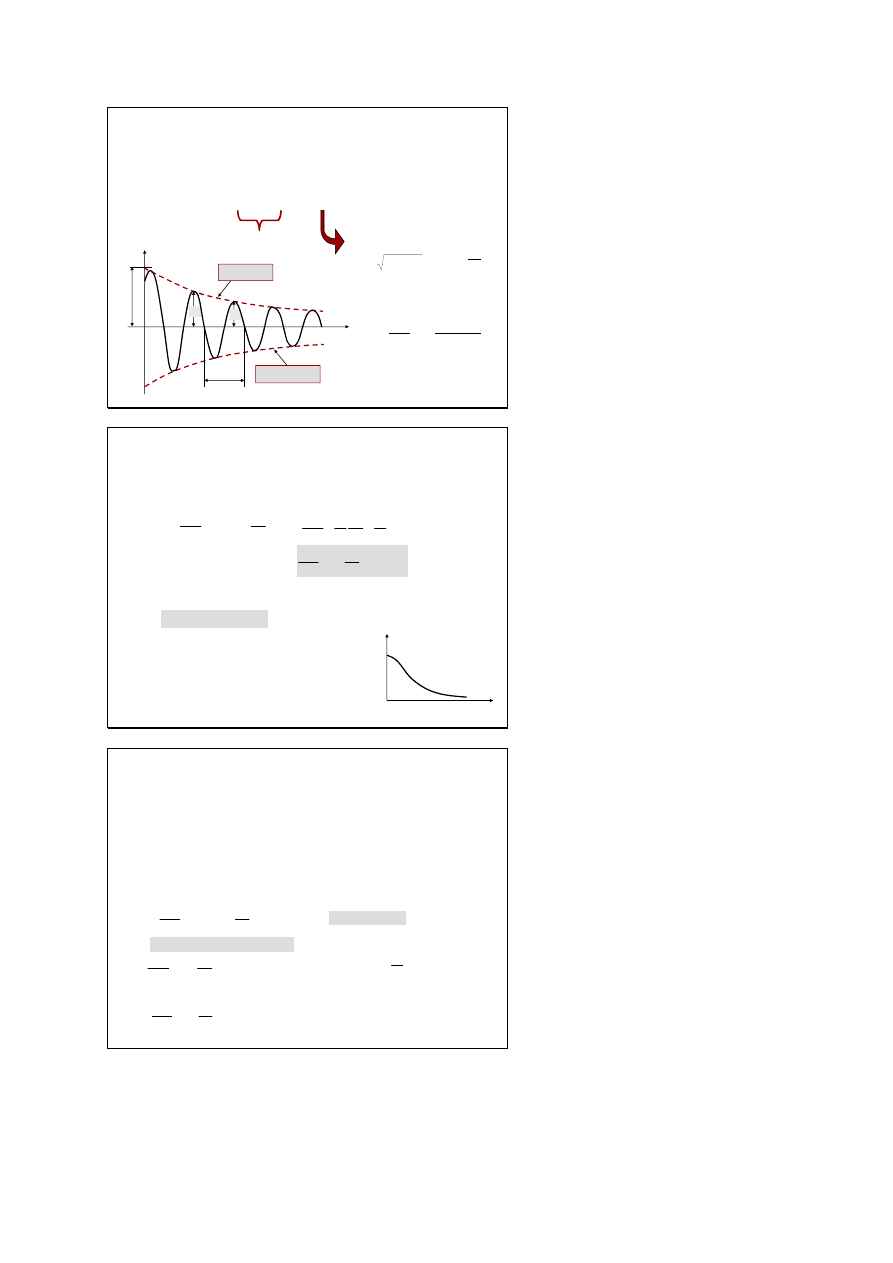
)
t
cos(
ϕ
+
ω
=
β
− t
o
e
A
s
amplituda malejąca
wykładniczo w czasie
częstość drgań tłumionych
2
2
β
−
ω
=
ω
o
t
o
e
A
A
β
−
=
t
o
e
A
A
β
−
−
=
s, A
t
T
A
o
A
1
A
2
o
T
T
>
ω
π
=
2
logarytmiczny dekrement tłumienia
(
)
T
e
e
A
e
A
A
A
T
T
t
o
t
o
n
n
⋅
=
=
=
=
=
Λ
+
−
−
+
β
β
β
β
ln
ln
ln
1
Drgania tłumione
Równanie drgań tłumionych
)
t
cos(
ϕ
ω
β
+
=
− t
o
e
A
x
v
r
F
t
−
=
dt
dx
r
kx
dt
x
d
m
−
−
=
2
2
0
2
2
=
+
+
x
m
k
dt
dx
m
r
dt
x
d
siły oporu
(
)
o
ω
β
<
Dla słabego tłumienia
0
2
2
2
2
=
+
+
x
dt
dx
dt
x
d
o
ω
β
Równanie drgań tłumionych:
(
)
2
2
2
β
−
ω
=
ω
o
Dla silnego tłumienia
(
)
o
ω
β
≥
ruch aperiodyczny – wychylenie zanika z czasem
x
t
A
o
0
drgania tłumione
Drgania wymuszone
aby utrzymać drgania nietłumione należy
skompensować straty energii
siła wymuszająca lub siła elektromotoryczna
t
cos ω
=
o
F
F
t
cos
ω
=
o
V
V
t
cos
2
2
2
2
ω
ω
β
o
o
x
x
dt
dx
dt
x
d
=
+
+
równanie drgań wymuszonych
t
i
o
o
e
x
z
dt
dz
dt
z
d
ω
=
ω
+
β
+
2
2
2
2
równanie drgań wymuszonych
w postaci zespolonej
t
cos ω
+
−
−
=
o
F
dt
dx
r
kx
dt
x
d
m
2
2
równanie ruchu
m
F
x
gdzie
o
o
=
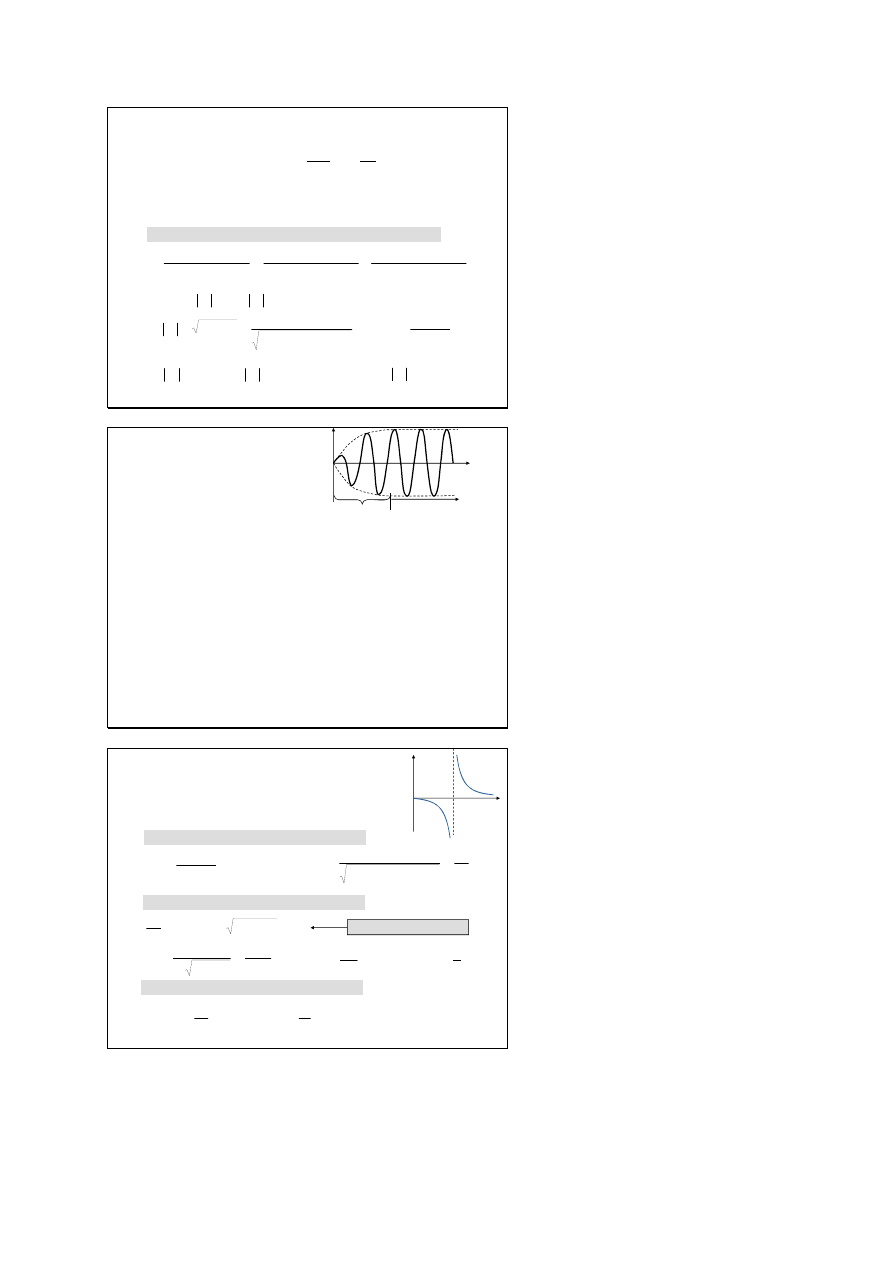
Rozwiązanie równania drgań
wymuszonych
t
i
o
o
e
x
z
dt
dz
dt
z
d
ω
=
ω
+
β
+
2
2
2
2
t
i
o
e
z
z
Ω
=
Rozwiązania tego równania szuka się w postaci:
t
i
o
t
i
o
o
t
i
o
t
i
o
e
x
e
z
e
z
i
e
z
ω
Ω
Ω
Ω
=
ω
+
Ω
β
+
Ω
−
2
2
2
równania musi być spełnione dla każdej chwili czasu więc Ω = ω
(
)
(
)
(
)
(
)
i
x
x
i
x
z
o
o
o
o
o
o
o
o
2
2
2
2
2
2
2
2
2
2
2
2
2
2
4
2
4
2
ω
β
ω
ω
βω
ω
β
ω
ω
ω
ω
βω
ω
ω
+
−
−
+
+
−
−
=
+
−
=
(
)
i
b
a
i
z
e
z
z
o
i
o
o
⋅
+
=
ϕ
+
ϕ
=
⋅
=
ϕ
sin
cos
(
)
2
2
2
2
2
2
2
4
ω
β
+
ω
−
ω
=
+
=
=
o
o
o
x
b
a
z
A
2
2
2
ω
−
ω
βω
−
=
ϕ
o
tg
(
)
ϕ
+
ω
ω
ϕ
⋅
=
⋅
⋅
=
t
i
o
t
i
i
o
e
z
e
e
z
z
(
)
ϕ
+
ω
⋅
=
=
t
z
z
s
o
cos
Re
Wnioski
po początkowym, nieustalonym stadium procesu
następują ustalone drgania wymuszone,
drgania wymuszone odbywają się z częstością
siły wymuszającej,
amplituda tych drgań zależy od amplitudy siły
wymuszającej, jej częstości i parametrów układu
drgającego,
faza drgań zależy od częstości siły wymuszającej
stan
nieustalony
ustalone drgania
wymuszone
s
t
Właściwości ustalonych
drgań wymuszonych
(
)
2
2
2
2
2
2
4
o
o
o
o
x
x
A
ω
≈
ω
β
+
ω
−
ω
=
a) Siła wymuszająca o małej częstości ω<<ω
o
b) Rezonans ω ≈ ω
o
o
o
r
d
dA
ω
≈
β
−
ω
=
ω
⇒
=
ω
2
2
2
0
o
o
o
o
r
x
x
A
βω
≈
β
−
ω
β
=
2
2
2
2
c) Siła wymuszająca o dużej częstości ω>>ω
o
2
ω
=
o
x
A
częstość rezonansowa
ϕ
tg
ω
o
ω
0
2
π
ϕ
β
ω
ϕ
−
→
⇒
−∞
→
−
=
tg
wychylenie opóźnia się w fazie o π/2
π
−
→
ϕ
⇒
→
ω
β
=
ϕ
0
2
tg
wychylenie opóźnia się w fazie o π
0
0
2
2
2
→
ϕ
⇒
→
ω
−
ω
βω
−
=
ϕ
o
tg
zgodność fazy siły z wychyleniem
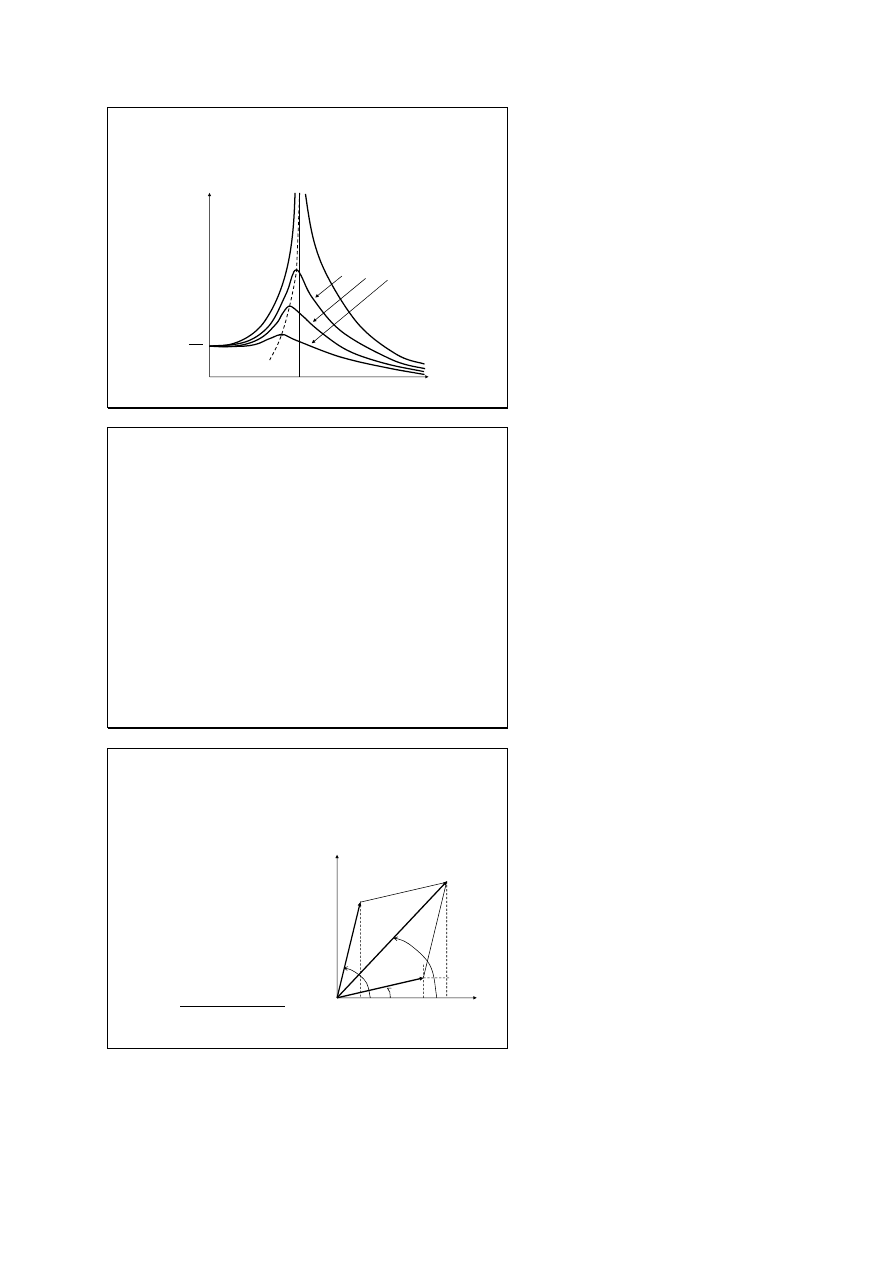
Amplituda drgań wymuszonych w
funkcji częstości siły wymuszającej
A
2
o
o
x
ω
ω
ω
o
ω
r
β=0
β
1
< β
2
<
β
3
0
odchylenie
statyczne
Składanie drgań i fale
Składanie drgań
Drgania normalne
Równanie falowe
Rodzaje fal
Składanie drgań jednakowych często-
ściach - metoda wykresów fazowych
(
)
1
1
1
ϕ
+
ω
=
t
A
x
o
cos
(
)
2
2
2
ϕ
+
ω
=
t
A
x
o
cos
(
)
ϕ
+
ω
=
+
=
t
A
x
x
x
o
cos
2
1
2
2
1
1
2
2
1
1
ϕ
+
ϕ
ϕ
+
ϕ
=
ϕ
cos
cos
sin
sin
A
A
A
A
tg
y
x
A
1
A
2
ϕ
1
ϕ
2
ϕ
A
(
)
1
2
2
1
2
2
2
1
2
2
ϕ
−
ϕ
+
+
=
cos
A
A
A
A
A
(
)
[
]
1
2
2
1
2
2
2
1
2
2
ϕ
−
ϕ
−
π
−
+
=
cos
A
A
A
A
A
z prawa cosinusów
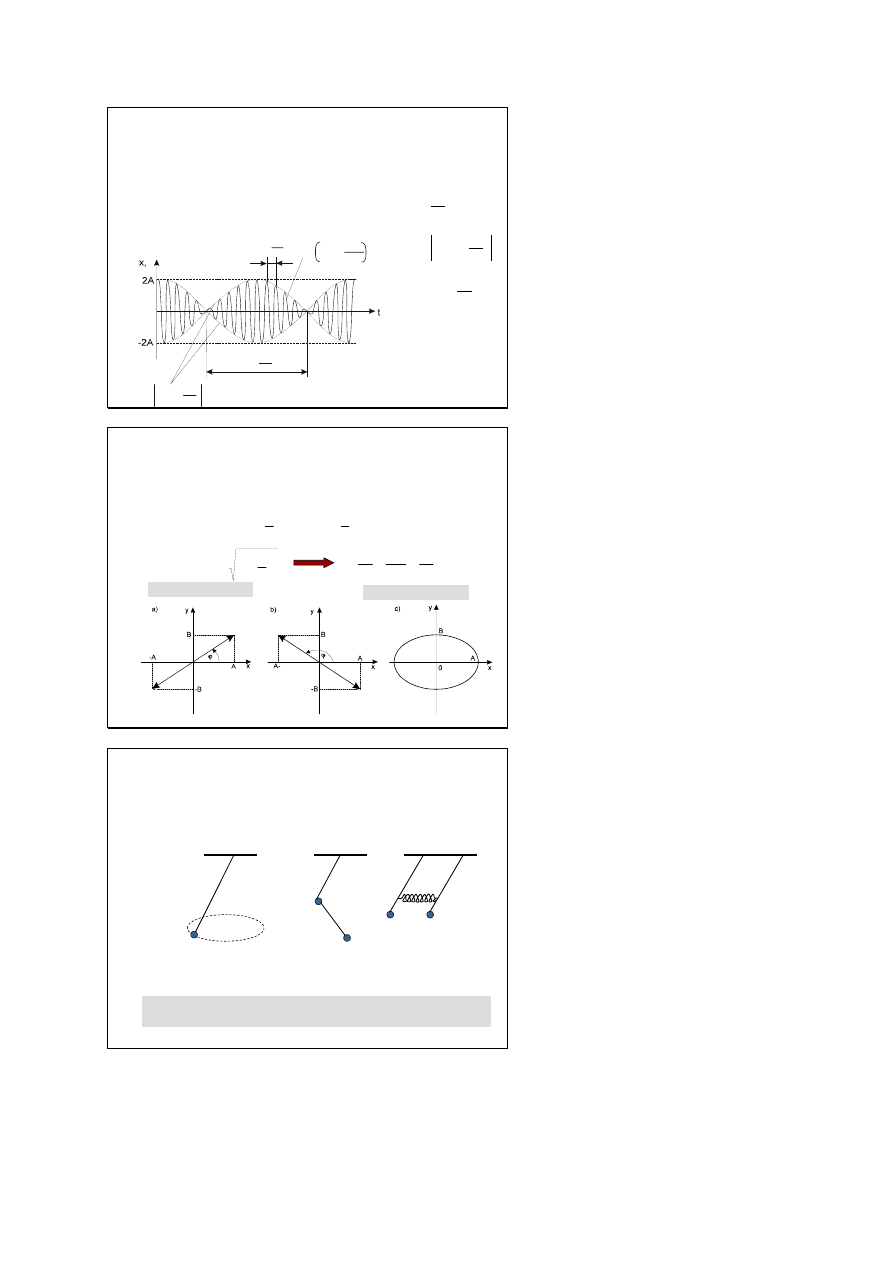
Dudnienia
t
cos
cos
ω
⎟
⎠
⎞
⎜
⎝
⎛
ω
Δ
=
t
A
x
2
2
t
A
A
2
2
ω
Δ
=
cos
~
ω
Δ
π
=
2
o
T
A
A
A
t
~
~
cos
= 2
2
Δω
A
2 cos
cos t
ω
t
2
T=
T =
o
2
π
2
π
ω
Δω
x=
Δω
2
1
x
x
x
+
=
t
cos ω
= A
x
1
t
A
x
)
cos(
ω
Δ
+
ω
=
2
ω
<<
ω
Δ
dwa drgania równoległe nieznacznie
różniące się częstościami (ϕ=0)
Składanie drgań wzajemnie
prostopadłych
)
t
cos(
t
cos
ϕ
+
ω
=
ω
=
B
y
A
x
ϕ
ω
−
ϕ
ω
=
ω
=
sin
t
sin
cos
t
cos
t
cos
B
y
;
A
x
2
1
⎟
⎠
⎞
⎜
⎝
⎛
−
=
ω
A
x
t
sin
ϕ
=
+
−
2
2
2
2
2
2
sin
B
y
AB
xy
A
x
m
=
± ±
0
2
4
,
,
m
= ± ±
±
1 3
5
,
,
,
Kształt krzywych Lissajous zależy od stosunku amplitud, częstości i początkowych faz drgań
.
Dla ϕ = mπ:
Dla ϕ = (2m+1)π/2:
Drgania o wielu stopniach
swobody
Wahadło sferyczne
Wahadło podwójne
Wahadło sprzężone
Układ fizyczny ma N stopni swobody, jeśli do opisu procesów
w nim zachodzących trzeba użyć N wielkości niezależnych
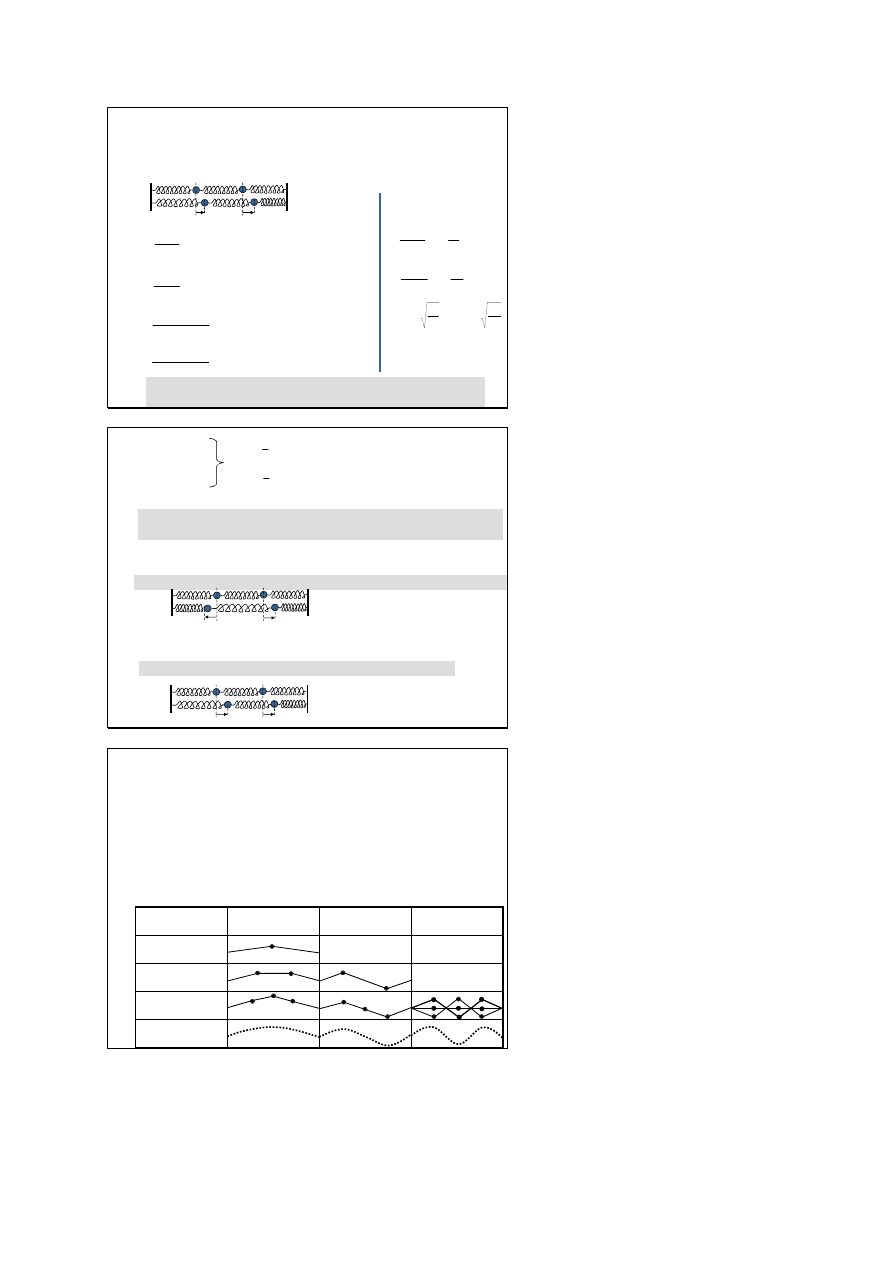
Drgania normalne oscylatora o
dwóch stopniach swobody
x
1
x
2
k
k
(
)
2
1
1
2
1
2
1
2
2
kx
kx
x
x
k
kx
dt
x
d
m
+
−
=
−
+
−
=
(
)
2
1
1
2
2
2
2
2
2kx
kx
x
x
k
kx
dt
x
d
m
−
=
−
−
−
=
(
)
(
)
2
1
2
2
1
2
x
x
k
dt
x
x
d
m
+
−
=
+
(
)
(
)
2
1
2
2
1
2
3
x
x
k
dt
x
x
d
m
−
−
=
−
2
1
1
x
x +
=
Ψ
2
1
2
x
x −
=
Ψ
1
2
1
2
Ψ
−
=
Ψ
m
k
dt
d
2
2
2
2
3 Ψ
−
=
Ψ
m
k
dt
d
m
k
=
ω
1
m
k
3
2
=
ω
(
)
1
1
1
1
2
ϕ
+
ω
=
Ψ
t
A
cos
(
)
2
2
2
2
2
ϕ
+
ω
=
Ψ
t
A
cos
Nowe współrzędne nazywamy normalnymi, a same drgania
drganiami własnymi czyli normalnymi
(
)
(
)
(
2
2
2
1
1
1
2
1
1
2
1
ϕ
+
ω
+
ϕ
+
ω
=
Ψ
+
Ψ
=
t
A
t
A
x
cos
cos
)
(
)
(
)
(
2
2
2
1
1
1
2
1
2
2
1
ϕ
+
ω
−
ϕ
+
ω
=
Ψ
−
Ψ
=
t
A
t
A
x
cos
cos
)
Drgania oscylatora o dwóch stopniach swobody są superpozycją
dwóch drgań normalnych o różnych częstościach własnych
x
2
(
)
2
2
2
2
1
1
0
ϕ
+
ω
=
−
=
⇒
=
t
A
x
x
A
cos
wahadła drgają z tą samą częstością w zgodnych fazach, przeciwnych kierunkach
x
1
k
k
(
)
1
1
1
2
1
2
0
ϕ
+
ω
=
=
⇒
=
t
A
x
x
A
cos
wahadła drgają z tą samą częstością w zgodnych fazach i kierunkach
x
1
x
2
k
k
2
1
1
x
x +
=
Ψ
2
1
2
x
x −
=
Ψ
Dla układu o N stopniach swobody:
istnieje N częstotliwości własnych,
układ może wykonywać N drgań normalnych,
dla drgań normalnych wszystkie elementy drgają w tej
samej fazie, zaś amplitudy drgań są wzajemnie zależne
Liczba stopni
swobody
Ψ
1
Ψ
2
Ψ
3
1
2
3
N
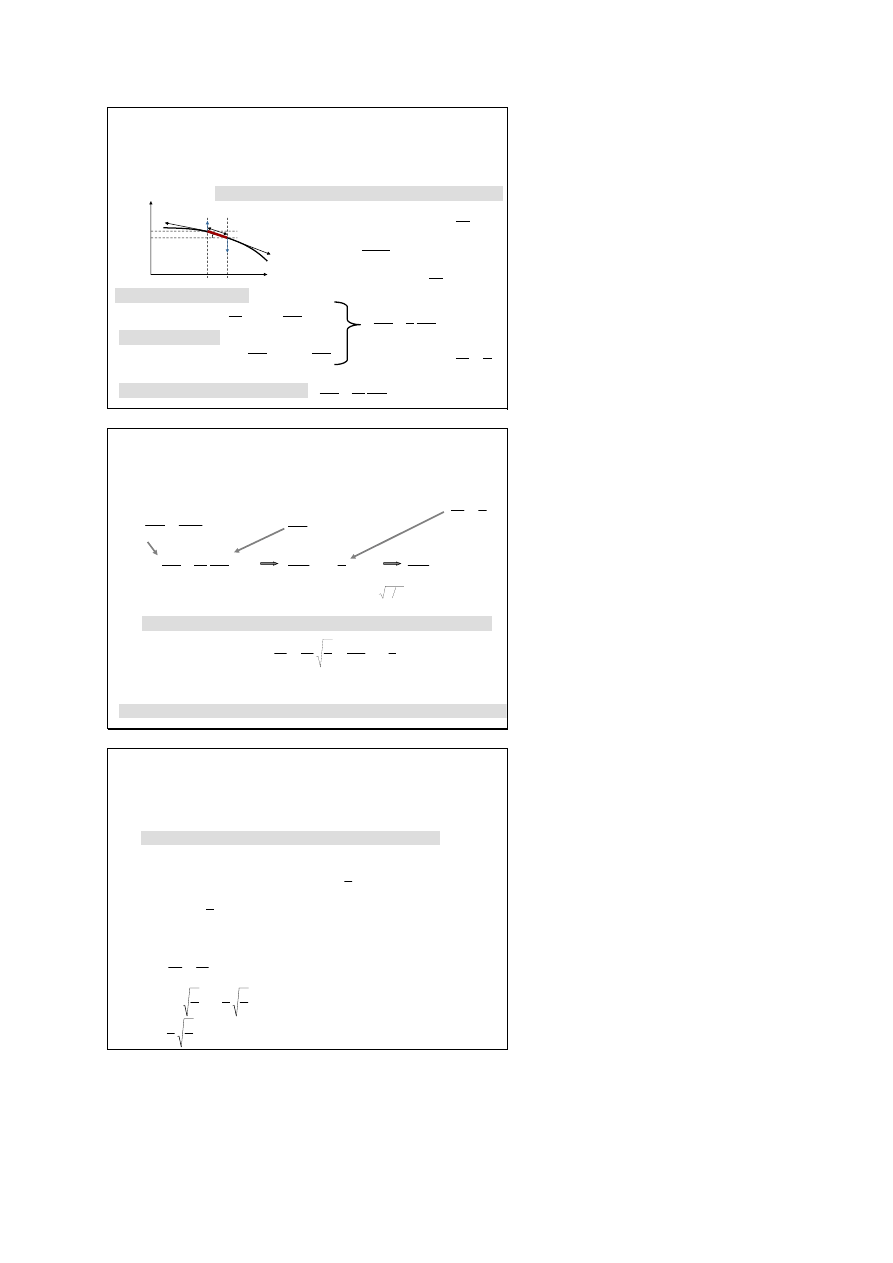
Drgania normalne struny rozpiętej wzdłuż
osi x ze stałym naciągiem T o masie
jednostki długości μ
Ψ=Ψ(x,y,z,t)
Ψ
x
x
tg
∂
ψ
∂
=
α
≈
α
≈
α
⇒
→
α
sin
,
cos
1
0
dΨ
dx
α
dl
Rozważmy element dl struny tworzący niewielki kąt
α
z osią x
dx
dx
dm
μ
≈
α
μ
=
cos
x
T
tg
T
T
F
∂
ψ
∂
=
α
⋅
≈
α
= sin
0
2
2
2
2
=
∂
ψ
∂
μ
−
∂
ψ
∂
t
T
x
T
v
ozn
μ
=
2
1
.
0
1
2
2
2
2
2
=
∂
ψ
∂
−
∂
ψ
∂
t
v
x
otrzymujemy klasyczne równanie falowe
2
2
2
2
t
dx
t
dm
dF
∂
ψ
∂
⋅
μ
=
∂
ψ
∂
=
II zas. dyn. Newtona
dx
x
T
dx
x
F
dF
2
2
∂
ψ
∂
=
∂
∂
=
Wypadkowa siła poprzeczna
T
T
F
F+dF
(
)
( )
(
)
ϕ
+
ω
⋅
=
Ψ
t
x
A
t
x
cos
,
0
1
2
2
2
2
2
=
∂
ψ
∂
−
∂
ψ
∂
t
v
x
(
)
ϕ
ω
ψ
+
=
∂
∂
t
x
d
A
d
x
cos
2
2
2
2
(
)
ϕ
+
ω
ω
−
=
∂
ψ
∂
t
A
t
cos
2
2
2
0
2
2
2
=
μ
ω
+
A
T
dx
A
d
0
2
2
2
=
+
A
k
dx
A
d
falowa
liczba
T
k
gdzie
−
μ
ω
=
( )
(
)
φ
+
⋅
=
x
k
A
x
A
o
cos
rozwiązaniem jest funkcja o okresie przestrzennym zwanym długością fali -λ
ν
=
πν
π
=
μ
ω
π
=
π
=
λ
⇒
π
=
λ
v
v
T
k
k
2
2
2
2
2
(
)
(
)
(
)
ϕ
+
ω
⋅
φ
+
=
Ψ
t
kx
A
t
x
o
cos
cos
,
Drganiom normalnym w układach ciągłych odpowiada powstanie w nich fal stojących
Drgania normalne, a fala stojąca
T
v
μ
=
2
1
Drgania własne struny
(
)
(
)
(
)
ϕ
+
ω
⋅
φ
+
=
Ψ
t
kx
A
t
x
o
cos
cos
,
dla struny o skończonej długości L zamocowanej na obu końcach
( )
( )
0
0
=
Ψ
=
Ψ
t
L
t
,
,
z warunków brzegowych wynika
( )
(
)
2
0
π
φ
ϕ
ω
φ
±
=
⇒
=
+
⋅
t
A
o
cos
cos
(
)
0
2
=
+
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
ϕ
ω
π
t
kL
A
o
cos
cos
( )
π
n
kL
kL
=
⇒
= 0
sin
...
,
, 2
1
0
2
2
=
=
=
n
n
L
k
n
n
π
λ
μ
π
μ
ω
T
L
n
T
k
n
n
=
=
μ
π
ω
T
L
=
1
podstawowa
częstość kołowa
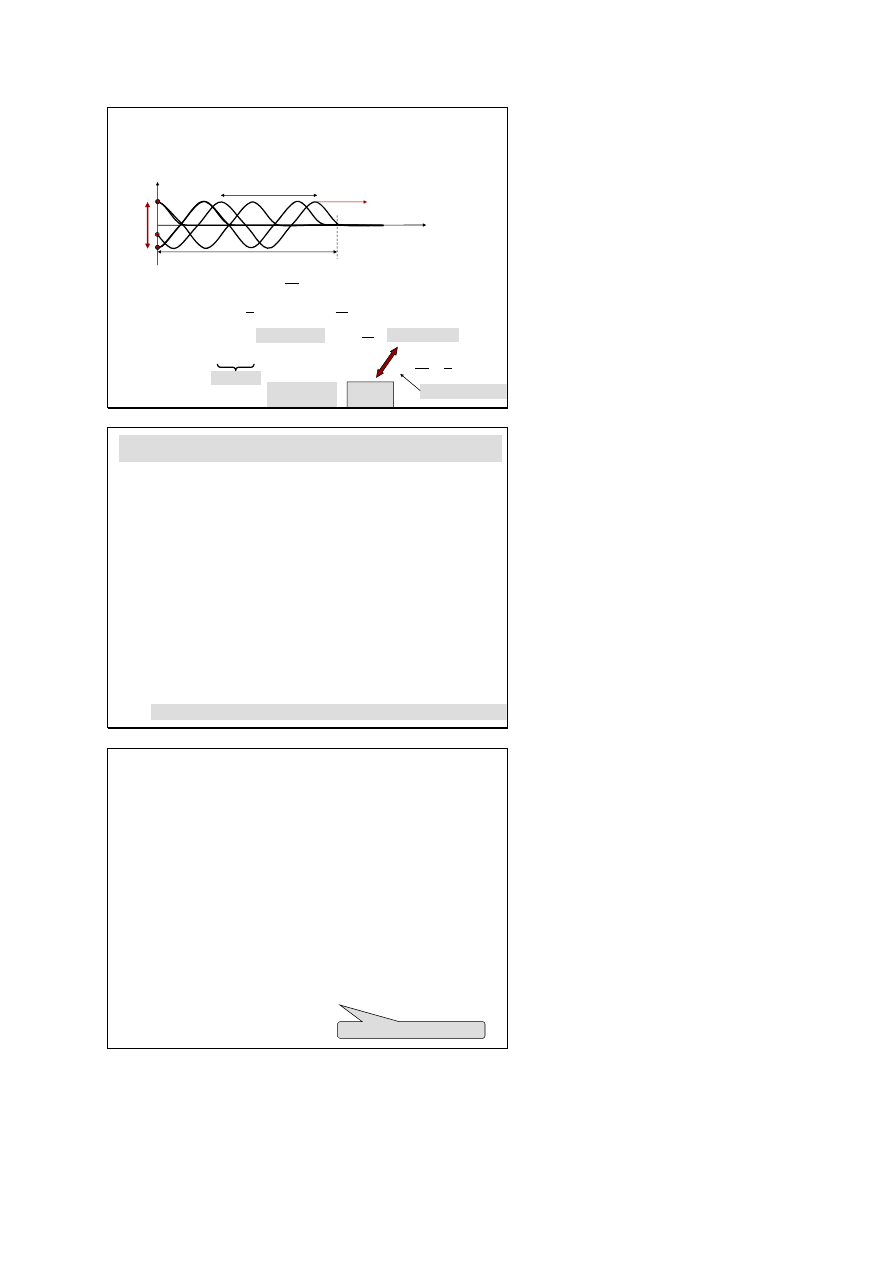
(
)
(
)
=
ω −
Ψ
k + ϕ
x t
A
t
x
Równanie falowe
x
Ψ
A
o
sinωt
λ
v
x
o
po czasie t
o
( )
( )
t
A
t
o
ω
=
Ψ
sin
,
0
x
(
)
(
)
o
o
o
t
t
A
t
x
−
ω
=
Ψ
sin
,
v
t
o
o
=
(
)
(
)
kx
t
A
x
t
A
v
x
t
A
t
x
o
o
o
−
ω
=
⎟
⎠
⎞
⎜
⎝
⎛
λ
π
−
ω
=
⎟
⎠
⎞
⎜
⎝
⎛ −
ω
=
Ψ
sin
sin
sin
,
2
o
sin
,
T
(
)
(
)
kx
t
A
t
x
o
−
ω
=
Ψ
sin
,
faza fali
const
kx
t
=
−
ω
0
=
⋅
−
⋅
ω
dx
k
dt
k
dt
dx
v
ω
=
=
prędkość fazowa
(
)
(
)
kx
t
A
t
x
o
+
ω
=
Ψ
sin
,
propagacja w
kierunku -x
wektor
falowy
v
gdzie
⋅
=
λ
λ
π
=
2
k
- liczba falowa
- długość fali,
Właściwości fal
fale harmoniczne opisane funkcją sinus lub cosinus
dowolny ruch falowy można przedstawić jako
superpozycję fal harmonicznych – analiza Fouriera
powierzchnia falowa (czoło fali) – zbiór punktów o
takiej samej fazie
linie prostopadłe do powierzchni falowej to
promień fali, wskazują kierunek propagacji
fale harmoniczną przedstawia się również w
zapisie zespolonym:
(
)
(
)
ikx
t
i
o
kx
t
i
o
e
e
A
e
A
t
x
−
ω
−
ω
=
=
Ψ ,
sens fizyczny ma tylko część rzeczywista zespolonej funkcji falowej
Zasada superpozycji:
jeśli w ośrodku propagują się dwie fale, to wypadkowe
zaburzenie ośrodka jest równe sumie zaburzeń wywołanych przez poszczególne fale
Rodzaje fal
w zależności od kształtu czoła fali:
płaskie
walcowe (koliste)
kuliste
w zależności od zmiennej wielkości
fizycznej:
skalarne (np. fale ciśnienia)
wektorowe (np. elektromagnetyczne)
•
podłużne
•
poprzeczne, tylko w ośrodkach sprężystych
•
powierzchniowe
mogą być spolaryzowane

Energia fal
Fale stojące
Prędkość grupowa
Paczka falowa
Fale dźwiękowe
Impedancja falowa
Rozpatrzmy falę biegnącą w kierunku osi x generowaną w punkcie x = 0
Obliczmy siłę z jaką struna działa na generator
v
T
0
ur
Wielkość Z nazywamy impedancją falową, która określa prędkość z jaką
struna absorbuje energię emitowaną przez źródło siły wymuszającej
(
)
(
)
kx
t
A
t
x
o
−
ω
=
Ψ
sin
,
μ
T
v
t
v
x
=
∂
Ψ
∂
−
=
∂
Ψ
∂
,
1
x
T
T
F
y
∂
Ψ
∂
=
=
α
sin
u
v
T
t
v
T
F
y
−
=
∂
Ψ
∂
−
=
T
v
T
Z
t
Z
F
y
⋅
=
=
∂
Ψ
∂
−
=
μ
,
dla małych
kątów
k
v
ω
=
Prędkość fazowa i impedancja są dwoma
naturalnymi parametrami dogodnymi do opisu fal biegnących w
ośrodku [stanowią kombinację parametru sprężystości ośrodka T
(naprężenie liny) oraz parametru bezwładności μ (gęstość liniowa)]
Energia przenoszona przez fale
2
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
⋅
=
∂
Ψ
∂
⎟
⎠
⎞
⎜
⎝
⎛
∂
Ψ
∂
=
∂
Ψ
∂
=
⋅
=
t
Z
t
t
Z
t
F
u
F
P
y
r
r
t
A
v
T
P
o
ω
ω
2
2
2
cos
=
2
1
2
/
cos
=
〉
〈
t
ω
2
2
2
o
A
v
T
P
ω
=
〉
〈
natężenie fali – średnia wartość
przenoszonej mocy przez falę
Obliczmy moc potrzebną do poruszania struną do góry i w dół z prędkością u
(
)
(
)
kx
t
A
t
x
o
−
ω
=
Ψ
sin
,
T
Z
⋅
=
μ
v
T
Z =
μ
T
v =
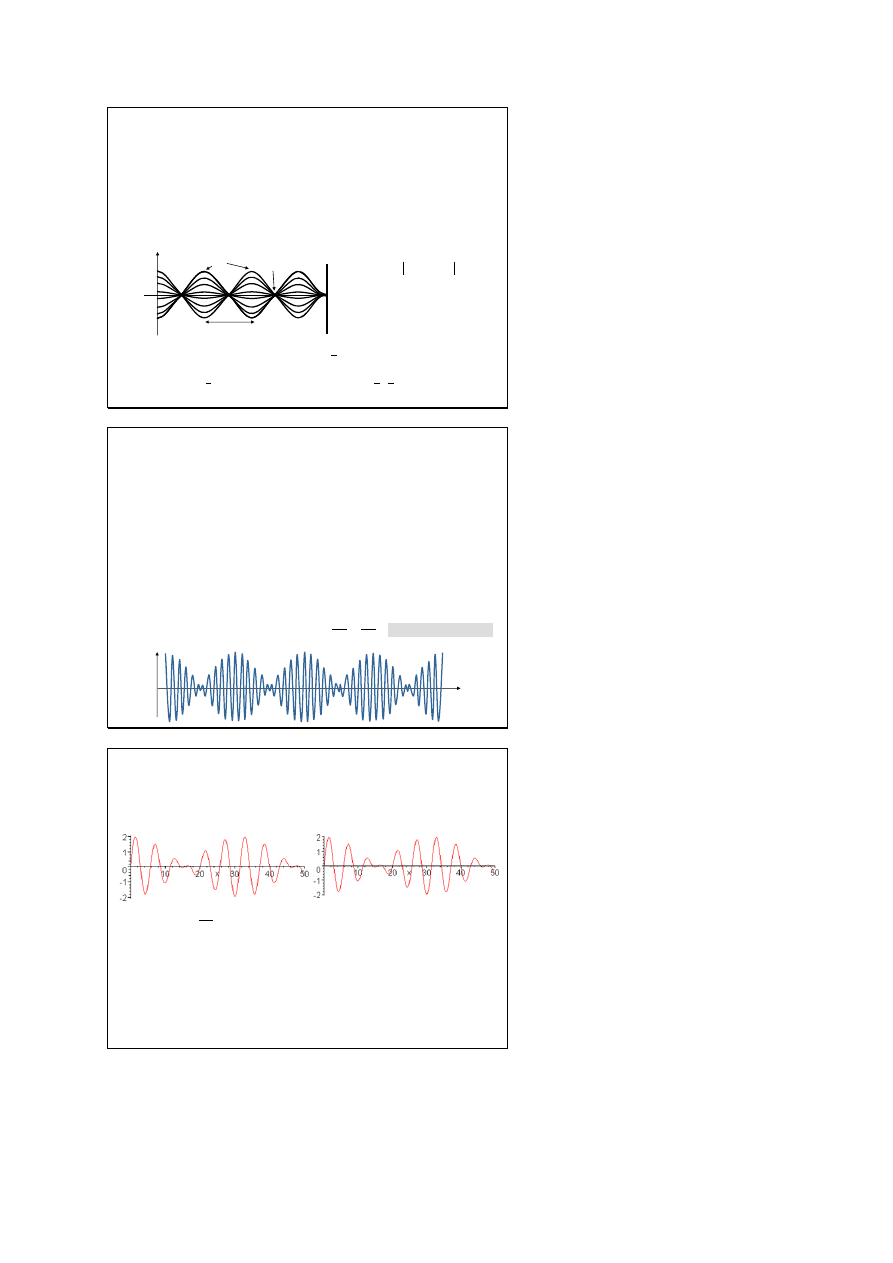
Fale stojące
x
Ψ
λ/2
strzałki
węzły
t
kx
A
ω
⋅
=
Ψ
+
Ψ
=
Ψ
cos
cos
2
2
1
(
)
A
A
n
x
n
n
kx
st
2
2
2
1
0
=
→
λ
±
=
⇒
=
π
±
=
...
,
,
(
)
0
2
2
1
2
1
0
2
1
=
→
λ
⎟
⎠
⎞
⎜
⎝
⎛ +
±
=
⇒
=
π
⎟
⎠
⎞
⎜
⎝
⎛ +
±
=
st
A
n
x
n
n
kx
...
,
,
(
)
kx
t
A
−
ω
=
Ψ
cos
1
(
)
kx
t
A
+
ω
=
Ψ
cos
2
Fala stojąca powstaje przy nakładaniu
się dwu harmonicznych fal biegnących
propagujących się w przeciwnych
kierunkach z jednakowymi
prędkościami i amplitudami
kx
A
A
st
cos
2
=
w każdym punkcie fali stojącej
zachodzą drgania o tej samej
częstotliwości z amplitudą
zależną od współrzędnej x
Superpozycja fal harmonicznych
- prędkość grupowa
(
) (
)
(
)
x
dk
k
t
d
A
o
−
−
−
=
Ψ
ω
ω
sin
2
(
) (
)
(
)
x
dk
k
t
d
A
o
+
−
+
=
Ψ
ω
ω
sin
1
Rozważmy dwie fale harmoniczne o nieco różnych częstościach
ω
<<
ω
d
(
)
(
)
kx
t
x
dk
t
d
A
o
−
⋅
⋅
−
⋅
=
Ψ
+
Ψ
=
Ψ
ω
ω
sin
cos
2
2
1
w wyniku superpozycji dwóch fal otrzymaliśmy fale harmoniczną o częstości
nośnej ω i modulowanej amplitudzie przenoszonej z prędkością grupową v
g
const
x
dk
t
d
=
⋅
−
⋅
ω
0
=
⋅
−
⋅
ω
dx
dk
dt
d
dk
d
dt
dx
v
g
ω
=
=
- prędkość grupowa
x
Ψ
Dyspersja fal
k
v
ω
=
szukamy związku pomiędzy prędkością grupową a fazową
dk
dv
k
v
dk
dkv
dk
d
v
g
+
=
=
ω
=
λ
λ
π
−
=
⎟
⎠
⎞
⎜
⎝
⎛
λ
π
=
d
d
dk
2
2
2
λ
λ
−
=
d
dv
v
v
g
prędkością grupową różni się od fazowej, gdy prędkość
fazowa zależy od częstości (długości fali). Zależność v
od λ nazywamy dyspersją.
ośrodki dyspersyjne – (v≠v
g
) fale o różnej długości
rozchodzą się z różną prędkością, np. pryzmat dla światła
ośrodki niedyspersyjne – (v=v
g
) fale o różnej długości
rozchodzą się z taką samą prędkością, np. w próżni
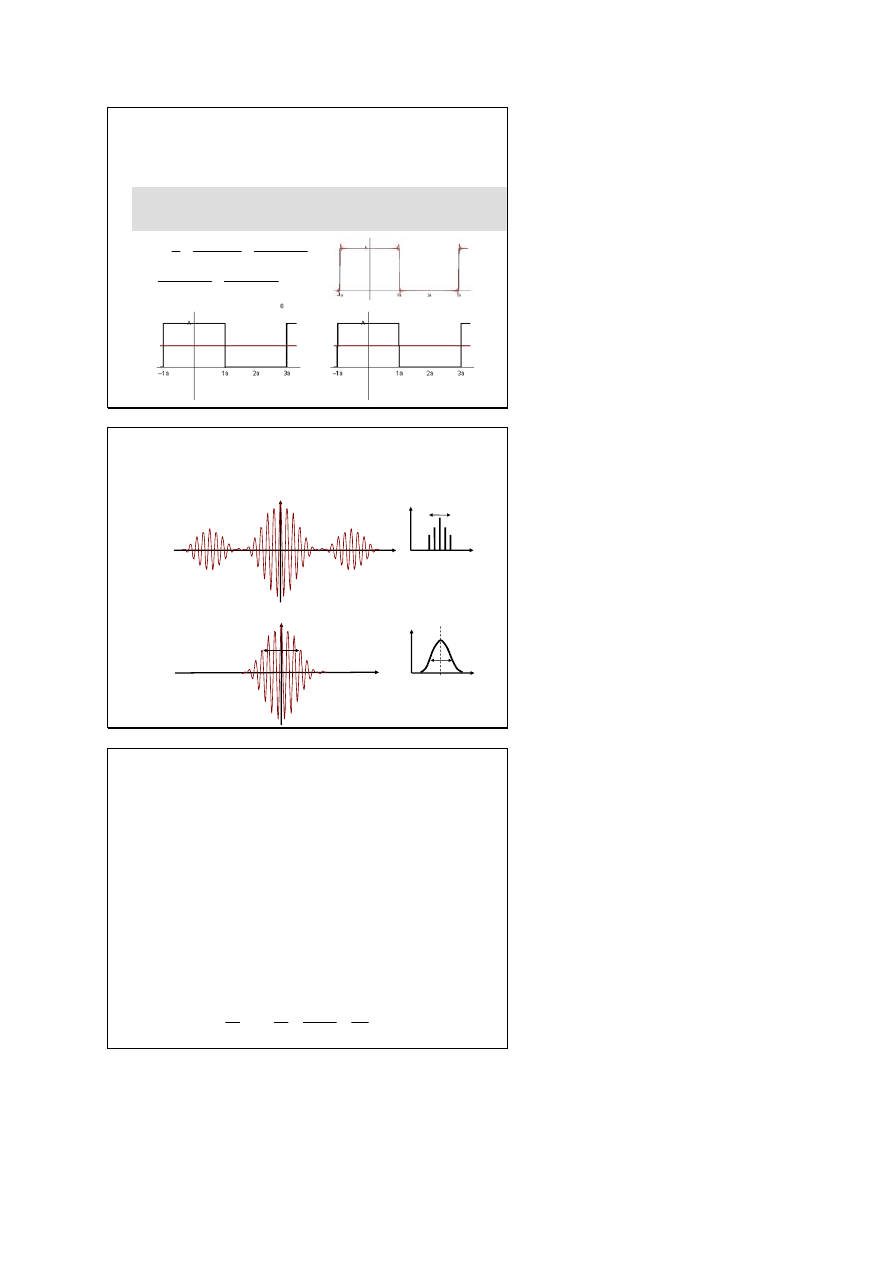
Analiza drgań Fouriera
Każde drganie okresowe nieharmoniczne można przedstawić w
postaci nieskończonego szeregu trygonometrycznego zwanego
szeregiem Fouriera, czyli w postaci sumy n drgań harmonicznych
składowe harmoniczne rzędu
suma drgań
rząd n = 99
π
ω
π
ω
π
ω
π
ω
7
7
2
5
5
2
3
3
2
2
2
t
A
t
A
t
A
t
A
A
cos
cos
cos
cos
−
+
+
−
+
=
Ψ
( )
(
)
∑
∞
=
+
+
=
Ψ
1
0
n
n
n
t
n
b
t
n
a
a
t
ω
ω
cos
sin
Superpozycja Fouriera
Dodając większą liczbę fal o częstościach bliskich ω
ο
boczne
dudnienia ulegają stłumieniu. Poniżej wykres dla sumy 5 fal.
Ψ
t
G(ω)
ω
ω
ο
Δω
Przy sumowaniu nieskończonej liczby fal o częstościach bliskich ω
ο
i
amplitudach opisanych funkcją Gaussa otrzymujemy pojedynczą paczkę falową
Ψ
t
G(ω)
ω
ω
ο
Δω
Δt
szerokość paczki
Δt=1/Δω
( )
( )
ω
ω
ω
d
t
G
t
cos
∫
∞
=
Ψ
0
Paczka falowa
w praktyce posługujemy się skończonymi
ciągami falowymi tzw. paczkami falowymi
paczka falowa powstaje w wyniku superpozycji
fal harmonicznych o częstościach z przedziału Δω
i amplitudach opisanych funkcją Gaussa
im mniejsze Δω tym bardziej paczka falowa
rozmyta jest w czasie
paczka falowa rozchodzi się z prędkością
grupową
danej paczce falowej przyporządkowujemy
odpowiednie pasmo liczb falowych Δk
x
t
v
v
d
dk
k
g
g
Δ
=
Δ
⋅
=
ω
Δ
=
ω
Δ
⎟
⎠
⎞
⎜
⎝
⎛
ω
=
Δ
1
1
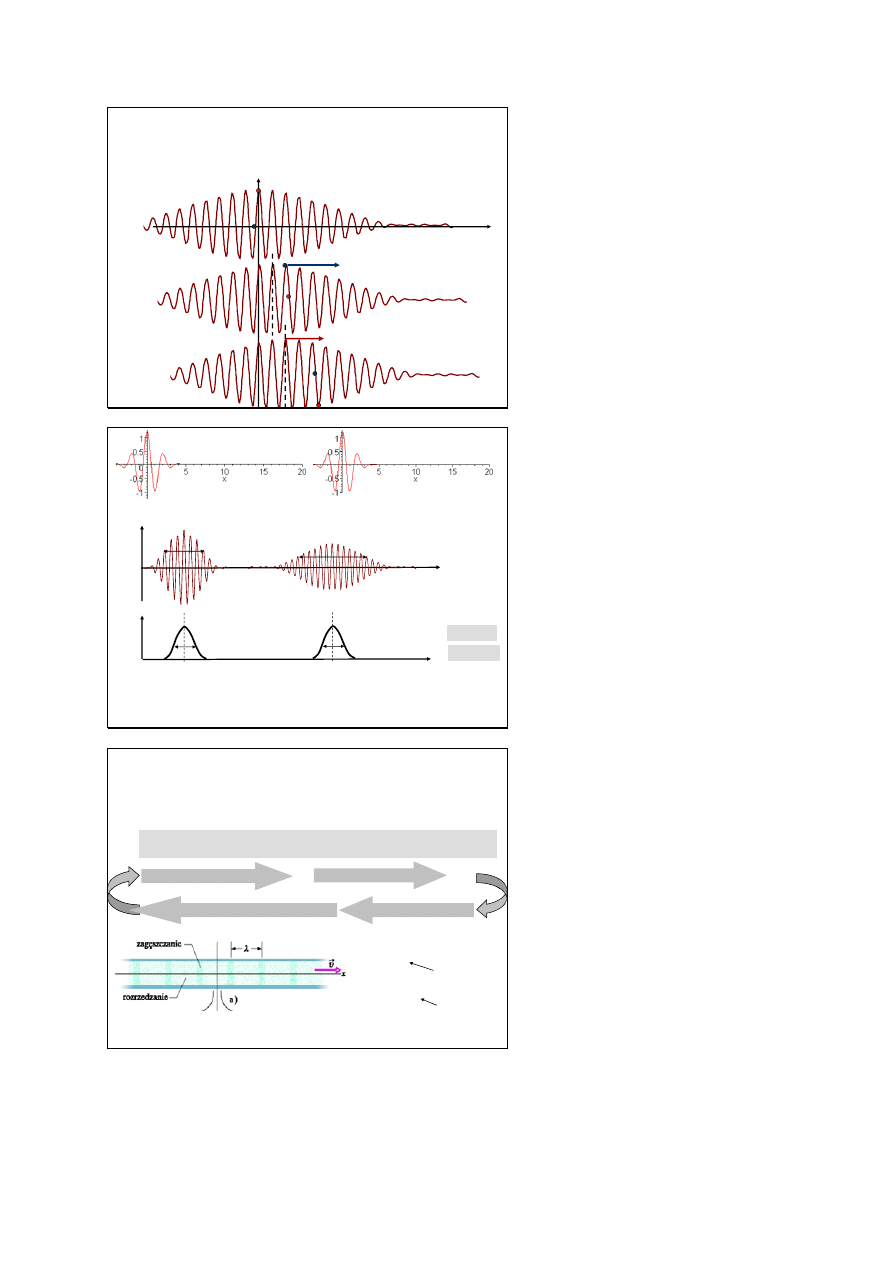
Prędkość grupowa, a prędkość
fazowa paczki falowej
x
v
v
g
Rozmycie paczki falowej
w ośrodku dyspersyjnym
Ψ(x,t)
t
G(ω)
ω
Δω
Δω⋅ Δt>1
w ośrodku dyspersyjnym paczka falowa ulega deformacji (rozmyciu), gdyż
poszczególne składowe propagują się z różnymi prędkościami
w ośrodku niedyspersyjnym paczka falowa nie ulega rozmyciu
Δt
Δt
Δω
Δk⋅ Δx>1
Fale akustyczne w powietrzu
Fale akustyczne w powietrzu są przykładem fal podłużnych
polegających na rozchodzeniu się zagęszczeń i rozrzedzeń powietrza
lokalny ruch cząsteczek
zmiana gęstości gazu
zmiana ciśnienia gazu
nierównomierny rozkład ciśnienia
)
cos(
)
,
(
kx
t
s
t
x
s
−
=
ω
0
)
sin(
)
,
(
kx
t
p
t
x
p
−
Δ
=
Δ
ω
0
(
)
0
0
s
v
p
ω
ρ
=
Δ
amplituda przemieszczeń
amplituda zmian ciśnienia
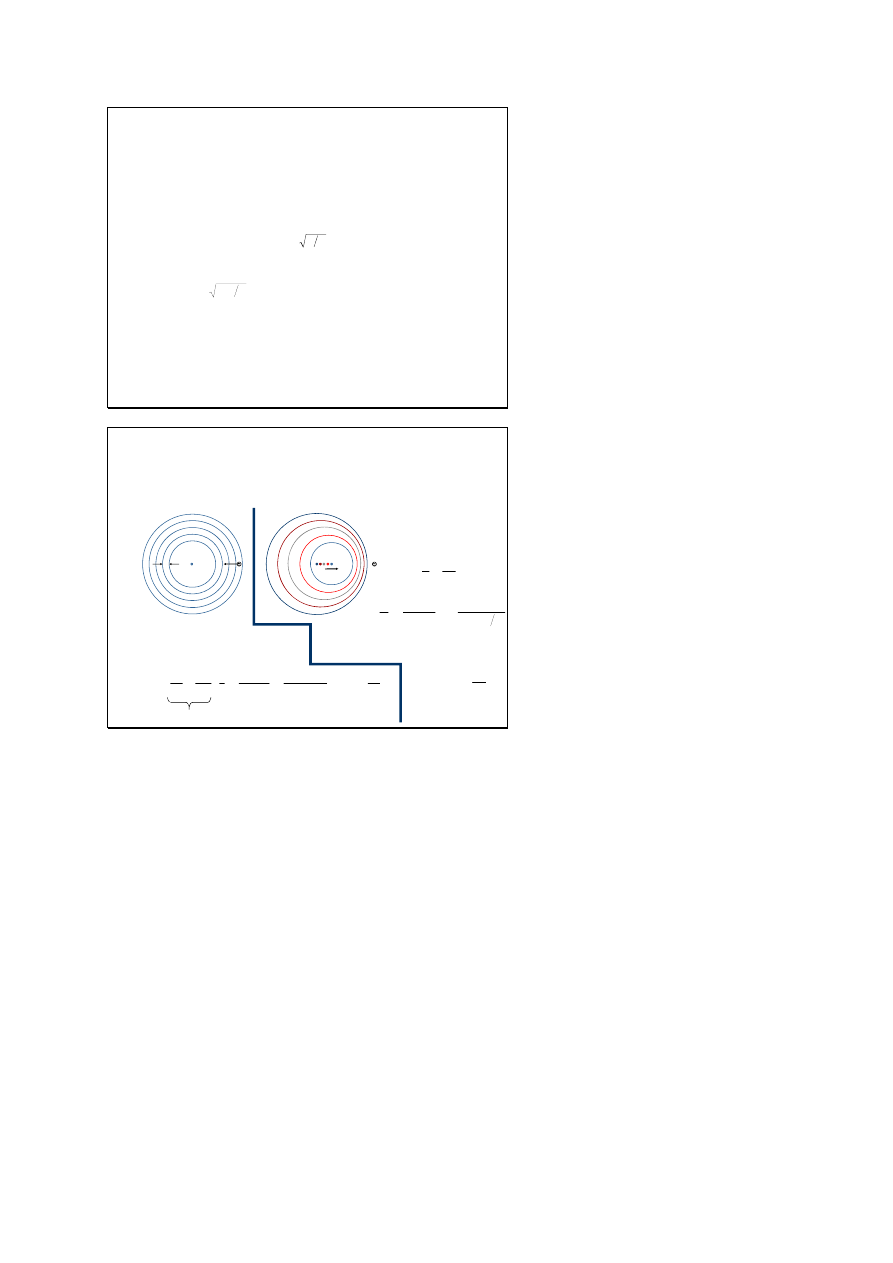
Fale dźwiękowe
(akustyczne)
dźwięki to podłużne fale sprężyste rozchodzące się w
ciałach stałych, cieczach i gazach o częstotliwościach
od 20 Hz (infradźwięki) do 20 KHz (ultradźwięki),
prędkość dźwięku B - moduł ściśliwości
ρ - gęstość ośrodka
powietrze 340 m/s, woda 1500 m/s, stal 6000 m/s
w powietrzu prędkość dźwięku zależy od ciśnienia
gdzie γ stała przemiany adiabatycznej
–fala harmoniczna o określonej częstotliwości,
– jego częstotliwość,
– zbiór fal o różnych częstotliwościach,
– moc na jednostkę powierzchni, ~ A
2
i ω
2
głośność - poziom natężenia dźwięku 10log(I/I
o
) [dB]
gdzie I
o
= 10
-12
W/m
2
to natężenie odniesienia - dolna
granica słyszalności (granica bólu 120 dB)
ton
wysokość dźwięku
barwa
natężenie
ρ
B
v =
ρ
γ
0
p
v =
γ
γ
0
0
V
p
pV =
Z
O
V
o
λ
Zjawisko Dopplera – zmiana częstości
wynikająca z wzajemnego ruchu
obserwatora O i źródła Z
(
)
⎟
⎠
⎞
⎜
⎝
⎛ +
=
+
=
+
=
⎟
⎠
⎞
⎜
⎝
⎛
+
=
u
v
f
u
f
v
u
v
u
t
t
v
ut
f
o
o
o
o
1
1
λ
λ
λ
'
zbliżający się obserwator odbiera
fale o większej częstotliwości
liczba rejestrowanych
fal w czasie t
f
v
f
u
z
−
=
λ'
(
)
u
v
f
v
u
uf
u
f
z
z
−
=
−
=
λ
=
1
1
'
'
źródło zbliża się do obserwatora
fala ma mniejszą długość z
przodu, a większą z tyłu
gdy prędkość źródła większa
jest od prędkości dźwięku
powstaje fala uderzeniowa
u
v
M
z
=
=
θ
sin
liczba Macha
1
1
2
2
3
3
4
4
5
5
Z
O
V
z
Wyszukiwarka
Podobne podstrony:
2 1 V 1 02 ark 07id 20006 Nieznany
bns kalisz 02 06 id 90842 Nieznany (2)
02 Identyfikacja zachowan konsu Nieznany (2)
Drgania 4 id 141931 Nieznany
02 2004 kurpiszid 3523 Nieznany
ORZ drgania id 340792 Nieznany
Cw 02 M 04A Badanie wlasciwos Nieznany
17 02 2011 2id 17062 Nieznany (2)
02 Charakteryzowanie typow i ro Nieznany (2)
02 Krotko i dlugoterminowe dec Nieznany
na5 pieszak 03 02 10 1 id 43624 Nieznany
1) Drgania w liniowych obwodach Nieznany
2009 02 17 test egzaminacyjny n Nieznany (2)
2003 02 Fosdem February 2003, K Nieznany
02 Zielona wiosenkaid 3865 Nieznany
02 07 azbestid 3506 Nieznany (2)
02 rozdzial 01 t4p4wqyl4oclhuae Nieznany (2)
24 02 2011 2 id 30494 Nieznany (2)
02 Przestrzeganie przepisow bez Nieznany (2)
więcej podobnych podstron