Politechnika Śląska

Gliwice

Wydział Automatyki, Elektroniki i Informatyki

Rok akademicki 2008/2009

Kierunek: Automatyka i Robotyka sem.4

Semestr letni

Metody Numeryczne

Laboratorium

Ćw. 6: Aproksymacja

Wykonali:

Tomasz LITWIN,

Bartosz GUDOWSKI

Grupa 3, sekcja 1

Data odbycia ćwiczenia:

24.04.2009r.

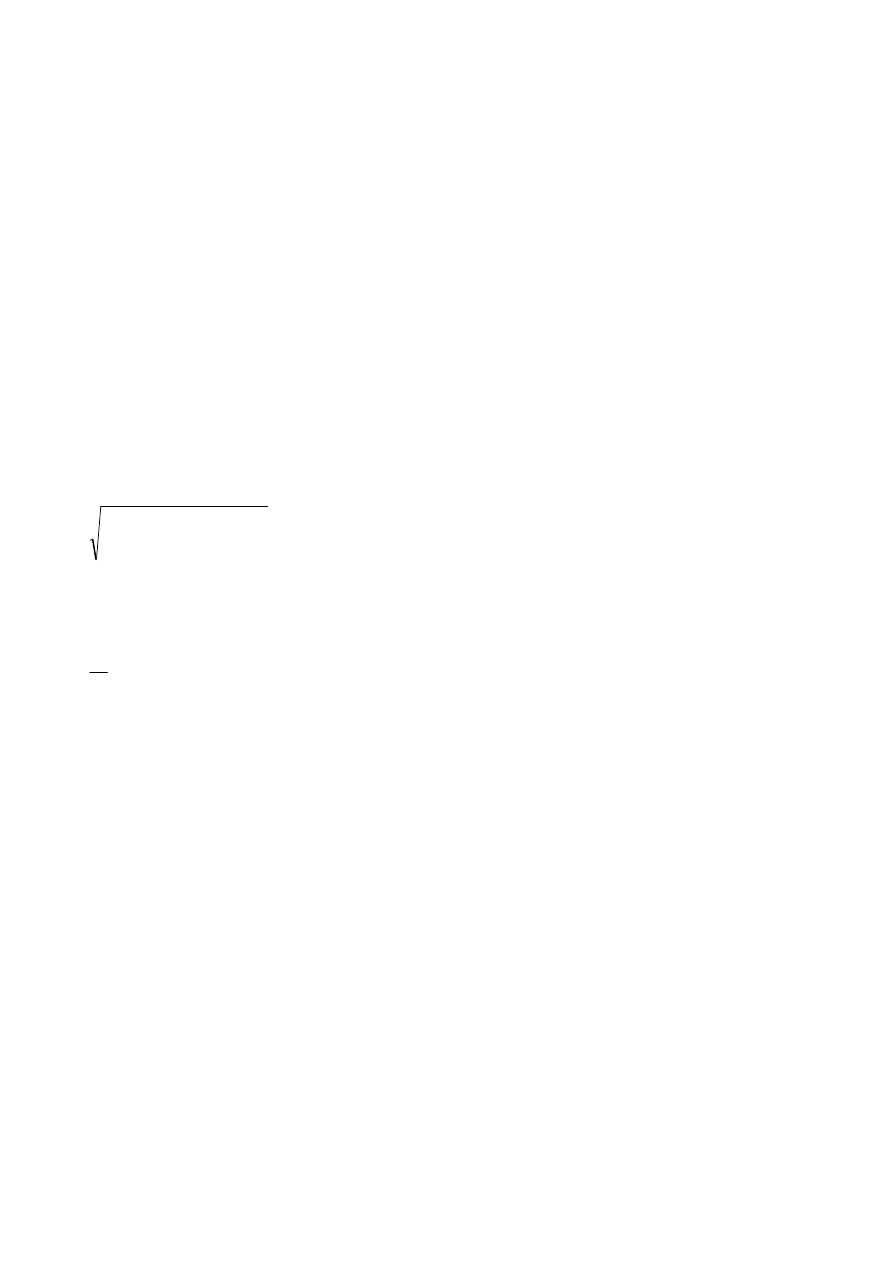
1. Aproksymacja średniokwadratowa z użyciem wielomianów ortogonalnych:

Opis metody:

Daną funkcję

]

,

[

)

(

2

b

a

L

x

f

p

∈

należy aproksymować z wagą

)

(x

p

funkcją

)

(x

q

o postaci :

∑

=

=

=

n

i

i

i

i

x

c

x

q

0

)

(

)

(

ϕ

gdzie:

)

(x

i

ϕ

]

,

[

2

b

a

L

p

∈

,

n

i

...,

,

1

,

0

=

są funkcjami tworzącymi układ ortogonalny w

]

,

[

2

b

a

L

p

, tzn.

∫







=

≠

=

b

a

j

i

dx

x

x

x

p

j

i

dla

const

j

i

dla

0

)

(

)

(

)

(

ϕ

ϕ

Miara odległości pomiędzy funkcjami jest zdefiniowana wzorem:

∫

−

=

b

a

dx

x

f

x

q

x

p

D

2

)]

(

)

(

)[

(

Współczynniki

i

c wyznaczamy z następującego wzoru (

n

i

...,

,

1

,

0

=

):

∫

=

b

a

i

i

i

dx

x

f

x

x

p

c

)

(

)

(

)

(

1

ϕ

λ

gdzie:

∫

=

b

a

i

i

dx

x

x

p

)

(

)

(

2

ϕ

λ

Otrzymane w programie wielomiany:

1 stopnia: y = 0.841471

2 stopnia: y = 0.465261x

2

+ 0.996558

3 stopnia: y = 0.465261x

2

+ 0.996558

4 stopnia: y = 0.0039554375x

4

+ 0.43135725x

2

+ 0.999948375

5 stopnia: y = 0.0039554375x

4

+ 0.43135725x

2

+ 0.999948375

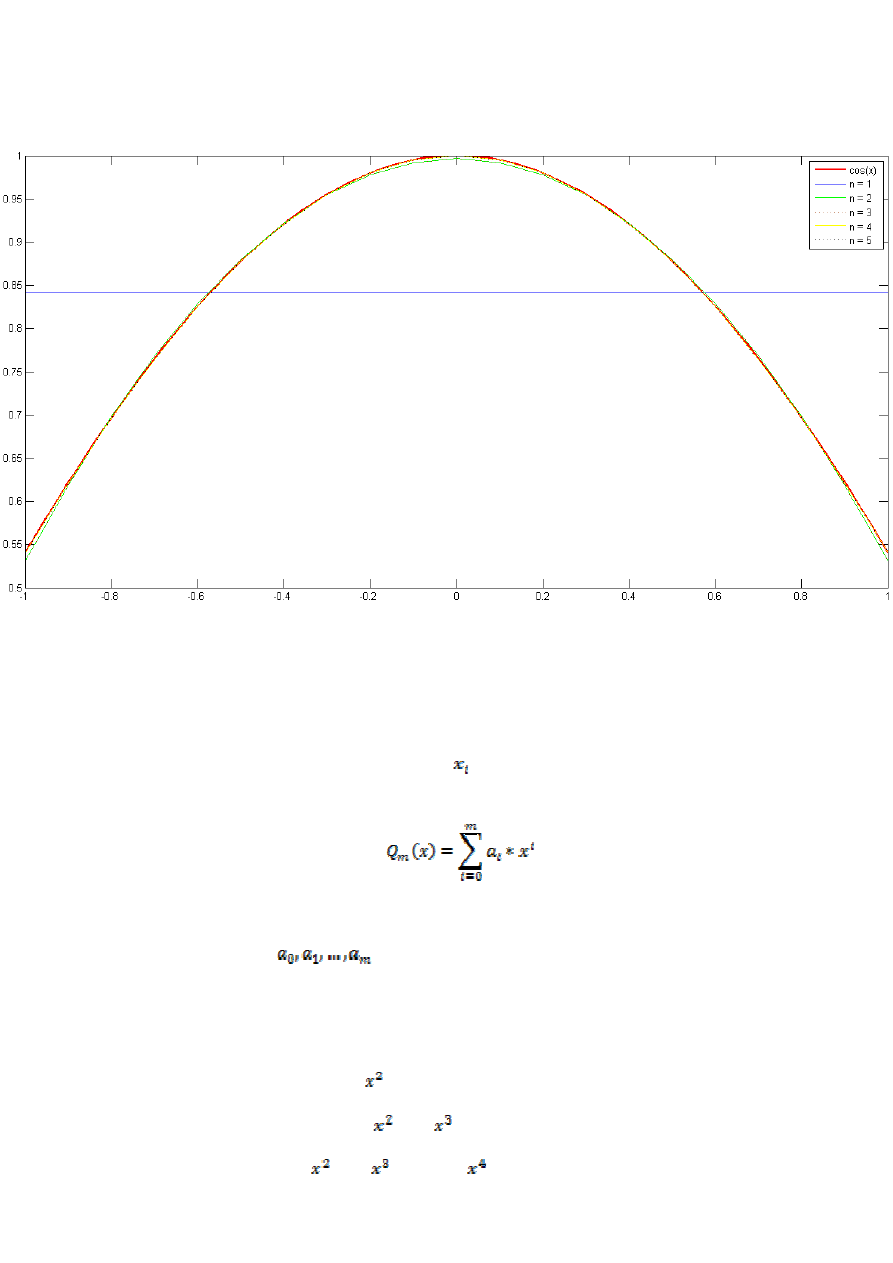
Wynik działania programu:

2. Metoda najmniejszych kwadratów(aproksymacja punktowa)

Opis metody:

Funkcję f(x) podaną w (n+1) punktach dyskretnych , (i=0,1,…,n) należy aproksymować wielomianem

potęgowym o postaci:

gdzie m-stopień wielomianu aproksymującego (m<n).

Poszczególne niewiadome

otrzymujemy rozwiązując układ równań

.

Otrzymane w programie wielomiany:

1 stopnia: y = 1,8-0,4x

2 stopnia: y = 1,514286-0,4x+0,142857

3 stopnia: y = 1,514286-1,25x+0,142857

+0,25

4 stopnia: y = 4-1,25x-5,208333

+0,25

+1,208333

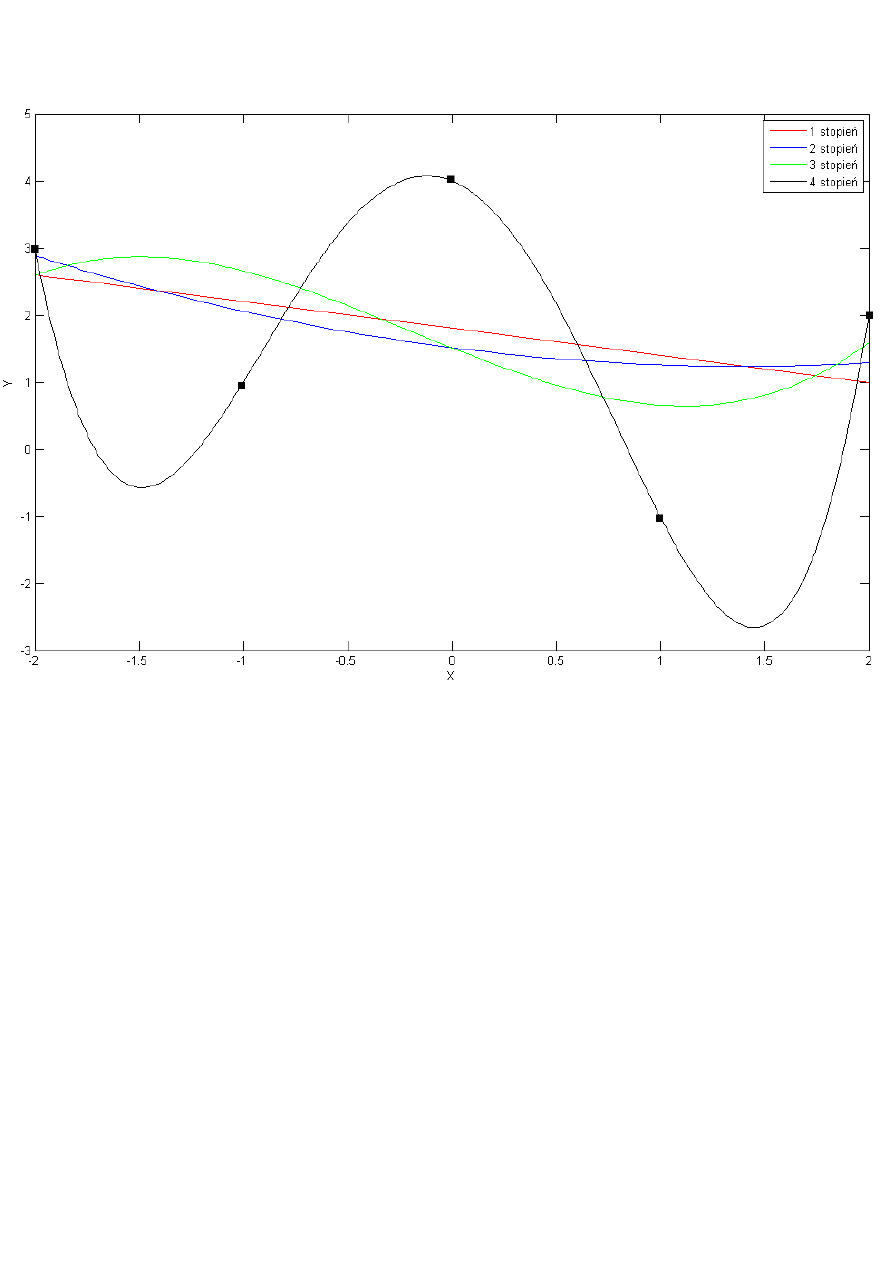
Wynik działania programu

3. Wnioski:

Wielomiany o stopniu powyżej trzeciego odwzorowują niemal idealnie przebieg funkcji w metodzie

aproksymacji średniokwadratowej. Przy stopniu wielomianu aproksymującego równym 2 i 3 można

jeszcze zauważyć„gołym okiem” różnice w przebiegu badanej funkcji i wielomianu aproksymującego ją.

W metodzie najmniejszych kwadratów widoczny jest wzrost dokładności aproksymacji wraz ze

zwiększaniem stopnia wielomianu aproksymującego. Dla maksymalnego stopnia wielomianu

aproksymującego jaki mogliśmy zastosować mając funkcję daną w pięciu punktach wielomian ten jest

jednocześnie wielomianem interpolacyjnym co doskonale widać na dołączonym wykresie.

4. Kody programów:

a) Aproksymacja średniokwadratowa

#include

<stdio.h>

#include

<stdlib.h>

#include

<math.h>

double

funka(

double

x)

{

return

cos(x);

//funkcja do aproksymacji

}

double

legendre(

double

x,

int

n,

int

opcja)

{

int

i;

double

Pn[10];

Pn[0] = 1;

for

(i = 0; i <= n; i++)

{
Pn[i+1] = ((2*i+1)*x*Pn[i]-i*Pn[i-1])/(i+1);
}

if

(opcja == 1)

return

pow(Pn[n],2);

if

(opcja == 2)

return

(Pn[n]*funka(x));

if

(opcja == 3)

return

Pn[n];

}

//simpson

double

simpson(

double

wezly[],

double

h,

int

ile_wezlow,

int

n,

int

opcja)

{

int

i;

double

suma = 0;

for

(i = 0; i <= (2*ile_wezlow); i++)

{

if

(i == 0 || i == (2*ile_wezlow)) suma += legendre(wezly[i],n,opcja);

else

{

if

(i%2 == 0) suma += 2*legendre(wezly[i],n,opcja);

if

(i%2 != 0) suma += 4*legendre(wezly[i],n,opcja);

}
}
suma = (h/3.0)*suma;

return

suma;

}

int

main()

{

int

n, i, ile_wezlow = 17;

double

j, a = -1, b = 1, h, wezly[50];

double

lambda[10], wsp_c[10], wynik;

//wyznaczanie wezlow do metody simpsona

h = (b-a)/(2*ile_wezlow);

for

(i = 0; i <= (2*ile_wezlow); i++)

{
wezly[i] = i*h + a;
}


printf(

"Podaj n: "

);

scanf(

"%d"

, &n);

//wyznaczanie wsp lambda (opcja simpson = 1) oraz wsp_c (opcja simpson = 2)

for

(i = 0; i <= n; i++)

{
lambda[i] = simpson(wezly,h,ile_wezlow,i,1);
wsp_c[i] = simpson(wezly,h,ile_wezlow,i,2)/lambda[i];
printf(

"lambda[%d] = %lf\n"

,i,lambda[i]);

printf(

"wsp_c[%d] = %lf\n"

,i,wsp_c[i]);

}

//wynik, wartosci pktow funkcji aproksymujacej

FILE *out;
out = fopen(

"wynik.txt"

,

"wt"

);

for

(j = -1; j <= 1; j+=0.1)

//przedzial wartosci

{
wynik = 0;

for

(i = 0; i <= n; i++)

{
wynik += wsp_c[i]*legendre(j,i,3);
}
fprintf(out,

"%lf,\n"

,wynik);

}
fclose(out);
system(

"pause"

);

return

0;

}

b) Metoda najmniejszych kwadratów

#include

<stdio.h>

#include

<math.h>

#include

<stdlib.h>

int

main()

{

double

x[5]={-2,-1,0,1,2} , y[5]={3,1,4,-1,2}, S[9]={0}, T[9]={0}, a[9][9]={0},

z[9]={0},roznica=0;

int

n=4,m,k,i,j;

printf(

"Podaj stopien wielomianu aproksymujacego\n"

);

scanf(

"%d"

,&m);

// obliczanie wartosci S

for

(k = 0; k <= 2*m; k++)

{

for

(i = 0; i <= n; i++)

{
S[k]+=pow(x[i],k);
}

// printf("S[%d] = %lf\n",k,S[k]);

}

// obliczanie wartosci T

for

(k = 0; k <= m; k++)

{

for

(i = 0; i <= n; i++)

{
T[k]+=pow(x[i],k)*y[i];
}

// printf("T[%d] = %lf\n",k,T[k]);

}

// stworzenie ukladu rownan

for

( j = 1;j <= m+2;j++)

{

for

( i = 1;i <= m+1;i++)

{

if

(j <= m+1)

a[i][j]=S[i+j-2];

if

(j == m+2)

a[i][j] = T[i-1];

//

printf("Rownanie %lf\n",a[i][j]);

}

}

//rozwiazanie ukladu rownan metoda Gaussa

n = m+1;

for

( i = 1; i <= n; i++)

{

for

(j = n+1; j >= i; j--)

{

a[i][j] = a[i][j] / a[i][i];

}

for

(k = i+1; k <= n; k++)

{

for

(j = n+1; j >= i; j--)

{

a[k][j] -= a[i][j] * a[k][i];

}
}
}
roznica;

for

(k = n;k >= 1;k--)

{

for

(i = n-1;i >= k;i--)

{

roznica+=a[k][i+1]*z[i+1];
}

z[k] = a[k][n+1]-roznica;

printf(

"Wspolczynnik a[%d] = %lf\n"

,k-1,z[k]);

roznica=0;

}
system(

"pause"

);

return

0;

}