D3. Wyznaczanie apertury numerycznej i zdolności rozdzielczej mikroskopu
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

1/3

Nr pary

Imię i nazwisko studenta

Wydział

grupa

data

Imię i nazwisko prowadzącego

Zaliczenie

D3.

Wyznaczanie apertury numerycznej i zdolności rozdzielczej mikroskopu

Celem ćwiczenia jest poznanie budowy i zasady działania mikroskopu oraz
eksperymentalne wyznaczenie apertury numerycznej oraz zdolności rozdzielczej
mikroskopu.

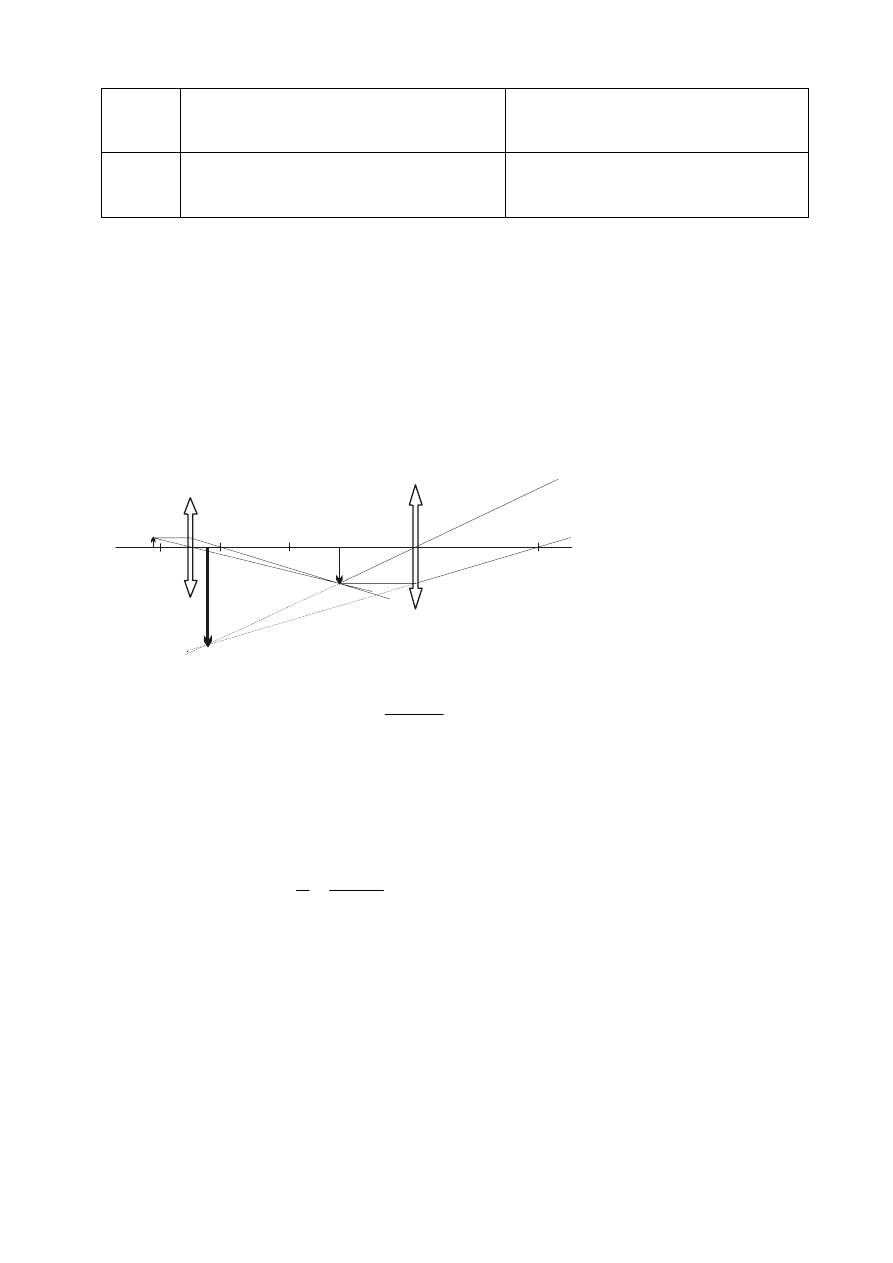
Mikroskop jest układem optycznym, składającym się z dwóch soczewek skupiających:
obiektywu, który daje powiększony, odwrócony i rzeczywisty obraz A’B’ przedmiotu AB,
i okularu, który - działając jak lupa – daje z kolei powiększony, prosty i pozorny obraz A’’B’’
pierwszego obrazu, czyli A’B’.

Rys. 1. Konstrukcja obrazu

w mikroskopie

Powiększenie mikroskopu równe – w przybliżeniu – iloczynowi powiększenia obiektywu

i okularu jest zdefiniowane jako:

ok

ob

f

f

D

l

p

⋅

⋅

=

,

(1)

gdzie l – jest długością tubusa, D – odległością dobrego widzenia, a f

ob

i f

ok

– ogniskowymi

obiektywu i okularu.

Zdolność rozdzielcza mikroskopu – to wielkość, która charakteryzuje mikroskop pod względem
rozróżniania drobnych szczegółów badanego przedmiotu. Określamy ją jako odwrotność
najmniejszej odległości d pomiędzy punktami, które jeszcze rozróżniamy jako oddzielne, a więc:

λ

u

n

d

z

sin

1

⋅

=

=

.

(2)

Wyrażenie:

n

⋅

sinu = A

(3)

nazywa się

aperturą numeryczną obiektywu mikroskopu, gdzie n oznacza współczynnik

załamania światła ośrodka pomiędzy obiektywem a oglądanym przedmiotem, u - jest połową
kąta, jaki tworzą skrajne promienie wchodzące do obiektywu.

Mikroskop jest tym lepszy, im większą ma zdolność rozdzielczą, gdyż tym więcej szczegółów
można rozróżnić w badanym przedmiocie.

Zdolność rozdzielczą mikroskopu można

zwiększyć poprzez:

wprowadzenie pomiędzy badany przedmiot a obiektyw tzw. cieczy immersyjnej, o dużym
współczynniku załamania n (tzw.

mikroskop immersyjny) lub poprzez

zastosowanie promieniowania o krótszej długości fali

λ

.

Najkrótsze fale uzyskuje się

w tzw.

mikroskopie elektronowym, w którym fale materii de Broglie’a, towarzyszące

A

B

A’

B’

A’‘

B’‘

Ob

Ok

F

Ob

F

Ob

F

Ok

F

Ok

D3. Wyznaczanie apertury numerycznej i zdolności rozdzielczej mikroskopu
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

2/3

poruszającym się elektronom, mają długość rzędu 10

3

– 10

4

razy mniejszą niż fale

ś

wietlne.

Wykonanie ćwiczenia

Przyrządy:

mikroskop optyczny, apertomierz (liniał z przesuwaną żarówką umieszczony prostopadle

do osi optycznej mikroskopu), miara metrowa, lampka podświetlająca.

1. Włączamy do sieci lampkę podświetlającą stolik mikroskopu.
2. Nastawiamy mikroskop na ostre widzenie otworu w przesłonie umieszczonej na stoliku

mikroskopu.

3. Zdejmujemy okular i ustawiamy tubus mikroskopu w położeniu poziomym.
4. Ustawiamy skalę apertomierza w określonej odległości od przesłony, np. L = 0.5 m.

Mierzymy tę odległość i zapisujemy w tabeli.

5. Przesuwamy wzdłuż liniału oświetloną strzałkę i wyznaczamy z obu stron osi optycznej

mikroskopu punkty, w których znika widziany przez obiektyw obraz strzałki.

6.

Mierzymy na skali odległość między tymi punktami równą 2S. Pomiar ten wykonujemy
conajmniej trzy razy, a otrzymane wartości uśredniamy.

Opracowanie wyników

1. Na podstawie przeprowadzonych pomiarów odległości 2S i L możemy wyznaczyć aperturę badanego

obiektywu korzystając ze wzoru(3):

u

n

A

sin

=

, przy czym:

2

2

sin

L

S

S

u

+

=

(4)*.

Przyjmując dla powietrza n = 1, otrzymujemy A = sin u.

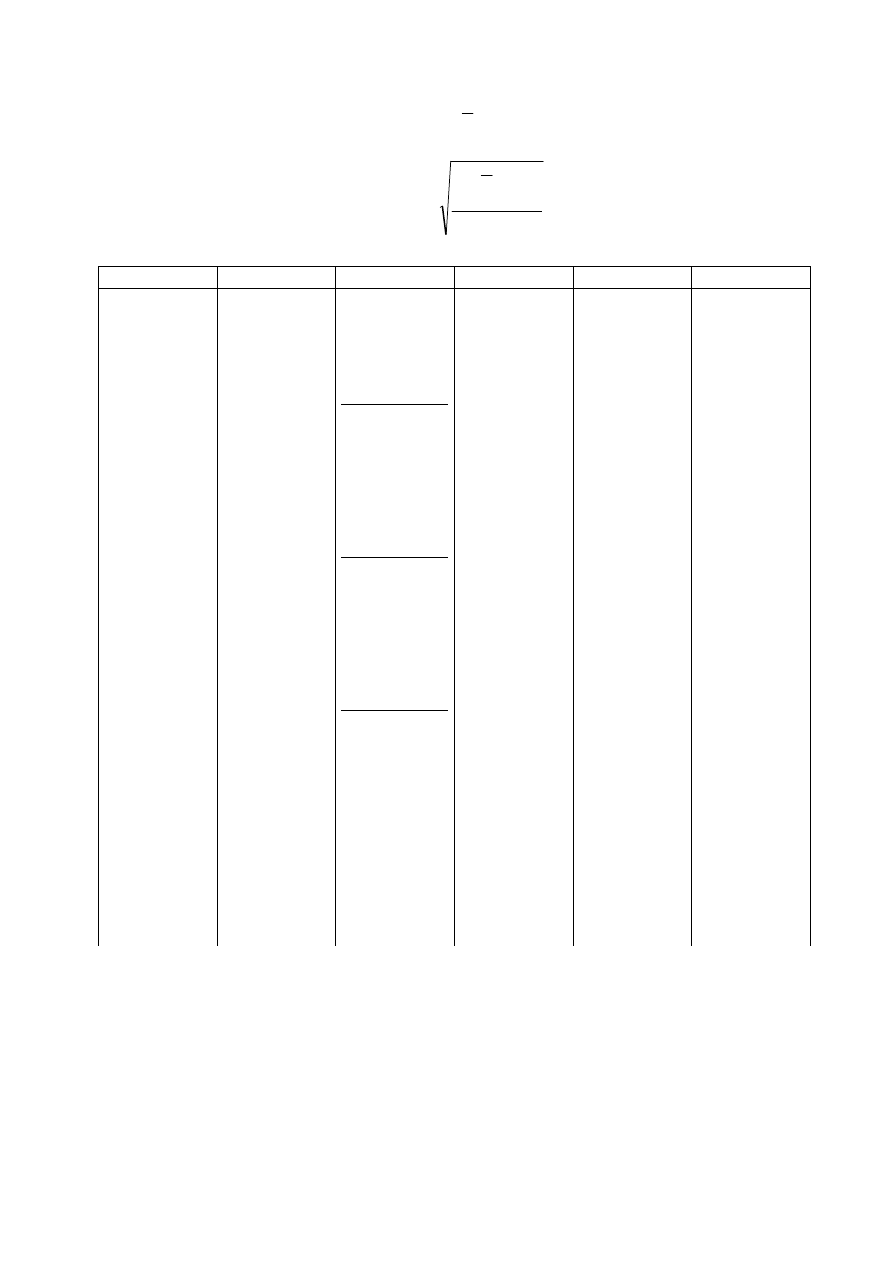
*Wyjaśnienie: na podstawie schematu obrazującego metodę wyznaczania apertury numerycznej obiektywu

(rysunek - powyżej), widzimy, że

L

S

tgu

=

(#). Jeżeli do równania

1

cos

sin

2

2

=

+

u

u

wstawimy:

tgu

u

u

sin

cos

=

,

to otrzymamy:

1

sin

2

2

2

+

=

u

tg

u

tg

u

.Po podstawieniu do ostatniego wzoru zależności (#) otrzymujemy wzór (4).

2. Mając znalezioną wartość apertury A dla danego obiektywu, obliczamy zdolność rozdzielczą

mikroskopu korzystając ze wzoru 2 i wstawiając

λ

= 550 nm.

3. Przeprowadzamy rachunek błędów pomiarowych: dla apertury A - metodą różniczki

zupełnej:

(

)

L

L

S

L

S

LS

S

L

S

L

S

L

L

L

A

S

S

A

A

∆

+

+

+

∆

+

+

=

∆

+

∆

=

∆

2

2

2

2

2

2

2

2

2

)

(

δ

δ

δ

δ

,

dla zdolności rozdzielczej z – metodą logarytmiczną:

A

A

z

z

∆

=

∆

stąd

A

A

z

z

∆

=

∆

.

L

2S

2u

O

o

b

ie

k

ty

w

l

D3. Wyznaczanie apertury numerycznej i zdolności rozdzielczej mikroskopu
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

3/3

Uwaga! Jeżeli dla tego samego obiektywu mierzymy n-krotnie aperturę (dla różnych

wartości L) i wyliczamy jej wartość średnią A , wówczas błąd bezwzględny

A

∆

możemy

obliczyć jako trójkrotną wartość odchylenia standardowego:

(

)

(

)

1

3

3

1

2

−

−

⋅

=

⋅

=

∆

∑

=

n

n

A

A

SD

A

n

i

i

.

Tabela

Lp.

L [m]

2S [m]

S [m]

A

z [nm

-1

]

1

2

3

=

.

2

ś

r

S

1

2

3

=

.

2

ś

r

S

1

2

3

=

.

2

ś

r

S