WYZNACZANIE WSPÓŁCZYNNIKA PRZEWODNO

Ś

CI CIEPLNEJ MATERIAŁÓW

IZOLACYJNYCH METOD

Ą

RURY

1. Cel

ć

wiczenia.

Celem

ć

wiczenia jest przedstawienie metody pomiaru wymiany ciepła w stanie

ustalonym, pozwalaj

ą

cej na okre

ś

lenie współczynnika przewodno

ś

ci cieplnej w

cylindrycznej

ś

cianie (warstwie izolacji okrywaj

ą

cej rur

ę

).

2. Podstawy teoretyczne.

Zjawisko przewodzenia ciepła polega na przenoszeniu energii wewn

ą

trz

o

ś

rodka materialnego z miejsc o temperaturze wy

ż

szej do miejsc o temperaturze

ni

ż

szej, przy czym poszczególne cz

ą

stki rozpatrywanego układu nie wykazuj

ą

wi

ę

kszych zmian poło

ż

enia.

Przewodzenie ciepła jest opisane prawem Fouriera, zgodnie z którym g

ę

sto

ść

strumienia ciepła jest proporcjonalna do gradientu temperatury mierzonego wzdłu

ż

kierunku przepływu ciepła.

Matematycznie prawo to wyra

ż

a si

ę

nast

ę

puj

ą

co:

x

T

q

∂

∂

λ

−

=

gdzie:

q – g

ę

sto

ść

strumienia ciepła[W/m

2

]

λ

- współczynnik przewodzenia ciepła [W/mK]

T – temperatura [K]

x – współrz

ę

dna liniowa [m]

Znak minus w równaniu wynika st

ą

d,

ż

e ciepło przepływa z miejsca o

temperaturze wy

ż

szej do miejsca o temperaturze ni

ż

szej, a wi

ę

c odcinkowi dx

mierzonemu wzdłu

ż

kierunku przepływu ciepła odpowiada ujemna warto

ść

przyrostu

temperatury dT. Współczynnik proporcjonalno

ś

ci

λ

nosi nazw

ę

współczynnika

przewodzenia ciepła i jest wielko

ś

ci

ą

charakteryzuj

ą

c

ą

dany o

ś

rodek pod wzgl

ę

dem

zdolno

ś

ci do przewodzenia ciepła.

Oznaczaj

ą

c przez A pole powierzchni prostopadłej do kierunku przepływu

ciepła otrzymuje si

ę

wyra

ż

enie na ilo

ść

ciepła przewodzonego w jednostce czasu

przez t

ę

powierzchni

ę

:

x

T

A

Q

∂

∂

λ

−

=

Całkuj

ą

c równanie przewodzenia ciepła dla ró

ż

nych (jednowymiarowych) układów,

przy zało

ż

eniu,

ż

e współczynnik przewodzenia ciepła ma warto

ść

stał

ą

, otrzymujemy

ilo

ś

ci przewodzonego ciepła w jednostce czasu dla:

-

ś

cianki płaskiej

(

)

z

w

T

T

A

Q

−

δ

λ

=

[W]

-

ś

cianki cylindrycznej (rury)

(

)

w

z

z

w

d

d

ln

1

l

T

T

2

Q

λ

−

Π

=

[W]

-

ś

cianki kulistej

(

)

z

w

z

w

d

1

d

1

T

T

2

Q

−

−

λ

Π

=

[W]

gdzie:

T

z

– temperatura zewn

ę

trznej powierzchni

ś

ciany [K]

T

w

- temperatura wewn

ę

trznej powierzchni

ś

ciany [K]

d

z

–

ś

rednica zewn

ę

trzna [m]

d

w

–

ś

rednica wewn

ę

trzna [m]

δ

- grubo

ść

ś

ciany płaskiej [m]

A – powierzchnia prostopadła do kierunku ciepła [m

2

]

l – długo

ść

ś

cianki cylindrycznej [m]

Współczynnik przewodzenia ciepła ciał stałych zawiera si

ę

w bardzo szerokich

granicach: od

λ

= 0,04 [W/mK] – (dobry izolator cieplny) do

λ

= 420 [W/mK] –

(srebro).

Współczynnik przewodzenia ciepła jest zale

ż

ny od temperatury. Zale

ż

no

ść

λ

od

temperatury dla ró

ż

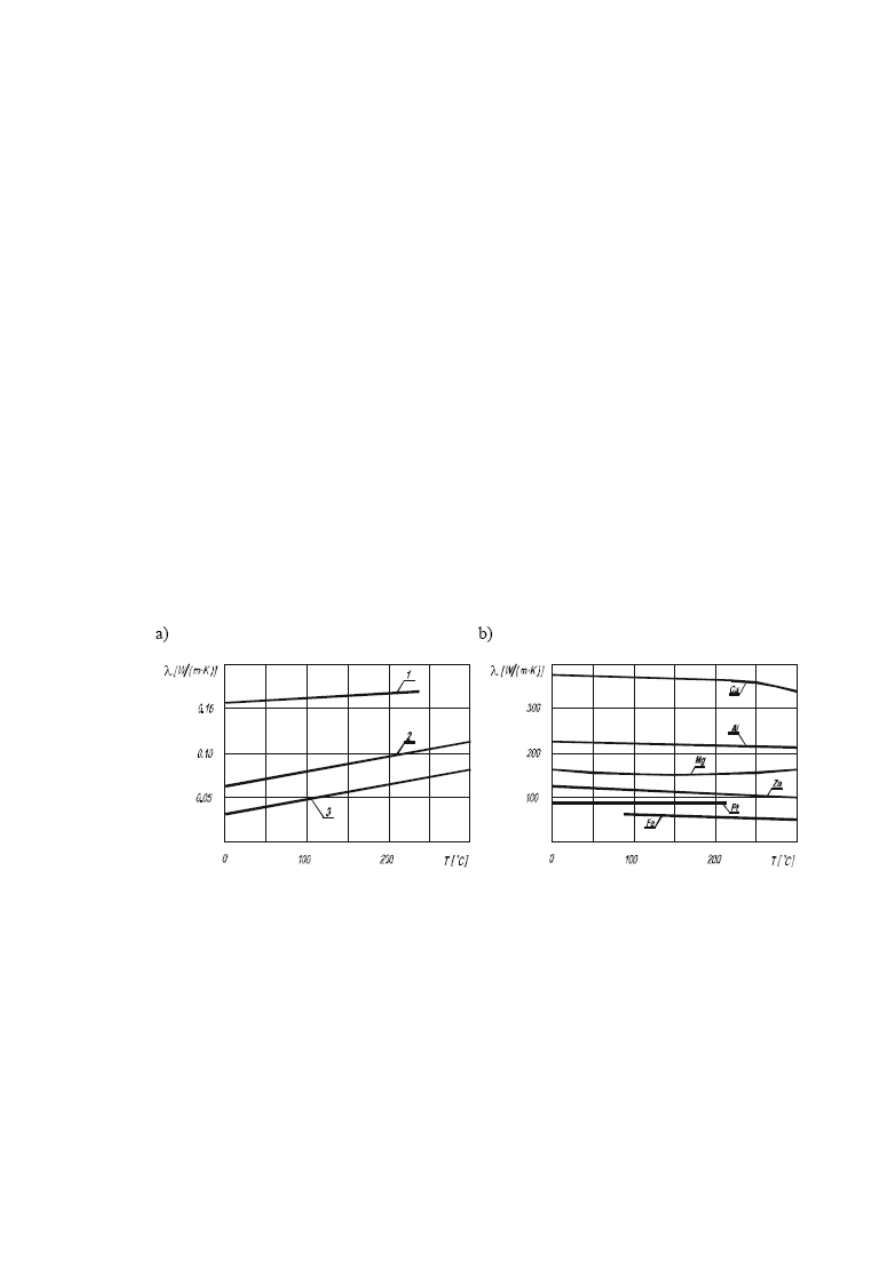
nych ciał stałych przedstawiono na rys.1.

Rys. 1. Przewodno

ść

cieplna w funkcji temperatury: a) materiały izolacyjne: 1-azbest,

2- wata

ż

u

ż

lowa, 3- wata mineralna, b) metale.

Jak wynika z wykresów, dla wi

ę

kszo

ś

ci materiałów w w

ą

skich przedziałach

temperatur mo

ż

na przyjmowa

ć

warto

ść

współczynnika przewodzenia ciepła

λ

jako

stał

ą

. Tak znaczne ró

ż

nice przewodno

ś

ci cieplnej dla ró

ż

nych materiałów wymagaj

ą

dokładnych pomiarów tej wielko

ś

ci dla ka

ż

dego materiału. W niektórych przypadkach

nawet niewielka zmiana składu lub struktury (np. przej

ś

cie z materiału litego na

porowaty) danego materiału mo

ż

e zasadniczo zmieni

ć

jego przewodno

ść

ciepln

ą

. W

tej sytuacji do dokładnych oblicze

ń

cieplnych nale

ż

y w zasadzie ka

ż

dorazowo w

sposób do

ś

wiadczalny okre

ś

li

ć

przewodno

ść

ciepln

ą

λ

.

Okre

ś

lenie eksperymentalne przewodno

ś

ci cieplnej jest tak

ż

e bardzo istotne

dla materiałów anizotropowych (np. grafit, drewno). Wiele nowoczesnych materiałów

kompozytowych ma przewodno

ś

ci cieplne ró

ż

ni

ą

ce si

ę

od siebie o rz

ą

d wielko

ś

ci,

zale

ż

nie od kierunku.

Jedn

ą

z najprostszych metod pomiaru przewodno

ś

ci cieplnej jest pomiar w

stanie ustalonym, którego zasadnicz

ą

wad

ą

jest stosunkowo długi czas ustalania

równowagi cieplnej. Mimo to, ze wzgl

ę

du na prostot

ę

ten sposób pomiaru nadal

stosowany jest w wielu aparatach firmowych do wyznaczania przewodno

ś

ci cieplnej.

Buduj

ą

c układ cieplny, w którym zostanie zapewnione jednowymiarowe

przewodzenie ciepła i mierz

ą

c spadek temperatury w elemencie przy znanej mocy

cieplnej przewodzonej przez ten element i znanych jego wymiarach geometrycznych

mo

ż

na wyznaczy

ć

przewodno

ść

ciepln

ą

. Na tej zasadzie zbudowane s

ą

aparaty

przeznaczone do pomiaru współczynnika przewodzenia ciepła (płytowe, rurowe,

kulowe). Aparat rurowy przeznaczony do pomiaru współczynnika przewodzenia

ciepła w

ś

cianie cylindrycznej opisany jest w nast

ę

pnym rozdziale.

3. Stanowisko pomiarowe.

Pomiar współczynnika przewodno

ś

ci cieplnej

λ

izolacji ruroci

ą

gów wykonuje si

ę

za

pomoc

ą

aparatu rurowego przedstawionego na schemacie:

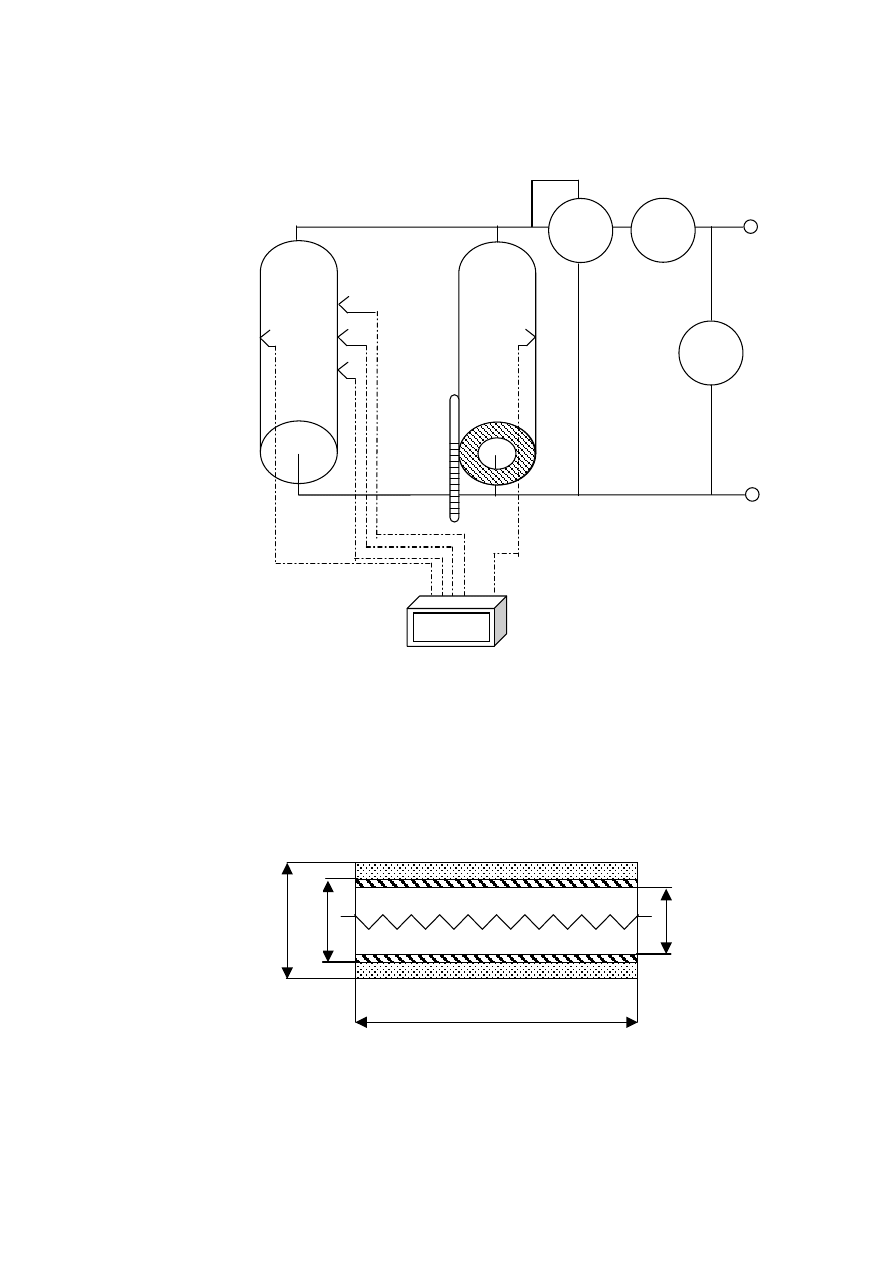
Schemat stanowiska pomiarowego.

Temperatury wewn

ę

trznej i zewn

ę

trznej powierzchni izolacji mierzone s

ą

przy

pomocy termoelementów, umieszczonych w cz

ęś

ci

ś

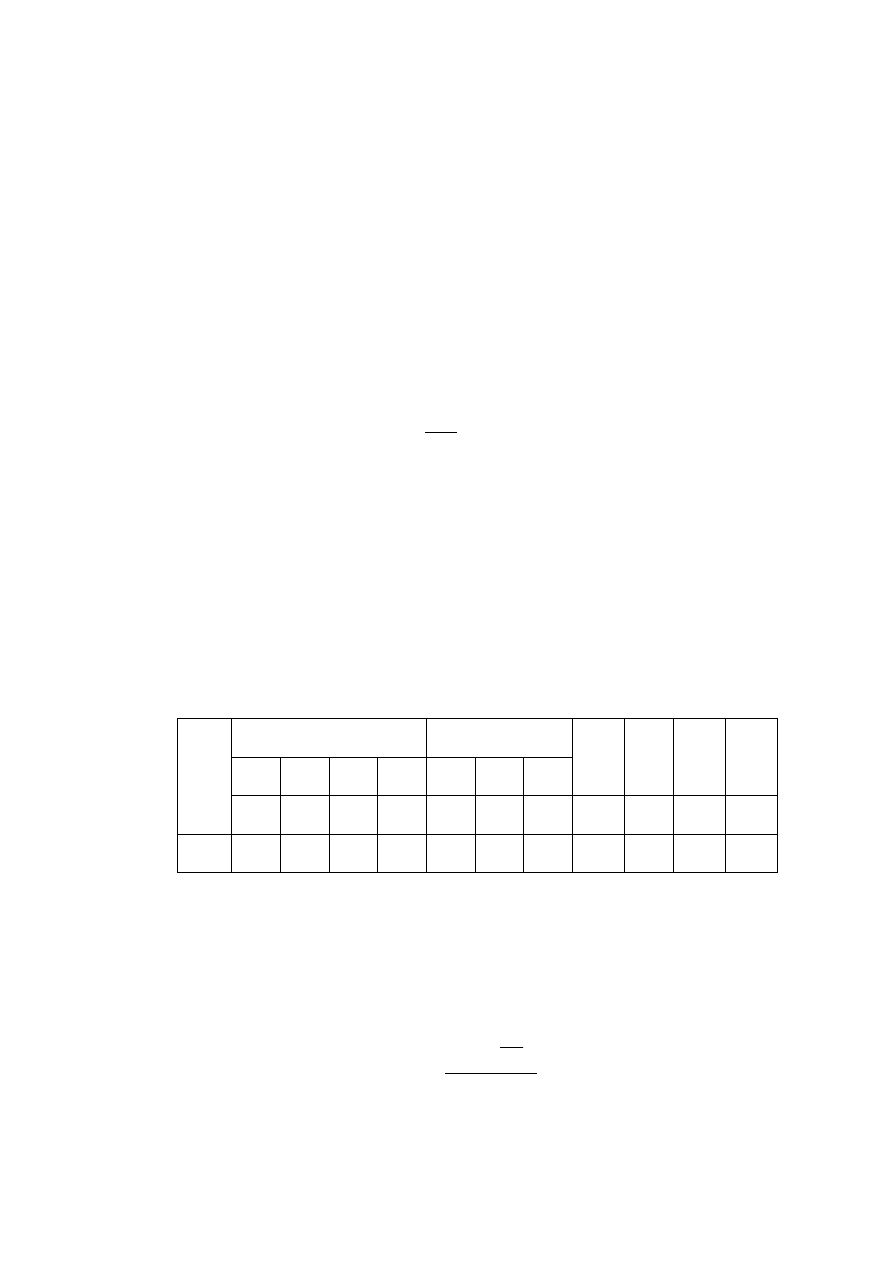
rodkowej rury, rozmieszczenie

termoelementów przedstawia rysunek . Strumie

ń

ciepła wydzielanego przez spiral

ę

,

po ustaleniu si

ę

równowagi cieplnej w układzie mierzony jest przy pomocy

watomierza.

Wymiary rur.

W

A

V

400,0 mV

7

,8

c

m

31,5 cm

8

,3

c

m

1

1

,3

c

m

4. Przebieg pomiarów i opracowanie wyników.

Wła

ś

ciwy pomiar jest poprzedzony długim okresem przygotowawczym, w

którym układ doprowadzony jest do stanu ustalonego. Nast

ę

pnie ju

ż

w stanie

równowagi cieplnej dokonuje si

ę

odczytów wskaza

ń

przyrz

ą

dów. Odczytuje si

ę

wskazania temperatur zewn

ę

trznych i wewn

ę

trznych oraz mocy P. Nale

ż

y dokona

ć

pomiarów kilkakrotnie, (np.5 razy) w odst

ę

pach czasowych co kilkana

ś

cie minut.

Przelicznik napi

ę

cia zmierzonego za pomoc

ą

termopar na tempertur

ę

:

o

x

x

t

100

*

37

,

5

U

t

+

=

[

0

C]

gdzie:
U

x

– napi

ę

cie [mV]

t

o

– temperatura otoczenia [

o

C]

Wyniki pomiarów nale

ż

y wpisa

ć

do tablicy pomiarowej.

Tablica 1. Wyniki pomiarów

Rura nie izolowana

Rura izolowana

t

w

t

z1

t

z2

t

z3

t

w

t

miz

t

z

U

I

P

λ

Lp

o

C

o

C

o

C

o

C

o

C

o

C

o

C

V

A

W

Współczynnik przewodzenia ciepła w

ś

cianie cylindrycznej wyznacza si

ę

z

zale

ż

no

ś

ci:

(

)

z

w

w

z

t

t

l

2

d

d

ln

*

P

−

Π

=

λ

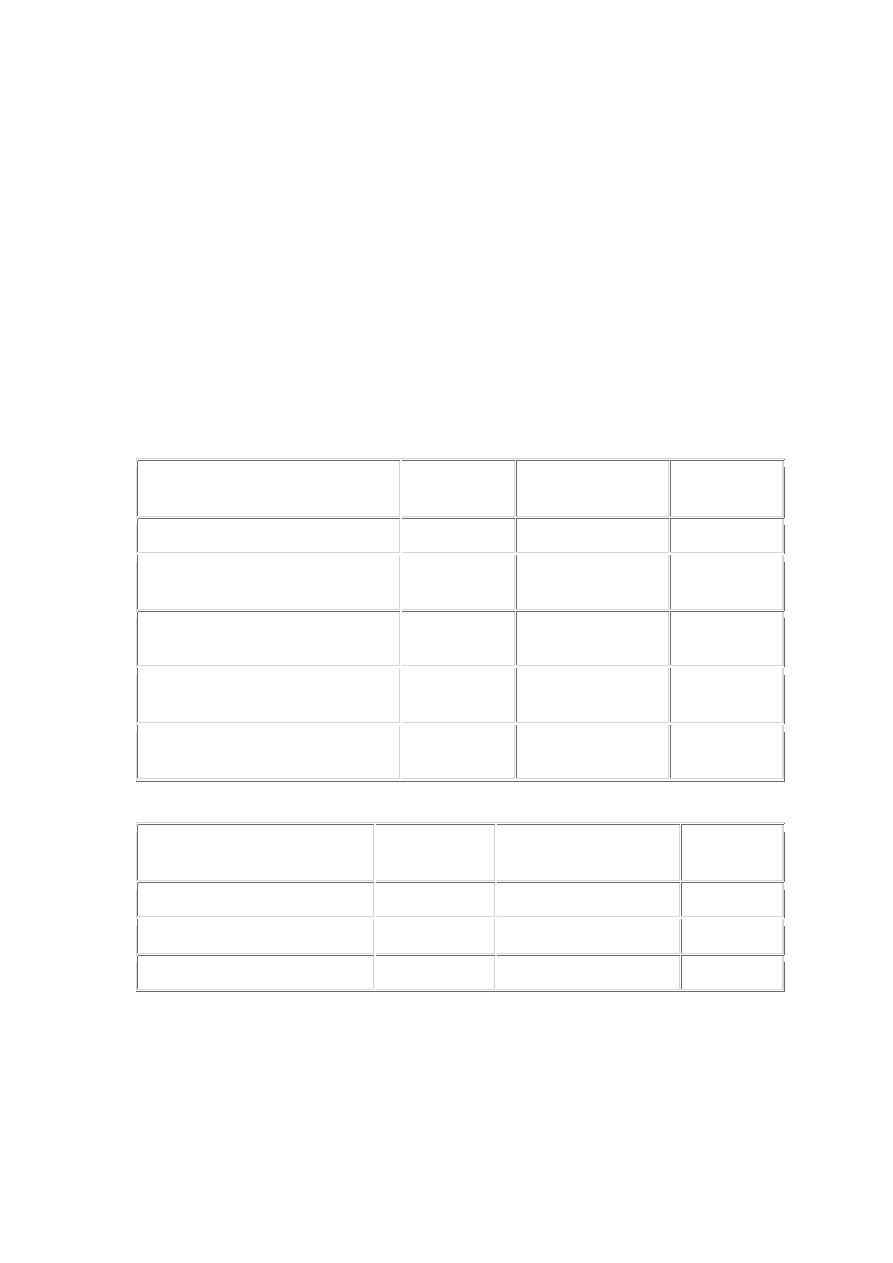
gdzie:

P- ilo

ść

przewodzonego ciepła (moc cieplna) [W]

t

z

– temperatura zewn

ę

trznej powierzchni

ś

ciany [

o

C]

t

w

– temperatura wewn

ę

trznej powierzchni

ś

ciany [

o

C]

d

z

–

ś

rednica zewn

ę

trzna izolacji [m]

d

w

–

ś

rednica wewn

ę

trzna izolacji (równa

ś

rednicy zewn

ę

trznej rury) [m]

l – długo

ść

ś

cianki cylindrycznej (rury) [m]

Przykładowe warto

ś

ci dla popularnych materiałów:

Materiały konstrukcyjne: Materiały osłonowe i izolacyjne

materiał

λ

[W/mK]

materiał

λ

[W/mK]

Ż

elbet

1,70

Styropian

0,037-0,045

Mur z cegły
ceramicznej pełnej

0,77

Wełna mineralna
granulowana

0,050

Płyty i bloki z gipsu

0,35

Tynk lub gład

ź

cementowa

1,00

Drewno sosnowe
lub

ś

wierkowe wzdłu

ż

włókien

0,163-0,300

Płyty gipsowo-
kartonowe

0,23

Beton komórkowy

0,160-0,275

Płyty pil

ś

niowe

porowate

0,058-0,069

Inne materiały

Metale

materiał

λ

[W/mK]

materiał

λ

[W/mK]

papa asfaltowa

0,18

stal budowlana

58,00

szkło okienne

0,05-1,05

ż

eliwo

50,00

pleksiglas

0,19

mied

ź

370,00

W sprawozdaniu nale

ż

y umie

ś

ci

ć

:

1. Krótki opis i schemat układu pomiarowego.

2. Otrzymane wyniki pomiarów ł

ą

cznie z tabel

ą

pomiarow

ą

.

4. Wnioski i uwagi na temat otrzymanych wyników i poprawno

ś

ci pomiaru.

Literatura:

1. „Pomiary w elektrowniach cieplnych”, Jerzy Wojciechowski, PWT 1958.

2. „Pomiary cieplne i energetyczne”, pod red. M. Mieszkowskiego, WNT 1981.

3. „Pomiary cieplne”, pod red. J. Kuleszy, tom 1 i 2, WNT 1993.

4. „Miernictwo energetyczne”, pod red. M. S

ą

siadka, skrypt Politechniki

Wrocławskiej.