Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 1
Opracowali: J. Felis, H. Jaworowski
ANALIZA KINEMATYCZNA PRZEKŁADNI KOŁOWYCH
Przekładnie kołowe są mechanizmami kołowymi przeznaczonymi zwykle
do przeniesienia napędu od wału silnika wykonującego ruch obrotowy do
członu napędowego maszyny roboczej, mechanizmu wykonawczego lub
wprost członu roboczego.
Przekładnie kołowe dzielimy:
- przekładnie zwykłe - przekładnie o osiach geometrycznych kół
nieruchomych względem podstawy. Rozróżniamy przekładnie zwykłe
szeregowe, równoległe, szeregowo-równoległe,
- przekładnie obiegowe lub inaczej planetarne - przekładnie o osiach
geometrycznych kół ruchomych względem podstawy. Rozróżniamy
przekładnie obiegowe proste, złożone, zamknięte.
W obliczeniach kinematycznych przekładni posługiwać się będziemy tzw.
przełożeniami kierunkowymi, które ogólnie można zapisać wzorem:
0
i
c
b
c
a
c
ab
=
=
ω
ω
(1)
gdzie: a, b – człony ruchome; a - napędzający (czynny) , b - napędzany
(bierny), c – człon nieruchomy
c
b
c
a
,
ω
ω
- prędkości kątowe członów czynnego a i biernego b przy
unieruchomionym członie c. Dalej te prędkości kątowe będziemy oznaczać
b
a
,
ω
ω
.
PRZEKŁADNIE ZWYKŁE
W przypadku analizy przekładni zwykłych ma potrzeby wprowadzania
pojęcia członu nieruchomego i wzór (1) można uprościć do postaci:
b
a
ab
i
ω
ω
=
lub
a
b
ba
i
ω
ω
=
(2)
Przełożenie kierunkowe
ab
i
przyjmujemy za ujemne
0
i
ab
<
, jeżeli
zwroty prędkości kątowych członu a i członu b są przeciwne. Jest to
przekładnia o zazębieniu zewnętrznym.
Przełożenie kierunkowe
ab
i
przyjmujemy za dodatnie
0
i
ab
>
, jeżeli
zwroty prędkości kątowych tych członów są zgodne. Jest to przekładnia
o zazębieniu wewnętrznym.
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 2
Opracowali: J. Felis, H. Jaworowski
Jeżeli moduł przełożenia kierunkowego
1
i
c
ab
>
, wówczas przekładnia słu-
ży do redukcji prędkości kątowej i jest nazywana reduktorem.
Jeżeli moduł przełożenia kierunkowego
1
i
c
ab
<
, wówczas przekładnia
służy do zwiększania prędkości kątowej i jest nazywana multiplikatorem.
Przełożenie przekładni można wyrazić za pomocą parametrów
geometrycznych kół uwzględniając podstawową zależność:
2
d
v
o
⋅
=
ω
(3)
gdzie:
v
o
– liniowa prędkość obwodowa wspólna dla obydwu kół,
s
m
d – średnica podziałowa koła zębatego lub średnica koła tocznego,
[ ]
m
ω
– prędkość kątowa koła,
[ ]
1
s
−
,
Jeżeli chcemy wyrażać przełożenie za pomocą prędkości obrotowej n to
należy uwzględnić zależność:
[ ]
1
s
30
n
60
n
2
−
⋅
=
⋅
=
π
π
ω
, gdzie
min
obr
n
.
Po uwzględnieniu powyższych związków jest:
a
b
b
a
b
a
ab
d
d
n
n
i
=
=
=
ω
ω
(4)
W przypadku przekładni zębatych, wzory na przełożenie możemy wyrazić
również jako stosunki odpowiednich liczb zębów.
Podstawowe zależności geometryczne i kinematyczne, wspólne dla
przekładni o zazębieniu wewnętrznym i zewnętrznym :
moduł
π
t
m
=
(5)
średnica podziałowa
m
z
t
z
d
⋅
=
⋅
=
π
(6)
prędkość obwodowa
2
d
2
d
v
2
2
1
1
0
⋅
=
⋅
=
ω
ω
(7)
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 3
Opracowali: J. Felis, H. Jaworowski
odległość osi pary kół
2
m
)
z
z
(
a
1
2
⋅
+
=
(8)
przełożenie kierunkowe
1
2
1
2
1
2
2
1
12
z
z
z
m
z
m
d
d
i
−
=
⋅
⋅
−
=
−
=
=
ω
ω
(9)
odległość osi pary kół
2
m
)
z
z
(
a
1
2
⋅
−
=
(10)
przełożenie kierunkowe
1
2
1
2
1
2
2
1
12
z
z
z
m
z
m
d
d
i
=
⋅
⋅
=
=
=
ω
ω
(11)
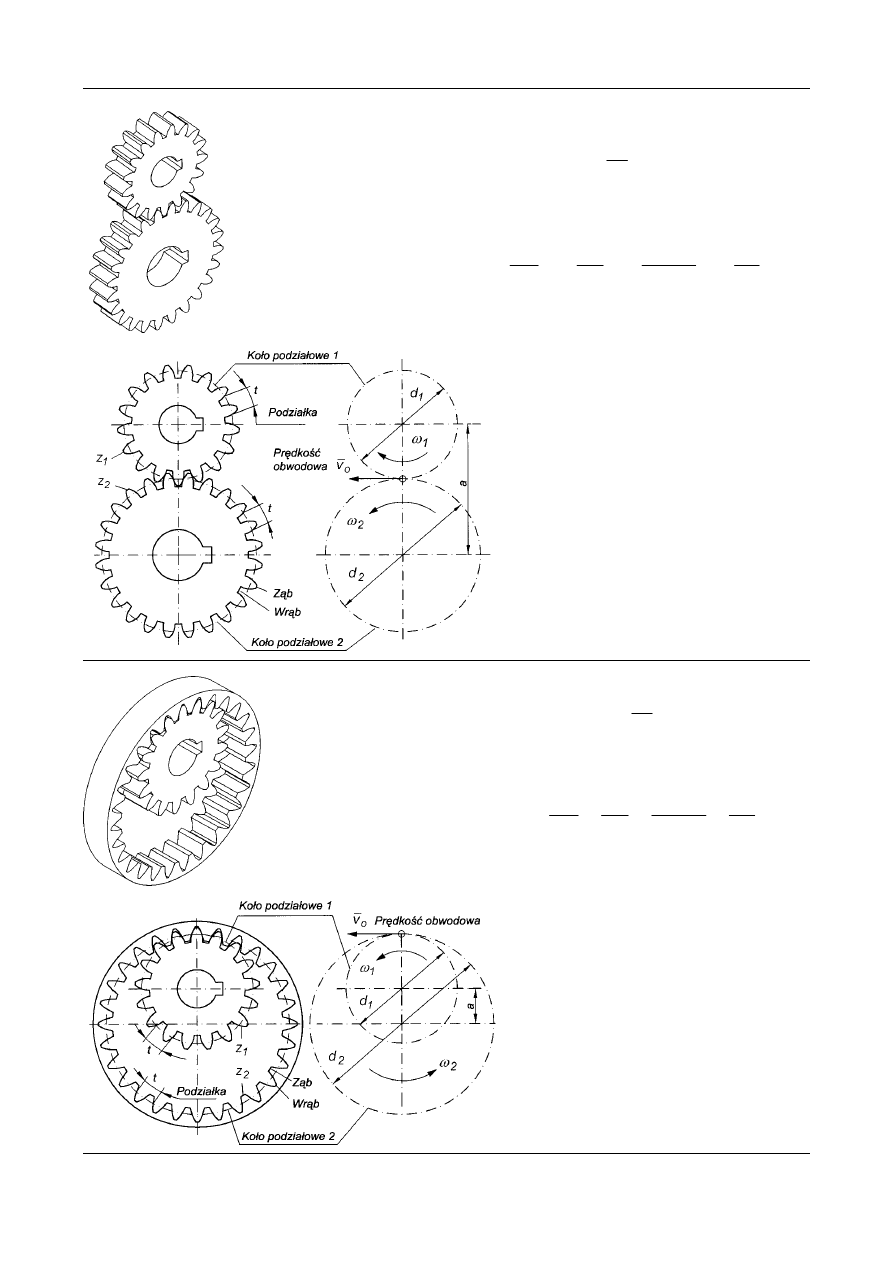
Rys. 1. Zależności geometryczne
i kinematyczne dla przekładni
zębatej o zazębieniu zewnętrznym
Rys. 2. Zależności geometryczne
i kinematyczne dla przekładni zę-
batej o zazębieniu wewnętrznym
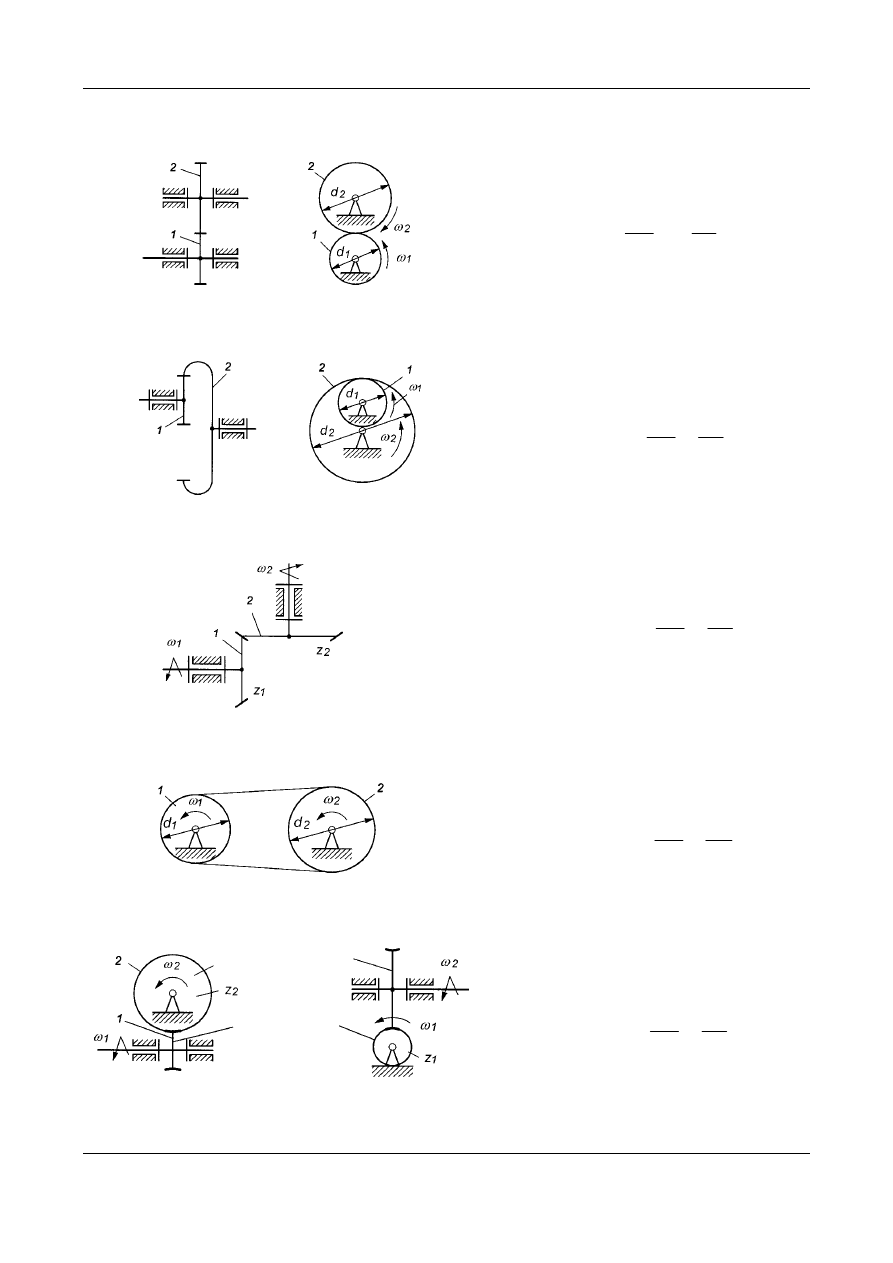
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 4
Opracowali: J. Felis, H. Jaworowski
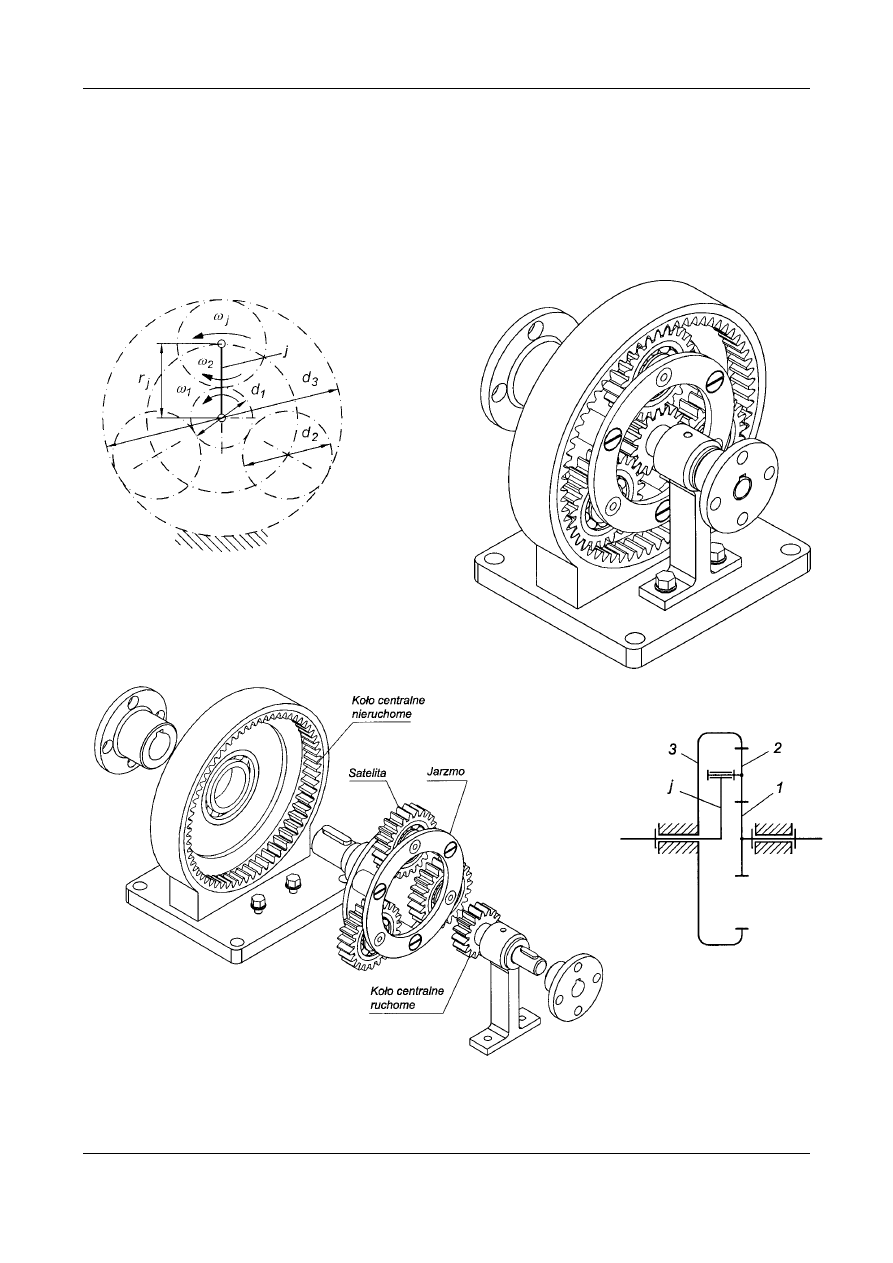
Typowe przekładnie kołowe.
z
z
i
1
2
2
1
12
−
=
=
ω
ω
(12)
Rys. 3. Przekładnia o zazębieniu zewnętrznym
z
z
i
1
2
2
1
12
=
=
ω
ω
(13)
Rys. 4. Przekładnia o zazębieniu wewnętrznym
z
z
i
1
2
2
1
12
=
=
ω
ω
(14)
W tym przypadku nie określa się znaku przeło-
żenia
Rys. 4. Przekładnia stożkowa
d
d
i
1
2
2
1
12
=
=
ω
ω
(15)
Rys. 4. Schemat przekładni cięgnowej, pasowej lub łańcuchowej
ślimacznica
ślimak
z
z
i
1
2
2
1
12
=
=
ω
ω
(16)
gdzie :
1
z
- zwojność ślimaka 1.
Rys. 5. Przekładnia ślimakowa
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 5
Opracowali: J. Felis, H. Jaworowski
PRZEKŁADNIE OBIEGOWE (PLANETARNE)
Przekładnie obiegowe w odróżnieniu od przekładni zwykłych cechują się
tym, że środki niektórych kół zwanych dalej satelitami poruszają się po torach
kołowych wokół osi geometrycznej przekładni z tym, że środki tych torów leżą
w geometrycznej osi przekładni. Koła przekładni, których środki leżą w osi
przekładni nazywane są kołami centralnymi natomiast człon, na którym
osadzone są satelity nazywa się jarzmem.
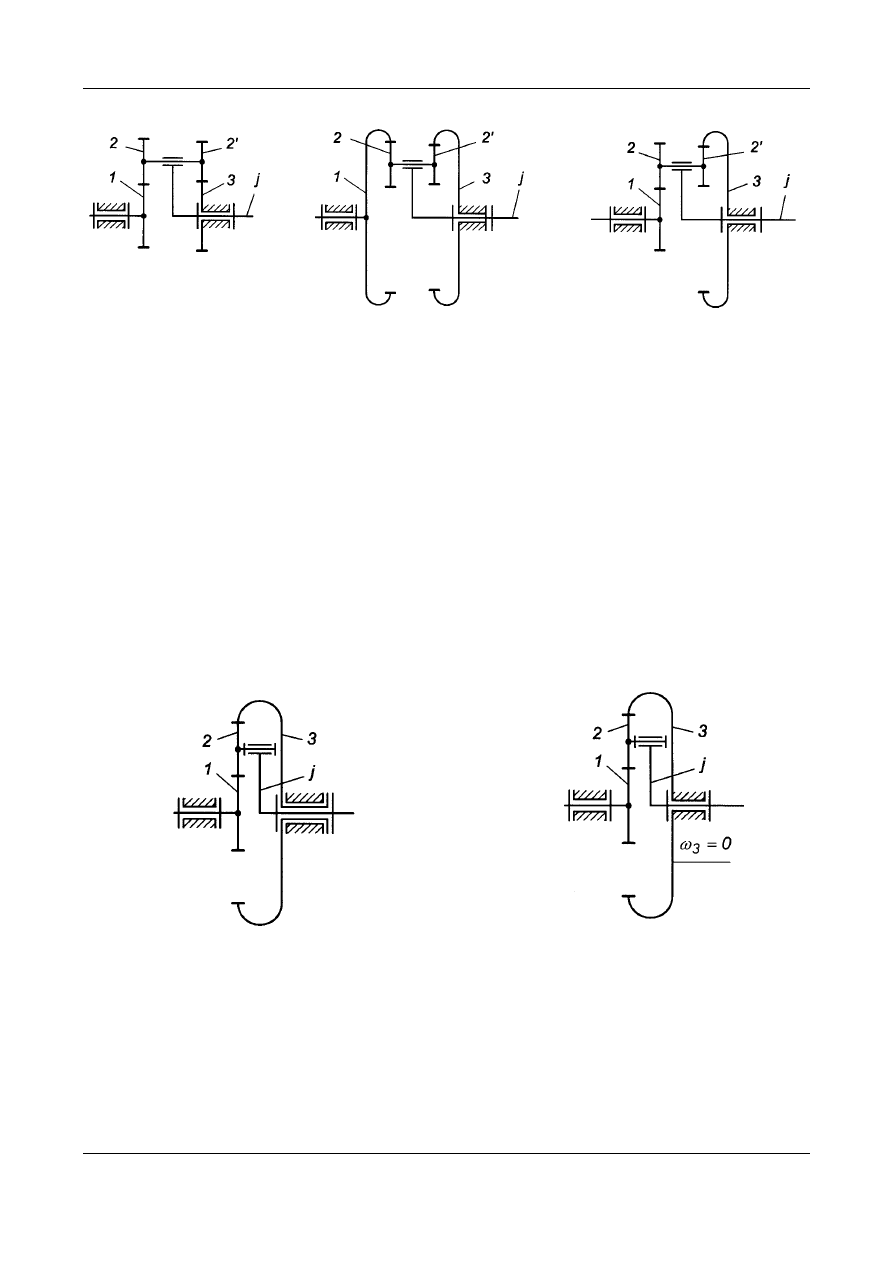
a)
Warunek współosiowości kół
2
1
3
d
2
d
d
+
=
,
2
1
3
z
2
z
z
+
=
b)
c) d)
Rys. 6. Jednorzędowa przekładnia obiegowa:
a) warunek współosiowości, b) i c) schemat konstrukcyjny, d) schemat kinematyczny
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 6
Opracowali: J. Felis, H. Jaworowski
Rys. 7. Warianty przekładni obiegowych dwurzędowych
Analiza kinematyczna przekładni obiegowych
Przekładnie obiegowe mają w ogólnym przypadku dwa stopnie swobody:
w = 2. Jeżeli jednak unieruchomimy względem podstawy jeden z członów np.
koło centralne lub jarzmo, to wówczas przekładnia będzie posiadać jeden
stopień swobody: w = 1. Przy tym należy zauważyć, że przekładnia
z unieruchomionym jarzmem nie jest już przekładnią obiegową.
Przekładnia obiegowa o dwóch stopniach swobody jest nazywana prze-
kładnią różnicową lub dyferencjałem
a) Przekładnia obiegowa o dwóch b) Przekładnia obiegowa o jednym
stopniach swobody stopniu swobody
n = 4 n= 3
p
4
= 2 p
4
= 2
p
5
= 4 p
5
= 3
w= 3n - p
4
- 2p
5
= 12 - 2 - 8 = 2 w= 3n - p
4
- 2p
5
= 9 - 2 - 6 = 1
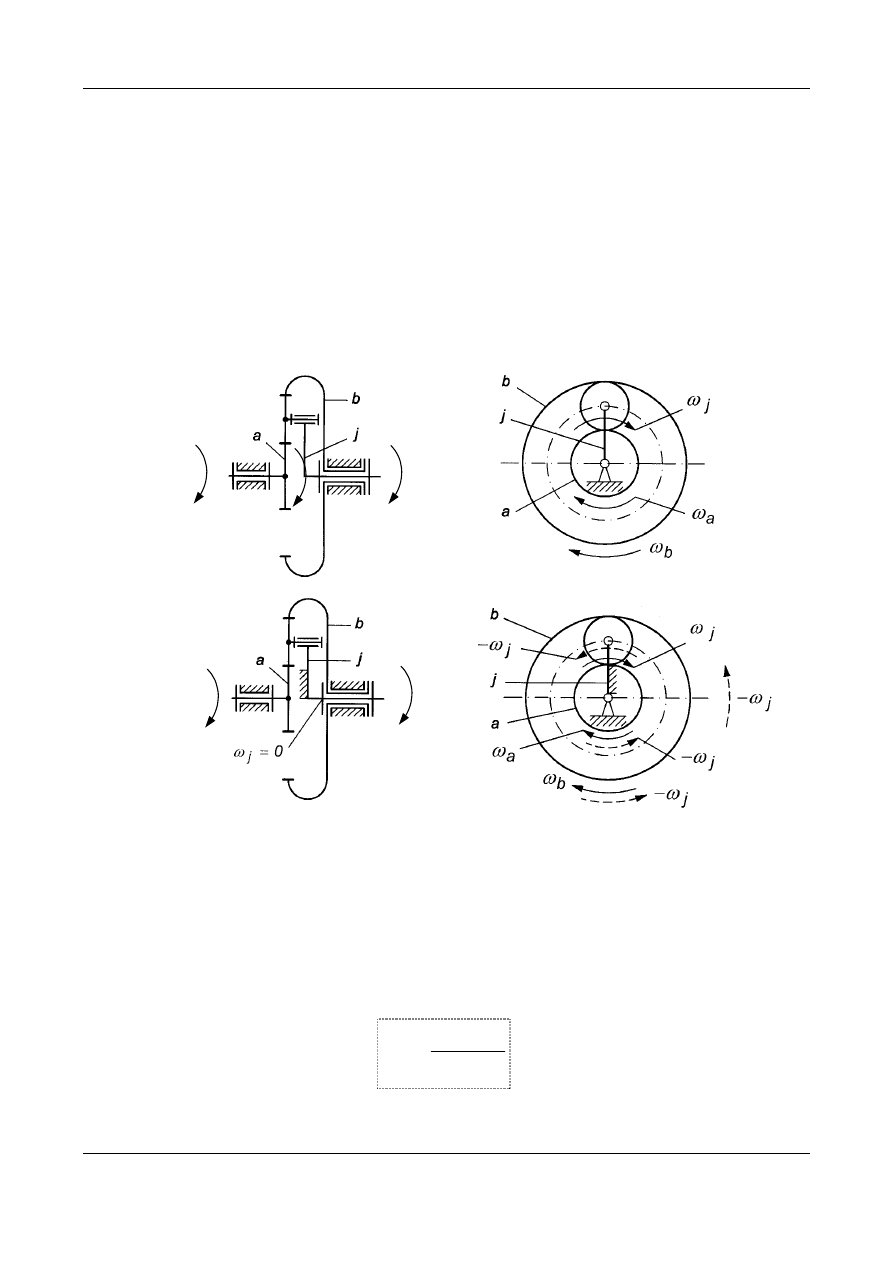
1, 3 - koła centralne, 2 - satelita, j - jarzmo,
Rys. 8. schematy kinematyczne jednorzędowej przekładni obiegowej:
a) przekładnia obiegowa o dwóch stopniach swobody,
b) przekładnia obiegowa o jednym stopniu swobody.
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 7
Opracowali: J. Felis, H. Jaworowski
Symbolami a i b oznaczone zostały tzw. osiowe elementy przekładni obiego-
wej tj. koła centralne, natomiast przez j - oznaczono jarzmo. Na Rys. 9a po-
kazano prędkości kątowe członów ruchomych tj.
a
ω
,
b
ω
i
j
ω
przekładni
obiegowej w przypadku kiedy posiada ona dwa stopnie swobody czyli dwa
człony (np. a i b ) są członami czynnymi.
Przyjmiemy, że cała przekładnia została wprawiona w ruch z prędkością
kątową (
j
ω
−
). W takim przypadku prędkości kątowe kół centralnych a i b
zostaną pomniejszone o wartość (
j
ω
−
), natomiast jarzmo stanie się nieru-
chome
0
j
j
=
−
ω
ω
, (Rys. 9b),
a)
a
ω
j
ω
b
ω
b)
j
b
ω
ω −
Rys. 9. Schematy przekładni obiegowej z zaznaczonymi prędkościami kątowymi:
a) bezwzględne prędkości kątowe członów przekładni o dwóch stopniach swobody tj.
a
ω
,
b
ω
,
j
ω
, b) względne prędkości kątowe członów przekładni po nadaniu całej
przekładni prędkości kątowej (
j
ω
−
) tj.
j
a
ω
ω −
,
j
b
ω
ω
−
,
0
j
j
=
−
ω
ω
.
Przełożenie kierunkowe pomiędzy kołem a i kołem b przekładni przy unie-
ruchomionym w ten sposób jarzmie, zapiszemy w postaci zależności zwanej
wzorem Willisa:
j
b
j
a
j
ab
i
ω
ω
ω
ω
−
−
=
(17)
gdzie:
j
ab
i
- przełożenie kierunkowe od członu a do b przy nieruchomym jarzmie j.
j
a
ω
ω −
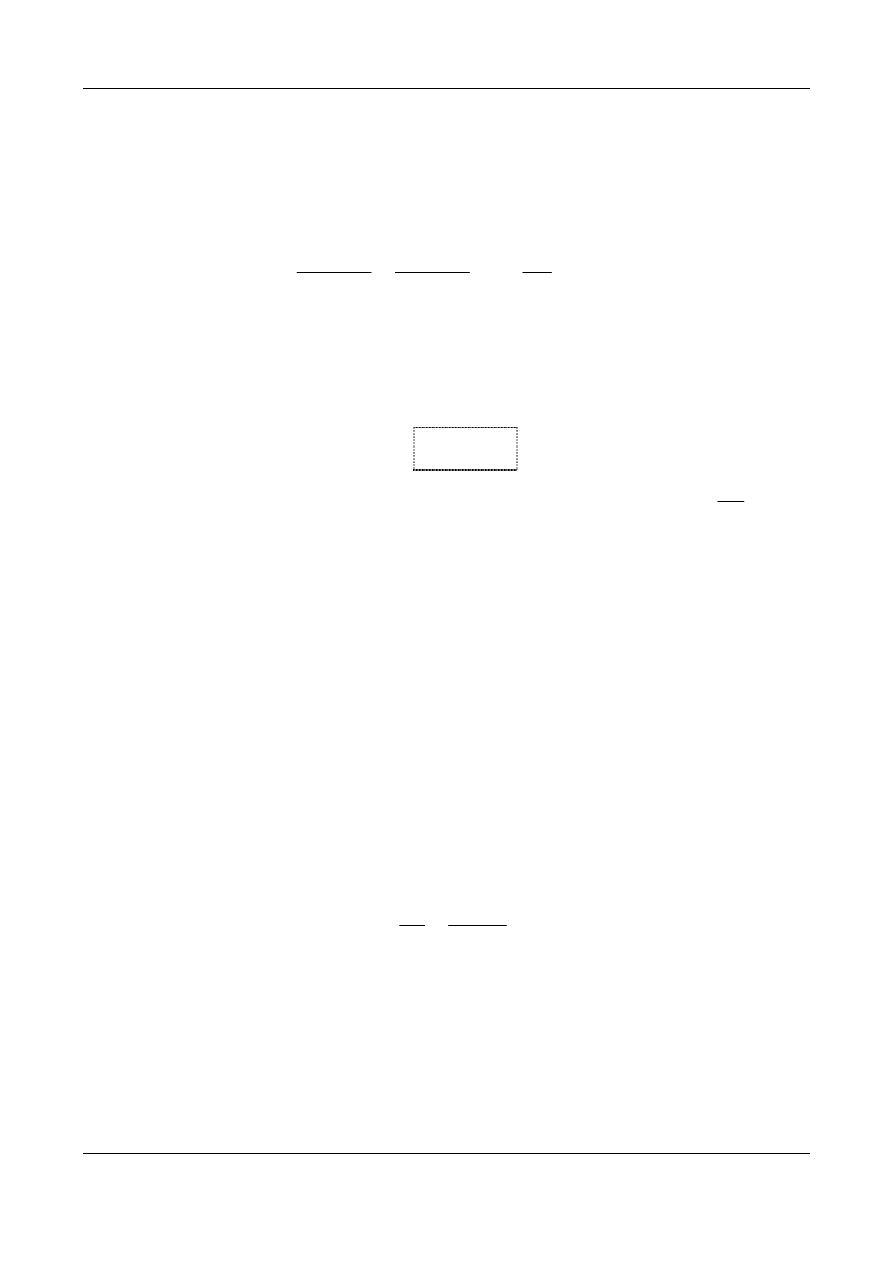
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 8
Opracowali: J. Felis, H. Jaworowski
Jest to podstawowy wzór, z którego można wyliczyć wszystkie możliwe
przełożenia przekładni obiegowej.
Dla przekładni o jednym stopniu swobody, w której koło b jest nieruchome
0
=
b
ω
, natomiast koło a i jarzmo j są członami ruchomymi, wzór Willisa
przyjmie postać:
b
aj
j
a
j
j
a
j
b
j
a
j
ab
i
1
1
0
i
−
=
−
=
−
−
=
−
−
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
(18)
Zauważymy jednak, że w rzeczywistości poszukiwanym przełożeniem
przekładni o jednym stopniu swobody jest przełożenie pomiędzy kołem a i
jarzmem j przy nieruchomym kole b czyli
b
aj
i . Wyznaczymy to przełożenie
przekształcając wzór (18):
j
ab
b
aj
i
1
i
−
=
(19)
W ten sposób przełożenie przekładni o osiach ruchomych
j
a
b
aj
i
ω
ω
=
udało
się wyrazić za pomocą prostego wzoru, w którym występuje przełożenie
j
ab
i
.
Przełożenie
j
ab
i
to bardzo łatwo wyznaczyć ponieważ dotyczy przekładni
zwykłej szeregowej lub równoległej o osiach nieruchomych, powstałej po-
przez myślowe unieruchomienie jarzma oraz myślowe uruchomienie ko-
ła w rzeczywistości nieruchomego.
W analogiczny sposób można wyznaczyć przełożenie kierunkowe prze-
kładni w przypadku kiedy koło a jest kołem nieruchomym (
0
a
=
ω
), natomiast
koło b i jarzmo są członami ruchomymi.
j
ba
a
bj
i
1
i
−
=
(20)
Jak zauważymy we wzorach (19) i (20) następuje zamiana wskaźników a,
b oraz j. Sposób zamiany wskaźników podaje wzór:
j
ab
b
aj
b
ja
i
1
1
i
1
i
−
=
=
(21)
gdzie:
b
ja
i - przełożenie przekładni obiegowej (jarzmo j ruchome, indeks j u
dołu),
j
ab
i - przełożenie przekładni z myślowo unieruchomionym jarzmem j (indeks j
u góry).
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 9
Opracowali: J. Felis, H. Jaworowski
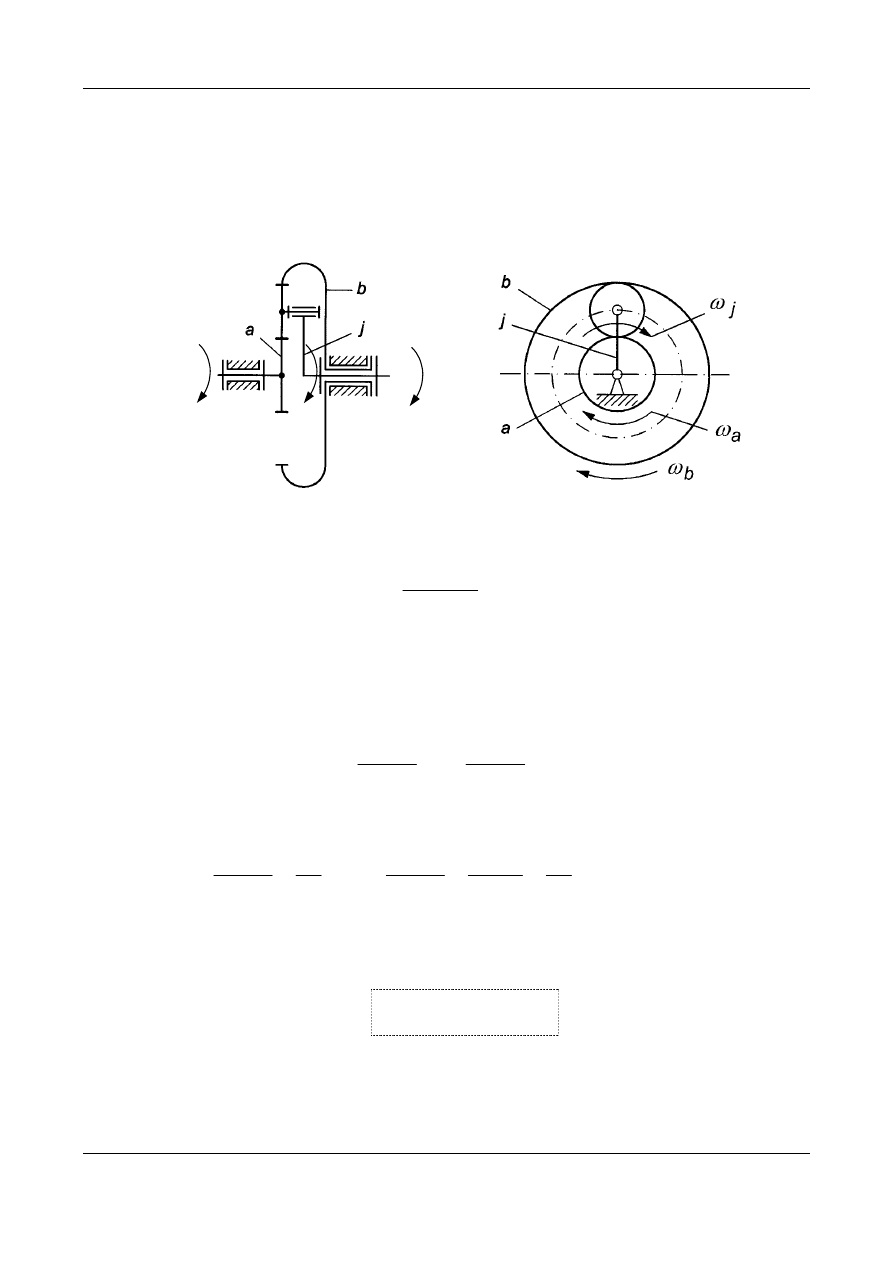
Dla przekładni o dwóch stopniach swobody ( Rys. 10), w której dwa człony są
członami napędzającymi np. koła a i b natomiast jarzmo j jest członem
biernym, wyznaczymy wpływ prędkości
a
ω
i
b
ω
na prędkość
j
ω
korzystając
ze wzoru Willisa:
a
ω
j
ω
b
ω
Rys. 10. Przekładnia o dwóch stopniach swobody
j
b
j
a
j
ab
i
ω
ω
ω
ω
−
−
=
(22)
(
)
j
a
j
ab
j
b
i
ω
ω
ω
ω
−
=
⋅
−
(23)
b
j
ab
j
ab
a
j
ab
j
i
1
i
i
1
1
ω
ω
ω
−
−
−
=
(24)
ponieważ zachodzą związki:
a
jb
b
ja
b
aj
b
aj
b
aj
j
ab
j
ab
b
ja
b
aj
j
ab
i
1
i
1
i
1
i
i
1
i
1
i
,
i
i
1
i
1
1
−
=
−
=
−
=
−
=
−
=
=
−
(25)
to ostatecznie możemy zapisać:
b
a
jb
a
b
ja
j
i
i
ω
ω
ω
+
=
(26)
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 10
Opracowali: J. Felis, H. Jaworowski
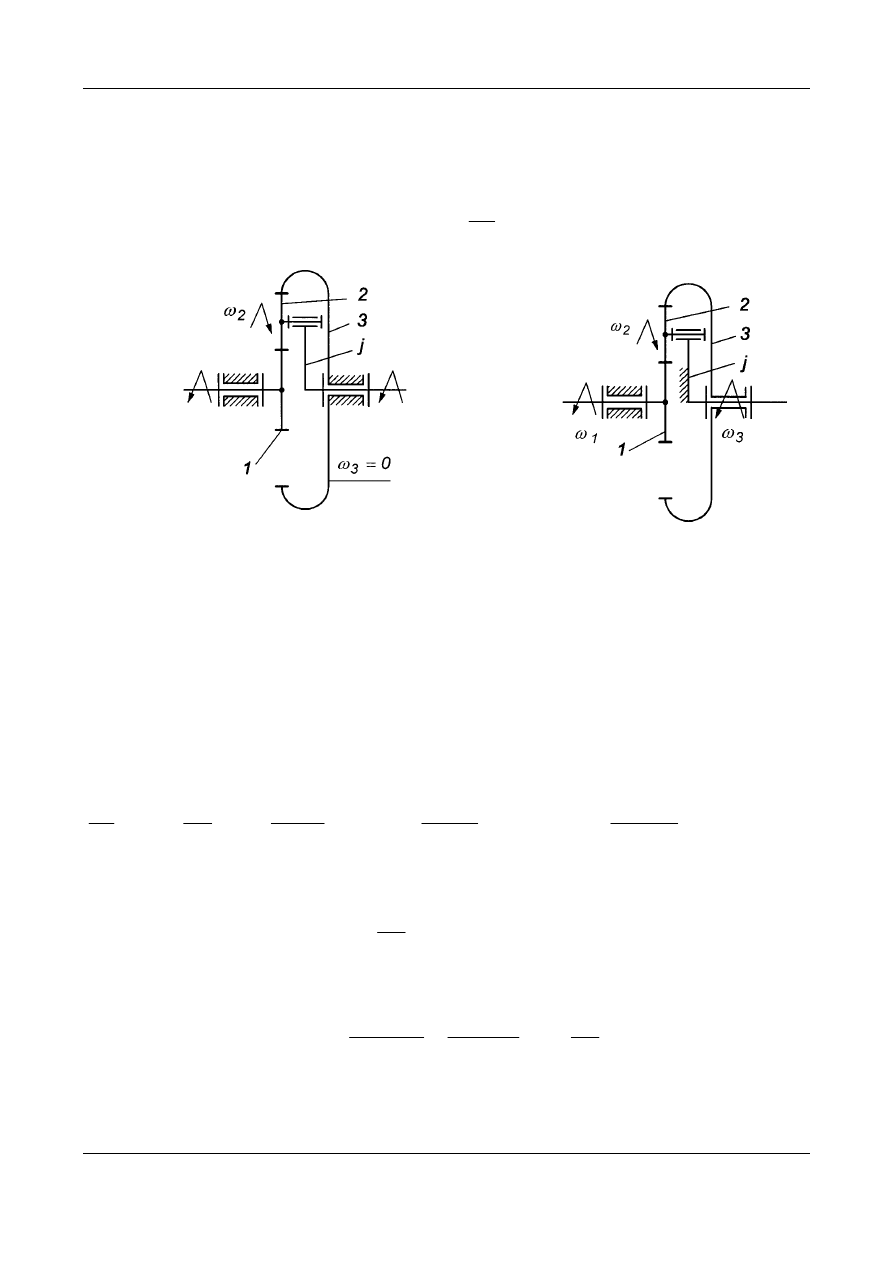
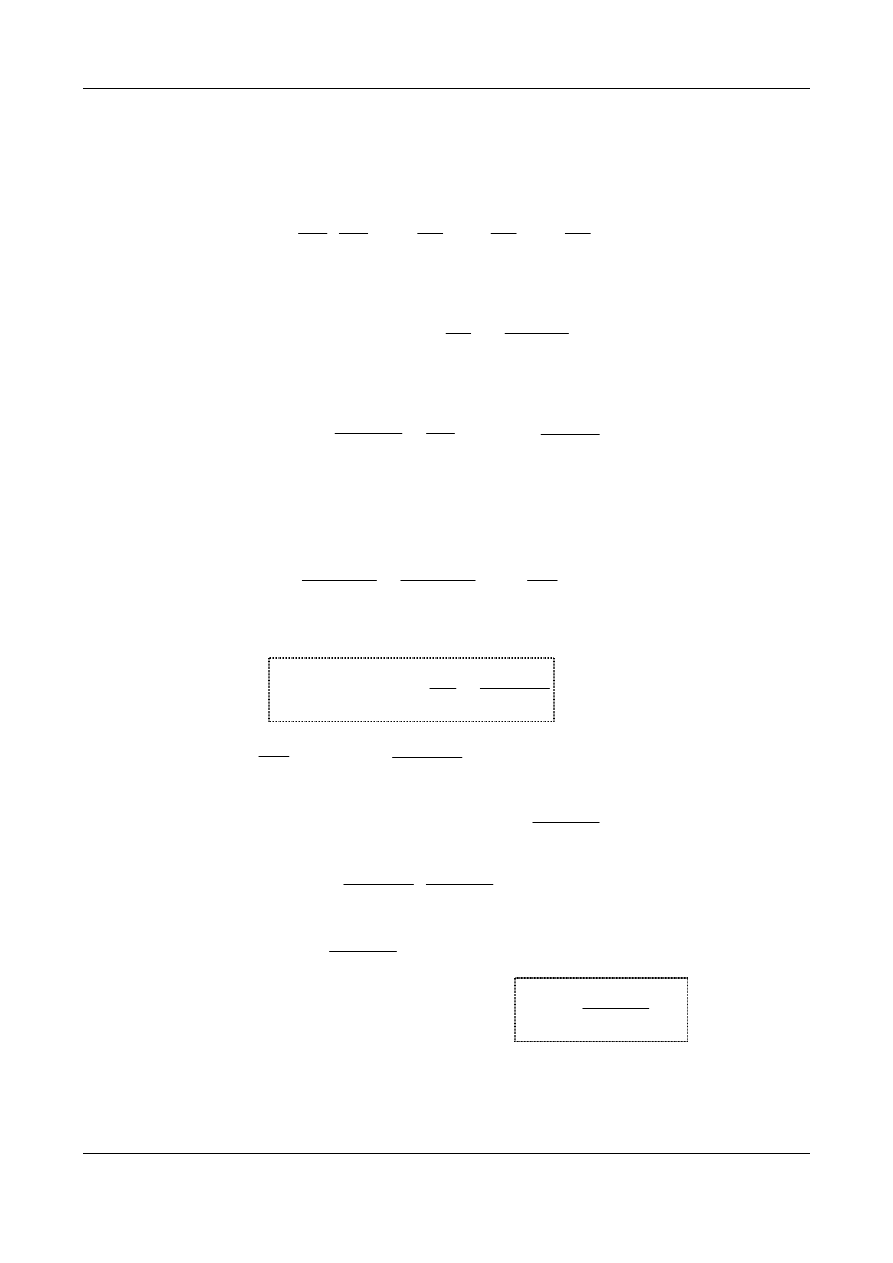
Przykład 1. Analiza kinematyczna jednorzędowej przekładni obiegowej
Schemat przekładni pokazano na Rys. 11.
Dane:
0
,
z
,
z
,
3
3
1
1
=
ω
ω
, ponieważ koło 3 jest członem nieruchomym.
Szukane: przełożenie przekładni
j
1
3
j
1
i
ω
ω
=
oraz
j
ω
,
2
ω
.
a) b)
we
1
ω
ω =
wy
j
ω
ω =
Rys. 11. Przekładnia obiegowa jednorzędowa o jednym stopniu swobody
a) schemat kinematyczny przekładni o ruchomym jarzmie,
b) schemat kinematyczny przekładni z unieruchomionym jarzmem
Liczby zębów koła 2 nie podano, gdyż wynika ona z tzw. warunku współo-
siowości przekładni. Warunek ten określa związek geometryczny pomiędzy
średnicami kół zębatych przekładni, które leżą w rozważanym przypadku
w jednej płaszczyźnie, mają wspólny moduł a ponadto dwa z nich mają
wspólną oś obrotu.
Dla rozważanej przekładni obiegowej warunek współosiowości można za-
pisać:
2
d
d
2
d
3
2
1
=
+
;
2
z
m
z
m
2
z
m
3
2
1
⋅
=
⋅
+
⋅
czyli:
2
z
z
z
1
3
2
−
=
(P1.1)
Przełożenie przekładni
j
1
3
j
1
i
ω
ω
=
wyznaczymy korzystając ze wzoru Willisa
przyjmując
0
3
=
ω
3
j
1
j
1
j
j
1
j
3
j
1
j
13
i
1
1
0
i
−
=
−
=
−
−
=
−
−
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
Po przekształceniu otrzymamy:
j
13
3
j
1
i
1
i
−
=
(P1.2)
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 11
Opracowali: J. Felis, H. Jaworowski
Przełożenie
j
13
i
przekładni z myślowo unieruchomionym jarzmem z Rys.
11b wyznaczymy z prostych związków obowiązujących dla przekładni szere-
gowej o osiach nieruchomych.
1
3
2
3
1
2
3
2
2
1
j
13
z
z
z
z
z
z
i
−
=
+
⋅
−
=
⋅
=
ω
ω
ω
ω
(P1.3)
Ostatecznie przełożenie przekładni obiegowej wyniesie:
1
3
1
1
3
j
13
3
j
1
z
z
z
z
z
1
i
1
i
+
=
−
−
=
−
=
(P1.4)
Poszukiwaną prędkość
kątową
ω
j
wyznaczamy z prostego
przekształcenia:
j
1
1
3
1
3
j
1
z
z
z
i
ω
ω
=
+
=
;
1
3
1
1
j
z
z
z
ω
ω
+
=
(P1.5)
W celu obliczenia prędkości kątowej satelity również wykorzystamy związki
wynikające ze wzoru Willisa:
3
j
2
j
2
j
j
2
j
3
j
2
j
23
i
1
1
0
i
−
=
−
=
−
−
=
−
−
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
(P1.6)
2
3
2
2
3
j
23
3
j
2
z
z
z
z
z
1
i
1
i
−
=
−
=
−
=
(P1.7)
Ponieważ
j
2
3
j
2
i
ω
ω
=
to
j
2
3
2
2
z
z
z
ω
ω
⋅
−
=
. Po podstawieniu uprzednio wy-
prowadzonego wzoru na prędkość jarzma
1
3
1
1
j
z
z
z
ω
ω
⋅
+
=
otrzymamy:
1
3
1
1
2
3
2
2
z
z
z
z
z
z
ω
ω
⋅
+
⋅
−
=
(P1.8)
Po podstawieniu
2
z
z
z
1
3
2
−
=
i prostych przekształceniach ostatecznie
otrzymamy wzór na prędkość kątową satelity:
1
1
3
1
2
z
z
z
ω
ω
⋅
−
−
=
.
Znak (-) w powyższym wzorze oznacza, że zwrot prędkości kątowej
satelity 2 jest przeciwny do zwrotu koła napędzającego 1.
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 12
Opracowali: J. Felis, H. Jaworowski
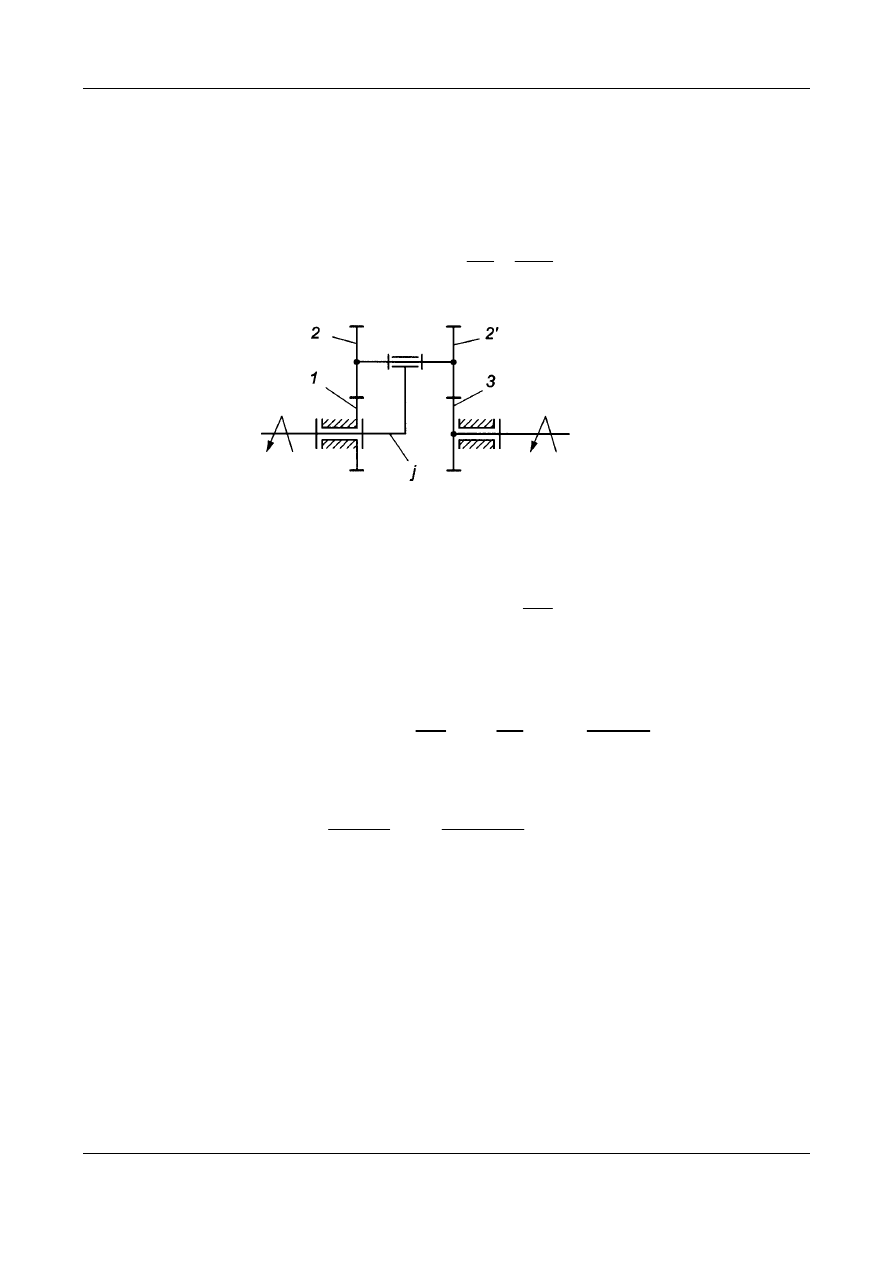
Przykład 2. Analiza kinematyczna dwurzędowej przekładni obiegowej
Dwurzędową przekładnię obiegową Pecquera przedstawia Rys. 12.
Dane:
we
j
ω
ω =
(jarzmo jest członem napędzającym - wejściowym),
99
z
1
=
,
100
z
2
=
,
101
'
z
2
=
,
100
z
3
=
Obliczyć przełożenie przekładni:
wy
we
3
j
1
3
j
i
ω
ω
ω
ω
=
=
gdzie koło 3 jest członem
wyjściowym przekładni)
we
j
ω
ω =
wy
ω
ω =
3
Rys. 12. Schemat kinematyczny przekładni dwurzędowej Pecquera
Przełożenie przekładni można zapisać
1
j
3
1
3
j
i
1
i
=
Wykorzystamy wzór na przełożenie przekładni o jednym stopniu swobody
3
2
2
1
2
1
3
2
j
31
1
j
3
z
z
'
z
z
1
z
z
z
'
z
1
i
1
i
⋅
⋅
−
=
−
⋅
−
−
=
−
=
(P2.1)
Po podstawieniu wartości liczbowych otrzymamy:
4
3
2
2
1
1
j
3
10
100
100
101
99
1
z
z
'
z
z
1
i
−
=
⋅
⋅
−
=
⋅
⋅
−
=
(P2.2)
Ostatecznie przełożenie analizowanej przekładni wynosi:
4
1
3
j
10
i
=
.
Przekładnia redukuje prędkość kątową 10000 razy.
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 13
Opracowali: J. Felis, H. Jaworowski
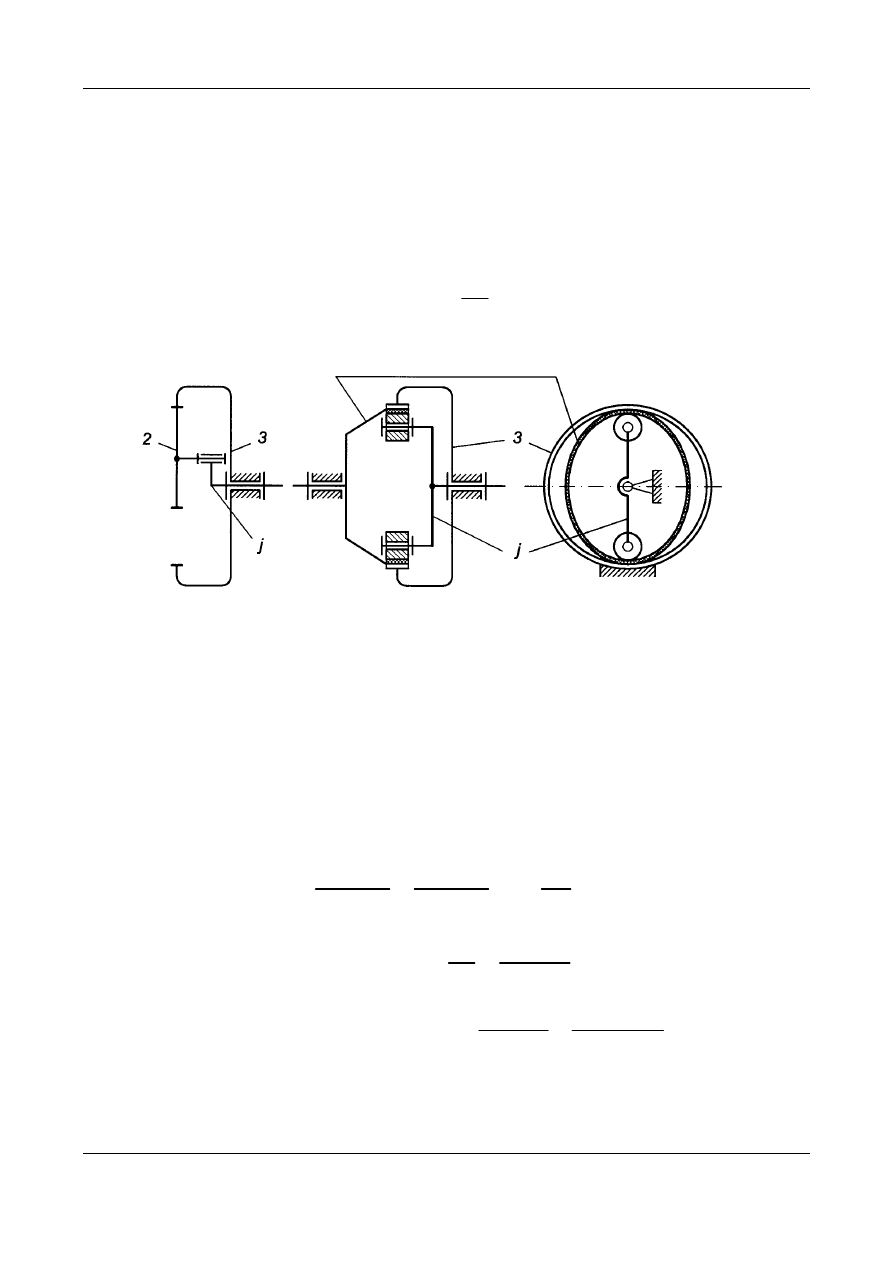
Przykład 3. Analiza kinematyczna przekładni falowej
Przekładnię falową pokazano na Rys. 13.
Dane:
100
z
2
=
,
102
z
3
=
, członem napędzającym jest jarzmo j,
członem wyjściowym elastyczny pierścień zębaty 2 (w zwykłej przekładni
obiegowej jest to satelita, Rys. 13a),
Obliczyć przełożenie przekładni:
2
j
1
2
j
i
ω
ω
=
.
Elastyczny pierścień zębaty 2
a) b)
Rys. 13. Schemat obliczeniowy i schemat kinematyczny przekładni falowej:
a) schemat obliczeniowy przekładni falowej,
b) schemat kinematyczny przekładni falowej
Przełożenie przekładni obliczamy podobnie jak przełożenie
j
23
i
w Przykładzie 1 korzystając ze wzoru Willisa. W obliczeniach posługujemy się
schematem obliczeniowym (Rys. 13a).
3
j
2
j
2
j
j
2
j
3
j
2
j
23
i
1
1
0
i
−
=
−
=
−
−
=
−
−
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
(P3.1)
2
3
2
2
3
j
23
3
j
2
z
z
z
z
z
1
i
1
i
−
=
−
=
−
=
(P3.2)
Poszukiwane przełożenie wynosi:
50
102
100
100
z
z
z
i
3
2
2
3
2
j
−
=
−
=
−
=
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 14
Opracowali: J. Felis, H. Jaworowski
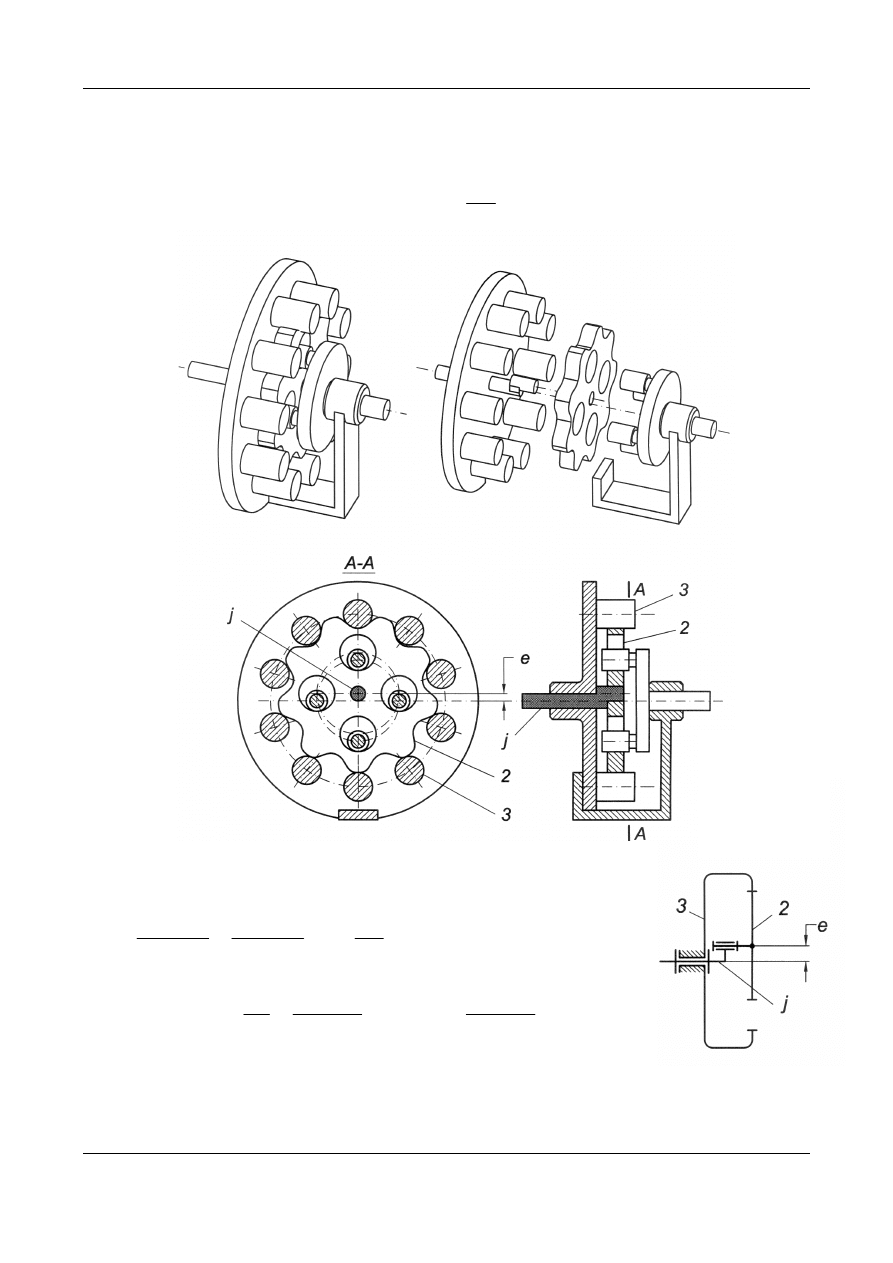
Przykład 4. Przekładnia kształtowo-toczna (cykloidalna)
Dane:
3
z - liczba palców koła 3,
2
z
- liczba zębów cykloidalnych satelity 2.
Obliczyć przełożenie przekładni:
2
j
3
2
j
i
ω
ω
=
.
0
3
=
ω
Przełożenie:
3
j
2
j
2
j
j
2
j
3
j
2
j
23
i
1
1
0
i
−
=
−
=
−
−
=
−
−
=
ω
ω
ω
ω
ω
ω
ω
ω
ω
(P4.1)
2
3
2
3
2
j
2
3
2
2
3
j
23
3
j
2
z
z
z
i
;
z
z
z
z
z
1
i
1
i
−
−
=
−
=
−
=
−
=
(P4.2)
Rys. 14. Schematy konstrukcyjny i kinematyczny przekładni kształtowo-tocznej
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 15
Opracowali: J. Felis, H. Jaworowski
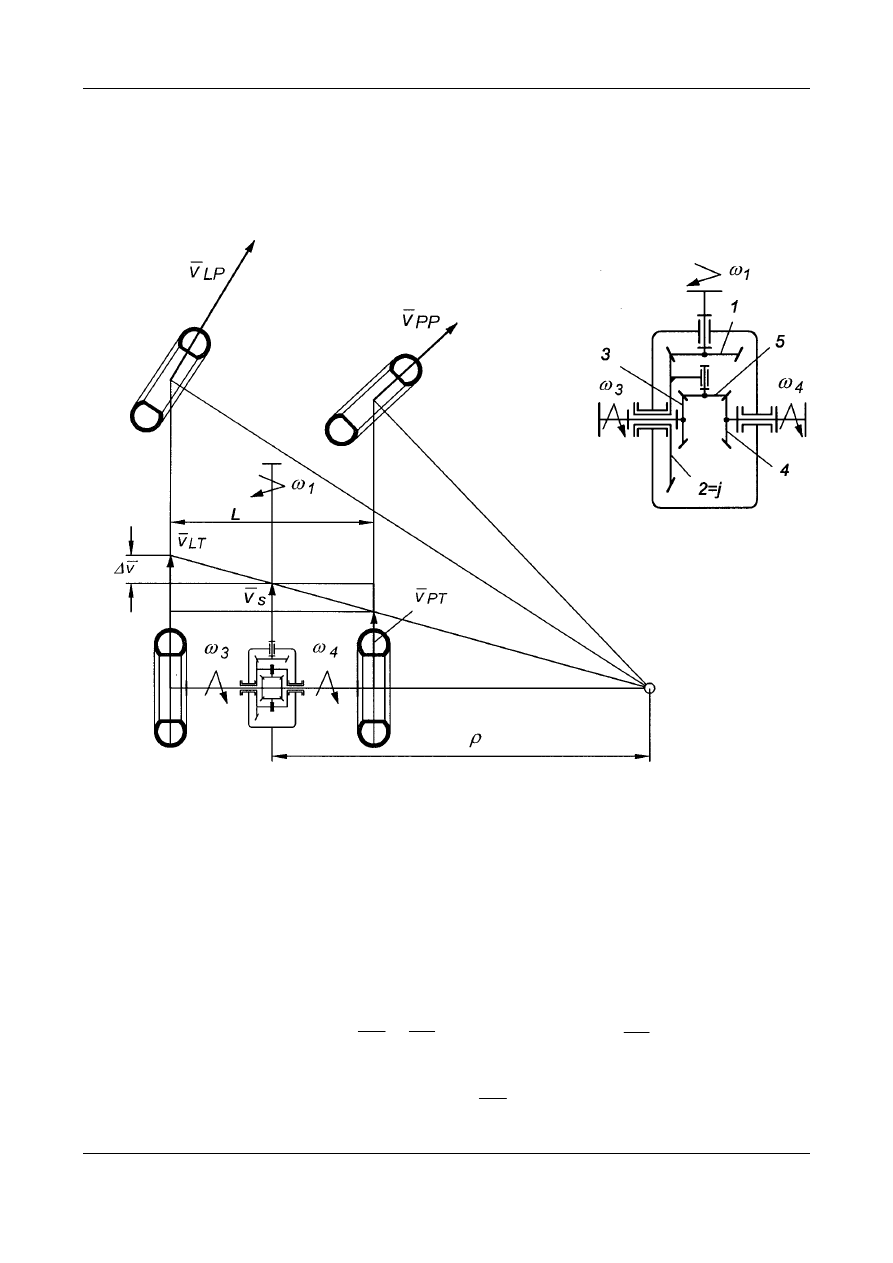
Przykład 5. Analiza kinematyczna stożkowej przekładni różnicowej.
Przekładnia różnicowa w pojazdach samochodowych ma za zadanie do-
stosować prędkość kątową kół napędowych (przednich lub tylnych) w taki
sposób, aby uniknąć zjawiska poślizgu na łukach drogi.
n = 5,
p
4
=3,
p
5
=5,
w = 2
Rys. 15. Zastosowanie przekładni obiegowej różnicowej do napędu kół pojazdu samocho-
dowego. Zasada poruszania się pojazdu po łuku drogi
Jeżeli samochód porusza się po prostej drodze, prędkości kątowe kół jezd-
nych są równe
4
3
ω
ω =
. Koło stożkowe 5 nie obraca się względem własnej
osi. Wówczas prędkość kątowa kół jezdnych wynika wyłącznie
z przełożenia przekładni stożkowej (1, 2). Ponieważ koło 2 jest zarazem
jarzmem j przekładni to możemy napisać:
1
2
j
1
12
j
1
z
z
i
i
=
=
=
ω
ω
oraz
2
1
1
j
z
z
ω
ω
=
(P5.1)
Samochód uzyskuje prędkość:
2
d
v
k
j
s
ω
=
, gdzie
k
d - średnica koła jezd-
nego. W ten sposób realizowany jest jeden stopień swobody.
Teoria maszyn i mechanizmów Kinematyka mechanizmów. Przekładnie kołowe 16
Opracowali: J. Felis, H. Jaworowski
Na łukach drogi prędkości liniowe kół jezdnych różnią się od siebie o
v
2
∆
,
oraz o v
∆
od prędkości środka tylnego mostu przy czym wartość v
∆
zależy
od promienia łuku i rozstawu kół. (Rys. 15).
ρ
∆
⋅
⋅
=
2
L
v
v
s
(P5.2)
gdzie L - rozstaw kół jezdnych,
ρ
- promień łuku drogi
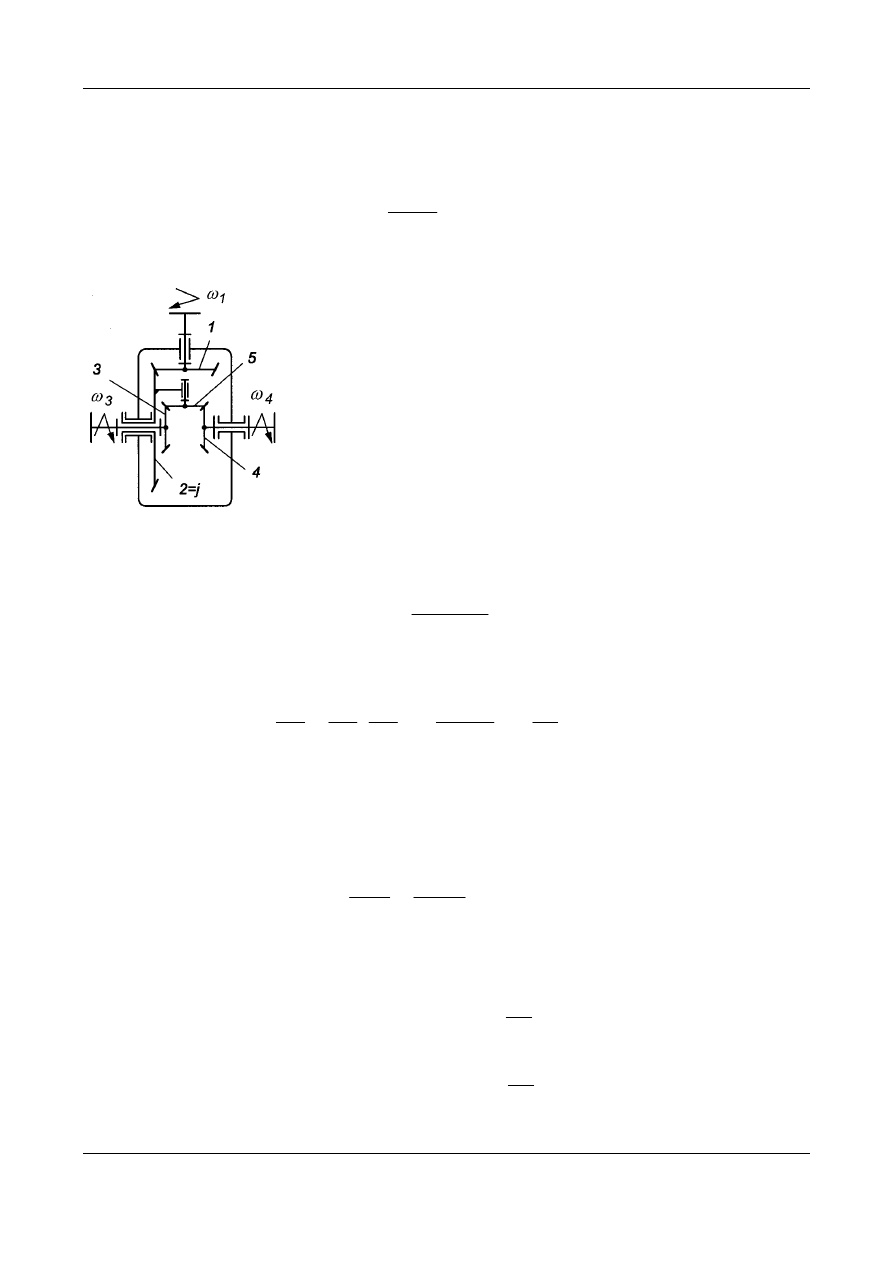
Rys. 16. Schemat przekładni różnicowej
bez członów kinematycznie zbędnych
Zróżnicowanie prędkości kół umożliwia przekładnia stożkowa złożona z kół
3, 4 i 5, której przełożenie wynosi:
2
3
2
4
j
43
i
ω
ω
ω
ω
−
−
=
(P5.3)
Zgodnie z wzorem Willisa
0
2
=
ω
. Zatem
1
z
z
z
z
z
z
4
3
5
4
3
5
3
5
5
4
3
4
−
=
−
=
⋅
⋅
−
=
⋅
=
ω
ω
ω
ω
ω
ω
(P5.4)
Ponieważ przełożenie pomiędzy kołami napędowymi wynosi dokładnie
i = – 1 to oznacza, że na łuku drogi koła 3 i 4 będą napędzane od drogi i gdy
prędkość kątowa jednego z kół wzrośnie o
ω
∆
to drugiego zmniejszy się o
ω
∆
.
k
s
k
d
L
v
d
v
2
⋅
⋅
=
=
ρ
∆
ω
∆
(P5.5)
W ten sposób realizowany jest drugi stopień swobody. Prędkość kątowa
tylnych kół napędowych wyniesie odpowiednio:
lewego
ω
∆
ω
ω
∆
ω
ω
ω
+
=
+
=
=
2
1
1
j
3
LT
z
z
(P5.6)
prawego
ω
∆
ω
ω
∆
ω
ω
ω
−
=
−
=
=
2
1
1
j
4
PT
z
z
(P5.7)