CAŁKA PODWÓJNA

1. Określić obszar normalny ograniczony liniami:
a)

x

y

,

x

y

,

x

2

1

0

2

1

b)

5

1

3

2

3

1

x

,

x

,

x

y

,

x

y

c)

x

y

,

x

y

,

x

2

1

2

2

2

1

d)

x

y

,

x

y

,

y

2

2

2

0

3

2

e)

2

2

2

0

2

1

x

y

,

x

y

,

y

2. Obliczyć całki
a)

D

xydxdy

y

x

)

(

, gdzie D jest ograniczony liniami:

b

y

y

a

x

x

,

0

,

,

0

, gdzie

0

b

,

a

.

b)

D

dxdy

x

y

, gdzie D jest ograniczony liniami:

6

,

2

,

,

1

3

y

y

e

x

x

.

c)

D

dxdy

y

x

)

cos(

, gdzie D jest ograniczony liniami:

2

,

0

,

,

0

y

y

x

x

d)

D

dxdy

y

x

2

10

1

,

gdzie D jest ograniczony liniami:

3

0

0

2

x

,

x

,

y

,

x

y

.

e)

D

dxdy

y

x

)

1

2

(

,

gdzie D jest wnętrzem trójkąta o wierzchołkach

)

,

(

C

),

,

(

B

),

,

(

A

5

5

3

5

1

1

.

f)

D

dxdy

y

x

)

2

(

, gdzie D jest ograniczony liniami:

1

,

,

2

1

y

x

y

x

y

.

g)

D

dxdy

x

)

1

(

2

, gdzie D jest ograniczony liniami::

1

,

,

2

1

2

1

y

x

y

x

y

h)

D

dxdy

y

x

)

1

(

2

,

gdzie D jest ograniczony liniami:

y

,

x

y

1

2

.

i)

D

dxdy

y

x

2

2

1

,

gdzie D jest wnętrzem okręgu o równaniu

y

x

1

2

2

.

j)

D

dxdy

xy

2

, gdzie

}

0

,

2

1

:

)

,

{(

2

2

x

y

x

y

x

D

.

k)

D

xdxdy

,

gdzie

}

0

0

,

1

:

)

,

{(

2

2

4

1

, y

x

y

x

y

x

D

.

l)

D

dxdy

y

x

sin

2

2

,

gdzie

}

2

:

{

2

2

y

x

(x,y)

D

.

3. Zamienić kolejność całkowania w całce iteracyjnej.

a)

2

0

0

)

,

(

x

dy

y

x

f

dx

b)

1

1

2

2

1

)

,

(

x

dy

y

x

f

dx

c)

2

4

3

1

)

,

(

y

dx

y

x

f

dy

d)

2

0

0

4

2

)

,

(

x

dx

y

x

f

dy

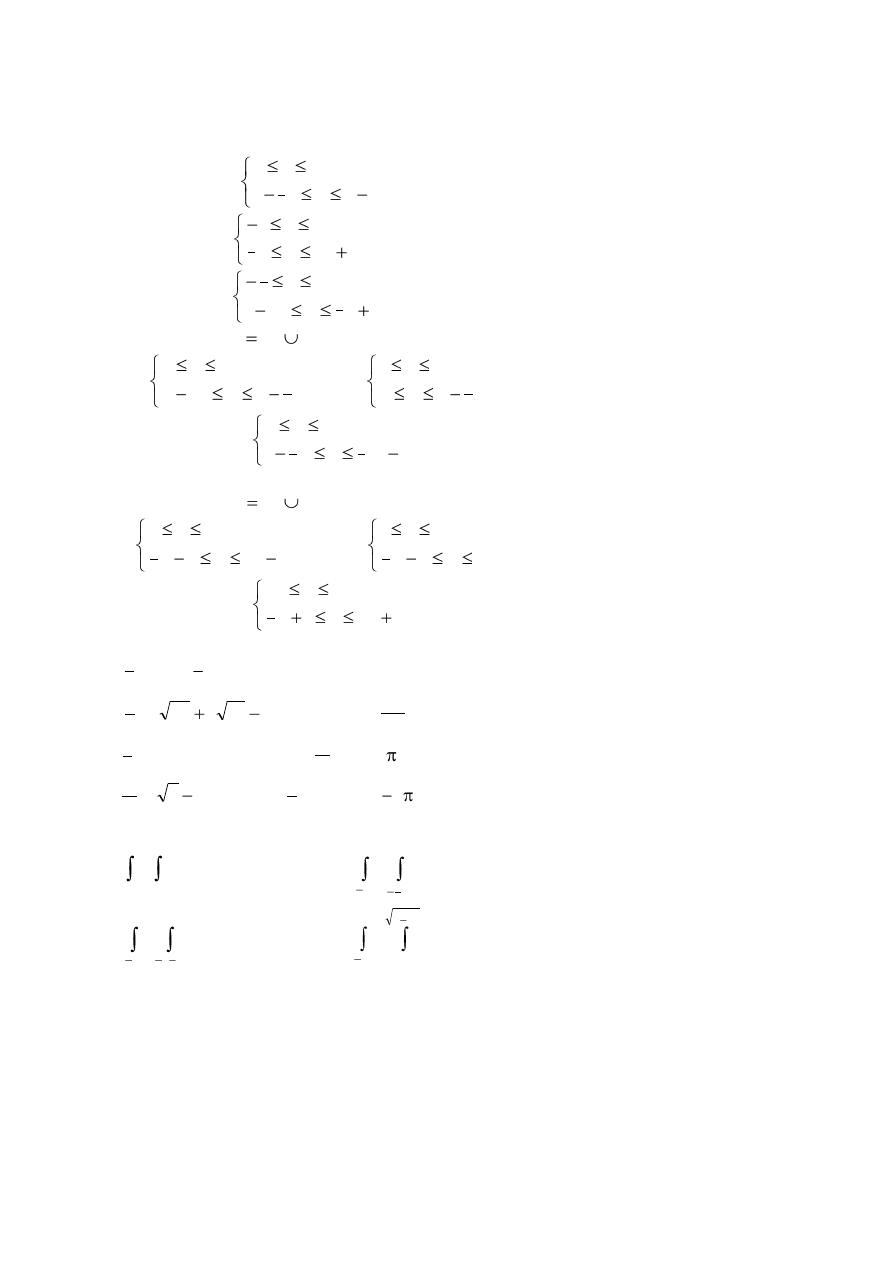
Odpowiedzi.

1 a) względem Ox:

x

y

x

x

2

1

2

0

2

1

b) względem Ox:

3

2

5

1

3

1

x

y

x

x

c) względem Ox:

2

2

1

2

2

1

5

2

x

y

x

x

d) względem Ox:

2

1

D

D

D

x

y

x

x

D

3

2

1

2

2

2

1

0

:

x

y

x

D

3

2

2

2

0

3

1

:

względem Oy:

)

y

(

x

y

y

0

:

E

2

1

2

1

2

2

3

e) względem Ox:

2

1

D

D

D

2

2

2

1

0

:

2

1

1

x

y

x

x

D

0

2

4

1

:

2

1

2

y

x

x

D

względem Oy:

4

2

1

0

y

x

y

y

2

-

:

E

2

1

2 a)

)

b

a

(

b

a

2

2

6

1

b) 48

c) -2

d)

)

64

10

5

22

11

(

3

2

e)

3

136

f)

3

4

g) 4

h)

5

12

i)

2

j)

)

(

1

2

4

15

2

k)

3

4

l )

2

3

3 a)

2

0

2

)

,

(

y

dx

y

x

f

dy

b)

1

2

1

2

1

)

,

(

y

dx

y

x

f

dy

c)

3

3

2

1

)

,

(

x

dy

y

x

f

dx

d)

0

2

4

0

2

)

,

(

x

dy

y

x

f

dx