
180%=TT
RACHUNEK CAŁKOWY FUNKCJI WIELU ZMIENNYCH.
CAŁKA PODWÓJNA.
Def.
Rozważmy w przestrzeni euklidesowej R
3
bryłę V ograniczoną
od góry powierzchnią S: z = f(x,y), z boków powierzchnią walcową
o tworzących równoległych do osi OZ i z dołu obszarem płaskim
D
na płaszczyźnie OXY.
.................................................................................................................................
Niech domknięty obszar
daje się opisać w sposób następujący:
D ⊂ R2
D = (x, y) ∈ R2 : a ≤ x ≤ b , ϕ(x) ≤ y ≤ ψ(x), ϕ, ψ ∈ C0([a, b]; R)
oraz
ϕ(x) < y < ψ(x) dla x ∈ (a, b)
Obszar taki nazywać będziemy obszarem normalnym względem osi OX.
.................................................................................................................................
Obszar domknięty będący sumą skończonej ilości obszarów normalnych
D
(względem osi OX lub OY ), które nie mają wspólnych punktów
wewnętrznych , nazywamy obszarem regularnym w przestrzeni R
2
.
.................................................................................................................................
Analogicznie okreslamy obszar
normalny względem osi OY.
D
⊂ R2
....................................................................................
Niech domknięty obszar daje się opisać w sposób następujący:
D
= (x, y) ∈ R2 : c ≤ x ≤ d ,
g
(y) ≤ x ≤ h(y),
g, h
∈ C0([c, d]; R)
oraz
g
(y) < x < h(y)
dla
y
∈ (c, d)
.................................................................................................................................
1

Def.
Niech
będzie funkcją określoną i ograniczoną w regularnym obszarze
f
(x, y)
domkniętym D.
.....................
Obszar D dzielimy na n obszarów oznaczonych D
1
,...D
n
o polach odpowiednio
.
∆p1, ...∆pn
Podział ten oznaczmy symbolicznie przez
.
∆n
.....................
Dla ustalonego podziału niech d
i
oznacza średnicę zbioru D
i
.
Średnicą podziału
nazywamy liczbę
.
∆n
δn
=
1
≤i≤n
max
di
........................
Rozważmy ciąg podziałów
obszaru D na podobszary D
1
,...D
n
takim,
{∆n}n∈N
że
.
n
→∞
lim
δn = 0
Taki ciąg podziałów obszaru D na podobszary nazywamy ciągiem normalnym
podziałów.
Wybierzmy w dowolny sposób różne punkty (x
i
,y
i
)
.
∈ Di.
Utwórzmy sumę postaci
.
σn =
n
i
=1
Σ
f
(xi, yi) ⋅ ∆pi
Nazywać ją będziemy sumą całkową f(x,y) w obszarze D.
.......................................
Weżmy następnie
n
→∞
lim
σn =
n
→∞
lim
n
i
=1
Σ
f
(xi, yi) ⋅ ∆pi
Jeżeli dla każdego normalnego ciągu podziałów obszaru D,
ciąg sum całkowych { }
odpowiadający tym podziałom,
σn n∈N
dąży do tej samej granicy właściwej,
niezależnie od wyboru punktów (x
i
,y
i
) i sposobu podziału obszaru D,
to granicę tę nazywać będziemy całką podwójną funkcji f w obszarze D
i oznaczać symbolem
.
D
∫ ∫
f
(x, y) dxdy
.........................................................................................................................
Jeżeli całka powyższa istnieje, to mówić będziemy,
że funkcja f(x,y) jest całkowalna w sensie Riemana w obszarze D
lub że funkcja f (x,y) jest całkowalna w obszarze D.
.........................................................................................................................
Funkcję f(x,y) nazywamy funkcją pocałkową, (x,y) nazywamy zmiennymi
całkowania, D obszarem całkowania.
.................................................................................................................................
2

Tw.
Jeżeli funkcja f(x,y) jest ciągła w obszarze domkniętym,
to jest całkowalna w tym obszarze.
...................................................................................................................................
Tw. O wartości średniej w regularnym obszarze domkniętym D.
Jeżeli funkcja f(x,y) jest ciągła w regularnym obszarze domkniętym D,
to istnieje punkt (x
o
,y
o
)
taki, że
∈ D
D
∫ ∫
f
(x, y) dxdy = f(xo, yo) ⋅ D
...............................................................................................................
3

Zamiana całki podwójnej na iterowaną.
.........................
Jeżeli funkcja f(x,y) jest ciągła i ograniczona w obszarze domkniętym
D
normalnym względem osi OX,
to
D
∫ ∫
f
(x, y) dxdy =
b
a
∫
ψ(x)
ϕ(x)
∫
f
(x, y)
dy
dx.
......................................................................................................................
Jeżeli funkcja f(x,y) jest ciągła i ograniczona w obszarze domkniętym
normalnym względem osi OY,
to
D
∫ ∫
f
(x, y) dxdy =
d
c
∫
h
(y)
g
(y)
∫
f
(x, y)
dx
dy.
=============================================================
W związku z powyższym twierdzeniem w dalszym ciągu na nasz użytek
ograniczać się będziemy do następujących stwierdzeń:
Niech f(x,y) będzie funkcją rzeczywistą dwóch zmiennych określoną na obszarze do-
mkniętym , normalnym względem osi OX lub odpowiednio względem osi OY.
.................................................................................................................................
Całkę podwójną funkcji F, ciągłej na obszarze normalnym względem osi OX lub od-
powiednio względem osi OY, możemy więc zdefiniować następująco:
(1)
D
∫ ∫
f
(x, y) dxdy
df
=
b
a
∫
ψ(x)
ϕ(x)
∫
f
(x, y)
dy
dx.
(2).
D
∫ ∫
f
(x, y) dxdy
df
=
d
c
∫
h
(y)
g
(y)
∫
f
(x, y)
dx
dy
4

Tw.
Całka podwójna funkcji F (x,y), na obszarze regularnym domkniętym w R
2
będącym sumą skończonej liczby obszarów normalnych
(względem osi OX lub OY),
które nie mają wspólnych punktów wewnętrznych, jest sumą całek podwójnych
tej funkcji na poszczególnych obszarach normalnych.
.................................................................................................................................
Wybrane własności całki podwójnej.
.................................................................................
Niech
(iloczyn wnętrz),(2)
F, G
∈ C0(D, R),
α, β ∈ R, D = D1 ∪ D2, intD1 ∩ intD2 = ∅
to
D
∫ ∫
[α F(x, y) + β G(x, y)] dxdy =
=
(3)
α
D
∫ ∫
F
(x, y) dxdy + β
D
∫ ∫
G
(x, y) dxdy
,
(4)
D
∫ ∫
F
(x, y) dxdy =
D
1
∫ ∫
F
(x, y) dxdy +
D
2
∫ ∫
F
(x, y) dxdy
.
(5)
D
∫ ∫
F
(x, y) dxdy ≥ 0
dla
F
(x, y) ≥ 0 na D
5
Tw. ( o zamianie zmiennych w całce podwójnej).
Jeżeli
1.
odwzorowanie
x = x(u,v), y = y(u,v) przekształca wzajemnie jednoznacznie
wnętrze obszaru regularnego na wnętrze obszaru regularnego ,
∆
∆
D
2.
funkcje
,
x, y
∈ C1( ∆ ; R)
3.
funkcja
,
F
∈ C0( D ; R)
4.
jakobian
J(u,v) =
na obszarze ,
∂x
∂u
∂x
∂v
∂y
∂u
∂y
∂v
≠ 0
∆
to
.
D
∫ ∫
F
(x, y) dxdy =
∆
∫ ∫
F
(x(u, v), y(u, v)) ⋅ J(u, v) ⋅ du ⋅ dv
(6)
..................................................................................
W przypadku, gdy obszar D jest kołem, pierścieniem lub wycinkiem jednej z tych figur,
a także i w niektórych innych przypadkach, wygodnie jest na ogół przy obliczaniu całki
podwójnej wprowadzić współrzędne biegunowe
.
x
= r cos ϕ,
y
= r sin ϕ
W tym przypadku jakobian przybiera postać:
J(r, ) =
ϕ
∂x
∂r
∂x
∂ϕ
∂y
∂r
∂y
∂ϕ
=
cos
ϕ −r cos ϕ
sin
ϕ r cos ϕ
= r
i wzór (6) ma postać
.
D
∫ ∫
F
(x, y) dxdy =
∆
∫ ∫
F
(r cos ϕ, r sin ϕ) ⋅ r ⋅ dr ⋅ dϕ
=.=.=.=.=.=.=.=.=.=.=.=.=.==.=.=.=.=.=.=.=.=.=.=.=.=.=.=.=.=..==.=..=
6

Zastosowania całki podwójnej.
1.
Obliczanie pola obszaru płaskiego .
Jeżeli D jest obszarem regularnym ,
, to
D
⊂ R2
.
D
=
D
∫ ∫
dxdy
2.
Obliczanie objętości brył.
Jeżeli
jest obszarem regularnym i
F
∈ C0(D; R), D ⊂ R2
F
(x, y) ≥ 0, to
objętość bryły
wyraża wzór:
V
= (x, y, z) ∈ R3 : (x, y) ∈ D ∧ 0 ≤ z ≤ F(x, y)
V
=
D
∫ ∫
F
(x, y) dxdy
3.
Obliczanie pola powierzchni .
Jeżeli
jest obszarem regularnym , płat powierzchniowy
D
⊂ R2
,
S
= (x, y, z) ∈ R3 : (x, y) ∈ D
∧
z
= f(x, y),
f
∈ C1(D; R)
to pole tego płata powierzchniowego wyraża wzór:
.
S
=
D
∫ ∫
1
+ fx(x, y)
2
+ fy(x, y)
2
dxdy
4.
Obliczanie masy obszaru.
Jeżeli F(x,y) jest gęstością powierzchniową masy obszaru regularnego
i
masę obszaru D wyraża wzór:
D
⊂ R2
F
∈ C0(D; R), to
m
=
D
∫ ∫
F
(x, y) dxdy
5.
Obliczanie momentów statycznych oraz momentów bezwładności.
Jeżeli F(x,y) jest gęstością powierzchniową masy obszaru regularnego
i
momenty statyczne
(względem osi OX)
D
⊂ R2
F
∈ C0(D; R), to
Mx
i
(względem osi
Oy) wyrażają wzory:
My
Mx =
D
∫ ∫
y F
(x, y) dxdy
oraz
,
My
=
D
∫ ∫
x F
(x, y) dxdy
zaś momenty bezwładności
(względem osi OX) ,
(względem osi OY)
Bx
By
7

oraz
względem osi OZ, wyrażają wzory:
Bz
,
Bx =
D
∫ ∫
y2 F
(x, y) dxdy
,
By =
D
∫ ∫
x2 F
(x, y) dxdy
.
Bz
=
D
∫ ∫
(x2+ y2) F(x, y) dxdy
6.
Obliczanie środka ciężkości.
Współrzędne
środka ciężkości
masy obszaru
ξ, η
S
(ξ, η)
D
⊂ R2
wyrażają wzory:
.
ξ =
My
m ,
η =
Mx
m
8
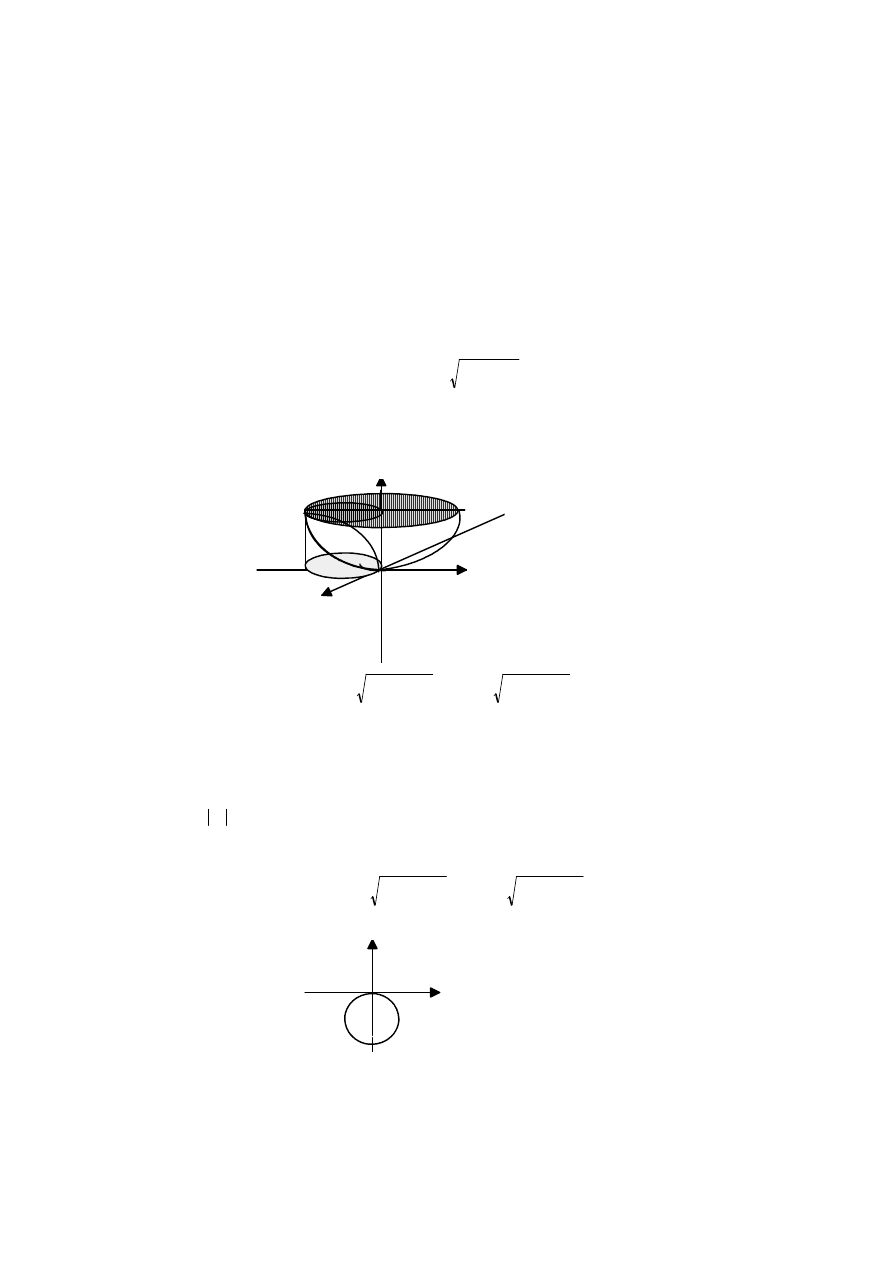
Przykład.
Obliczmy objętość bryły
, ograniczonej częściami powierzchni
V
⊂ R3
a)
,
S1 :
z
= x2 + y2
S2 :
x2
+ y2 + 2y = 0
S3 :
z
= 0
b)
S1 :
z
= x2 + y2
S2 :
x2
+ y2 − 2x = 0
S3 :
z
= 0
x
y
z
a)
,
P
(x, y, z) ∈ V ⇔
− −2y − y2 ≤ x ≤
−2y − y2
−2
≤ y ≤
0
0
≤ z ≤
x2
+ y2
Zatem
,
V
=
D
∫∫
x
2 + y2dxdy
gdzie
.
D
=
(x, y) ∈ R2 :
− −2y − y2 ≤ x ≤
−2y − y2
−2
≤ y ≤
0
x
y
Ponieważ obszar D jest normalny względem osi OY , zatem
9
=
V
=
D
∫∫
x
2 + y2dxdy =
−2
0
∫
− −2y−y
2
−2y−y
2
∫
x
2 + y2dx
dy
=
=
−2
0
∫
x
3
3
+ x ⋅ y2
− −2y−y
2
−2y−y
2
dy
=
=
−2
0
∫
−2y−y
2
3
3
+
−2y − y
2
⋅ y
2
−
− −2y−y
2
3
3
+
− −2y − y
2
⋅ y
2
dy
=2
−2
0
∫
−2y−y
2
3
3
+
−2y − y
2
⋅ y
2
dy
Wobec złożonej postaci wyrażenia podcałkowego zastosujmy twierdzenie
o zamianie zmiennych w całce podwójnej:
,
x
= r cos ϕ
y
= r sin ϕ
wówczas
x2
+ y2 + 2y ≤ 0
,
dla
.
r2
+ 2r sin ϕ ≤ 0
0
≤ r ≤ −2 sin ϕ
π
≤ ϕ ≤
2
π
Zatem
=
D
∫∫
x
2 + y2dxdy =
2
π
π
∫
−2 sin ϕ
0
∫
r
3
dr
d
ϕ =
2
π
π
∫
r
4
4
0
−2 sin ϕ
d
ϕ
=
2
π
π
∫
[−2 sin ϕ]4
4
d
ϕ = 4
2
π
π
∫
sin4
ϕ dϕ = 4
2
π
π
∫
1
− cos 2ϕ
2
2
d
ϕ =
=
=
=
2
π
π
∫
1 − 2 cos 2ϕ + cos
22ϕ dϕ
2
π
π
∫
1 − 2 cos 2ϕ +
1
+ cos 4ϕ
2
dϕ
=
+
ϕ − sin 2ϕ +
ϕ +
sin 4
ϕ
4
2
π
2
π
=
2
π − sin (2 ⋅ 2π) +
2
π +
sin (4
⋅2π)
4
2
10

_
=
-
.
π − sin (2 ⋅ π) +
π +
sin (4
⋅π)
4
2
2π +
2
π
2
π + π
2
= π − π
2
= π
2
Ćwiczenia. Oblicz całki:
1.
, gdzie
,
D
∫ ∫
ex dxdy
D
=
obszar ograniczony liniami
x
= o,
y
= 2,
x
= ln y
2.
,
D
∫ ∫
2y dxdy ,
gdzie D
=
obszar ograniczony liniami
y
= x ,
y
= 0,
x
+ y = 2
3.
,
D
∫ ∫
x
2 + y2 dxdy, gdzie D =
obszar ograniczony linia
x2
+ y2 = 4
4.
,
D
∫ ∫
2 dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 = 2x
5.
,
D
∫ ∫
dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 = −2y
6.
,
D
∫ ∫
dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 = −2x + 2y
7.
,
D
∫ ∫
x2
+ y2 dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 ≤ 2
8.
D
∫ ∫
1
+ x2 + y2 dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 ≤ 4
,
9.
D
∫ ∫
x2
+ y2 dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 ≤ 2x
,
10.
,
D
∫ ∫
1
x2
+ y2
dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 ≤ 9
11.
.
D
∫ ∫
1
1
+ x2 + y2
dxdy ,
gdzie D
=
obszar ograniczony linia
x2
+ y2 ≤ 1
11

12
13
Wyszukiwarka
Podobne podstrony:
C 06 Całka podwójna
09Calki wielokrotne, 1 Całka podwójna w prostokącie
AMII, am2.11a, CAŁKA PODWÓJNA W PROSTOKĄCIE
AMII, am2.11a, CAŁKA PODWÓJNA W PROSTOKĄCIE
Calka podwojna id 107925 Nieznany
calka podwojna w obszarze normalnym
Całka podwójna
Microsoft Word W19 Calka podwojna
całka podwójna i potrójna
Monte Carlo calka podwojna prezentacja 1
Całka Podwójna 2, Prywatne, Budownictwo, Matematyka
Calka podwójna
całka podwójna (3)
Całka Podwójna 1, Prywatne, Budownictwo, Matematyka
Całka podwójna - zastosowania, ciag dalszy
Calka podwojna zadania
Monte Carlo calka podwojna prezentacja 3
11 Całka podwójna
więcej podobnych podstron